Вы можете увидеть призмы как на уроке математики, так и на протяжении всей вашей повседневной жизни. Кирпич – это прямоугольная призма. Упаковка апельсинового сока – это тип призмы. Коробка из ткани представляет собой прямоугольную призму. Амбары представляют собой тип пятиугольной призмы. Пентагон – это пятиугольная призма. Аквариум представляет собой прямоугольную призму. Этот список можно продолжать и продолжать.
Призмы по определению – это сплошные объекты с одинаковыми концевыми формами, одинаковыми сечениями и плоскими боковыми гранями (без кривых) И хотя большинство математических задач и примеров из реальной жизни, касающихся вычислений призмы, связаны с формулой объема или формулой площади поверхности, прежде чем вы сможете это сделать, вам нужно сначала понять один расчет: периметр призмы.
Что такое призма?
Общее определение призмы – это трехмерная сплошная форма, которая имеет следующие характеристики:
- Это многогранник (то есть это сплошная фигура).
- Поперечное сечение объекта является одинаковым по всей длине объекта.
- Это параллелограмм (четырехсторонняя форма, в которой противоположные стороны параллельны друг другу).
- Грани объекта плоские (без изогнутых граней).
- Две концевые формы идентичны.
Название призмы происходит от формы двух концов, которые известны как основания. Это может быть любая форма (кроме кривых или кругов). Например, призма с треугольными основаниями называется треугольной призмой. Призма с прямоугольными основаниями называется прямоугольной призмой. Этот список можно продолжить.
Рассматривая характеристики призм, это исключает сферы, цилиндры и конусы как призмы, потому что они имеют изогнутые грани. Это также устраняет пирамиды, потому что они не имеют одинаковых основных форм или идентичных поперечных сечений повсюду.
Периметр призмы
Говоря о периметре призмы, вы на самом деле имеете в виду периметр базовой формы. Периметр основания призмы такой же, как периметр вдоль любого поперечного сечения призмы, поскольку все поперечные сечения одинаковы по всей длине призмы.
Периметр измеряет сумму длин любого многоугольника. Таким образом, для каждого типа призмы вы найдете сумму длин любой формы, являющейся основанием, и это будет периметр призмы.
Например, формула для нахождения периметра треугольной призмы будет суммой трех длин треугольника, составляющего основание, или:
Периметр треугольника = a + b + c, где a , b и c – три длины треугольника.
Это будет периметр формулы прямоугольной призмы:
Периметр прямоугольника: 2l + 2w, где l – длина прямоугольника, а w – ширина.
Примените стандартные расчеты периметра к базовой форме призмы, и это даст вам периметр.
Зачем вам нужно рассчитывать периметр призмы?
Поиск периметра призмы не кажется слишком сложным, если вы понимаете, о чем идет речь. Однако периметр является важным расчетом, который учитывает формулы площади и объема поверхности для некоторых призм.
Например, это формула для определения площади поверхности правой призмы (правая призма имеет идентичные основания и стороны, которые все прямоугольные):
Площадь поверхности = 2b + ph
где b равно площади основания, p равно периметру основания, а h равно высоте призмы. Вы можете видеть этот периметр, необходимый для определения площади поверхности.
Пример задачи: периметр прямоугольной призмы
Допустим, у вас есть проблема с правильной прямоугольной призмой, и вас попросили найти периметр. Вам даны следующие значения:
Длина = 75 см
Ширина = 10 см
Высота = 5 см
Чтобы найти периметр, используйте формулу для нахождения периметра прямоугольной призмы, поскольку имя говорит о том, что основание представляет собой прямоугольник:
Периметр = 2l + 2w = 2 (75 см) + 2 (10 см) = 150 см + 20 см = 170 см
Затем вы можете продолжить, чтобы найти площадь поверхности, потому что у вас есть высота, у вас есть периметр основания, и это считается, что эта призма является правой призмой.
Площадь основания равна длине × ширине (как всегда для прямоугольника), которая равна:
Площадь основания = 75 см × 10 см = 750 см 2
Теперь у вас есть все значения для расчета площади поверхности:
Площадь поверхности = 2b + ph = 2 (750 см 2) + 170 см (5 см) = 1500 см 2 + 850 см = 2350 см 2
You can see prisms in both math class and throughout your everyday life. A brick is a rectangular prism. A carton of orange juice is a type of prism. A tissue box is a rectangular prism. Barns are a type of pentagonal prism. The pentagon is a pentagonal prism. A fish tank is a rectangular prism. This list goes on and on.
Prisms by definition are solid objects with identical end shapes, identical cross sections and flat side faces (no curves). And while most math problems and real world examples regarding prism calculations have to do with a volume formula or a surface area formula, there’s one calculation that you need to understand first before you can do that: the perimeter of a prism.
What Is a Prism?
The general definition of a prism is a 3-dimensional solid shape that has the following characteristics:
- It is a polyhedron (meaning it is a solid figure).
- The cross section of the object is the exact same throughout the length of the object.
- It is a parallelogram (a 4-sided shape where the opposite sides are parallel to each other).
- The faces of the object are flat (no curved faces).
- The two end shapes are identical.
The name of the prism comes from the shape of the two ends, which are known as the bases. This can be any shape (besides curves or circles). For example, a prism with triangular bases is called a triangular prism. A prism with rectangular bases is called a rectangular prism. This list goes on.
Looking at the characteristics of prisms, this eliminates spheres, cylinders and cones as prisms because they have curved faces. This also eliminates pyramids because they don’t have identical base shapes or identical cross sections throughout.
Perimeter of Prism
When talking about the perimeter of the prism, you’re actually referring to the perimeter of the base shape. The perimeter of the base of a prism is the same as the perimeter along any cross section of the prism since all cross sections are the same along the length of the prism.
Perimeter measures the sum of the lengths of any polygon. So for each prism type, you’d find the sum of the lengths of whatever shape is the base, and that would be the perimeter of the prism.
The formula for finding the perimeter of a triangular prism, for example, would be the sum of the three lengths of the triangle that makes up the base, or:
text{Perimeter of triangle } = a + b + c
where a, b and c are the three lengths of the triangle.
This would be the perimeter of a rectangular prism formula:
text{ Perimeter of rectangle } = 2l + 2w
where l is the length of the rectangle and w is the width.
Apply standard perimeter calculations to the base shape of the prism, and that gives you the perimeter.
Why Would You Need to Calculate the Perimeter of a Prism?
Finding the perimeter of a prism doesn’t seem too complex once you understand what’s being asked. However, the perimeter is an important calculation that factors into surface area and volume formulas for some prisms.
For example, this is the formula for finding the surface area of a right prism (a right prism has identical bases and sides that are all rectangular):
text{Surface Area } = 2b + ph
where b is equal to area of the base, p is equal to the perimeter of the base and h is equal to the height of the prism. You can see that perimeter essential for finding the surface area.
Example Problem: Perimeter of a Rectangular Prism
Let’s say you’re given a problem with a right rectangular prism and you’re asked to find the perimeter. You’re given the following values:
Length = 75 cm
Width = 10 cm
Height = 5 cm
To find the perimeter, use the formula for finding the perimeter of a rectangular prism since the name tells you the base is a rectangle:
begin{aligned} text{Perimeter } &= 2l + 2w \ &= 2(75 text{ cm}) + 2(10 text{ cm} ) \ &= 150 text{ cm} + 20 text{ cm} \ &= 170 text{ cm} end{aligned}
You can then go on to find the surface area because you’re given the height, you have the perimeter of the base and it’s given that this prism is a right prism.
The area of the base is equal to length × width (as it always is for a rectangle), which is:
begin{aligned} text{ Area of base } &= 75 text{ cm} × 10 text{ cm} \ &= 750 text{ cm}^2 end{aligned}
Now you have all the values for a surface area calculation:
begin{aligned} text{ Surface Area } &= 2b + ph \ &= 2(750 text{ cm}^2) + 170 text{ cm}(5 text{ cm}) \ &= 1500 text{ cm}^2 + 850 text{ cm}^2 \ &= 2350 text{ cm}^2 end{aligned}
Лучший ответ
FILIN
Искусственный Интеллект
(114607)
6 месяцев назад
Как узнать маршрут автобуса, если известен его объем и число пассажиров? Ты, вообще, думаешь или не думаешь?
Остальные ответы
Оркот Нроков
Ученик
(226)
6 месяцев назад
Призма?
Murat KasumovГуру (3428)
6 месяцев назад
🙂 присоединяюсь вопросу!:)
Murat Kasumov, Не нужно присоединяться к глупым вопросам.
Лучше свой задай, может у тебя лучше получится.
Мария Фил
Ученик
(130)
6 месяцев назад
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Зная боковое ребро и высоту основания треугольной призмы можно рассчитать ее сторону основания, площадь основания, а также радиусы вписанной и описанной окружностей и периметр треугольной призмы.
Сторона основания через высоту основания треугольной призмы будет равна высоте, умноженной на корень из двух. Чтобы найти площадь основания, нужно это выражение возвести в квадрат и умножить на корень из трех, деленный на четыре. Радиусы вписанной и описанной окружности в основание, вычисляются по формулам для равностороннего треугольника, в которые нужно подставить выражение через высоту, а для того чтобы найти периметр призмы, необходимо сложить вместе три боковых ребра и шесть сторон основания.
a=h√2
S_(осн.)=(√3 h^2)/2
r= h/√6
R=(a√2)/√3
P=3(2a+b)
Зная площадь основания треугольной призмы через высоту, можно вычислить также площадь боковой поверхности, и, сложив их вместе, найти площадь полной поверхности треугольной призмы через боковое ребро и высоту основания. Объем треугольной призмы зависит той же площади основания и бокового ребра.
S_(б.п.)=3ab=3√2 hb
S_(п.п.)=3ab+(√3 a^2)/2=3√2 hb+√3 h^2
V=S_(осн.) b=(√3 a^2 b)/4=(√3 h^2 b)/2
Диагональ боковой грани треугольной призмы можно найти по теореме Пифагора из прямоугольного треугольника, в котором она является гипотенузой при катетах – боковом ребре и стороне основания.
d=√(a^2+b^2 )
В треугольную сферу можно вписать сферу, только если боковое ребро призмы совпадает с диаметром окружности, вписанной в основание, тогда радиус вписанной в треугольную призму сферы равен радиусу этой окружности. Радиус же описанной вокруг призмы сферы всегда равен корню из пяти шестых, умноженному на сторону основания призмы, поскольку описать такую сферу можно вокруг любой треугольной призмы.
r_1=r
R_1=√(5/6) a=√(5/3) h
Как найти периметр призмы
Любая геометрическая фигура имеет несколько измерений. Одно из них – периметр. Найти его, как правило, проще всего. Нужно лишь знать размер всех сторон геометрической фигуры.
Вам понадобится
- Линейка, лист бумаги, ручка.
Инструкция
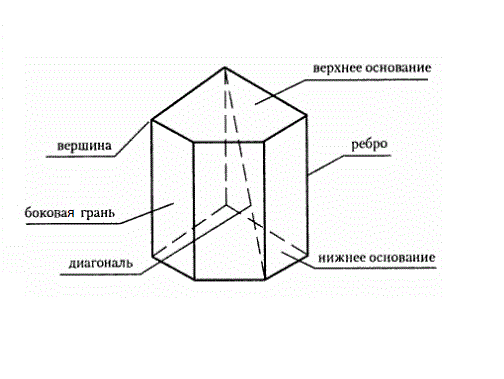
Разберитесь, что такое призма, и какой вид эта геометрическая фигура может иметь. Учтите, что слово «призма» переводится с латинского как «нечто отпиленное». Этот многогранник, всегда имеет два основания, которые расположены в параллельных плоскостях и являются равными многоугольниками. Они могут быть треугольными, четырехугольными, а также n-угольными.
Запомните, что количество остальных (боковых) граней зависит от вида основания. Если в основании треугольник, боковых граней соответственно окажется три, четырехугольник – четыре и так далее.
Имейте в виду, что ребра боковое ребро располагается под углом 90о к основанию, призма именуется прямой. В противном случае – наклонной. Если у прямой призмы в основании окажется правильный многоугольник, она превратится в правильную призму. Пример подобной геометрической фигуры – куб.
Чтобы вычислить периметр призмы, найдите периметры оснований и боковых граней призмы, и все размеры сложите друг с другом. Для этого измерьте при помощи линейки длины сторон (или ребра) каждой из граней. И посчитайте периметр каждого многоугольника.
Упростите свою задачу. Так как размер обоих оснований одинаков, померяйте длины ребер только у одного из них. Сложите размеры всех сторон и умножьте получившуюся сумму на два.
Если у оснований есть ребра равного размера, найдите количество одинаковых боковых граней. Измерьте длины сторон одной из этих граней, вычислите ее периметр. Умножьте получившееся значение на общее число одинаковых граней.
Отдельно посчитайте периметр каждой из тех боковых граней, которая ни разу не повторяется.
Сложите все посчитанные периметры – двух оснований, повторяющихся боковых граней, и тех боковых граней, которые не имеют аналога. Общая сумма будет равна периметру призмы.
Обратите внимание
Вычисление периметра не зависит от вида призмы. Он подсчитывается одинаково и для прямой, и для наклонной призмы.
