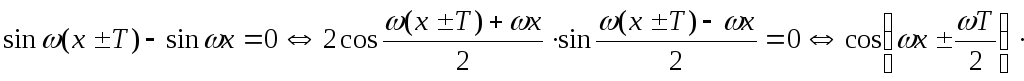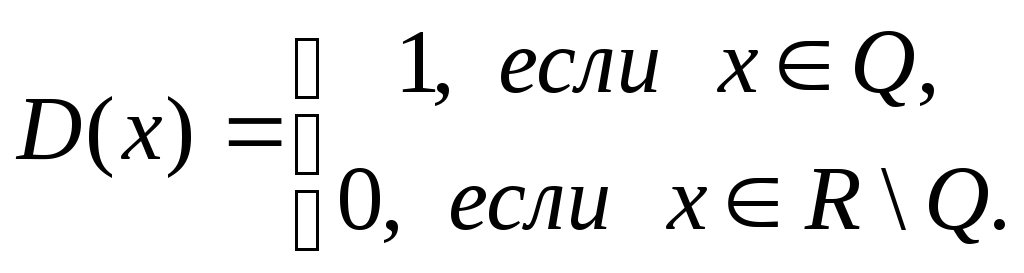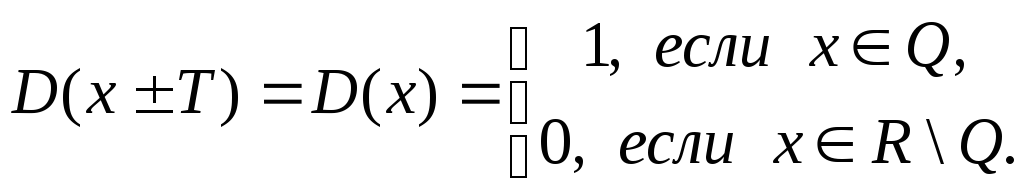Способы задания функции
Пусть функция задается формулой: y=2x^{2}-3. Назначая любые значения независимой переменной x, можно вычислить, пользуясь данной формулой соответствующие значения зависимой переменной y. Например, если x=-0,5, то, пользуясь формулой, получаем, что соответствующее значение y равно y=2 cdot (-0,5)^{2}-3=-2,5.
Взяв любое значение, принимаемое аргументом x в формуле y=2x^{2}-3, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x. Наиболее часто, это будет приближенное значение функции.
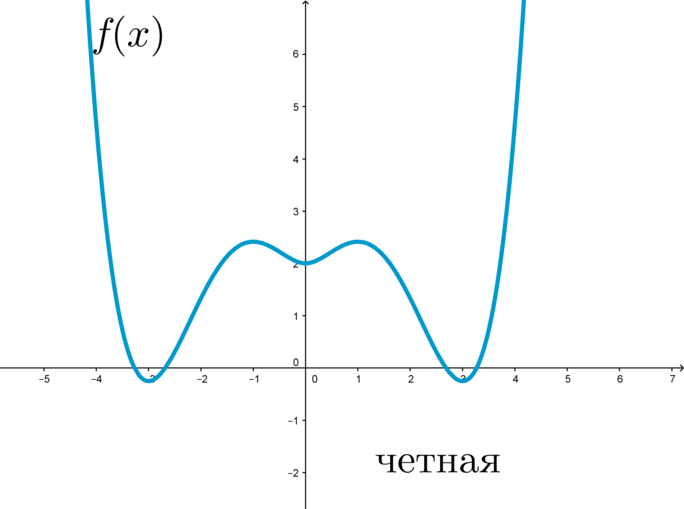
Четная и нечетная функция
Функция является четной функцией, когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy.
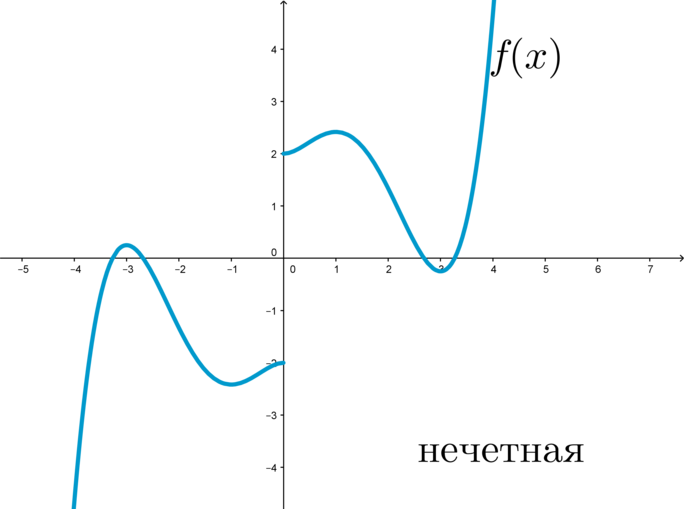
Функция является нечетной функцией, когда f(-x)=-f(x) для любого x из области определения. Такая функция будет симметрична относительно начала координат O (0;0).
Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.
Исследуем на четность нижеприведенную функцию:
f(x)=3x^{3}-7x^{7}
D(f)=(-infty ; +infty ) с симметричной областью определения относительно начала координат. f(-x)= 3 cdot (-x)^{3}-7 cdot (-x)^{7}= -3x^{3}+7x^{7}= -(3x^{3}-7x^{7})= -f(x).
Значит, функция f(x)=3x^{3}-7x^{7} является нечетной.
Периодическая функция
Функция y=f(x), в области определения которой для любого x выполняется равенство f(x+T)=f(x-T)=f(x), называется периодической функцией с периодом T neq 0.
Повторение графика функции на любом отрезке оси абсцисс, который имеет длину T.
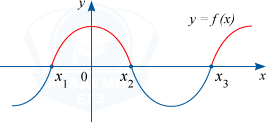
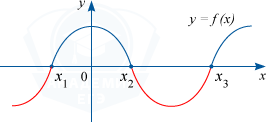
Промежутки, где функция положительная, то есть f(x) > 0 – отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих выше оси абсцисс.
f(x) > 0 на (x_{1}; x_{2}) cup (x_{3}; +infty )
Промежутки, где функция отрицательная, то есть f(x) < 0 – отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.
f(x) < 0 на (-infty; x_{1} ) cup (x_{2}; x_{3} )
Ограниченность функции
Ограниченной снизу принято называть функцию y=f(x), x in X тогда, когда существует такое число A, для которого выполняется неравенство f(x) geq A для любого x in X.
Пример ограниченной снизу функции: y=sqrt{1+x^{2}} так как y=sqrt{1+x^{2}} geq 1 для любого x.
Ограниченной сверху называется функция y=f(x), x in X тогда, когда существует такое число B, для которого выполняется неравенство f(x) neq B для любого x in X.
Пример ограниченной снизу функции: y=sqrt{1-x^{2}}, x in [-1;1] так как y=sqrt{1+x^{2}} neq 1 для любого x in [-1;1].
Ограниченной принято называть функцию y=f(x), x in X тогда, когда существует такое число K > 0, для которого выполняется неравенство left | f(x) right | neq K для любого x in X.
Пример ограниченной функции: y=sin x ограничена на всей числовой оси, так как left | sin x right | neq 1.
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) > y(x_{2}).
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) < y(x_{2}).
Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0).
а) Если при x > 0 четная функция возрастает, то убывает она при x < 0
б) Когда при x > 0 четная функция убывает, то возрастает она при x < 0
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x < 0
г) Когда нечетная функция будет убывать при x > 0, то она будет убывать и при x < 0
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняться неравенство f(x) > f(x_{0}). y_{min} – обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняется неравенство f(x) < f(x^{0}). y_{max} – обозначение функции в точке max.
Необходимое условие
Согласно теореме Ферма: f'(x)=0 тогда, когда у функции f(x), что дифференцируема в точке x_{0}, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} – будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}.
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f'(x);
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку [a; b];
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции, а большее — наибольшим.
Определение 1. Функцияназываетсячетной (нечетной),
если вместе с каждым значением переменнойзначение –хтакже принадлежит
и выполняется равенство
(11.1)
Таким образом, функция может быть четной
или нечетной только тогда, когда ее
область определения симметрична
относительно начала координат на
числовой прямой (числа х и –ходновременно принадлежат).
Например, функцияне является четной и нечетной, так как
ее область определенияне симметрична относительно начала
координат.
Функция
четная, так как
симметрична относительно начала
координат и.
Функция
нечетная, так как
и
.
Функция
не является четной и нечетной, так как
хотяи симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,.
График четной функции симметричен
относительно оси Оу, так как если
точкапринадлежит графику, то и точка
тоже принадлежит графику. График нечетной
функции симметричен относительно начала
координат, так как еслипринадлежит графику, то и точка
тоже принадлежит графику.
При доказательстве четности или
нечетности функции бывают полезны
следующие утверждения.
Теорема 1. а) Сумма двух четных
(нечетных) функций есть функция четная
(нечетная).
б) Произведение двух четных (нечетных)
функций есть функция четная.
в) Произведение четной и нечетной функций
есть функция нечетная.
г) Если f– четная
функция на множествеХ, а функцияg определена на
множестве,
то функция–
четная.
д) Если f– нечетная
функция на множествеХ, а функцияg определена на
множествеи четная (нечетная), то функция
–
четная (нечетная).
Доказательство. Докажем, например,
б) и г).
б) Пусть
и
–
четные функции. Тогда,
поэтому.
Аналогично рассматривается случай
нечетных функцийи
.
г) Пусть f – четная
функция. Тогда.
Остальные утверждения теоремы доказываются
аналогично. Теорема доказана.
Теорема 2. Любую функцию,
заданную на множествеХ, симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
Доказательство. Функциюможно записать в виде
.
Функция
– четная, так как
,
а функция– нечетная, поскольку
.
Таким образом,,
где–
четная, а–
нечетная функции. Теорема доказана.
Определение 2. Функцияназываетсяпериодической, если
существует число,
такое, что при любомчисла
и
также
принадлежат области определенияи выполняются равенства
.
Такое число Tназываетсяпериодом функции.
Из определения 1 следует, что если Т
– период функции,
то и число –Т тоже является
периодом функции (так
как при заменеТ на –Т равенство
сохраняется). С помощью метода
математической индукции можно показать,
что еслиТ– период функцииf,
то и,
тоже является периодом. Отсюда следует,
что если функция имеет период, то она
имеет бесконечно много периодов.
Определение 3. Наименьший из
положительных периодов функции называется
ееосновным периодом.
Теорема 3. ЕслиТ– основной
период функцииf, то
остальные периоды кратны ему.
Доказательство. Предположим
противное, то есть что существует периодфункцииf (
>0),
не кратныйТ. Тогда, разделивнаТ с остатком, получим
,
где.
Поэтому
,
то есть
– период функцииf,
причем,
а это противоречит тому, чтоТ–
основной период функцииf.
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические
функции являются периодическими.
Основной период
и
равен
,
и
.
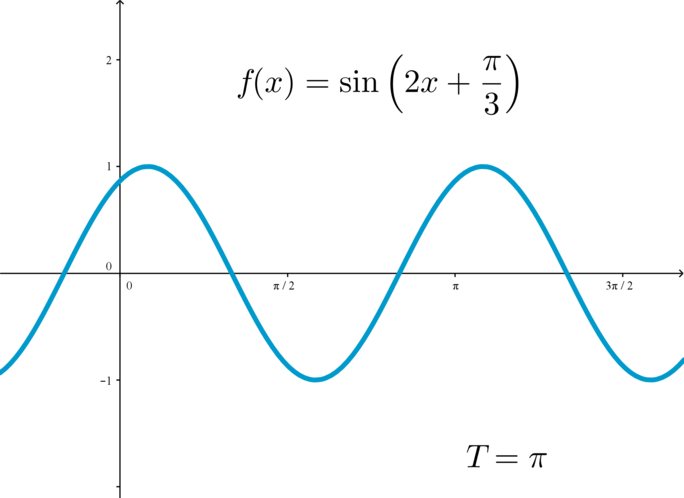
Найдем период функции.
Пусть– период этой функции. Тогда
(так как
.
Отсюда
или
или
или
.
Значение T, определяемое
из первого равенства, не может быть
периодом, так как зависит отх, т.е.
является функцией отх, а не постоянным
числом. Период определяется из второго
равенства:.
Периодов бесконечно много, принаименьший
положительный период получается при:
.
Это – основной период функции.
Примером более сложной периодической
функции является функция Дирихле
Заметим, что если T–
рациональное число, тои
являются рациональными числами при
рациональномхи иррациональными
при иррациональномх. Поэтому
при любом рациональном числе T.
Следовательно, любое рациональное числоTявляется периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное числоможно сделать выборомnсколь угодно близким к нулю).
Теорема 4. Если функцияf
задана на множествеХи имеет
периодТ, а функцияg
задана на множестве,
то сложная функциятоже имеет периодТ.
Доказательство. Имеем,
поэтому
,
то есть утверждение теоремы доказано.
Например, так как cos
x имеет период,
то и функцииимеют период
.
Определение 4. Функции, не являющиеся
периодическими, называютсянепериодическими.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье обсуждаем периодичность функций: как определить, периодична ли функция, и каков ее период.
Функция периодична, если некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом. Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.
Тогда, если мы знаем период, мы можем, зная все значения функции на протяжении данного периода, достроить функцию, либо узнать ее значения в любой точке числовой оси – то есть при любом аргументе.
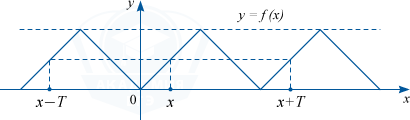
Периодичная функция
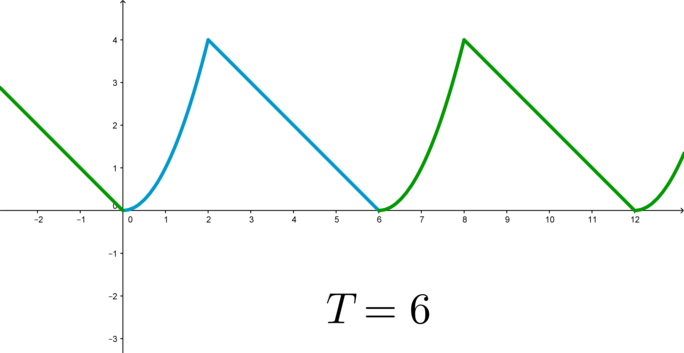
Пример 1: функция 


![x in[-2; 0] x in[-2; 0]](https://easy-physic.ru/img_formuls/math_985.5_76563737120aaab9a7fd96ee3cb53fce.png)

Раз наша функция принимает форму части параболы на отрезке [-2; 0] при периоде, равном 2, значит, такую же форму она будет иметь и на следующем отрезке – [0;2], и на отрезке [2;4]. Изобразим ее:
Определение значения периодичной функции
Видно, что функция принимает одинаковые значения в точках, отстоящих друг от друга на 2, 4, 6 единиц и т.д., тогда 


Теперь найдем значение искомого выражения: 
Строго говоря, функция периодична, если есть такое число Т, что 
Попробуем научиться определять, периодична ли функция или нет. Для этого рассмотрим несколько примеров.
Пример 2. Проверим, периодична ли функция 
Установим, выполняется ли условие: 

Пример 3. Проверим, периодична ли функция 
Функцию для удобства представим в виде: 
Установим, выполняется ли условие: 


Пример 4. Проверим, периодична ли функция 










Определение периода функции
В данном примере делать проверку необязательно, но проверка бывает очень полезна в более сложных задачах, поэтому сделаем ее здесь для тренировки: 
Пример 5. Определить периодичность функции 
Если Т – период, то 
В это равенство подставим какие-нибудь «удобные» точки, например, 
Далее есть два пути отыскания периода, первый – решение этого уравнения, второй – составление еще одного уравнения такого же вида. Если функция имеет период Т, то верно и следующее: 

Пользуясь четностью косинуса и нечетностью синуса можем записать:
Имеем систему:
Уравнения сложим, и получим




Теперь испробуем второй путь, решим это уравнение: 
Оставим в левой части только корень:
Возведем в квадрат:
Тогда либо 


Это уравнение имеет два решения, одно из которых (второе) – посторонний корень, появившийся при возведении в квадрат. Проверка подстановкой его в исходное уравнение позволит нам выявить его и отбросить. Таким образом, получаем:



Здесь также необходимо сделать проверку. Подставим полученный период в условие 

период данной функции – 
Определение периода функции
Пример 6. Определить периодичность функции 
Если Т – период, то
Подставим 

Или 



Проверим:
Определение периода функции
Пример 7. Определим период функции 
Запишем условие периодичности:











Определение периода функции
Пример 8. Доказать, что периодом функции 

Тогда:
Пример 9. Доказать, что периодом функции 

Тогда:
Если 



Удачи вам в учебе и надеюсь, эта статья вам помогла.
Алгебра и начала математического анализа, 11 класс
Урок №2 Чётность и нечётность тригонометрических функций. Периодичность.
Перечень вопросов, рассматриваемых в теме
- Изучение чётности функции,
- Построение периодичности функции,
- Определение четности или нечетности тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|,
- Объяснение зависимости четности или нечетность функции вида y=af(kx+b)+c и y=|f(k|x|+b)|,
- Определение периодичности тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|,
- Объяснение зависимости периодичности функции вида y=af(kx+b)+c и y=|f(k|x|+b)|,
Глоссарий по теме
Функцию y=f(x), x∈X называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x).
Функцию y=f(x), x∈X называют нечётной, если для любого значения x из множества X выполняется равенство f(−x)=−f(x).
Период функций, представляющих собой сумму непрерывных и периодических функций, равен наименьшему кратному периодов слагаемых, если он существует.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |ОА| к длине гипотенузы |ОВ|.
Область. определения функции (D) — множество R всех действительных чисел
Множество значений функции (E) — отрезок [-1; 1], т.е. косинус функция —ограниченная.
Для того, чтобы определить чётность функции косинус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, cos(60°) = ½ = cos(–60°)–это значит, что : cos(−x)=cos x для всех x∈R и у=сosx–чётная
Сиинус(sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |АВ| к длине гипотенузы |ОВ|.
Область определения функции (D) — множество R всех действительных чисел.
Множество значений функции (E) — отрезок [-1; 1], т.е. синус функция —ограниченная.
Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, sin(30°) = ½ sin(–30°) = –½ –это значит, что : sin(−x)=–sin (x) для всех x∈R и y=sinx–нечётная


Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π.
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Выясним, является ли функция
чётной или нечётной?
Пример 2. Доказать, что число 2π является наименьшим положительным периодом функции y=cos x
Пусть Т>0 – период косинуса, т.е. для любого х выполняется равенство cos (x+T)= cos x. Положив х=0, получим cos T=1. Отсюда Т=2πk, x∈R. Так как Т>0, то может принимать значения 2π, 4π, 6π,…, и поэтому период не может быть меньше 2π
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Четные и нечетные функции
(blacktriangleright) Функция (f(x)) называется четной, если при всех (x) из ее области определения верно: (f(-x)=f(x)).
График четной функции симметричен относительно оси (y):
Пример: функция (f(x)=x^2+cos x) является четной, т.к. (f(-x)=(-x)^2+cos{(-x)}=x^2+cos x=f(x)).
(blacktriangleright) Функция (f(x)) называется нечетной, если при всех (x) из ее области определения верно: (f(-x)=-f(x)).
График нечетной функции симметричен относительно начала координат:
Пример: функция (f(x)=x^3+x) является нечетной, т.к. (f(-x)=(-x)^3+(-x)=-x^3-x=-(x^3+x)=-f(x)).
(blacktriangleright) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
Например, функция (f(x)=x^2-x) является суммой четной функции (f_1=x^2) и нечетной (f_2=-x).
(blacktriangleright) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
5) Если (f(x)) — четная функция, то уравнение (f(x)=c (cin
mathbb{R})) имеет единственный корень тогда и только когда, когда (x=0).
6) Если (f(x)) — четная или нечетная функция, и уравнение (f(x)=0) имеет корень (x=b), то это уравнение обязательно будет иметь второй корень (x=-b).
(blacktriangleright) Функция (f(x)) называется периодической на (X), если для некоторого числа (Tne 0) выполнено (f(x)=f(x+T)), где (x,
x+Tin X). Наименьшее (T), для которого выполнено данное равенство, называется главным (основным) периодом функции.
У периодической функции любое число вида (nT), где (nin mathbb{Z}) также будет являться периодом.
Пример: любая тригонометрическая функция является периодической;
у функций (f(x)=sin x) и (f(x)=cos x) главный период равен (2pi), у функций (f(x)=mathrm{tg},x) и (f(x)=mathrm{ctg},x) главный период равен (pi).
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной (T) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
(blacktriangleright) Область определения (D(f)) функции (f(x)) — это множество, состоящее из всех значений аргумента (x), при которых функция имеет смысл (определена).
Пример: у функции (f(x)=sqrt x+1) область определения: (xin
[0;+infty)).
(blacktriangleright) Область значений (E(f)) функции (f(x)) — это множество, состоящее из всех значений функции (f(a)), где (ain
D(f)).
Пример: у функции (f(x)=sqrt x +1) область значений: (f(x)in
[1;+infty)).
(blacktriangleright) Уравнение (f(x)=a) имеет решение тогда и только тогда, когда (a) принадлежит области значений функции (f(x)), т.е. (ain E(f)).
(blacktriangleright) Если область значений функции (f(x)) не превышает некоторого числа (A), т.е. (f(x)leq A) при всех (xin
D(f)), а функция (g(x)geq A) при всех (xin D(g)), то уравнение [{large{f(x)=g(x)}} Leftrightarrow begin{cases} f(x)=A\g(x)=Aend{cases}]
Задание
1
#6364
Уровень задания: Равен ЕГЭ
При каких значениях параметра (a) уравнение
[2x^2+amathrm{tg},(cos x)+a^2=0]
имеет единственное решение?
Заметим, что так как (x^2) и (cos x) — четные функции, то если уравнение будет иметь корень (x_0), оно также будет иметь и корень (-x_0).
Действительно, пусть (x_0) – корень, то есть равенство (2x_0^2+amathrm{tg},(cos x_0)+a^2=0) верно. Подставим (-x_0): (2
(-x_0)^2+amathrm{tg},(cos(-x_0))+a^2=2x_0^2+amathrm{tg},(cos
x_0)+a^2=0).
Таким образом, если (x_0ne 0), то уравнение уже будет иметь как минимум два корня. Следовательно, (x_0=0). Тогда:
[2cdot 0+amathrm{tg},(cos 0)+a^2=0 quad Rightarrow quad
a^2+amathrm{tg},1=0 quad Rightarrow quad left[
begin{gathered}begin{aligned}
&a=0\
&a=-mathrm{tg},1 end{aligned} end{gathered}right.]
Мы получили два значения параметра (a). Заметим, что мы использовали то, что (x=0) точно является корнем исходного уравнения. Но мы нигде не использовали то, что он единственный. Следовательно, нужно подставить получившиеся значения параметра (a) в исходное уравнение и проверить, при каких именно (a) корень (x=0) действительно будет единственным.
1) Если (a=0), то уравнение примет вид (2x^2=0). Очевидно, что это уравнение имеет лишь один корень (x=0). Следовательно, значение (a=0) нам подходит.
2) Если (a=-mathrm{tg},1), то уравнение примет вид [2x^2-mathrm{tg},1cdot mathrm{tg},(cos x)+mathrm{tg}^2,1=0] Перепишем уравнение в виде [2x^2+mathrm{tg}^2,1=mathrm{tg},1cdot mathrm{tg},(cos x)qquad (*)] Так как (-1leqslant cos xleqslant 1), то (-mathrm{tg},1leqslant mathrm{tg},(cos x)leqslant
mathrm{tg},1). Следовательно, значения правой части уравнения (*) принадлежат отрезку ([-mathrm{tg}^2,1; mathrm{tg}^2,1]).
Так как (x^2geqslant 0), то левая часть уравнения (*) больше или равна (0+
mathrm{tg}^2,1).
Таким образом, равенство (*) может выполняться только тогда, когда обе части уравнения равны (mathrm{tg}^2,1). А это значит, что [begin{cases} 2x^2+mathrm{tg}^2,1=mathrm{tg}^2,1 \
mathrm{tg},1cdot mathrm{tg},(cos x)=mathrm{tg}^2,1
end{cases}
quadLeftrightarrowquad begin{cases} x=0\
mathrm{tg},(cos x)=mathrm{tg},1
end{cases}quadLeftrightarrowquad x=0] Следовательно, значение (a=-mathrm{tg},1) нам подходит.
Ответ:
(ain {-mathrm{tg},1;0})
Задание
2
#3923
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых график функции [f(x)=3mathrm{tg},dfrac{ax}5 +2sin dfrac{8pi a-3x}4]
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено (f(-x)=-f(x)) для любого (x) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено (f(-x)=-f(x).)
[begin{aligned}
&3mathrm{tg},left(-dfrac{ax}5right)+2sin dfrac{8pi a+3x}4=
-left(3mathrm{tg},left(dfrac{ax}5right)+2sin dfrac{8pi
a-3x}4right)quad Rightarrowquad -3mathrm{tg},dfrac{ax}5+2sin
dfrac{8pi a+3x}4=
-left(3mathrm{tg},left(dfrac{ax}5right)+2sin dfrac{8pi
a-3x}4right) quad Rightarrow\[3ex]
Rightarrowquad &sin dfrac{8pi a+3x}4+sin dfrac{8pi a-3x}4=0
quad Rightarrow quad2sin dfrac12left(dfrac{8pi
a+3x}4+dfrac{8pi a-3x}4right)cdot cos dfrac12
left(dfrac{8pi a+3x}4-dfrac{8pi a-3x}4right)=0 quad
Rightarrowquad sin (2pi a)cdot cos frac34 x=0
end{aligned}]
Последнее уравнение должно быть выполнено для всех (x) из области определения (f(x)), следовательно, (sin(2pi a)=0 Rightarrow
a=dfrac n2, ninmathbb{Z}).
Ответ:
(dfrac n2, ninmathbb{Z})
Задание
3
#3069
Уровень задания: Равен ЕГЭ
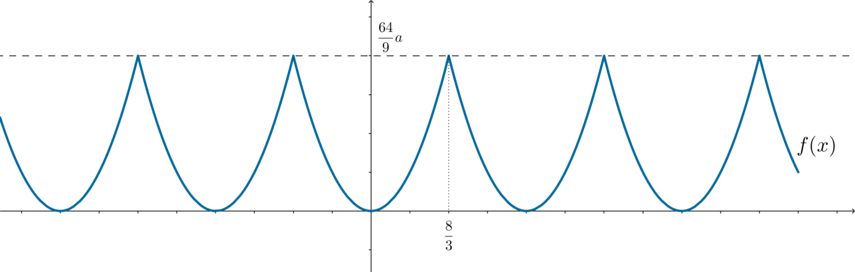
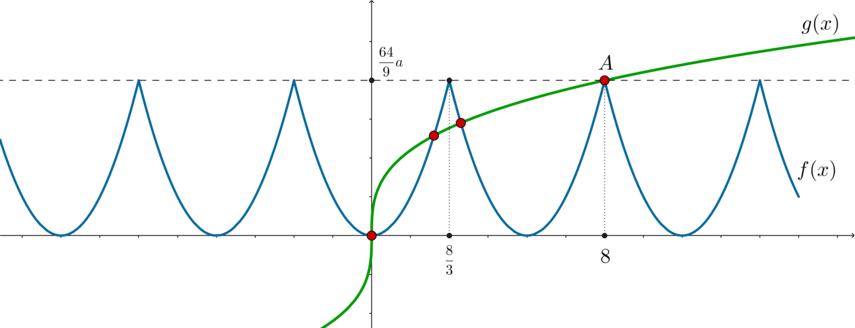
Найдите все значения параметра (a), при каждом из которых уравнение [f(x)=|a+2|sqrt[3]x] имеет 4 решения, где (f) – четная периодическая с периодом (T=dfrac{16}3) функция, определенная на всей числовой прямой, причем (f(x)=ax^2) при (0leqslant xleqslant dfrac83.)
(Задача от подписчиков)
Так как (f(x)) – четная функция, то ее график симметричен относительно оси ординат, следовательно, при (-dfrac83leqslant
xleqslant 0) (f(x)=ax^2). Таким образом, при (-dfrac83leqslant
xleqslant dfrac83), а это отрезок длиной (dfrac{16}3), функция (f(x)=ax^2).
1) Пусть (a>0). Тогда график функции (f(x)) будет выглядеть следующим образом:
Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график (g(x)=|a+2|cdot sqrt[3]x) проходил через точку (A):
Следовательно, [dfrac{64}9a=|a+2|cdot sqrt[3]8 quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &9(a+2)=32a\
&9(a+2)=-32a end{aligned} end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &a=dfrac{18}{23}\[2ex]
&a=-dfrac{18}{41} end{aligned} end{gathered}right.] Так как (a>0), то подходит (a=dfrac{18}{23}).
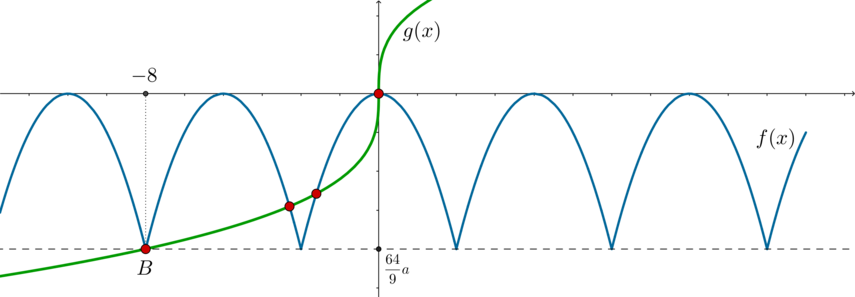
2) Пусть (a<0). Тогда картинка окажется симметричной относительно начала координат:
Нужно, чтобы график (g(x)) прошел через точку (B): [dfrac{64}9a=|a+2|cdot sqrt[3]{-8} quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &a=dfrac{18}{23}\[2ex]
&a=-dfrac{18}{41} end{aligned} end{gathered}right.] Так как (a<0), то подходит (a=-dfrac{18}{41}).
3) Случай, когда (a=0), не подходит, так как тогда (f(x)=0) при всех (x), (g(x)=2sqrt[3]x) и уравнение будет иметь только 1 корень.
Ответ:
(ain left{-dfrac{18}{41};dfrac{18}{23}right})
Задание
4
#3072
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [a^2-7a+7sqrt{2x^2+49}=3|x-7a|-6|x|]
имеет хотя бы один корень.
(Задача от подписчиков)
Перепишем уравнение в виде [7sqrt{2x^2+49}=3|x-7a|-6|x|-a^2+7a] и рассмотрим две функции: (g(x)=7sqrt{2x^2+49}) и (f(x)=3|x-7a|-6|x|-a^2+7a).
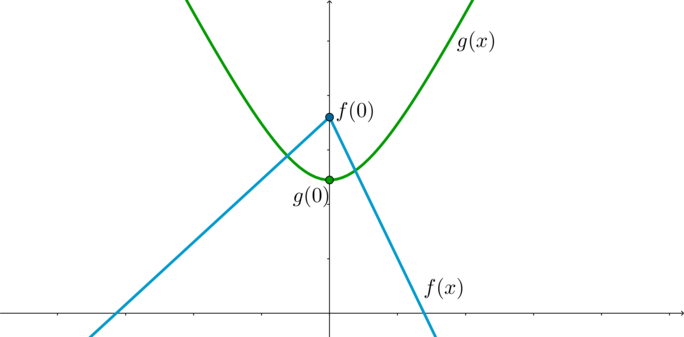
Функция (g(x)) является четной, имеет точку минимума (x=0) (причем (g(0)=49)).
Функция (f(x)) при (x>0) является убывающей, а при (x<0) – возрастающей, следовательно, (x=0) – точка максимума.
Действительно, при (x>0) второй модуль раскроется положительно ((|x|=x)), следовательно, вне зависимости от того, как раскроется первый модуль, (f(x)) будет равно (kx+A), где (A) – выражение от (a), а (k) равно либо (-9), либо (-3). При (x<0) наоборот: второй модуль раскроется отрицательно и (f(x)=kx+A), где (k) равно либо (3), либо (9).
Найдем значение (f) в точке максимума: [f(0)=-a^2+7a+21|a|]
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций (f) и (g) имели хотя бы одну точку пересечения. Следовательно, нужно: [f(0)geqslant g(0) quadRightarrowquad -a^2+7a+21|a|geqslant 49
quadLeftrightarrowquad left[ begin{gathered} begin{aligned}
&begin{cases} a>0\
a^2-28a+49leqslant 0 end{cases}\
&begin{cases} a<0\
a^2+14a+49leqslant 0 end{cases}\
&begin{cases} a=0\
0geqslant 49end{cases} end{aligned} end{gathered}right.] Решая данную совокупность систем, получим ответ: [ain {-7}cup [14-7sqrt3;14+7sqrt3]]
Ответ:
(ain {-7}cup[14-7sqrt3;14+7sqrt3])
Задание
5
#3912
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [2^{x^3-3x^2+4}+(a-10)cdot (sqrt2)^{x^3-3x^2+4}+12-a=0]
имеет шесть различных решений.
Сделаем замену ((sqrt2)^{x^3-3x^2+4}=t), (t>0). Тогда уравнение примет вид [t^2+(a-10)t+12-a=0quad (*)] Будем постепенно выписывать условия, при которых исходное уравнение будет иметь шесть решений.
Заметим, что квадратное уравнение ((*)) может максимум иметь два решения. Любое кубическое уравнение (Ax^3+Bx^2+Cx+D=0) может иметь не более трех решений. Следовательно, если уравнение ((*)) имеет два различных решения (положительных!, так как (t) должно быть больше нуля) (t_1) и (t_2), то, сделав обратную замену, мы получим: [left[begin{gathered}begin{aligned}
&(sqrt2)^{x^3-3x^2+4}=t_1\[2ex]
&(sqrt2)^{x^3-3x^2+4}=t_2end{aligned}end{gathered}right.] Так как любое положительное число можно представить как (sqrt2) в какой-то степени, например, (t_1=(sqrt2)^{log_{sqrt2} t_1}), то первое уравнение совокупности перепишется в виде [x^3-3x^2+4=log_{sqrt2} t_1] Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение ((*)) должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение ((*)) будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение ((*)) имело два различных решения, его дискриминант должен быть положительным: [D=a^2-16a+52>0quadLeftrightarrowquad
ain (-infty;8-2sqrt3)cup(8+2sqrt3;+infty)]
2) Также нужно, чтобы оба корня были положительными (так как (t>0)). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: [begin{cases} 12-a>0\-(a-10)>0end{cases}quadLeftrightarrowquad a<10]
Таким образом, мы уже обеспечили себе два различных положительных корня (t_1) и (t_2).
3) Давайте посмотрим на такое уравнение [x^3-3x^2+4=log_{sqrt2} t] При каких (t) оно будет иметь три различных решения?
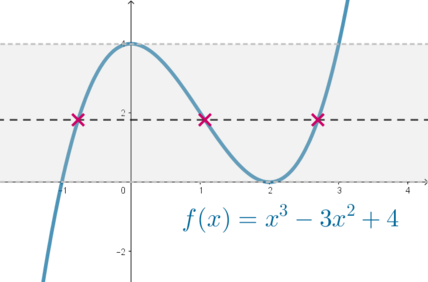
Рассмотрим функцию (f(x)=x^3-3x^2+4).
Можно разложить на множители: [x^3-3x^2+4=x^3+x^2-4x^2+4=x^2(x+1)-4(x+1)(x-1)=(x+1)(x-2)^2] Следовательно, ее нули: (x=-1;2).
Если найти производную (f'(x)=3x^2-6x), то мы получим две точки экстремума (x_{max}=0, x_{min}=2).
Следовательно, график выглядит так:
Мы видим, что любая горизонтальная прямая (y=k), где (0<k<4), пересекает график в трех точках. При всех остальных значениях (k) будет меньше трех точек пересечения. Следовательно, для того, чтобы уравнение (x^3-3x^2+4=log_{sqrt2} t) имело три различных решения, нужно, чтобы (0<log_ {sqrt2}t<4).
Таким образом, нужно: [begin{cases} 0<log_{sqrt2}t_1<4\ 0<log_{sqrt2}t_2<4end{cases}qquad (**)] Давайте также сразу заметим, что если числа (t_1) и (t_2) различны, то и числа (log_{sqrt2}t_1) и (log_{sqrt2}t_2) будут различны, значит, и уравнения (x^3-3x^2+4=log_{sqrt2} t_1) и (x^3-3x^2+4=log_{sqrt2} t_2) будут иметь несовпадающие между собой корни.
Систему ((**)) можно переписать так: [begin{cases} 1<t_1<4\
1<t_2<4end{cases}]
Таким образом, мы определили, что оба корня уравнения ((*)) должны лежать в интервале ((1;4)). Как записать это условие?
В явном виде выписывать корни мы не будем.
Рассмотрим функцию (g(t)=t^2+(a-10)t+12-a). Ее график – парабола с ветвями вверх, которая имеет две точки пересечения с осью абсцисс (это условие мы записали в пункте 1)). Как должен выглядеть ее график, чтобы точки пересечения с осью абсцисс были в интервале ((1;4))? Так:
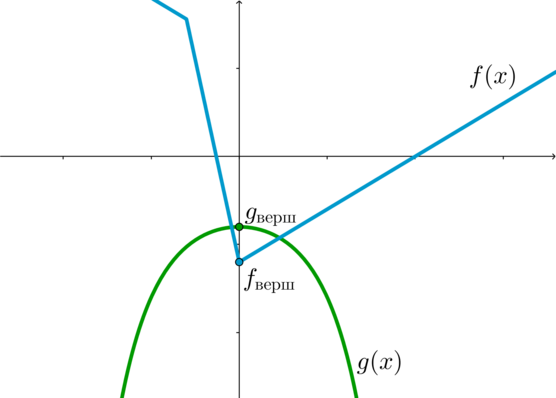
Во-первых, значения (g(1)) и (g(4)) функции в точках (1) и (4) должны быть положительными, во-вторых, вершина параболы (t_0) должна также находиться в интервале ((1;4)). Следовательно, можно записать систему: [begin{cases}
1+a-10+12-a>0\[1ex]
4^2+(a-10)cdot 4+12-a>0\[2ex]
1<dfrac{-(a-10)}2<4end{cases}quadLeftrightarrowquad 4<a<8]
Таким образом, нам нужно пересечь значения параметра (a), найденные в 1-ом, 2-ом и 3-ем пунктах, и мы получим ответ: [begin{cases} ain (-infty;8-2sqrt3)cup(8+2sqrt3;+infty)\ a<10\
4<a<8end{cases}quadLeftrightarrowquad 4<a<8-2sqrt3]
Ответ:
((4;8-2sqrt3))
Задание
6
#1828
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение
[25x^5+25(a-1)x^3-4(a-7)x=0]
имеет ровно пять различных решений, а сами решения, упорядоченные по возрастанию, образуют арифметическую прогрессию.
Заметим, что данное уравнение при любых значениях (a) всегда имеет как минимум один корень (x=0). Значит, для выполнения условия задачи нужно, чтобы уравнение [25x^4+25(a-1)x^2-4(a-7)=0 qquad (*)]
имело четыре различных корня, отличных от нуля, представляющих вместе с (x=0) арифметическую прогрессию.
Заметим, что функция (y=25x^4+25(a-1)x^2-4(a-7)) является четной, значит, если (x_0) является корнем уравнения ((*)), то и (-x_0) будет являться его корнем. Тогда необходимо, чтобы корнями этого уравнения были упорядоченные по возрастанию числа: (-2d, -d, d, 2d) (тогда (d>0)). Именно тогда данные пять чисел будут образовывать арифметическую прогрессию (с разностью (d)).
Чтобы этими корнями являлись числа (-2d, -d, d, 2d), нужно, чтобы числа (d^{,2}, 4d^{,2}) являлись корнями уравнения (25t^2+25(a-1)t-4(a-7)=0). Тогда по теореме Виета:
[begin{cases}
-dfrac{4(a-7)}{25}=d^{,2}cdot 4d^{,2}\[4pt]
-dfrac{25(a-1)}{25}=d^{,2}+4d^{,2}
end{cases} quad Rightarrow quad begin{cases}
d^{,4}=dfrac{7-a}{25}\
dfrac{7-a}{25}=left(dfrac{1-a}{5}right)^2
end{cases} quad Rightarrow quad
left[begin{gathered}begin{aligned} &a=-2\&a=3
end{aligned} end{gathered} right.]
Причем при (a=-2) (d=pm sqrt{frac35}), а при (a=3) (din
varnothing). Значит, подходит значение (a=-2) и (d=sqrt{frac35}) (т.к. должно быть (d>0)).
Ответ:
(ain {-2})
Задание
7
#3198
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [a^2+13|x|+2^{x^2+2}=20a+2|5x+12a|]
имеет хотя бы один корень.
Перепишем уравнение в виде [13|x|-2|5x+12a|=20a-a^2-2^{x^2+2}] и рассмотрим две функции: (g(x)=20a-a^2-2^{x^2+2}) и (f(x)=13|x|-2|5x+12a|).
Функция (g(x)) имеет точку максимума (x=0) (причем (g_{text{верш}}=g(0)=-a^2+20a-4)):
(g'(x)=-2^{x^2+2}cdot ln 2cdot 2x). Ноль производной: (x=0). При (x<0) имеем: (g’>0), при (x>0): (g'<0).
Функция (f(x)) при (x>0) является возрастающей, а при (x<0) – убывающей, следовательно, (x=0) – точка минимума.
Действительно, при (x>0) первый модуль раскроется положительно ((|x|=x)), следовательно, вне зависимости от того, как раскроется второй модуль, (f(x)) будет равно (kx+A), где (A) – выражение от (a), а (k) равно либо (13-10=3), либо (13+10=23). При (x<0) наоборот: первый модуль раскроется отрицательно и (f(x)=kx+A), где (k) равно либо (-3), либо (-23).
Найдем значение (f) в точке минимума: [f_{text{верш}}=f(0)=-24|a|]
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций (f) и (g) имели хотя бы одну точку пересечения. Следовательно, нужно: [f(0)leqslant g(0) quadRightarrowquad a^2-20a+4leqslant 24|a|
quadLeftrightarrowquad left[ begin{gathered} begin{aligned}
&begin{cases} ageqslant 0\
a^2-44a+4leqslant 0 end{cases}\
&begin{cases} a<0\
a^2+4a+4leqslant 0 end{cases} end{aligned}
end{gathered}right.] Решая данную совокупность систем, получим ответ: [ain {-2}cup[22-4sqrt{30};22+4sqrt{30}]]
Ответ:
(ain {-2}cup[22-4sqrt{30};22+4sqrt{30}])

УСТАЛ? Просто отдохни
.png)
.png)