Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.
Колебательные движения. Формулы
Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.
Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).
Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.
Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.
Гармонические колебания. Определение
В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.
Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.
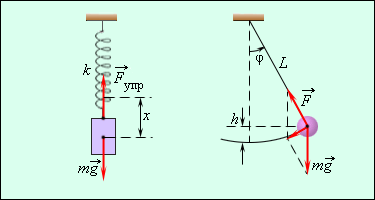
Функция x=f(t) объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок 2.1.1 наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.
Рисунок 2.1.1. Механические колебательные системы.
Механические колебания подразделяют на свободные и вынужденные.
Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.
Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x=xmcos (ωt+φ0), где x– смещение тела от положения равновесия, xm – амплитуда колебаний, ω– циклическая или круговая частота, t – время.
Величина, располагаемая под знаком косинуса, получила название фазы гармонического процесса: φ=ωt+φ0. Если t=0, φ=φ0, тогда φ0 рассматривается в качестве начальной фазы.
Период колебаний Т – это минимальный промежуток времени, через который происходят повторения движения тела. Величина, обратная периоду колебаний, называют частотой колебаний f=1T.
Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах (Г). Связь с циклической частотой ω и периодом T выражается с помощью формулы:
ω=2πf=2πT.
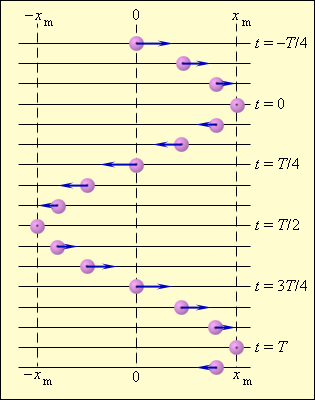
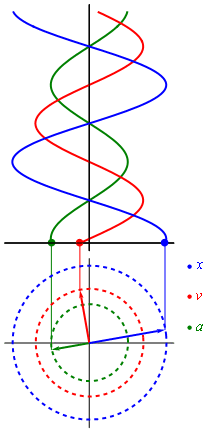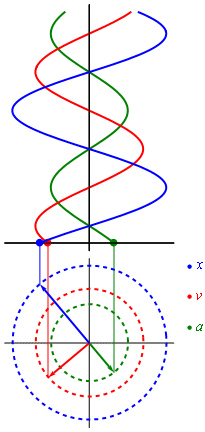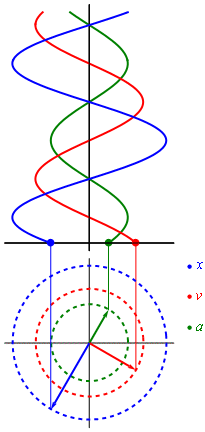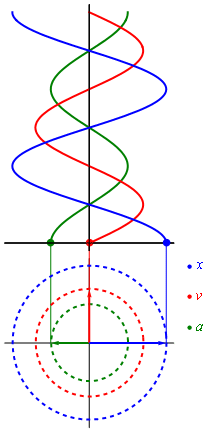
Рисунок 2.1.2 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.
Рисунок 2.1.2. Стробоскопическое изображение гармонических колебаний. Начальная фаза φ0=0. Интервал времени между последовательными положениями тела τ = T12.
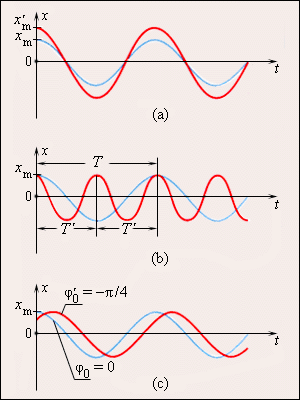
На графике 2.1.3. показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний xm, или периода Т (частоты f), или начальной фазы φ0.
Рисунок 2.1.3. Во всех трех случаях для синих кривых φ0=0: a – красная кривая отличается от синей только большей амплитудой (x’m>xm); b – красная кривая отличается от синей только значением периода (T’=T2); с – красная кривая отличается от синей только значением начальной фазы φ0’=-π2 рад.
Гармонический закон
Если колебания совершаются вдоль прямой Ох, тогда направление вектора скорости аналогично. Определение скорости движения тела υ=υx определяют из выражения υ=∆x∆t; ∆t→0.
Отношение ∆x∆t при ∆t→0 математика трактует как вычисление производной функции x(t) за определенное время t. Обозначение принимает вид dx (t)dt, x'(t) или x˙.
Гармонический закон движения записывается в качестве x=xmcos (ωt+φ0). После вычисления производной формула приобретает вид:
υ=x˙(t)=-ωxmsin (ωt+φ0)=ωxmcos ωt+φ0+π2.
Слагаемое +π2 считают изменением начальной фазы. Достижение максимального значения скорости по модулю υ=ωxmпроизводится при прохождении тела через положение равновесия, то есть x=0. Аналогично определяют ускорение a=ax. Тогда a=∆υ∆t, ∆t→0. Отсюда следует, что a равняется производной функции υ(t) за время t или второй производной функции x(t). Подставив выражения, получим
a=υ˙(t)=x¨(t)=-ω2xmcos (ωt+φ0)=-ω2x(t).
Наличие отрицательного знака указывает на то, что ускорение a(t) имеет противоположный смещению x(t) знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия x=0.
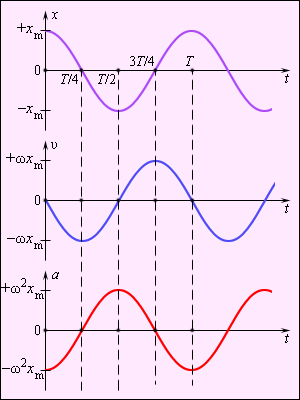
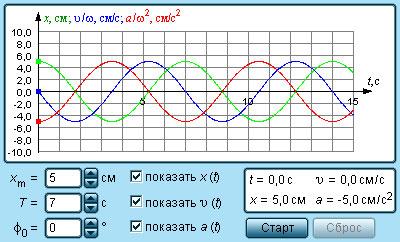
На рисунке 2.1.4 изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания.
Рисунок 2.1.4. Графики координаты x (t), скорости υ (t) и ускорения a (t) тела, совершающего гармонические колебания.
Рисунок 2.1.5. Модель гармонических колебаний.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 апреля 2020 года; проверки требуют 3 правки.
Графики функций f(x) = sin(x) (красная линия) и g(x) = cos(x) (зелёная линия) в декартовой системе координат. По оси абсцисс отложены значения полной фазы.
Гармони́ческие колеба́ния — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Математическое описание[править | править код]
Уравнение гармонического колебания имеет вид
или
,
где
- х — отклонение колеблющейся величины в текущий момент времени t от среднего за период значения (например, в кинематике — смещение, отклонение колеблющейся точки от положения равновесия);
- А — амплитуда колебания, т.е. максимальное за период отклонение колеблющейся величины от среднего за период значения, размерность A совпадает с размерностью x;
- ω (радиан/с, градус/с) — циклическая частота, показывающая, на сколько радиан (градусов) изменяется фаза колебания за 1 с;
(радиан, градус) — полная фаза колебания (сокращённо — фаза, не путать с начальной фазой);
(радиан, градус) — начальная фаза колебаний, которая определяет значение полной фазы колебания (и самой величины x) в момент времени t = 0.
Дифференциальное уравнение, описывающее гармонические колебания, имеет вид
Любое нетривиальное[1] решение этого дифференциального уравнения — гармоническое колебание с циклической частотой 
Примеры[править | править код]
При равномерном движении точки по окружности гармоническое колебание совершает проекция (ортогональная) этой точки на любую прямую, лежащую в той же плоскости[2]. Колебания, близкие к гармоническим, совершает под действием силы тяготения маленький грузик, подвешенный на тонкой длинной нити — математический маятник — при малых амплитудах[3]. Гармонические колебания под действием силы упругости совершает закреплённый между двумя пружинами на горизонтальной направляющей грузик[4]. Гармоническими являются крутильные колебания раскручивающегося под действием силы упругости подвешенного вертикально грузика, такие же колебания совершает балансир механических часов[5].
Вообще, материальная точка совершает гармонические колебания, если они происходят в результате воздействия на точку силы, пропорциональной смещению колеблющейся точки от положения равновесия и направленной противоположно этому смещению.
Примеры гармонических колебаний имеются не только в механике — так, в LC-контуре без диссипативных потерь изменения заряда на ёмкости, напряжения и тока в цепи со временем происходят по гармоническому закону.
Виды колебаний[править | править код]
Эволюция во времени перемещения, скорости и ускорения при гармоническом движении
- Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (при ненулевой диссипации, в системе после возбуждения происходят затухающие колебания).
- Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы вынужденные колебания были гармоническими, достаточно, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила (воздействие) менялась со временем как гармоническое колебание (то есть, чтобы зависимость от времени этой силы тоже, в свою очередь, была синусоидальной).
Применение[править | править код]
Гармонические колебания выделяются из всех остальных видов колебаний по следующим причинам:
- Очень часто[6] малые колебания, как свободные, так и вынужденные, которые происходят в реальных системах, можно считать имеющими форму гармонических колебаний или очень близкую к ней.
- Как установил в 1822 году Фурье, широкий класс периодических функций может быть разложен на сумму тригонометрических компонентов — в ряд Фурье. Другими словами, любое периодическое колебание может быть представлено как сумма гармонических колебаний с соответствующими амплитудами, частотами и начальными фазами. Среди слагаемых этой суммы существует гармоническое колебание с наименьшей частотой, которая называется основной частотой, а само это колебание — первой гармоникой или основным тоном, частоты же всех остальных слагаемых, гармонических колебаний, кратны основной частоте, и эти колебания называются высшими гармониками или обертонами — первым, вторым и т.д.[7]
- Для широкого класса систем откликом на гармоническое воздействие является гармоническое колебание (свойство линейности), при этом связь воздействия и отклика является устойчивой характеристикой системы. С учётом предыдущего свойства это позволяет исследовать прохождение колебаний произвольной формы через системы.
См. также[править | править код]
- Гармонический осциллятор
- Математический маятник
- Физический маятник
- Псевдогармонические колебания
- Биения
Примечания[править | править код]
- ↑ То есть не равное тождественно нулю.
- ↑ Ландсберг, 2003, с. 17.
- ↑ Ландсберг, 2003, с. 2,25.
- ↑ Ландсберг, 2003, с. 27—29.
- ↑ Ландсберг, 2003, с. 29—30.
- ↑ Подразумеваемым условием здесь является то, что свойства системы должны быть постоянны во времени (что в реальности достаточно часто выполняется, по крайней мере, приближенно).
- ↑ Ландсберг, 2003, с. 43.
Литература[править | править код]
- Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика.
- Хайкин С. Э. Физические основы механики. — М., 1963.
- А. М. Афонин. Физические основы механики. — Изд. МГТУ им. Баумана, 2006.
- Горелик Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику. — М.: Физматлит, 1959. — 572 с.
Основные формулы по физике – КОЛЕБАНИЯ И ВОЛНЫ
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна – это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Смотрите также основные формулы квантовой физики
Таблица формул: колебания и волны
|
Физические законы, формулы, переменные |
Формулы колебания и волны |
||||
|
Уравнение гармонических колебаний: где х – смещение (отклонение) колеблющейся величины от положения равновесия; А – амплитуда; ω – круговая (циклическая) частота; t – время; α – начальная фаза; (ωt+α ) – фаза. |
|
||||
|
Связь между периодом и круговой частотой: |
|
||||
|
Частота: |
|
||||
|
Связь круговой частоты с частотой: |
|
||||
|
Периоды собственных колебаний 1) пружинного маятника: где k – жесткость пружины; 2) математического маятника: где l – длина маятника, g – ускорение свободного падения; 3) колебательного контура: где L – индуктивность контура, С – емкость конденсатора. |
|||||
|
Частота собственных колебаний: |
|
||||
|
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А1 и А2 – амплитуды составляющих колебаний, α1 и α2 – начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания |
|
||||
|
Уравнение затухающих колебаний: е = 2,71… – основание натуральных логарифмов. |
|
||||
|
Амплитуда затухающих колебаний: где А0 – амплитуда в начальный момент времени; β – коэффициент затухания; t – время. |
|
||||
|
Коэффициент затухания: колеблющегося тела где r – коэффициент сопротивления среды, m – масса тела; колебательного контура где R – активное сопротивление, L – индуктивность контура. |
|
||||
|
Частота затухающих колебаний ω: |
|
||||
|
Период затухающих колебаний Т: |
|
||||
|
Логарифмический декремент затухания: |
|
||||
|
Связь логарифмического декремента χ и коэффициента затухания β: |
|
||||
|
Амплитуда вынужденных колебаний где ω – частота вынужденных колебаний, fо – приведенная амплитуда вынуждающей силы, при механических колебаниях: при электромагнитных колебаниях: |
|
||||
|
Резонансная частота |
|
||||
|
Резонансная амплитуда |
|
||||
|
Полная энергия колебаний: |
|
||||
|
Уравнение плоской волны: где ξ – смещение точек среды с координатой х в момент времени t; k – волновое число: |
|
||||
|
Длина волны: где v скорость распространения колебаний в среде, Т – период колебаний. |
|
||||
|
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: |
|
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
Колебательное движение – движение (изменение состояния), обладающее той или иной степенью повторяемости во времени.
Т.е. колебанием можно назвать любой вид движения, при котором через одинаковые промежутки времени повторяются кинематические характеристики движения (координата, скорость, ускорение).
Гармоническими колебаниями называются колебания, кинематические характеристики в которых меняются по закону синуса или косинуса.
Рис. 1. Колебательное движение. Вывод через окружность. Начальные условия
Для визуализации, представим вращательное движение в виде колебательного движения вдоль двух взаимно перпендикулярных осей.
Пусть тело, вращающееся по окружности радиуса A, в начале движения находилось в точке C. Пусть в начале движения радиус-вектор, описывающий выбранную точку, наклонён под углом к оси OX. Определим начальные координаты тела (исходя из проекций радиуса на оси):
(1)
(2)
Рис. 2. Колебательное движение. Вывод через окружность
Пусть через время тело, вращаясь с угловой скоростью
, переместилось в точку D. При этом угол поворота радиус-вектора, относительно начального положения составил
(рис. 2).
Определим текущие координаты тела тем же методом:
(3)
(4)
Учитывая, что при равномерном движении по окружности , получим:
(5)
(6)
Уравнения (5) и (6) являются законом движения материальной точки при гармонических колебаниях. Причём, одним и тем же законом, так как с тригонометрической точки зрения , тогда из (5):
=
(7)
- где
— новый параметр, характеризующий некое другое начальное положение тела.
Таким образом, уравнения (5) и (6), по сути, являются одинаковыми уравнениями только при разных начальных условиях.
Разберём уравнение (5). Каждый из введённых параметров, имея аналог во вращательном движении, описывается по-другому в колебательном движении:
Зная общий вид колебательного движения, можем найти зависимости скорости и ускорения от времени. Для уравнения (5):
(7)
(8)
Аналогичным образом можно провести рассмотрение уравнения (6).
Проанализируем (5) и (8), исходя из внешнего вида правой части обоих уравнений, можем вывести:
(9)
Уравнение (9) называется основным уравнением гармонических колебаний.
Среди параметров колебаний также присутствуют параметры, знакомые нам по вращательному движению:
(10)
(11)
Вывод: для школьных задач почти все колебания являются гармоническими и описываются соотношениями (5), (6). Соответствующие скорость и ускорение частицы рассчитываются исходя из конкретного колебания. Параметры колебания также рассчитываются формульно.
Что такое колебательный процесс
Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.
Систему, совершающую колебания, называют колебательной системой или осциллятором.
Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.
Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.
При механических колебаниях, которые относят к категории вынужденных:
(F=F_{0}cos cot)
Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.
Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.
Определение периода колебаний, формула
Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:
(x(t)=Atimes cos left(omega _{0}t+phi _{0} right))
Где (x(t)) является отклонением колеблющейся физической величины от равновесного значения;
А представляет собой амплитуду гармонических колебаний;
(omega _{0}) равно циклической или круговой частоте колебаний;
(phi _{0}) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;
(cp(t)=(co_{0}t+cp_{0})) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.
В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
(cos left(alpha +2pi right)=cos alpha,)
то х остается без изменений при фазе колебаний, получающей приращение в $$2pi$$
Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.
В этом случае фаза будет увеличена на (2pi:)
(omega _{0}(t+T)+phi _{0}=left(omega _{0}t+phi _{0} right)+2pi)
Из данного равенства можно вычислить период колебаний:
(T=frac{2pi }{omega _{0}})
Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:
(v=frac{omega _{0}}{2pi})
На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.
Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.
Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:
Смещение (x=Atimes cos left(omega _{0}t+phi _{0} right))
Скорость (v_{x}=dot{x}=-Aomega _{0}times sin left(omega _{0} t+phi_{0} right)=Aomega _{0}times cos left(omega _{0} t+phi_{0} +frac{pi }{2}right))
Ускорение
(a_{x}=dot{v_{x}}=ddot{x}=-Aomega _{0}times cos left(omega _{0} t+phi_{0} right)=Aomega _{0}^{2}times cos left(omega _{0} t+phi_{0} +pi right))
Как найти период для физического маятника
В случае, когда углы отклонения (varphi) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:
(F=mgtimes sin varphi)
Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла (alpha)
Учитывая малый угол (varphi) уравнение можно записать в следующем виде:
(F=mgtimesvarphi)
С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:
(J=ml^{2})
При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:
(frac{d^{2}varphi }{dt^{2}}+frac{mgl}{J}varphi =0)
В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:
(alpha _{x}(t)+omega ^{2}x(t)=0)
Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:
(omega =sqrt{frac{mgl}{J}})
В таком случае для расчета периода колебаний математического маятника будет использоваться формула:
(T =frac{2pi }{omega }=2pi sqrt{frac{J}{mgl}})
Исходя из расчетов, можно сделать следующие выводы:
- Период пружинного маятника (T =2pi sqrt{frac{m}{k}})
- Период математического маятника (T =2pi sqrt{frac{L}{g}})
- Период крутильного маятника (T =2pi sqrt{frac{I}{K}})
В приведенных формулах:
- T — период физического маятника;
- J — момент силы маятника относительно оси вращения;
- l — расстояние от оси вращения до центра масс;
- m — масса маятника;
- g=9.8 — ускорение свободного падения.
Примеры решений
Задача № 1
Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.
Решение
(T =frac{t}{N}=frac{120}{60}=2)
(V=frac{1}{T}=frac{1}{2}=0.5)
Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.
Задача № 2
Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.
Решение
А = 20
Т = 0,8
(V=frac{1}{T}=frac{1}{0,8}=1,25)
(x(t)=Asin 2pi Vt=0.2sin 2pi times 1.25t=0.2sin 2.5pi t)
Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: (x(t)=0.2sin 2.5pi t)
Задача № 3
Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.
Решение
Период колебаний математического маятника рассчитывается по формуле:
(T =2pi sqrt{frac{L}{g}})
Согласно определению:
(V=frac{1}{T})
Тогда:
(T=frac{1}{V})
Получим равенство:
(frac{1}{V}=2pi sqrt{frac{l}{g}})
Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:
(frac{1}{V^{2}}=4pi ^{2}times frac{l}{g}Rightarrow l=frac{g}{4pi ^{2}V^{2}})
(l=frac{1.5}{4*3.14 ^{2}*0.5^{2}}approx 0.16)
Ответ: длина математического маятника примерно составляет 0,16 метра.