В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F – частота (Гц) , v – скорость распространения колебаний в среде (м/с) , λ – длина волны (м) .
Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T – период колебаний (с) , F – частота (Гц) .
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F – частота (Гц) , T – период колебаний (с) .
Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω – циклическая частота (радиан в секунду) , F – обычная частота (Гц)
Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω/(2π), где F – обычная частота (Гц) , ω – циклическая частота (радиан в секунду) .
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:
– скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину) ;
– скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
– число «пи» (до пятидесятого знака) : π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).
Период и частота колебаний, теория и онлайн калькуляторы
Период и частота колебаний
Период колебаний
Определение
Период – это отрезок времени, которое необходимо для совершения одного цикла периодического процесса.
Периодом ($T$) колебаний называют время, за которое совершается одно полное колебание.
За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:
[T=frac{2pi }{{omega }_0}left(1right).]
Разные периодические процессы, (процессы, повторяющиеся через равные промежутки времени) можно представить в виде совокупности наложенных гармонических колебаний.
Гармонические колебания некоторого параметра $xi $ описываются уравнением:
[xi =A{cos ({omega }_0t+varphi ) } left(2right),]
где $A={xi }_{max}$ – амплитуда колебаний; ${omega }_0$ – циклическая (круговая) частота колебаний; $varphi $ – начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ –
фаза колебаний. Величина $xi $ лежит в пределах $-Ale sle $+A.
Формулы для вычисления периода простейших колебательных систем
Период колебаний пружинного маятника определим как:
[T=2pi sqrt{frac{m}{k}} left(3right),]
на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$.
Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)
[T=2pi sqrt{frac{l}{g}}left(4right).]
Формула для вычисления периода колебаний физического маятника представляет собой выражение:
[T=2pi sqrt{frac{J}{mga}left(5right),}]
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние от центра масс тела до оси вращения.
Единицами измерения периода служат единицы времени, например секунды.
[left[Tright]=c.]
Частота колебаний
Определение
Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $).
Частота – это количество полных колебаний, которые колебательная система совершает за единицу времени.
[nu =frac{1}{T}left(6right).]
Частота колебаний связана с циклической частотой как:
[{omega }_0=2pi nu left(7right).]
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
[left[nu right]=с^{-1}=Гц.]
Примеры задач с решением
Пример 1
Задание. Каковы период ($T$) и частота ($nu $) колебаний, которые происходят в соответствии с уравнением: $x=A{sin ({omega }_0(t+tau )) }$, где ${omega }_0=2,5 pi (frac{рад}{с})$; $tau =0,4 $с?
Решение. Из уравнения колебаний:
[x=A{sin left({omega }_0left(t+tau right)right)left(1.1right), }]
заключаем, что это гармонические колебания, так как они происходят по закону синуса следовательно, они являются периодическими. Период найдем, зная циклическую частоту колебаний:
[T=frac{2pi }{{omega }_0}left(1.1right).]
Подставляя имеющиеся данные, вычислим период колебаний:
[T=frac{2pi }{2,5pi }=0,8 left(сright).]
Частоту колебаний найдем как величину, обратную периоду:
[nu =frac{1}{T}left(1.2right).]
Вычислим частоту:
[nu =frac{1}{0,8}=1,25 left(Гцright).]
Ответ. $T=0,8$ с; $nu =1,25 Гц$
Пример 2
Задание. Какими будут период и частота малых колебаний тонкого обруча, который висит на гвозде (точка А), вбитом горизонтально в стену (рис.1)? Колебания совершаются в плоскости параллельной стене. Радиус обруча R.
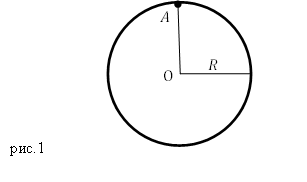
Решение. В этой задаче мы имеем дело с физическим маятником период которого, найдем, используя формулу:
[T=2pi sqrt{frac{J}{mga}left(2.1right).}]
Осью вращения обруча является гвоздь, находящийся в точке А. Цент масс обруча находится в его геометрическом центре, точке О, следовательно, расстояние от центра масс до оси вращения обруча (рис.1) равно:
[a=R left(2.2right).]
Найдем момент инерции обруча относительно оси, перпендикулярной плоскости обруча, проходящей через точку $A$. Для этого воспользуемся теоремой Штейнера:
[J=J_0+mR^2 left(2.3right),]
где $J_0=mR^2$ – момент инерции обруча, относительно оси, проходящей через его центр (т.О), перпендикулярно плоскости обруча; расстояние между осями равно радиусу обруча. Получаем, момент инерции обруча относительно гвоздя равен:
[J=mR^2+mR^2=2mR^2left(2.4right).]
Используя формулы (2.1) (2.2) и (2.4), имеем:
[T=2pi sqrt{frac{2mR^2}{mgR}}=2pi sqrt{frac{2R}{g}}.]
Отталкиваясь от полученного результата, найдем частоту колебаний как:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{g}{2R}}.]
Ответ. $T=2pi sqrt{frac{2R}{g}},$ $nu =frac{1}{2pi }sqrt{frac{g}{2R}}$
Читать дальше: полная энергия колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Для школьников.
Любое тело подвешенное так, что его центр масс находится ниже точки подвеса, называют физическим маятником.
Маятник находится в состоянии устойчивого равновесия, если его центр масс расположен на вертикали под точкой подвеса.
Если маятник вывести из состояния равновесия, отклонив его на некоторый угол и предоставив самому себе, то он начнёт колебаться около положения равновесия.
Чтобы описать колебание маятника, надо знать уравнение его движения, то есть зависимость координаты от времени, и период его колебаний.
Но найти период колебаний физического маятника сложно, так как он зависит от многих причин – от формы и размера маятника, от распределения массы тела, расстояния от точки подвеса до центра масс тела.
Много проще описать поведение математического маятника. Для этого физический маятник заменяют математическим маятником такой длины, чтобы частоты колебаний этих маятников были одинаковы.
Длина математического маятника, частота колебаний которого равна частоте колебаний данного физического маятника, называется приведённой длиной физического маятника.
Под математическим маятником понимается тело малого размера, подвешенного на длинной нерастяжимой нити. Нить считаем невесомой, а тело можно принять за материальную точку.
Наблюдения за колебаниями маятников, подобных математическому, позволили установить следующие законы:
1) Период колебаний математического маятника не зависит от массы тела;
2) Период колебаний математического маятника не зависит от амплитуды колебаний (при малых амплитудах).
Впервые второй закон был установлен Галилеем в 1655 году, при наблюдении им в соборе качания паникадила на длинной цепи, которое толкнули при зажигании. Его колебания постепенно затухали, но период колебаний оставался прежним. Для измерения периода колебаний Галилей пользовался своим пульсом.
Посмотрим теперь, как получили формулу, по которой можно найти период колебаний математического маятника.
На рис а) показан математический маятник, отклонённый от положения равновесия (от точки А) на малый угол (в точку В).
Буквой Р обозначена сила тяжести груза, а буквой Р (с индексом 1) обозначена переменная возвращающая сила, действующая на груз.
Так как возвращающая сила меняется в процессе колебания, то рассчитать движение колеблющегося тела сложно.
Для упрощения расчётов заставляют маятник колебаться не в одной плоскости, как показано на рис.а), а описывать конус (рис. б), чтобы грузик двигался по окружности.
Движение маятника по конусу может рассматриваться как сложение двух независимых колебаний (в плоскости рисунка и в перпендикулярной рисунку плоскости).
Период этих колебаний одинаков. Тогда период обращения маятника можно выразить через отношение длины окружности к скорости движения
При малом угле отклонения маятника (малой амплитуде) можно считать, что возвращающая сила направлена к центру окружности (является центростремительной, равной произведению массы тела на центростремительное или нормальное ускорение), то есть
С другой стороны, из подобия треугольников ОВС и ДВЕ можно записать, что
Приравняв правые части последних выражений, получим уравнение для скорости обращения груза
Подставив скорость в выражение периода, получим искомую формулу для нахождения периода гармонических колебаний математического маятника
Таким образом, период колебаний математического маятника зависит только от ускорения свободного падения и от длины маятника (расстояния от точки подвеса до центра масс груза), и не зависит от его массы и амплитуды (при малых значениях амплитуд), то есть теоретические расчёты подтверждают установленные путём наблюдений первый и второй законы, записанные выше.
К тому же полученная формула
позволила установить количественную зависимость между периодом колебаний маятника, его длиной и ускорением свободного падения g
На практике эту формулу можно использовать для точного нахождения ускорения свободного падения g в разных точках земной поверхности, где g имеет разные значения из-за неравномерной плотности земной коры.
Задачи.
Зададим себе вопросы:
Вопрос: Изменится ли период колебания качелей, если на доску положить груз?
Ответ: Качели могут рассматриваться как математический маятник, а период колебаний математического маятника не зависит от его массы. Значит, если во время колебаний качели на её доску положить груз, то период колебаний качели не изменится.
Вопрос: Как объяснить раскачивание изображённых на рисунке качелей?
Ответ: Качели раскачиваются, так как человек периодически приседает и выпрямляет ноги, изменяя этим центр масс качелей (колебательной системы). Период колебаний качелей меняется и поддерживается за счёт совершённой людьми на качелях работы.
Выше говорилось о колебаниях математического маятника в инерциальной системе отсчёта.
Если маятник колеблется в неинерциальной системе отсчёта, то
Задача.
Итак, мы рассмотрели, как было получено выражение для периода колебаний математического маятника в инерциальных системах отсчёта. В неинерциальных системах отсчёта для расчёта периода колебаний математического маятника кроме ускорения свободного падения надо учитывать ещё ускорение, входящее в выражение силы инерции.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Решение задач на тему: “Гармонические колебания”.
Следующая запись: Упругие колебания. Крутильные колебания.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70
Как найти период и частоту колебаний
У любой волны, распространяющейся в той или иной среде, имеются три взаимосвязанных между собой параметра: длина, период колебаний и их частота. Любой из них можно найти, зная любой другой, при этом в некоторых случаях необходима также информация о скорости распространения колебаний в среде.

Инструкция
Независимо от того, какой из параметров вы собираетесь вычислять, переведите все исходные величины в систему СИ. Тогда и результат получится в единицах той же системы. При необходимости пользуйтесь калькулятором, способным, помимо мантиссы, отображать и порядок числа, поскольку при решении задач по теме «Колебания и волны» приходится иметь дело как с очень малыми, так и с очень большими величинами.
В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F – частота (Гц), v – скорость распространения колебаний в среде (м/с), λ – длина волны (м).
Скорость света в вакууме обычно обозначают другой буквой – c (латинской). Помните, что скорость распространения света в любой другой среде, кроме вакуума, меньше скорости света в вакууме. Если та или иная частица пролетает через среду со скоростью, хотя и меньшей скорости света в вакууме, но большей скорости света в этой среде, возникает так называемое свечение Черенкова.
Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T – период колебаний (с), F – частота (Гц).
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F – частота (Гц), T – период колебаний (с).
Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω – циклическая частота (радиан в секунду), F – обычная частота (Гц).
Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω/(2π), где F – обычная частота (Гц), ω – циклическая частота (радиан в секунду).
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:
– скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину);
– скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
– число «пи» (до пятидесятого знака): π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).
Скорость света в веществе с показателем преломления, равным n (также безразмерная величина), вычислите, поделив скорость света на показатель преломления.
После окончания вычислений при необходимости переведите результат из системы СИ в удобные для вас единицы измерения.
Источники:
- как будет изменяться период колебаний
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Что такое колебательный процесс
Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.
Систему, совершающую колебания, называют колебательной системой или осциллятором.
Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.
Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.
При механических колебаниях, которые относят к категории вынужденных:
(F=F_{0}cos cot)
Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.
Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.
Определение периода колебаний, формула
Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:
(x(t)=Atimes cos left(omega _{0}t+phi _{0} right))
Где (x(t)) является отклонением колеблющейся физической величины от равновесного значения;
А представляет собой амплитуду гармонических колебаний;
(omega _{0}) равно циклической или круговой частоте колебаний;
(phi _{0}) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;
(cp(t)=(co_{0}t+cp_{0})) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.
В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
(cos left(alpha +2pi right)=cos alpha,)
то х остается без изменений при фазе колебаний, получающей приращение в $$2pi$$
Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.
В этом случае фаза будет увеличена на (2pi:)
(omega _{0}(t+T)+phi _{0}=left(omega _{0}t+phi _{0} right)+2pi)
Из данного равенства можно вычислить период колебаний:
(T=frac{2pi }{omega _{0}})
Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:
(v=frac{omega _{0}}{2pi})
На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.
Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.
Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:
Смещение (x=Atimes cos left(omega _{0}t+phi _{0} right))
Скорость (v_{x}=dot{x}=-Aomega _{0}times sin left(omega _{0} t+phi_{0} right)=Aomega _{0}times cos left(omega _{0} t+phi_{0} +frac{pi }{2}right))
Ускорение
(a_{x}=dot{v_{x}}=ddot{x}=-Aomega _{0}times cos left(omega _{0} t+phi_{0} right)=Aomega _{0}^{2}times cos left(omega _{0} t+phi_{0} +pi right))
Как найти период для физического маятника
В случае, когда углы отклонения (varphi) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:
(F=mgtimes sin varphi)
Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла (alpha)
Учитывая малый угол (varphi) уравнение можно записать в следующем виде:
(F=mgtimesvarphi)
С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:
(J=ml^{2})
При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:
(frac{d^{2}varphi }{dt^{2}}+frac{mgl}{J}varphi =0)
В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:
(alpha _{x}(t)+omega ^{2}x(t)=0)
Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:
(omega =sqrt{frac{mgl}{J}})
В таком случае для расчета периода колебаний математического маятника будет использоваться формула:
(T =frac{2pi }{omega }=2pi sqrt{frac{J}{mgl}})
Исходя из расчетов, можно сделать следующие выводы:
- Период пружинного маятника (T =2pi sqrt{frac{m}{k}})
- Период математического маятника (T =2pi sqrt{frac{L}{g}})
- Период крутильного маятника (T =2pi sqrt{frac{I}{K}})
В приведенных формулах:
- T — период физического маятника;
- J — момент силы маятника относительно оси вращения;
- l — расстояние от оси вращения до центра масс;
- m — масса маятника;
- g=9.8 — ускорение свободного падения.
Примеры решений
Задача № 1
Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.
Решение
(T =frac{t}{N}=frac{120}{60}=2)
(V=frac{1}{T}=frac{1}{2}=0.5)
Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.
Задача № 2
Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.
Решение
А = 20
Т = 0,8
(V=frac{1}{T}=frac{1}{0,8}=1,25)
(x(t)=Asin 2pi Vt=0.2sin 2pi times 1.25t=0.2sin 2.5pi t)
Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: (x(t)=0.2sin 2.5pi t)
Задача № 3
Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.
Решение
Период колебаний математического маятника рассчитывается по формуле:
(T =2pi sqrt{frac{L}{g}})
Согласно определению:
(V=frac{1}{T})
Тогда:
(T=frac{1}{V})
Получим равенство:
(frac{1}{V}=2pi sqrt{frac{l}{g}})
Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:
(frac{1}{V^{2}}=4pi ^{2}times frac{l}{g}Rightarrow l=frac{g}{4pi ^{2}V^{2}})
(l=frac{1.5}{4*3.14 ^{2}*0.5^{2}}approx 0.16)
Ответ: длина математического маятника примерно составляет 0,16 метра.
