Содержание:
- Колебания материальной точки
- Свободные гармонические колебания материальной точки
- Влияние постоянной силы на свободные колебания
- Порядок решения задач на свободные колебания
- Примеры решения задач на тему: Колебания материальной точки
- Затухающие колебания материальной точки
- Примеры решения задач на тему: Затухающие колебания материальной точки
- Вынужденные колебания материальной точки без учета сопротивления
- Амплитуда вынужденных колебаний
- Явление резонанса
- Примеры решения задач на тему: Вынужденные колебания точки
Прямолинейные колебания материальной точки – колебательное движение материальной точки – движение, происходящее при условии: имеется восстанавливающая сила, стремящаяся вернуть точку в положение равновесия при любом отклонении ее из этого положения. Свободные колебания – происходят под действием только восстанавливающей силы.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Колебания материальной точки
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Свободные гармонические колебания материальной точки
Свободные гармонические колебания материальной точки происходят под действием восстановительной силы, которая пытается вернуть точку в положение равновесия. Примером такой силы может быть сила упругости пружины.
Восстановительная сила меняется по линейному закону. Если на материальную точку действует сила упругости пружины  , то:
, то:

где  – деформация пружины,
– деформация пружины,
 – коэффициент жесткости.
– коэффициент жесткости.
Коэффициент жесткости  многочисленно равен силе, которую необходимо приложить к пружине для того, чтобы деформировать ее на единицу длины.
многочисленно равен силе, которую необходимо приложить к пружине для того, чтобы деформировать ее на единицу длины.
Единицей измерения коэффициента жесткости  в системе единиц Си является
в системе единиц Си является  .
.
В практике чаще применяется единица  .
.
Движение материальной точки  с массой
с массой  по горизонтальной оси (рис.3.1) под действием восстановительной силы
по горизонтальной оси (рис.3.1) под действием восстановительной силы  , которая равна по модулю
, которая равна по модулю  , описывается дифференциальным уравнением:
, описывается дифференциальным уравнением:


Решение этого уравнения, или закон изменения координаты  от времени
от времени  , выглядит так:
, выглядит так:

где  и
и  – постоянные интегрирования, которые определяются по первоначальным условиям.
– постоянные интегрирования, которые определяются по первоначальным условиям.
В амплитудной форме уравнение движения записывается следующим образом:

где  – амплитуда колебаний, то есть наибольшее отклонение колеблющейся точки от положения равновесия;
– амплитуда колебаний, то есть наибольшее отклонение колеблющейся точки от положения равновесия;
 – фаза колебаний;
– фаза колебаний;
 – начальная фаза колебаний;
– начальная фаза колебаний;
 – круговая частота колебаний, то есть количество колебаний материальной точки за
– круговая частота колебаний, то есть количество колебаний материальной точки за  секунд:
секунд:

Если исходные условия движения материальной точки при  имеют вид
имеют вид  то:
то:

Периодом колебаний  материальной точки называется наименьший промежуток времени, по истечении которого точка будет иметь ту же самую координату:
материальной точки называется наименьший промежуток времени, по истечении которого точка будет иметь ту же самую координату:

Из приведенных зависимостей вытекает, что амплитуда  и начальная фаза
и начальная фаза  зависят от первоначальных условий, а период
зависят от первоначальных условий, а период  и круговая частота
и круговая частота  – не зависят от первоначальных условий.
– не зависят от первоначальных условий.
Влияние постоянной силы на свободные колебания
В этом случае начало отсчета выбирается в положении статического равновесия, то есть на расстоянии, которое откладывается в направлении постоянной силы и определяется по соотношению:

где  – модуль постоянной силы.
– модуль постоянной силы.
Дифференциальное уравнение движения при наличии постоянной силы совпадает по форме с дифференциальным уравнением свободных колебаний. Отсюда выходит, что
Период колебаний и круговая частота равны:

Порядок решения задач на свободные колебания
Решение задач на свободные колебания материальной точки рекомендуется делать в следующем порядке:
1. Изобразить материальную точку в произвольном положении и показать силы, которые на нее действуют.
2. Выбрать систему отсчета, начало координат разместить в положении статического равновесия и направить ось в сторону движения точки.
3. Записать начальные условия движения материальной точки.
4. Составить дифференциальное уравнение движения материальной точки в проекции на соответствующую ось.
5. Проинтегрировать дифференциальное уравнение движения.
6. Определить постоянные интегрирования, используя исходные условия.
7. Записать окончательное уравнение движения.
Примеры решения задач на тему: Колебания материальной точки
Задача № 1
Определить максимальное удлинение  пружины
пружины  (рис. 3.2, а) в сантиметрах при свободных вертикальных колебаниях груза, если он прикреплен в точке
(рис. 3.2, а) в сантиметрах при свободных вертикальных колебаниях груза, если он прикреплен в точке  к недеформированной пружине и отпущен из состояния покоя. Статическая деформация пружины под действием груза равняется
к недеформированной пружине и отпущен из состояния покоя. Статическая деформация пружины под действием груза равняется 
Решение. Изобразим груз в произвольном положении (рис.3.2, б) и покажем силы, которые на него действуют: силу упругости пружины  , которая является восстановительной силой, и силу тяжести груза
, которая является восстановительной силой, и силу тяжести груза  .
.
Поскольку на груз помимо восстановительной силы  , действует и постоянная сила – сила тяжести груза
, действует и постоянная сила – сила тяжести груза  , то центр колебаний сместим относительно конца недеформированной пружины в направлении силы тяжести на
, то центр колебаний сместим относительно конца недеформированной пружины в направлении силы тяжести на  (точка
(точка  ). Ось
). Ось  направим в направлении движения груза.
направим в направлении движения груза.
Когда груз будет находиться в крайнем нижнем положении (рис.3.2, б), то максимальное удлинение пружины будет состоять из статической деформации  и амплитуды
и амплитуды  свободных колебаний:
свободных колебаний:

Величину амплитуды можно определить из выражения:

где  – исходное положение груза;
– исходное положение груза;
 – начальная скорость груза.
– начальная скорость груза.
По условию задачи при 
Подставляя значения  и
и  в уравнение (1), достанем:
в уравнение (1), достанем:

Таким образом, максимальное удлинение пружины равно:

Ответ: 
Задача № 2
Груз массой  подвешен к пружине с коэффициентом жесткости
подвешен к пружине с коэффициентом жесткости  и находится в свободном прямолинейном колебательном движении.
и находится в свободном прямолинейном колебательном движении.
Определить модуль ускорения  груза в момент времени, когда его центр тяжести находится на расстоянии 5 см от положения статического равновесия.
груза в момент времени, когда его центр тяжести находится на расстоянии 5 см от положения статического равновесия.
Решение. При изучении свободных колебаний под действием восстановительной (сила  упругости пружины) и постоянной силы (в данном случае – силы тяжести
упругости пружины) и постоянной силы (в данном случае – силы тяжести  ) начало координат лучше всего выбрать в положении статического равновесия (точка
) начало координат лучше всего выбрать в положении статического равновесия (точка  ) (рис.3.3), то есть смещенным на
) (рис.3.3), то есть смещенным на  относительно недеформированного состояния в направлении силы
относительно недеформированного состояния в направлении силы  . Тогда уравнение движения груза будет иметь вид:
. Тогда уравнение движения груза будет иметь вид:


Для нахождения ускорения груза два раза продифференцируем это уравнение по времени:

Последнее выражение представим в виде:

поскольку 
Определим круговую частоту колебаний, которая входит в правую часть уравнения (2):

По условиям задачи необходимо определить модуль ускорения груза, когда его центр тяжести находится на расстоянии 5 см от положения статического равновесия, то есть 
Окончательно:

Ответ: 
Задача № 3
Определить эквивалентный коэффициент жесткости  двух пружин и период колебаний груза
двух пружин и период колебаний груза  весом
весом  , подвешенного к этим пружинам, если пружины соединены последовательно (рис. 3.4,а) и параллельно (рис. 3.5). Коэффициенты жесткости пружин:
, подвешенного к этим пружинам, если пружины соединены последовательно (рис. 3.4,а) и параллельно (рис. 3.5). Коэффициенты жесткости пружин:


Решение: в случае последовательного соединения пружин общее статическое удлинение  будет равняться сумме статических удлинений первой и второй пружины:
будет равняться сумме статических удлинений первой и второй пружины:

Поскольку каждая из пружин в статическом положении растягивается силой  , то согласно (3.7):
, то согласно (3.7):

С учетом последних соотношений формула (1) примет вид:

Для эквивалентной расчетной схемы с одной пружиной (рис. 3.4, б):

где  – коэффициент жесткости эквивалентной пружины, заменяющей две последовательно соединенные пружины.
– коэффициент жесткости эквивалентной пружины, заменяющей две последовательно соединенные пружины.
Поскольку статическое удлинение заданной (рис. 3.4,а) и эквивалентной (рис. 3.4,б) схем должно быть равным, то:

С учетом числовых данных:

Период колебаний по формуле (3.8):

В случае параллельного соединения пружин (рис. 3.5) их статическое удлинение будет одинаковым:


Исходя из формулы (3.7) пружины будут растянуты усилиями:

Таким образом, сила тяжести груза  будет уравновешиваться двумя вертикальными усилиями
будет уравновешиваться двумя вертикальными усилиями  и
и  пружин, то есть,
пружин, то есть, 
или

С другой стороны, для эквивалентной расчетной схемы с одной пружиной (рис. 3.4, б):

де  – коэффициент жесткости эквивалентной пружины, заменяющей две параллельные пружины.
– коэффициент жесткости эквивалентной пружины, заменяющей две параллельные пружины.
Отсюда

С учетом числовых данных:

Период колебаний по формуле (3.8):

Ответ: 

Задача № 4
Пружина  , которая закреплена одним концом в точке
, которая закреплена одним концом в точке  , является такой, что для удлинения ее на
, является такой, что для удлинения ее на  необходимо приложить в точке
необходимо приложить в точке  при статической нагрузке силу
при статической нагрузке силу  . В некоторый момент времени к нижнему концу
. В некоторый момент времени к нижнему концу  недеформированной пружины подвешивают гирю
недеформированной пружины подвешивают гирю  , массой
, массой  и отпускают ее без начальной скорости. Пренебрегая массой пружины, написать уравнение дальнейшего движения гири и определить амплитуду
и отпускают ее без начальной скорости. Пренебрегая массой пружины, написать уравнение дальнейшего движения гири и определить амплитуду  и период
и период  ее колебаний, относя движение гири к оси, которая проведена вниз из положения статического равновесия гири.
ее колебаний, относя движение гири к оси, которая проведена вниз из положения статического равновесия гири.
Определить: 
Решение. Изобразим гирю  в промежуточном положении (рис.3.6). На нее действуют сила тяжести
в промежуточном положении (рис.3.6). На нее действуют сила тяжести  и сила упругости
и сила упругости  . Ось
. Ось  направим вертикально вниз, а начало отсчета
направим вертикально вниз, а начало отсчета
возьмем в точке  , которая отдалена от конца
, которая отдалена от конца  недеформированной пружины на величину
недеформированной пружины на величину  .
.
Начальные условия при  имеют вид:
имеют вид:

Уравнение движения гири  запишем в дифференциальной форме:
запишем в дифференциальной форме:

С другой стороны

Тогда

Статическое отклонение равно:
 или
или 
Подставив в (1) выражение для  , получим:
, получим:

Решение этого дифференциального уравнения в амплитудной форме имеет вид:

Круговая частота  колебаний гири
колебаний гири  определяется зависимостью (3.4):
определяется зависимостью (3.4):

где 
Тогда

Определим амплитуду колебаний гири по формуле (3.5):

где 
Тогда,

а поскольку

то амплитуда колебаний гири

Начальную фазу колебаний  найдем по формуле (3.5):
найдем по формуле (3.5):

С учетом найденных величин  ,
,  и
и  уравнение (1) движения гири имеет вид:
уравнение (1) движения гири имеет вид:

Период свободных колебаний гири равен (3.8):

Ответ: 
Задача № 5
Во время равномерного опускания груза весом  со скоростью
со скоростью  , от зажатия троса в обойме блока (рис.3.7), случилась внезапная задержка верхнего конца троса, на котором опускался груз.
, от зажатия троса в обойме блока (рис.3.7), случилась внезапная задержка верхнего конца троса, на котором опускался груз.

Определить наибольшее натяжение  троса во время колебания груза, если коэффициент жесткости троса
троса во время колебания груза, если коэффициент жесткости троса  . Весом троса пренебречь.
. Весом троса пренебречь.
Решение. Начало координат выбираем в положении статического равновесия на расстоянии  от начального состояния (точка
от начального состояния (точка  ).
).
Из условия задачи вытекает, что максимальное натяжение троса будет при крайнем нижнем положении груза  . В этом случае деформация будет равна сумме статического отклонения и амплитуды колебаний груза
. В этом случае деформация будет равна сумме статического отклонения и амплитуды колебаний груза  . Таким образом:
. Таким образом:

Итак, задача сводится к определению амплитуды колебаний.
Амплитуда колебаний определяется с помощью начальных условий:

где  – исходное положение груза
– исходное положение груза  ;
;
 – начальная скорость груза Q .
– начальная скорость груза Q .
В данной задаче начальные условия при  имеют вид:
имеют вид:

Определяем круговую частоту колебаний:

и величину статического отклонения:

Тогда

Максимальное натяжение троса равно:

Надо обратить внимание на то, что груз весом  при зажатии троса вызывает в нем усилие в 23 раза больше, чем его вес, что может привести к разрыву троса и аварии.
при зажатии троса вызывает в нем усилие в 23 раза больше, чем его вес, что может привести к разрыву троса и аварии.
Ответ: 
Задача № 6
Груз  , падающий с высоты
, падающий с высоты  без начальной скорости, бьется о середину упругой горизонтальной балки, концы которой
без начальной скорости, бьется о середину упругой горизонтальной балки, концы которой  и
и  закреплены (рис.3.8).
закреплены (рис.3.8).

Определить уравнение  последующего движения груза вместе с балкой относительно оси, которая проведена вертикально вниз из положения статического равновесия балки вместе с грузом. При статической нагрузке балки в средней ее части силой, равной силе тяжести груза
последующего движения груза вместе с балкой относительно оси, которая проведена вертикально вниз из положения статического равновесия балки вместе с грузом. При статической нагрузке балки в средней ее части силой, равной силе тяжести груза  , прогиб составляет
, прогиб составляет  Массой балки пренебречь.
Массой балки пренебречь.
Решение. Изобразим груз в промежуточном положении. На груз действует: сила тяжести  и сила упругости балки
и сила упругости балки  . Ось
. Ось  направим вниз, начало отсчета берем в точке
направим вниз, начало отсчета берем в точке  , которая находится на расстоянии
, которая находится на расстоянии  от горизонтального положения балки.
от горизонтального положения балки.
Запишем начальные условия движения.
Координата  груза в начале колебательного движения равна
груза в начале колебательного движения равна  . Скорость средней точки балки, которая колеблется вместе с грузом, в начале движения будет равна скорости груза при его падении с высоты
. Скорость средней точки балки, которая колеблется вместе с грузом, в начале движения будет равна скорости груза при его падении с высоты  :
:

Таким образом, при  :
:

Если начало отсчета совпадает с положением статического равновесия, то уравнение движения имеет вид:

Для определения постоянных интегрирования  и
и  нам кроме закона движения надо иметь и закон изменения скорости:
нам кроме закона движения надо иметь и закон изменения скорости:

Для определения круговой частоты колебаний  найдем коэффициент жесткости балки.
найдем коэффициент жесткости балки.
Поскольку  то
то 
Тогда 
Из начальных условий (при  ) и закона движения (1) находим постоянную интегрирования
) и закона движения (1) находим постоянную интегрирования  :
:

Из уравнения (2) и начальных условий (при  :
:  ) находим постоянную интегрирования
) находим постоянную интегрирования  :
:

Окончательно, уравнение движения груза примет вид

Ответ: 
Задача № 7
В клапанном механизме (рис. 3.9,а) закон движения толкателя 2 задается профилем кулачка 1 и передается на клапан 3. На клапане 3 установлена пружина 4, которая обеспечивает постоянный контакт между рабочими поверхностями кулачка 1 и толкателя 2. При проектировании быстроходных кулачковых механизмов приходится учитывать характеристики реальных деталей, которые отличаются от характеристик абсолютно твердых тел. Например, низкая жесткость, значительные массы и большие ускорения при движении деталей газораспределительных механизмов двигателей внутреннего сгорания приводят к возникновению упругих колебаний, которые накладываются на заданное движение деталей.
Считается, что податливость имеют кулачок 1, толкатель 2 и клапан 3 с пружиной 4. При создании динамической модели механизма, которая отражает влияние упругости деталей реального механизма, используют одномассовую модель (рис. 3.9, б). Масса  учитывает массы кулачка, толкателя и клапана, пружина с коэффициентом жесткости
учитывает массы кулачка, толкателя и клапана, пружина с коэффициентом жесткости  клапанную пружину 4, а пружина коэффициентом жесткости
клапанную пружину 4, а пружина коэффициентом жесткости  жесткость кулачка, толкателя и клапана.
жесткость кулачка, толкателя и клапана.

Определить коэффициент жесткости  и частоту колебаний
и частоту колебаний  деталей такого механизма, если:
деталей такого механизма, если:  коэффициент жесткости клапанной пружины
коэффициент жесткости клапанной пружины  и статическую нагрузку величиной
и статическую нагрузку величиной  вызывает деформацию
вызывает деформацию  Силами трения в направляющих толкателя и клапана пренебречь.
Силами трения в направляющих толкателя и клапана пренебречь.
Решение. При статической нагрузке на тело массой  (рис. 3.9) действуют три силы: статическая нагрузка
(рис. 3.9) действуют три силы: статическая нагрузка  и силы упругости пружин
и силы упругости пружин  и
и  .
.
Сила упругости пружины  , длина которой в недеформированном состоянии
, длина которой в недеформированном состоянии  , пропорциональна статическому удлинению
, пропорциональна статическому удлинению  :
:

и направлена вверх, поскольку пружина сжата.
Сила упругости пружины  , длина которой в недеформированном состоянии
, длина которой в недеформированном состоянии  , пропорциональна статическому удлинению
, пропорциональна статическому удлинению  :
:

и направлена вверх, поскольку пружина растянута.
Спроектировав эти силы  ,
,  и
и  на ось
на ось  , получим:
, получим:

или

Исходя из условия совместимости деформации системы имеем:

Тогда

Из уравнения (1) определяем коэффициент жесткости пружины  :
:

Для эквивалентной расчетной схемы с одной пружиной (рис. 3.4, б):

где  – коэффициент жесткости эквивалентной пружины.
– коэффициент жесткости эквивалентной пружины.
Приравняв уравнения (1) и (2) получим коэффициент жесткости эквивалентной пружины:

Круговая частота колебаний (3.4):

Ответ: 
Задачи, которые рекомендуются для самостоятельной работы: 32.11; 32.15; 32.24 [2].
Затухающие колебания материальной точки
Материальная точка, которая колеблется при реальных условиях, испытывает сопротивление движению (силы трения, сопротивление воздуха и т.п.). Это значит, что помимо восстановительной силы, которая направлена к центру колебаний, действует сила сопротивления, которая направлена всегда в сторону, противоположную направлению движения точки.
Рассмотрим колебания материальной точки (рис.3.10) под действием восстановительной силы  и силы сопротивления
и силы сопротивления  , которая пропорциональна модулю скорости точки
, которая пропорциональна модулю скорости точки  .
.

Векторное уравнение движения точки в этом случае имеет вид:

В проекции на ось  :
:

поскольку  , где
, где  – коэффициент сопротивления среды.
– коэффициент сопротивления среды.
После преобразований, уравнение (3.11) примет вид:

Если обозначить:  то
то

Уравнение (3.12) является дифференциальным уравнением движения материальной точки под действием восстанавливающей силы и силы сопротивления, пропорциональной скорости точки.
Решение уравнения (3.12) имеет разный вид в зависимости от соотношения коэффициентов  и
и  .
.
а) Случай малого сопротивления 
В этом случае решение уравнения (3.12) имеет вид:

Движение, которое соответствует уравнению (3.13), имеет колебательный характер, потому что координата  периодически меняет свой знак, что зависит от знака синуса, который входит в уравнение. Множитель
периодически меняет свой знак, что зависит от знака синуса, который входит в уравнение. Множитель  показывает на то, что амплитуда колебаний с течением времени уменьшается. Колебания такого вида называются затухающими.
показывает на то, что амплитуда колебаний с течением времени уменьшается. Колебания такого вида называются затухающими.
В уравнении (3.13):
 ,
,  – постоянные интегрирования (определяются по начальным условиям);
– постоянные интегрирования (определяются по начальным условиям);
 – коэффициент затухания;
– коэффициент затухания;
 – частота затухающих колебаний,
– частота затухающих колебаний, 
График затухающих колебаний показан на рис.3.11.
Поскольку:

то координата  затухающих колебаний размещается между двумя симметричными относительно оси абсцисс кривыми, которые соответствуют уравнению
затухающих колебаний размещается между двумя симметричными относительно оси абсцисс кривыми, которые соответствуют уравнению


Промежуток  времени, который равен
времени, который равен

называется периодом затухающих колебаний, то есть, это есть время, за которое точка совершает полное колебание.
Выражение (3.14) можно представить в виде:

где  – период свободных колебаний.
– период свободных колебаний.
Амплитудой затухающих колебаний называют наибольшее отклонение точки в ту или иную сторону от положения равновесия.
На рис.3.11 показаны амплитуда  и
и  в промежуток половины одного периода:
в промежуток половины одного периода:

Отношение следующей амплитуды к предыдущей представляет собой знаменатель геометрической прогрессии, который не изменяется во время всего колебательного процесса, и называется декрементом колебаний.

Модуль натурального логарифма декремента колебаний называется логарифмическим декрементом.

б) Предельный случай 
В этом случае уравнение движения точки имеет вид

Движение точки, которое соответствует уравнению (3.18), называется апериодическим и не является колебательным. Точка из любого положения приближается к положению  . График этого движения приведен на рисунке 3.12.
. График этого движения приведен на рисунке 3.12.

в) Случай большого сопротивления 
Решение дифференциального уравнения (3.12) в этом случае имеет вид:

где

Поскольку функции  и
и  с течением времени монотонно уменьшаются, приближаясь к нулю, то движение точки в этом случае не будет колебательным и она под действием восстанавливающей силы будет постепенно приближаться к положению равновесия. Движение также будет апериодическим.
с течением времени монотонно уменьшаются, приближаясь к нулю, то движение точки в этом случае не будет колебательным и она под действием восстанавливающей силы будет постепенно приближаться к положению равновесия. Движение также будет апериодическим.
В зависимости от начальных условий материальная точка может совершать одно из апериодических движений, графики которых показаны на рис. 3.13.

Рис. 3.13, а характеризует движение точки с начальной скоростью  , совпадающей с положительным направлением оси
, совпадающей с положительным направлением оси  . Сначала точка отдаляется от положения равновесия, а затем под действием восстановительной силы постепенно приближается к этому положению.
. Сначала точка отдаляется от положения равновесия, а затем под действием восстановительной силы постепенно приближается к этому положению.
Графики, приведенные на рис. 3.13,б и рис 3.13,в, соответствуют движению точки с начальной скоростью  , которая направлена противоположно положительному направлению оси
, которая направлена противоположно положительному направлению оси  . При достаточно большой начальной скорости точка может совершить переход через положение равновесия и после этого при обратном движении приблизиться к этому положению (рис 3.13,б).
. При достаточно большой начальной скорости точка может совершить переход через положение равновесия и после этого при обратном движении приблизиться к этому положению (рис 3.13,б).
Примеры решения задач на тему: Затухающие колебания материальной точки
Решение задач на затухающие колебания состоит из 2-х частей. В первой части основное внимание отводится ознакомлению с важнейшими понятиями и характеристиками затухающего колебательного процесса. Вторая часть занятия посвящена составлению и решению уравнений затухающих колебаний.
Задача №8
Дифференциальное уравнение движения материальной точки имеет вид 
Определить максимальное значение массы точки, при котором движение будет апериодическим.
Решение. Движение точки будет апериодическим, если выполняется условие:

где  – коэффициент сопротивления,
– коэффициент сопротивления,
 – частота свободных незатухающих колебаний.
– частота свободных незатухающих колебаний.
Заданное дифференциальное уравнение  приведем к каноническому виду, разделив на массу:
приведем к каноническому виду, разделив на массу:

Отсюда:

С учетом полученных значений  и
и  , условие (1) примет вид:
, условие (1) примет вид:

Решаем неравенство (2) относительно массы  :
:

Ответ: максимальное значение массы 
Задача №9
Дифференциальное уравнение движения материальной точки имеет вид:  , где
, где  в см .
в см .
Определить максимальное значение коэффициента жесткости  , при котором движение будет апериодическим.
, при котором движение будет апериодическим.
Решение. Движение точки будет апериодическим, если выполняется условие:

Исходное дифференциальное уравнение движения материальной точки приводим к виду:

Тогда:

Таким образом, условие (1) имеет вид:

Откуда
 и
и 
Ответ: максимальное значение коэффициента жесткости 
Задача № 10
Тело весом  , что подвешенное на пружине, которую сила
, что подвешенное на пружине, которую сила  растягивает на
растягивает на  , при движении встречает сопротивление, величина которого пропорциональна первой степени скорости. Сила сопротивления при скорости
, при движении встречает сопротивление, величина которого пропорциональна первой степени скорости. Сила сопротивления при скорости  равна
равна  . В начальный момент пружина была растянута относительно положения равновесия на
. В начальный момент пружина была растянута относительно положения равновесия на  , и тело начало двигаться без начальной скорости, то есть,
, и тело начало двигаться без начальной скорости, то есть,  .
.
Определить уравнение движения тела  .
.
Решение. Перед тем, как записать общее уравнение движения точки, необходимо выяснить, при каком сопротивлении происходит движение, то есть сравнить значения коэффициента  и круговой частоты
и круговой частоты  :
:

Из условия задачи вытекает:

Таким образом,  , то есть коэффициент сопротивления равен круговой частоте, и движение точки будет апериодическим.
, то есть коэффициент сопротивления равен круговой частоте, и движение точки будет апериодическим.
В этом случае закон движения точки определяется зависимостью (3.18):

Начальные условия: 
Подставляя их в уравнение (1), получим:

Ответ: 
Найдя по формуле (2) значение  в зависимости от времени
в зависимости от времени  (табл. 3.1), построим график
(табл. 3.1), построим график  (рис.3.14).
(рис.3.14).
Таблица 3.1
 |
0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
 |
5 | 3,68 | 2,0 | 0,99 | 0,46 | 0,2 |

Из графика видно, что при  точка не колеблется и быстро приближается к положению равновесия (
точка не колеблется и быстро приближается к положению равновесия ( ) . Выясним теперь, переходит ли груз положения статического равновесия. Для этого приравняем
) . Выясним теперь, переходит ли груз положения статического равновесия. Для этого приравняем  в уравнении (2) к нулю:
в уравнении (2) к нулю:

Моменты времени, в которые груз находится в положении статического равновесия определяются из уравнений:
 и
и 
Из первого уравнения вытекает: 
Из второго уравнения: 
Значение  соответствует угасанию движения, отрицательное значение
соответствует угасанию движения, отрицательное значение  показывает на отсутствие перехода тела через положение статического равновесия.
показывает на отсутствие перехода тела через положение статического равновесия.
Задача № 11
Грузы весом  и
и  подвешены (рис.3.15, а) в положении статического равновесия к пружине 1, коэффициент жесткости которой
подвешены (рис.3.15, а) в положении статического равновесия к пружине 1, коэффициент жесткости которой  , и масляного демпфера 2, которая влечет пропорциональную первой степени скорости силу сопротивления, равную
, и масляного демпфера 2, которая влечет пропорциональную первой степени скорости силу сопротивления, равную  , где
, где  . Груз
. Груз  вдруг сняли.
вдруг сняли.

Определить уравнение  движения груза
движения груза  после снятия груза
после снятия груза  .
.
Решение. Изобразим расчетную схему для движения груза  (рис.3.15, б).
(рис.3.15, б).
На схеме обозначено:
 – длина недеформированной пружины;
– длина недеформированной пружины;
 – деформация пружины под действием силы тяжести груза
– деформация пружины под действием силы тяжести груза  ;
;
 – деформация пружины под действием силы тяжести груза
– деформация пружины под действием силы тяжести груза  .
.
 – деформация пружины под действием сил тяжести грузов
– деформация пружины под действием сил тяжести грузов  и
и  .
.
Ось колебаний направим вниз (ось  ). Начало отсчета возьмем в точке
). Начало отсчета возьмем в точке  , в положении статического равновесия пружины под действием силы тяжести груза
, в положении статического равновесия пружины под действием силы тяжести груза  , поскольку во время движения груз
, поскольку во время движения груз  отсутствует.
отсутствует.
Исходя из принятой схемы, исходные условия будут:
исходное положение груза  :
:

начальная скорость груза  :
:

Для определения вида движения груза  необходимо сравнить значения коэффициента затухания
необходимо сравнить значения коэффициента затухания  и круговой частоты свободных колебаний
и круговой частоты свободных колебаний  .
.

где  – масса груза
– масса груза  ;
;
 – коэффициент жесткости пружины;
– коэффициент жесткости пружины;
 – коэффициент сопротивления среды.
– коэффициент сопротивления среды.
После подстановки числовых данных получим:

Итак, 
Таким образом, в задаче рассматривается случай большого сопротивления ( ) и уравнение движения груза
) и уравнение движения груза  имеет вид (3.20):
имеет вид (3.20):

где  и
и  – постоянные интегрирования, которые определяются по начальным условиям.
– постоянные интегрирования, которые определяются по начальным условиям.
Подсчитаем величину коэффициента  :
:

С учетом того, что  уравнение (1) примет вид:
уравнение (1) примет вид:

Для определения постоянных интегрирования  и
и  выразим зависимость скорости груза
выразим зависимость скорости груза  от времени:
от времени:

Подставим в уравнение (2)  а в уравнение (3)
а в уравнение (3) 
Получим:

Из уравнений (2′) и (3′) находим:

Окончательно, уравнение движения груза  имеет вид:
имеет вид:

Как и в предыдущей задаче, построим график изменения координаты  (табл. 3.2) в зависимости от времени (рис.3.16).
(табл. 3.2) в зависимости от времени (рис.3.16).
Таблица 3.2
 |
0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
 |
7,5 | 3,45 | 1,43 | 0,59 | 0,25 | 0,1 |

Ответ: 
Задача № 12
Тело весом  , которое подвешено к пружине, при отсутствии силы сопротивления колеблется с периодом
, которое подвешено к пружине, при отсутствии силы сопротивления колеблется с периодом  а если действует сила сопротивления, пропорциональная скорости, то с периодом
а если действует сила сопротивления, пропорциональная скорости, то с периодом 
Определить силу сопротивления  при скорости
при скорости  и определить уравнение движения
и определить уравнение движения  , если в начальный момент пружина была растянута из положения статического равновесия на
, если в начальный момент пружина была растянута из положения статического равновесия на 
Решение. Если скорость тела  то сила сопротивления численно будет равна коэффициенту силы сопротивления, поскольку
то сила сопротивления численно будет равна коэффициенту силы сопротивления, поскольку 
Коэффициент пропорциональности  связан с коэффициентом затухания зависимостью:
связан с коэффициентом затухания зависимостью:

Итак, для определения  необходимо найти значение коэффициента затухания
необходимо найти значение коэффициента затухания  , который можно определить из выражения:
, который можно определить из выражения:

где  – частота свободных колебаний при отсутствии сопротивления,
– частота свободных колебаний при отсутствии сопротивления,
 – частота затухающих колебаний.
– частота затухающих колебаний.
Поскольку

то
 и
и 
и

Следовательно, сила сопротивления  при скорости движения
при скорости движения  равна:
равна:

Переходим к определению закона движения тела. Составим расчетную схему (рис.3.17).

На схеме
 – длина недеформированной пружины,
– длина недеформированной пружины,
 – статическое удлинение пружины под действием силы тяжести тела,
– статическое удлинение пружины под действием силы тяжести тела,
 – переменная координата положения тела,
– переменная координата положения тела,
 – исходное положение тела.
– исходное положение тела.
Ось колебаний направляется вниз (ось  ), а начало координат (точка
), а начало координат (точка  ) выбирается в положении статического равновесия.
) выбирается в положении статического равновесия.
Поскольку  (случай малого сопротивления), то закон движения тела под действием силы тяжести
(случай малого сопротивления), то закон движения тела под действием силы тяжести  , восстанавливающей силы
, восстанавливающей силы  и силы сопротивления
и силы сопротивления  выражается уравнением:
выражается уравнением:

Учитывая, что  то:
то:

Для определения постоянных интегрирования  и
и  , кроме уравнения (2), запишем уравнение зависимости скорости от времени:
, кроме уравнения (2), запишем уравнение зависимости скорости от времени:

В уравнения (2) и (3) подставим начальные условия:
при  ,
, 

Из уравнения (3′) определяем постоянную  :
:

Из уравнения (2′) находим постоянную  :
:

С учетом полученных значений 
 , уравнение движения тела будет:
, уравнение движения тела будет:

Построим график зависимости  (рис.3.18)
(рис.3.18)
Таблица 3.3

Задача № 13
Материальная точка  совершает прямолинейные колебания под действием восстанавливающей силы, модуль которой пропорционален расстоянию от точки к некоторому неподвижному центру
совершает прямолинейные колебания под действием восстанавливающей силы, модуль которой пропорционален расстоянию от точки к некоторому неподвижному центру  , и силы сопротивления среды, модуль которой пропорционален скорости точки. В начальный момент времени смещение точки
, и силы сопротивления среды, модуль которой пропорционален скорости точки. В начальный момент времени смещение точки  и ее скорость
и ее скорость 
Определить закон движения точки, если период колебаний равен  , а декремент колебаний –
, а декремент колебаний – 
Решение. Выберем начало координат в неподвижном центре  , а ось
, а ось  направим вдоль прямолинейной траектории точки
направим вдоль прямолинейной траектории точки  . Покажем силы, действующие на материальную точку (рис.3.19):
. Покажем силы, действующие на материальную точку (рис.3.19):
 – восстановительная сила, модуль которой пропорционален отклонению точки от положения равновесия
– восстановительная сила, модуль которой пропорционален отклонению точки от положения равновесия  , где
, где  – коэффициент жесткости;
– коэффициент жесткости;
 – сила сопротивления среды, модуль которой пропорционален скорости точки
– сила сопротивления среды, модуль которой пропорционален скорости точки  , где
, где  – коэффициент сопротивления среды.
– коэффициент сопротивления среды.
Дифференциальное уравнение движения точки  массой
массой  будет иметь следующий вид:
будет иметь следующий вид:

или

Сведем записанное уравнение к виду:

или

где

Мы получили дифференциальное уравнение (3.12) затухающих колебаний.
Решение дифференциального уравнения (1) будет иметь вид:

Чтобы найти коэффициенты  и
и  воспользуемся формулами (3.14) и (3.16):
воспользуемся формулами (3.14) и (3.16):

Из первой из этих формул найдем  :
:

Из второй формулы найдем  :
:

С учетом найденных значений  и
и  уравнение (2) примет вид:
уравнение (2) примет вид:

Учитывая, что

то уравнение движения точки будет иметь вид:

Постоянные  и
и  определим из начальных условий. При
определим из начальных условий. При  начальная скорость
начальная скорость  и начальная координата
и начальная координата 
После предварительного дифференцирования уравнения (2) по времени  :
:

Поскольку при  , то:
, то:

Из уравнения (4) определим постоянную  . Поскольку
. Поскольку  , то
, то  , то есть
, то есть  .
.
Из уравнения (5) после подстановки  найдем
найдем  :
:

С учетом найденных значений  и
и  , уравнение (2) движения точки примет вид:
, уравнение (2) движения точки примет вид:

Ответ: 
Задачи, которые рекомендуются для самостоятельной работы: 32.55; 32.58; 32.59; 32.64 [2]
Вынужденные колебания материальной точки без учета сопротивления
Вынужденные колебания совершает материальная точка (рис.3.20), на которую вместе с восстановительной силой  действует возбуждающая сила
действует возбуждающая сила  , периодически изменяющаяся.
, периодически изменяющаяся.

Пусть проекция возбуждающей силы на ось, которая совпадает с направлением движения точки меняется по закону:

где  – максимальное значение возбуждающей силы;
– максимальное значение возбуждающей силы;
 – частота изменения возбуждающей силы;
– частота изменения возбуждающей силы;
 – фаза изменения возбуждающей силы;
– фаза изменения возбуждающей силы;
 – начальная фаза изменения возбуждающей силы.
– начальная фаза изменения возбуждающей силы.
Дифференциальное уравнение движения точки  в проекции на ось
в проекции на ось  имеет вид:
имеет вид:

или

Если обозначить

то получим дифференциальное уравнение вынужденных колебаний материальной точки:

Решение уравнения (3.22) в амплитудной форме, то есть, зависимость координаты  от времени
от времени  , имеет вид:
, имеет вид:

где  – амплитуда вынужденных колебаний имеет вид:
– амплитуда вынужденных колебаний имеет вид:

Из уравнения (3.22) вытекает, что движение точки представляет собой наложение двух колебательных движений.
Колебания, определяемые первым слагаемым:

имеют частоту  свободных гармонических колебаний и называются собственными колебаниями материальной точки.
свободных гармонических колебаний и называются собственными колебаниями материальной точки.
Колебания, определяемые вторым слагаемым

имеют частоту  возбуждающей силы
возбуждающей силы  и называются вынужденными колебаниями материальной точки.
и называются вынужденными колебаниями материальной точки.
Таким образом, при одновременном действии восстанавливающей и возбуждающей сил точка совершает сложное колебательное движение, которое представляет собой результат наложения свободных и вынужденных колебаний точки.
Из уравнения (3.24) вытекает, что вынужденные колебания не зависят от начальных условий.
Необходимо подчеркнуть, что частота  и период
и период  вынужденных колебаний являются также частотой и периодом возбуждающей силы.
вынужденных колебаний являются также частотой и периодом возбуждающей силы.
Вынужденные колебания, частота которых меньше частоты свободных колебаний точки, называют вынужденными колебаниями малой частоты.
Вынужденные колебания, частота которых больше частоты свободных колебаний, называют вынужденными колебаниями большой частоты.
Фаза вынужденных колебаний
Если  (случай вынужденных колебаний малой частоты), то
(случай вынужденных колебаний малой частоты), то  , и фаза вынужденных колебаний совпадает с частотой возбуждающей силы. В этом случае:
, и фаза вынужденных колебаний совпадает с частотой возбуждающей силы. В этом случае:

Если вынужденные колебания происходят с большой частотой  то
то  и для того, чтобы амплитуда колебаний была положительной, ее записывают в виде:
и для того, чтобы амплитуда колебаний была положительной, ее записывают в виде:

При этом, фаза вынужденных колебаний большой частоты равна  и отличается от фазы возбуждающей силы
и отличается от фазы возбуждающей силы  на величину
на величину  , то есть фазы возбуждающей силы и вынужденных колебаний противоположны.
, то есть фазы возбуждающей силы и вынужденных колебаний противоположны.
В случае вынужденных колебаний малой частоты точка  всегда отклонена от начала координат
всегда отклонена от начала координат  в ту сторону, в которую направлена в данный момент возбуждающая сила
в ту сторону, в которую направлена в данный момент возбуждающая сила  .
.
В случае вынужденных колебаний большой частоты отклонение точки  от начала координат
от начала координат  всегда противоположное направлению возбуждающая сила
всегда противоположное направлению возбуждающая сила  . При этом в обоих случаях максимальное отклонение точки от начала координат происходит в тот момент времени, когда модуль возбуждающей силы достигает максимума.
. При этом в обоих случаях максимальное отклонение точки от начала координат происходит в тот момент времени, когда модуль возбуждающей силы достигает максимума.
Амплитуда вынужденных колебаний
Статическим отклонением точки называется величина  (рис.3.21), которая определяется из условия:
(рис.3.21), которая определяется из условия:

Отсюда

где  – максимальное значение возбуждающей силы.
– максимальное значение возбуждающей силы.

Отношение амплитуды вынужденных колебаний  к статическому отклонению
к статическому отклонению  называется коэффициентом динамичности.
называется коэффициентом динамичности.
При 

При 

График изменения коэффициента динамичности в зависимости от изменения частоты возбуждающей силы (рис.3.22) имеет разрыв при значении  В этом случае коэффициент динамичности
В этом случае коэффициент динамичности  увеличивается к бесконечности и наступает так называемое явление резонанса.
увеличивается к бесконечности и наступает так называемое явление резонанса.
Явление резонанса
Явление резонанса возникает когда частоты вынужденных и свободных колебаний точки совпадают, то есть:

При этом амплитуда  вынужденных колебаний точки равна бесконечности и большинство уравнений вынужденных колебаний, полученных при условии
вынужденных колебаний точки равна бесконечности и большинство уравнений вынужденных колебаний, полученных при условии  , теряют смысл.
, теряют смысл.
Дифференциальное уравнение движения при  , примет вид:
, примет вид:

Уравнение (3.28) отличается от уравнения (3.22) тем, что в правой части стоит частота  , которая равна частоте собственных колебаний точки.
, которая равна частоте собственных колебаний точки.

Решение дифференциального уравнения (3.28) имеет вид:

При резонансе частота и период вынужденных колебаний равны, соответственно, частоте  и периоду
и периоду  свободных колебаний точки, а фаза вынужденных колебаний
свободных колебаний точки, а фаза вынужденных колебаний  отстает от фазы возбуждающей силы
отстает от фазы возбуждающей силы  на величину
на величину 
Графиком отклонений для вынужденных колебаний во время резонанса является периодическая кривая, напоминающая синусоиду (рис.3.23), что вписывается в область, ограниченную прямыми  и
и  поскольку
поскольку  не больше единицы. При
не больше единицы. При  точки графика лежат на этих прямых.
точки графика лежат на этих прямых.
Из графика видно, что амплитуды колебаний увеличиваются со временем.

Примеры решения задач на тему: Вынужденные колебания точки
Задачи на вынужденные колебания точки рекомендуется решать в следующей последовательности:
1. Выбрать систему координат, взяв за начало положение статического равновесия точки;
2. Записать начальные условия движения точки;
3. Изобразить на рисунке силы, приложенные к точке;
4. Составить дифференциальное уравнение движения в проекции на соответствующую ось;
5. Проинтегрировать дифференциальное уравнение движения, использовав начальные условия для определения постоянных интегрирования, определить искомые величины.
При решении задачи материальную точку рекомендуется изображать в промежуточном положении, где ее координата на оси будет положительной.
Если составленное дифференциальное уравнение движения точки тождественно с одним из выше записанных уравнений, то не интегрируя это уравнение, можно сразу получить решение по приведенным формулам.
Задача № 14
На тело, которое подвешено к пружине, действует вертикальная возбуждающая сила 
Определить коэффициент динамичности, если круговая частота свободных колебаний тела 
Решение. Сравнивая заданное в условиях значение для возбуждающей силы с выражением (3.21):

получим, что частота ее изменения 
Поскольку  , то в данной задаче имеем вынужденные колебания малой частоты.
, то в данной задаче имеем вынужденные колебания малой частоты.
Коэффициент динамичности  в этом случае соответственно с (3.26) равен:
в этом случае соответственно с (3.26) равен:

Ответ: 
Задача № 15
Дифференциальное уравнение колебательного движения материальной точки имеет вид: 
Определить коэффициент динамичности  .
.
Решение. Сравнивая заданное в условиях задачи уравнение колебательного движения с (3.22):

получим:

Поскольку  , то имеем вынужденные колебания малой частоты и коэффициент динамичности
, то имеем вынужденные колебания малой частоты и коэффициент динамичности  равен:
равен:

Ответ: 
Задача № 16
Статическое удлинение пружины 
Определить коэффициент динамичности, если на груз действует вертикальная возбуждающая сила 
Решение. Сравнивая заданное в условиях задачи выражение для возбуждающей силы с (3.21):

получим: 
Для определения коэффициента динамичности  необходимо найти частоту собственных колебаний
необходимо найти частоту собственных колебаний  .
.
Учитывая, что

а статическое удлинение пружины

то
 или
или 
Поскольку  то из (3.26) получим:
то из (3.26) получим:

Ответ: 
Задача №17
Материальная точка  массой
массой  совершает прямолинейные колебания вдоль оси
совершает прямолинейные колебания вдоль оси  (рис.3.24) под действием возбуждающей силы
(рис.3.24) под действием возбуждающей силы  и восстановительной силы
и восстановительной силы  , модуль которой пропорционален расстоянию точки от начала координат (коэффициент пропорциональности равен
, модуль которой пропорционален расстоянию точки от начала координат (коэффициент пропорциональности равен  ).
).

Определить закон движения точки, если в начальный момент  и
и 
Решение. Дифференциальное уравнение движения материальной точки  в данном случае имеет вид:
в данном случае имеет вид:

или

Уравнение (1) является дифференциальным уравнением вынужденных колебаний (3.22), в котором:  (то есть
(то есть  );
);  и
и 
Поскольку  , то общее решение уравнения (1) находим из формулы (3.23):
, то общее решение уравнения (1) находим из формулы (3.23):

В нашем случае это уравнение будет иметь вид:

или

Учитывая, что  , то
, то 
Окончательно,

Перейдем к нахождению постоянных  и α. Для этого продифференцируем уравнение (2) по времени
и α. Для этого продифференцируем уравнение (2) по времени  :
:

Подставим в уравнение (2) и (3) начальные условия: при 
Тогда

или

Из второго уравнения находим постоянную  . Поскольку
. Поскольку  , то нулю равен
, то нулю равен  , то есть
, то есть 
Из первого уравнения находим постоянную  :
:

Таким образом, искомый закон движения точки  будет иметь вид:
будет иметь вид:

Ответ: 
Задача № 18
Точка  массой
массой  движется прямолинейно и притягивается к неподвижному центру
движется прямолинейно и притягивается к неподвижному центру  силой, которая пропорциональна расстоянию точки к этому центру, причем коэффициент пропорциональности равен
силой, которая пропорциональна расстоянию точки к этому центру, причем коэффициент пропорциональности равен  Кроме того, на точку действует возбуждающая сила
Кроме того, на точку действует возбуждающая сила  , которая выражена в Ньютонах (рис.3.24).
, которая выражена в Ньютонах (рис.3.24).
Определить закон движения точки  , если в начальный момент
, если в начальный момент  и
и 
Решение. Составим дифференциальное уравнение движения материальной точки  , выбрав при этом начало координат в центре
, выбрав при этом начало координат в центре  и направив ось
и направив ось  (рис.3.24) вдоль траектории точки:
(рис.3.24) вдоль траектории точки:

Получим дифференциальное уравнение в виде (3.22), в котором:

Поскольку частота свободных колебаний  и частота вынужденных колебаний
и частота вынужденных колебаний  совпадают, то имеет место явление резонанса. Закон движения точки
совпадают, то имеет место явление резонанса. Закон движения точки  определим из формулы (3.29):
определим из формулы (3.29):

В нашем случае эта формула приобретет вид:

Постоянные  и
и  найдем из начальных условий. Продифференцировав уравнение (2) по времени
найдем из начальных условий. Продифференцировав уравнение (2) по времени  , получим:
, получим:

Подставим в уравнение (2) и (3) начальные условия: при 
Тогда:

или

Из первого уравнения находим постоянную  . Поскольку
. Поскольку  , то нулю равно
, то нулю равно  , то есть
, то есть 
Из второго уравнения находим постоянную  :
:

Таким образом, закон движения точки  будет иметь вид:
будет иметь вид:

Ответ: 
Задача № 19
К вертикальной пружине, верхний конец которой закреплен, подвешен груз весом  , который придает статическое удлинение пружине
, который придает статическое удлинение пружине  . На груз действует вертикальная возбуждающая сила
. На груз действует вертикальная возбуждающая сила  При
При  пружина была растянута на
пружина была растянута на  и грузу предоставлена вниз скорость
и грузу предоставлена вниз скорость 
Определить закон движения груза 
Решение. Изобразим схему движения груза (рис.3.25).

Вертикаль, по которой движется груз, принимаем за ось  , положительным выбираем направление вниз. Начало координат совпадает с положением статического равновесия груза (точка
, положительным выбираем направление вниз. Начало координат совпадает с положением статического равновесия груза (точка  ). В начальный момент времени тело находилось в точке
). В начальный момент времени тело находилось в точке  , то есть на расстоянии
, то есть на расстоянии  от конца недеформированной пружины.
от конца недеформированной пружины.
Начальные условия для точки  (при
(при  ) будут иметь следующий вид:
) будут иметь следующий вид:

Для определения закона движения груза необходимо сравнить значения частоты собственных колебаний  и частоты возбуждающей силы
и частоты возбуждающей силы  .
.
Из уравнения возбуждающего силы  вытекает, что
вытекает, что 
Вычислим значение частоты собственных колебаний  , исходя из того, что
, исходя из того, что

Поскольку  а
а  то
то 
Тогда

Следовательно,  , то есть имеет место резонанс, и уравнение движения тела записывается в виде:
, то есть имеет место резонанс, и уравнение движения тела записывается в виде:

где

Следовательно,

или

Для определения постоянных интегрирования  и
и  необходимо иметь два уравнения. Одно уравнение получено – это зависимость (2) координаты точки
необходимо иметь два уравнения. Одно уравнение получено – это зависимость (2) координаты точки  от времени
от времени  .
.
Второе уравнение получим, продифференцировав уравнение (2) по времени:

или

Подставим в уравнение (2) и (3) начальные условия: при 

После упрощений:

Решая эти уравнения, находим:

Таким образом, закон движения груза имеет вид:

Построим график  (рис.3.26) по уравнению (4) в соответствии с координатами
(рис.3.26) по уравнению (4) в соответствии с координатами  и
и  , которые приводятся в таблице.
, которые приводятся в таблице.

Ответ: 
Задача № 20
Определить, какова должна быть величина статического прогиба рессор железнодорожного вагона, чтобы при скорости  к
к  вагон не попал в резонанс с толчками на стыках колеи, расстояние между которыми
вагон не попал в резонанс с толчками на стыках колеи, расстояние между которыми 
Решение. Резонанс наступает тогда, когда период свободных колебаний вагона совпадает с периодом возбуждающего силы, которой будут толчки на стыках рельсов.

Период собственных колебаний вагона равен

Найдем круговую частоту свободных колебаний:

Следовательно, период собственных колебаний равен:

где 
Вычислим период  возбуждающей силы, который равен времени прохождения вагоном длины рейки
возбуждающей силы, который равен времени прохождения вагоном длины рейки  :
:

Определим  , при котором будет явление резонанса, то есть когда
, при котором будет явление резонанса, то есть когда  :
:
 или
или 
Откуда

Таким образом, для избежания резонанса вагона необходимо, чтобы выполнялась неровность:

Ответ: 
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
| Период | |
|---|---|
 |
|
| Размерность | T |
| Единицы измерения | |
| СИ | с |

Пери́од колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором она находилась в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное обозначение периода колебаний: 


Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.
Период колебаний связан соотношением взаимной обратности с частотой:
Для волновых процессов период связан кроме того очевидным образом с длиной волны 
где 
В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота[3] колебаний его волновой функции).
Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).
Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).
Периоды колебаний в природе[править | править код]
Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).
Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот электромагнитных колебаний (см. Электромагнитный спектр) .
Периоды колебаний слышимого человеком звука находятся в диапазоне
- от 5·10−5с до 0,2с
(четкие границы его несколько условны).
Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне
- от 1,1·10−15с до 2,3·10−15с.
Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц.
В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.
Периоды колебаний простейших физических систем[править | править код]
Пружинный маятник[править | править код]
Период колебаний пружинного маятника может быть вычислен по следующей формуле:

где 

Математический маятник[править | править код]
Период малых колебаний математического маятника:

где 

Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью[5] равен 2 секундам.
Физический маятник[править | править код]
Период малых колебаний физического маятника:

где 


Крутильный маятник[править | править код]
Период колебаний крутильного маятника:

где 

Электрический колебательный (LC) контур[править | править код]
Период колебаний электрического колебательного контура (формула Томсона):

где 

Эту формулу вывел в 1853 году английский физик Уильям Томсон.
Примечания[править | править код]
- ↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
- ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
- ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
- ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
- ↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.
Ссылки[править | править код]
- [bse.sci-lib.com/article088257.html Период колебаний] — статья из Большой советской энциклопедии
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|
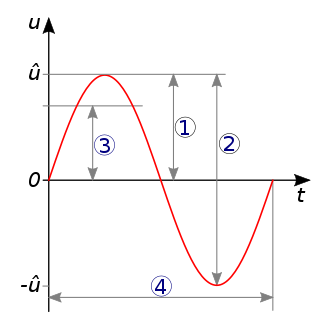
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Что такое колебательный процесс
Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.
Систему, совершающую колебания, называют колебательной системой или осциллятором.
Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.
Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.
При механических колебаниях, которые относят к категории вынужденных:
(F=F_{0}cos cot)
Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.
Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.
Определение периода колебаний, формула
Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:
(x(t)=Atimes cos left(omega _{0}t+phi _{0} right))
Где (x(t)) является отклонением колеблющейся физической величины от равновесного значения;
А представляет собой амплитуду гармонических колебаний;
(omega _{0}) равно циклической или круговой частоте колебаний;
(phi _{0}) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;
(cp(t)=(co_{0}t+cp_{0})) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.
В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
(cos left(alpha +2pi right)=cos alpha,)
то х остается без изменений при фазе колебаний, получающей приращение в $$2pi$$
Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.
В этом случае фаза будет увеличена на (2pi:)
(omega _{0}(t+T)+phi _{0}=left(omega _{0}t+phi _{0} right)+2pi)
Из данного равенства можно вычислить период колебаний:
(T=frac{2pi }{omega _{0}})
Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:
(v=frac{omega _{0}}{2pi})
На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.
Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.
Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:
Смещение (x=Atimes cos left(omega _{0}t+phi _{0} right))
Скорость (v_{x}=dot{x}=-Aomega _{0}times sin left(omega _{0} t+phi_{0} right)=Aomega _{0}times cos left(omega _{0} t+phi_{0} +frac{pi }{2}right))
Ускорение
(a_{x}=dot{v_{x}}=ddot{x}=-Aomega _{0}times cos left(omega _{0} t+phi_{0} right)=Aomega _{0}^{2}times cos left(omega _{0} t+phi_{0} +pi right))
Как найти период для физического маятника
В случае, когда углы отклонения (varphi) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:
(F=mgtimes sin varphi)
Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла (alpha)
Учитывая малый угол (varphi) уравнение можно записать в следующем виде:
(F=mgtimesvarphi)
С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:
(J=ml^{2})
При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:
(frac{d^{2}varphi }{dt^{2}}+frac{mgl}{J}varphi =0)
В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:
(alpha _{x}(t)+omega ^{2}x(t)=0)
Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:
(omega =sqrt{frac{mgl}{J}})
В таком случае для расчета периода колебаний математического маятника будет использоваться формула:
(T =frac{2pi }{omega }=2pi sqrt{frac{J}{mgl}})
Исходя из расчетов, можно сделать следующие выводы:
- Период пружинного маятника (T =2pi sqrt{frac{m}{k}})
- Период математического маятника (T =2pi sqrt{frac{L}{g}})
- Период крутильного маятника (T =2pi sqrt{frac{I}{K}})
В приведенных формулах:
- T — период физического маятника;
- J — момент силы маятника относительно оси вращения;
- l — расстояние от оси вращения до центра масс;
- m — масса маятника;
- g=9.8 — ускорение свободного падения.
Примеры решений
Задача № 1
Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.
Решение
(T =frac{t}{N}=frac{120}{60}=2)
(V=frac{1}{T}=frac{1}{2}=0.5)
Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.
Задача № 2
Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.
Решение
А = 20
Т = 0,8
(V=frac{1}{T}=frac{1}{0,8}=1,25)
(x(t)=Asin 2pi Vt=0.2sin 2pi times 1.25t=0.2sin 2.5pi t)
Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: (x(t)=0.2sin 2.5pi t)
Задача № 3
Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.
Решение
Период колебаний математического маятника рассчитывается по формуле:
(T =2pi sqrt{frac{L}{g}})
Согласно определению:
(V=frac{1}{T})
Тогда:
(T=frac{1}{V})
Получим равенство:
(frac{1}{V}=2pi sqrt{frac{l}{g}})
Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:
(frac{1}{V^{2}}=4pi ^{2}times frac{l}{g}Rightarrow l=frac{g}{4pi ^{2}V^{2}})
(l=frac{1.5}{4*3.14 ^{2}*0.5^{2}}approx 0.16)
Ответ: длина математического маятника примерно составляет 0,16 метра.
Период и частота колебаний, теория и онлайн калькуляторы
Период и частота колебаний
Период колебаний
Определение
Период – это отрезок времени, которое необходимо для совершения одного цикла периодического процесса.
Периодом ($T$) колебаний называют время, за которое совершается одно полное колебание.
За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:
[T=frac{2pi }{{omega }_0}left(1right).]
Разные периодические процессы, (процессы, повторяющиеся через равные промежутки времени) можно представить в виде совокупности наложенных гармонических колебаний.
Гармонические колебания некоторого параметра $xi $ описываются уравнением:
[xi =A{cos ({omega }_0t+varphi ) } left(2right),]
где $A={xi }_{max}$ – амплитуда колебаний; ${omega }_0$ – циклическая (круговая) частота колебаний; $varphi $ – начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ –
фаза колебаний. Величина $xi $ лежит в пределах $-Ale sle $+A.
Формулы для вычисления периода простейших колебательных систем
Период колебаний пружинного маятника определим как:
[T=2pi sqrt{frac{m}{k}} left(3right),]
на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$.
Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)
[T=2pi sqrt{frac{l}{g}}left(4right).]
Формула для вычисления периода колебаний физического маятника представляет собой выражение:
[T=2pi sqrt{frac{J}{mga}left(5right),}]
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние от центра масс тела до оси вращения.
Единицами измерения периода служат единицы времени, например секунды.
[left[Tright]=c.]
Частота колебаний
Определение
Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $).
Частота – это количество полных колебаний, которые колебательная система совершает за единицу времени.
[nu =frac{1}{T}left(6right).]
Частота колебаний связана с циклической частотой как:
[{omega }_0=2pi nu left(7right).]
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
[left[nu right]=с^{-1}=Гц.]
Примеры задач с решением
Пример 1
Задание. Каковы период ($T$) и частота ($nu $) колебаний, которые происходят в соответствии с уравнением: $x=A{sin ({omega }_0(t+tau )) }$, где ${omega }_0=2,5 pi (frac{рад}{с})$; $tau =0,4 $с?
Решение. Из уравнения колебаний:
[x=A{sin left({omega }_0left(t+tau right)right)left(1.1right), }]
заключаем, что это гармонические колебания, так как они происходят по закону синуса следовательно, они являются периодическими. Период найдем, зная циклическую частоту колебаний:
[T=frac{2pi }{{omega }_0}left(1.1right).]
Подставляя имеющиеся данные, вычислим период колебаний:
[T=frac{2pi }{2,5pi }=0,8 left(сright).]
Частоту колебаний найдем как величину, обратную периоду:
[nu =frac{1}{T}left(1.2right).]
Вычислим частоту:
[nu =frac{1}{0,8}=1,25 left(Гцright).]
Ответ. $T=0,8$ с; $nu =1,25 Гц$
Пример 2
Задание. Какими будут период и частота малых колебаний тонкого обруча, который висит на гвозде (точка А), вбитом горизонтально в стену (рис.1)? Колебания совершаются в плоскости параллельной стене. Радиус обруча R.
Решение. В этой задаче мы имеем дело с физическим маятником период которого, найдем, используя формулу:
[T=2pi sqrt{frac{J}{mga}left(2.1right).}]
Осью вращения обруча является гвоздь, находящийся в точке А. Цент масс обруча находится в его геометрическом центре, точке О, следовательно, расстояние от центра масс до оси вращения обруча (рис.1) равно:
[a=R left(2.2right).]
Найдем момент инерции обруча относительно оси, перпендикулярной плоскости обруча, проходящей через точку $A$. Для этого воспользуемся теоремой Штейнера:
[J=J_0+mR^2 left(2.3right),]
где $J_0=mR^2$ – момент инерции обруча, относительно оси, проходящей через его центр (т.О), перпендикулярно плоскости обруча; расстояние между осями равно радиусу обруча. Получаем, момент инерции обруча относительно гвоздя равен:
[J=mR^2+mR^2=2mR^2left(2.4right).]
Используя формулы (2.1) (2.2) и (2.4), имеем:
[T=2pi sqrt{frac{2mR^2}{mgR}}=2pi sqrt{frac{2R}{g}}.]
Отталкиваясь от полученного результата, найдем частоту колебаний как:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{g}{2R}}.]
Ответ. $T=2pi sqrt{frac{2R}{g}},$ $nu =frac{1}{2pi }sqrt{frac{g}{2R}}$
Читать дальше: полная энергия колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!


