В первой части нашей работы мы должны будем с вами с
помощью экспериментальной установки исследовать зависимость периода свободных
колебаний нитяного маятника от его длины.
Для выполнения этой работы нам предлагается использовать
оборудование из комплекта № 5 в составе: штатив с муфтой и креплением для нити,
груз с крючком, нить, электронный секундомер и метровую линейку или мерную
ленту.
Прежде чем приступить к работе давайте с вами вспомним, что маятником
называется твёрдое тело, совершающее под действием приложенных сил
колебания около неподвижной точки или вокруг оси.
Существует несколько видов маятников. Но наиболее часто
встречающиеся, это пружинный маятник, представляющий собой груз,
прикреплённый к пружине, и способный совершать колебания вдоль горизонтальной
или вертикальной оси.
И нитяной маятник — шарик, подвешенный на нити,
способный совершать колебательное движение.
Теперь давайте вспомним, что любое колебательное движение
характеризуется амплитудой, частотой и периодом колебаний.
Амплитуда колебаний — это наибольшее смещение
колеблющегося тела от положения равновесия.
Частота
колебаний — это
число колебаний, совершаемых телом за единицу времени. Обозначается она
греческой буквой ν. А единицей её измерения в системе СИ является герц
[Гц]:
И, наконец, период
колебаний — это наименьший промежуток времени, через который полностью
повторяется состояние колебательной системы. Обозначается период большой буквой
Т. Единица измерения — секунда [с]:
Ещё в
середине XVII века нидерландский учёный Христиан Гюйгенс показал, что «период малых
колебаний математического маятника зависит от длины подвеса и ничего более»:
И в первой
части нашей работы мы с вами должны будем проверить, как зависит период
колебаний маятника от его длины.
Итак, для
начала давайте соберём экспериментальную установку. Для этого закрепим
перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе
так, чтобы конец перекладины выступал за край поверхности стола. Далее подвесим
к перекладине с помощью нити груз из набора. И сразу же установим длину нити в
1 м. Электронный секундомер переведём в ручной режим работы.
Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.
Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний равен отношению промежутка времени,
в течение которого тело совершило N полных колебаний, к числу этих
колебаний:
Так как нам необходимо будет провести несколько измерений, то
давайте с вами составим таблицу. В первой колонке мы укажем номера опытов. Во
второй колонке мы запишем значения длины маятника, которые нам даны в условии
задания. Число колебаний маятника мы запишем в третью колонку (во всех опытах
оно будет одинаковым и равно 30). Четвёртую колонку мы отведём для записи
времени совершения заданного числа колебаний. А в последнюю колонку будем
записывать значения периода колебаний маятника.
Теперь приступим непосредственно к работе. Итак, отклоняем
нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем
отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы
процесс колебаний стал установившимся. В момент прохождения маятником крайнего
положения запускаем секундомер. Теперь нам остаётся только дождаться, пока
маятник не совершит 30 полных колебаний. По окончании последнего колебаний
останавливаем секундомер.
Значение промежутка времени, за которое маятник совершил
заданное число колебаний, записываем в таблицу с учётом погрешности измерения:
Теперь уменьшим длину нити маятника в два раза и повторим
эксперимент. По окончании тридцатого колебания останавливаем секундомер и
записываем значение промежутка времени в таблицу.
Наконец уменьшаем длину маятника до 25 см и, включив секундомер,
вновь отсчитываем 30 полных колебаний. Не забываем записать в таблицу значение
промежутка времени с учётом погрешности измерения:
Прямые измерения мы с вами завершили. Теперь определяем
период колебаний. Для этого подставляем в расчётную формулу значения
промежутков времени и числа полных колебаний для каждого из трёх случаев:
Теперь хорошо видно, что чем меньше длина нити маятника, тем
меньше его период колебаний. Поэтому в выводе напишем: при уменьшении
длины нити период свободных колебаний нитяного маятника уменьшается.
Во второй части работы мы с вами должны будем
проверить, зависит ли период колебаний нитяного маятника от массы груза.
Оборудование мы будем использовать практически то же самое:
штатив с муфтой и креплением для нити, набор грузов с крючками, нить,
электронный секундомер и метровую линейку или мерную ленту.
Итак, для
начала давайте соберём экспериментальную установку. Для этого закрепим
перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе
так, чтобы конец перекладины выступал за край поверхности стола. Далее подвесим
к перекладине с помощью нити один груз из набора. Длина маятника по условию
задания у нас должна быть равна 1 м. Электронный секундомер переведём в ручной
режим работы.
Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.
Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний равен отношению промежутка времени,
в течение которого тело совершило N полных колебаний, к числу этих
колебаний:
Так как нам необходимо будет провести несколько измерений, то
давайте с вами составим таблицу. В первой колонке мы укажем номера опытов. Во
второй колонке мы запишем значения массы маятника, которые нам даны в условии
задания. Число колебаний маятника мы запишем в третью колонку (во всех опытах
оно будет одинаковым и равно 30). Четвёртую колонку мы отведём для записи
времени совершения заданного числа колебаний. А в последнюю колонку будем
записывать значения периода колебаний маятника.
Теперь приступим непосредственно к работе. Итак, отклоняем
нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем
отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы
процесс колебаний стал установившимся. В момент прохождения маятником крайнего
положения запускаем секундомер. Теперь нам остаётся только дождаться, пока
маятник не совершит 30 полных колебаний. По окончании последнего колебаний
останавливаем секундомер. Значение промежутка времени, за которое маятник
совершил 30 колебаний, записываем в таблицу с учётом погрешности измерения:
Теперь подвесим к маятнику второй груз и повторим
эксперимент. По окончании тридцатого колебания останавливаем секундомер и
записываем значение промежутка времени в таблицу.
Наконец, увеличиваем массу маятника до 300 г и, включив секундомер,
вновь отсчитываем 30 полных колебаний. Не забываем записать в таблицу значение
промежутка времени с учётом погрешности измерения:
Прямые измерения мы с вами завершили. Теперь определяем
период колебаний. Для этого подставляем в расчётную формулу значения
промежутков времени и числа полных колебаний для каждого из трёх случаев:
Таким образом видим, что в пределах погрешности измерений
период колебаний маятника остаётся неизменным. Поэтому в выводе мы
напишем: период колебаний нитяного маятника не зависит от массы груза.
Что касается исследования зависимости частоты колебаний
маятника от его длины, то вся работа остаётся примерно такой же,
что и в нашей первой работе, где мы определяли период колебаний. Отличие будет
состоять только в расчётной формуле. Ведь частота определяет число колебаний,
совершаемых телом за единицу времени:
То же самое
касается и исследования зависимости
частоты колебаний нитяного маятника от массы груза. Ведь в любом
случае, частота — это величина, обратная периоду колебаний.
По данным таблицы, относящимся к колебаниям математического маятника, составьте и решите задачи.
| № п/п | t,с | N | T, с | ν, Гц |
|---|---|---|---|---|
| 1 | 25 | 50 | ? | ? |
| 2 | 15 | ? | ? | 100 |
| 3 | ? | 10 | 2 | ? |
| 4 | ? | 200 | ? | 50 |
| 5 | 200 | ? | 2 | ? |
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Механические колебания. Номер №1799
Решение 1
Груз, колеблющийся на пружине, за 25 с совершил 50 колебаний. Найдите период и частоту колебаний.
Дано:
t = 25 c;
N = 50 колебаний.
Найти:
T − ?
ν − ?
Решение:
T
=
t
N
;
T
=
25
50
=
0
,
5
с;
ν
=
N
t
;
ν
=
50
25
=
2
Гц.
Ответ: 0,5 с; 2 Гц.
Решение 2
Математический маятник колеблется с частотой 100 Гц. Найдите период колебаний и число колебаний за 15 с.
Дано:
t = 15 c;
ν = 100 Гц.
Найти:
T − ?
N − ?
Решение:
Найдем период колебания маятника:
T
=
1
ν
;
T
=
1
100
=
0
,
01
с;
Найдем число колебаний:
T
=
t
N
;
N
=
t
T
;
N
=
15
0
,
01
=
1500
колебаний.
Ответ: 0,01 с; 1500 колебаний.
Решение 3
Период колебания маятника 2 с. За какое время он совершит 10 колебаний? Определите частоту колебаний маятника.
Дано:
T = 2 c;
N = 10 колебаний.
Найти:
t − ?
ν − ?
Решение:
Найдем время колебания маятника:
T
=
t
N
;
t = TN;
t = 2 * 10 = 20 c;
Найдем частоту колебаний:
ν
=
1
T
;
ν
=
1
2
=
0
,
5
Гц.
Ответ: 20 с; 0,5 Гц.
Решение 4
Груз, колеблющийся на пружине, совершил 200 колебаний. Частота колебаний груза 50 Гц. Найдите период и время колебания груза.
Дано:
N = 200 колебаний;
ν = 50 Гц.
Найти:
t − ?
T − ?
Решение:
Найдем период колебания маятника:
T
=
1
ν
;
T
=
1
50
=
0
,
02
с;
Найдем время колебания маятника:
T
=
t
N
;
t = TN;
t = 0,02 * 200 = 4 c.
Ответ: 0,02 с; 4 с.
Решение 5
Период колебания маятника 2 с. Найдите частоту колебаний и число колебаний за 200 с.
Дано:
t = 200 c;
T = 2 c.
Найти:
N − ?
ν − ?
Решение:
Найдем частоту колебаний:
ν
=
1
T
;
ν
=
1
2
=
0
,
5
Гц.
Найдем число колебаний:
T
=
t
N
;
N
=
t
T
;
N
=
200
2
=
100
колебаний.
Ответ: 0,5 Гц; 100 колебаний.
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Период колебания пружинного маятника, теория и онлайн калькуляторы
Период колебания пружинного маятника
Рассмотрим простейшую систему, в которой возможна реализация механических колебаний. Допустим, что на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$. Груз движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. Массу пружины считаем малой в сравнении с массой груза.
Уравнение движения груза при таких колебаниях имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${omega }^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=B{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ и $B$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
Частота и период колебаний пружинного маятника
Косинус (синус) – периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют
периодом колебаний. Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):
[T=frac{1}{nu }left(3right).]
Период связан с циклической частотой колебаний как:
[T=frac{2pi }{{omega }_0}left(4right).]
Зная, что для пружинного маятника ${omega }_0=sqrt{frac{k}{m}}$, период колебаний его определим как:
[T=2pi sqrt{frac{m}{k}} left(5right).]
Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:
[left[Tright]=с.]
Примеры задач на период колебания пружинного маятника
Пример 1
Задание. К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?
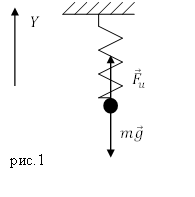
Решение. Сделаем рисунок.
Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:
[moverline{g}+{overline{F}}_u=0 left(1.1right).]
Запишем проекцию уравнения (1.1) на ось Y:
[mg=F_uleft(1.2right).]
Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:
[F_u=kDelta x left(1.3right).]
Используя выражения (1.2) и (1.3) найдем отношение $frac{m}{k}$:
[mg=kDelta xto frac{m}{k}=frac{Delta x }{g}left(1.4right).]
Период колебаний пружинного маятника при малых колебаниях можно найти, используя выражение:
[T=2pi sqrt{frac{m}{k}} left(1.5right).]
Заменяя отношение массы груза к жесткости пружины на правую часть выражения (1.4), получим:
[T=2pi sqrt{frac{Delta x }{g}.}]
Вычислим период колебаний нашего маятника, если $g=9,8 frac{м}{с^2}$:
[T=2pi sqrt{frac{0,09 }{9,8} approx 0,6 (с)}]
Ответ. $T$=0,6 с
Пример 2
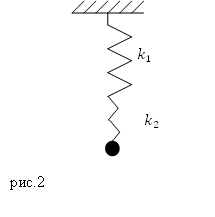
Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.
Решение.Период колебаний пружинного маятника равен:
[T=2pi sqrt{frac{m}{k}} left(2.1right).]
Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}to k=frac{k_1k_2}{k_1{+k}_2}left(2.2right).]
Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
[T=2pi sqrt{frac{m(k_1{+k}_2)}{k_1k_2}}.]
Ответ. $T=2pi sqrt{frac{m(k_1{+k}_2)}{k_1k_2}}$
Читать дальше: плечо силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!