Для школьников.
Любое тело подвешенное так, что его центр масс находится ниже точки подвеса, называют физическим маятником.
Маятник находится в состоянии устойчивого равновесия, если его центр масс расположен на вертикали под точкой подвеса.
Если маятник вывести из состояния равновесия, отклонив его на некоторый угол и предоставив самому себе, то он начнёт колебаться около положения равновесия.
Чтобы описать колебание маятника, надо знать уравнение его движения, то есть зависимость координаты от времени, и период его колебаний.
Но найти период колебаний физического маятника сложно, так как он зависит от многих причин – от формы и размера маятника, от распределения массы тела, расстояния от точки подвеса до центра масс тела.
Много проще описать поведение математического маятника. Для этого физический маятник заменяют математическим маятником такой длины, чтобы частоты колебаний этих маятников были одинаковы.
Длина математического маятника, частота колебаний которого равна частоте колебаний данного физического маятника, называется приведённой длиной физического маятника.
Под математическим маятником понимается тело малого размера, подвешенного на длинной нерастяжимой нити. Нить считаем невесомой, а тело можно принять за материальную точку.
Наблюдения за колебаниями маятников, подобных математическому, позволили установить следующие законы:
1) Период колебаний математического маятника не зависит от массы тела;
2) Период колебаний математического маятника не зависит от амплитуды колебаний (при малых амплитудах).
Впервые второй закон был установлен Галилеем в 1655 году, при наблюдении им в соборе качания паникадила на длинной цепи, которое толкнули при зажигании. Его колебания постепенно затухали, но период колебаний оставался прежним. Для измерения периода колебаний Галилей пользовался своим пульсом.
Посмотрим теперь, как получили формулу, по которой можно найти период колебаний математического маятника.
На рис а) показан математический маятник, отклонённый от положения равновесия (от точки А) на малый угол (в точку В).
Буквой Р обозначена сила тяжести груза, а буквой Р (с индексом 1) обозначена переменная возвращающая сила, действующая на груз.
Так как возвращающая сила меняется в процессе колебания, то рассчитать движение колеблющегося тела сложно.
Для упрощения расчётов заставляют маятник колебаться не в одной плоскости, как показано на рис.а), а описывать конус (рис. б), чтобы грузик двигался по окружности.
Движение маятника по конусу может рассматриваться как сложение двух независимых колебаний (в плоскости рисунка и в перпендикулярной рисунку плоскости).
Период этих колебаний одинаков. Тогда период обращения маятника можно выразить через отношение длины окружности к скорости движения
При малом угле отклонения маятника (малой амплитуде) можно считать, что возвращающая сила направлена к центру окружности (является центростремительной, равной произведению массы тела на центростремительное или нормальное ускорение), то есть
С другой стороны, из подобия треугольников ОВС и ДВЕ можно записать, что
Приравняв правые части последних выражений, получим уравнение для скорости обращения груза
Подставив скорость в выражение периода, получим искомую формулу для нахождения периода гармонических колебаний математического маятника
Таким образом, период колебаний математического маятника зависит только от ускорения свободного падения и от длины маятника (расстояния от точки подвеса до центра масс груза), и не зависит от его массы и амплитуды (при малых значениях амплитуд), то есть теоретические расчёты подтверждают установленные путём наблюдений первый и второй законы, записанные выше.
К тому же полученная формула
позволила установить количественную зависимость между периодом колебаний маятника, его длиной и ускорением свободного падения g
На практике эту формулу можно использовать для точного нахождения ускорения свободного падения g в разных точках земной поверхности, где g имеет разные значения из-за неравномерной плотности земной коры.
Задачи.
Зададим себе вопросы:
Вопрос: Изменится ли период колебания качелей, если на доску положить груз?
Ответ: Качели могут рассматриваться как математический маятник, а период колебаний математического маятника не зависит от его массы. Значит, если во время колебаний качели на её доску положить груз, то период колебаний качели не изменится.
Вопрос: Как объяснить раскачивание изображённых на рисунке качелей?
Ответ: Качели раскачиваются, так как человек периодически приседает и выпрямляет ноги, изменяя этим центр масс качелей (колебательной системы). Период колебаний качелей меняется и поддерживается за счёт совершённой людьми на качелях работы.
Выше говорилось о колебаниях математического маятника в инерциальной системе отсчёта.
Если маятник колеблется в неинерциальной системе отсчёта, то
Задача.
Итак, мы рассмотрели, как было получено выражение для периода колебаний математического маятника в инерциальных системах отсчёта. В неинерциальных системах отсчёта для расчёта периода колебаний математического маятника кроме ускорения свободного падения надо учитывать ещё ускорение, входящее в выражение силы инерции.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Решение задач на тему: “Гармонические колебания”.
Следующая запись: Упругие колебания. Крутильные колебания.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70
Формула периода колебаний пружинного маятника в физике
Формула периода колебаний пружинного маятника
Определение
Период – это минимальное время, за которое совершается одно полное колебательное движение.
Обозначают период буквой $T$.
[T=frac{Delta t}{N}left(1right),]
где $Delta t$ – время колебаний; $N$ – число полных колебаний.
Уравнение колебаний пружинного маятника
Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.
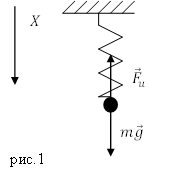
Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:
[mg=kb left(2right).]
Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
[F_u=-kleft(x+bright)left(3right).]
Ускорение груза запишем, помня, что движение происходит по оси X, как:
[a=frac{d^2x}{dt^2}=ddot{x }left(4right).]
Второй закон Ньютона для груза принимает вид:
[mddot{x}=-kleft(x+bright)+mg left(5right).]
Учтем равенство (2), формулу (5) преобразуем к виду:
[mddot{x}=-kx-kb+mg=-kx-mg+mg=-kx left(6right).]
Если ввести обозначение: ${omega }^2_0=frac{k}{m}$, то уравнение колебаний запишем как:
[ddot{x}+{omega }^2_0x=0left(7right),]
где ${omega }^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(8right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
Формулы периода колебаний пружинного маятника
Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний.
Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):
[T=frac{1}{nu }left(9right).]
Период связан с циклической частотой колебаний как:
[T=frac{2pi }{{omega }_0}left(10right).]
Выше мы получали для пружинного маятника ${omega }_0=sqrt{frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:
[T=2pi sqrt{frac{m}{k}} left(11right).]
Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Примеры задач на период колебаний
Пример 1
Задание. Пружинный маятник совершил 50 полных колебаний за время равное 10 с . Каков период колебаний маятника? Чему равна частота этих колебаний?
Решение. Так как период – это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:
[T=frac{Delta t}{N}left(1.1right).]
Вычислим период:
[T=frac{10}{50}=0,2 left(сright).]
Частота – величина обратная периоду, следовательно:
[nu =frac{1}{T}left(1.2right).]
Вычислим частоту колебаний:
[nu =frac{1}{0,2}=5 left(Гцright).]
Ответ. $1) T=0,2$ с; 2) 5Гц
Пример 2
Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?
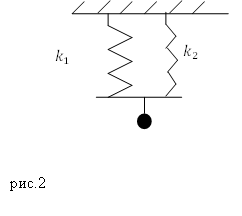
Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:
[T=2pi sqrt{frac{M}{k}} left(2.1right).]
При параллельном соединении пружин результирующая жесткость системы находится как:
[k=k_1{+k}_2left(2.2right).]
Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
[T=2pi sqrt{frac{M}{k_1{+k}_2}}.]
Ответ. $T=2pi sqrt{frac{M}{k_1{+k}_2}}$
Читать дальше: формула плеча силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Что такое колебательный процесс
Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.
Систему, совершающую колебания, называют колебательной системой или осциллятором.
Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.
Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.
При механических колебаниях, которые относят к категории вынужденных:
(F=F_{0}cos cot)
Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.
Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.
Определение периода колебаний, формула
Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:
(x(t)=Atimes cos left(omega _{0}t+phi _{0} right))
Где (x(t)) является отклонением колеблющейся физической величины от равновесного значения;
А представляет собой амплитуду гармонических колебаний;
(omega _{0}) равно циклической или круговой частоте колебаний;
(phi _{0}) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;
(cp(t)=(co_{0}t+cp_{0})) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.
В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
(cos left(alpha +2pi right)=cos alpha,)
то х остается без изменений при фазе колебаний, получающей приращение в $$2pi$$
Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.
В этом случае фаза будет увеличена на (2pi:)
(omega _{0}(t+T)+phi _{0}=left(omega _{0}t+phi _{0} right)+2pi)
Из данного равенства можно вычислить период колебаний:
(T=frac{2pi }{omega _{0}})
Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:
(v=frac{omega _{0}}{2pi})
На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.
Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.
Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:
Смещение (x=Atimes cos left(omega _{0}t+phi _{0} right))
Скорость (v_{x}=dot{x}=-Aomega _{0}times sin left(omega _{0} t+phi_{0} right)=Aomega _{0}times cos left(omega _{0} t+phi_{0} +frac{pi }{2}right))
Ускорение
(a_{x}=dot{v_{x}}=ddot{x}=-Aomega _{0}times cos left(omega _{0} t+phi_{0} right)=Aomega _{0}^{2}times cos left(omega _{0} t+phi_{0} +pi right))
Как найти период для физического маятника
В случае, когда углы отклонения (varphi) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:
(F=mgtimes sin varphi)
Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла (alpha)
Учитывая малый угол (varphi) уравнение можно записать в следующем виде:
(F=mgtimesvarphi)
С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:
(J=ml^{2})
При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:
(frac{d^{2}varphi }{dt^{2}}+frac{mgl}{J}varphi =0)
В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:
(alpha _{x}(t)+omega ^{2}x(t)=0)
Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:
(omega =sqrt{frac{mgl}{J}})
В таком случае для расчета периода колебаний математического маятника будет использоваться формула:
(T =frac{2pi }{omega }=2pi sqrt{frac{J}{mgl}})
Исходя из расчетов, можно сделать следующие выводы:
- Период пружинного маятника (T =2pi sqrt{frac{m}{k}})
- Период математического маятника (T =2pi sqrt{frac{L}{g}})
- Период крутильного маятника (T =2pi sqrt{frac{I}{K}})
В приведенных формулах:
- T — период физического маятника;
- J — момент силы маятника относительно оси вращения;
- l — расстояние от оси вращения до центра масс;
- m — масса маятника;
- g=9.8 — ускорение свободного падения.
Примеры решений
Задача № 1
Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.
Решение
(T =frac{t}{N}=frac{120}{60}=2)
(V=frac{1}{T}=frac{1}{2}=0.5)
Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.
Задача № 2
Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.
Решение
А = 20
Т = 0,8
(V=frac{1}{T}=frac{1}{0,8}=1,25)
(x(t)=Asin 2pi Vt=0.2sin 2pi times 1.25t=0.2sin 2.5pi t)
Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: (x(t)=0.2sin 2.5pi t)
Задача № 3
Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.
Решение
Период колебаний математического маятника рассчитывается по формуле:
(T =2pi sqrt{frac{L}{g}})
Согласно определению:
(V=frac{1}{T})
Тогда:
(T=frac{1}{V})
Получим равенство:
(frac{1}{V}=2pi sqrt{frac{l}{g}})
Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:
(frac{1}{V^{2}}=4pi ^{2}times frac{l}{g}Rightarrow l=frac{g}{4pi ^{2}V^{2}})
(l=frac{1.5}{4*3.14 ^{2}*0.5^{2}}approx 0.16)
Ответ: длина математического маятника примерно составляет 0,16 метра.
Период колебаний, формула
Повторяющиеся движения или процессы, которые воспроизводят все состояния предыдущего цикла являются периодическими.
Одной из характеристик периодических процессов или колебаний является период.
Период колебаний — Это время за которое периодический процесс проходит полностью один цикл.
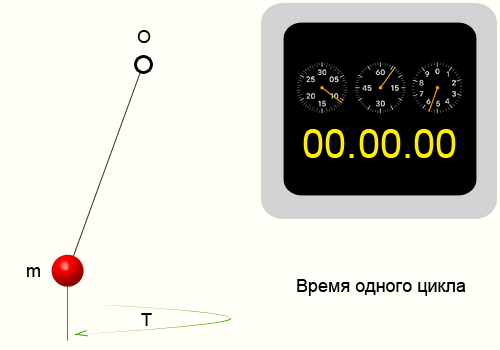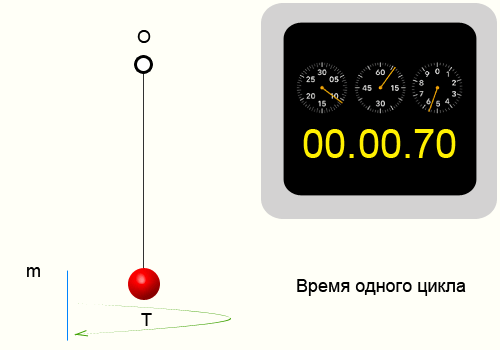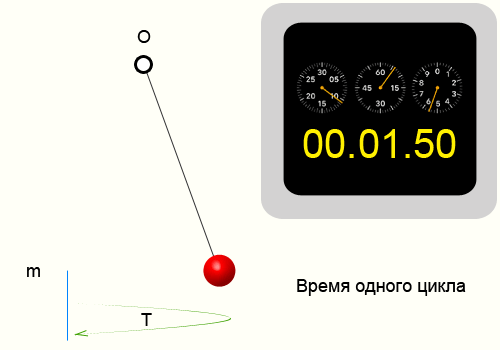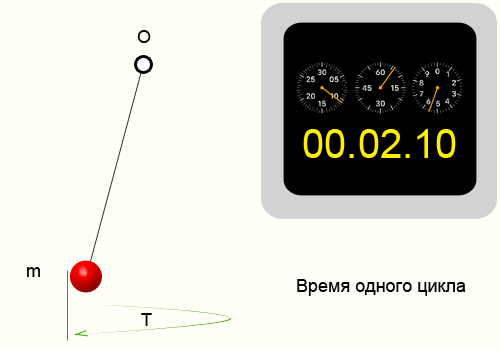
Период колебаний, формула
Для того чтобы найти период колебаний, необходимо взять определенный временной интервал и подсчитать количество циклов, после чего воспользоваться формулой:
Если
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| f | частота колебаний (число циклов в одну секунду), | Герц |
то
[ T = frac{∆t}{N} = frac{1}{f} ]
Пример определения периода колебаний
Например возьмем кусочек пластилина и подвесим его на нитке.
Отведем нитку от положения равновесия и отпустим. На сотовом телефоне в момент отпускания запустим секундомер.
Отсчитаем 10 циклов, т.е. нить 10 раз вернется в ту же точку из которой мы ее отпустили.
Секундомер показал 14.35 секунд, соответственно приблизительный период колебаний нити 1.435 секунд.
Вычислить, найти период колебаний по формуле 1
Как найти период колебаний зная частоту
Период колебаний, формула |
стр. 533 |
|---|
| Период | |
|---|---|
 |
|
| Размерность | T |
| Единицы измерения | |
| СИ | с |

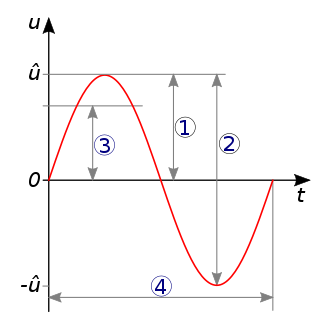
Пери́од колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором она находилась в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное обозначение периода колебаний: 


Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.
Период колебаний связан соотношением взаимной обратности с частотой:
Для волновых процессов период связан кроме того очевидным образом с длиной волны 
где 
В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота[3] колебаний его волновой функции).
Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).
Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).
Периоды колебаний в природе[править | править код]
Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).
Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот электромагнитных колебаний (см. Электромагнитный спектр) .
Периоды колебаний слышимого человеком звука находятся в диапазоне
- от 5·10−5с до 0,2с
(четкие границы его несколько условны).
Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне
- от 1,1·10−15с до 2,3·10−15с.
Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц.
В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.
Периоды колебаний простейших физических систем[править | править код]
Пружинный маятник[править | править код]
Период колебаний пружинного маятника может быть вычислен по следующей формуле:

где 

Математический маятник[править | править код]
Период малых колебаний математического маятника:

где 

Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью[5] равен 2 секундам.
Физический маятник[править | править код]
Период малых колебаний физического маятника:

где 


Крутильный маятник[править | править код]
Период колебаний крутильного маятника:

где 

Электрический колебательный (LC) контур[править | править код]
Период колебаний электрического колебательного контура (формула Томсона):

где 

Эту формулу вывел в 1853 году английский физик Уильям Томсон.
Примечания[править | править код]
- ↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
- ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
- ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
- ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
- ↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.
Ссылки[править | править код]
- [bse.sci-lib.com/article088257.html Период колебаний] — статья из Большой советской энциклопедии
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|


