Как связаны между собой частота колебаний и период?
Онлайн калькуляторы: перевод частоты колебаний в период и, наоборот –
перевод периода в частоту
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического
(в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
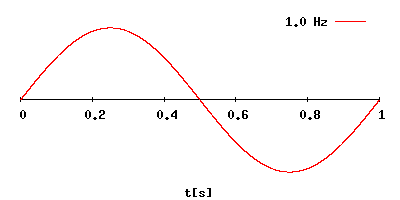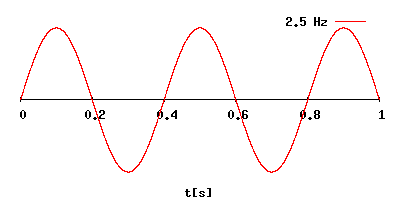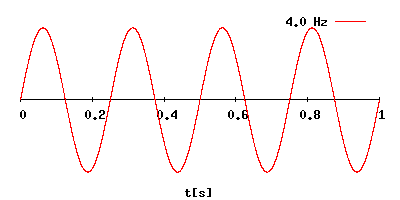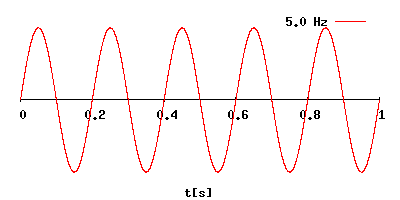
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом:
F(Гц) = 1/T(с) и соответственно:
T(с) = 1/F(Гц)
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое может оказаться довольно громоздким,
а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим
пройденный материал парой простых онлайн калькуляторов.
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ПЕРИОДА КОЛЕБАНИЙ ПО ЧАСТОТЕ
Частота колебаний F |
||
Период Т |
А теперь всё то же самое, но наоборот:
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ПЕРИОДУ КОЛЕБАНИЙ
Период колебаний Т |
||
Частота F |
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина –
циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω.
В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно:
ω (рад/с) = 2πF(Гц).
Период колебаний, формула
Повторяющиеся движения или процессы, которые воспроизводят все состояния предыдущего цикла являются периодическими.
Одной из характеристик периодических процессов или колебаний является период.
Период колебаний — Это время за которое периодический процесс проходит полностью один цикл.
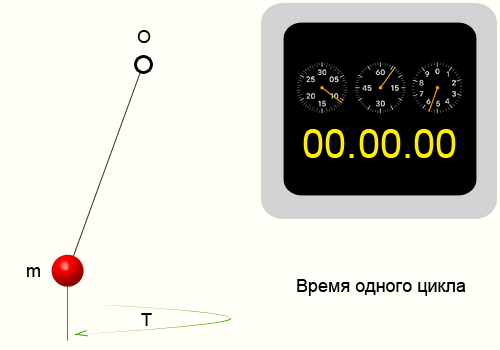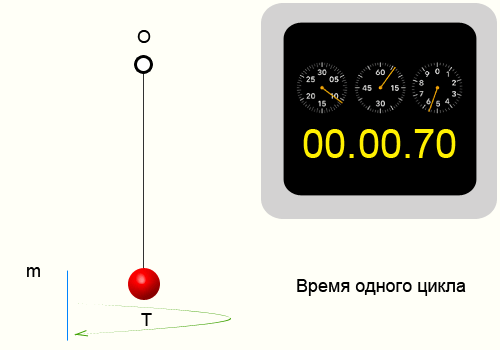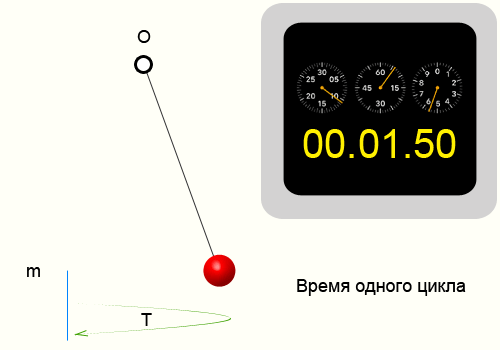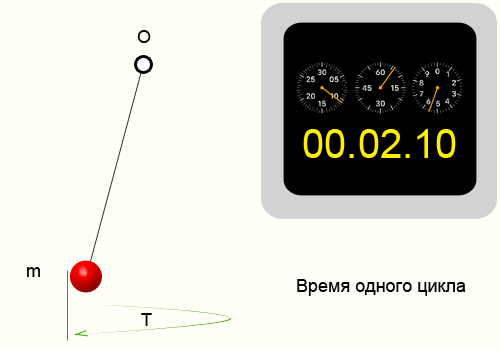
Период колебаний, формула
Для того чтобы найти период колебаний, необходимо взять определенный временной интервал и подсчитать количество циклов, после чего воспользоваться формулой:
Если
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| f | частота колебаний (число циклов в одну секунду), | Герц |
то
[ T = frac{∆t}{N} = frac{1}{f} ]
Пример определения периода колебаний
Например возьмем кусочек пластилина и подвесим его на нитке.
Отведем нитку от положения равновесия и отпустим. На сотовом телефоне в момент отпускания запустим секундомер.
Отсчитаем 10 циклов, т.е. нить 10 раз вернется в ту же точку из которой мы ее отпустили.
Секундомер показал 14.35 секунд, соответственно приблизительный период колебаний нити 1.435 секунд.
Вычислить, найти период колебаний по формуле 1
Как найти период колебаний зная частоту
Период колебаний, формула |
стр. 533 |
|---|
Период колебаний маятника это наименьший промежуток времени, за который он совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно).
.
Калькулятор расчета периода колебания маятника
Ускорение свободного падения (g, м/с2)
Период колебания (t, сек.)
Законы колебания простого маятника
Всякому известно, что, чем короче маятник, тем быстрее его колебания. Очевидно, период колебания уменьшается с уменьшением длины маятника. Но такое
знание имеет небольшое значение, пока мы не узнаем, насколько колебания становятся чаще при определенном уменьшении длины маятника. Другой фактор, который мог бы оказать влияние на период,— это масса маятника. Однако опытным путем было установлено, что мааса тут не причем.
Формула колебания маятника: 
где t — время в сек, l — длина маятника в м, a g — ускорение в м/сек2.
- Период (время полного колебания) не зависит от материала и массы маятника.
- Период не зависит от длины дуги (до 16°).
- Период пропорционален корню квадратному из длины маятника.
An online period of oscillation calculator to calculate the period of simple pendulum, which is the term that refers to the oscillation of the object in a pendulum, spring, etc. This motion of oscillation is called as the simple harmonic motion (SHM), which is a type of periodic motion along a path whose magnitude is proportional to the distance from the fixed point. In the below period of pendulum calculator enter the length and acceleration of gravity to know the period of oscillation.
Period of Pendulum Calculator
An online period of oscillation calculator to calculate the period of simple pendulum, which is the term that refers to the oscillation of the object in a pendulum, spring, etc. This motion of oscillation is called as the simple harmonic motion (SHM), which is a type of periodic motion along a path whose magnitude is proportional to the distance from the fixed point. In the below period of pendulum calculator enter the length and acceleration of gravity to know the period of oscillation.
Code to add this calci to your website 

Formula:
Period of Oscillation = 2 π √(L / g)
Where,
T = Period
L = Length
g = Acceleration of Gravity
Example:
A simple pendulum having a length of 7 cm and acceleration of gravity as 12 m/s2
Solution:
Period of Oscillation = 2 π √(L / g)
= 2 x 3.14 √(7 / 12)
= 0.4799 s
Период колебаний Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Затухающая собственная частота: 22.88 Герц –> 22.88 Герц Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.27461474244666 Второй –> Конверсия не требуется
17 Система второго порядка Калькуляторы
16 Система второго порядка Калькуляторы
25 Проект системы управления Калькуляторы
Период колебаний формула
Период времени для колебаний = (2*pi)/Затухающая собственная частота
T = (2*pi)/ωd
Сколько колебаний в периоде?
Период – это время, за которое частица совершает одно полное колебание. Обозначается буквой T. Частоту колебаний можно получить, взяв обратную величину частоты.
