Как найти период колебания кольца

ЗАДАНИЕ ПО
ОБРАБОТКЕ РЕЗУЛЬТАТОВ:

Расчетная формула:
Т_к=,
где t_k
– время, за
которое совершались колебания, n=10
– количество колебаний, совершенных
маятником.

T_k1==1,31
с

Т_k2==1,316
с

Т_k3==1,322
с

Т_k4==1,319
с

Т_k5==1,325
с

1) Вычисление среднего результата
измерения

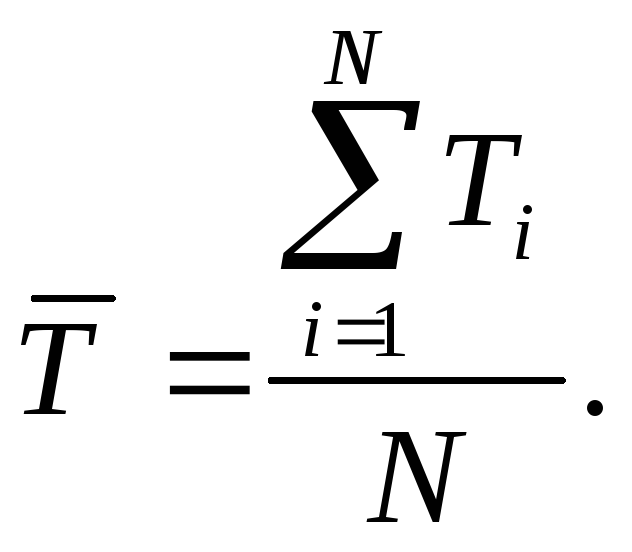
2)

равенство нулю или близость к нулю суммы
отклонений подтверждает правильность
расчёта отклонений X_i.

2.1.

следовательно, расчёт отклонений
произведён правильно!

3) Вычисление СКО результата наблюдения

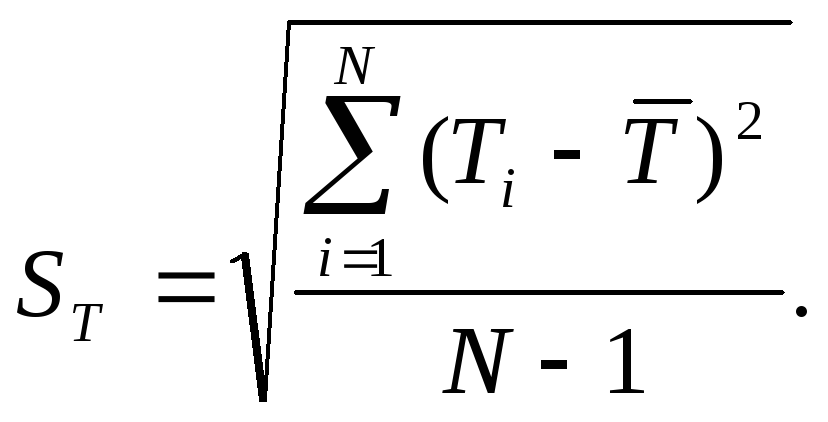
с

4) Проверка на промахи

P =95% N
= 5 V_PN
=1,67

=>
Следовательно, промахов нет!

5) СКО результата
измерения:

с

6) Вычислим
границу случайной погрешности измерения
периода:

с

Приборная погрешность

с

7) Вычислим полную
погрешность:

с

8) Запишем результат
статистической обработки

с p=95%

T_k=1,3180,017
с
P=95%

1. Вычислим периоды колебаний маятника без кольца Tд :

Расчетная формула:
Т_д=,
где t_д
– время, за
которое совершались колебания, n=10
– количество колебаний, совершенных
маятником.

T_д1==0,947
с

T_д2==0,938
с

T_д3==0,931
с

T_д4==0,941
с

T_д5==0,946
с

1) Вычисление среднего результата
измерения

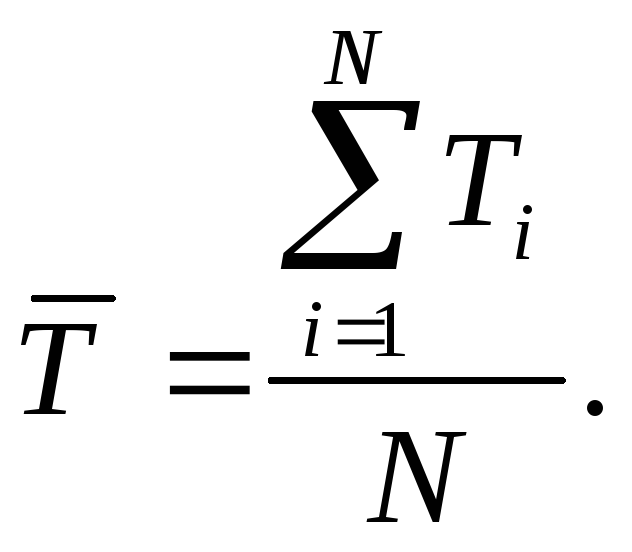
2)

равенство нулю или близость к нулю суммы
отклонений подтверждает правильность
расчёта отклонений X_i.

2.1.

следовательно, расчёт отклонений
произведён правильно!

3) Вычисление СКО результата наблюдения

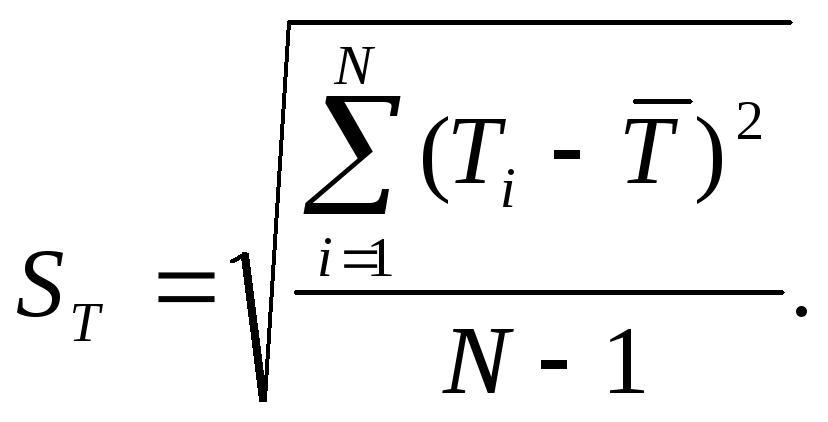
с

4) Проверка на промахи

P =95% N
= 5 V_PN
=1,67

=>
Следовательно, промахов нет!

5) СКО результата
измерения:

с

6) Вычислим
границу случайной погрешности измерения
периода:

с

Приборная погрешность

с

7) Вычислим полную
погрешность:

с

8) Запишем результат
статистической обработки

с P=95%

T_k=0,9400,013
с P=95%
III.
Вычислим
частоты колебаний
_к
для
маятника с кольцом:

Расчетная формула:
=,
где Т
– период колебаний.

_k1==4,794
Гц

_k2==4,772
Гц

_k3==4,75
Гц

_k4==
4,761 Гц

_k5==
4,74 Гц

1) Вычисление среднего результата
измерения

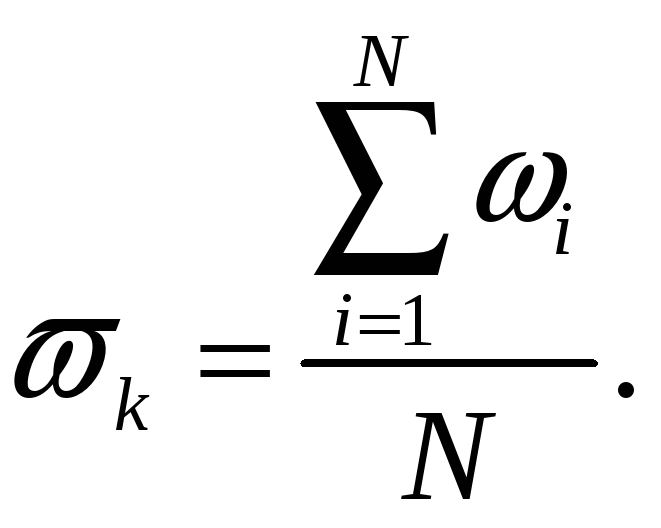
Гц

2)

равенство нулю или близость к нулю суммы
отклонений подтверждает правильность
расчёта отклонений X_i.

2.1.

следовательно, расчёт отклонений
произведён правильно!

3) Вычисление СКО результата наблюдения

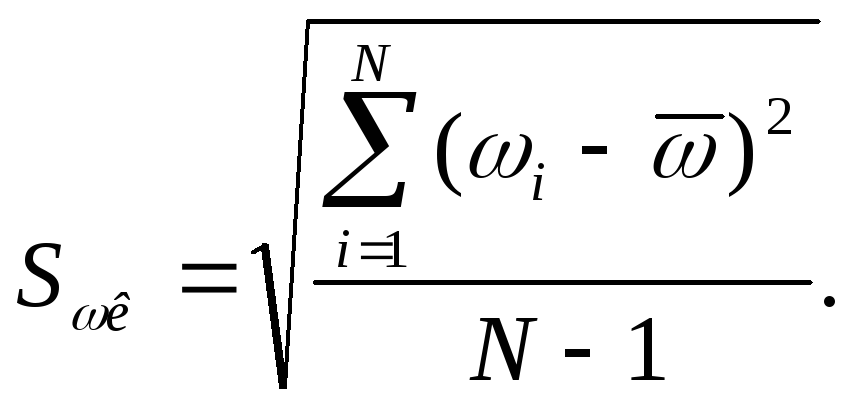
Гц

4) Проверка на промахи

P =95% N
= 5 V_PN
=1,67

=>
Следовательно, промахов нет!

5) СКО результата
измерения:

Гц

6) Вычислим
границу случайной погрешности измерения
периода:

Гц

Вычислим приборную
погрешность

с

Приборная погрешность вычисляется по
формуле:

Вычислим среднюю приборную погрешность:

7) Вычислим полную
погрешность:

Гц

8) Запишем результат
статистической обработки

с P=95%

=4,760,06
Гц P=95%

IV. Вычислим частоты колебаний для маятника без кольца:

Расчетная формула:
=,
где Т
– период колебаний.

_д1==6,631
Гц

_д2==6,695
Гц

_д3==6,745
Гц

_д4==
6,674 Гц

_д5==
6,638 Гц

1) Вычисление среднего результата
измерения

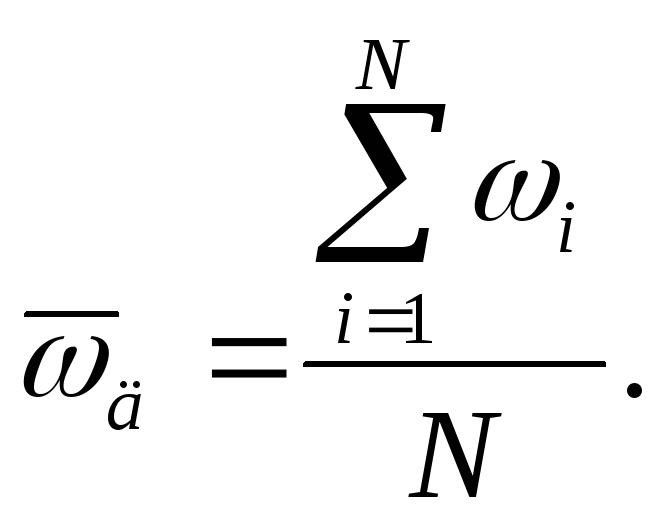
Гц

2)

равенство нулю или близость к нулю суммы
отклонений подтверждает правильность
расчёта отклонений X_i.

2.1.

следовательно, расчёт отклонений
произведён правильно!

3) Вычисление СКО результата наблюдения

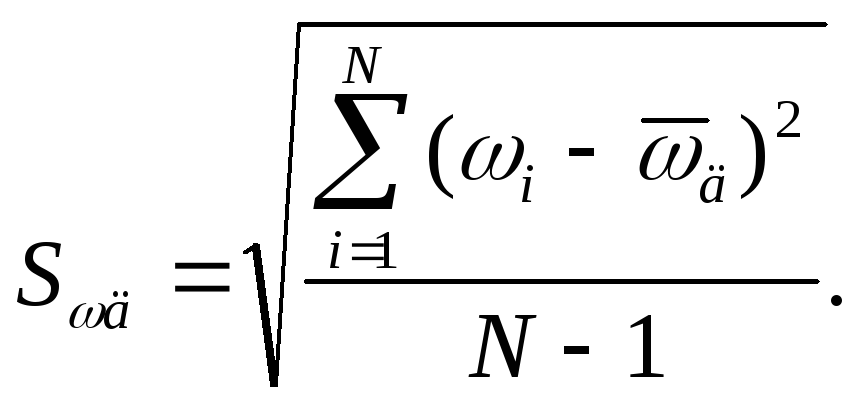
Гц

4) Проверка на промахи

P =95% N
= 5 V_PN
=1,67

=>
Следовательно, промахов нет!

5) СКО результата
измерения:

Гц

6) Вычислим
границу случайной погрешности измерения
периода:

Гц

Приборная погрешность

с

Вычислим приборную
погрешность

с

Приборная погрешность вычисляется по
формуле:

Вычислим среднюю приборную погрешность:

7) Вычислим полную
погрешность:

Гц

8) Запишем результат
статистической обработки

с P=95%

=6,680,13
Гц P=95%

2017-10-18   

Тонкое проволочное кольцо радиуса $R$ закреплено так, что его плоскость вертикальна. Кольцо имеет заряд $Q$. Вдоль оси кольца расположена гладкая непроводящая спица, на которую надета бусинка массы $m$, имеющая заряд $- q$, противоположный по знаку заряду кольца. К бусинке с двух сторон прикреплены изолированные от нее одинаковые невесомые пружины жесткостью $k$ каждая, оси которых совпадают со спицей, а концы закреплены так, что в положении равновесия бусинка находится в центре кольца. Найти период малых колебаний бусинки.

Решение:

Поскольку оси пружин и спицы совпадают с осью кольца, и размерами бусинки, которая может перемещаться только по спице, как обычно, можно пренебречь, имеет место осевая симметрия в расположении тел. Поэтому можно считать, что по тонкому проводящему кольцу заряд Q распределен равномерно. Учитывая это и то, что в положении равновесия бусинка находится в центре кольца, можно утверждать, что при равновесном положении бусинки деформации одинаковых пружины должны быть одинаковы. Отсюда следует, что при смещении бусинки вдоль оси кольца на расстояние $x$ от равновесного положения равнодействующая сил упругих деформаций пружин $vec{F}_{п}$ будет направлена к положению равновесия вдоль оси пружин, а по величине, согласно закону Гука, она должна быть равна $2kx$.

Наряду с силами упругих деформаций пружин, на бусинку при ее смещении от положения равновесия будут действовать электрические силы со стороны заряженного кольца. Чтобы определить величину и направление этих сил, рассмотрим часть дуги кольца, ограниченную центральным углом $Delta phi$, показанным на рисунке. При достаточно малой величине угла $Delta phi$ размерами указанного участка дуги кольца можно пренебречь. Учитывая, что заряд этого участка, согласно сказанному выше, должен быть равен $Delta Q = Q Delta phi /(2 pi)$, можно утверждать, что напряженность поля $Delta vec{E}$, создаваемого этим зарядом в точке, находящейся на оси на расстоянии х от центра кольца, будет направлена так, как показано на рисунке (считая, конечно, заряд кольца положительным), а ее величина должна быть равна

$Delta E = frac{Q Delta phi}{8 pi^{2} epsilon_{0} (R^{2} + x^{2})}$,

где $epsilon_{0}$ – электрическая постоянная. Диаметрально противоположный участок кольца таких же размеров в рассматриваемой точке создает поле с напряженностью $Delta vec{E}_{1}$, составляющая которой, перпендикулярная оси ОХ, имеет ту же величину, но направлена противоположно аналогичной компоненте поля $Delta vec{E}$. Поэтому на основании принципа суперпозиции можно утверждать, что напряженность поля, создаваемого всем кольцом, направлена вдоль оси ОХ и равна

$E = frac{Q cos alpha}{4 pi epsilon_{0} (R^{2} + x^{2})} = frac{Qx}{ 4 pi epsilon_{0} sqrt{(R^{2} + x^{2})^{3}}}$.

Отсюда, пренебрегая размерами бусинки, получаем, что электрическая сила, действующая на нее, в соответствии с определением напряженности электрического поля равна $F_{э} = qE$ и направлена вдоль оси к плоскости кольца, т.к. знаки зарядов кольца и бусинки противоположны.

Будем, как это обычно и делается, считать лабораторную систему отсчета, относительно которой кольцо неподвижно, инер-циальной и пренебрегать силами трения, действующими на движущиеся части. Тогда, пренебрегая в соответствии с условием массой пружин, на основании II закона Ньютона уравнение движения бусинки в проекции на ось ОХ можно представить в виде

$m ddot{x} = – F_{п} – F_{э} = – left ( 2k + frac{qQ}{4 pi epsilon_{0} sqrt{ (R^{2} + x^{2})^{3} }} right )x$,

где $ddot{x}$ – проекция ускорения бусинки на ось ОХ. Поскольку требуется определить период малых колебаний, то следует считать, что амплитуда колебаний бусинки много меньше радиуса кольца, а потому всегда должно соблюдаться неравенство $|x| ll R$, и уравнение движения можно представить в виде

$m ddot{x} = – left ( 2k + frac{qQ}{4 pi epsilon_{0} R^{3} } right ) x$.

Из полученного уравнения видно, что ускорение бусинки прямо пропорционально ее смещению от положения равновесия и направлено к этому положению. Следовательно, после малого отклонения от положения равновесия бусинка будет совершать гармонические колебания. Вспоминая, что при прямолинейных гармонических колебаниях квадрат угловой частоты $omega$ равен модулю отношения ускорения колеблющегося тела к его смещению от положения равновесия в тот же момент времени, а период колебаний обратно пропорционален угловой частоте, получим, что искомый период малых колебаний равен

$T = frac{2 pi}{ omega} = 2 pi sqrt{ frac{m}{2k + qQ / (4 pi epsilon_{0} R^{3}) }}$.

Данное кольцо есть физический маятник с париодом колебаний
Т =2п·sqrt(J/mgd),где J—момент инерции кольца относительно точки О, J=2mR^2,
d=R—расстояние от О до центра масс кольца. Подставимвсе в формулу и найдем период Т=1,418 с.
Частота v=1/Т=0,7 с^(-1) =7 Гц

Гость3

Всего 1 ответ.

Другие интересные вопросы и ответы

Как связана длина волны и скорость распространения?

Александр Смуров3

Источник: st03.kakprosto.ru

Длина волны равна произведению скорости распространения волны на ее период колебаний (курс 9 класса общеобразовательной школы). Соответственно, если нужно получить скорость, то нужно длину волны разделить на период колебаний. 

Илья Левин4

Всего 1 ответ.

Как определяется амплитуда, период и частота гармонических колебаний?

Гость5

Гармоническое колебание, это колебание, описывающееся уравнением x = x0*cos(ω *t). В этом уравнении x0 – амплитуда. ω – циклическая частота, равная 2*π/Т, где Т – период. Отсюда Т = 2*π/ω. Частота ν = 1/T. Отсюда ν = ω/(2*π).

КЛХ6

Всего 1 ответ.

Как найти период колебаний зная частоту

Как найти период колебаний зная частотуТатьяна Владимировна6

Подумать головой. Частота – это сколько колебаний происходит в секунду.

Следовательно, одно колебание происходит за какое время?

Александр Шеруда2

Всего 4 ответа.

Что такое период колебания?

Алеkсей6

Период колебания – это физическая величина, которая равняется промежутку времени,за которое тело, что движется равномерно по кругу, совершает один полный оборот. Период колебания измеряется в секундах. Его можно вычислить за формулой T=t/N, где T-период, N-количество полных оборотов, t-время.

Зная период колебания и радиус, легко определить скорость, с которой движется тело.

ozerk­a1

Всего 10 ответов.

• Переведите пожалуйста устойчивое выражение старославянское: старьци людьсции
• Как повысить скорость мышления?
• Почему ещё никто не додумался выкопать яму до ядра Земли?
• Укажите, что из перечисленного является гражданско-правовой ответственностью:
• Срочно! Тест на ETXT! Он на грамотность! Только быстро 7 минут!