Период колебания пружинного маятника, теория и онлайн калькуляторы
Период колебания пружинного маятника
Рассмотрим простейшую систему, в которой возможна реализация механических колебаний. Допустим, что на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$. Груз движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. Массу пружины считаем малой в сравнении с массой груза.
Уравнение движения груза при таких колебаниях имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${omega }^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=B{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ и $B$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
Частота и период колебаний пружинного маятника
Косинус (синус) – периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют
периодом колебаний. Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):
[T=frac{1}{nu }left(3right).]
Период связан с циклической частотой колебаний как:
[T=frac{2pi }{{omega }_0}left(4right).]
Зная, что для пружинного маятника ${omega }_0=sqrt{frac{k}{m}}$, период колебаний его определим как:
[T=2pi sqrt{frac{m}{k}} left(5right).]
Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:
[left[Tright]=с.]
Примеры задач на период колебания пружинного маятника
Пример 1
Задание. К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?
Решение. Сделаем рисунок.
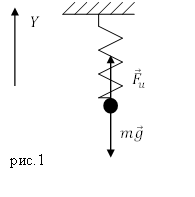
Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:
[moverline{g}+{overline{F}}_u=0 left(1.1right).]
Запишем проекцию уравнения (1.1) на ось Y:
[mg=F_uleft(1.2right).]
Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:
[F_u=kDelta x left(1.3right).]
Используя выражения (1.2) и (1.3) найдем отношение $frac{m}{k}$:
[mg=kDelta xto frac{m}{k}=frac{Delta x }{g}left(1.4right).]
Период колебаний пружинного маятника при малых колебаниях можно найти, используя выражение:
[T=2pi sqrt{frac{m}{k}} left(1.5right).]
Заменяя отношение массы груза к жесткости пружины на правую часть выражения (1.4), получим:
[T=2pi sqrt{frac{Delta x }{g}.}]
Вычислим период колебаний нашего маятника, если $g=9,8 frac{м}{с^2}$:
[T=2pi sqrt{frac{0,09 }{9,8} approx 0,6 (с)}]
Ответ. $T$=0,6 с
Пример 2
Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.
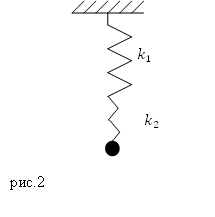
Решение.Период колебаний пружинного маятника равен:
[T=2pi sqrt{frac{m}{k}} left(2.1right).]
Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}to k=frac{k_1k_2}{k_1{+k}_2}left(2.2right).]
Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
[T=2pi sqrt{frac{m(k_1{+k}_2)}{k_1k_2}}.]
Ответ. $T=2pi sqrt{frac{m(k_1{+k}_2)}{k_1k_2}}$
Читать дальше: плечо силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Для школьников.
Любое тело подвешенное так, что его центр масс находится ниже точки подвеса, называют физическим маятником.
Маятник находится в состоянии устойчивого равновесия, если его центр масс расположен на вертикали под точкой подвеса.
Если маятник вывести из состояния равновесия, отклонив его на некоторый угол и предоставив самому себе, то он начнёт колебаться около положения равновесия.
Чтобы описать колебание маятника, надо знать уравнение его движения, то есть зависимость координаты от времени, и период его колебаний.
Но найти период колебаний физического маятника сложно, так как он зависит от многих причин – от формы и размера маятника, от распределения массы тела, расстояния от точки подвеса до центра масс тела.
Много проще описать поведение математического маятника. Для этого физический маятник заменяют математическим маятником такой длины, чтобы частоты колебаний этих маятников были одинаковы.
Длина математического маятника, частота колебаний которого равна частоте колебаний данного физического маятника, называется приведённой длиной физического маятника.
Под математическим маятником понимается тело малого размера, подвешенного на длинной нерастяжимой нити. Нить считаем невесомой, а тело можно принять за материальную точку.
Наблюдения за колебаниями маятников, подобных математическому, позволили установить следующие законы:
1) Период колебаний математического маятника не зависит от массы тела;
2) Период колебаний математического маятника не зависит от амплитуды колебаний (при малых амплитудах).
Впервые второй закон был установлен Галилеем в 1655 году, при наблюдении им в соборе качания паникадила на длинной цепи, которое толкнули при зажигании. Его колебания постепенно затухали, но период колебаний оставался прежним. Для измерения периода колебаний Галилей пользовался своим пульсом.
Посмотрим теперь, как получили формулу, по которой можно найти период колебаний математического маятника.
На рис а) показан математический маятник, отклонённый от положения равновесия (от точки А) на малый угол (в точку В).
Буквой Р обозначена сила тяжести груза, а буквой Р (с индексом 1) обозначена переменная возвращающая сила, действующая на груз.
Так как возвращающая сила меняется в процессе колебания, то рассчитать движение колеблющегося тела сложно.
Для упрощения расчётов заставляют маятник колебаться не в одной плоскости, как показано на рис.а), а описывать конус (рис. б), чтобы грузик двигался по окружности.
Движение маятника по конусу может рассматриваться как сложение двух независимых колебаний (в плоскости рисунка и в перпендикулярной рисунку плоскости).
Период этих колебаний одинаков. Тогда период обращения маятника можно выразить через отношение длины окружности к скорости движения
При малом угле отклонения маятника (малой амплитуде) можно считать, что возвращающая сила направлена к центру окружности (является центростремительной, равной произведению массы тела на центростремительное или нормальное ускорение), то есть
С другой стороны, из подобия треугольников ОВС и ДВЕ можно записать, что
Приравняв правые части последних выражений, получим уравнение для скорости обращения груза
Подставив скорость в выражение периода, получим искомую формулу для нахождения периода гармонических колебаний математического маятника
Таким образом, период колебаний математического маятника зависит только от ускорения свободного падения и от длины маятника (расстояния от точки подвеса до центра масс груза), и не зависит от его массы и амплитуды (при малых значениях амплитуд), то есть теоретические расчёты подтверждают установленные путём наблюдений первый и второй законы, записанные выше.
К тому же полученная формула
позволила установить количественную зависимость между периодом колебаний маятника, его длиной и ускорением свободного падения g
На практике эту формулу можно использовать для точного нахождения ускорения свободного падения g в разных точках земной поверхности, где g имеет разные значения из-за неравномерной плотности земной коры.
Задачи.
Зададим себе вопросы:
Вопрос: Изменится ли период колебания качелей, если на доску положить груз?
Ответ: Качели могут рассматриваться как математический маятник, а период колебаний математического маятника не зависит от его массы. Значит, если во время колебаний качели на её доску положить груз, то период колебаний качели не изменится.
Вопрос: Как объяснить раскачивание изображённых на рисунке качелей?
Ответ: Качели раскачиваются, так как человек периодически приседает и выпрямляет ноги, изменяя этим центр масс качелей (колебательной системы). Период колебаний качелей меняется и поддерживается за счёт совершённой людьми на качелях работы.
Выше говорилось о колебаниях математического маятника в инерциальной системе отсчёта.
Если маятник колеблется в неинерциальной системе отсчёта, то
Задача.
Итак, мы рассмотрели, как было получено выражение для периода колебаний математического маятника в инерциальных системах отсчёта. В неинерциальных системах отсчёта для расчёта периода колебаний математического маятника кроме ускорения свободного падения надо учитывать ещё ускорение, входящее в выражение силы инерции.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Решение задач на тему: “Гармонические колебания”.
Следующая запись: Упругие колебания. Крутильные колебания.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70
Алексей . Малеев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Период колебаний – минимальное время, за которое циклически движущаяся система возвращается в исходное состояние.
Период колебаний можно найти как
$T = frac{t}{n}$,
где $t$ – время всех колебаний, $n$ – их количество.
Закономерности, связанные с колебаниями, удобно изучать с помощью модели движущегося в горизонтальной плоскости пружинного маятника, поскольку внутри такой системы действует всего одна сила – сила упругости пружины (ее весом и силами сопротивления среды можно пренебречь). Такое устройство относится к т.н. линейным гармоническим осцилляторам – системам, графиком зависимости скорости тела от времени для которых является синусоида.
Функция силы от времени, действующая в пружинном маятнике, может быть выражена как:
$F(t) = m cdot a (t) = -m cdot omega^2 cdot x$ (t), где:
- $m$ – масса,
- $a$ – ускорение,
- $omega$ – круговая частота гармонических колебаний,
- $x$ – приращение длины в данный момент времени.
Сила упругости зависит лишь от коэффициента упругости пружины и растяжения пружины:
$F_{упр} = -k cdot x$
Объединив эти две формулы, получим:
$m cdot a = -kx = m cdot omega_0^2 cdot x$,
Величина $omega_0$ называется собственной частотой колебательной пружинного маятника. Ее можно выразить, исходя из вышеизложенного, как
$omega_0 = sqrtfrac{k}{m}$.
Период колебаний связан с собственной частотой отношением
$T = frac{2pi}{omega_0}$,
где $2pi$ – длина одного цикла, выраженная в радианах. Из этого можно выразить период как зависимость от массы и упругости:
$T = 2pi cdot sqrtfrac{m}{k}$.
Для других колебательных систем класса гармонических осцилляторов (математического маятника, крутильного маятника) периоды колебаний находятся аналогично. Различаются лишь системы сил, действующие на тело. Так, период колебаний математического маятника зависит (при небольших углах отклонения от вертикали) от длины подвеса.
Пример 1
Найти жёсткость пружины пружинного маятника с грузом массой 0,1 кг, если период его колебаний составляет 1 с.
Подставляем значения в формулу:
$1 = 2 cdot 3,14 cdot sqrtfrac{0,1}{k}$
$1^2 = 4 cdot 3,14^2 cdot frac{0,01}{k^2}$
$k = sqrt {4 cdot 3,14^2 cdot 0,01} = 0,628 frac{Н}{м}$
Ответ: $0,628 frac{Н}{м}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается
![]()
Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.
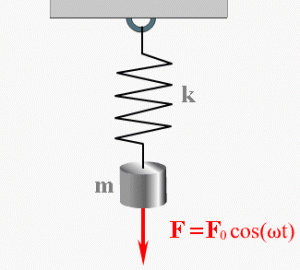
Давайте выведем формулу периода пружинного маятника.
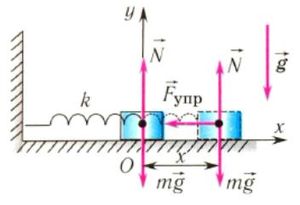
На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :
![]()
Все проецируем на ось ОХ:
![]()
Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:
![]()
Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:
![]()
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
![]()
Тогда период колебаний пружинного маятника будет равен:
![]()
Так же есть:
Период математического маятника ![]()
Период физического маятника ![]()
Период крутильного маятника ![]()
В Формуле мы использовали :
![]() — Период пружинного маятника маятника
— Период пружинного маятника маятника
![]() — Масса груза
— Масса груза
![]() — Изменение длины пружины
— Изменение длины пружины
![]() — Коэффициент упругости пружины
— Коэффициент упругости пружины
![]() — Ускорение свободного падения
— Ускорение свободного падения
![]() — Циклическая частота пружинного маятника
— Циклическая частота пружинного маятника
![]() — Сила реакции опоры
— Сила реакции опоры
![]() — Сила упругости
— Сила упругости
Пружинный маятник .
Пружинный маятник представляет из себя груз на пружине.
(T=2 pi sqrt{dfrac{m}{k}} )
(k) – жесткость пружины маятника
(m) – масса груза
Задача 1.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=8 Н/м ), а масса его груза
(m=0,5 кг ) ,
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 2.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=81 Н/м ), а масса его груза
(m=1 кг ) ,
(pi=3,14 )
Ответ округлить до десятых
Показать ответ
Показать решение
Видеорешение
Задача 3.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=400 Н/м ), а масса его груза
(m=0,25 кг ) ,
(pi=3,14 )
Ответ округлить до сотых
Показать ответ
Показать решение
Видеорешение
Задача 4.
Найти массу груза пружинного маятника, если его период ( T=1 с )
, а коэффициент жесткости пружины ( k=400 Н/м ; )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 5.
Найти массу груза пружинного маятника, если его период ( T=0,3 с )
, а коэффициент жесткости пружины ( k=350 Н/м ; )
(pi=3,14 ).
Ответ округлить до десятых.
Показать ответ
Показать решение
Видеорешение
Задача 6.
Найти массу груза пружинного маятника, если его период ( T=0,07 с )
, а коэффициент жесткости пружины ( k=150 Н/м ; )
(pi=3,14 ).
Ответ округлить до сотых.
Показать ответ
Показать решение
Видеорешение
Задача 7.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,07 с )
, а масса груза ( m=0,0186 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 8.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,32 с )
, а масса груза ( m=0,8 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 9.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,6 с )
, а масса груза ( m=4 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 10.
Найти частоту колебаний ( nu ) пружинного маятника, если жесткость его пружины (k=400 Н/м ), а масса его груза
(m=0,25 кг ) ,
(pi=3,14 )
Ответ округлить до сотых
Показать ответ
Показать решение
Видеорешение
Задача 15.
Массу груза пружинного маятника увеличили в 4 раза. Во сколько раз увеличился период колебаний этого
пружинного маятника?
Показать ответ
Показать решение
Видеорешение
Задача 16.
Массу груза пружинного маятника увеличили в 25 раза. Во сколько раз увеличился период колебаний этого
пружинного маятника?
Показать ответ
Показать решение
Видеорешение
Задача 25.
Пружинный маятник совершает гармонические колебания с периодом (T_1=0,4 с. ;; )
Масса его груза (m_1=1 кг ).
В какой-то момент
к грузу пружинного маятника жестко прикрепили дополнительный груз массой (m_2=3 кг. ; )
Вычислить период колебаний пружинного маятника после присоединения дополнительного груза.
Показать ответ
Показать решение
Видеорешение
Задача 30.
Пружинный маятник совершает гармонические колебания с периодом (T_1=0,15 с. ;; )
Масса его груза (m_1= 0,6 кг ).
В какой-то момент
к грузу пружинного маятника жестко прикрепили дополнительный груз , после чего
его период стал равен (T_2=0,45 с )
Найти массу (m_2 ) дополнительного груза.
Показать ответ
Показать решение
Видеорешение
