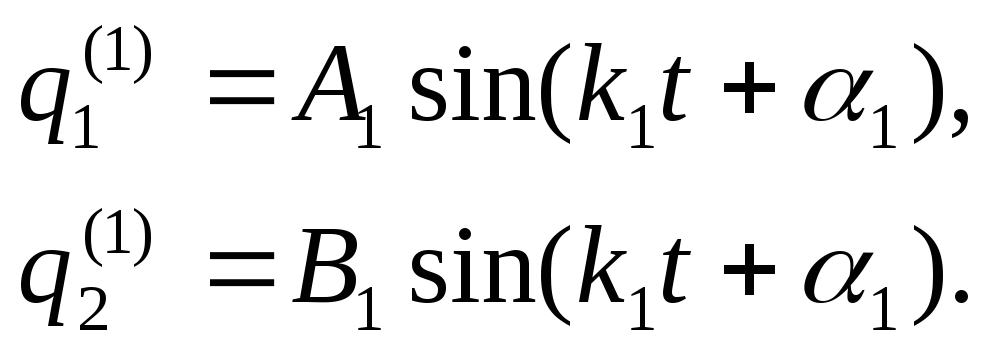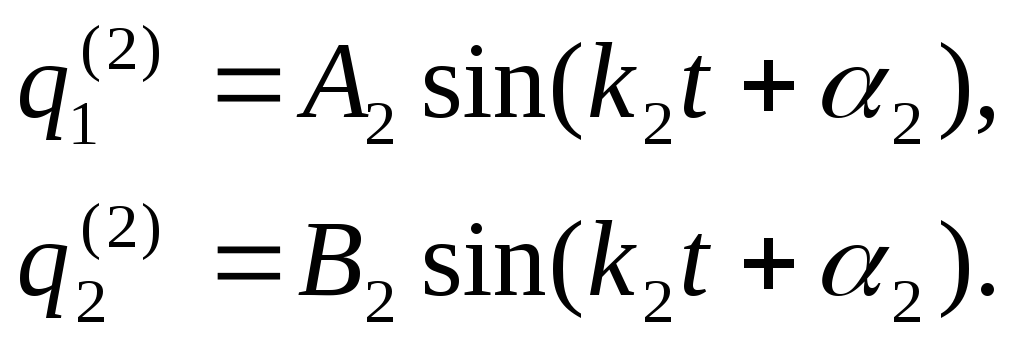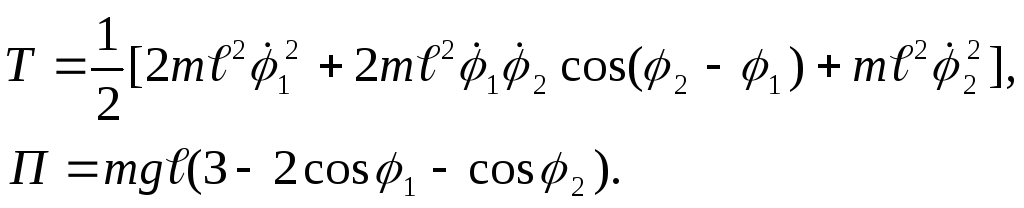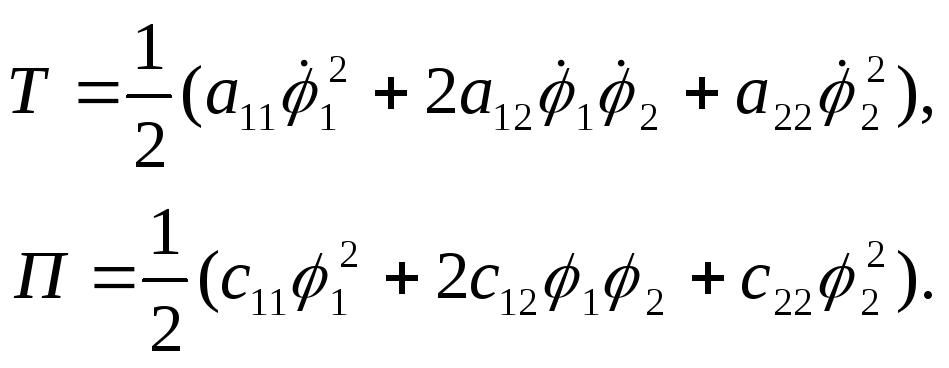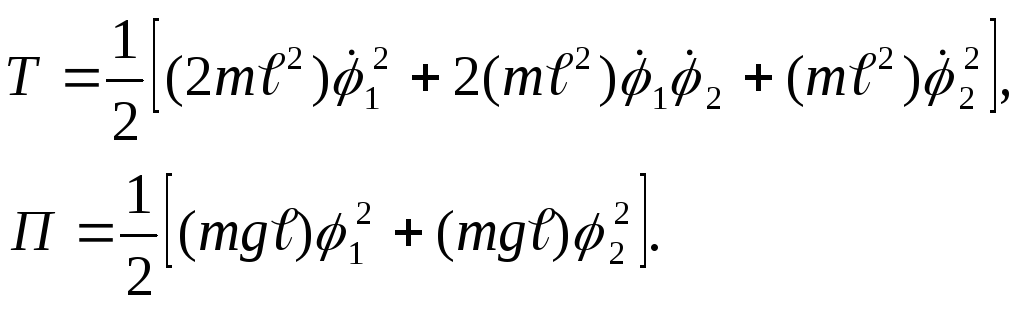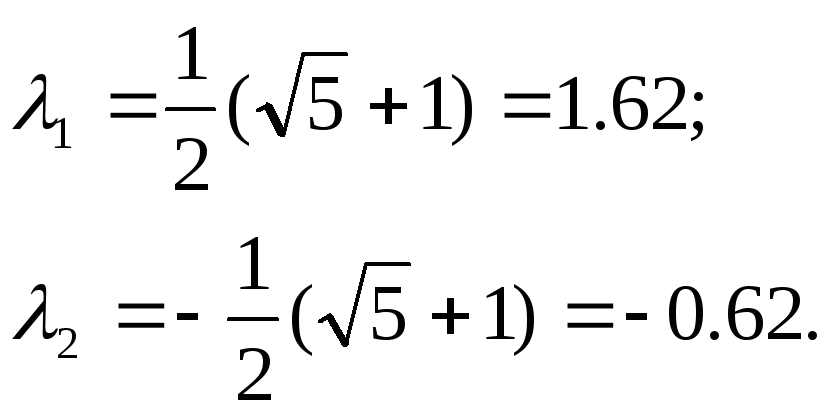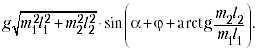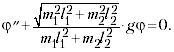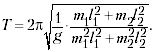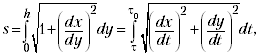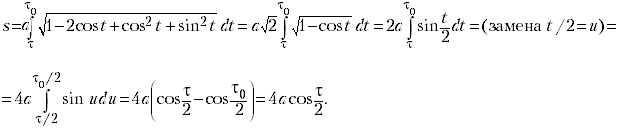Как найти период малых колебаний системы

Для системы с одной степенью свободы
уравнения Лагранжа при малых колебаниях:

Кинетическая и потенциальная энергия:

.

Выполняя над Т и П указанные действия,
получим:

(10.5)

или

(10.6)

где
– угловая частота колебаний,– период.

Общее решение уравнения (10.6) можно
принять в одной из таких форм:

,

(10.7)

,

где
– произвольные постоянные, определяемые
по начальным условиям; А – амплитуда,
α – начальная фаза. Приняв во внимание
разложение функции,
нетрудно установить связь между одной
и другой парой постоянных:

.

(10.8)

Остановимся на первом представлении и
найдем постоянные Aи α.
Положим, что в начальный момент времениt= 0 задано:

(10.9)

Исходим из того, что

Сюда подставим t = 0и
(10.9):

Решая данную систему, найдем:

(10.10)

Замечание. Если в задаче требуется
определить лишь частоту или период
малых колебаний, то нет необходимости
в составлении и решении дифференциального
уравнения колебаний. В этом случае
достаточно составить кинетическую и
потенциальную энергию в форме
,
и затем найти то, что требуется:

Пример.

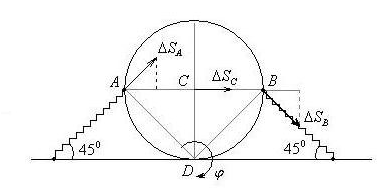
Однородный цилиндр радиуса Rи массыMможет кататься
без скольжения по горизонтальной
плоскости. В точках и цилиндра шарнирно
прикреплены пружины длинойи жесткостью каждая. Другие концы пружин
закреплены на плоскости катания. Когда
диаметрABгоризонтален
(положение равновесия), пружины не
напряжены. Определить период малых
колебаний цилиндра.

Рис. 49

Система имеет одну степень свободы. В
качестве обобщенной координаты возьмем
угол
поворота цилиндра. ТочкаDявляется мгновенным центром скоростей.
При малых колебаниях её можно считать
неподвижной. В решении задачи ничего
не изменится, если в точкеDввести неподвижный шарнир. Колебания
можно считать малыми до тех пор, пока
можно считать постоянными углы наклона
пружин к плоскости.

Перемещения точек при малых колебаниях
направлены по скоростям этих точек.
Причем для малых перемещений также
выполняется теорема о равенстве проекций.
Например, в нашей задаче:

Итак, сообщим цилиндру бесконечно малый
поворот
вокруг точкиD. Производнаябудет угловой скоростью. Кинетическая
энергия найдется по формуле:

где
.

Потенциальная энергия вызывается силами
упругости двух пружин. Перемещения
точек AиB:

направлены по осям пружин;
– удлинение,– осадка. Отсюда следует:

,

где
.

Период малых колебаний равен:

23.4 Малые свободные колебания системы с двумя степенями свободы

Пусть дана система с двумя степенями
свободы и
– обобщенные координаты. Кинетическая
и потенциальная энергия системы дается
формулами (10.2):

Функции Т и П определенно положительны,
а потому:

(10.11)

Уравнения Лагранжа для соответствующих
координат:

(10.12)

(9.46)

Подставив (10.2) в (10.12), получим дифференциальные
уравнения малых колебаний системы с
двумя степенями свободы:

(10.13)

Примем решение системы в виде:

,

(10.14)

где A,B,k,α– некоторые постоянные.
Подставив (10.14) в (10.13), и сократив на,
получим:

(10.15)

Система имеет нулевое решение A=B=0,
соответствующее устойчивому положению
равновесия. Для ненулевых решений
составим из (10.15) отношение:

.

(10.16)

Из первого равенства находим:

.

(10.17)

Данное условие, служащее для определения
частот, называют уравнением частот.
Запишем его в виде:

(10.18)

где
;.

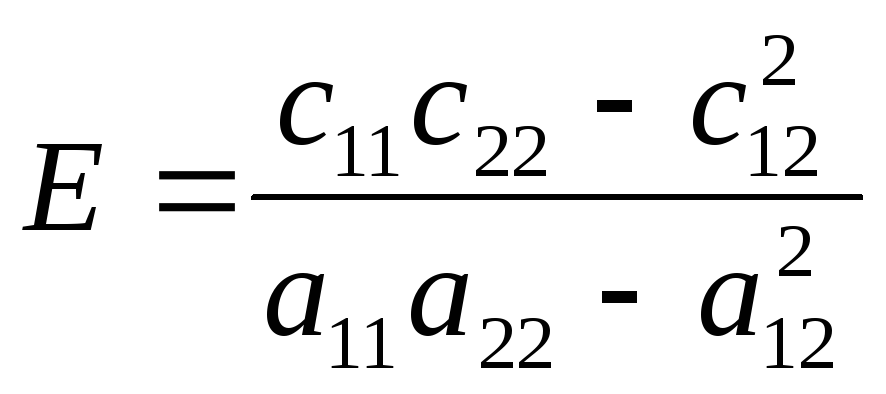
Квадратное (относительно
)
уравнение (10.18) в силу неравенств
устойчивости имеет два вещественных
положительных корня. Расположим их в
порядке возрастания:

(10.19)

Отсюда найдем две частоты. Одна из них
– низшая, другая– высшая. Это собственные частоты системы.
Колебание с частотойназывают первым главным колебанием, с
частотой– вторым главным колебанием системы.

Вернувшись к решению (10.14), мы можем
теперь записать – для первого главного
колебания:

(10.20)

Для второго главного колебания:

(10.21)

Главные колебания являются колебаниями
гармоническими.

Подставив поочередно
ив (10.16 ), найдем связи между амплитудамиAиBв главных
колебаниях:.
Множителииназывают коэффициентами собственных
форм (коэффициентами распределения
амплитуд). Они могут быть как положительными,
так и отрицательными. Приобе координаты в главном колебании
находятся в одной фазе; при– в противофазе.

Результирующее движение по каждой
координате будет суммой двух главных
колебаний:

(10.22)

где
– зависят от начальных условий,– от начальных условий не зависят и
определяются параметрами самой
колебательной системы. В общем случае
частотыинесоизмеримы, а потому результирующее
движение не будет периодическим.

Примеры.

1. Определить собственные частоты и
собственные формы колебаний (малых)
двойного математического маятника,
образованного двумя материальными
точками равной массы mи
двумя стержнями длинойкаждый.

Подобная система в общем виде была
рассмотрена в примере 2 (§34). Воспользуемся
полученными там формулами (2) и (3).

При
,
получим:

(1)

Функции Tи П должны быть
приведены к квадратичным формам:

(2)

Так как колебания малые, то с точностью
до малых второго порядка включительно:

(3)

С учетом (3) из (1), замечаем:

(4)

Сравнивая (4) и (2), замечаем:

Раскрывая уравнение (7.52) частот, получим:

Из (9.50) находим коэффициенты распределения:
.

Первое главное колебание:

Движение в фазе – в каждое мгновение
стержни вращаются в одном направлении.

Второе главное колебание:

Движение в противофазе – в каждое
мгновение стержни вращаются в прямо
противоположных направлениях.

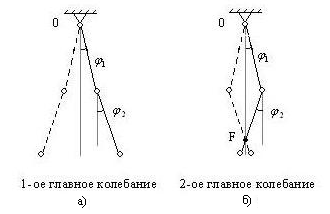
Формы колебаний показаны на рис. 50. Во
втором главном колебании имеется
особенная точка F, которая
остается неподвижной. Такие точки
называют узлами. Концевая точкаOк узлам не относится.

Рис. 50

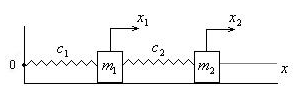
2. Два твердых тела с массами
ии две пружины, жесткостьюи,
объединены в систему, которая располагается
на гладкой горизонтальной плоскости и
может совершать малые прямолинейные
колебания.

Определить собственные частоты и
установить формы колебаний.

Рис. 51

Пусть
– обобщенные координаты, отсчитываемые
от положений равновесия тел. Кинетическая
и потенциальная энергия:

Для упрощения выкладок возьмем упрощенный
вариант:
.

В результате:

.

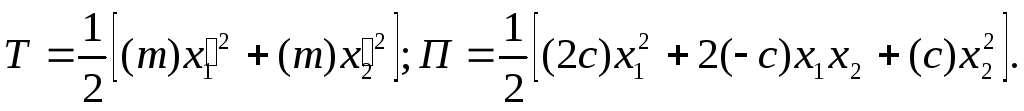
Коэффициенты квадратичных форм:

Уравнение для вычисления частот:

Его решение:

По формулам ( 9.50) находим:

Картина движения показана на рис. 52. При
втором главном колебании точка Fостается неподвижной (узел).

Рис. 52

Первое главное колебание:

Тела движутся в фазе, либо вправо либо
влево. Амплитуда колебаний второго тела
в 1,62 раза больше.

Второе главное колебание:

Тела движутся в противофазе: либо
навстречу друг другу, к узлу, либо
расходятся от узла. Амплитуда колебаний
второго тела составляет 0,62 амплитуды
первого.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Период
Размерность	T
Единицы измерения
СИ	с

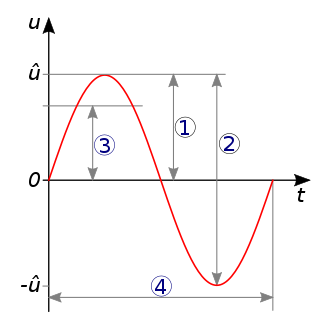
Пери́од колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором она находилась в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: (хотя могут применяться и другие, наиболее часто это , иногда и т. д.).

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

Для волновых процессов период связан кроме того очевидным образом с длиной волны

где  — скорость распространения волны (точнее^[2] — фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота^[3] колебаний его волновой функции).

Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Периоды колебаний в природе[править | править код]

Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот электромагнитных колебаний (см. Электромагнитный спектр) .

Периоды колебаний слышимого человеком звука находятся в диапазоне

от 5·10⁻⁵с до 0,2с

(четкие границы его несколько условны).

Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне

от 1,1·10⁻¹⁵с до 2,3·10⁻¹⁵с.

Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц.

В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено^[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.

Периоды колебаний простейших физических систем[править | править код]

Пружинный маятник[править | править код]

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

,

где  — масса груза,  — жёсткость пружины.

Математический маятник[править | править код]

Период малых колебаний математического маятника:

где  — длина подвеса (к примеру, нити),  — ускорение свободного падения. Отсюда видно, что период колебаний маятника зависит только от длины подвеса и ничего более.

Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью^[5] равен 2 секундам.

Физический маятник[править | править код]

Период малых колебаний физического маятника:

где  — момент инерции маятника относительно оси вращения,  — масса маятника,  — расстояние от оси вращения до центра масс.

Крутильный маятник[править | править код]

Период колебаний крутильного маятника:

где  — момент инерции маятника относительно оси кручения, а  — вращательный коэффициент жёсткости маятника.

Электрический колебательный (LC) контур[править | править код]

Период колебаний электрического колебательного контура (формула Томсона):

,

где  — индуктивность катушки,  — ёмкость конденсатора.

Эту формулу вывел в 1853 году английский физик Уильям Томсон.

Примечания[править | править код]

Ссылки[править | править код]

• [bse.sci-lib.com/article088257.html Период колебаний] — статья из Большой советской энциклопедии

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок bse.sci-lib.com/article088257.html

2018-05-31   

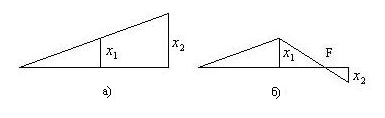
Найти период малых вертикальных колебаний тела массы $m$ в системе (рис.). Жесткости пружинок равны $chi_{1}$ и $chi_{2}$, а их массы пренебрежимо малы.

Решение:

Во время вертикального колебаний тело находится на расстоянии х от положения равновесия. В этот момент, если $x_{1}$ и $x_{3}$ являются дополнительными удлинениями верхних и нижних пружин относительно положения равновесия, то неуравновешенная сила на теле будет $chi_{2} x_{2}$, направленная вверх. Следовательно

$- chi_{2} x_{2} = m ddot{x}$ (1)

Мы также значем, что $x= x_{1} + x_{2}$ (2)

Поскольку пружины безмассовые, и изначально сила на пружине также равна нулю, поэтому

$chi_{1} x_{1} = chi_{2}x_{2}$ (3)

Решая уравнения (1), (2) и (3) одновременно, получаем

$- frac{ chi_{1} chi_{2} }{ chi_{1} + chi_{2} } x = m ddot{x}$

Таким образом $ddot{x} = – frac{( chi_{1} chi_{2} / chi_{1} + chi_{2} ) }{m}x$

Следовательно, искомый период колебаний $T = 2 pi sqrt{ m frac{ chi_{1} + chi_{2} }{ chi_{1} chi_{2} } }$

Период гармонических колебаний

В.Б.ДРОЗДОВ, г. Рязань

Период гармонических колебаний

В учебнике «Физика-11» (Г.Я.Мякишев,
Б.Б.Буховцев. – М.: Просвещение, 2004) дан вывод
формулы Томсона
основанный на постоянстве полной
электромагнитной энергии колебательного
контура. Представляет интерес применить этот
метод к различным колебательным системам, в
которых происходят свободные незатухающие
гармонические колебания, для определения
периода этих колебаний. Данный способ позволяет
получить дифференциальное уравнение колебаний откуда следует
формула для периода колебаний При этом достигается
единообразие в решении различных задач на
определение периода колебаний, а также
достигается элементарное решение ряда задач.
Становится возможным, не выходя за рамки
школьного курса, определить период колебаний
некоторых физических маятников. Такого рода
задачи предлагаются на вступительных экзаменах
в вузы с повышенными требованиями по физике.
Рассмотрим конкретные примеры.

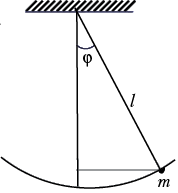
1. Математический маятник.

Пусть
– мгновенное значение скорости маятника,
соответствующее отклонению нити от вертикали на
угол . Тогда
кинетическая энергия маятника потенциальная энергия

E_p = mgl(1 – cos ).

По закону сохранения энергии,

Дифференцируем равенство по времени t,
учитывая что
Так как ‘ = 0
лишь в моменты максимального отклонения
маятника от положения равновесия, то – дифференциальное
уравнение движения математического маятника.
Пусть 1, значит, sin . Тогда из уравнения
гармонических колебаний получим период

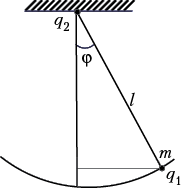
Рассмотрим маятник, несущий
электрический заряд q₁, если в точку
подвеса помещён заряд q₂. Имеем:

Слагаемое

не зависит от времени, следовательно,
получится такое же уравнение колебаний, что и для
незаряженного маятника. Поэтому период
колебаний от зарядов q₁ и q₂
не зависит.

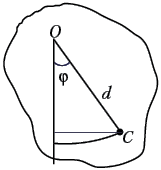
2. Физический маятник.
Физический маятник – это твёрдое тело, которое
может качаться вокруг неподвижной
горизонтальной оси. Масса маятника m, момент
инерции относительно оси J. Расстояние между
центром масс маятника C и точкой подвеса O
равно d.

Пусть – мгновенное значение угловой
скорости маятника, соответствующее отклонению
отрезка OC от вертикали на угол . По закону сохранения
энергии,

Дифференцируем это равенство по
времени t, учитывая, что = ‘. В результате имеем
дифференциальное уравнение колебаний:

а для
малых углов –
уравнение гармонических колебаний с периодом

3. Задача Ф 477 («Квант», 1977, № 9).

Резиновое кольцо массой M лежит на
гладкой горизонтальной плоскости. Кольцо
немного растягивают так, что оно сохраняет форму
окружности и центр его остаётся неподвижным.
После этого кольцо отпускают. Опишите дальнейшее
поведение кольца. Коэффициент упругости
резинового жгута равен k.

Решение. Пусть на рисунке x –
мгновенное смещение элементов кольца от
положения равновесия, соответствующее скорости этих элементов. Так
как все элементы кольца движутся с одной и той же
скоростью, то его кинетическая энергия E_k
= M²/2.

Поскольку кольцо растянуто на 2x, то его потенциальная
энергия По закону  сохранения энергии,

Дифференцируем это равенство по
времени, принимая во внимание, что = x’. Получим: – уравнение гармонических
колебаний с периодом

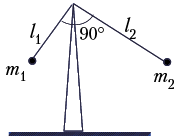
4. Задача Ф 380 («Квант», 1976, № 2).

Найдите период малых колебаний
системы из двух жёстко скреплённых под прямым
углом стержней с шарами на концах. Стержни
считать невесомыми, их длины l₁ и l₂,
массы шаров m₁ и m₂.

Решение. Определим угол , который образует стержень l₂
с вертикалью в положении равновесия, исходя из
того, что в состоянии равновесия потенциальная
энергия системы минимальна: откуда m₁gl_lsin + m₂gl₂cos = max.

Применяя формулу

получим: минимум потенциальной
энергии системы будет при

         (1)

Кинетическая энергия колебательной
системы

где –
угловая скорость вращения стержней l₁
и l₂ вокруг точки O. Пусть 1
рад – угол, на который отклонились стержни от
положения равновесия, тогда потенциальная
энергия системы

E_p = m₁gh – m₁gl₁
+ m₂gh
– m₂gl₂cos( + ) =
(m₁ + m₂)gh – g[m₁l₁sin( + ) + m₂l₂cos( + )] =

= (m₁ + m₂)gh –

С учётом равенства (1) имеем:

E_p = (m₁ + m₂)
gh –

Закон сохранения энергии даёт
уравнение

откуда при 1 получим
уравнение гармонических колебаний:

Период колебаний

Энергетический метод позволяет
упростить элементарное решение задачи (без
использования формулы для периода колебаний
физического маятника). Наиболее же простое
решение получится, если применить формулу

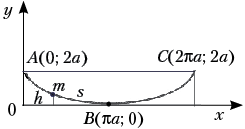
5. Циклоидальный маятник.

Рассмотрим материальную точку,
скользящую без трения по траектории, имеющей
форму одной арки циклоиды, обращённой
выпуклостью вниз. Параметрические уравнения
циклоиды:

По закону сохранения энергии,

где и h
– соответствующие дуге s скорость точки и её
высота над осью абсцисс. Длину дуги s
отсчитываем от положения равновесия точки на
циклоиде.

Скорость точки  = s’.
Из системы уравнений нетрудно получить h = s²/(8a).
Тогда Из
последнего уравнения имеем: – уравнение гармонических
колебаний с периодом

КОММЕНТАРИЙ РЕДАКЦИИ: «Так ли уж
„нетрудно” получить?»

Задав циклоиду в параметрическом виде

x = a(t – sin t),

y = a(1 + cos t).

вычислим длину дуги циклоиды от её
нижней точки до точки, где у = h, лежащей
левее нижней точки (в точности, как у автора).
Сведения из математического анализа дают рецепт:

где ₀
= отвечает нижней
точке циклоиды,
< отвечает точке
циклоиды, в которой y = h;

В таком случае

Как мы договорились выше, y() = a(1+cos) = h. Поэтому

В итоге как и
обещал любезный автор. И никаких особенных
умений не нужно. Какой-то вузовский курс
матанализа плюс некие навыки нехитрого
интегрирования. И вот: не прошло и получаса, как
ответ готов.

Мы в редакции будем весьма
признательны автору, если он пришлёт нам
вычисления, которые действительно покажут, что
ответ в задаче «нетрудно получить».

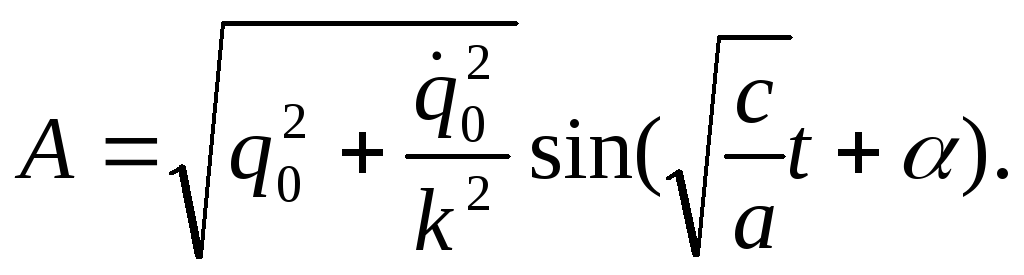
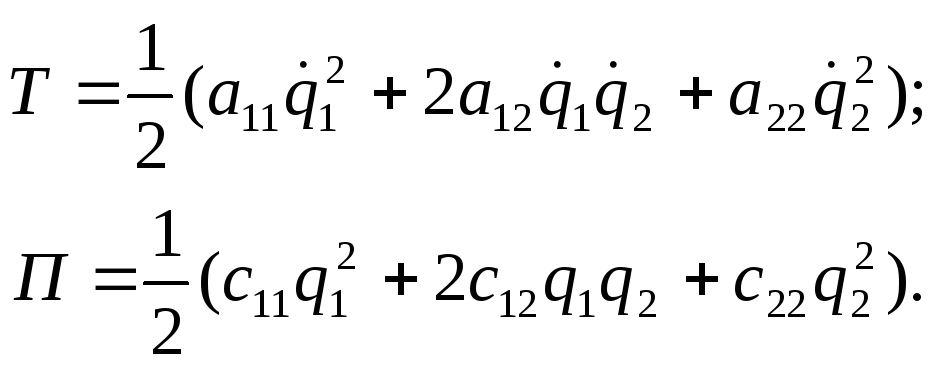
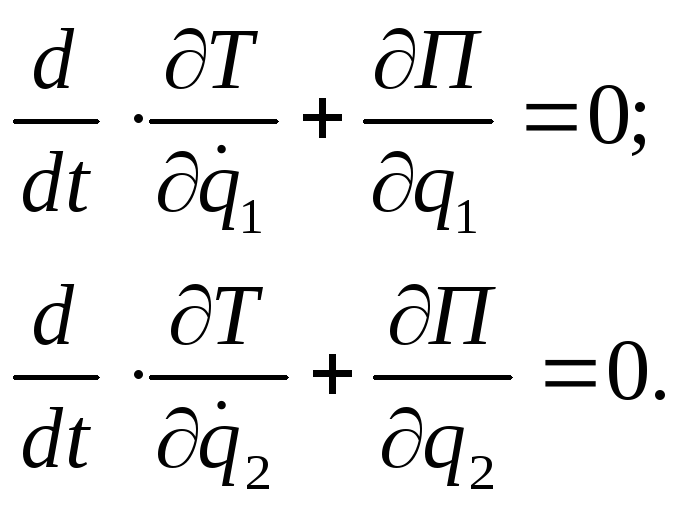
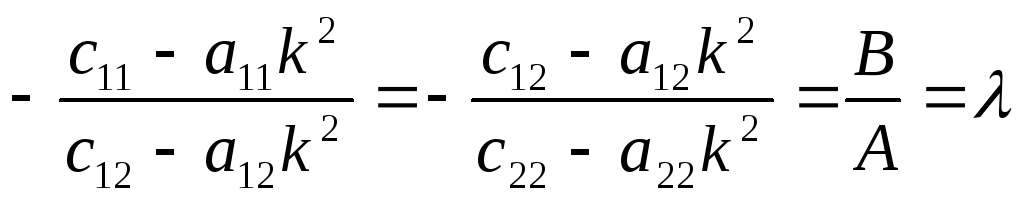В.Г.ГРИБОВ, к.ф.-м.н.,
доцент физфака МГУ им. М.В.Ломоносова