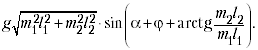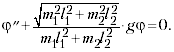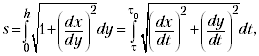Тема: Определить период Т малых колебаний стержня (Прочитано 7431 раз)
0 Пользователей и 1 Гость просматривают эту тему.
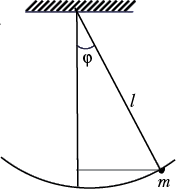
Тонкий однородный стержень длиной 0,48м может вращаться вокруг горизонтальной оси, проходящей на расстоянии 1/3 его длины от одного из его концов. Определить период Т малых колебаний стержня.
Решение:
Имеем физический маятник, период колебаний которого определяется формулой
( T=2*pi*sqrt{frac{J}{mgd}} )
где J – момент инерции стержня относительно точки подвеса, который надо посчитать при помощи теоремы Штейнера
( J=J_0+md^2 )
Здесь
( J_0=frac{ml^2}{12} ) – момент инерции стержня, когда ось колебания проходит через центр тяжести, – расстояние от центра тяжести до точки подвеса ( d=0.16 ) м
Окончательно
( T=2*pi*sqrt{frac{J}{mgd}}=2*pisqrt{frac{l^2+12d^2}{12gd}} )
Правильно?
« Последнее редактирование: 19 Января 2012, 01:18:55 от Asix »

“d – расстояние от центра тяжести до точки подвеса” сами же написали.
Стержень однородный, т.е. его центр тяжести расположен в его геометрическом центре, т.е. на расстоянии L/2 от края стержня, где L – длина стержня. Точка подвеса расположена на расстоянии L/3 от края стержня по условию. Тогда d = L/2 – L/3 = L/6 = 0,08 м.
Остальное верно.
Благодарю за поправку
Период колебаний стержня
#5812
2011-05-03 14:31 GMT
Найти период колебаний стержня длиной 0,70 м, совер-
шающего малые колебания в вертикальной плоскости около
горизонтальной оси, если ось проходит через точку, нахо-
дящуюся на расстоянии 10 см от его верхнего конца.
#5828
2011-05-04 14:57 GMT
Имеем физический маятник, период колебаний которого определяется формулой
(T=2pisqrt{frac{J}{mgd}}),
где (J) – момент инерции стержня относительно точки подвеса, который надо посчитать при помощи теоремы Штейнера
(J=J_0+md^2).
Здесь
(J_0=frac{ml^2}{12}) – момент инерции стержня, когда ось колебания проходит через центр тяжести, (d) – расстояние от центра тяжести до точки подвеса (d=0,25{м})
Окончательно
(T=2pisqrt{frac{J}{mgd}}=2pisqrt{frac{l^2+12d^2}{12gd}})
Найти период малых колебаний стержня.
ech pochma
Ученик
(53),
закрыт
1 год назад
Однородный тонкий стержень длины 50 см подвешен за верхний конец. Найти период малых колебаний стержня.
Владимир Александрович
Высший разум
(102904)
1 год назад
См. Картинки 1 и 2:
Т = 2п*sqrt(J/(mgL)).
Длина стержня l = 2L = 0,50 м. Масса — m.
Для нашего случая: J = m*(2L)^2/3.
Значит, Т = 2п*sqrt(m*(2L)^2/(3*mgL)) = {{масса m сокращается) = 2*3.14*sqrt(4*L/(3g)) = 2*3.14*sqrt(4*0.25/(3*9.8)) = 1.1582 = 1,16 с.
Ответ: Т = 1,16 с. 
ech pochmaУченик (53)
1 год назад
Огромное спасибо!) Все понятно и не сложно оказалось!
Владимир Александрович
Высший разум
(102904)
ech pochma, — УСПЕХОВ !!!Все есть в учебнике и даже в интернете.
Уравнение колебаний стержня относительно оси проходящей через его конец
Вращательное движение твердых тел
Однородный стержень длиной l = 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальный оси, проходящей через его верхний конец. Найти период колебаний T стержня.
Дано:
Решение:
Стержень, совершающий колебания вокруг оси, проходящей через его верхний конец, представляет физический маятник. Период колебаний физического маятника
Момент инерции стержня находим по теореме Штейнера
Колебания механических систем
3. Колебания механических систем
3.1. Физический маятник
3.1.1. Физический маятник представляет собой однородный стержень длины l = 2 м. Колебания происходят вокруг горизонтальной оси, перпендикулярной стержню и проходящей через его верхний конец.
1. Момент инерции стержня относительно горизонтальной оси колебаний определится как
. (1)
2. Период малых колебаний физического маятника при расстоянии от центра масс до оси колебаний d = l/2, определится посредствам уравнения

3.1.2. Физический маятник представляет собой тонкий стержень длиной l = 2 ми массой m0 = 1 кг, на концах которого закреплены свинцовые шарики массами m1 = m2 = 0,5 кг. Маятник совершает малые колебания вокруг оси, проходящей через середину стержня перпендикулярно его оси. Определить период колебаний.
1. Период колебаний физического маятника определяется уравнением

где Jz – момент инерции маятника относительно оси колебаний z, M – масса маятника, lС – расстояние от центра масс маятника до оси.
2. Маятник состоит из двух точечных масс m1 и m2 и массы стержня m0, поэтому его суммарный момент инерции определится как

3. Поскольку маятник симметричен, то ось вращения будет проходить через центр масс, т. е. lC = l/2, поэтому период маятника определится следующим уравнением

3.1.3. В условиях предыдущей задачи массы шаров равны m1 = 0,3 кг, m2 = 0,6 кг. Определить период колебаний стержня, длина и масса которого остались неизменными.
1. В этом случае момент инерции стержня с шарами определится посредствам уравнения

2. Так как на концах стержня закреплены шары разной массы, то ось z, вокруг которой происходят колебания, не будет совпадать с центром масс. Определим положение центра масс маятника



3. Период колебаний маятника

3.1.4. Однородный диск радиусом R = 30см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Определите период колебаний этого физического маятника.
1. В данном случае расстояние между осью, относительно которой происходят колебания и центром масс диска равно радиусу диска, т. е. lC = R.
2. Момент инерции диска относительно оси, проходящий через образующую диска определяется как
. (1)
3. Период колебаний такого физического маятника будет равен
. (2)
3.1.5. На концах невесомого тонкого стержня длиной l = 1 м укреплены одинаковые грузы. Стержень совместно с грузами колеблется вокруг вертикальной оси, проходящей через точку, удалённую на расстояние d = 0,25 м от одного из грузов. Определить период колебаний маятника и его приведённую длину.
1. Определим расстояние между центром масс и осью z, вокруг которой происходят колебания
. (2)
2. Определим момент инерции маятника
. (3)
3. Период колебаний данного физического маятника
. (4)
4. Приведённая длина маятника определится как
. (5)
3.1.6. На концах невесомого тонкого стержня длиной l = 0,3 м укреплены одинаковые точечные грузы. Стержень совместно с грузами колеблется вокруг горизонтальной оси, проходящей через точку, удалённую на расстояние d = 0,1 м от одного из концов стержня. Определить период колебаний маятника и его приведённую длину.
1. В отличие от предыдущей задачи, где колебания происходили в плоскости перпендикулярной вектору силы тяжести, т. е. при движении системы потенциальная энергия не изменялась, в данном случае изменение относительного положения грузов будет сопровождаться изменением потенциальной энергии системы. Момент инерции, при этом, определится как
. (1)
2. Период колебаний такого физического маятника, при учёте того, что lC = l/4, будет определяться уравнением (4) предыдущей задачи
. (2)
3. Приведённая длина маятника
. (3)
3.1.7. На невесомом стержне длиной l = 0,3 м закреплены два одинаковых шарика: один в середине стержня, а второй – на одном из его концов. Система тел колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить период колебаний и приведённую длину этого физического маятника.
1. Определим положение центра масс данной механической системы
. (1)
2. Найдём далее момент инерции маятника относительно горизонтальной оси вращения
. (2)
3. Приведённая длина физического маятника, с учётом того, что расстояние между центром масс маятника и осью, вокруг которой происходят колебания d = 3l/4
. (4)
4. Период колебаний маятника
. (5)
3.1.8. Физический маятник представляет собой систему трёх точечных грузов, соединённых невесомыми стержнями одинаковой длины l = 0,3 м колеблется вокруг горизонтальной оси, проходящей перпендикулярно плоскости чертежа через общую точку О стержневой системы. Определить период колебаний маятника.
1. Определим положение центра масс относительно оси колебаний, проходящих через точку О
, (1)
. (2)
2. Расстояние между центром масс и осью колебаний составит
. (3)
3. Момент инерции анализируемой колебательной системы относительно оси, проходящей через точку О перпендикулярно плоскости чертежа
. (4)
4. Период колебаний маятника
. (5)
3.1.9. Тонкий обруч радиусом R = 0,3 м колеблется вокруг вбитого горизонтально в стену гвоздя, так что плоскость колебания параллельна стене. Определить период колебаний такого физического маятника.
1. В данном случае центр масс обруча не совпадает с осью колебаний, для определения момента инерции относительно оси колебаний х, перпендикулярной плоскости чертежа необходимо воспользоваться теоремой Гюйгенса – Штейнера
. (1)
2. Период колебаний обруча
. (2)
3.1.10. Однородный диск радиусом R = 0,3 м колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Определить период колебаний.
1. Так же как и в предыдущей задаче, центр масс диска не совпадает с положением оси х, относительно которой колеблется физический маятник. Для определения момента инерции диска относительно оси х воспользуемся теоремой Гюйгенса – Штейнера
. (3)
2. Период колебаний маятника с учётом того, что d = R, определится посредствам следующего уравнения
. (4)
3.1.11. Диск радиусом R = 0,24 м колеблется вокруг горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведённую длину и период колебаний маятника.
1. По методике, использованной в предыдущих задачах определим момент инерции диска относительно горизонтальной оси х, которая разнесена с осью колебаний на расстояние d = R
. (2)
2. Приведённая длина физического маятника
. (3)
3. Период колебаний
. (4)
3.1.12. Математический маятник длиной l1 = 0,4 м и физический маятник в виде тонкого прямоугольного стержня длиной l2 = 0,6 м синхронно колеблются около одной горизонтальной оси. Определить расстояние d между центром масс стержня и осью его колебаний.
1. Поскольку колебания математического и физического маятников синхронные, то периоды будут одинаковыми
.
3.1.13. Физический маятник представляет собой однородный диск радиусом r = 0,4 м, горизонтальная ось колебаний которого проходит на расстоянии d = r/4 от центра масс диска. Определить период малых колебаний диска.
1. Момент инерции диска относительно оси, проходящей центр масс, определяется уравнением
. (1)
2. Момент инерции относительно параллельной оси, отстоящей на расстоянии d, определим с помощью теоремы Гюйгенса – Штейнера
. (2)
3. Период малых колебаний этого физического маятника запишется следующим образом
. (3)
3.2. Свободные колебания механических систем
3.2.1. Определить частоту малых колебаний тонкого однородного стержня массой m = 1 кг длиной l = 1 м вокруг горизонтальной оси, проходящей через точку О, если противоположный конец стержня присоединён к пружине жёсткости k = 100 Н/м. В статическом положении стержень вертикален и пружина не деформирована.
1. Момент инерции стержня относительно оси колебаний
. (1)
2. Рассматриваемая конструкция физического маятника в соответствие с уравнением (1) имеет следующее значение приведённой массы
(2)
3. Циклическая частота колебаний стержня при условии равенства расстояния от оси колебаний до центра масс d = l/2 определится уравнением
. (3)
4. Циклическая частота собственных колебаний стержня, один конец которого присоединён к пружине жёсткостью k
. (4)
5. Период собственных малых колебаний физического маятника
. (4)
3.2.2. Однородный стержень массой m = 1 кг совершает колебания вокруг горизонтальной оси, проходящей через точку О, свободный конец стержня соединён с вертикальной пружиной жёсткости k = 10 Н/м. Определить период малых колебаний физического маятника.
1. Физический маятник в данном случае можно рассматривать как часть массы стержня подвешенной к вертикальной пружине. Присоединённую к пружине массу определим их уравнения момента инерции стержня относительно горизонтальной оси, проходящей через точку О перпендикулярно плоскости чертежа
. (1)
2. Период колебаний в этом случае запишется как
. (2)
3.2.3. Найти циклическую частоту собственных малых свободных горизонтальных колебаний однородного диска массой m = 0,33 кг, соединённого с пружиной жёсткостью k = 50 Н/м. Качение диска по горизонтальной плоскости происходит без проскальзывания.
1. Если в качестве обобщённой координаты принять горизонтальное перемещение диска х, то уравнение его кинетической энергии можно представить в виде суммы энергии поступательного движения и энергии вращения
. (1)
2. Момент инерции диска относительно оси z, перпендикулярной плоскости чертежа и проходящей через точку крепления пружины к диску
. (2)
3. Подставим уравнение (2) в уравнение (1)
, (3)
приведённая масса, при этом, равна .
4. Определим частоту собственных колебаний
. (4)
3.2.4. Определить собственную частоту колебаний системы, состоящей из упруго закреплённой горизонтальной рейки А, которая лежит на подпружиненном цилиндре В и катке С. Массы рейки m1 = 1 кг и цилиндра m2 = 0,5 кг, жёсткости пружин: k1 = 20 Н/м, k2 = 10 Н/м, радиус качения цилиндра составляет r = 0,2 м. Расстояние от точки крепления вертикальной пружины до оси цилиндра l = 0,22 м.
1. Рассматриваемая в задаче колебательная система имеет одну степень свободы, поэтому положение любой движущейся точки, принадлежащей системе, можно однозначно охарактеризовать одной обобщённой координатой, в качестве которой целесообразно взять линейное перемещение рейки с началом системы отсчёта в положении статического равновесия.
3. При перемещении рейки на расстояние х каток поворачивается на угол .
4. Запишем уравнение кинетической энергии колебательной системы
. (2)
5. Подставим в уравнение кинетической энергии значение момента инерции цилиндра и его угловой скорости
. (3)
. (4)
6. Из уравнения (4) определим приведённую массу (инерционный коэффициент)
. (2)
7. Коэффициент упругости системы определим путём анализа уравнения потенциальной энергии системы
. (3)
8. Коэффициент упругости системы, таким образом, равен
. (4)
9. Циклическая частота собственных колебаний системы
. (5)
10. Собственная частота колебаний
. (6)
3.2.5. Найти циклическую частоту собственных колебаний механической системы, состоящей из балки длиной 2l с грузом на конце массой m = 1 кг. Второй конец балки закреплён шарнирно, в своей средней части балка опирается на пружину жёсткости k =36 H/м.
1. В положении равновесия пружина под действием веса груза деформируется на величину lj0, т. е. на середину балки действует сила упругости
. (1)
2. Уравнение моментов относительно центра шарнирной опоры позволяет определить величину j0
. (2)
3. Предположим далее, что после сообщения грузу импульса угол отклонения балки составит j + j0, что обеспечит действие со стороны пружины силы
. (3)
4. Уравнение вращательного движения балки относительно шарнира будет иметь следующий вид
, (4)
, (5)
. (6)
5. Приведённая масса системы, таким образом, определяется как
. (7)
6. Циклическая частота собственных колебаний
. (8)
3.2.6. Модель крыла самолёта или рулей глубины подводной лодки или торпеды можно представить в виде жёсткой пластинки с шарнирным закреплением одного конца и подпружиненным вторым концом. Пластинка обтекается потоком газа или жидкости со скоростью v, направленной вдоль пластины. Определить критическое значение скорости, соответствующее потере устойчивости пластинкой, т. е. возникновению колебаний.
1. При отклонении пластинки от горизонтального положения статического равновесия, когда на неё действует сила тяжести и реакции опор, возникают силы, обусловленные гидродинамическими давлениями. Главный вектор этих сил, приложенных в сечении пластинки, отстоящем на расстоянии b от упругой опоры
(1)
где СХ, СY – постоянные коэффициенты, r – плотность жидкости или газа, j – угол отклонения пластинки, l – длина пластинки.
2. Момент сил относительно шарнирного закрепления
, (2)
. (3)
3. Дифференциальное уравнение движения
. (4)
4. Условие устойчивости
. (5)
3.2.7. Вычислить кинетическую энергию механической системы, состоящей из пружины массой m и прикрепленного к ней груза массой M, совершающего малые гармонические свободные колебания. Смещение точек пружины пропорционально их расстоянию до подвеса О.
1. Кинетическая энергия колебательной системы будет складываться из энергии возвратно-поступательного движения груза и кинетической энергии движущейся пружины
, (1)
где KМ – кинетическая энергия тела массой М, Km – кинетическая энергия пружины.
2. Если выбрать вертикальную ось oy, направленную вниз, то кинетическую энергию тела можно представить в традиционном виде
. (2)
3. Энергию пружины будем рассматривать, задавшись её длиной в статическом состоянии l и линейной плотностью r (кг/м). Выделим на длине пружины элемент её длины ds, который будет иметь смещения x одинаковые по всей длине пружины и совпадающие со смещениями груза. Это даёт основание записать следующее соотношение
. (3)
4. Кинетическая энергия элемента пружины длины dy определится на основании уравнения (3) следующим образом
. (4)
. (5)
5. Энергию всей пружины определится посредствам определённого интеграла взятого в пределах от 0 до l:
(6)
. (7)
6. Реализуем уравнение (1), используя значения полученных энергий груза и пружины
, (8)
величина, стоящая в скобках называется приведённой массой колебательной системы.
Таким образом, уравнение (8) при заданном законе движения груза позволяет определить величину кинетической энергии колебательной системы в любой момент времени, включая и амплитудные значения, которые будут иметь место при sin(wt+j0) = 1.
Раздел 6. Свободные колебания систем с распределёнными параметрами
Основная особенность процесса свободных колебаний систем с бесконечным числом степеней свободы выражается в бесконечности числа собственных частот и форм колебаний. С этим связаны и особенности математического характера: вместо обыкновенных дифференциальных уравнений, описывающих колебания систем с конечным числом степеней свободы, здесь приходится иметь дело с дифференциальными уравнениями в частных производных. Кроме начальных условий, определяющих начальные смещения и скорости, необходимо учитывать и граничные условия, характеризующие закрепление системы.
6.1. Продольные колебания стержней
При анализе продольных колебаний прямолинейного стержня (рис.67,а) будем считать, что поперечные сечения остаются плоскими и что частицы стержня не совершают поперечных движений, а перемещаются только в продольном направлении.
Пусть u – продольное перемещение текущего сечения стержня при колебаниях; это перемещение зависит от расположения сечения (координаты x ) и от времени t . Таким образом, есть функция двух переменных; её определение и представляет основную задачу. Перемещение бесконечно близкого сечения равно , следовательно, абсолютное удлинение бесконечно малого элемента равно (рис.67,б), а относительное его удлинение .
Соответственно продольная сила в сечении с координатой х может быть записана в виде
, (173)
где жёсткость стержня при растяжении (сжатии). Сила N также является функцией двух аргументов – координаты х и времени t .
Рассмотрим элемент стержня, расположенный между двумя бесконечно близкими сечениями (рис.67,в). К левой грани элемента приложена сила N, а к правой – сила . Если обозначить через плотность материала стержня, то масса рассматриваемого элемента составляет . Поэтому уравнение движения в проекции на ось х
,
. (174)
Учитывая (173) и принимая A = const , получим
, (175)
. (176)
Следуя методу Фурье, ищем частное решение дифференциального уравнения (175) в виде
, (177)
т.е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента х , а другая только от аргумента t . Тогда вместо определения функции двух переменных u ( x , t ) необходимо определять две функции X( x ) и T( t ), каждая из которых зависит только от одной переменной.
Подставив (177) в (174), получим
,
где штрихами обозначена операция дифференцирования по x , а точками – по t . Перепишем это уравнение таким образом:
.
Здесь левая часть зависит только от x,а правая – только от t . Для тождественного выполнения этого равенства (при любых x и t ) необходимо, чтобы каждая из его частей была равна постоянной, которую обозначим через :
; . (178)
Отсюда следуют два уравнения:
; . (179)
Первое уравнение имеет решение:
, (180)
указывающее на колебательный характер, причём из (180) видно, что неизвестная величина имеет смысл частоты свободных колебаний.
Второе из уравнений (179) имеет решение:
, (181)
определяющее форму колебаний.
Частотное уравнение, определяющее величину , составляется путём использования граничных условий. Это уравнение всегда трансцендентное и имеет бесконечное число корней. Таким образом, число собственных частот бесконечно, причём каждому значению частоты соответствует своя функция Tn ( t ), определяемая зависимостью (180), и своя функция Xn ( x ), определяемая зависимостью (181). Решение (177) является лишь частным и не даёт полного описания движения. Полное решение получается путём наложения всех частных решений:
.
Функции Xn ( x ) называются собственными функциями задачи и описывают собственные формы колебаний. Они не зависят от начальных условий и удовлетворяют условию ортогональности, которое при А=const имеет вид
, если .
Рассмотрим некоторые варианты граничных условий.
Закреплённый конец стержня (рис.68,а). В концевом сечении перемещение u должно быть равно нулю; отсюда следует, что в этом сечении
Свободный конец стержня (рис.68,б). В концевом сечении продольная сила
(183)
должна тождественно равняться нулю, что возможно, если в концевом сечении X’=0.
Упругозакреплённый конец стержня (рис.68,в).
При перемещении u концевого стержня возникает упругая реакция опоры , где Со – жёсткость опоры. Учитывая (183) для продольной силы, получим граничное условие
,
если опора расположена на левом конце стержня (рис.68,в), и
,
если опора расположена на правом конце стержня (рис.68,г).
Сосредоточенная масса на конце стержня.
Развиваемая массой сила инерции:
.
Так как, согласно первому из уравнений (179), , то сила инерции может быть записана в виде . Получаем граничное условие
,
если масса находится на левом конце (рис.68,д), и
, (184)
если масса связана с правым концом (рис.68,е).
Определим собственные частоты консольного стержня (рис.68,a’).
Согласно (182) и (183), граничные условия
X’=0 при х= .
Подставляя поочерёдно эти условия в решение (181), получим
D=0; .
Условие С 0 приводит к частотному уравнению:
.
Корни этого уравнения
(n=1,2,…)
определяют собственные частоты:
(n=1,2,…). (185)
Первая (низшая) частота при n=1:
.
Вторая частота (при n=2):
и т. д.
Определим собственные частоты стержня с массой на конце (рис.68,е).
Согласно (182) и (184), имеем
при х= .
Подставляя эти условия в решение (181), получим:
D=0; .
Следовательно, частотное уравнение при учёте (176) имеет вид
.
Здесь правая часть представляет собой отношение массы стержня к массе концевого груза.
Для решения полученного трансцендентного уравнения необходимо воспользоваться каким-либо приближённым способом.
При и значения наиболее важного низшего корня будут соответственно 0.32 и 0.65 .
При малом отношении решающее влияние оказывает груз и хорошие результаты даёт приближённое решение
.
Для стержней переменного сечения, т.е. при А const , из (173) и (174) получается уравнение движения в виде
.
Это дифференциальное уравнение не поддаётся решению в замкнутом виде. Поэтому в подобных случаях приходится прибегать к приближённым методам определения собственных частот.
6.2. Крутильные колебания валов
Крутильные колебания вала с непрерывно распределенной массой (рис.69,а) описываются уравнениями, которые по структуре полностью совпадают с приведенными выше уравнениями продольных колебаний стержней.
Крутящий момент М в сечении с абсциссой х связан с углом поворота дифференциальной зависимостью, аналогичной (173):
, (186)
где Jp-полярный момент инерции поперечного сечения.
В сечении, расположенном на расстоянии dx , крутящий момент равен (рис.69,б):
.
Обозначая через (где – плотность материала вала) интенсивность момента инерции массы вала относительно его оси (т.е. момент инерции единицы длины), уравнение движения элементарного участка вала можно записать так:
,
или подобно (174):
.
Подставляя сюда выражение (186), при Jp=const получим, аналогично (175):
, (187)
.
Общее решение уравнения (187), как и уравнения (175), имеет вид
,
(188)
Собственные частоты и собственные функции при этом определяются конкретными граничными условиями.
В основных случаях закрепления концов аналогично случаю продольных колебаний получим
а) закрепленный конец ( =0): Х=0;
б) свободный конец (М=0): Х’=0;
в) упругозакрепленный левый конец: СоХ=GJpX ‘ ( Со-коэффициент жёсткости);
г) упругозакрепленный правый конец: – СоХ=GJpX ‘;
д ) диск на левом конце: (Jo-момент инерции диска относительно оси стержня);
е) диск на правом конце: .
Если вал закреплён на левом конце (х=0), а правый конец ( х= ) свободен, то Х=0 при х=0 и Х’=0 при x= ; собственные частоты определяются аналогично (185):
(n=1,2,…).
Если левый конец закреплён, а на правом конце имеется диск, получим трансцендентное уравнение:
.
Если оба конца вала закреплены, то граничные условия будут X=0 при х=0 и х= . В этом случае из (188) получим
; D=0,
(n=1,2,…),
отсюда находим собственные частоты:
.
Если левый конец вала свободен, а на правом конце имеется диск, то X’=0 при х=0 ; Jo X=GJpX ‘ при х= .
При помощи (188) находим
С=0; ,
или трансцендентное частотное уравнение:
.
6.3.Изгибные колебания балок
6.3.1.Основное уравнение
Из курса сопротивления материалов известны дифференциальные зависимости при изгибе балок:
; (189)
, (190)
где EJ – жёсткость при изгибе; y=y ( x , t ) – прогиб; M=M( x , t ) – изгибающий момент; q – интенсивность распределённой нагрузки.
Объединяя (189) и (190), получим
. (191)
В задаче о свободных колебаниях нагрузкой для упругого скелета являются распределённые силы инерции:
,
где m – интенсивность массы балки (масса единицы длины), и уравнение (191) принимает вид
.
В частном случае постоянного поперечного сечения, когда EJ = const , m = const , имеем:
. (192)
Для решения уравнения (192) полагаем, как и выше,
y = X ( x ) × T ( t ). (193)
Подставляя (193) в (192), приходим к уравнению:
.
Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через , получим два уравнения:
; (194)
. (195)
Первое уравнение указывает на то, что движение носит колебательный характер с частотой .
Второе уравнение определяет форму колебаний. Решение уравнения (195) содержит четыре постоянных и имеет вид
,
. (196)
Удобно использовать вариант записи общего решения, предложенный А.Н.Крыловым:
, (197)
(198)
представляют собой функции А.Н.Крылова.
Обратим внимание на то, что S=1, T=U=V=0 при x=0. Функции S,T,U,V связаны между собой следующим образом:
(199)
Поэтому производные выражения (197) записываются в виде
(200)
В задачах рассматриваемого класса число собственных частот бесконечно велико; каждой из них отвечает своя функция времени Tn и своя фундаментальная функция Xn . Общее решение получится путём наложения частных решений вида (193)
. (201)
Для определения собственных частот и формул необходимо рассмотреть граничные условия.
6.3.2. Граничные условия
Для каждого конца стержня можно указать два граничных условия .
Свободный конец стержня (рис. 70,а). Нулю равны поперечная сила Q=EJX”’T и изгибающий момент M=EJX”T. Поэтому граничные условия имеют вид
Шарнирно-опёртый конец стержня (рис.70,б). Нулю равны прогиб y=XT и изгибающий момент M=EJX”T. Следовательно, граничные условия таковы:
Защемленный конец (рис.70,в). Нулю равны прогиб y=XT и угол поворота . Граничные условия:
На конце стержня имеется точечный груз массы (рис.70,г). Его сила инерции может быть при помощи уравнения (194) записана так: ; она должна быть равна поперечной силе Q=EJX”’T , поэтому граничные условия принимают вид
; X”=0 . (205)
В первом условии знак плюс принимается в случае, когда точечный груз связан с левым концом стержня, и знак минус, когда он связан с правым концом стержня. Второе условие вытекает из отсутствия изгибающего момента .
Упруго-опертый конец стержня (рис.70,д). Здесь изгибающий момент равен нулю, а поперечная сила Q=EJX”’T равна реакции опоры (Co-коэффициент жёсткости опоры).
X”=0 ; (206)
(знак минус принимается в случае, когда упругая опора является левой, и знак плюс, когда она является правой).
6.3.3. Частотное уравнение и собственные формы
Развёрнутая запись граничных условий приводит к однородным уравнениям относительно постоянных C1, C2, C3, C4.
Чтобы эти постоянные не равнялись нулю, должен равняться нулю определитель, составленный из коэффициентов системы; это приводит к частотному уравнению. При этих операциях выясняются соотношения между C1, C2, C3, C4, т.е. определяются собственные формы колебаний (с точностью до постоянного множителя).
Проследим составление частотных уравнений на примерах.
Для балки с шарнирно-опёртыми концами согласно (203) имеем следующие граничные условия: X=0; X”=0 при x=0 и x= . При помощи (197)-(200) получим из первых двух условий: C1=C3=0. Два оставшихся условия можно записать в виде
Чтобы C2 и C4 не были равны нулю, необходимо равенство нулю определителя:
.
Таким образом, частотное уравнение имеет вид
.
Подставляя выражения T и U, получим
.
Так как , то окончательно частотное уравнение записывается так:
. (207)
Корни этого уравнения:
, ( n =1,2,3. ).
Учитывая (196), получим
. (208)
Перейдём к определению собственных форм. Из записанных выше однородных уравнений вытекает следующее соотношение между постоянными C2 и C4:
.
Следовательно, (197) приобретает вид
Согласно (207), имеем
, (209)
где – новая постоянная, значение которой остаётся неопределённым, пока не введены в рассмотрение начальные условия.
6.3.4. Определение движения по начальным условиям
Если требуется определить движение, следующее после начального возмущения, то необходимо указать для всех точек балки как начальные смещения, так и начальные скорости:
(210)
и использовать свойство ортогональности собственных форм:
.
Общее решение (201) запишем так:
. (211)
Скорость определяется выражением
. (212)
Подставляя в правые части уравнений (211) и (212) , а в левые части – предполагаемые известными начальные смещения и скорости, получим
.
Умножая эти выражения на и интегрируя по всей длине, имеем
(213)
Бесконечные суммы в правых частях исчезли вследствие свойства ортогональности. Из (213) следуют формулы для постоянных и
(214)
Теперь эти результаты нужно подставить в решение (211).
Снова подчеркнём, что выбор масштаба собственных форм несущественен. Если, например, в выражении собственной формы (209) принять вместо величину в раз большую, то (214) дадут результаты в раз меньшие; после подстановки в решение (211) эти различия компенсируют друг друга. Тем не менее часто пользуются нормированными собственными функциями, выбирая их масштаб таким, чтобы знаменатели выражений (214) равнялись единице, что упрощает выражения и .
6.3.5. Влияние постоянной продольной силы
Рассмотрим случай, когда колеблющаяся балка испытывает действие продольной силы N , величина которой не меняется в процессе колебаний. В этом случае уравнение статического изгиба усложняется и приобретает вид (при условии, что сжимающая сила считается положительной)
.
Полагая и считая жёсткость постоянной, получаем уравнение свободных колебаний
. (215)
Принимаем по-прежнему частное решение в виде .
Тогда уравнение (215) распадается на два уравнения:
Первое уравнение выражает колебательный характер решения, второе определяет форму колебаний, а также позволяет найти частоты. Перепишем его таким образом:
(216)
где K определяется формулой (196), а
. (217)
Решение уравнения (216) имеет вид
Рассмотрим случай, когда оба конца стержня имеют шарнирные опоры. Условия на левом конце дают . Удовлетворяя те же условия на правом конце, получим
Приравнивая нулю определитель, составленный из коэффициентов при величинах и , приходим к уравнению
,
. (218)
Корни этого частотного уравнения:
.
Следовательно, собственная частота определится из уравнения
.
Отсюда при учёте (217) находим
. (219)
При растяжении частота увеличивается, при сжатии уменьшается. Когда сжимающая сила N приближается к критическому значению, корень стремится к нулю.
6.3.6. Влияние цепных усилий
Ранее продольная сила считалась заданной и не зависящей от перемещений системы. В некоторых практических задачах сопровождающая процесс поперечных колебаний продольная сила возникает вследствие изгиба балки и носит характер реакции опоры. Рассмотрим, например, балку на двух шарнирно-неподвижных опорах. При её изгибе возникают горизонтальные реакции опор, вызывающие растяжение балки; соответствующее горизонтальное усилие принято называть цепным усилием. Если балка совершает поперечные колебания, то цепное усилие будет изменяться во времени.
Если в мгновение t прогибы балки определяются функцией , то удлинение оси можно найти по формуле
.
Соответствующее цепное усилие найдём при помощи закона Гука
.
Подставим этот результат в (215) вместо продольной силы N (с учётом знака)
. (220)
Полученное нелинейное интегродифференциальное уравнение упрощается при помощи подстановки
, (221)
где безразмерная функция времени, максимальное значение которой можно положить равным любому числу, например, единице; амплитуда колебаний.
Подставляя (221) в (220), получим обыкновенное дифференциальное уравнение
, (222)
коэффициенты которого имеют следующие значения:
; .
Дифференциальное уравнение (222) является нелинейным, следовательно, частота свободных колебаний зависит от их амплитуды.
Точное решение для частоты поперечных колебаний имеет вид
,
где частота поперечных колебаний, вычисленная без учёта цепных усилий; поправочный коэффициент, зависящий от отношения амплитуды колебаний к радиусу инерции поперечного сечения ; величина приводится в справочной литературе.
При соизмеримости амплитуды и радиуса инерции поперечного сечения поправка к частоте становится значительной. Если, например, амплитуда колебаний стержня круглого сечения равна его диаметру, то , и частота почти в два раза больше, чем в случае свободного смещения опор.
Случай соответствует нулевому значению радиуса инерции, когда изгибная жёсткость балки исчезающе мала – струна. При этом формула для даёт неопределённость. Раскрывая эту неопределённость, получим формулу для частоты колебаний струны
.
Эта формула относится к случаю, когда в положении равновесия натяжение равно нулю. Часто задачу о колебаниях струны ставят в других предположениях: считают, что перемещения малы, а растягивающая сила задана и остаётся неизменной в процессе колебаний.
При этом формула для частоты имеет вид
,
где N – постоянная растягивающая сила.
6.4. Влияние вязкого трения
Ранее предполагалось, что материал стержней идеально упругий и трение отсутствует. Рассмотрим влияние внутреннего трения, считая, что оно является вязким; тогда связь напряжений с деформациями описывается соотношениями
; . (223)
Пусть стержень с распределёнными параметрами совершает свободные продольные колебания. В этом случае продольная сила запишется в виде
. (224)
Из уравнения движения элемента стержня было получено соотношение (174)
.
Подставляя сюда (224), приходим к основному дифференциальному уравнению
, (225)
которое отличается от (175) вторым слагаемым, выражающим влияние сил вязкого трения.
Следуя методу Фурье, ищем решение уравнения (225) в виде
, (226)
где функция только координаты x , а функция только времени t .
При этом каждый член ряда должен удовлетворять граничным условиям задачи, а вся сумма – также и начальным условиям. Подставляя (226) в (225) и требуя, чтобы равенство удовлетворялось для любого номера r , получим
, (227)
где штрихи обозначают дифференцирование по координате x , а точки – дифференцирование по времени t .
Разделив (227) на произведение , приходим к равенству
, (228)
левая часть, которого может зависеть только от координаты x , а правая – только от времени t . Для тождественного выполнения равенства (228) необходимо, чтобы обе части были равны одной и той же постоянной, которую обозначим через .
Из этого следуют уравнения
(229)
. (230)
Уравнение (229) не зависит от коэффициента вязкости K и, в частности, остаётся таким же в случае идеально упругой системы, когда . Поэтому числа полностью совпадают с найденными ранее; однако, как будет показано ниже, величина даёт лишь приближённое значение собственной частоты. Отметим, что собственные формы совершенно не зависят от вязких свойств стержня, т.е. формы свободных затухающих колебаний совпадают с формами свободных незатухающих колебаний.
Теперь перейдём к уравнению (230), описывающему процесс затухающих колебаний; его решение имеет вид
, (231)
; (232)
. (233)
Выражение (232) определяет темп затухания, а (233) – частоту колебаний.
Таким образом, полное решение уравнения задачи
. (234)
Постоянные и всегда можно найти по заданным начальным условиям. Пусть начальные смещения и начальные скорости всех сечений стержня заданы следующим образом:
; , (235)
где и – известные функции.
Тогда при , согласно (211) и (212), имеем
умножая обе части этих равенств на и интегрируя в пределах всей длины стержня, получим
(236)
Соответственно условию ортогональности собственных форм все остальные слагаемые, входящие в правые части этих равенств, обращаются в нуль. Теперь из равенств (236) легко найти и для любого номера r .
Рассматривая (232) и (234), заметим, что чем выше номер формы колебаний , тем быстрее её затухание. Кроме того, слагаемые, входящие в (234), описывают затухающие колебания, если есть действительное число. Из (233) видно, что это имеет место лишь для нескольких начальных значений r , пока выполняется неравенство
. (237)
При достаточно больших значениях r неравенство (237) нарушается и величина становится мнимой. При этом соответствующие члены общего решения (234) уже не будут описывать затухающие колебания, но будут представлять апериодическое затухающее движение. Другими словами, колебания, в обычном смысле слова, выражает только некоторая конечная часть суммы (234).
Все эти качественные выводы относятся не только к случаю продольных колебаний, но и к случаям крутильных и изгибных колебаний.
6.5. Колебания стержней переменного сечения
В тех случаях, когда распределённая масса и сечение стержня переменны по его длине, следует вместо уравнения продольных колебаний (175) исходить из уравнения
. (238)
Уравнение крутильных колебаний (187) должно быть заменено уравнением
, (239)
а уравнение поперечных колебаний (192) – уравнением
. (240)
Уравнения (238)-(240) при помощи однотипных подстановок ; ; можно привести к обыкновенным дифференциальным уравнениям для функции
(241)
(242)
(243)
и одному однотипному уравнению для функции .
Уравнения (241)-(243) в отличие от уравнений, решённых выше, имеют переменные коэффициенты.
Замкнутую форму решений можно получить лишь в отдельных случаях, когда переменные определены специальными зависимостями. В общем случае неизбежен переход к приближённым методам. В частности, возможен путь, основанный на сосредоточении распределённой массы в ряде точек по длине стержня, после чего система сохраняет лишь конечное число степеней свободы, равное числу точек приведения. Используются также различные варианты вариационного метода и некоторые другие приближённые методы, о которых речь пойдёт ниже.
6.6. Колебания круговых колец
6.6.1. Колебания в плоскости кольца
Рассмотрим круговой брус малой кривизны постоянного сечения с радиусом R осевой линии (рис.71,а). Будем считать груз нерастяжимым. Перемещение центра тяжести поперечного сечения, зафиксированного угловой координатой , можно разложить на радиальный и окружной компоненты – соответственно и . Из условия нерастяжимости оси бруса следует, что перемещения и связаны зависимостью:
. (244)
Угол поворота поперечного сечения бруса в процессе движения определяется формулой
. (245)
Изменение кривизны бруса равно производной от по дуге:
. (246)
Изгибающий момент в поперечном сечении кольца:
. (247)
Теперь составим уравнение движения элемента бруса (рис.71,б).
Помимо перечисленных сил, на элемент действует также сила инерции:
,
где масса единицы длины бруса.
Проектируя приложенные к элементу силы на радиус, получим
. (248)
Равенство нулю суммы проекций всех сил на направление касательной приводит к уравнению:
. (249)
Уравнение моментов имеет вид
. (250)
Исключим из (248) и (249) нормальную силу N , а поперечную силу Q заменим её значением из (250):
. (251)
Подставляя сюда значение M из (247), получим уравнение движения в перемещениях , и, наконец, исключая один из компонентов перемещения, с помощью условия нерастяжимости (244) придём к уравнению, в которое входит единственная переменная :
. (252)
Решение уравнения движения (252) будем искать в виде
; .
При этом для получается обыкновенное дифференциальное уравнение
, (253)
.
Согласно общим правилам решения дифференциальных уравнений, следует найти общее решение уравнения (253), включающее шесть постоянных, и подчинить его граничным условиям. На каждом конце бруса должны быть равны нулю либо компоненты перемещений , либо соответствующие им внутренние силы. Равенство нулю определителя системы, выражающей граничные условия, приводит к частотному уравнению.
Для замкнутого кольца граничные условия заменяются условиями периодичности, которые выполняются, если принять
; . (254)
Подставляя (254) в (253), устанавливаем, что последнее удовлетворяется тождественно, если
. (255)
Формула (255) определяет частоты собственных колебаний кольца в своей плоскости. Значению соответствует нулевая частота, так как при формулы (254) описывают смещение кольца как жёсткого тела.
6.6.2. Колебания, перпендикулярные плоскости кольца
В этом случае положение поперечного сечения кольца в процессе движения характеризуется смещением его центра тяжести из плоскости кольца и углом поворота сечения х4 (рис.72,а). В поперечном сечении кольца возникают изгибающие и крутящие моменты (рис.72,б), а также поперечная сила, перпендикулярная плоскости кольца.
Установим зависимость моментов от перемещений. Так как задача линейная, то рассмотрим сначала силовые факторы, связанные со смещением х3, а затем – с х4.
Если х3 постоянно по длине окружности, то кольцо смещается как жёсткое целое, и внутренние силы не возникнут. Если х3 изменяется в зависимости от центрального угла по линейному закону , то ось бруса превращается в винтовую линию, т.е. брус деформируется подобно витку пружины при растяжении. Известно, что в этом случае в поперечных сечениях возникает крутящий момент
,
где GJ кр – крутильная жёсткость бруса.
Если при этом отлична от нуля и вторая производная , то меняется кривизна бруса и возникает изгибающий момент
,
где J 1 – момент инерции сечения относительно центральной оси, лежащей в плоскости кривизны.
Найдём силовые факторы, связанные с поворотом х4. Если х4 постоянно, то происходит осесимметричный изгиб кольца, причём в его сечениях возникает изгибающий момент
.
При переменном по длине повороте х4 соседние сечения поворачиваются друг относительно друга и возникает крутящий момент
.
Суммируя силовые факторы, связанные с перемещениями х3 и х4, ,получаем
(256)
Составим уравнение движения элемента Rd бруса (рис.73).
Будем пренебрегать инерцией поворота элемента вокруг своей оси.
Условие динамического равновесия в направлении нормали к плоскости кольца приводит к уравнению:
. (257)
Сумма моментов относительно нормали к оси элемента:
. (258)
Сумма моментов относительно касательной к оси элемента:
. (259)
Исключая поперечную силу из (257) и (258) и заменяя моменты в полученном уравнении и уравнении (259) их значениями (256), приходим к системе уравнений, в которую входят только перемещения х3 и х4:
(260)
Ограничиваясь исследованием собственных колебаний замкнутого кольца, решение уравнений (260) можно представить в виде
x3 = Acosk j × cos w t , x4 = Bcosk j × cos w t . (261)
Подставляя значения (261) в уравнение движения (260), получим
(262)
Из равенства нулю определителя этой системы получим частотное уравнение, корни которого – собственные частоты – таковы:
(263)
Наименьшая отличная от нуля частота соответствует k =2.
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
[spoiler title=”источники:”]
http://pandia.ru/text/78/558/21860.php
http://www.detalmach.ru/lectdinamika6.htm
[/spoiler]
Период гармонических колебаний
В.Б.ДРОЗДОВ, г. Рязань
Период гармонических колебаний
В учебнике «Физика-11» (Г.Я.Мякишев,
Б.Б.Буховцев. – М.: Просвещение, 2004) дан вывод
формулы Томсона
основанный на постоянстве полной
электромагнитной энергии колебательного
контура. Представляет интерес применить этот
метод к различным колебательным системам, в
которых происходят свободные незатухающие
гармонические колебания, для определения
периода этих колебаний. Данный способ позволяет
получить дифференциальное уравнение колебаний откуда следует
формула для периода колебаний При этом достигается
единообразие в решении различных задач на
определение периода колебаний, а также
достигается элементарное решение ряда задач.
Становится возможным, не выходя за рамки
школьного курса, определить период колебаний
некоторых физических маятников. Такого рода
задачи предлагаются на вступительных экзаменах
в вузы с повышенными требованиями по физике.
Рассмотрим конкретные примеры.
1. Математический маятник.
Пусть
– мгновенное значение скорости маятника,
соответствующее отклонению нити от вертикали на
угол . Тогда
кинетическая энергия маятника потенциальная энергия
Ep = mgl(1 – cos ).
По закону сохранения энергии,
Дифференцируем равенство по времени t,
учитывая что
Так как ‘ = 0
лишь в моменты максимального отклонения
маятника от положения равновесия, то – дифференциальное
уравнение движения математического маятника.
Пусть
1, значит, sin
. Тогда из уравнения
гармонических колебаний получим период
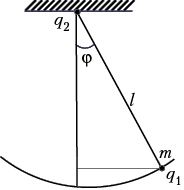
Рассмотрим маятник, несущий
электрический заряд q1, если в точку
подвеса помещён заряд q2. Имеем:
Слагаемое
не зависит от времени, следовательно,
получится такое же уравнение колебаний, что и для
незаряженного маятника. Поэтому период
колебаний от зарядов q1 и q2
не зависит.
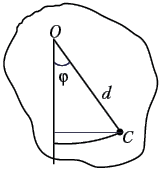
2. Физический маятник.
Физический маятник – это твёрдое тело, которое
может качаться вокруг неподвижной
горизонтальной оси. Масса маятника m, момент
инерции относительно оси J. Расстояние между
центром масс маятника C и точкой подвеса O
равно d.
Пусть – мгновенное значение угловой
скорости маятника, соответствующее отклонению
отрезка OC от вертикали на угол . По закону сохранения
энергии,
Дифференцируем это равенство по
времени t, учитывая, что =
‘. В результате имеем
дифференциальное уравнение колебаний:
а для
малых углов –
уравнение гармонических колебаний с периодом
3. Задача Ф 477 («Квант», 1977, № 9).
гладкой горизонтальной плоскости. Кольцо
немного растягивают так, что оно сохраняет форму
окружности и центр его остаётся неподвижным.
После этого кольцо отпускают. Опишите дальнейшее
поведение кольца. Коэффициент упругости
резинового жгута равен k.
Решение. Пусть на рисунке x –
мгновенное смещение элементов кольца от
положения равновесия, соответствующее скорости этих элементов. Так
как все элементы кольца движутся с одной и той же
скоростью, то его кинетическая энергия Ek
= M2/2.
Поскольку кольцо растянуто на 2x, то его потенциальная
энергия По закону сохранения энергии,
Дифференцируем это равенство по
времени, принимая во внимание, что = x’. Получим:
– уравнение гармонических
колебаний с периодом
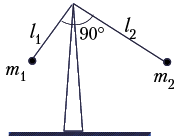
4. Задача Ф 380 («Квант», 1976, № 2).
Найдите период малых колебаний
системы из двух жёстко скреплённых под прямым
углом стержней с шарами на концах. Стержни
считать невесомыми, их длины l1 и l2,
массы шаров m1 и m2.
Решение. Определим угол , который образует стержень l2
с вертикалью в положении равновесия, исходя из
того, что в состоянии равновесия потенциальная
энергия системы минимальна: откуда m1gllsin
+ m2gl2cos
= max.
Применяя формулу
получим: минимум потенциальной
энергии системы будет при
(1)
Кинетическая энергия колебательной
системы
где –
угловая скорость вращения стержней l1
и l2 вокруг точки O. Пусть
1
рад – угол, на который отклонились стержни от
положения равновесия, тогда потенциальная
энергия системы
Ep = m1gh – m1gl1
+ m2gh
– m2gl2cos( +
) =
(m1 + m2)gh – g[m1l1sin( +
) + m2l2cos(
+
)] =
= (m1 + m2)gh –
С учётом равенства (1) имеем:
Ep = (m1 + m2)
gh –
Закон сохранения энергии даёт
уравнение
откуда при
1 получим
уравнение гармонических колебаний:
Период колебаний
Энергетический метод позволяет
упростить элементарное решение задачи (без
использования формулы для периода колебаний
физического маятника). Наиболее же простое
решение получится, если применить формулу
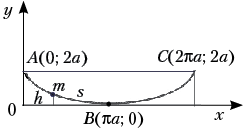
5. Циклоидальный маятник.
Рассмотрим материальную точку,
скользящую без трения по траектории, имеющей
форму одной арки циклоиды, обращённой
выпуклостью вниз. Параметрические уравнения
циклоиды:
По закону сохранения энергии,
где и h
– соответствующие дуге s скорость точки и её
высота над осью абсцисс. Длину дуги s
отсчитываем от положения равновесия точки на
циклоиде.
Скорость точки = s’.
Из системы уравнений нетрудно получить h = s2/(8a).
Тогда Из
последнего уравнения имеем: – уравнение гармонических
колебаний с периодом
КОММЕНТАРИЙ РЕДАКЦИИ: «Так ли уж
„нетрудно” получить?»
Задав циклоиду в параметрическом виде
x = a(t – sin t),
y = a(1 + cos t).
вычислим длину дуги циклоиды от её
нижней точки до точки, где у = h, лежащей
левее нижней точки (в точности, как у автора).
Сведения из математического анализа дают рецепт:
где 0
= отвечает нижней
точке циклоиды,
< отвечает точке
циклоиды, в которой y = h;
В таком случае
Как мы договорились выше, y() = a(1+cos
) = h. Поэтому
В итоге как и
обещал любезный автор. И никаких особенных
умений не нужно. Какой-то вузовский курс
матанализа плюс некие навыки нехитрого
интегрирования. И вот: не прошло и получаса, как
ответ готов.
Мы в редакции будем весьма
признательны автору, если он пришлёт нам
вычисления, которые действительно покажут, что
ответ в задаче «нетрудно получить».