Орбитальный период — время, за которое небесное тело совершает полный оборот на орбите вокруг внешнего центра притяжения или вокруг общего с другим небесным телом центра масс. Является предметом изучения небесной механики.
Орбитальный период не зависит от размера небесного тела. Соотношение орбитальных периодов двух (или более) небесных тел равное небольшому натуральному числу приводит к орбитальному резонансу, а при таком соотношении орбитального периода тела и его периода вращения вокруг своей оси — к спин-орбитальному резонансу. Орбитальный период пылевых частиц в Солнечной системе может уменьшаться вследствие эффекта Пойнтинга — Робертсона.
Сводка формул[править | править код]
Большая (а) и малая (б) полуось эллипса
Согласно третьему закону Кеплера, орбитальный период T (в секундах) двух тел, вращающихся друг вокруг друга по круговой или эллиптической орбите, равен:
где:
а — большая полуось орбиты
μ = GM — стандартный гравитационный параметр
G — гравитационная постоянная
М — масса более массивного тела.
Для всех эллиптических орбит с одинаковой большой полуосью период обращения одинаков, независимо от эксцентриситета.
И наоборот, формула для расчёта расстояния, на котором тело должно вращаться, чтобы иметь заданный орбитальный период:
![{displaystyle a={sqrt[{3}]{frac {GMT^{2}}{4pi ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acc0794d19344d83b82ba93518c68a0fccd0b31b)
Например, для завершения движения каждые 24 часа при массе тела 100 кг небольшое тело должно вращаться на расстоянии 1,08 метра от его центра масс.
Когда сравнительно маленькое тело движется по круговой орбите и зависит от плотности центра масс — р (в кг/м³), приведённое выше уравнение упрощается:
.
Когда два тела вращаются друг вокруг друга, орбитальный период T можно рассчитать следующим образом (необходимо учитывать массы обоих орбитальных тел):
М1+М2 — сумма масс двух тел.
Виды[править | править код]
Существует несколько видов орбитальных периодов (при рассмотрении небесных тел в Солнечной системе):
- Сидерический период — промежуток времени, в течение которого какое-либо небесное тело-спутник совершает вокруг главного тела полный оборот относительно звёзд.
- Синодический период — промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.
- Драконический период — интервал времени, состоящий из 223 синодических месяцев (в среднем приблизительно 6585,3211 суток или 18,03 тропического года), по прошествии которого затмения Луны и Солнца приблизительно повторяются в прежнем порядке.
- Аномалистический период — промежуток времени, за который тело, перемещаясь по эллиптической орбите, дважды последовательно проходит через перицентр. Этот период может несколько отличаться от сидерического, потому что ориентация линии апсид орбиты медленно меняется из-за её прецессии. Например, аномалистический период Луны — 27,55455 дня, Земли — 365,25964 дня.
- Тропический период — отрезок времени, за который Солнце завершает один цикл смены времён года, как это видно с Земли, например, время от одного весеннего равноденствия до следующего, или от одного дня летнего солнцестояния до другого.
Ссылки[править | править код]
- Bate, Roger B.; Mueller, Donald D. & White, Jerry E. (1971), Fundamentals of Astrodynamics, Dover
Синодическим периодом обращения(S) планеты называется промежуток времени
между ее двумя последовательными
одноименными конфигурациями.
Сидерическим или звездным периодом
обращения(Т) планеты называется
промежуток времени, в течение которого
планета совершает один полный оборот
вокруг Солнца по своей орбите.
Сидерический период обращения Земли
называется звездным годом (Т☺).
Между этими тремя периодами можно
установить простую математическую
зависимость из следующих рассуждений.
Угловое перемещение по орбите за сутки
у планеты равно
,
а у Земли
.
Разность суточных угловых перемещений
планеты и Земли (или Земли и планеты)
есть видимое смещение планеты за сутки,
т.е.
.
Отсюда для нижних планет
(2.1)
для верхних планет
(2.2)
Эти равенства называются уравнениями
синодического движения.
Непосредственно из наблюдений могут
быть определены только синодические
периоды обращений планет S и сидерический
период обращения Земли, т.е. звездный
год Т☺. Сидерические же периоды
обращений планет Т вычисляются по
соответствующему уравнению синодического
движения.
Продолжительность звездного года равна
365,26… средних солнечных суток.
7.4. Законы Кеплера
Кеплер был сторонником учения Коперника
и поставил перед собой задачу
усовершенствовать его систему по
наблюдениям Марса, которые на протяжении
двадцати лет производил датский астроном
Тихо Браге (1546-1601) и в течение нескольких
лет — сам Кеплер.
Вначале Кеплер разделял традиционное
убеждение, что небесные тела могут
двигаться только по кругам, и поэтому
он потратил много времени на то, чтобы
подобрать для Марса круговую орбиту.
После многолетних и очень трудоемких
вычислений, отказавшись от общего
заблуждения о кругообразности движений,
Кеплер открыл три закона планетных
движений, которые в настоящее время
формулируются следующим образом:
1. Все планеты движутся по эллипсам, в
одном из фокусов которых (общем для всех
планет) находится Солнце.
2. Радиус-вектор планеты в равные
промежутки времени описывает равновеликие
площади.
3. Квадраты сидерических периодов
обращений планет вокруг Солнца
пропорциональны кубам больших полуосей
их эллиптических орбит.
Как известно, у эллипса сумма расстояний
от какой-либо его точки до двух неподвижных
точек f1и f2, лежащих на его
оси АП и называемых фокусами, есть
величина постоянная, равная большой
оси АП (рис. 27). Расстояние ПО (или ОA), где
О — центр эллипса, называется большой
полуосью
,
а отношение
— эксцентриситетом эллипса. Последний
характеризует отклонение эллипса от
окружности, у которой е = 0.
Орбиты планет мало отличаются от
окружностей, т.е. их эксцентриситеты
невелики. Наименьший эксцентриситет
имеет орбита Венеры (е = 0,007), наибольший
— орбита Плутона (е = 0,247). Эксцентриситет
земной орбиты
е = 0,017.
Согласно первому закону Кеплера Солнце
находится в одном из фокусов эллиптической
орбиты планеты. Пусть на рис. 27,а это
будет фокус f1(С — Солнце). Тогда
наиболее близкая к Солнцу точка орбиты
П называетсяперигелием, а наиболее
удаленная от Солнца точка A —афелием.
Большая ось орбиты АП называетсялинией
апсид, а линия f2P, соединяющая
Солнце и планету Р на ее орбите, —радиусом-вектором планеты.
Расстояние планеты от Солнца в перигелии
q = а (1 — е), (2.3)
в афелии
Q = a (l + e). (2.4)
За среднее расстояние планеты от Солнца
принимается большая полуось орбиты
Согласно второму закону Кеплера площадь
СР1Р2, описанная радиусом-вектором
планеты за время
t
вблизи перигелия, равна площади СР3Р4, описанной им за то же время
t
вблизи афелия (рис. 27, б). Так как дуга
Р1Р2больше дуги Р3Р4, то, следовательно, планета вблизи
перигелия имеет скорость большую, чем
вблизи афелия. Иными словами, ее движение
вокруг Солнца неравномерно.
Скорость движения планеты в перигелии
(2.5)
в афелии
(2.6)
где vc— средняя или круговая
скорость планеты при r = а. Круговая
скорость Земли равна 29,78 км/сек = 29,8
км/сек.
Третий закон Кеплера записывается так:
(2.7)
где Т1и T2— сидерические
периоды обращений планет, а1и a2— большие полуоси их орбит.
Если большие полуоси орбит планет
выражать в единицах среднего расстояния
Земли от Солнца (в астрономических
единицах), а периоды обращений планет
—
в годах, то для Земли а =1 и Т = 1 и
период обращения вокруг Солнца любой
планеты
(2.8)
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
Законы движения планет в Солнечной системе
- Виды траекторий небесных тел
- Законы Кеплера
- Задачи
п.1. Виды траекторий небесных тел
При движении небесного тела вблизи другого массивного тела (планеты или звезды), его траектория может иметь различную форму, что связано с соотношением скорости движения и космических скоростей (см. §23 данного справочника).
Например, при движении в гравитационном поле Земли с первой космической скоростью (v_1=7,92 text{км/с}) тело будет описывать окружность на относительно небольшой высоте вокруг планеты. При скорости выше первой космической, но ниже второй, орбита тела становится вытянутой – тело описывает эллипс, то приближаясь, то удаляясь от Земли. По эллиптическим орбитам движутся Луна, более мелкие естественные объекты, захваченные гравитационным полем, и искусственные спутники Земли.
Начина со второй космической скорости (v_2=11,18 text{км/с}), траектория становится незамкнутой – тело улетает от планеты по кривой, которая называется параболой. По параболе движутся межпланетные станции, которые запускаются с Земли, а также астероиды и кометы, пролетающие мимо.
Наконец, при третьей космической скорости (v_3=16,67 text{км/с}) и выше, траектория вытягивается еще больше, тело движется по гиперболе за пределы Солнечной системы.
п.2. Законы Кеплера
Законы Кеплера – три эмпирических соотношения, которые были предложены Иоганном Кеплером в 1609-1619 гг. как обобщение результатов астрономических наблюдений, полученных к тому времени.
| «Где материя – там и геометрия».
Иоганн Кеплер (1571-1630), |
 |
Первый закон Кеплера
Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которых находится Солнце.
 |
Эллипс – это плоская замкнутая кривая, для любой точки которой сумма расстояний до двух фокусов является постоянной величиной: $$ MF_1+MF_2=2a $$ где (a) – большая полуось эллипса. Ближайшая к Солнцу точка орбиты называется перигелием, а самая дальняя – афелием. |
Длина большой полуоси принимается за средний радиус орбиты.
Большая полуось земной орбиты является единицей измерения расстояний – астрономической единицей: 1 а.е. = 149 597 870 700 м ≈ 150 млн.км
Второй закон Кеплера
Каждая планета движется в плоскости, проходящей через центр Солнца, причем за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. $$ frac{Delta S}{Delta t}=const=frac{S_{text{элл}}}{T}=frac{pi ab}{T} $$ где (S_{text{элл}}=pi ab) – площадь эллипса, (T) – период обращения планеты.
 |
Из второго закона Кеплера следует, что планета движется по орбите неравномерно: быстрее в перигелии и медленнее в афелии. |
Третий закон Кеплера
Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. $$ frac{T_1^2}{T_2^2}=frac{a_1^3}{a_2^3} $$
Из третьего закона Кеплера следует, что период обращения увеличивается по мере удаления планет от Солнца.
Ньютон в 1684-1686 гг. дал теоретическое обоснование законов Кеплера и уточнил формулировку 3-го закона: $$ frac{T_1^2(M+m_1)}{T_2^2(M+m_2)}=frac{a_1^3}{a_2^3}, frac{T^2(M+m)}{a^3}=frac{4pi ^2}{G}=const $$ где (M) – масса Солнца, (m_1) и (m_2) – массы планет (или масса планет и их спутников соответственно). Эту уточненную формулу используют для определения масс планет и спутников, если из наблюдений становятся известны их орбиты и орбитальные периоды.
п.3. Задачи
Задача 1. Найдите среднее расстояние от Юпитера до Солнца (в астрономических единицах), если период обращения Юпитера вокруг Солнца равен 11,9 лет.
Дано:
(T_1=11,9 text{лет})
(T_2=1 text{год})
(a_2=1 text{а.е.})
__________________
(a_1-?)
Применяем 3-й закон Кеплера и в качестве «эталонной планеты» берем Землю. begin{gather*} frac{T_1^2}{T_2^2}=frac{a_1^3}{a_2^3} Rightarrow a_1^3=frac{T_1^2}{T_2^2}a_2^3 Rightarrow a_1=a_2sqrt[{3}]{left(frac{T_1}{T_2}right)^2}\[6pt] a_1=1cdot sqrt[{3}]{left(frac{11,9}{1}right)^2}=sqrt[{3}]{141,61}approx 5,2 (text{а.е.}) end{gather*} Ответ: 5,2 а.е.
Задача 2. Чему равна масса Солнца, если период обращения Земли равен 1 году, а средний радиус земной орбиты 1 а.е.≈150 млн.км?
Дано:
(T=1 text{год}approx 3,156cdot 10^7 text{с})
(a=150 text{млн.км}=1,5cdot 10^{11} text{м})
__________________
(M-?)
По формуле Ньютона для 3-го закона Кеплера begin{gather*} frac{T^2(M+m)}{a^3}=frac{4pi ^2}{G} end{gather*} Считаем массу Земли малой по сравнению с массой Солнца. Тогда begin{gather*} frac{T^2M}{a^3}approx frac{4pi ^2}{G} Rightarrow M=frac{4pi ^2}{G}cdot frac{a^3}{T^2}\[6pt] M=frac{4pi^2}{6,67cdot 10^{-11}}cdot frac{(1,5cdot 10^{11})^3}{(3,156cdot 10^7)^2}approx 2,0cdot 10^{30} (text{кг}) end{gather*} Ответ: 2,0·1030 кг
Задача 3. Период обращения Ганимеда вокруг Юпитера равен 7,15 дней, средний радиус орбиты 1,07 млн.км. Чему равна масса Юпитера?
Дано:
(T=7,15 text{дней}=7,15cdot 24cdot 3600 text{с}=617760 text{с})
(a=1,07 text{млн.км}=1,07cdot 10^9 text{м})
__________________
(M-?)
По формуле Ньютона для 3-го закона Кеплера begin{gather*} frac{T^2(M+m)}{a^3}=frac{4pi ^2}{G} end{gather*} Считаем массу спутника малой по сравнению с массой Юпитера. Тогда begin{gather*} frac{T^2M}{a^3}approx frac{4pi ^2}{G} Rightarrow M=frac{4pi ^2}{G}cdot frac{a^3}{T^2}\[6pt] M=frac{4pi^2}{6,67cdot 10^{-11}}cdot frac{(1,07cdot 10^{9})^3}{(617760)^2}approx 1,9cdot 10^{27} (text{кг}) end{gather*} Ответ: 1,9· 1027 кг
Как найти период обращения
Период обращения тела, которое движется по замкнутой траектории можно измерить при помощи часов. Если же обращение происходит слишком быстро, это делается после изменения некоторого числа полных обращений. Если тело вращается по окружности, и известна его линейная скорость, эта величина рассчитывается по формуле. Период обращения планеты рассчитывается по третьему закону Кеплера.
Вам понадобится
- — секундомер;
- — калькулятор;
- — справочные данные по орбитам планет.
Инструкция
Измерьте при помощи секундомера время, требующееся вращающемуся телу, чтобы прийти в исходную точку. Это и будет период его вращения. Если измерить вращения тела затруднительно, то измерьте время t, N полных обращений. Найдите отношение этих величин, это и будет период вращения данного тела T (T=t/N). Период измеряется в тех же величинах, что и время. В интернациональной системе измерения это секунда.
Если известна частота вращения тела, то найдите период, поделив число 1 на значение частоты ν (T=1/ν).
Если тело вращается по круговой траектории и известна его линейная скорость, рассчитайте период его вращения. Для этого измерьте радиус R траектории, по которой вращается тело. Убедитесь, что модуль скорости не изменяется со временем. Затем произведите расчет. Для этого поделите длину окружности, по которой движется тело, которая равна 2∙π∙R (π≈3,14), на скорость его вращения v. Результатом будет период вращения данного тела по окружности T=2∙π∙R/v.
Если нужно рассчитать период обращения планеты, которая движется вокруг звезды, используйте третий закон Кеплера. Если две планеты вращаются вокруг одной звезды, то квадраты периодов их обращения относятся как кубы больших полуосей их орбит. Если обозначить периоды обращения двух планет T1 и T2, большие полуоси орбит (они эллиптичные), соответственно, a1 и a2, то T1²/ T2²= a1³/a2³. Данные расчеты верны в том случае, если массы планет значительно уступают массе звезды.
Пример: Определите период обращения планеты Марс. Чтобы рассчитать эту величину, найдите длину большей полуоси орбиты Марса, a1 и Земли, a2 (как планеты, которая тоже вращается вокруг Солнца). Они равны a1=227,92∙10^6 км и a2=149,6∙10^6 км. Период вращения земли T2=365,25 суток (1 земной год). Тогда найдите период обращения марса, преобразовав формулу из третьего закона Кеплера, для определения периода вращения Марса Т1=√( T2²∙ a1³/a2³)=√( 365,25²∙ (227,92∙10^6)³/(149,6∙10^6)³)≈686,86 суток.
Источники:
- как найти обращения в тексте
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
1. Теоретическая разрешающая способность телескопа:
, где λ – средняя длина световой волны (5,5·10-7 м), D – диаметр объектива телескопа, или 
, где D – диаметр объектива телескопа в миллиметрах.
2. Увеличение телескопа:
, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра.
3. Высота светил в кульминации:
высота светил в верхней кульминации, кульминирующих к югу от зенита ( ):
, где – широта места наблюдения, – склонение светила;
высота светил в верхней кульминации, кульминирующих к северу от зенита ( ):
, где – широта места наблюдения, – склонение светила;
высота светил в нижней кульминации:
, где – широта места наблюдения, – склонение светила.
4. Астрономическая рефракция:
приближенная формула для вычисления угла рефракции, выраженного в секундах дуги (при температуре +10°C и атмосферном давлении 760 мм. рт. ст.):
, где z – зенитное расстояние светила (для z
5. Время:
звездное время:
, где – прямое восхождение какого-либо светила, t – его часовой угол;
среднее солнечное время (местное среднее время):
Tm=T+, где T – истинное солнечное время, – уравнение времени;
всемирное время:
, где – долгота пункта с местным средним временем Tm, выраженная в часовой мере, T0 – всемирное время в этот момент;
поясное время:
, где T0 – всемирное время; n – номер часового пояса (для Гринвича n=0, для Москвы n=2, для Красноярска n=6);
декретное время:
или 
6. Формулы, связывающие сидерический (звездный) период обращения планеты T с синодическим периодом ее обращения S:
для верхних планет:
;
для нижних планет:
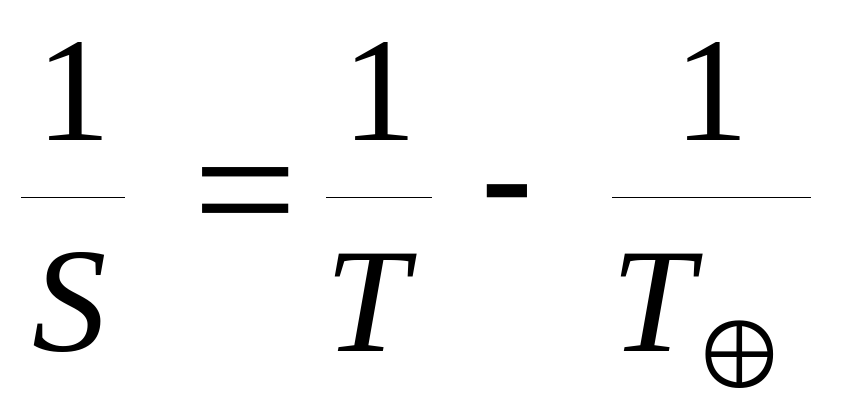, где T – звездный период обращения Земли вокруг Солнца.
7. Третий закон Кеплера:
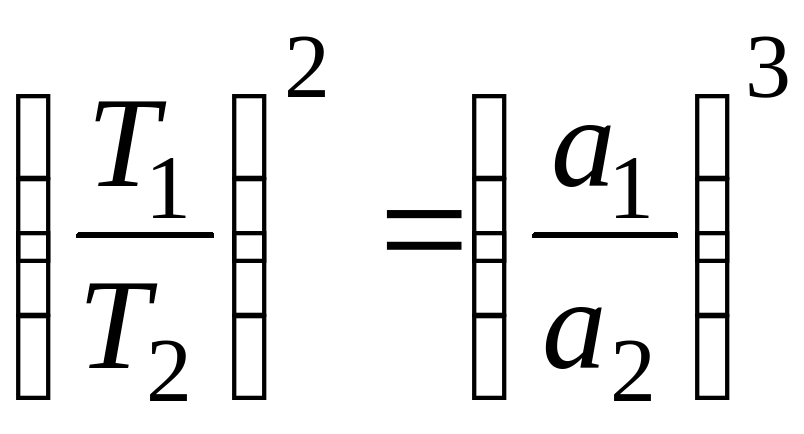, где Т1 и Т2 – периоды обращения планет, a1 и a2 – большие полуоси их орбиты.
8. Закон всемирного тяготения:
, где m1 и m2 – массы притягивающихся материальных точек, r – расстояние между ними, G – гравитационная постоянная.
9. Третий обобщенный закон Кеплера:
, где m1 и m2 – массы двух взаимно притягивающихся тел, r – расстояние между их центрами, Т – период обращения этих тел вокруг общего центра масс, G – гравитационная постоянная;
для системы Солнце и две планеты:
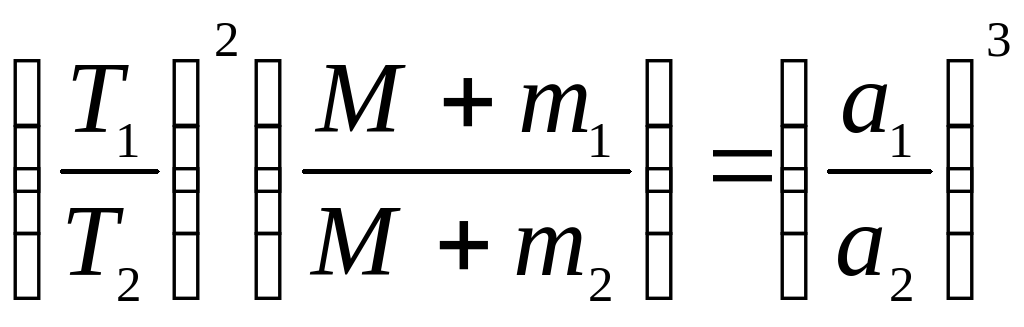, где Т1 и Т2 – сидерические (звездные) периоды обращения планет, М – масса Солнца, m1 и m2 – массы планет, a1 и a2 –большие полуоси орбит планет;
для систем Солнце и планета, планета и спутник:
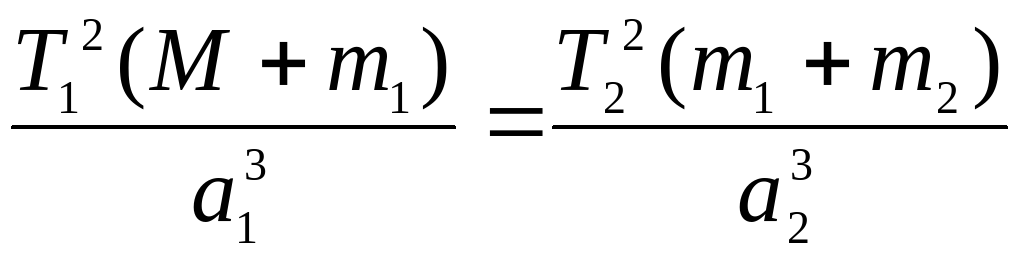, где M – масса Солнца; m1 – масса планеты; m2 – масса спутника планеты; Т1 и a1 – период обращения планеты вокруг Солнца и большая полуось ее орбиты; Т2 и a2 – период обращения спутника вокруг планеты и большая полуось его орбиты;
при M m1, а m1 m2,
.
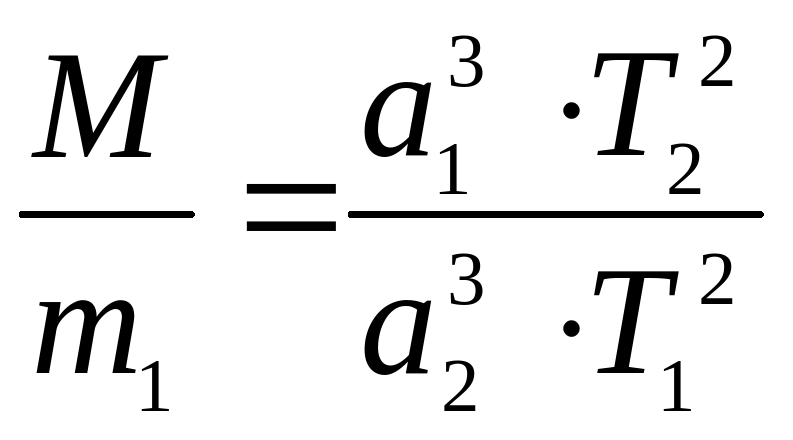10. Линейная скорость движения тела по параболической орбите (параболическая скорость):
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки параболической орбиты.
11. Линейная скорость движения тела по эллиптической орбите в избранной точке:
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки эллиптической орбиты, a – большая полуось эллиптической орбиты.
12. Линейная скорость движения тела по круговой орбите (круговая скорость):
, где G – гравитационная постоянная, M – масса центрального тела, R – радиус орбиты, vp – параболическая скорость.
13. Эксцентриситет эллиптической орбиты, характеризующий степень отклонение эллипса от окружности:
, где c – расстояние от фокуса до центра орбиты, a – большая полуось орбиты, b – малая полуось орбиты.
14. Связь расстояний перицентра и апоцентра с большой полуосью и эксцентриситетом эллиптической орбиты:
, , , где rП – расстояния от фокуса, в котором находится центральное небесное тело, до перицентра, rА – расстояния от фокуса, в котором находится центральное небесное тело, до апоцентра, a – большая полуось орбиты, e – эксцентриситет орбиты.
15. Расстояние до светила (в пределах Солнечной системы):
, где R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила, выраженный в секундах дуги,
или , где D1 и D2 – расстояния до светил, ρ1 и ρ2 – их горизонтальные параллаксы.
16. Радиус светила:
, где ρ – угол, под которым с Земли виден радиус диска светила (угловой радиус), R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила.
17. Расстояние до звезд:
в парсеках: , где – годичный параллакс звезды, выраженный в радианах;
в астрономических единицах: , где – годичный параллакс звезды, выраженный в секундах дуги;
в километрах: , где – годичный параллакс звезды, выраженный в секундах дуги, a – средний радиус (большая полуось) земной орбиты.
18. Связь блеска звезды и ее звездной величины (формула Погсона):
, где I1 – освещенность, создаваемая звездой, звездная величина которой равна m1, и I2 – освещенность, создаваемая другой звездой, звездная величина которой равна m2.
19. Абсолютная звездная величина:
, где m – видимая звездная величина, R – расстояние до звезды в парсеках.
20. Закон Стефана–Больцмана:
ε=σT4, где ε – энергия, излучаемая в единицу времени с единицы поверхности, Т – температура (в кельвинах), а σ – постоянная Стефана–Больцмана.
21. Закон Вина:
, где λmax – длина волны, на которую приходится максимум излучения абсолютно черного тела (в сантиметрах), Т – абсолютная температура в кельвинах.
22. Закон Хаббла:
, где v – лучевая скорость удаления галактики, c – скорость света, Δλ – доплеровское смещение линий в спектре, λ – длина волны источника излучения, z – красное смещение, r – расстояние до галактики в мегапарсеках, H – постоянная Хаббла, равная 75 км / (сМпк).
4
