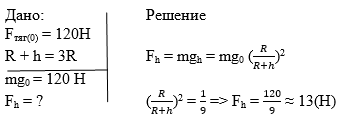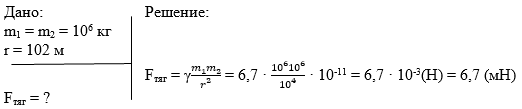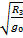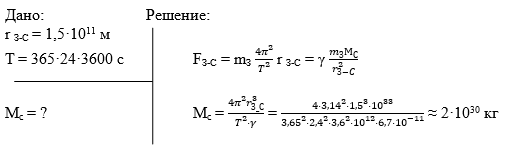В этой главе. . .
- Постигаем равномерное вращательное движение
- Изучаем угловое ускорение
- Испытываем влияние центростремительной силы
- Учитываем перемещение, скорость и ускорение
- Движемся по орбите под действием законов Ньютона и силы гравитационного притяжения
- Поддерживаем вращение в вертикальной плоскости
Вращательное движение выполняют искусственные спутники вокруг планет, гоночные автомобили по трекам и даже пчелы вокруг ульев. В предыдущих разделах рассматривались такие характеристики прямолинейного движения, как перемещение, скорость и ускорение. В этой главе мы снова рассмотрим их, но теперь уже для вращательного движения.
Для перечисленных выше характеристик прямолинейного движения есть аналоги, характеризующие вращательное движение, а именно: угловое перемещение, угловая скорость и угловое ускорение. Как видно из их названия, роль перемещения во вращательном движении играет угол. Угловая скорость обозначает величину угла поворота за единицу времени, а угловое ускорение — изменение угловой скорости за единицу времени. Все, что нужно сделать, чтобы освоить премудрости вращательного движения, это взять уравнения прямолинейного движения и заменить в них одни характеристики другими: перемещение поменять на угол, скорость — на угловую скорость и ускорение — на угловое ускорение.
Содержание
- Держим курс: равномерное вращательное движение
- Меняем направление: центростремительное ускорение
- Управляем скоростью с помощью центростремительного ускорения
- Определяем величину центростремительного ускорения
- Стремимся к центру: центростремительная сила
- Вписываемся в повороты: учитываем радиус и наклон
- Вращательное движение: перемещение, скорость и ускорение
- Бросаем яблоко: закон всемирного тяготения Ньютона
- Вычисляем силу гравитационного притяжения на поверхности Земли
- Исследуем орбитальное движение с помощью закона всемирного тяготения
- Вычисляем скорость спутника
- Вычисляем период обращения спутника
- Вращаемся вдоль вертикальной плоскости
Держим курс: равномерное вращательное движение
Если объект движется с постоянной по величине скоростью по окружности, то такое движение называется равномерным вращательным движением. Примерами такого движения являются движение гоночного автомобиля по круглому треку и стрелки на циферблате часов. На рис. 7.1 показан мяч для игры в гольф, привязанный нитью к шесту и совершающий движение по окружности. Мяч совершает движение с одинаковой по величине скоростью, но с изменяющимся направлением. Потому такое движение мяча называется равномерным вращательным движением.
Время, которое требуется мячику (или какому-либо другому объекту), чтобы полностью обогнуть окружность, называется периодом и обозначается символом ( T ). Период и линейную скорость можно легко связать, если известно пройденное расстояние, т.е. длина окружности ( 2pi r ), а точнее ее радиус ( r ). Итак, линейная скорость мячика ( v ) равна:
а период вращения ( T ) равен:
Допустим, что длина нити равна 1 м, а период вращения равен 0,5 с. Чему в таком случае будет равна линейная скорость мячика? Подставим численные значения в одно из предыдущих соотношений и получим:
Итак, мячик вращается с линейной скоростью 13 м/с!
Меняем направление: центростремительное ускорение
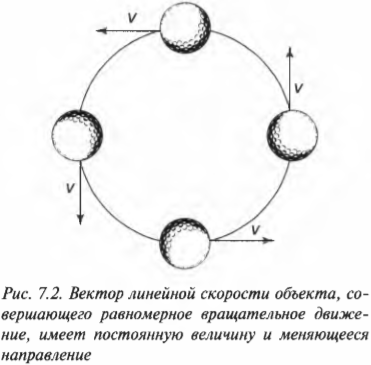
При вращательном движении по окружности линейная скорость мячика постоянно меняет направление, как показано на рис. 7.2. Ускорение, характеризующее такое изменение скорости, называется центростремительным (или центробежным). В любой точке вращательного движения с постоянной величиной и меняющимся направлением вектор линейной скорости перпендикулярен радиусу.
Это правило справедливо для всех объектов: вектор линейной скорости объекта, равномерно вращающегося по окружности, всегда перпендикулярен радиусу окружности.
Если в показанных на рис. 7.2 положениях нить, удерживающая мяч, оборвется, то куда полетит мяч? Если в этот момент вектор линейной скорости направлен влево, то мяч полетит влево, а если этот вектор направлен вправо, то мяч полетит вправо, и т.д. Этот, казалось бы, простой и интуитивно понятный момент часто вызывает трудности у тех, кто впервые постигает физику.
Всегда следует помнить, что вектор линейной скорости объекта, выполняющего равномерное вращательное движение, всегда направлен под прямым углом к радиусу вращения в текущей точке траектории. (В общем случае неравномерного криволинейного движения эта компонента вектора скорости, перпендикулярная радиусу вращения и касательная к траектории движения, называется тангенциальной компонентой, а перпендикулярная ей компонента — нормальной компонентой. — Примеч. ред.)
Управляем скоростью с помощью центростремительного ускорения
Особенностью равномерного вращательного движения является постоянство величины линейной скорости. Это значит, что вектор ускорения не имеет компоненты, параллельной вектору линейной скорости, поскольку в противном случае величина линейной скорости менялась бы. Однако при равномерном вращательном движении меняется только направление линейной скорости. Такое изменение линейной скорости поддерживается центростремительным ускорением, направленным к центру окружности вращения и перпендикулярно вектору линейной скорости.
В примерах на рис. 7.1 и 7.2 на мяч со стороны нити действует сила натяжения нити, которая поддерживает его движение по окружности. Именно эта сила сообщает мячу центростремительное ускорение ( a_ц ), вектор которого показан на рис. 7.1. (Попробуйте раскрутить мяч с помощью привязанной к нему нити, и вы сразу же почувствуете действие этой силы со стороны нити.)
Часто возникает вопрос: если вектор ускорения мяча направлен к центру окружности, то почему мяч не движется к центру? Дело в том, что при равномерном вращательном движении это ускорение меняет только направление, а не величину линейной скорости.
Определяем величину центростремительного ускорения
Нам уже известно направление вектора центростремительного ускорения, а чему же равна его величина? Итак, величина центростремительного ускорения объекта, равномерно движущегося с линейной скоростью ( v ) по окружности с радиусом ( r ), равна:
Как видите, величина центростремительного ускорения обратно пропорциональна радиусу окружности ( r ) и прямо пропорциональна квадрату скорости ( v ). Поэтому не удивительно, что автомобиль на более крутых поворотах испытывает более сильное центростремительное ускорение.
Стремимся к центру: центростремительная сила
На крутых поворотах действие центростремительного ускорения обеспечивается трением шин по дороге. Какую силу нужно приложить, чтобы удержать движущийся со скоростью ( v ) автомобиль на повороте с радиусом кривизны ( r )?
Допустим, что в примере на рис. 7.1 легкий мяч заменили на тяжелое пушечное ядро. Теперь, чтобы поддерживать движение ядра по окружности с тем же радиусом и периодом вращения, потребуется гораздо большая сила.
Дело в том, что сила ( F=ma ) равна произведению ускорения ( a ) и массы ( m ), а значит, увеличение массы объекта (замена мяча на ядро) неизбежно приводит к необходимости увеличения силы для обеспечения прежнего ускорения.
Центростремительная сила ( F_ц ), необходимая для равномерного вращения по окружности с радиусом ( r ) объекта массой ( m ) с постоянной скоростью ( v ), равна:
С помощью этого уравнения можно легко определить силу, необходимую для равномерного вращения объекта по окружности с известной массой, скоростью и радиусом окружности.
Обратите внимание, что если объект движется по той же окружности, но с разной скоростью, то он будет испытывать разную центростремительную силу.
В примерах на рис. 7.1 и 7.2 мяч движется со скоростью ( v ) = 13 м/с и удерживается нитью длиной 1,0 м, т.е. в данном случае радиус окружности ( r ) = 1 м. Какая сила потребуется, чтобы поддерживать такое же движение для пушечного ядра с массой 10 кг? Подставляя численные значения в уже известную нам формулу, получим:
Приличная сила! Остается только надеяться, что ваши руки достаточно сильны, чтобы удержать ядро.
Является ли центростремительная сила реальной силой?
Центростремительная сила не является каким-то особым типом взаимодействия. Она имеет отношение только к объекту, движущемуся по криволинейной траектории, и необходима для удержания объекта на данной траектории. Поэтому ее часто называют центростремительно-необходимой силой. Довольно часто новички считают центростремительную силу каким-то новым фундаментальным типом взаимодействия. И это понятно, поскольку известные нам силы (например, сила гравитации и сила трения) имеют вполне определенный источник, который не зависит от траектории движения. Но это совсем не так для центростремительной силы. Центростремительная сила возникает из необходимости удержания объекта на криволинейной траектории. Сумма всех остальных сил, действующих на объект, который движется по криволинейной траектории, должна быть равна центростремительной силе. (Если объект движется по прямолинейной траектории, а затем ему нужно изменить направление движения, то для этого придется приложить силу, равную центростремительной силе. — Примеч. ред.)
Вписываемся в повороты: учитываем радиус и наклон
Если вам приходилось ехать на автомобиле или велосипеде или даже бежать трусцой, то наверняка вы заметили, что в крутой поворот проще вписаться, если поверхность дороги немного наклонена внутрь поворота. Из опыта известно, что чем больше наклон, тем проще вписаться в поворот. Это объясняется тем, что в таком случае на вас действует меньшая центростремительная сила. Центростремительная сила обеспечивается силой трения о поверхность дороги. Если поверхность дороги покрыта льдом, то сила трения становится меньше и потому часто не удается вписаться в поворот на обледеневшей дороге на большой скорости.
Представьте, что автомобилю с массой 1000 кг нужно вписаться в поворот с радиусом Юм, а коэффициент трения покоя (подробнее о нем см. главу6) равен 0,8. (Здесь используется коэффициент трения покоя, поскольку предполагается, что шины по поверхности дороги.) Какую максимальную скорость может развить этот автомобиль без риска не вписаться в поворот. Итак, сила трения покоя шин о поверхность дороги ( F_{трение,покоя} ) должна обеспечивать центростремительную силу:
где ( m ) — это масса автомобиля, ( v ) — его скорость, ( r ) — радиус, ( mu_п ) — коэффициент трения покоя, a ( g ) = 9,8 м/с2 — ускорение свободного падения под действием силы гравитации. Отсюда легко находим скорость:
(Обратите внимание, что максимальная безопасная скорость прохождения поворота не зависит от массы автомобиля. — Примеч. ред.)
Это выражение выглядит очень просто, а после подстановки в него численных значений получим:
Итак, максимальная скорость безопасного проезда при таком повороте равна 8,9 м/с. Пересчитаем в единицы “км/ч”, в которых скорость указана на спидометре, и сравним. Получается, что 8,9 м/с = 32 км/ч, а на спидометре всего 29 км/ч. Прекрасно, но далеко не все водители умеют так быстро рассчитывать безопасную скорость прохождения поворотов. Поэтому конструкторы дорог часто строят повороты с наклоном внутрь, чтобы обеспечить центростремительное ускорение не только за счет силы трения, но и за счет горизонтальной компоненты силы гравитации.
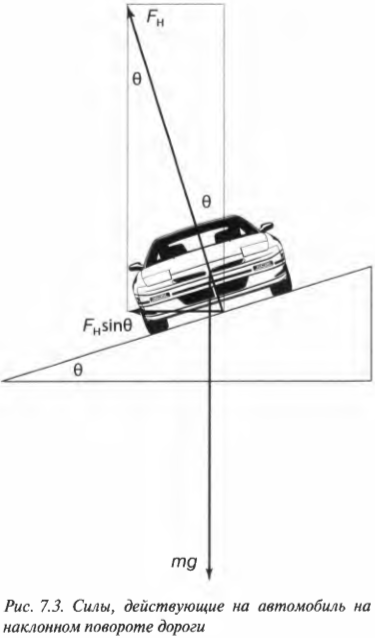
На рис. 7.3 показан пример поворота дороги с некоторым наклоном под углом ( theta ) к горизонтали. Предположим, что конструкторы решили полностью обеспечить центростремительное ускорение только за счет горизонтальной компоненты силы гравитации (т.е. без учета силы трения) ( F_нsintheta ), где ( F_н ) — это нормальная сила (подробнее о ней см. в главе 6). Тогда:
В вертикальном направлении на автомобиль действует сила гравитации ( mg ), которая уравновешивается вертикальной компонентой нормальной силы ( F_нcostheta ):
или, иначе выражая это соотношение, получим:
Подставляя это выражение в прежнее соотношение между центростремительной силой и нормальной силой, получим:
Поскольку ( sintheta/!costheta=tg,theta ) в то
Отсюда легко получаем, что угол наклона поворота дороги ( theta ) равен:
Именно это уравнение используют инженеры при проектировании дорог. Обратите внимание, что масса автомобиля не влияет на величину угла, при котором центростремительная сила полностью обеспечивается только горизонтальной компонентой нормальной силы. Попробуем теперь определить величину угла наклона поворота с радиусом 200 м для автомобиля, движущегося со скоростью 100 км/ч или 27,8 м/с:
Для обеспечения безопасного движения автомобиля со скоростью 100 км/ч в повороте с радиусом 200 м без учета силы трения, инженеры должны создать наклон около 22°. Отлично, из вас может получиться неплохой инженер-конструктор автомагистралей!
Вращательное движение: перемещение, скорость и ускорение
Если вы привыкли решать задачи о прямолинейном движении типа “некто движется из пункта А в пункт Б”, то задачи о вращательном движении можно формулировать аналогично, но для этого нужно приобрести некоторый опыт. На рис. 7.1 мяч движется криволинейно по окружности, а не прямолинейно по линии. Это движение можно было бы описать как комбинацию прямолинейных движений с координатами X и Y. Однако гораздо удобнее характеризовать его иначе, а именно как вращательное движение с одной координатой ( theta ). В данном примере вращательного движения перемещение можно характеризовать углом ( theta ) так же, как в прямолинейном движении перемещение характеризуется расстоянием ( s ). (Более подробно перемещение при прямолинейном движении описывается в главе 3.)
Стандартной единицей измерения перемещения при вращательном движении является радиан (рад), а не градус. Полная окружность охватывает угол величиной ( 2pi ) радиан, что равно 360°. Соответственно, половина окружности охватывает угол величиной ( pi ) радиан, а четверть окружности — ( pi/2 ).
Как преобразуются величины углов из градусов в радианы и обратно? Достаточно определить, сколько радиан приходится на один градус, т.е. вычислить отношение ( 2pi )/360°. Например, величина угла 45° в радианах равна:
Аналогично, для преобразования величины угла из радианов в градусы следует определить, сколько градусов приходится на один радиан, т.е. вычислить отношение 360°/( 2pi ). Например, величина угла ( pi/2 ) в градусах равна:
Формулировка вращательного движения в терминах прямолинейного движения очень удобна. Напомним основные формулы прямолинейного движения, которые подробно описываются в главе 3:
Теперь для вывода аналогичных основных формул вращательного движения достаточно в формулах прямолинейного движения вместо расстояния ( s ), которое характеризует прямолинейное перемещение, подставить угол ( theta ), который характеризует угловое перемещение. А как определяется угловая скорость? Очень просто. Угловая скорость ( omega ) определяется аналогично, как изменение угла за единицу времени, и равна количеству радианов, пройденных за секунду:
Обратите внимание, как похоже это выражение для угловой скорости на выражение для линейной скорости:
Давайте теперь вычислим угловую скорость мяча на рис. 7.1. Он совершает полный круг, охватывающий ( 2pi ) радиан, за 1/2 с, а значит, его угловая скорость равна:
(Величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине ее радиуса. Поэтому радиан — это безразмерная величина, и ее обозначение (рад) часто опускается. Соответственно, угловую скорость принято указывать “в обратных секундах” как с-1, т.е. без указания единицы измерения углов. — Примеч. ред.)
Угловое ускорение ( alpha ) определяется аналогично линейному ускорению:
Оно определяется как изменение угловой скорости за единицу времени и измеряется в радианах на секунду в квадрате. Если скорость за 2 с изменилась от величины ( 4pi c^{-1} ) до величины ( 8pi c^{-1} ), то чему равно угловое ускорение? Подставим эти численные значения в предыдущую формулу и получим:
Итак, для описания вращательного движения у нас есть следующие аналоги: для линейного перемещения ( s ) — угловое перемещение ( theta ), для линейной скорости ( v ) — угловая скорость ( omega ) и для линейного ускорения ( a ) — угловое ускорение ( alpha ).
На основании этой аналогии можно легко вывести основные формулы вращательного движения (подобно основным формулам прямолинейного движения, которые подробно описываются в главе 3):
Более подробно эти выражения рассматриваются далее в главе 10 при описании момента импульса и момента силы.
Бросаем яблоко: закон всемирного тяготения Ньютона
Чтобы проводить опыты с вращательным движением, необязательно привязывать мячики к нитям и вращать их вокруг себя. Например, Луне совсем не нужны никакие нити, чтобы вращаться вокруг Земли. А дело в том, что необходимую центростремительную силу, вместо силы натяжения нити, обеспечивает сила гравитационного притяжения.
Один из важнейших законов физики, а именно закон всемирного тяготения, вывел еще сэр Исаак Ньютон. Согласно этому закону любые два тела притягиваются друг к другу с некоторой силой. Величина этой силы притяжения между телами с массами ( m_1 ) и ( m_2 ), которые находятся на расстоянии ( r ) друг от друга, равна:
где ( G ) — это константа, равная 6,67·10-11 Н·м2/кг2.
Благодаря этому уравнению можно легко вычислить силу гравитационного притяжения между двумя телами. Например, какова сила гравитационного притяжения между Землей и Солнцем? Солнце имеет массу около 1,99·1030 кг, Земля — 5,97·1024 кг, а расстояние между ними равно 1,50·1011 м. Подставляя эти числа в закон всемирного тяготения Ньютона, получим:
Историческая яблоня
Как известно, яблоко упало на голову Исаака Ньютона, и он открыл закон всемирного тяготения. Неужели это так и было? Правда ли, что какое-то падающее яблоко натолкнуло его на верную мысль или, по крайней мере, привлекло внимание Ньютона к данной теме? Согласно последним историческим исследованиям, весьма маловероятно, что именно падение яблока на голову великого ученого вдохновило его. Скорее всего, глядя в окно на падающие яблоки в саду, он нашел еще один пример всемирного тяготения. Историки до сих пор спорят, какое именно дерево является “яблоней Ньютона”. Сотрудники поместья матери Ньютона в Вулсторпе возле Грантхэма в Линкольншире (Великобритания) утверждают, в ее семейном саду до сих пор сохранились потомки “яблони Ньютона”.
Возвращаясь с небес на грешную землю, давайте вычислим силу притяжения между двумя влюбленными на парковой скамейке. Какой величины может быть сила гравитационного притяжения между ними, если, едва встретившись, они обнимают друг друга все сильнее и сильнее? Допустим, что они весят по 75 кг и находятся на расстоянии не больше полуметра. Подставляя эти значения в уже известную нам формулу, получим:
Ничтожная сила в несколько миллионных долей ньютона!
Вычисляем силу гравитационного притяжения на поверхности Земли
Описанное выше уравнение ( F=(Gm_1m_2)/r^2 ) для силы гравитационного притяжения справедливо независимо от расстояния между двумя массивными телами. В обыденных ситуациях часто приходится иметь дело с небольшими (по сравнению с размерами Земли) объектами на поверхности Земли, т.е. на фиксированном расстоянии между центром Земли и центром небольшого объекта. Силу гравитационного притяжения (или силу тяжести), действующую на небольшой объект, часто называют весом. Вес ( F_g ) равен произведению массы ( m ) на ускорение свободного падения ( g ), т.е. ( F_g = mg ). Массу измеряют в граммах, килограммах, центнерах, каратах и т.д., а вес — в динах, ньютонах и даже фунт-силах.
Попробуем вычислить ускорение свободного падения на поверхности Земли, пользуясь законом всемирного тяготения. Формула веса тела с массой ( m_1 ) нам известна:
Она создается силой гравитационного притяжения между этим телом и Землей и равна этой силе:
Здесь ( r ) — это радиус Земли, равный 6,38·106 м, а ( m_2 ) — ее масса, равная 5,97·1024 кг.
Сокращая массу тела ( m_1 ) в обеих половинах предыдущего равенства, получим:
Подставляя численные значения, получим:
Так, благодаря закону всемирного тяготения Ньютона мы смогли вычислить значение ускорения свободного падения, уже известное нам из прежних глав. Как видите, для этого нам потребовались значения константы всемирного тяготения ( G ), радиуса Земли ( r ) и ее массы ( m_2 ). (Конечно, значение ускорения свободного падения ( g ) можно определить экспериментально, измеряя время падения предмета с известной высоты. Но, согласитесь, гораздо интересней использовать последнюю формулу, для применения которой потребуется экспериментально измерить… радиус и массу Земли. Шутка!)
Исследуем орбитальное движение с помощью закона всемирного тяготения
Небесные тела в космическом пространстве из-за силы гравитационного притяжения вращаются друг относительно друга: спутники — вокруг своих планет (как Луна — вокруг Земли), планеты — вокруг звезд (как Земля — вокруг Солнца в Солнечной системе), а звезды — вокруг центра Галактики (как Солнце — вокруг центра нашей галактики, т.е. Млечного пути), а Галактика — вокруг местной группы галактик (как Млечный путь — вокруг нашей Местной группы галактик). Во всех этих случаях тела удерживаются центростремительной силой, которую обеспечивает сила гравитации. Как показано ниже, такая центростремительная сила несколько отличается от той, которая известна нам по прежнему примеру с вращающимся на нитке мячом для игры в гольф. В следующих разделах рассматриваются широко известные законы вращения тел под действием силы гравитационного притяжения, так называемые законы Кеплера, т.е. соотношения между параметрами вращательного движения: периодами вращения, радиусами и площадями орбит вращения.
Вычисляем скорость спутника
Чему равна скорость спутника, вращающегося вокруг планеты по орбите с постоянным радиусом? Ее можно легко определить, приравнивая центростремительную силу:
и силу гравитации:
В итоге получаем:
После простых алгебраических операций получим следующее выражение для скорости вращения:
Это уравнение определяет скорость вращения спутника по постоянной орбите независимо от его происхождения, будь-то искусственный спутник Земли, как рукотворный космический корабль на постоянной орбите, или естественный спутник Земли, как Луна.
Подсчитаем скорость вращения искусственного спутника Земли, вращающегося вокруг Земли. Для этого нужно в предыдущую формулу подставить массу Земли и расстояние от космического орбитального спутника до центра Земли.
Рукотворные спутники Земли обычно вращаются на высоте около 640 км, а радиус Земли, как известно, равен 6,38·106 м. Можно считать, что искусственные спутники вращаются на круговой орбите с радиусом около 7,02·106 м. Подставляя это и другие известные нам численные значения в предыдущую формулу, получим:
В этом месте нужно сделать несколько важных замечаний.
Значение 7,02·106 м в знаменателе обозначает расстояние от спутника до центра Земли, а не расстояние от спутника до поверхности Земли, равное 640 км. Помните, что в законе всемирного тяготения под расстоянием между телами подразумевается расстояние между их центрами масс, а не между их поверхностями.
В данном примере предполагается, что космический корабль находится достаточно высоко и не испытывает влияние атмосферы, например силу трения от соприкосновения с ней. На самом деле это не так. Даже на такой большой высоте как 640 км, космический корабль теряет скорость, вследствие трения в разреженных слоях атмосферы. В результате его скорость уменьшается, а сам корабль постепенно снижается. (Более подробно об этом рассказывается ниже.)
Движение искусственного спутника вокруг Земли можно рассматривать как “вечное” падение. От фактического падения его “удерживает” только то, что вектор скорости всегда направлен перпендикулярно радиусу окружности вращения. Действительно, именно из-за такого “вечного” падения космонавты испытывают чувство невесомости. Дело в том, что космонавты и их космический корабль “вечно” падают по касательной к орбите вращения вокруг Земли, но при этом нисколько не приближаются к Земле.
В практических целях часто важнее знать период обращения искусственного спутника, а не его скорость. Это нужно, например, в ситуации, когда требуется определить момент выхода на связь с космическим кораблем.
Вычисляем период обращения спутника
Периодом обращения спутника называется время, которое необходимо ему, чтобы совершить полный цикл вращательного движения по орбите. Если нам известна орбитальная скорость движения ( v ) спутника по окружности с радиусом ( r ) (см. предыдущий раздел), то можно легко и просто вычислить период обращения ( T ). За период обращения спутник преодолевает расстояние, равное длине окружности ( 2pi r ). Это значит, что орбитальная скорость ( v ) спутника равна ( 2pi r/T ). Приравнивая это соотношение и полученное ранее выражение для орбитальной скорости
где ( m ) — масса Земли, получим:
Отсюда легко получить следующее выражение для периода обращения спутника:
А на какой высоте должен находиться спутник, чтобы вращаться с периодом обращения Земли вокруг своей оси, равным 24 часам или 86400 с? Это вовсе не праздный вопрос. Такие спутники действительно существуют и используются для обеспечения непрерывной связи в данном регионе. Действительно, ведь, обращаясь вокруг Земли с тем же периодом, что и Земля, спутник на такой геостационарной орбите постоянно находится над одной и той же точкой поверхности Земли. Несколько таких спутников образуют систему глобального позиционирования. Итак, с помощью предыдущей формулы вычислим радиус окружности вращения спутника на стационарной орбите:
Подставляя численные значения, получим:
Отнимая от этой величины 4,23·107 м, значение радиуса Земли, равное 6,38·106 м, получим приблизительно 3,59·107 м, т.е. около 35900 км. Именно на таком расстоянии от Земли вращаются спутники глобальной системы позиционирования.
На практике спутники на геостационарной орбите все же теряют скорость из- за взаимодействия с магнитным полем Земли (подробнее о магнитном поле рассказывается в следующих главах). Поэтому спутники оборудованы небольшими двигателями для корректировки их положения на геостационарной орбите.
Вращаемся вдоль вертикальной плоскости
Наверняка вам приходилось наблюдать, как отважные мотоциклисты, велосипедисты или скейтбордисты вращаются внутри круглого трека, расположенного в вертикальной плоскости. Почему сила тяжести не опрокидывает их в самой верхней точке, где они находятся вверх ногами? Как быстро им нужно двигаться, чтобы сила гравитации не превышала центростремительной силы?
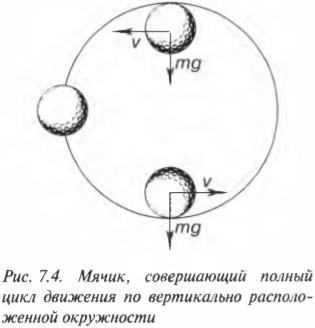
Рассмотрим эту ситуацию подробнее с помощью схемы на рис. 7.4. Для простоты предположим, что вместо отважных спортсменов маленький мячик совершает движение по окружности, расположенной в вертикальной плоскости. Итак, предыдущий вопрос формулируется следующим образом: “Какой минимальной скоростью должен обладать мячик, чтобы совершить полный цикл движения по вертикально расположенной окружности?”. Какому основному условию должно отвечать движение мячика, чтобы он совершил полный цикл движения по такой окружности и не упал в самой верхней точке?
Для прохождения самой верхней точки без падения мячик должен обладать минимальной скоростью, достаточной для создания такой центростремительной силы, которая была бы не меньше силы гравитации.
При таких условиях нормальная сила со стороны трека будет равна нулю, а единственной силой, которая будет удерживать объект на окружности, является сила гравитации. Поскольку центростремительная сила равна:
а сила гравитации равна:
то, приравнивая их, получим:
Отсюда получим выражение для минимально необходимой скорости для безопасного движения по окружности, расположенной в вертикальной плоскости:
Обратите внимание, что на величину минимально необходимой скорости для безопасного движения объекта по окружности, расположенной в вертикальной плоскости, не влияет масса объекта, будь-то мячик, мотоцикл или гоночный автомобиль.
Любой объект, движущийся с меньшей скоростью, в самой верхней точке трека неизбежно отклонится от траектории движения по окружности и упадет. Давайте вычислим величину минимально необходимой скорости для безопасного движения по окружности с радиусом 20 м. Подставляя численные значения в предыдущую формулу, получим:
Итак, для безопасного движения по окружности с радиусом 20 м объект (мячик, мотоцикл или гоночный автомобиль) должен иметь скорость не менее 14 м/с, т.е. около 50 км/ч.
Учтите, что для безопасного движения по окружности такую минимальную скорость объект должен иметь в самой верхней точке! Для того чтобы развить такую скорость в верхней точке, объекту в нижней точке нужно иметь гораздо большую скорость. Действительно, ведь чтобы добраться до верхней точки объекту придется какое-то время преодолевать силу гравитации с неизбежной потерей скорости.
Возникает вопрос: какую минимальную скорость в нижней точке должен иметь объект для безопасного движения по такой окружности? Подробный ответ на этот вопрос будет дан в части III этой книги, в которой рассматриваются такие понятия, как “кинетическая энергия”, “потенциальная энергия” и “преобразование энергии из одной формы в другую”.
Глава 7. Движемся по орбитам
3 (59.17%) 24 votes
Содержание
- Как найти период обращения спутника по круговой орбите?
- Что такое период обращения спутника?
- Формула для вычисления периода обращения спутника
- Пример вычисления периода обращения спутника
- Общий итог
- Как найти период обращения спутника по круговой орбите
- Что такое период обращения спутника
- Формула расчета периода обращения спутника
- Пример расчета периода обращения спутника
- Вывод
- Как найти период обращения спутника по круговой орбите
- Понимание круговой орбиты
- Использование закона Кеплера
- Использование скорости и радиуса
- Использование радара
- Итог
Как найти период обращения спутника по круговой орбите?
Существует множество спутников, которые обращаются вокруг Земли на круговых орбитах. Некоторые из них являются геостационарными, другие — находятся на низких орбитах. Но как вычислить период обращения спутника по круговой орбите? В этой статье мы рассмотрим методики и формулы, которые вам помогут решить эту задачу.
Что такое период обращения спутника?
Период обращения спутника — это время, за которое спутник полностью совершает один оборот вокруг Земли. Это важный параметр для определения траектории полета спутника, а также для планирования космических миссий и обеспечения связи со спутником.
Формула для вычисления периода обращения спутника
Для вычисления периода обращения спутника по круговой орбите можно использовать следующую формулу:
Т = 2π√(a³/GM)
где:
- Т — период обращения спутника
- π — математическая константа (3,1415926…)
- a — радиус орбиты спутника
- G — гравитационная постоянная (6,67430×10^−11 м³/(кг·с²))
- M — масса Земли
Для использования этой формулы необходимо знать радиус орбиты спутника и массу Земли. Радиус орбиты может быть вычислен, используя орбитальную высоту спутника. Для спутников на геостационарной орбите радиус орбиты составляет примерно 42 164 км, но для спутников на других орбитах этот параметр может отличаться.
Пример вычисления периода обращения спутника
Давайте рассмотрим пример вычисления периода обращения спутника. Предположим, что у нас есть спутник, находящийся на орбите в 1000 км от поверхности Земли.
Сначала необходимо вычислить радиус орбиты:
R = r + h = 6 371 + 1 000 = 7 371 км
где:
- R — радиус орбиты
- r — радиус Земли (6 371 км)
- h — высота орбиты (1 000 км)
Теперь, используя формулу, мы можем вычислить период обращения спутника:
Т = 2π√(a³/GM) = 2π√((7 371 000)³/(6,67430×10^−11 × 5,972×10^24)) ≈ 101.3 минуты
Итак, период обращения спутника составляет примерно 101.3 минуты, что означает, что спутник совершает один оборот вокруг Земли каждые 101.3 минуты.
Общий итог
Найти период обращения спутника по круговой орбите может показаться сложной задачей, но на самом деле все достаточно просто. Для вычисления периода необходимо знать радиус орбиты и провести небольшой расчет, используя формулу, которую мы описали в этой статье. Более подробно с формулами и практическими примерами можно ознакомиться в учебниках по астрономии и космическим наукам. Надеемся, что эта статья была для вас полезной и помогла лучше понять, как вычислить период обращения спутника по круговой орбите.
Как найти период обращения спутника по круговой орбите
Каждый спутник на орбите Земли имеет свой период обращения вокруг планеты. Для определения точного времени этого периода и формулы его вычисления, необходимы астрономические знания и некоторые математические умения. Если вы хотите узнать, как найти период обращения спутника по круговой орбите, то в данной статье мы детально рассмотрим этот вопрос.
Что такое период обращения спутника
Период обращения спутника — это время, которое тратит спутник на полный оборот по орбите вокруг планеты. Его измеряют в днях, часах, минутах и секундах. Он зависит от нескольких факторов, таких как масса планеты, высота орбиты спутника и его начальная скорость. Зная период обращения спутника, можно предсказать его положение относительно Земли в любой момент времени и проследить его траекторию движения.
Формула расчета периода обращения спутника
Математически формула для расчета периода обращения спутника выглядит следующим образом:
T = 2π√(a³/GM)
где:
- T — период обращения спутника
- π — математическая константа, приблизительно равная 3,14159
- a — радиус орбиты спутника
- G — гравитационная постоянная
- M — масса планеты, вокруг которой вращается спутник
Обратим внимание на то, что радиус орбиты спутника и масса планеты должны быть выражены в одинаковых единицах измерения. Например, если радиус задан в метрах, то масса должна быть выражена в килограммах.
Пример расчета периода обращения спутника
Предположим, что у нас есть спутник на орбите Земли, находящейся на высоте 200 км. Необходимо рассчитать его период обращения.
Сначала определим радиус орбиты спутника. Если считать Землю идеальной сферой, то ее радиус составляет 6 371 км. Прибавив к этому значению 200 км, получим общий радиус орбиты спутника, который составит 6 571 км.
Затем необходимо определить гравитационную постоянную. Это значение составляет 6,674 × 10^-11 м³/кг*с². Масса Земли равна 5,972 × 10^24 кг.
Теперь, подставив эти значения в формулу расчета периода обращения спутника, мы получаем следующий результат:
T = 2π√((6571000 м + 6371000 м)³ / (6,674 × 10^-11 м³/кг*с² × 5,972 × 10^24 кг)) = 5 399 секунд, что равно примерно 90 минутам.
Таким образом, период обращения спутника по круговой орбите на высоте 200 км составляет 90 минут.
Вывод
Расчет периода обращения спутника по круговой орбите может показаться сложной задачей, но с помощью вышеуказанной формулы и знаний о гравитационной постоянной и массе планеты, всё становится несколько проще. Знание периода обращения спутника позволяет предсказать его движение и местоположение в любой момент времени, что очень важно для астрономических и навигационных целей.
Как найти период обращения спутника по круговой орбите
При работе со спутниками, одним из наиболее важных параметров является период обращения. Знание периода обращения спутника позволяет правильно распределять его рабочие ресурсы, что может оказать влияние на проведение международных коммуникаций и даже экономические операции. Ниже описаны несколько способов, которые могут помочь определить период обращения спутника по круговой орбите.
Понимание круговой орбиты
Круговая орбита возникает, когда спутник движется вокруг шара по окружности. При круговой орбите скорость спутника постоянна, а сила, действующая на него, направлена к центру шара. Остановимся на некоторых основных концепциях, чтобы понять круговую орбиту.
- Центральное поле — это гравитационное поле, создаваемое центром шара;
- Радиус-вектор — это вектор, который соединяет центр шара и центр спутника;
- Закон Гравитации — это закон, который предписывает, как сила гравитации между двумя телами уменьшается по мере того, как расстояние между ними увеличивается.
В круговой орбите, радиус-вектор и скорость спутника будут перпендикулярны друг другу. Это значит, что центральное поле всегда направлено вдоль радиус-вектора.
Использование закона Кеплера
Для определения периода обращения спутника можно использовать закон Кеплера, который говорит о том, что квадрат периода обращения спутника пропорционален кубу его средней дистанции до центра планеты. Математически это выглядит так:
T^2 = (4 * П^2 / G * M) * r^3
где:
- T — период обращения;
- П — число Пи;
- G — гравитационная постоянная;
- M — масса центрального объекта;
- r — средняя дистанция между центром планеты и спутником.
Используя эту формулу, можно рассчитать период обращения спутника.
Использование скорости и радиуса
Другой способ определения периода обращения спутника по круговой орбите — использование его скорости и радиуса. Период обращения связан со скоростью спутника следующим образом:
T = 2 * П * r / v
где:
- T — период обращения;
- П — число Пи;
- r — радиус круговой орбиты;
- v — скорость спутника.
Таким образом, если известна скорость спутника и его радиус, можно рассчитать его период обращения.
Использование радара
Радар — это устройство, которое используется для измерения расстояний и скоростей. Для определения периода обращения спутника можно использовать радар. Существуют радиолокационные станции, способные отслеживать перемещение спутников и определять их параметры, включая период обращения.
Как правило, такие станции находятся под управлением космических агентств и используются для контроля над спутниками, чтобы пережить любые возможные неполадки и поддерживать работоспособность в течение всего срока их работы
Итог
В расчетах и определениях периода обращения, требуется знание нескольких величин, т.е знание математических формул и законов. Закон Кеплера и скорость спутника, являются базовыми компонентами, необходимыми для определения периода, также возможна требовательная для дополнительной аппаратуры (радара) работа. Понимание этих методов и компонентов крайне важно, особенно для инженеров и специалистов, работающих в космической индустрии.
Орбитальный период — время, за которое небесное тело совершает полный оборот на орбите вокруг внешнего центра притяжения или вокруг общего с другим небесным телом центра масс. Является предметом изучения небесной механики.
Орбитальный период не зависит от размера небесного тела. Соотношение орбитальных периодов двух (или более) небесных тел равное небольшому натуральному числу приводит к орбитальному резонансу, а при таком соотношении орбитального периода тела и его периода вращения вокруг своей оси — к спин-орбитальному резонансу. Орбитальный период пылевых частиц в Солнечной системе может уменьшаться вследствие эффекта Пойнтинга — Робертсона.
Сводка формул[править | править код]
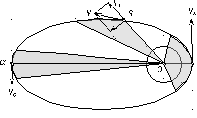
Большая (а) и малая (б) полуось эллипса
Согласно третьему закону Кеплера, орбитальный период T (в секундах) двух тел, вращающихся друг вокруг друга по круговой или эллиптической орбите, равен:
где:
а — большая полуось орбиты
μ = GM — стандартный гравитационный параметр
G — гравитационная постоянная
М — масса более массивного тела.
Для всех эллиптических орбит с одинаковой большой полуосью период обращения одинаков, независимо от эксцентриситета.
И наоборот, формула для расчёта расстояния, на котором тело должно вращаться, чтобы иметь заданный орбитальный период:
Например, для завершения движения каждые 24 часа при массе тела 100 кг небольшое тело должно вращаться на расстоянии 1,08 метра от его центра масс.
Когда сравнительно маленькое тело движется по круговой орбите и зависит от плотности центра масс — р (в кг/м³), приведённое выше уравнение упрощается:
.
Когда два тела вращаются друг вокруг друга, орбитальный период T можно рассчитать следующим образом (необходимо учитывать массы обоих орбитальных тел):
М1+М2 — сумма масс двух тел.
Виды[править | править код]
Существует несколько видов орбитальных периодов (при рассмотрении небесных тел в Солнечной системе):
- Сидерический период — промежуток времени, в течение которого какое-либо небесное тело-спутник совершает вокруг главного тела полный оборот относительно звёзд.
- Синодический период — промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.
- Драконический период — интервал времени, состоящий из 223 синодических месяцев (в среднем приблизительно 6585,3211 суток или 18,03 тропического года), по прошествии которого затмения Луны и Солнца приблизительно повторяются в прежнем порядке.
- Аномалистический период — промежуток времени, за который тело, перемещаясь по эллиптической орбите, дважды последовательно проходит через перицентр. Этот период может несколько отличаться от сидерического, потому что ориентация линии апсид орбиты медленно меняется из-за её прецессии. Например, аномалистический период Луны — 27,55455 дня, Земли — 365,25964 дня.
- Тропический период — отрезок времени, за который Солнце завершает один цикл смены времён года, как это видно с Земли, например, время от одного весеннего равноденствия до следующего, или от одного дня летнего солнцестояния до другого.
Ссылки[править | править код]
- Bate, Roger B.; Mueller, Donald D. & White, Jerry E. (1971), Fundamentals of Astrodynamics, Dover
-
Элементы орбиты и законы Кеплера. Основные формулы невозмущённого движения.
От постоянных интегрирования
обычно переходят к другим параметрам,
по которым можно вычислять координаты
и скорости спутника на любой момент
времени в инерциальной системе отсчёта.
Их называют элементами орбиты. По своему
назначению элементы орбиты делятся на
три группы. К первой группе относят
элементы, характеризующие размеры и
форму орбиты. Это большая полуосьи эксцентриситет обиты е:
К этой же группе элементов относятся:
фокальный параметр
,
малая полуось,
радиусы орбиты в перигееи
апогее:
а так же период обращения и среднее
движение:
Периодом обращения спутника
вокруг центрального тела называется
промежуток времени между моментами
двух последовательных прохождений
через произвольную точку орбиты. Среднее
движениеинтерпретируется
как средняя угловая скорость движения
спутника.
Элементы второй группы задают ориентировку
орбиты в пространстве. Они связаны с
векторными интегралами площадей и
Лапласа. К этим элементам относятся:
наклонение
,
долготаи аргумент перигея
.
Наклонениемназывают угол между
плоскостью экватора и плоскостью орбиты.
Его можно вычислить по формуле:
Очевидно, что
.
Орбиты с наклонением, равным 0º или 180º
называют экваториальными, а с наклонением
90º– полярными. Орбиты сназывают с прямым движением спутника,
а с– орбиты с обратным движением спутника
( по отношению к направлению вращения
Земли).
Долготой орбитыназывается угол,
отсчитываемый в плоскости экватора от
направления на точку весеннего
равноденствия

до направления на восходящий узел орбиты

Долготу определяют по формуле:
Аргументом перигеяназывается уголмежду направлениями на восходящий узел
и на перигей, отсчитываемый по направлению
движения спутника:
.
Для долготы и аргумента перигея
справедливо:
,
.
Элементы третьей группы задают положение
спутника на орбите. Оно устанавливается
с помощью момента прохождения перигея
или любой из аномалий (обычно истинной
или средней) с указанием эпохи.Истинной аномалией
называется угол между направлениями
на перигей и на спутник, отсчитываемый
в сторону движения спутника:
Средняя аномалияпредставляет
собой угол от направления на перигей
до направления на некоторое фиктивное
положение спутника, движущегося
равномерно по орбите:
.
Уравнение для средней аномалии иногда
называют динамическим интегралом, в
котором содержится шестая независимая
постоянная интегрирования – момент
проходжения перигея
.
Для связи истинной и средней аномалии
вводится эксцентрическая аномалия.
Чтобы её показать, вокруг орбитального
эллипса описывается окружность с центром
в точке С – геометрическом центре
эллипса, с радиусом, равным его большей
полуоси.
Через положение спутника – точку–
проводится перпендикуляр к большей
полуосидо
пересечения с окружностью в точке.
Соединяются точки С и.
Угол,
отсчитываемый при центре эллипса от
направления на перигей до направления
на точку,
называетсяэксцентрической аномалией.
Истинная и эксцентрическая аномалии
связаны соотношением:
,
а средняя и эксцентрическая аномалии
связаны уравнением Кеплера:
.
Часто используется угол от направления
на восходящий узел до направления на
спутник, называемый аргументом широты:
.
Существует множество других систем
элементов. Приведенные здесь параметры
называют Кеплеровыми элементами орбиты.
Законы движения спутника вокруг
центрального тела были открыты И.Кеплером
в начале XVIIв. Выведенные
вначале для вращающихся вокруг Солнца
планет, они оказались пригодными для
всех других тел, поскольку в их основе
лежит закон всемирного тяготения.
1-й закон Кеплера. Движение спутника
вокруг притягивающего тела всегда
происходит по коническому сечению
(окружности, эллипсу, параболе, гиперболе,
прямой), в одном из фокусов которого
находится притягивающий центр. Закон
выражается с помощью уравнения орбиты,
имеющей вид:
.
В зависимости от величины эксцентриситета
различают отбиты в виде окружности
(е=0), эллипса (0 < е < 1), параболы (е = 1),
гиперболы (е > 1) и прямой (е = ∞). В
дальнейшем мы будем рассматривать
только эллиптические орбиты.
Для описания 2-го закона Кеплера
потребуется ввести понятие секториальной
скорости
.
Это площадь, описываемая радиусом-вектором
спутника за единицу времени. Она связана
со скалярной константой площадей С:
.
Площадь, описываемую радиусом-вектором
спутника за промежуток времени
,
можно получить в виде определённого
интеграла:

что является математической записью
2-го закона Кеплера: за равные
промежутки времени радиус-вектор
спутника описывает равные площади.
Вследствии этого, линейная скорость
движения спутника по орбите в перигеебольше,
чем скорость в апогее.
3-й закон Кеплераформулируется
следующим образом: квадраты периодов
обращения спутников пропорциональны
кубам больших полуосей. Математическое
выражение для него получается из формулыЕсли у центрального тела (Земли) имеется
два спутника, соответственно, с периодамиР1 иР2и с большими полуосями
и
,
то для квадратов их периодов можно
записать:
А отношение этих выражение даёт формулу
3-го закона Кеплера:
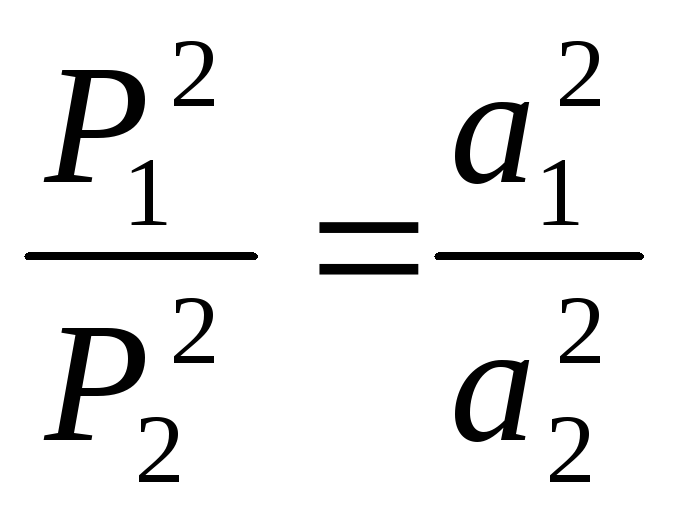
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
Закон всемирного тяготения. Движение планет и спутников
Закон всемирного тяготения
Соображения Ньютона состояли в следующем.
– Если сила притяжения тела к Земле пропорциональна массе тела Fтяг = mg, а каждой силе действия есть сила противодействия F1,2 = F2,1 и если тело притягивается к Земле, то и Земля притягивается к телу. Тогда сила тяготения должна быть пропорциональна как массе одного тела, так и массе второго тела Fтяг ~ m1m2, то есть сила тяготения пропорциональна произведению масс, взаимодействующих тел.
– Ньютон заметил, что ускорение на планете Земля, ускорение свободного падения
g = Fтяг / m – это примерно 10 м/с2, а ускорение, с которым движется Луна по своей орбите ал = Fтяг / Мл = g / 3600, – это центростремительное ускорение, в 3600 раз меньше ускорения свободного падения. Ньютон догадался, почему такая разница в числах: дело в том, что расстояние от Земли до Луны составляет примерно шестьдесят земных радиусов rз-л ≈ 60Rз. Их, а также ускорение 3600 Ньютон объединил следующим выводом: сила тяготения обратно пропорциональна квадрату расстояния между взаимодействующими телами Fтяг ~ 1 / r2.
Учитывая эти два посыла, Ньютон дал общую формулировку: сила всемирного тяготения прямо пропорциональна массам взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними.
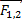
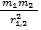
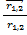
γ – коэффициент пропорциональности (гамма), а направление силы – это сила притяжения друг к другу, и направление в этой формуле дается следующим образом: это единичный вектор, приведенный из первого тела ко второму, то есть отношение самого вектора к его модулю. Знак минус означает, что сила тяготения направлена не от первого тела ко второму, а от второго тела к первому.
Коэффициент пропорциональности измерил Кавендиш в своем эксперименте:
γ = G = 6,62 · 10-11 Нм2 / кг2
Из закона всемирного тяготения следуют формулы ускорения свободного падения:
1. Ускорение свободного падения у поверхности планеты:
g0 = Fтяг / m = γmМз / R2з · m = γ · Мз / R2з.
Зная ускорение на планете Земля, радиус Земли, значение гравитационной постоянной, можно при необходимости вычислить массу Земли.
2. Ускорение свободного падения на каком-то расстоянии h от поверхности планеты:
gh = γ· Мз / (Rз + h)2 = (γ · Мз / R2з) · R2з / (Rз + h)2.
Так как в такой форме ее трудно применить, то пользуются приведенной формулой:
gh = g0 · (Rз / Rз + h)2
3. Ускорение свободного падения на глубине: gh↓ = g0 · (Rз – h / Rз).
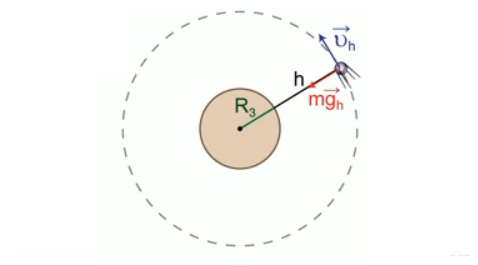
На основе закона всемирного тяготения можно рассчитать скорость спутников планет (рис. 1).
Рис. 1. Пример расчета скорости спутника
m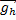
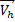
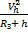
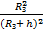
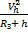
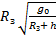
при h << 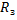
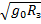
В этом случае сила притяжения будет перпендикулярна скорости спутника при движении по круговой орбите, она вызывает центростремительное движение. Зная ускорение свободного падения на высоте h, получаем формулу скорости спутника на высоте h. Очевидно, что с ростом высоты скорость будет уменьшаться, а у самой поверхности Земли при очень малых h по сравнению с радиусом Земли применяется упрощение. То есть h пренебрегают, вносят радиус Земли под корень, производят сокращения и получают формулу первой космической скорости, которая равна 7,9 км/с. При такой скорости спутник недалеко от поверхности Земли может двигаться по круговой орбите.
Пример решения задачи 1
У поверхности Луны на космонавта действует сила тяготения 120 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?
1. 0 Н; 2. 39 Н; 3. 21 Н; 4. 13 Н.
Запишем краткое условие задачи и рассмотрим решение:
Ответ: вариант 4. 13 Н.
Пример решения задачи 2
Два тела массой по 1000 тонн удалены на 0,1 км друг от друга. Найти силу их гравитационного притяжения.
1. 6,7 мН; 2. 0,67 Н; 3. 6,7 Н; 4. 6,7 кН.
Записываем краткое условие задачи, переводя тонны в килограммы, расстояние в метры, и решение.
Ответ: вариант 1. 6,7 мН.
Применяя закон всемирного тяготения, мы получаем правильный ответ 1.
Пример решения задачи 3
Чему равна скорость спутника Земли на круговой орбите на высоте 500 км от ее поверхности? Радиус Земли принять равным 6400 км.
1. 7,6 км/с; 2. 7,8 км/с; 3. 7,9 км/с; 4. 8,2 км/с.
Записываем краткое условие задачи и вычисления.
Ответ: вариант 1. 7,6 км/с.
Используя формулу спутника на высоте, мы вносим радиус планеты под знак радикала и разбиваем его на два множителя. У нас под корнем получилась первая космическая скорость, которую мы можем вынести за знак радикала и, подставив значения, получим, что скорость будет равна 7,6 км/с – это соответствует 1 ответу.
Движение планет и спутников
На основе закона всемирного тяготения рассчитывают период обращения спутников, как естественных, так и искусственных. Зная период обращения, мы можем найти массу спутников. Период обращения находится по формуле: Т = 2πR / V, то есть длина окружности, деленная на скорость по орбите. При малых высотах по сравнению с радиусом Земли для вычисления скорости спутника, который летит недалеко от поверхности Земли, период мы находим по формуле:
То = 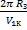
Помним о том, что в числителе у нас длина экватора, а в знаменателе первая космическая скорость. Произведя расчеты мы получим, что То ≈ 5060 с ≈ 1 ч 24 мин = 1,4 ч – это время, за которое искусственный спутник Земли, двигающийся недалеко от поверхности, совершает полный оборот. Если спутник летит по орбите, высота которой соизмерима с радиусом Земли, мы пользуемся формулой:
Тh = 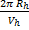
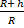
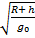
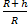
Эту формулу мы получили, внеся (R + h) под знак радикала и используя уже полученное значение То.
Рассмотрим задачу, по которой была вычислена масса Солнца.
Радиус земной орбиты составляет 1,5 · 1011 м. Чему равна масса Солнца?
Обычно эта задача вызывает затруднение, так как дан всего лишь один параметр, но нужно помнить, что Земля вокруг Солнца совершает один оборот за 365 дней, в сутках у нас 24 часа и в каждом часе 3600 секунд, так что нам известен период обращения Земли как спутника Солнца. Поэтому записываем краткое условие задачи и решение.
Ответ: 2·1030 кг.
Сила, с которой Земля притягивается к Солнцу, приводит к центростремительному ускорению, поэтому применяем формулу, которая выражается через период обращения. С другой стороны, это сила тяготения, и по закону всемирного тяготения выражается через гравитационную постоянную, массу Земли и массу Солнца, деленные на квадрат расстояния между ними. Сокращаем массу Земли в двух последних членах этого равенства, неизвестным остается только масса Солнца, которую мы можем вычислить, подставляя все данные.
Рассмотрим еще одну задачу.
В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли уменьшается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения по орбите и период обращения вокруг Земли? Для каждой величины определите соответствующий характер изменения:
1. увеличилась; 2. уменьшилась; 3. не изменилась.
При решении задач с выбором ответа необходимо перед решением выписать формулы величин, которые фигурируют в условии задачи. Сказано о том, что центростремительное ускорение уменьшилось, а центростремительное ускорение спутника есть не что иное, как ускорение свободного падения на его орбите: gh = g0 · (Rз / Rз + h)2, если g уменьшилось, значит, h увеличилось.
Скорость спутника на орбите, находящегося на высоте, – Vh = 
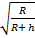
Формулу для периода обращения применяем Тh = То (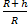
Ответ: в результате перехода радиус орбиты спутника увеличился, скорость его движения по орбите уменьшилась, период обращения вокруг Земли увеличился.
Заключение
Наличие всемирного тяготения объясняет устойчивость Солнечной системы, движение планет и других небесных тел. С открытием закона всемирного тяготения к людям пришло понимание принципа строения вселенной. Ярчайшим примером применения закона всемирного тяготения является запуск искусственного спутника Земли. Спутник все время находится на равном расстоянии над поверхностью Земли. Земля притягивает одинаково во всех направлениях.

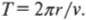

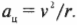
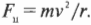
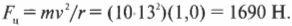
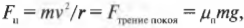
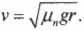
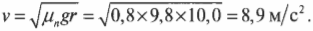
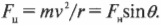
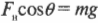
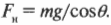
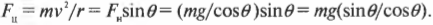
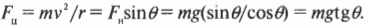
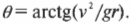
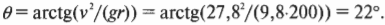
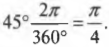
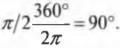
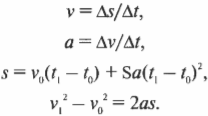
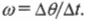
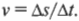
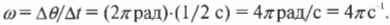
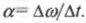
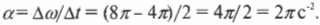
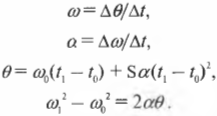
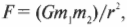
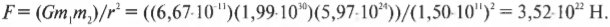
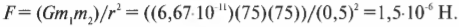
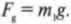
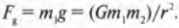
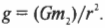
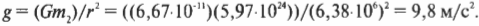
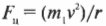
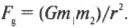

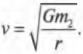
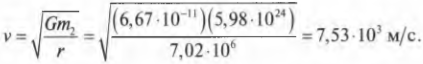
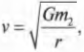
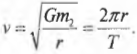
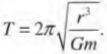
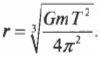
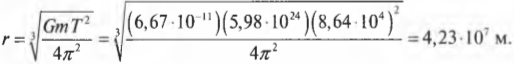
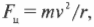
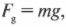
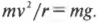
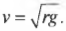
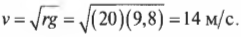








![{displaystyle a={sqrt[{3}]{frac {GMT^{2}}{4pi ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acc0794d19344d83b82ba93518c68a0fccd0b31b)