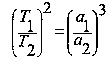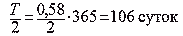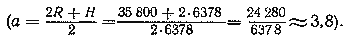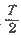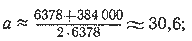Как найти период обращения вокруг эллипса - Сайт, где вы сможете решить свои вопросы

Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.

Эллипс[править | править код]

Основные параметры эллипса. Большая полуось обозначена как .

Большой осью эллипса называется его наибольший диаметр — отрезок проходящий через центр и два фокуса. Большая полуось составляет половину этого расстояния и идёт от центра эллипса к его краю через фокус.

Под углом в 90° к большой полуоси располагается малая полуось — минимальное расстояние от центра эллипса до его края. У частного случая эллипса — круга — большая и малая полуоси равны и являются радиусами. Таким образом, можно рассматривать большую и малую полуоси как некоего рода радиусы эллипса.

Длина большой полуоси связана с длиной малой полуоси через эксцентриситет , фокальный параметр и фокальное расстояние (полурасстояние между фокусами) следующим образом:

${displaystyle b=a{sqrt {1-e^{2}}},}$

${displaystyle p=a(1-e^{2}),}$

${displaystyle ap=b^{2}.}$

${displaystyle a^{2}=b^{2}+c^{2}}$

Большая полуось представляет собой среднее арифметическое между расстояниями от любой точки эллипса до его фокусов.

Рассмотрев уравнение в полярных координатах, с точкой в начале координат (полюс) и лучом, начинающейся из этой точки (полярная ось):

Получим средние значения и
и большую полуось ${displaystyle a={p over 1-e^{2}}.}$

Парабола[править | править код]

График построения параболы простейшей функции y = x²

Параболу можно получить как предел последовательности эллипсов, где один фокус остаётся постоянным, а другой отодвигается в бесконечность, сохраняя постоянным. Таким образом и стремятся к бесконечности, причём быстрее, чем .

Гипербола[править | править код]

Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:

${frac {left(x-hright)^{2}}{a^{2}}}-{frac {left(y-kright)^{2}}{b^{2}}}=1.$

Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:

${displaystyle a={p over e^{2}-1}}$

Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы.^[1]

Астрономия[править | править код]

Орбитальный период[править | править код]

В небесной механике орбитальный период обращения малых тел по эллиптической или круговой орбите вокруг более крупного центрального тела рассчитывается по формуле:

$T=2pi {sqrt {a^{3} over mu }}$

где:

— это размер большой полуоси орбиты

— это стандартный гравитационный параметр (произведение гравитационной постоянной на массу объекта

)

Следует обратить внимание, что в данной формуле для всех эллипсов период обращения определяется значением большой полуоси, независимо от эксцентриситета.

В астрономии большая полуось, наряду с орбитальным периодом, является одним из самых важных орбитальных элементов орбиты космического тела.

Для объектов Солнечной системы большая полуось связана с орбитальным периодом по третьему закону Кеплера.

$frac{T_1^2}{T_2^2} = frac{a_1^3}{a_2^3}$

где:

— орбитальный период в годах;

— большая полуось в астрономических единицах.

Это выражение является частным случаем общего решения задачи двух тел Исаака Ньютона:

${displaystyle T^{2}={frac {4pi ^{2}}{G(M+m)}}a^{3}}$

где:

— гравитационная постоянная

— масса центрального тела

— масса обращающегося вокруг него спутника. Как правило, масса спутника настолько мала по сравнению с массой центрального тела, что ею можно пренебречь. Поэтому, сделав соответствующие упрощения в этой формуле, получим данную формулу в упрощённом виде, который приведён выше.

Орбита движения спутника вокруг общего с центральным телом центра масс (барицентра), представляет собой эллипс. Большая полуось используется в астрономии всегда применительно к среднему расстоянию между планетой и звездой, в результате орбиты планет Солнечной системы приведены к гелиоцентрической системе, а не к системе движения вокруг центра масс. Эту разницу удобнее всего проиллюстрировать на примере системы Земля—Луна. Отношение масс в этом случае составляет 81,30059. Большая полуось геоцентрической орбиты Луны составляет 384 400 км, в то время как расстояние до Луны относительно центра масс системы Земля—Луна составляет 379 730 км — из-за влияния массы Луны центр масс находится не в центре Земли, а на расстоянии 4670 км от него. В итоге средняя орбитальная скорость Луны относительно центра масс составляет 1,010 км/с, а средняя скорость Земли — 0,012 км/с. Сумма этих скоростей даёт орбитальную скорость Луны 1,022 км/с; то же самое значение можно получить, рассматривая движение Луны относительно центра Земли, а не центра масс.

Среднее расстояние[править | править код]

Часто говорят, что большая полуось является средним расстоянием между центральным и орбитальным телом. Это не совсем верно, так как под средним расстоянием можно понимать разные значения — в зависимости от величины, по которой производят усреднение:

усреднение по эксцентрической аномалии. В таком случае среднее расстояние будет точно равно большой полуоси орбиты.
усреднение по истинной аномалии, тогда среднее расстояние будет точно равно малой полуоси орбиты.
усреднение по средней аномалии даст значение среднего расстояния, усреднённое по времени:

${displaystyle aleft(1+{frac {e^{2}}{2}}right).}$

усреднение по радиусу, которое получают из следующего соотношения:

${displaystyle {sqrt {ab}}=a{sqrt[{4}]{1-e^{2}}}.}$

Энергия; расчёт большой полуоси методом векторов состояния[править | править код]

В небесной механике большая полуось может быть рассчитана методом векторов орбитального состояния:

{displaystyle a={-mu over {2varepsilon }}}

для эллиптических орбит

для гиперболической траектории

$varepsilon ={v^{2} over {2}}-{mu over left|{mathbf {r}}right|}$

(удельная орбитальная энергия)

(стандартный гравитационный параметр),
где:

— орбитальная скорость спутника, на основе вектора скорости,

— вектор положения спутника в координатах системы отсчёта, относительно которой должны быть вычислены элементы орбиты (например, геоцентрический в плоскости экватора — на орбите вокруг Земли, или гелиоцентрический в плоскости эклиптики — на орбите вокруг Солнца),

— гравитационная постоянная,

— массы тел.

Большая полуось рассчитывается на основе общей массы и удельной энергии, независимо от значения эксцентриситета орбиты.

Большие и малые полуоси орбит планет[править | править код]

Орбиты планет всегда приводятся в качестве главных примеров эллипсов (первый закон Кеплера). Однако минимальная разница между большой и малой полуосями показывает, что они практически круговые по внешнему виду. Эта разница (или соотношение) основывается на эксцентриситете и вычисляется как ${displaystyle a/b=1/{sqrt {1-e^{2}}}}$ , что для типичных эксцентриситетов планет дает очень малые значения. Причина предположения о значительной эллиптичности орбит, вероятно, кроется в гораздо большей разнице между афелием и перигелием. Эта разница (или соотношение) также основывается на эксцентриситете и рассчитывается как ${displaystyle r_{text{a}}/r_{text{p}}=(1+e)/(1-e)}$ . Из-за большой разницы между афелием и перигелием второй закон Кеплера легко изобразить графически.

	Эксцентриситет	Большая полуось a (а. е.)	Малая полуось b (а. е.)	Разница (%)	Перигелий (а. е.)	Афелий (а. е.)	Разница (%)
Меркурий	0.206	0.38700	0.37870	2.2	0.307	0.467	52
Венера	0.007	0.72300	0.72298	0.002	0.718	0.728	1.4
Земля	0.017	1.00000	0.99986	0.014	0.983	1.017	3.5
Марс	0.093	1.52400	1.51740	0.44	1.382	1.666	21
Юпитер	0.049	5.20440	5.19820	0.12	4.950	5.459	10
Сатурн	0.057	9.58260	9.56730	0.16	9.041	10.124	12
Уран	0.046	19.21840	19.19770	0.11	18.330	20.110	9.7
Нептун	0.010	30.11000	30.10870	0.004	29.820	30.400	1.9

См. также[править | править код]

Элементы орбиты
Кеплеровы элементы орбиты
Эксцентриситет
Апоцентр и перицентр

Примечания[править | править код]

↑ 7.1 Alternative Characterization. Дата обращения: 15 сентября 2010. Архивировано 24 октября 2018 года.

Ссылки[править | править код]

Semi-major and semi-minor axes of an ellipse Архивная копия от 2 апреля 2012 на Wayback Machine With interactive animation

Источник

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения

— это время, за которое совершается один оборот.

Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:

Итак,
чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов
.

Другой характеристикой равномерного движения по окружности является частота обращения.

Частота обращения

— это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой
V
(читается: ню) и определяется по формуле:
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.

Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому

Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения
V
. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела
V
и радиус окружности r, по которой оно движется.

Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l

окр = 2
П
r, где
П
≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
. 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?

Отослано читателями из интернет-сайтов

Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку.

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Номинальная скорость вращения

Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:

К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.

Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.

Формула расчета сидерического периода

Для определения реального периода обращения планеты вокруг своей звезды или естественного спутника вокруг своей планеты, необходимо воспользоваться третьим законом Кеплера, который устанавливает взаимосвязь между реальным орбитальным периодом объекта и полудлиной его большой оси. В общем случае форма орбиты любого космического тела представляет собой эллипс.

Формула для определения сидерического периода имеет вид: T = 2*pi*√(a3/(G*M)), где pi = 3,14 — число пи, a — полудлина большой оси эллипса, G = 6,674*10-11 м3/(кг*с2) — универсальная гравитационная постоянная, M — масса объекта, вокруг которого осуществляется вращение.

Таким образом, зная параметры орбиты любого объекта, а также массу звезды, можно легко вычислить значение реального периода обращения этого объекта по своей орбите.

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

где:

ω – угловая скорость (рад./с);
∆ϕ – изменение угла отклонения при повороте (рад.);
∆t – время, затраченное на отклонение ©.

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

Описывающие вращение физические величины

Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.

В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:

n = θ/(2*pi);

L = θ*r.

Где r — радиус окружности или радиус вращения.

Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:

ω = θ/t

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать ½, ¼ оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

Расчет синодического временного периода

Как вычислить? Синодический период планеты или ее естественного спутника можно рассчитать, если знать значение реального ее периода обращения вокруг рассматриваемого объекта и реального периода обращения этого объекта вокруг своей звезды.

Формула, которая позволяет провести подобный расчет, имеет вид: 1/P = 1/T ± 1/S, здесь P — реальный период обращения рассматриваемого объекта, T — реальный период обращения объекта, относительно которого рассматривается движение, вокруг своей звезды, S — неизвестный синодический временной период.

Знаком «±» в формуле следует пользоваться так: если T > S, тогда формула используется со знаком «+», если же T

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

ν = 2*π*R / Т = 2*π*R* ν.

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Использование формулы на примере Луны

Чтобы показать, как правильно пользоваться приведенным выражением, возьмем для примера вращение Луны вокруг Земли и синодический период обращения Луны рассчитаем.

Источник

Равномерное движение по прямой линии

Это идеализированный тип движения, который предполагает, что тело в течение некоторого промежутка времени движется вдоль прямой в пространстве. При этом скорость тела не меняется. Обозначая пройденный путь символом l, получаем формулу:

l = v*t.

Здесь v = const.

Этот тип движения рассматривался еще философами Античной Греции. Они полагали, что для движения тел необходимо прикладывать некоторую силу, поэтому естественным состоянием всех окружающих объектов является покой. Только с приходом эпохи Возрождения благодаря работам Галилея и Ньютона было показано, что если на тело не воздействуют внешние силы, то равномерность и прямолинейность его движения не нарушается.

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Что касается обозначений, — ЗАПОМНИТЕ пожалуйста — НЕ СУЩЕСТВУЕТ жёстких правил обозначений, в принципе — обозначайте как хотите, хоть буквами «щ» и «ъ» Другое дело, что есть ТРАДИЦИЯ, период принято обозначать разными буквами «Т» (от английского time-время) , греческая «тау» используется много реже.. . А для частоты применяются (опять же ТРАДИЦИОННО) разные, большие и маленькие, буквы F, f (от англиского frequency) и (не знаю почему) греческая «ню».

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Мгновенная и средняя скорости

Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:

v¯ = dl¯/dt.

Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.

Вам будет интересно:Основные новообразования дошкольного возраста: общая характеристика развития ребенка

Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:

v¯ = Δl¯/Δt, где Δt>>dt.

В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.

При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности.

Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T

. Путь, который преодолевает точка — это есть длина окружности.

Линейная скорость вращения, частота и частота угловая

В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.

Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:

μ = 1/T

Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:

f = 2*pi*μ

Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.

Линейная скорость v связана со скоростью угловой ω следующим равенством:

v = ω*r

Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:

f = v/r

Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.

Источник

При движении по эллипсу вокруг Солнца продолжительность полного обращения может быть определена с помощью третьего закона Кеплера, по которому квадраты времен обращения планет относятся как кубы их средних расстояний от Солнца (то есть кубы больших полуосей эллиптических орбит):

где Т — продолжительность одного обращения;

а — большая полуось эллиптической орбиты.

Проще всего производить сравнение с периодом обращения Земли, равным, как известно, одному году, или 365 суткам. Тогда

Т = 365·a^3/2

где Т — в сутках, а — в астрономических единицах.

При движении вокруг Земли период обращения можно сравнивать с периодом обращения кругового спутника у самой поверхности, то есть на высоте Н = О. Этот период равен, как указывалось выше, 5070 секундам.

Поэтому

Т = 5070·a^3/2

где Т — в секундах,

а — в радиусах земного шара.

Примеры использования формул

1. Какова продолжительность полета корабля с Земли до Меркурия по наивыгоднейшему касательному полуэллипсу?

Период обращения по наивыгоднейшему эллипсу

Т = а^3/2 = 0,693^3/2 ? 0,58 лет.

Продолжительность полета

2. Какова продолжительность полета грузовой ракеты с Земли до суточной орбиты по касательному полуэллипсу (сопротивлением воздуха и активным участком траектории пренебрегаем)?

Т=5070·3,8^3/2 = 37 600 секунд

Продолжительность полета

= 18 800 секунд, или ?5,2 часа.

3. Какова продолжительность полета на Луну по наивыгоднейшему касательному полуэллипсу?

В этом случае поэтому Т = 5070 · 30,6^3/2 ? 860 000 секунд, или около 240 часов.

Продолжительность полета

? 120 часов (5 суток).

4. Какова величина больших полуосей орбит советских искусственных спутников?

В начале движения периоды обращения советских искусственных спутников равнялись:

первого спутника

Т₁ = 96,17 минуты = 5770 секунд;

второго спутника

Т₂ = 103,75 минуты = 6225 секунд;

третьего спутника

Т₃ = 106 минут= 6360 секунд.

По формуле Т = 5070 ^3/2 находим:

Истинные величины больших полуосей отличаются от приведенных выше приближенных, которые даны лишь в качестве иллюстрации.

5. Каков период обращения советской искусственной планеты, запущенной 2 января 1959 года?

Так как для этого случая а =1,145 (см. выше), то

Т = 365·1,145^3/2? 450 суток,

что соответствует данным, опубликованным в советской печати.

Источник

“Небесная механика”, как было принято называть науку о звездах во времена Исаака Ньютона, подчиняется классическим законам движения тел. Одними из важных характеристик этого движения являются различные периоды обращения космических объектов по своим орбитам. В статье пойдет речь о сидерическом и синодическом периодах обращения звезд, планет и их естественных спутников.

Понятие о синодическом и сидерическом временных периодах

Практически каждый из нас знает, что планеты движутся по эллиптическим орбитам вокруг своих звезд. Звезды, в свою очередь, совершают орбитальные движения вокруг друг друга или вокруг центра Галактики. Иными словами, все массивные объекты космоса имеют определенные траектории движения, включая кометы и астероиды.

Важной характеристикой для всякого космического объекта является время, которое он затрачивает, чтобы совершить один полный оборот по своей траектории. Это время принято называть периодом. Чаще всего в астрономии при изучении Солнечной системы пользуются двумя периодами: синодическим и сидерическим.

Сидерический временной период – это время, которое требуется объекту, чтобы он совершил полный оборот по своей орбите вокруг своей звезды, при этом за точку отчета берется другая удаленная звезда. Этот период также называют реальным, поскольку именно такое значение времени обращения по орбите получит неподвижный наблюдатель, который будет следить за процессом вращения объекта вокруг его звезды.

Синодический период – это время, через которое объект появится в одной и той же точке на небосводе, если смотреть на него с какой-либо планеты. Например, если взять Луну, Землю и Солнце и задаться вопросом о том, через какое время Луна будет находиться в точке на небе, в которой она находится в данный момент, ответом на него будет значение синодического периода Луны. Этот период также называют кажущимся, поскольку от реального орбитального периода он отличается.

Главное отличие между сидерическим и синодическим периодами

Как уже было сказано, сидерический – это реальный период обращения, а синодический – это кажущийся, однако в чем же главная разница между этими понятиями?

Вся разница заключается в количестве объектов, относительно которых измеряется временная характеристика. Понятие “сидерический период” принимает во внимание всего один относительный объект, например, Марс вращается вокруг Солнца, то есть движение рассматривается только относительно одной звезды. Синодический же временной период – это характеристика, которая учитывает относительное положение двух и более объектов, например, два одинаковых положения Юпитера относительно земного наблюдателя. То есть здесь необходимо учитывать положение Юпитера не только относительно Солнца, но и относительно Земли, которая также вращается вокруг Солнца.

Формула расчета сидерического периода

Формула для определения сидерического периода имеет вид: T = 2*pi*√(a3/(G*M)), где pi = 3,14 – число пи, a – полудлина большой оси эллипса, G = 6,674*10-11 м3/(кг*с2) – универсальная гравитационная постоянная, M – масса объекта, вокруг которого осуществляется вращение.

Расчет синодического временного периода

Формула, которая позволяет провести подобный расчет, имеет вид: 1/P = 1/T ± 1/S, здесь P – реальный период обращения рассматриваемого объекта, T – реальный период обращения объекта, относительно которого рассматривается движение, вокруг своей звезды, S – неизвестный синодический временной период.

Знаком “±” в формуле следует пользоваться так: если T > S, тогда формула используется со знаком “+”, если же T < S, тогда нужно подставить знак “-“.

Использование формулы на примере Луны

Известно, что наша планета имеет реальный период обращения по орбите вокруг Солнца, равный T = 365,256363 дней. В свою очередь, из наблюдений можно установить, что на небосводе Луна появляется в рассматриваемой точке через каждые S = 29,530556 дня, то есть это ее синодический период. Поскольку S < T, то формулу, связывающую разные периоды, следует брать со знаком “+”, получаем: 1/P = 1/365,256363 + 1/29,530556 = 0,0366, откуда P = 27,3216 дней. Как можно видеть, Луна на 2 дня быстрее совершает свой оборот вокруг Земли, чем земной наблюдатель снова может ее увидеть в отмеченном месте на небосводе.

Источник

From Wikipedia, the free encyclopedia

Animation of Orbit by eccentricity
0.0 ·

0.2 ·

0.4 ·

0.6 ·

0.8

Two bodies with similar mass orbiting around a common barycenter with elliptic orbits.

Two bodies with unequal mass orbiting around a common barycenter with circular orbits.

Two bodies with highly unequal mass orbiting a common barycenter with circular orbits.

An elliptical orbit is depicted in the top-right quadrant of this diagram, where the gravitational potential well of the central mass shows potential energy, and the kinetic energy of the orbital speed is shown in red. The height of the kinetic energy decreases as the orbiting body’s speed decreases and distance increases according to Kepler’s laws.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 (thus excluding the circular orbit). In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.

In a gravitational two-body problem with negative energy, both bodies follow similar elliptic orbits with the same orbital period around their common barycenter. Also the relative position of one body with respect to the other follows an elliptic orbit.

Examples of elliptic orbits include: Hohmann transfer orbit, Molniya orbit, and tundra orbit.

Velocity[edit]

Under standard assumptions, no other forces acting except two spherically symmetrical bodies m₁ and m₂,^[1] the orbital speed () of one body traveling along an elliptic orbit can be computed from the vis-viva equation as:^[2]

{displaystyle v={sqrt {mu left({2 over {r}}-{1 over {a}}right)}}}

where:

The velocity equation for a hyperbolic trajectory has either + , or it is the same with the convention that in that case a is negative.

Orbital period[edit]

Under standard assumptions the orbital period( T,! ) of a body travelling along an elliptic orbit can be computed as:^[3]

$T=2pisqrt{a^3over{mu}}$

where:

Conclusions:

The orbital period is equal to that for a circular orbit with the orbital radius equal to the semi-major axis (),
For a given semi-major axis the orbital period does not depend on the eccentricity (See also: Kepler’s third law).

Energy[edit]

Under standard assumptions, the specific orbital energy ( epsilon ) of an elliptic orbit is negative and the orbital energy conservation equation (the Vis-viva equation) for this orbit can take the form:^[4]

${v^2over{2}}-{muover{r}}=-{muover{2a}}=epsilon<0$

where:

Conclusions:

For a given semi-major axis the specific orbital energy is independent of the eccentricity.

Using the virial theorem we find:

the time-average of the specific potential energy is equal to −2ε
- the time-average of r⁻¹ is a⁻¹
the time-average of the specific kinetic energy is equal to ε

Energy in terms of semi major axis[edit]

It can be helpful to know the energy in terms of the semi major axis (and the involved masses). The total energy of the orbit is given by

${displaystyle E=-G{frac {Mm}{2a}}}$

where a is the semi major axis.

Derivation[edit]

Since gravity is a central force, the angular momentum is constant:

{displaystyle {dot {mathbf {L} }}=mathbf {r} times mathbf {F} =mathbf {r} times F(r)mathbf {hat {r}} =0}

At the closest and furthest approaches, the angular momentum is perpendicular to the distance from the mass orbited, therefore:

The total energy of the orbit is given by^[5]

${displaystyle E={frac {1}{2}}mv^{2}-G{frac {Mm}{r}}}$

We may substitute for v and obtain

${displaystyle E={frac {1}{2}}{frac {L^{2}}{mr^{2}}}-G{frac {Mm}{r}}}$

This is true for r being the closest / furthest distance so we get two simultaneous equations which we solve for E:

${displaystyle E=-G{frac {Mm}{r_{1}+r_{2}}}}$

Since ${textstyle r_{1}=a+aepsilon }$ and ${displaystyle r_{2}=a-aepsilon }$ , where epsilon is the eccentricity of the orbit, we finally have the stated result.

Flight path angle[edit]

The flight path angle is the angle between the orbiting body’s velocity vector (= the vector tangent to the instantaneous orbit) and the local horizontal. Under standard assumptions of the conservation of angular momentum the flight path angle phi satisfies the equation:^[6]

where:

psi is the angle between the orbital velocity vector and the semi-major axis. is the local true anomaly. ${displaystyle phi =nu +{frac {pi }{2}}-psi }$ , therefore,

${displaystyle cos phi =sin(psi -nu )=sin psi cos nu -cos psi sin nu ={frac {1+ecos nu }{sqrt {1+e^{2}+2ecos nu }}}}$

${displaystyle tan phi ={frac {esin nu }{1+ecos nu }}}$

where is the eccentricity.

The angular momentum is related to the vector cross product of position and velocity, which is proportional to the sine of the angle between these two vectors. Here phi is defined as the angle which differs by 90 degrees from this, so the cosine appears in place of the sine.

This section needs expansion. You can help by adding to it. (June 2008)

Equation of motion[edit]

From initial position and velocity[edit]

An orbit equation defines the path of an orbiting body $m_{2},!$ around central body $m_{1},!$ relative to $m_{1},!$ , without specifying position as a function of time. If the eccentricity is less than 1 then the equation of motion describes an elliptical orbit. Because Kepler’s equation has no general closed-form solution for the Eccentric anomaly (E) in terms of the Mean anomaly (M), equations of motion as a function of time also have no closed-form solution (although numerical solutions exist for both).

However, closed-form time-independent path equations of an elliptic orbit with respect to a central body can be determined from just an initial position () and velocity ().

For this case it is convenient to use the following assumptions which differ somewhat from the standard assumptions above:

The central body’s position is at the origin and is the primary focus () of the ellipse (alternatively, the center of mass may be used instead if the orbiting body has a significant mass)
The central body’s mass (m1) is known
The orbiting body’s initial position() and velocity() are known
The ellipse lies within the XY-plane

The fourth assumption can be made without loss of generality because any three points (or vectors) must lie within a common plane. Under these assumptions the second focus (sometimes called the “empty” focus) must also lie within the XY-plane: ${displaystyle mathbf {F2} =left(f_{x},f_{y}right)}$ .

Using vectors[edit]

The general equation of an ellipse under these assumptions using vectors is:

{displaystyle |mathbf {F2} -mathbf {p} |+|mathbf {p} |=2aqquad mid z=0}

where:

The semi-major axis length (a) can be calculated as:

${displaystyle a={frac {mu |mathbf {r} |}{2mu -|mathbf {r} |mathbf {v} ^{2}}}}$

where ${displaystyle mu =Gm_{1}}$ is the standard gravitational parameter.

The empty focus ( ${displaystyle mathbf {F2} =left(f_{x},f_{y}right)}$ ) can be found by first determining the Eccentricity vector:

${displaystyle mathbf {e} ={frac {mathbf {r} }{|mathbf {r} |}}-{frac {mathbf {v} times mathbf {h} }{mu }}}$

Where is the specific angular momentum of the orbiting body:^[7]

{displaystyle mathbf {h} =mathbf {r} times mathbf {v} }

Then

{displaystyle mathbf {F2} =-2amathbf {e} }

Using XY Coordinates[edit]

This can be done in cartesian coordinates using the following procedure:

The general equation of an ellipse under the assumptions above is:

${displaystyle {sqrt {left(f_{x}-xright)^{2}+left(f_{y}-yright)^{2}}}+{sqrt {x^{2}+y^{2}}}=2aqquad mid z=0}$

Given:

${displaystyle r_{x},r_{y}quad }$

the initial position coordinates

${displaystyle v_{x},v_{y}quad }$

the initial velocity coordinates

and

${displaystyle mu =Gm_{1}quad }$

the gravitational parameter

Then:

${displaystyle h=r_{x}v_{y}-r_{y}v_{x}quad }$

specific angular momentum

${displaystyle r={sqrt {r_{x}^{2}+r_{y}^{2}}}quad }$

initial distance from F1 (at the origin)

${displaystyle a={frac {mu r}{2mu -rleft(v_{x}^{2}+v_{y}^{2}right)}}quad }$

the semi-major axis length

${displaystyle e_{x}={frac {r_{x}}{r}}-{frac {hv_{y}}{mu }}quad }$

the Eccentricity vector coordinates

${displaystyle e_{y}={frac {r_{y}}{r}}+{frac {hv_{x}}{mu }}quad }$

Finally, the empty focus coordinates

${displaystyle f_{x}=-2ae_{x}quad }$

${displaystyle f_{y}=-2ae_{y}quad }$

Now the result values fx, fy and a can be applied to the general ellipse equation above.

Orbital parameters[edit]

The state of an orbiting body at any given time is defined by the orbiting body’s position and velocity with respect to the central body, which can be represented by the three-dimensional Cartesian coordinates (position of the orbiting body represented by x, y, and z) and the similar Cartesian components of the orbiting body’s velocity. This set of six variables, together with time, are called the orbital state vectors. Given the masses of the two bodies they determine the full orbit. The two most general cases with these 6 degrees of freedom are the elliptic and the hyperbolic orbit. Special cases with fewer degrees of freedom are the circular and parabolic orbit.

Because at least six variables are absolutely required to completely represent an elliptic orbit with this set of parameters, then six variables are required to represent an orbit with any set of parameters. Another set of six parameters that are commonly used are the orbital elements.

Solar System[edit]

In the Solar System, planets, asteroids, most comets and some pieces of space debris have approximately elliptical orbits around the Sun. Strictly speaking, both bodies revolve around the same focus of the ellipse, the one closer to the more massive body, but when one body is significantly more massive, such as the sun in relation to the earth, the focus may be contained within the larger massing body, and thus the smaller is said to revolve around it. The following chart of the perihelion and aphelion of the planets, dwarf planets and Halley’s Comet demonstrates the variation of the eccentricity of their elliptical orbits. For similar distances from the sun, wider bars denote greater eccentricity. Note the almost-zero eccentricity of Earth and Venus compared to the enormous eccentricity of Halley’s Comet and Eris.

Distances of selected bodies of the Solar System from the Sun. The left and right edges of each bar correspond to the perihelion and aphelion of the body, respectively, hence long bars denote high orbital eccentricity. The radius of the Sun is 0.7 million km, and the radius of Jupiter (the largest planet) is 0.07 million km, both too small to resolve on this image.

Radial elliptic trajectory[edit]

A radial trajectory can be a double line segment, which is a degenerate ellipse with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1, this is not a parabolic orbit. Most properties and formulas of elliptic orbits apply. However, the orbit cannot be closed. It is an open orbit corresponding to the part of the degenerate ellipse from the moment the bodies touch each other and move away from each other until they touch each other again. In the case of point masses one full orbit is possible, starting and ending with a singularity. The velocities at the start and end are infinite in opposite directions and the potential energy is equal to minus infinity.

The radial elliptic trajectory is the solution of a two-body problem with at some instant zero speed, as in the case of dropping an object (neglecting air resistance).

History[edit]

The Babylonians were the first to realize that the Sun’s motion along the ecliptic was not uniform, though they were unaware of why this was; it is today known that this is due to the Earth moving in an elliptic orbit around the Sun, with the Earth moving faster when it is nearer to the Sun at perihelion and moving slower when it is farther away at aphelion.^[8]

In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun at one focus, and described this in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.

References[edit]

^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 11–12. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Lissauer, Jack J.; de Pater, Imke (2019). Fundamental Planetary Sciences: physics, chemistry, and habitability. New York, NY, USA: Cambridge University Press. pp. 29–31. ISBN 9781108411981.
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 33. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. pp. 27–28. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 15. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 18. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Bate, Mueller, White (1971). Fundamentals Of Astrodynamics (First ed.). New York: Dover. p. 17. ISBN 0-486-60061-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ David Leverington (2003), Babylon to Voyager and beyond: a history of planetary astronomy, Cambridge University Press, pp. 6–7, ISBN 0-521-80840-5

Sources[edit]

D’Eliseo, Maurizio M. (2007). “The First-Order Orbital Equation”. American Journal of Physics. 75 (4): 352–355. Bibcode:2007AmJPh..75..352D. doi:10.1119/1.2432126.
D’Eliseo, Maurizio M.; Mironov, Sergey V. (2009). “The Gravitational Ellipse”. Journal of Mathematical Physics. 50 (2): 022901. arXiv:0802.2435. Bibcode:2009JMP….50a2901M. doi:10.1063/1.3078419.
Curtis, Howard D. (2019). Orbital Mechanics for Engineering Students (4th ed.). Butterworth-Heinemann. ISBN 978-0-08-102133-0.

External links[edit]

Java applet animating the orbit of a satellite in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.
Apogee – Perigee Lunar photographic comparison
Aphelion – Perihelion Solar photographic comparison
http://www.castor2.ca

Источник

Эллипс[править | править код]

Парабола[править | править код]

Гипербола[править | править код]

Астрономия[править | править код]

Орбитальный период[править | править код]

Среднее расстояние[править | править код]

Энергия; расчёт большой полуоси методом векторов состояния[править | править код]

Большие и малые полуоси орбит планет[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Номинальная скорость вращения

Формула расчета сидерического периода

Угловая скорость

Угловая скорость в конкретных случаях

Описывающие вращение физические величины

Угол поворота и период обращения

Расчет синодического временного периода

Переход от угловой к линейной скорости

Использование формулы на примере Луны

Равномерное движение по прямой линии

Движение по циклоиде*

Связь со вторым законом Ньютона

Мгновенная и средняя скорости

Линейная скорость

Линейная скорость вращения, частота и частота угловая

Понятие о синодическом и сидерическом временных периодах

Главное отличие между сидерическим и синодическим периодами

Формула расчета сидерического периода

Расчет синодического временного периода

Использование формулы на примере Луны

Velocity[edit]

Orbital period[edit]

Energy[edit]

Energy in terms of semi major axis[edit]

Derivation[edit]

Flight path angle[edit]

Equation of motion[edit]

From initial position and velocity[edit]

Using vectors[edit]

Using XY Coordinates[edit]

Orbital parameters[edit]

Solar System[edit]

Radial elliptic trajectory[edit]

History[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

Вам также может понравиться

Как найти вирус через диспетчер задач

Как найти девушку в майнкрафте видео

Как составить карту схему по географии

Добавить комментарий Отменить ответ