Как найти период в магнитном однородном поле
Магнитное поле – это особый вид материи, возникающий вокруг движущихся заряженных частиц. Простейший способ его обнаружения заключается в использовании магнитной стрелки.

Инструкция
Магнитное поле бывает неоднородным и однородным. Во втором случае его характеристики таковы: линии магнитной индукции (то есть воображаемые линии, по направлению которых располагаются магнитные стрелки, помещенные в поле) представляют собой параллельные прямые, густота этих линий везде одинакова. Сила, с которой поле воздействует на магнитную стрелку, также одинакова в любой точке поля, как по величине, так и по направлению.
Иногда приходится решать задачу по определению периода оборота заряженной частицы в однородном магнитном поле. Например, частица с зарядом q и массой m влетела в однородное магнитное поле с индукцией В, имея начальную скорость v. Каков период ее оборота?
Начните решение с поиска ответа на вопрос: какая сила действует в данный момент на частицу? Это сила Лоренца, которая всегда перпендикулярна к направлению движения частицы. Под ее воздействием частица будет двигаться по окружности радиуса r. Но перпендикулярность векторов силы Лоренца и скорость частицы означает, что работа силы Лоренца равна нулю. Значит, и скорость частицы, и ее кинетическая энергия при движении по круговой орбите остаются постоянными. Тогда и величина силы Лоренца постоянна, и вычисляется по формуле: F = qvB
C другой стороны, радиус окружности, по которой движется частица, связан с этой же силой таким соотношением: F = mv^2/r, или qvB = mv^2/r. Следовательно, r = vm/qB.
Период обращения заряженной частицы по окружности радиуса r вычисляется по формуле: Т = 2πr/v. Подставляя в эту формулу определенное выше значение радиуса окружности, вы получите: T = 2πvm/qBv. Сократив в числителе и знаменателе одинаковую величину скорости, получите окончательный результат: T = 2πm/qB. Задача решена.
Вы видите, что при вращении частицы в однородном магнитном поле период ее обращения зависит только от величины магнитной индукции поля, а также заряда и массы самой частицы.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Пусть в однородном магнитном поле, индукция которого , движется частица со скоростью
, направленной перпендикулярно линиям индукции. Масса частицы m и заряд q. Так как сила Лоренца
перпендикулярна скорости
движения частицы (см. рис. 170), то эта сила изменяет только направление скорости, сообщая частице центростремительное ускорение, модуль которого согласно второму закону Ньютона:
В результате частица движется по окружности, радиус которой можно определить из формулы :
Период Т обращения частицы, движущейся по окружности в однородном магнитном поле:
(30.2)
Как следует из выражения (30.2), период обращения частицы не зависит от модуля скорости её движения и радиуса траектории, а определяется только модулем заряда частицы, её массой и значением индукции магнитного поля.
От теории к практике
В однородном магнитном поле, модуль индукции которого В = 4,0 мТл, перпендикулярно линиям индукции поля движется электрон. Чему равен модуль ускорения электрона, если модуль скорости его движения ? Масса и модуль заряда электрона mе = 9,1 · 10–31 кг и е = 1,6 · 10–19 Кл соответственно.
![]()
Подобное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Движущиеся с огромными скоростями заряженные частицы из космоса захватываются магнитным полем Земли и образуют так называемые радиационные пояса (рис. 170.2), в которых частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами туда и обратно за промежуток времени порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния (рис. 170.3).
Если заряженная частица в момент возникновения внешнего электрического поля покоилась, то , где U — напряжение между точками, в которых находилась частица в моменты возникновения внешнего электрического поля и выхода из него, q — модуль заряда частицы. Поэтому модуль скорости частицы при выходе из электрического поля:
Если после этого частица попадает в однородное магнитное поле, индукция которого перпендикулярна направлению её скорости, то радиус окружности, по дуге которой будет двигаться частица,
, откуда
Величину называют удельным зарядом частицы. Поэтому если опытным путём определить радиус траектории движения частицы в магнитном поле, то, зная индукцию магнитного поля и ускоряющее напряжение электрического поля, можно рассчитать удельный заряд частицы. Этот метод используют при конструировании приборов, которые называют масс–спектрометрами.
Интересно знать
Поскольку сила Лоренца направлена под углом 90° к скорости движения заряженной частицы в каждой точке траектории (рис. 171), то работа этой силы при движении заряженной частицы в магнитном поле равна нулю. Поэтому кинетическая энергия частицы, движущейся в стационарном (не изменяющемся во времени) магнитном поле, не изменяется, т. е. стационарное магнитное поле нельзя использовать для ускорения заряженных частиц.
Увеличение кинетической энергии частицы, т. е. её разгон, возможно под действием электрического поля (в этом случае изменение кинетической энергии частицы равно работе силы поля). Поэтому в современных ускорителях (рис. 172) заряженных частиц электрическое поле используют для ускорения, а магнитное — для «формирования» траектории движения заряженных частиц.

![]()
1. Как определить модуль силы, действующей со стороны магнитного поля на движущуюся в нём заряженную частицу?
2. Как определяют направление силы Лоренца?
3. Заряженная частица движется в однородном магнитном поле со скоростью, направленной перпендикулярно линиям индукции. По какой траектории движется частица?
4. От чего зависит период обращения заряженной частицы в однородном магнитном поле?
![]()
5. Почему сила Лоренца изменяет направление скорости движения частицы, но не влияет на её модуль?
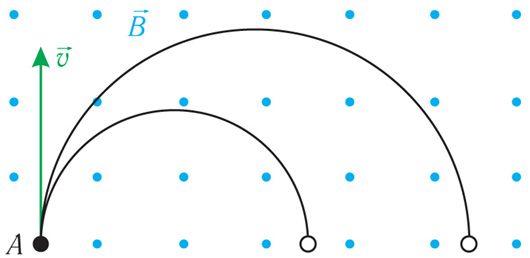
6. На рисунке 172.1 представлены траектории движения двух частиц, имеющих одинаковые заряды. Частицы влетают в однородное магнитное поле из одной точки А с одинаковыми скоростями. Определите знак заряда частиц. Объясните причину несовпадения траекторий их движения.
Как найти период обращения частицы по окружности в магнитном поле
Задание 18. Протон массой m и зарядом q движется перпендикулярно линиям индукции однородного магнитного поля B по окружности со скоростью v. Действием силы тяжести пренебречь.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
А) период обращения протона по окружности
Б) модуль ускорения протона

Сила Лоренца, действующая на частицу со стороны магнитного поля равна

и так как в данном случае  , то
, то
 .
.
Перепишем это выражение в соответствии со вторым законом Ньютона, получим:
 ,
,
откуда модуль ускорения протона равен:
 .
.
Это центростремительное ускорение  , поэтому:
, поэтому:
 ,
,
откуда радиус окружности
 .
.
Период обращения частицы по окружности – это время, за которое она проходит по этой окружности. Длина окружности равна
 ,
,
тогда время прохождения будет равно
 .
.
Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле
Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы FB, которую поле оказывает на частицу при ее движении в нем со скоростью v.
Общие свойства магнитной силы
Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:
- Величина FB магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
- Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
- Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, FB перпендикулярна плоскости, образованной v и B (см.рис. ниже).
- Величина и направление FB зависит от скорости частицы и от величины и направления магнитного поля B.
- Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
- Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.
Сила Лоренца
Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде FB = qv х B.
Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца FB при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.
Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно FЛ = qE + qv х В. Его принято называть так: полная сила Лоренца.
Движение заряженных частиц в однородном магнитном поле
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.
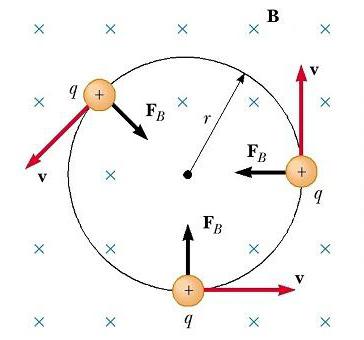
Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила FB направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и FB изменяются непрерывно, как показано на рисунке. Так как FB всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.
Динамика кругового движения частицы
Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем FB центробежной силе, требуемой для сохранения круговой траектории движения:
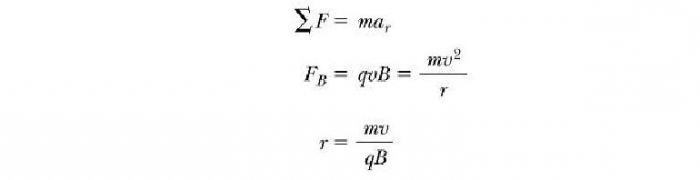
То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы
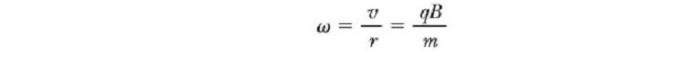
Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:
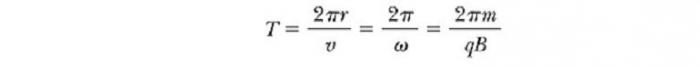
Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.
Движение частицы под углом к вектору магнитного поля
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы FB в этом направлении. В результате составляющая ускорения ax= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила FB = qv х В вызывает изменение во времени компонентов скорости vy и vz. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν⊥ = √(νу 2 + νz 2 ).
Неоднородное магнитное поле: как в нем движутся частицы
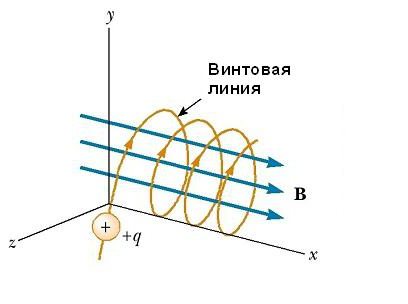
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.
Как Земля влияет на движение космических частиц
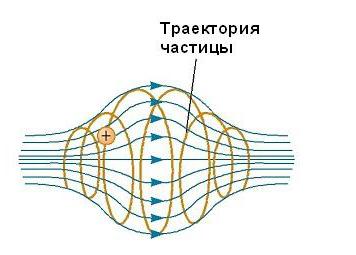
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.
Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.
Селектор скоростей
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).
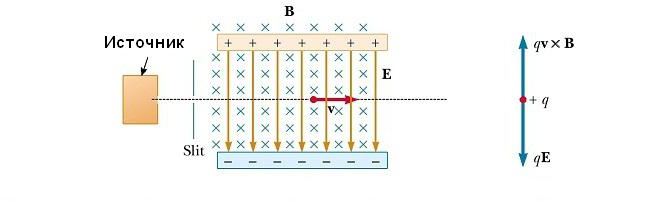
Масс-спектрометр
Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B0, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q
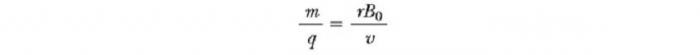
и затем, используя уравнение v=E/B, мы находим, что
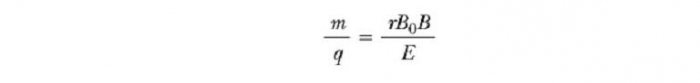
Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B0, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/mе для электронов.
Циклотрон
Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.
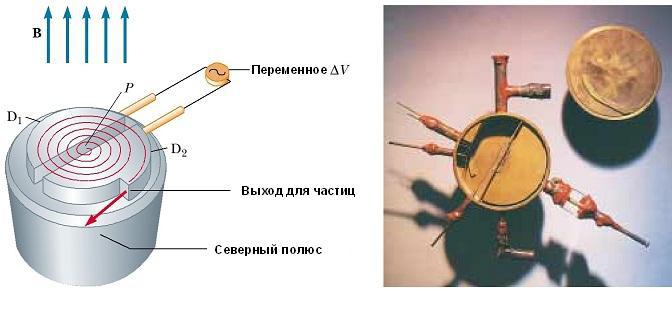
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).
Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.
Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D2 получает более низкий электрический потенциал, чем D1 на величину qΔV, то ион ускоряется в зазоре перед входом в D2, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D2 по полукруглой траектории большего радиуса (потому что его скорость увеличилась).
Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия
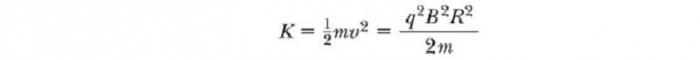
Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.
Эффект Холла
Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.
Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.
Как найти период обращения частицы по окружности в магнитном поле
Протон в однородном магнитном поле между полюсами магнита под действием силы Лоренца движется по окружности радиусом r. В этом же поле по окружности с таким же радиусом стала двигаться α-частица. Как изменились период обращения в магнитном поле и модуль импульса α-частицы по сравнению с протоном?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период обращения | Модуль импульса |
При движении заряженной частицы в однородном магнитном поле по окружности параметры системы связаны между собой соотношениями
Значит, радиус обращения частицы равен А скорость частицы равна Модуль импульса частицы будет равен
Период обращения равен Заряд альфа-частицы в два раза больше заряда протона, а её масса в четыре раза больше массы протона, следовательно, период обращения альфа-частицы в два раза больше, чем у протона, её импульс также в два раза больше, чем у протона.
[spoiler title=”источники:”]
http://www.syl.ru/article/203046/new_dvijenie-zaryajennoy-chastitsyi-v-magnitnom-pole-formulyi-dvijenie-zaryajennyih-chastits-v-odnorodnom-magnitnom-pole
http://phys-ege.sdamgia.ru/problem?id=16858
[/spoiler]
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
Движение заряженной частицы в магнитном поле
Работа силы Лоренца
может быть вычислена по формуле
![]() . (5)
. (5)
где
![]() – вектор перемещения частицы.
– вектор перемещения частицы.
Из
(2) следует, что сила Лоренца всегда
перпендикулярна вектору скорости
![]() заряженной частицы, и следовательно,
заряженной частицы, и следовательно,
перпендикулярна вектору перемещения
частицы![]() .
.
Тогда в выражении (5)![]() =
=
0, и работа силы Лоренца равна нулю.
Таким
образом, сила
Лоренца, действующая со стороны магнитного
поля на движущуюся заряженную частицу,
работы не совершает. Следовательно,
кинетическая энергия частицы при
движении в магнитном поле не изменяется,
т.е. величина
скорости движения частицы остается
постоянной.
Для
вывода основных закономерностей движения
заряженных частиц в магнитном поле
будем полагать, что магнитное поле
однородно.
Рассмотрим
три случая движения заряженной частицы
в магнитном поле:
1)
частица движется в магнитном поле со
скоростью
![]() вдоль линий магнитной индукции, то есть
вдоль линий магнитной индукции, то есть
угол α между векторами![]() и
и
![]()
равен 0 или π;
2)
частица движется в магнитном поле со
скоростью
![]() ,
,
перпендикулярной вектору магнитной
индукции (рис.4);
3)
частица движется со скоростью
![]() ,
,
вектор которой направлен под произвольным
углом α к вектору
![]()
(рис.5).
В
первом случае
сила Лоренца согласно формуле (3) равна
нулю. Магнитное поле на частицу не
действует, и заряженная частица движется
равномерно и прямолинейно вдоль линии
индукции магнитного поля.
Во
втором случае
сила Лоренца сообщает частице только
центростремительное ускорение. Поэтому
частица будет двигаться по окружности
радиуса R
с периодом обращения Т.
Для
определения радиуса окружности R
воспользуемся вторым законом Ньютона:
![]() .
.
(6)
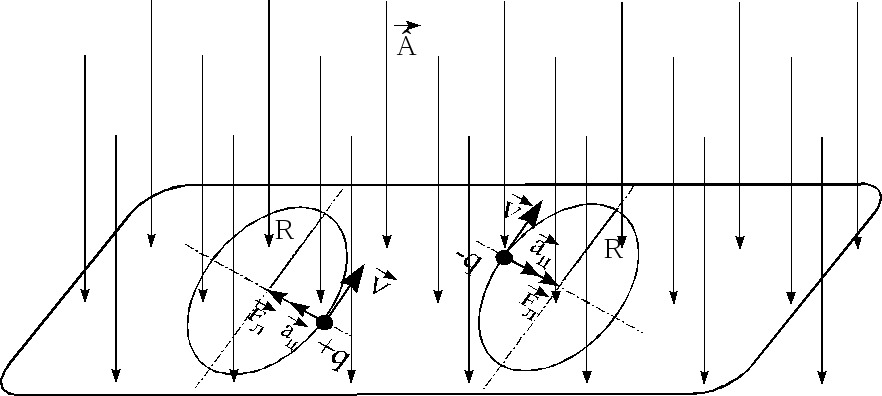
Рис.4.
Движение заряженных частиц под действием
силы Лоренца в магнитном поле в случае,
когда вектор скорости
![]() перпендикулярен
перпендикулярен
вектору магнитной индукции
![]()
Центростремительное
ускорение сообщает частице только сила
Лоренца, поэтому
![]()
, (7)
так
как
![]() .
.
Поскольку
![]() ,
,
(8)
то
![]() .
.
(9)
Из
(9) находим выражение для радиуса
окружности R,
по которой движется частица:
![]() .
.
(10)
Учитывая,
что длина окружности L
равна:
L = 2πR,
(11)
вычислим
период
обращения Т
частицы по окружности:
![]() .
.
(12)
С учётом (10)
получим:
![]()
(13)
Из
выражения (13) следует, что
период обращения Т не зависит от величины
скорости движения частицы V,
а определяется величиной индукции поля
![]()
и отношением q/m,
называемым удельным зарядом заряженной
частицы.
В
третьем
случае, когда
угол α ≠ 90°, траектория движения частицы
представляет собой спираль, ось которой
параллельна магнитному полю (рис.5).
Разложим
вектор скорости
![]() на две составляющие: параллельную и
на две составляющие: параллельную и
перпендикулярную полю
![]() ,
,
величины которых соответственно равны:
V׀׀= Vcosα
(14)
V= Vsinα
(15)
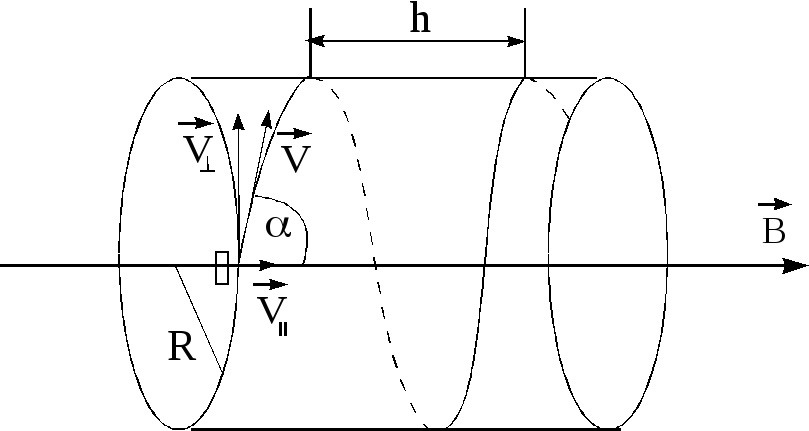
Рис.5. Движение
заряженной частицы в магнитном поле
по спирали
Тогда сила Лоренца,
действующая на частицу, может быть
представлена в виде:
![]() (16)
(16)
Так
как вектора
![]() и
и
![]()
сонаправлены, то второе слагаемое в
(16) равно нулю. Поэтому действие силы
Лоренца обусловлено только перпендикулярной
составляющей скорости частицы:
![]() .
.
(17)
В
этом случае частица будет двигаться по
окружности с центростремительным
ускорением
![]() ,
,
сообщаемым силой Лоренца (17). Радиус
окружностиR
согласно (10) будет равен:
![]() . (18)
. (18)
Период обращения
по окружности Т определяется формулой
(13).
Движение
частицы вдоль линий магнитного поля
![]() представляет собой равномерное
представляет собой равномерное
прямолинейное движение с постоянной
скоростью![]() .
.
За время одного полного оборота Т частица
сместится вдоль направления индукции
поля![]() на расстоянииh,
на расстоянииh,
равное:
![]() .
.
(19)
Величина
h
называется шагом
спирали (рис.5).
Направление, в котором закручивается
спираль, зависит от знака заряда частицы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
