Как найти период по математике - Сайт, где вы сможете решить свои вопросы

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:

Функция y=f(x) называется периодической, если существует такое число , не равное нулю, что для любого из ее области определения

Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.

Например, — периодические функции.

Для функций и период T = 2pi ,

Для функций tg x и период T = pi.

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках будут также равны пяти. Здесь k — целое число.

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

Значения функции в точках -3 и 7 равны пяти. Мы получим:

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем f(4)

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен 2pi.

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Значит, у функции частота в 3 раза больше, чем у функции , а наименьший положительный период в 3 раза меньше и равен $frac{{rm 2}pi }{{rm 3}}$ . Значит, на отрезке 2pi укладывается ровно 3 полных волны функции

Рассуждая аналогично, получим, что для функции наименьший положительный период равен $frac{{rm 2}pi }{{rm 5}}.$ На отрезке 2pi укладывается ровно 5 полных волн функции

Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен 2pi .

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

По условию, период функции равен 12. Это значит, что все значения повторяются через 12, через . Если мы выберем любую точку x_0 на графике функции то через значение функции будет такое же, как и в точке x_0.

Аналогично, все значения функции повторяются через . В этих точках значения будут такие же, как и в точке x_0.

На каком же расстоянии от точки x_0 расположена точка, в которой значение функции такое же, что и в точке x_0 ? Очевидно, на расстоянии Это значит, что число делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, T = 24 .

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Периодические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

$[{T_1} = frac{T}{{left| k right|}}]$

где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.

Найти период функции:

1) y=5sin(3x-п/8).

Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| 3 right|}} = frac{{2pi }}{3}.]$

$[2)y = frac{2}{7}cos (frac{pi }{5} - frac{x}{{11}})]$

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| { - frac{1}{{11}}} right|}} = 2pi cdot 11 = 22pi .]$

$[3)y = 0,3tg(frac{{5x}}{9} - frac{pi }{7})]$

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {frac{5}{9}} right|}} = frac{{9pi }}{5}.]$

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {0,4} right|}} = frac{{10pi }}{4} = frac{{5pi }}{2}.]$

Источник

Периодические десятичные дроби

10 февраля 2012

Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.

Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.

Периодическая десятичная дробь — это любая десятичная дробь, у которой:

Значащая часть состоит из бесконечного количества цифр;

Через определенные интервалы цифры в значащей части повторяются.

Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:

Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:

В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.

Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».

При этом будет происходить следующее:

Сначала разделится целая часть, если она есть;
Возможно, будет несколько чисел после десятичной точки;
Через некоторое время цифры начнут повторяться.

Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.

Задача. Переведите обыкновенные дроби в периодические десятичные:

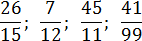
Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:

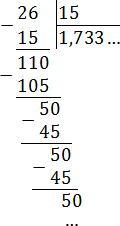
Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 … = 1,7(3).

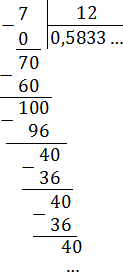
В итоге получается дробь: 0,5833 … = 0,58(3).

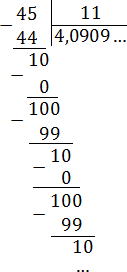
Записываем в нормальном виде: 4,0909 … = 4,(09).

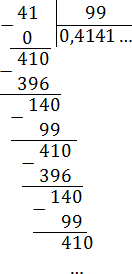
Получаем дробь: 0,4141 … = 0,(41).

Переход от периодической десятичной дроби к обыкновенной

Рассмотрим периодическую десятичную дробь X = abc(a₁b₁c₁). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:

Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
Найдите значение выражения X · 10^k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.

Задача. Приведите к обыкновенной неправильной дроби числа:

9,(6);

32,(39);

0,30(5);

0,(2475).

Работаем с первой дробью: X = 9,(6) = 9,666 …

В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10^k = 10¹ = 10. Имеем:

10X = 10 · 9,6666 … = 96,666 …

Вычитаем исходную дробь и решаем уравнение:

10X − X = 96,666 … − 9,666 … = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.

Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 …

Период k = 2, поэтому умножаем все на 10^k = 10² = 100:

100X = 100 · 32,393939 … = 3239,3939 …

Снова вычитаем исходную дробь и решаем уравнение:

100X − X = 3239,3939 … − 32,3939 … = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.

Приступаем к третьей дроби: X = 0,30(5) = 0,30555 … Схема та же самая, поэтому я просто приведу выкладки:

Период k = 1 ⇒ умножаем все на 10^k = 10¹ = 10;

10X = 10 · 0,30555 … = 3,05555 …
10X − X = 3,0555 … − 0,305555 … = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.

Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 … Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:

k = 4 ⇒ 10^k = 10⁴ = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 …
10 000X − X = 2475,2475 … − 0,2475 2475 … = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.

Смотрите также:

Сравнение дробей
Тест к уроку «Десятичные дроби» (2 вариант)
Четырехугольная пирамида в задаче C2
Как сдать ЕГЭ по математике
Задача B5: площадь сектора
Задача B4: тарифы на сотовую связь

Источник

Как определить периодичность функции

По школьным урокам математики каждый помнит график синуса, равномерными волнами уходящий вдаль. Аналогичным свойством — повторяться через определенный промежуток — обладают и многие другие функции. Они называются периодическими. Периодичность — очень важное свойство функции, часто встречающееся в различных задачах. Поэтому полезно уметь определять, является ли функция периодической.

Инструкция

Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.

Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.

Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете график функции по горизонтали именно в столько раз

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Однако если соотношение периодов иррационально, то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.

Источники:

Теоретические сведения о функциях

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Это очень просто

Время на прочтение
2 мин

Количество просмотров 19K

Рассмотрим следующую задачу. Найти период дроби 1/81. Уверяю, что для решения не потребуется ни калькулятор, ни деление столбиком. Для начала вспомним чему равно 81*(Период). Пусть длина периода n, тогда исходная дробь запишется как:

$frac{1}p=frac{Период}{10^n}+frac{Период}{10^{2n}}+frac{Период}{10^{3n}}+...$

Перепишем данное представление в следующем виде:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotleft(frac{Период}{10^{n}}+frac{Период}{10^{2n}}+..right)$

Последнее выражение можно представить так:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotfrac{1}p$

Ну а теперь то соотношение, которое мы искали:

Для нашего случая это тождество будет следующим:

Разделим левую и правую часть на 9, получим:

Первое число, составленное из одних единиц, которое делится на 9 равно 111111111, это следует из признака делимости на 9. Делить будем через сумму цифр исходного числа. Двигаемся слева направо, складываем цифры делимого и на каждом шаге записываем полученную сумму. Результат работы данного алгоритма — число 12345678,9999… Здесь надо пояснить, что когда мы достигаем крайней правой цифры, то ставим запятую и полученную сумму цифр исходного числа дублируем как бесконечную десятичную дробь. Вспоминаем, что 0,999…=1 и получаем ответ, который мы искали 12345679. Если рассмотреть более общую задачу нахождения периода дроби $frac{1}{9^n}$ , то окажется, что период такой дроби имеет длину ${9^{n-1}}$ и если известен период для случая n-1, то следующий равен произведению данного периода на число вида 11111… (повторяется ${9^{n-1}}$ раз)22222… (повторяется ${9^{n-1}}$ раз)33333… (повторяется ${9^{n-1}}$ раз). Самая правая секция будет иметь вид 8888..889. Последняя цифра девятка.
И еще одно наблюдение, теперь для дробей вида $frac{1}{11^{n}}$ . В этом случае длина периода равна $2cdot{11^{n-1}}$ . И если известен период для случая n-1, то следующий период равен произведению данного периода на число, составленное из 10 блоков, где длина каждого блока $2cdot{11^{n-2}}$ . Блоки имеют следующую структуру:
09090909…
18181818…
27272727…
36363636…
…
последний блок 90909091. Для $frac{1}{11}$ период 09, для $frac{1}{11^{2}}$ период будет 09182736455463728191*9=0082644628099173553719.
Проверил формулу для $frac{1}{11^{3}}$ . Получил

75131480090157776108189331329827197595792637114951164537941397445529676934635612
32156273478587528174305033809166040570999248685199098422238918106686701728024042
0736288504883546205860255447032306536438767843726521412471825694966190833959429,

что совпадает с периодом без ведущих нулей.

Приведу код процедур, которые я использовал для проверки своих выводов.

Function GreatestCommonDivisor(x,y)

    if x=y then
        return x;
    endif;  

    a=min(x,y);
    if a=1 then
        return 1;
    endif;  
    b=x+y-a;

    while TRUE do
     c=b%a; 
     if c=0 then
         return a;
     endif;  
     b=a;
     a=c;
    enddo;

EndFunction

Function NumeratorFractionPeriod(numerator,denumerator)

    // дробь a/b

    a=numerator;
    b=denumerator;

    while b%2=0 do
        b=b/2;
        a=a*5;
    enddo;  

    while b%5=0 do
        b=b/5;
        a=a*2;
    enddo;  
    //наибольший общий делитель
    c=GreatestCommonDivisor(a,b);
    a=a/c;
    b=b/c;

    if b=1 then
        Period=string(a);
        return Period;
    endif;

    if a>b then
        Period=string((a-a%b)/b);
        a=a%b;
        if a=0 then
            return Period;
        endif;  
        Period=Period+"(";
    else
        Period="(";
    endif;      

    while a%10=0 do
        a=a/10;
    enddo;  

    i=a;
    while TRUE do
        j=0;
        while i<b do
            i=i*10;
            j=j+1;
            if j>1 then
             Period=Period+"0";
            endif; 
        enddo;  

        check=i-a;
        if (check%b)=0 then
            Period=Period+(check)/b;
            break;
        else
            j=i%b;
            Period=Period+(i-j)/b;
            i=j;
        endif;    
    enddo;

    return Period+")";
EndFunction

Источник

Периодические десятичные дроби

Переход к периодической десятичной дроби

Переход от периодической десятичной дроби к обыкновенной

Как определить периодичность функции

Это очень просто

Вам также может понравиться

Как найти изображение в инете

Как исправить вздутую вагонку

Как исправить часы на телефоне айфон

Добавить комментарий Отменить ответ