|
0 / 0 / 0 Регистрация: 02.01.2014 Сообщений: 11 |
|
|
1 |
|
Найти период сгенерированных определенным образом чисел06.03.2014, 21:07. Показов 10384. Ответов 19
Допустим я генерирую числа определенным способом(Митчелла и Мура, Линейный конгруэнтный метод и т.д).
0 |
|
294 / 265 / 48 Регистрация: 09.04.2013 Сообщений: 1,037 |
|
|
07.03.2014, 22:14 |
2 |
|
Примерный алгоритм: Саму проверку на повторы периода можно целиком позаимствовать из алгоритмов проверки равенства строк.
1 |
|
22 / 15 / 7 Регистрация: 27.10.2013 Сообщений: 95 |
|
|
08.03.2014, 23:10 |
3 |
|
Нужно вывести все числа, кроме тех, что относятся к повторяющимся? Каков критерий определения повторяющихся чисел? Могут по 2е цифры часто повторятся, по 3 и т.д. Повторяющиеся числа это самая длинная, из повторяющихся последовательностей чисел? Длина периода всегда одна и та же? Если немного уточните условия задачи, то выложу код на c#.
1 |
|
0 / 0 / 0 Регистрация: 02.01.2014 Сообщений: 11 |
|
|
10.03.2014, 22:48 [ТС] |
4 |
|
Нужно найти период последовательности псевдослучайных чисел.
0 |
|
294 / 265 / 48 Регистрация: 09.04.2013 Сообщений: 1,037 |
|
|
11.03.2014, 00:28 |
5 |
|
Xn=(a*Xn-1+c) mod(m);
-Как определить длину предпериода? a,c,m константы ? тогда из-за рекурсивности формулы получаем что для определения предпериода достаточно найти сам период, потом запустить генератор с начала и ждать любое число из периода, когда нашли – сделать шаг назад. Полученный порядковый номер числа и будет длинной пред периода.
-Как без запоминания всей последовательности найти период? – она ведь может быть гигантской А ведь и не надо её всю запоминать, нужно только найти период. Кстати, а не может ли быть математического описания когда появятся повторения ? Добавлено через 7 минут
2 |
|
831 / 639 / 101 Регистрация: 20.08.2013 Сообщений: 2,524 |
|
|
12.03.2014, 18:25 |
6 |
|
Допустим набор чисел сгенерирован линейным конгруэнтным методом. Тогда надо генерировать последовательность двумя счётчиками – один с единичным шагом, второй – с двойным. Когда получится одинаковое число, запомнить его и продолить генерировать до тех пор пока оно не повторится. Это позволяет найти период. Чтобы найти предпериод, начинаем генерировать сначала, но одним из счётчиков пролистываем начало, по длинне равное периоду, после чего считаем обоими счётчиками синхронно. Когда числа совпадут, предпериод найден.
1 |
|
Potanin 22 / 15 / 7 Регистрация: 27.10.2013 Сообщений: 95 |
||||
|
12.03.2014, 19:49 |
7 |
|||
|
Не уверен что правильно понял задания, но, если понял правильно, то этот алгоритм создает одну и ту же постоянно повторяющуюся последовательность чисел. То есть например 123123123123, тогда здесь периодом будет 123.
1 |
|
831 / 639 / 101 Регистрация: 20.08.2013 Сообщений: 2,524 |
|
|
14.03.2014, 11:46 |
8 |
|
Potanin, просто ужас…
0 |
|
294 / 265 / 48 Регистрация: 09.04.2013 Сообщений: 1,037 |
|
|
14.03.2014, 12:50 |
9 |
|
x = (a * x + c) * m; } Не умножить, а найти модуль от деления на m Не по теме: Про поиск в строке промолчу, ибо думаю что я недостаточно знаю этот ЯП, вдруг что-то не то подумаю… Но спинным мозгом чувствую что что-то не то
2 |
|
22 / 15 / 7 Регистрация: 27.10.2013 Сообщений: 95 |
|
|
14.03.2014, 16:02 |
10 |
|
Так тоже работает, хоть и поиздевался над алгоритмом)))) Если просто удвоенный счетчик использовать то могут быть проблемы с, например 11311341131134. Первые три цифры и последующие три может ошибочно посчитать за период. Если посмотреть удлиненную версию (для этого берется +10 но тут можно +1) то такой ошибки можно избежать.
1 |
|
831 / 639 / 101 Регистрация: 20.08.2013 Сообщений: 2,524 |
|
|
14.03.2014, 18:11 |
11 |
|
Так тоже работает, хоть и поиздевался над алгоритмом)))) Я не про сдвиг 10, а про саму реализацию. Использование строк подобным образом – это извращение.
Если просто удвоенный счетчик использовать то могут быть проблемы с, например 11311341131134. Я ответил на конкретный вопрос. Для всех последовательностей, где каждый последующий элемент определяется ровно одним предыдущим, этот способ верный, причём есть доказательство этого факта.
1 |
|
294 / 265 / 48 Регистрация: 09.04.2013 Сообщений: 1,037 |
|
|
16.03.2014, 02:21 |
12 |
|
) Если просто удвоенный счетчик использовать то могут быть проблемы с, например 11311341131134 У тебя изначально задание сохранять последовательность в одну и ту же строку без символов-разделителей или ты так сам себе выбрал? В обоих случаях это плохая задумка, тут нужно либо массив чисел, либо добавлять разделители между строковым представлением чисел.
0 |
|
22 / 15 / 7 Регистрация: 27.10.2013 Сообщений: 95 |
|
|
16.03.2014, 08:56 |
13 |
|
Последнее замечание не совсем понятно. В итоге выводятся сам период и его длина, а не вся строка. Или суть в том, что необходимо сохранить не последовательность цифр в str, а последовательность чисел, формирующих период? Тогда тут возникает проблема. Допустим у меня началась генерация и мы получаем: 1 2 3 4 5 (затем) 12 34 51 и какую тут последовательность чисел приписать к периоду во втором случае?
0 |
|
831 / 639 / 101 Регистрация: 20.08.2013 Сообщений: 2,524 |
|
|
16.03.2014, 12:40 |
14 |
|
Не надо вообще использовать строки.
0 |
|
294 / 265 / 48 Регистрация: 09.04.2013 Сообщений: 1,037 |
|
|
16.03.2014, 18:55 |
15 |
|
Последнее замечание не совсем понятно. Нужно работать с числами чтобы правильно находить период, а не цифрами в числах, поэтому и получается у вас, что “могут быть проблемы с, например 11311341131134”. Желательно отказаться от строк вообще и перейти на целочисленные массивы.
0 |
|
22 / 15 / 7 Регистрация: 27.10.2013 Сообщений: 95 |
|
|
16.03.2014, 19:18 |
16 |
|
Все еще не ясно как, если работать не с цифрами, а с числами, получать период целиком. В любом же случае, если, как я указывал выше, есть 1 2 3 4 5 и 12 34 51, чтобы во втором случае вычислить период необходимо от последнего числа отделить последнюю цифру. Или же соответствующие алгоритмы генерации чисел устроены таким образом, что данной проблемы не возникает?
0 |
|
831 / 639 / 101 Регистрация: 20.08.2013 Сообщений: 2,524 |
|
|
16.03.2014, 23:04 |
17 |
|
Или же соответствующие алгоритмы генерации чисел устроены таким образом, что данной проблемы не возникает? Нужно найти период в последовательности чисел, а не цифр.
1 |
|
22 / 15 / 7 Регистрация: 27.10.2013 Сообщений: 95 |
|
|
17.03.2014, 09:58 |
18 |
|
Но ведь по линейному конгруэнтному методу каждое последующее число больше предыдущего, в следствие чего повторение последовательности именно из чисел невозможно.
0 |
|
Qwertiy 831 / 639 / 101 Регистрация: 20.08.2013 Сообщений: 2,524 |
||||
|
17.03.2014, 13:26 |
19 |
|||
|
Но ведь по линейному конгруэнтному методу каждое последующее число больше предыдущего Неправда. Там же по модулю.
1 |
|
Potanin 22 / 15 / 7 Регистрация: 27.10.2013 Сообщений: 95 |
||||
|
17.03.2014, 13:54 |
20 |
|||
|
Неправда. Там же по модулю.
Не о том модуле подумал, разобрался, спасибо
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
17.03.2014, 13:54 |
|
20 |
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 января 2022 года; проверки требуют 4 правки.
Периодическая последовательность — это последовательность, для которой те же самые элементы повторяются снова и снова:
Число p повторяющихся элементов называется периодом[1].
Определение[править | править код]
Периодическая последовательность (с периодом p) или p-периодическая последовательность — это последовательность 

Примеры[править | править код]
Любая постоянная функция 1-периодична[4].
Последовательность 
Последовательность цифр в десятичном представлении 1/7 является периодической последовательностью с периодом 6:
Вообще, последовательность цифр в десятичном представлении любого рационального числа является, в конечном счёте, периодической (см. ниже)[7].
Последовательность степеней −1 периодична с периодом два:
Вообще, последовательность степеней любого корня из единицы периодична. То же выполняется для степеней любого элемента конечного порядка в группе.
Периодическая точка для функции f : X → X — это точка x, орбита[en] которой
является периодической последовательностью. Здесь 
Тождества[править | править код]
Частичные суммы[править | править код]
Где k и m<p являются натуральными числами.
Частичные произведения[править | править код]
Где k и m<p являются натуральными числами.
Периодические 0, 1 последовательности[править | править код]
Любую периодическую последовательность можно построить поэлементным сложением, вычитанием, умножением и делением периодических последовательностей, состоящих из нулей и единиц. Периодические последовательности из нулей и единиц можно выразить через суммы тригонометрических функций:
последовательность с периодом N
Обобщения[править | править код]
Последовательность в конечном итоге периодическая, если её можно сделать периодической путём отбрасывания некоторого конечного набора членов с начала. Например, последовательность цифр в десятичном представлении числа 1/56 в конечном итоге периодична:
- 1 / 56 = 0,017 857142 857142 857142 …[1].
Последовательность асимптотически периодична, если её члены стремятся к периодической последовательности. То есть, последовательность 

[4][8][9]
Например, последовательность
- 1 / 3, 2 / 3, 1 / 4, 3 / 4, 1 / 5, 4 / 5, …
асимптотически периодична, поскольку её члены стремятся к периодической последовательности 0, 1, 0, 1, 0, 1, …
Примечания[править | править код]
- ↑ 1 2 3 4 Ultimately periodic sequence – Encyclopedia of Mathematics. encyclopediaofmath.org (7 февраля 2011). Дата обращения: 13 августа 2021. Архивировано 11 декабря 2021 года.
- ↑ 1 2 Weisstein, Eric W. Periodic Sequence (англ.). mathworld.wolfram.com. Дата обращения: 13 августа 2021. Архивировано 13 августа 2021 года.
- ↑ Bosma, Wieb Complexity of Periodic Sequences. www.math.ru.nl. Дата обращения: 13 августа 2021. Архивировано 17 февраля 2022 года.
- ↑ 1 2 3 Janglajew, Schmeidel, 2012, с. 195.
- ↑ Menezes, van Oorschot, Vanstone, 2018.
- ↑ 1 2 Weisstein, Eric W. Least Period (англ.). mathworld.wolfram.com. Дата обращения: 13 августа 2021. Архивировано 13 августа 2021 года.
- ↑ Hosch, William L. Rational number (англ.). Encyclopedia Britannica (1 июня 2018). Дата обращения: 13 августа 2021. Архивировано 11 декабря 2021 года.
- ↑ Cheng, 2017.
- ↑ Shlezinger, Todros, 2019, с. 260–271.
Литература[править | править код]
- Klara Janglajew, Ewa Schmeidel. Periodicity of solutions of nonhomogeneous linear difference equations // Advances in Difference Equations. — 2012. — Ноябрь (т. 2012, вып. 1). — ISSN 1687-1847. — doi:10.1186/1687-1847-2012-195.
- Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone. Handbook of Applied Cryptography. — CRC Press, 2018. — ISBN 978-0-429-88132-9.
- SuiSun Cheng. New Developments in Difference Equations and Applications: Proceedings of the Third International Conference on Difference Equations. — Routledge, 2017. — ISBN 978-1-351-42880-4.
- Nir Shlezinger, Koby Todros. Performance analysis of LMS filters with non-Gaussian cyclostationary signals // Signal Processing. — 2019. — Январь (т. 154). — ISSN 0165-1684. — doi:10.1016/j.sigpro.2018.08.008. — arXiv:1708.00635.
Найти период конечной периодической последовательности
краткое объяснение.
у меня есть последовательность чисел [0, 1, 4, 0, 0, 1, 1, 2, 3, 7, 0, 0, 1, 1, 2, 3, 7, 0, 0, 1, 1, 2, 3, 7, 0, 0, 1, 1, 2, 3, 7]. Как видите, из 3-го значения последовательность периодическая с периодом [0, 0, 1, 1, 2, 3, 7].
Я пытаюсь автоматически извлечь этот период из этой последовательности. Проблема в том, что я не знаю ни длины периода, ни положения, из которого последовательность становится периодической.
полное описание (может потребоваться math)
Я изучаю комбинаторную теорию игр, и краеугольный камень этой теории требует расчета Grundy values игры графика. Это порождает бесконечную последовательность, которая во многих случаях становится в конце концов периодические.
я нашел способ эффективно вычислять значения grundy (он возвращает мне последовательность). Я хотел бы автоматически извлечь смещение и период этой последовательности. Я знаю, что вижу часть последовательности [1, 2, 3, 1, 2, 3] вы не можете быть уверены в том, что [1, 2, 3] – это точка (кто знает, может быть, следующее число –4, что нарушает предположение), но меня не интересуют такие тонкости (я предполагаю, что последовательности достаточно, чтобы найти реальный период). Также проблема в том, что последовательность может остановиться в середине периода:[1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, ...] (период по-прежнему 1, 2, 3).
мне нужно найти наименьшее смещение и период. Например, для исходной последовательности, смещение может быть [0, 1, 4, 0, 0] и период [1, 1, 2, 3, 7, 0, 0], а самый маленький –[0, 1, 4] и [0, 0, 1, 1, 2, 3, 7].
мой неэффективный подход заключается в том, чтобы попробовать все возможные смещения и каждый возможный период. Постройте последовательность, используя эти данные, и проверьте, совпадает ли она с оригиналом. Я не делал никакого нормального анализа, но похоже, что он по крайней мере квадратичен с точки зрения сложности времени.
вот мой быстрый код python (не протестировали его должным образом):
def getPeriod(arr):
min_offset, min_period, n = len(arr), len(arr), len(arr)
best_offset, best_period = [], []
for offset in xrange(n):
start = arr[:offset]
for period_len in xrange(1, (n - offset) / 2):
period = arr[offset: offset+period_len]
attempt = (start + period * (n / period_len + 1))[:n]
if attempt == arr:
if period_len < min_period:
best_offset, best_period = start[::], period[::]
min_offset, min_period = len(start), period_len
elif period_len == min_period and len(start) < min_offset:
best_offset, best_period = start[::], period[::]
min_offset, min_period = len(start), period_len
return best_offset, best_period
который возвращает мне то, что я хочу для моей первоначальной последовательности:
offset [0, 1, 4]
period [0, 0, 1, 1, 2, 3, 7]
есть ли что-нибудь более эффективное?
3 ответов
-
я бы начал с построения гистограммы значений в последовательности
поэтому вы просто составляете список всех чисел, используемых в последовательности (или значительной ее части), и подсчитываете их появление. Это
O(n)здесьn– размер последовательности. -
сортировка по возрастанию гистограмме
это
O(m.log(m))здесьm– количество различных значений. Вы также можете игнорировать низкий вероятные числа (count<treshold), которые, скорее всего, в смещении или просто неровности дальнейшего сниженияm. Для периодических последовательностейm <<< nтаким образом, вы можете использовать его в качестве первого маркера, если последовательность периодическая или нет. -
узнайте срок
на гистограмма the
countsдолжно быть вокруг кратныхn/period. Так приблизительно / найти GCD гистограммы отсчетов. Проблема в том, что ты необходимо учитывать, что в графах, а также вn(смещенная часть), поэтому вам нужно вычислить GCD приблизительно. например:sequence = { 1,1,2,3,3,1,2,3,3,1,2,3,3 }заказал гистограммы:
item,count 2 3 1 4 3 6the
GCD(6,4)=2иGCD(6,3)=3вы должны проверить, по крайней мере+/-1вокругGCDрезультаты так что возможные периоды вокруг:T = ~n/2 = 13/2 = 6 T = ~n/3 = 13/3 = 4так что проверьте
T={3,4,5,6,7}просто чтобы быть уверенным. Использовать всегда GCD между наивысшими значениями и низкой счету. Если последовательность имеет много различных чисел, вы также можете сделать гистограмму подсчетов, проверяя только наиболее распространенные значения.чтобы проверить срок действия, просто возьмите любой элемент в конце или середине последовательности (просто используйте вероятную периодическую область). Затем ищите его в непосредственной близости от вероятного периода до (или после) его возникновения. Если найдено несколько раз, вы получили правильный период (или его несколько)
-
вам точный период
просто проверьте найденные фракции периода (
T/2, T/3,…) или сделайте гистограмму на найденном периоде и наименьшемcountговорит вам, сколько реальных периодов вы инкапсулировали так разделить на него. -
найти смещение
когда вы знаете период, это легко. Просто сканируйте с начала возьмите первый элемент и посмотрите, есть ли после периода снова. Если не помните положение. Остановиться в конце или в середине последовательность… или на каких-то последующих успехах. Это
O(n)и последнее запоминающееся положение-это последний элемент вoffset.
[edit1] было любопытно, поэтому я пытаюсь закодировать его на C++
я упростил / пропустил несколько вещей (предполагая, что по крайней мере половина массива является периодической), чтобы проверить, не сделал ли я какую-то глупую ошибку в своем алгоритме, и здесь результат (работает как ожидалось):
const int p=10; // min periods for testing
const int n=500; // generated sequence size
int seq[n]; // generated sequence
int offset,period; // generated properties
int i,j,k,e,t0,T;
int hval[n],hcnt[n],hs; // histogram
// generate periodic sequence
Randomize();
offset=Random(n/5);
period=5+Random(n/5);
for (i=0;i<offset+period;i++) seq[i]=Random(n);
for (i=offset,j=i+period;j<n;i++,j++) seq[j]=seq[i];
if ((offset)&&(seq[offset-1]==seq[offset-1+period])) seq[offset-1]++;
// compute histogram O(n) on last half of it
for (hs=0,i=n>>1;i<n;i++)
{
for (e=seq[i],j=0;j<hs;j++)
if (hval[j]==e) { hcnt[j]++; j=-1; break; }
if (j>=0) { hval[hs]=e; hcnt[hs]=1; hs++; }
}
// bubble sort histogram asc O(m^2)
for (e=1,j=hs;e;j--)
for (e=0,i=1;i<j;i++)
if (hcnt[i-1]>hcnt[i])
{ e=hval[i-1]; hval[i-1]=hval[i]; hval[i]=e;
e=hcnt[i-1]; hcnt[i-1]=hcnt[i]; hcnt[i]=e; e=1; }
// test possible periods
for (j=0;j<hs;j++)
if ((!j)||(hcnt[j]!=hcnt[j-1])) // distinct counts only
if (hcnt[j]>1) // more then 1 occurence
for (T=(n>>1)/(hcnt[j]+1);T<=(n>>1)/(hcnt[j]-1);T++)
{
for (i=n-1,e=seq[i],i-=T,k=0;(i>=(n>>1))&&(k<p)&&(e==seq[i]);i-=T,k++);
if ((k>=p)||(i<n>>1)) { j=hs; break; }
}
// compute histogram O(T) on last multiple of period
for (hs=0,i=n-T;i<n;i++)
{
for (e=seq[i],j=0;j<hs;j++)
if (hval[j]==e) { hcnt[j]++; j=-1; break; }
if (j>=0) { hval[hs]=e; hcnt[hs]=1; hs++; }
}
// least count is the period multiple O(m)
for (e=hcnt[0],i=0;i<hs;i++) if (e>hcnt[i]) e=hcnt[i];
if (e) T/=e;
// check/handle error
if (T!=period)
{
return;
}
// search offset size O(n)
for (t0=-1,i=0;i<n-T;i++)
if (seq[i]!=seq[i+T]) t0=i;
t0++;
// check/handle error
if (t0!=offset)
{
return;
}
код все еще не оптимизированный. Для n=10000 к 5ms настройки мои. Результат в t0 (смещение) и T (период). возможно, вам придется немного поиграть с константами treshold
Примечание: если есть срок P1 длиной L, тогда есть также Точка P2 С такая же длина, L, так что входная последовательность заканчивается точно на P2 (то есть у нас нет частичного периода в конце).
действительно, другой период той же длины всегда может быть получен путем изменения смещения. Новый период быть ротацией начального периода.
например, следующая последовательность имеет период длины 4 и смещение 3:
0 0 0 (1 2 3 4) (1 2 3 4) (1 2 3 4) (1 2 3 4) (1 2 3 4) (1 2
но он также имеет период с той же длиной 4 и смещением 5, без частичного периода в конце:
0 0 0 1 2 (3 4 1 2) (3 4 1 2) (3 4 1 2) (3 4 1 2) (3 4 1 2)
подразумевается, что мы можем найти минимальную длину периода путем обработки последовательности в обратном порядке и поиска минимального периода с использованием нулевого смещения от конец. Один из возможных подходов-просто использовать текущий алгоритм в обратном списке, без необходимости циклических смещений.
теперь, когда мы знаем длину желаемого периода, мы также можем найти его минимальное смещение. Один из возможных подходов-попробовать все различные смещения (с тем преимуществом, что цикл не нужен по длине, поскольку длина известна), однако при необходимости возможны дальнейшие оптимизации, например, продвигая как можно больше, когда обработка списка с конца, позволяющая окончательное повторение периода (то есть тот, который ближе всего к началу не обращенной последовательности), чтобы быть частичным.
однажды мне пришлось сделать что-то подобное. Я использовал грубую силу и здравый смысл, решение не очень элегантное, но оно работает. Решение всегда работает,но вы должны установить правильные параметры (k, j, con) в функции.
- последовательность сохраняется в виде списка в переменной seq.
- k размер массива последовательности, если вы думаете, что ваша последовательность займет много времени, чтобы стать периодической, то установите это k большой число.
- переменная нашел сообщит нам, прошел ли массив периодический тест с периодом j
- j – это период.
- если вы ожидаете огромный период, то вы должны установить j в большом количестве.
- мы проверяем периодичность, проверяя последний J в+30 чисел последовательности.
- чем больше период (j) еще надо проверить.
- As как только один из тест пройден, мы выходим из функции и возвращаем меньший период.
Как вы можете заметить, что точность зависит от переменных j и k но если вы установите их на очень большие числа, это всегда будет правильно.
def some_sequence(s0, a, b, m):
try:
seq=[s0]
snext=s0
findseq=True
k=0
while findseq:
snext= (a*snext+b)%m
seq.append(snext)
#UNTIL THIS PART IS JUST TO CREATE THE SEQUENCE (seq) SO IS NOT IMPORTANT
k=k+1
if k>20000:
# I IS OUR LIST INDEX
for i in range(1,len(seq)):
for j in range(1,1000):
found =True
for con in range(j+30):
#THE TRICK IS TO START FROM BEHIND
if not (seq[-i-con]==seq[-i-j-con]):
found = False
if found:
minT=j
findseq=False
return minT
except:
return None
упрощенная версия
def get_min_period(sequence,max_period,test_numb):
seq=sequence
if max_period+test_numb > len(sequence):
print("max_period+test_numb cannot be bigger than the seq length")
return 1
for i in range(1,len(seq)):
for j in range(1,max_period):
found =True
for con in range(j+test_numb):
if not (seq[-i-con]==seq[-i-j-con]):
found = False
if found:
minT=j
return minT
здесь max_period это максимальный период, который вы хотите найти, и test_numb сколько номеров последовательности вы хотите проверить, чем больше, тем лучше, но вы должны сделать max_period+test_numb
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Предел функции
В математическом
анализе рассматриваются функциональные
зависимости двух или более переменных.
Особый интерес представляет изучение
поведения функции при упорядоченном
изменении независимой переменной, т.е.
предельный переход, который является
одной из основных операций математического
анализа. Понятие предела является базой,
на которой строится классическое учение
о функциях. Выясним сначала это понятие
применительно к числовым последовательностям.
2.1. Числовая последовательность. Предел числовой последовательности
а) Рассмотрим
некоторую функцию натурального аргумента,
а именно функцию f(n),
определенную на множестве всех натуральных
чисел.
1, 2, 3, 4, …, N, …
Определение.
Всякая функция у=f(п),
заданная
на множестве
всех натуральных чисел, называется
(бесконечной) числовой последовательностью.
Закон соответствия
f
сопоставляет каждому натуральному
числу п
определенное значение функции f(п)
f(1),
f(2),
f(3),
…, f(п),
…
Значение функции
удобно обозначать одной буквой, снабженной
индексом (значком), указывающим, какому
натуральному числу соответствует взятое
значение функции f(п)
у1=
f(1),
у2=f(2),
у3=f(3),
…, уп=f(п),
…
Числа у1,
у2,
у3,
…, уп,
… называют
членами последовательности, член уп,
стоящий в последовательности на п-ом
месте, называется п-ым
ее членом.
Числовую
последовательность обозначают символом
{yn}.
Графиком числовой
последовательности является множество
изолированных точек.
Чаще всего
последовательность задается аналитическим
способом, т.е. при помощи формулы уп=f(п).
Примеры числовых
последовательностей.
1)
Члены последовательности
2)
Члены последовательности
б)
Виды числовых последовательностей.
Определение.
Числовая последовательность {yn}
называется монотонно возрастающей,
если при всех натуральных значениях n
выполняется неравенство
yn+1>yn
У монотонно
возрастающей последовательности каждый
последующий член больше предыдущего.
Определение.
Числовая последовательность {yn}
называется монотонно убывающей, если
при всех натуральных значениях п
выполняется
неравенство
yn+1<yn
Определение.
Последовательность {yn}
называется ограниченной, если можно
указать такое положительное число М,
что при
всех натуральных значениях п
имеет место
неравенство
|yn|<M
Определение.
Последовательность называется
неограниченной, если для любого
положительного числа М
имеет
место
неравенство
|yn|>M
в)
Предел числовой последовательности.
Рассмотрим
последовательность:
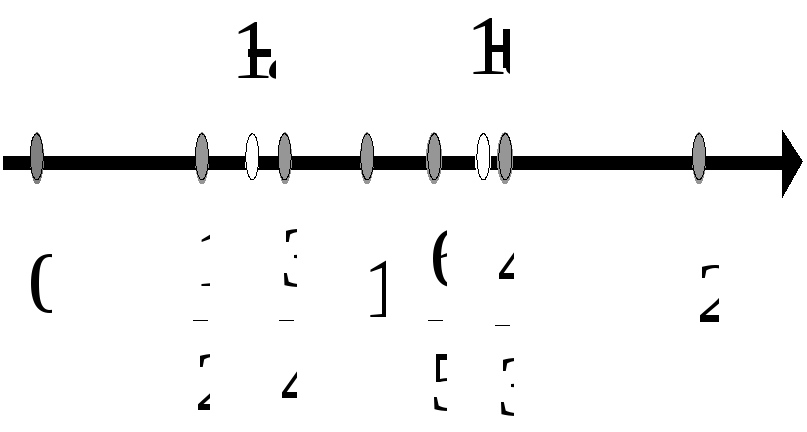
Изобразим члены
последовательности точками прямой
Из рисунка видно,
что точки, изображающие члены
последовательности, с увеличением
номера п все
ближе и ближе подходят к точке 1, они как
бы “накапливаются” около единицы.
Возьмем любое
положительное число .
Изобразим на прямой отрезок длиной 2
с центром в точке 1. Очевидно, что точки,
изображающие члены последовательности,
попадут в интервал (1,
1+)
только тогда, когда расстояние между
ними и точкой, изображающей единицу,
будет меньше .
Как известно, расстояние между точками
числовой прямой выражается числом
|yn
–1|,
независимо от того, будет ли точка уп
слева или справа от точки 1.
Число 1, по отношению
к которому члены взятой последовательности
{yn}
обладают указанным свойством, называется
пределом
этой последовательности.
Очевидно также,
что с ростом номера члена числовой
последовательности, все члены числовой
последовательности попадут в интервал
(1,
1+).
Определение.
Число А
называется пределом последовательности
{yn},
если для любого положительного числа
существует такое натуральное число N,
что все значения yn
, у
которых номер п>N,
удовлетворяют
неравенству
|yn–А|<
Тот факт, что А
является пределом последовательности
записывают так:
Еще одна графическая
иллюстрация понятия предела
Интервал (А-,
А+)
образует –полосу.
Все точки, которым соответствуют члены
числовой последовательности, у которых
номер n>N,
попадут в –полосу.
г)
Свойства пределов последовательностей.
Теорема Последовательность
{yn}
может иметь лишь один предел
Теорема Последовательность,
имеющая предел, является ограниченной.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Есть ли возможность найти длину цикла в очень большой части чисел (больше максимального значения самого большого целочисленного типа в C / C ++, скажем, 2 ^ 20), не задействуя диск для ее выполнения? Лучше всего было бы проанализировать их последовательно, поскольку они поступают со стандартного ввода, но я почти уверен, что это невозможно, и мне нужно хранить их в памяти. Но я надеюсь, что я не прав. Числовые значения являются целыми числами, они поступают из стандартного ввода.
Пример:
Ввод: (1 2 3 … (2 ^ 20 троек из 1 2 3) … 1 2 3)
Желаемый результат: 3
РЕДАКТИРОВАТЬ
давайте думать о цикле как о периоде (f (x) = f (x + t) для некоторого t) — ищем значение t
давайте предположим, что оперативной памяти слишком мало для хранения всех чисел (числа могут быть больше 2 ^ 20) и могут быть типы gmp.
0
Решение
Другие решения
Стандартный способ определения длины периода состоит в том, чтобы представить, что ваша последовательность представляет собой строку S над алфавитом целых чисел, а затем найти крайнюю левую позицию (больше 0), где S можно найти в строке SS (конкатенация строки S с собой). То есть если S = 'abcabc'нужно найти первую позицию i больше нуля, так что S находится в положении i в строке SS = 'abcabcabcabc', В данном случае это 3, и это длина периода.
Это может быть сделано любым алгоритмом поиска строк с линейной производительностью, и он должен прекрасно работать для 2 ^ 20 чисел на современном компьютере. Я сомневаюсь, что вы можете избежать сохранения чисел в памяти, хотя.
1