Как найти период собственных колебаний маятника - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 февраля 2023 года; проверки требует 1 правка.

Математический маятник. Чёрный пунктир — положение равновесия, theta — угол отклонения от вертикали в некоторый момент

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения^[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен

${displaystyle T_{0}=2pi {sqrt {L over g}}}$

и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.

Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.

Характер движения маятника[править | править код]

Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).

При колебаниях в одной плоскости маятник движется по дуге окружности радиуса , а при наличии двух степеней свободы может описывать кривые на сфере того же радиуса^[1]. Нередко, в том числе в случае нити, ограничиваются анализом плоского движения; оно и рассматривается далее.

Уравнение колебаний маятника[править | править код]

Маятник (схема с обозначениями)

Если в записи второго закона Ньютона для математического маятника выделить тангенциальную составляющую ( ${displaystyle ma_{tau }=F_{tau })}$ , получится выражение

{displaystyle mL{ddot {theta }}=-mgsin theta }

так как ${displaystyle a_{tau }={dot {v}}=d/dt(Ldtheta /dt)}$ , а из действующих на точку сил тяжести и натяжения ненулевую компоненту ${displaystyle F_{tau }}$ даёт только первая. Следовательно, колебания маятника описываются обыкновенным дифференциальным уравнением (ДУ) вида

${displaystyle {ddot {theta }}+{frac {g}{L}}sin theta =0}$

где неизвестная функция ― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах, ― длина подвеса, ― ускорение свободного падения. Предполагается, что потерь энергии в системе нет. В области малых углов это уравнение превращается в

${displaystyle {ddot {theta }}+{frac {g}{L}}theta =0}$

Для решения ДУ второго порядка, то есть для определения закона движения маятника, необходимо задать два начальных условия — угол theta и его производную при t=0 .

Решения уравнения движения[править | править код]

Возможные типы решений[править | править код]

В общем случае решение ДУ с начальными условиями для маятника может быть получено численно. Варианты движения (в случае, если маятник — это материальная точка на лёгком стержне), качественно, представлены на анимации. В каждом окне вверху показана зависимость угловой скорости от угла theta . По мере нарастания размаха поведение маятника всё сильнее отклоняется от режима гармонических колебаний.

Маятник висит
Малые колебания (размах 45°)
Колебания с размахом 90°
Колебания с размахом 135°
Колебания с размахом 170°
Фиксация в верхнем положении
Движение близкое к сепаратрисе
Вращение маятника

Гармонические колебания[править | править код]

Уравнение малых колебаний маятника около нижнего положения равновесия, когда уместна замена , называется гармоническим уравнением:

${displaystyle {ddot {theta }}+omega _{0}^{2}theta =0}$

где ${displaystyle omega _{0}={sqrt {g/L}}}$ ― положительная константа, определяемая только из параметров маятника и имеющая смысл собственной частоты колебаний. Кроме того, может быть осуществлён переход к переменной «горизонтальная координата» (ось лежит в плоскости качания и ортогональна нити в нижней точке):

${displaystyle {ddot {x}}+omega _{0}^{2}x=0}$

Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону^[2]:

${displaystyle x=Asin(omega _{0}t+alpha )}$

где — амплитуда колебаний маятника, alpha — начальная фаза колебаний.

Если пользоваться переменной , то при t=0 необходимо задать координату $x_{0}$ и скорость ${displaystyle v_{x0}}$ , что позволит найти две независимые константы , alpha из соотношений ${displaystyle x_{0}=Asin alpha }$ и ${displaystyle v_{x0}=Aomega _{0}cos alpha }$ .

Случай нелинейных колебаний[править | править код]

Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:

${displaystyle sin {frac {theta }{2}}=varkappa cdot operatorname {sn} (omega _{0}t;varkappa ),}$

где — это синус Якоби. Для он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом.

Параметр определяется выражением

${displaystyle varkappa ={frac {varepsilon +omega _{0}^{2}}{2omega _{0}^{2}}},quad varepsilon ={frac {E}{mL^{2}}}}$

Период колебаний нелинейного маятника составляет

${displaystyle T={frac {2pi }{Omega }},quad Omega ={frac {pi }{2}}{frac {omega _{0}}{K(varkappa )}}}$

где K — эллиптический интеграл первого рода.

Для вычислений практически удобно разлагать эллиптический интеграл в ряд:

${displaystyle T=T_{0}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {theta _{0}}{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {theta _{0}}{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {theta _{0}}{2}}right)+dots right}}$

где $T_{0}=2pi {sqrt {frac {L}{g}}}$ — период малых колебаний, $theta _{0}$ — максимальный угол отклонения маятника от вертикали.

При углах до 1 радиана (≈ 60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:

${displaystyle T=T_{0}left(1+{frac {1}{4}}sin ^{2}left({frac {theta _{0}}{2}}right)right)}$

Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года^[3]:

${displaystyle T={frac {2pi }{M{big (}cos(theta _{0}/2){big )}}}{sqrt {frac {L}{g}}}}$

где — арифметико-геометрическое среднее чисел 1 и .

Движение по сепаратрисе[править | править код]

Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.

Факты[править | править код]

Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.

Если амплитуда колебания маятника близка к , то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения^[4].
Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).

См. также[править | править код]

Физический маятник
Маятник Фуко
Маятник Дубошинского

Примечания[править | править код]

↑ ¹ ² Главный редактор А. М. Прохоров. Маятник // Физический энциклопедический словарь. — М.: Советская энциклопедия. — 1983. — Статья в Физическом энциклопедическом словаре
↑ Скорость и ускорение маятника при гармонических колебаниях также изменяются во времени по синусоидальному закону.
↑ Adlaj S. An Eloquent Formula for the Perimeter of an Ellipse (англ.) // Notices of the AMS. — 2012. — Vol. 59, no. 8. — P. 1096—1097. — ISSN 1088-9477.
↑ В. В. Вечеславов. Хаотический слой маятника при низких и средних частотах возмущений // Журнал технической физики. — 2004. — Т. 74, № 5. — С. 1—5. Архивировано 14 февраля 2017 года.

Ссылки[править | править код]

Коллекция Java-апплетов, моделирующая поведение математических маятников, в частности маятника Капицы.
Java-апплет, моделирующий колебание математического маятника при наличии вязкого трения с черчением фазовой траектории.
Учебный фильм «Математический и физический маятник», производство СССР

Источник

Механические колебания.

Гармонические колебания.
Уравнение гармонических колебаний.
Пружинный маятник.
Математический маятник.
Свободные и вынужденные колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания – это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания – это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия – это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела – это величина его наибольшего отклонения от положения равновесия.

Период колебаний – это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний – это величина, обратная периоду: nu =1/T . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение x=0 . Основная задача механики в данном случае состоит в нахождении функции x(t) , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них – синус и косинус – являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на pi /2 , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания – это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому – амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина alpha , равная значению фазы при t=0 , называется начальной фазой. Начальная фаза отвечает начальной координате тела: $x_{0}=Acos alpha$ .

Величина называется omega циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное 2 pi радиан: , откуда

$omega = frac{displaystyle 2pi }{displaystyle T}$ (2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

$x=Acos(frac{displaystyle 2pi t }{displaystyle T}+ alpha), x=Acos(2 pi nu t + alpha)$ .

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину $x_{0}$ и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае $x_{0}=A$ , поэтому можно положить alpha=0 . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае $x_{0}=0$ , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

$v_{x}=dot{x}=-Aomega sin(omega t+alpha )$ . (4)

Теперь дифференцируем полученное равенство (4):

$a_{x}=ddot{x}=-Aomega^{2} cos(omega t+alpha )$ . (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем $-omega^{2}$ :

$a_{x}=-omega^{2}x$ . (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

$ddot{x}+omega^{2}x=0$ . (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой omega и только их. Две константы определяются из начальных условий – по начальным значениям координаты и скорости.

к оглавлению ▴

Пружинный маятник.

Пружинный маятник – это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате x=0 отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости vec F со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

$ma_{x}=F_{x}$ . (8)

Если x>0 (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и $F_{x}<0$ . Наоборот, если x<0 , то $F_{x}>0$ . Знаки и $F_{x}$ всё время противоположны, поэтому закон Гука можно записать так:

$F_{x}=-kx$

Тогда соотношение (8) принимает вид:

$ma_{x}=-kx$

или

$a_{x}=-frac{displaystyle k}{displaystyle m}x$ .

Мы получили уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle k}{displaystyle m}$ .

Циклическая частота колебаний пружинного маятника, таким образом, равна:

$omega =sqrt{frac{displaystyle k}{displaystyle m}}$ . (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

$T=2 pi sqrt{frac{displaystyle m}{displaystyle k}}$ . (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник – это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

$ma_{x}=T_{x}$ .

Если маятник занимает положение как на рисунке (т. е. x>0 ), то:

$T_{x}=-Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Если же маятник находится по другую сторону от положения равновесия (т. е. x<0 ), то:

$T_{x}=Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Итак, при любом положении маятника имеем:

$ma_{x}=-Tfrac{displaystyle x}{displaystyle l}$ . (11)

Когда маятник покоится в положении равновесия, выполнено равенство T=mg . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

$ma_{x}=-mgfrac{displaystyle x}{displaystyle l}$ ,

или

$a_{x}=-frac{displaystyle g}{displaystyle l}x$ .

Это – уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle g}{displaystyle l}$ .

Следовательно, циклическая частота колебаний математического маятника равна:

$omega =sqrt{frac{displaystyle g}{displaystyle l}}$ . (12)

Отсюда период колебаний математического маятника:

$T=2pi sqrt{frac{displaystyle l}{displaystyle g}}$ . (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания – это колебания, совершаемые системой под воздействием внешней силы F(t) , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна $omega_{0}$ , а вынуждающая сила зависит от времени по гармоническому закону:

$F(t)=F_{0}cos omega t$ .

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
omega вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты $omega=omega_{r}$ наступает резонанс – явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: $omega_{r} approx omega_{0}$ , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, $omega_{r} = omega_{0}$ , а амплитуда колебаний возрастает до бесконечности при $omega Rightarrow omega_{0}$ .

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Формула периода колебаний математического маятника

Математический маятник

Определение

Математический маятник – это частный случай физического маятника, масса которого находится в одной точке.

Обычно математическим маятником считают маленький шарик (материальную точку), имеющий большую массу, подвешенный на длинной нерастяжимой нити (подвесе). Это идеализированная система, которая совершает колебания под воздействием силы тяжести. Только для углов порядка 50-100 математический маятник является гармоническим осциллятором, то есть совершает гармонические колебания.

Изучая качание паникадила на длинной цепи Галилей изучал свойства математического маятника. Он понял, что период колебаний данной системы не зависит от амплитуды при малых углах отклонения.

Формула для периода колебаний математического маятника

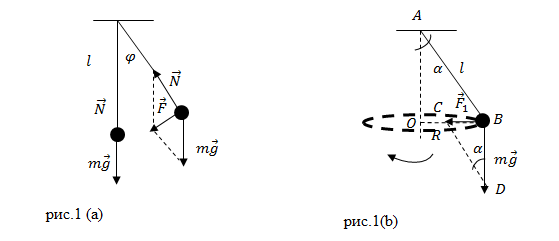
Пусть точка подвеса маятника неподвижна. Груз, подвешенный к нити маятника, движется по дуге окружности (рис.1(a)) с ускорением, на него действует некоторая возвращающая сила ($overline{F}$). Данная сила изменяется при движении груза. В результате чего расчет движения становится сложным. Введем некоторые упрощения. Пусть маятник совершает колебания не в плоскости, а описывает конус (рис.1 (b)). Груз в этом случае перемещается по окружности. Период интересующих нас колебаний будет совпадать с периодом конического движения груза. Период обращения конического маятника по окружности равен времени, которое тратит груз на один виток по окружности:

[T=frac{L}{v}=frac{2pi R}{v}left(1right),]

где $L$ – длина окружности; $v$ – скорость движения груза. Если углы отклонения нити от вертикали малые (небольшие амплитуды колебаний) то полагают, что возвращающая сила ($F_1$) направлена по радиусу окружности, которую описывает груз. Тогда эта сила равна центростремительной силе:

[F_1=frac{mv^2}{R}left(2right).]

Рассмотрим подобные треугольники: AOB и DBC (рис.1 (b)).

[F_1=mg{sin alpha =mgfrac{R}{l} }left(3right).]

Приравниваем правые части выражений (2) и (3), выражаем скорость движения груза:

[frac{mv^2}{R}=mgfrac{R}{l} to v=Rsqrt{frac{g}{l}}left(4right).]

Полученную скорость подставим в формулу (1), имеем:

[T=frac{2pi R}{Rsqrt{frac{g}{l}}}to ]

[T=2pi sqrt{frac{l}{g}}left(5right).]

Из формулы (5) мы видим, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения. Формулу (5) для периода математического маятника называют формулой Гюйгенса, она выполняется, когда точка подвеса маятника не движется.

Используя зависимость периода колебаний математического маятника от ускорения свободного падения, определяют величину данного ускорения. Для этого измеряют длину маятника, рассматривая большое количество колебаний, находят период $T$, затем вычисляют ускорение свободного падения.

Примеры задач с решением

Пример 1

Задание. Как известно, величина ускорения свободного падения зависит от широты. Каково ускорение свободного падения на широте Москвы, если период колебаний математического маятник длиной $l=2,485cdot {10}^{-1}$м равен T=1 c?textit{}

Решение. За основу решения задачи примем формулу периода математического маятника:

[T=2pi sqrt{frac{l}{g}}left(1.1right).]

Выразим из (1.1) ускорение свободного падения:

[g=lfrac{4{pi }^2}{T^2}.]

Вычислим искомое ускорение:

[g=0,2485cdot frac{4{pi }^2}{1^2}=9,81 (frac{м}{с^2}).]

Ответ. $g=9,81frac{м}{с^2}$

Пример 2

Задание. Каким будет период колебаний математического маятника, если точка его подвеса движется вертикально вниз 1) с постоянной скоростью? 2) с ускорением $a$? Длина нити этого маятника равна $l.$

Решение. Сделаем рисунок.

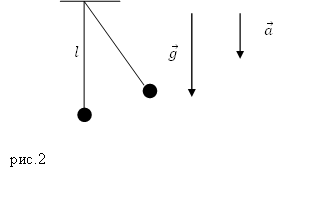
1) Период математического маятника, точка подвеса которого движется равномерно, равен периоду маятника с неподвижной точкой подвеса:

[T_1=2pi sqrt{frac{l}{g}}left(2.1right).]

2) Ускорение точки подвеса маятника можно рассматривать как появление дополнительной силы, равной $F=ma$, которая направлена против ускорения. То есть, если ускорение направлено вверх, то дополнительная сила направлена вниз, значит, она складывается с силой тяжести ($mg$). Если точка подвеса движется с ускорением, направленным вниз, то дополнительная сила вычитается из силы тяжести.

Период математического маятника, который совершает колебания и у которого точка подвеса движется с ускорением, найдем как:

[T_2=2pi sqrt{frac{l}{a_p}}left(2.2right),]

где:

[a_p=g-a left(2.3right),]

тогда:

[T_1=2pi sqrt{frac{l}{g-a}}.]

Ответ. 1) $T_1=2pi sqrt{frac{l}{g}}$; 2) $T_1=2pi sqrt{frac{l}{g-a}}$

Читать дальше: формула периода колебаний пружинного маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Пружинный маятник – колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.

Приняты следующие обозначения:

m – масса тела;
k – коэффициент жесткости пружины.

Общий вид маятника:

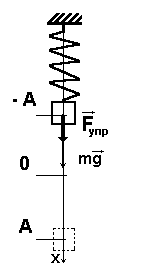
Особенностями пружинных маятников являются:

Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;
У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;
Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;
Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;
От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Виды пружинных маятников

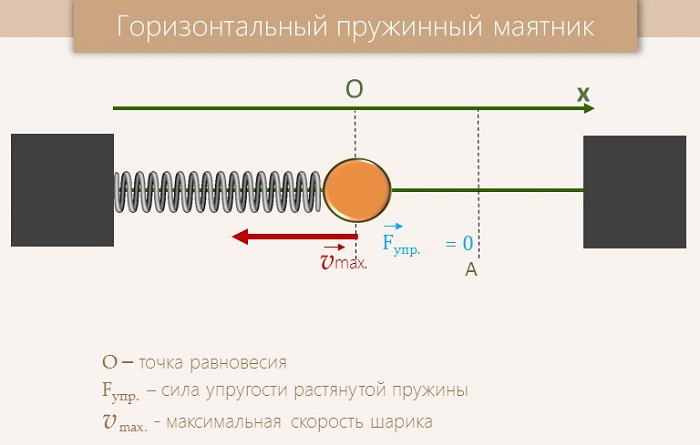
Существует два типа данной системы:

Вертикальный маятник – на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.
Горизонтальный – в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

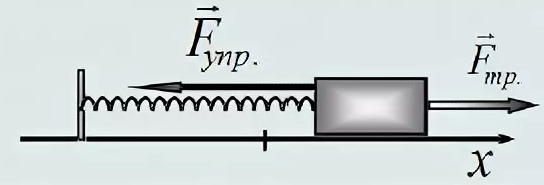
Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

F_упр = – k*x

где k — коэффициент жесткости пружины (Нм),

x – смещение (м).

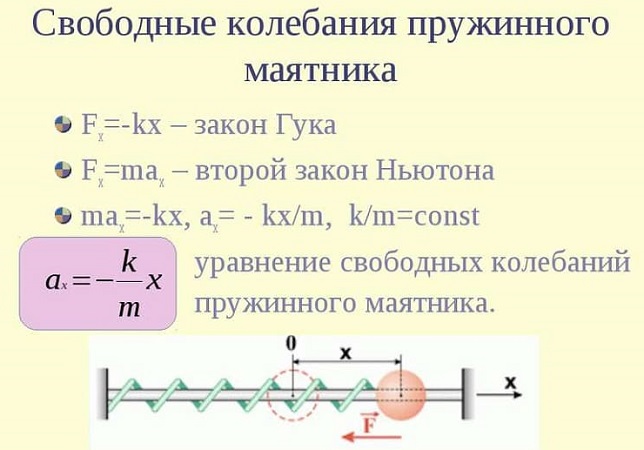
Уравнения колебаний пружинного маятника

Свободные колебания пружинного маятника описываются с помощью гармонического закона.

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = – mw2x(t),

где w – радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

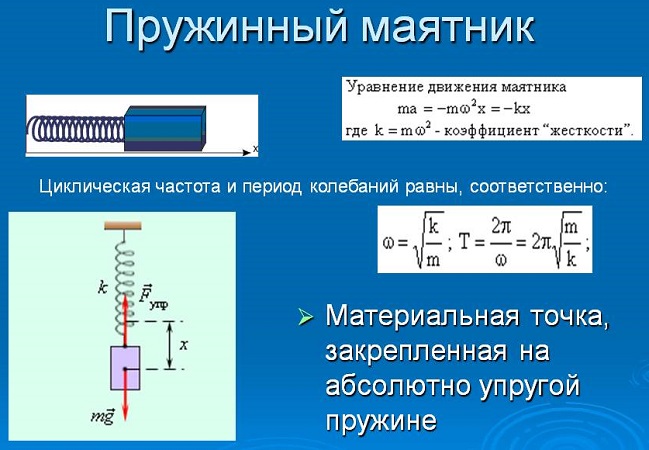
Факторы, от которых зависит частота:

Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.
Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

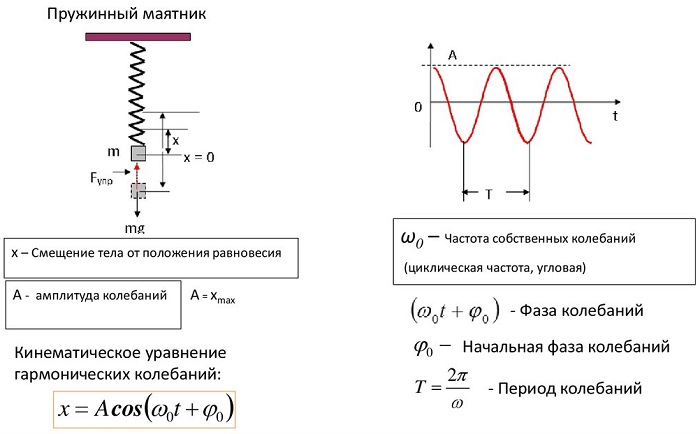
Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Потенциальная энергия:

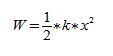
Кинетическая энергия:

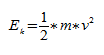
Полная энергия:

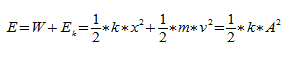
Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

Колебания проходят в двух плоскостях: вертикальной и горизонтальной.
В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.
Влияние силы трения при расчете не учитывают.

Дифференциальное уравнение гармонических колебаний пружинного маятника

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.

Источник

Что такое колебательный процесс

Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.

Систему, совершающую колебания, называют колебательной системой или осциллятором.

Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.

Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.

При механических колебаниях, которые относят к категории вынужденных:

(F=F_{0}cos cot)

Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.

Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.

Определение периода колебаний, формула

Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:

(x(t)=Atimes cos left(omega _{0}t+phi _{0} right))

Где (x(t)) является отклонением колеблющейся физической величины от равновесного значения;

А представляет собой амплитуду гармонических колебаний;

(omega _{0}) равно циклической или круговой частоте колебаний;

(phi _{0}) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;

(cp(t)=(co_{0}t+cp_{0})) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.

В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:

(cos left(alpha +2pi right)=cos alpha,)

то х остается без изменений при фазе колебаний, получающей приращение в $$2pi$$

Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.

В этом случае фаза будет увеличена на (2pi:)

(omega _{0}(t+T)+phi _{0}=left(omega _{0}t+phi _{0} right)+2pi)

Из данного равенства можно вычислить период колебаний:

(T=frac{2pi }{omega _{0}})

Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:

(v=frac{omega _{0}}{2pi})

На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.

Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.

Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:

Смещение (x=Atimes cos left(omega _{0}t+phi _{0} right))

Скорость (v_{x}=dot{x}=-Aomega _{0}times sin left(omega _{0} t+phi_{0} right)=Aomega _{0}times cos left(omega _{0} t+phi_{0} +frac{pi }{2}right))

Ускорение

(a_{x}=dot{v_{x}}=ddot{x}=-Aomega _{0}times cos left(omega _{0} t+phi_{0} right)=Aomega _{0}^{2}times cos left(omega _{0} t+phi_{0} +pi right))

Как найти период для физического маятника

В случае, когда углы отклонения (varphi) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:

(F=mgtimes sin varphi)

Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла (alpha)

Учитывая малый угол (varphi) уравнение можно записать в следующем виде:

(F=mgtimesvarphi)

С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:

(J=ml^{2})

При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:

(frac{d^{2}varphi }{dt^{2}}+frac{mgl}{J}varphi =0)

В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:

(alpha _{x}(t)+omega ^{2}x(t)=0)

Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:

(omega =sqrt{frac{mgl}{J}})

В таком случае для расчета периода колебаний математического маятника будет использоваться формула:

(T =frac{2pi }{omega }=2pi sqrt{frac{J}{mgl}})

Исходя из расчетов, можно сделать следующие выводы:

Период пружинного маятника (T =2pi sqrt{frac{m}{k}})
Период математического маятника (T =2pi sqrt{frac{L}{g}})
Период крутильного маятника (T =2pi sqrt{frac{I}{K}})

В приведенных формулах:

T — период физического маятника;
J — момент силы маятника относительно оси вращения;
l — расстояние от оси вращения до центра масс;
m — масса маятника;
g=9.8 — ускорение свободного падения.

Примеры решений

Задача № 1

Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.

Решение

(T =frac{t}{N}=frac{120}{60}=2)

(V=frac{1}{T}=frac{1}{2}=0.5)

Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.

Задача № 2

Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.

Решение

А = 20

Т = 0,8

(V=frac{1}{T}=frac{1}{0,8}=1,25)

(x(t)=Asin 2pi Vt=0.2sin 2pi times 1.25t=0.2sin 2.5pi t)

Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: (x(t)=0.2sin 2.5pi t)

Задача № 3

Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.

Решение

Период колебаний математического маятника рассчитывается по формуле:

(T =2pi sqrt{frac{L}{g}})

Согласно определению:

(V=frac{1}{T})

Тогда:

(T=frac{1}{V})

Получим равенство:

(frac{1}{V}=2pi sqrt{frac{l}{g}})

Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:

(frac{1}{V^{2}}=4pi ^{2}times frac{l}{g}Rightarrow l=frac{g}{4pi ^{2}V^{2}})

(l=frac{1.5}{4*3.14 ^{2}*0.5^{2}}approx 0.16)

Ответ: длина математического маятника примерно составляет 0,16 метра.

Источник

Характер движения маятника[править | править код]

Уравнение колебаний маятника[править | править код]

Решения уравнения движения[править | править код]

Возможные типы решений[править | править код]

Гармонические колебания[править | править код]

Случай нелинейных колебаний[править | править код]

Движение по сепаратрисе[править | править код]

Факты[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Механические колебания.

Гармонические колебания.

Уравнение гармонических колебаний.

Пружинный маятник.

Математический маятник.

Свободные и вынужденные колебания.

Формула периода колебаний математического маятника

Математический маятник

Формула для периода колебаний математического маятника

Примеры задач с решением

Что такое пружинный маятник

Виды пружинных маятников

Сила упругости в пружинном маятнике

Уравнения колебаний пружинного маятника

Период и частота свободных колебаний пружинного маятника

Амплитуда и начальная фаза пружинного маятника

Энергия пружинного маятника

Дифференциальное уравнение гармонических колебаний пружинного маятника

Что такое колебательный процесс

Определение периода колебаний, формула

Как найти период для физического маятника

Примеры решений

Вам также может понравиться

Как найти пароль от wifi на айфоне

Как составить схему древа предков

Как найти сумму выплат кредита

Добавить комментарий Отменить ответ