Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период – время одного колебания; Аплитуда – его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
1000 мкс = 1 мс.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами


Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2![]() .
.

Рисунок 2. Радиан.
Тогда,
1рад = 360°/2![]()
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2![]() ). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
Итак,
?= 6,28*f = 2f![]()
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
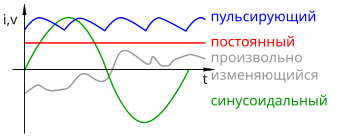
Пульсирующий переменный ток Постоянный ток Произвольно изменяющийся переменный ток Синусоидальный переменный ток

Переме́нный ток — электрический ток, который с течением времени изменяется по величине, обычно и по направлению в электрической цепи[1].
Хотя переменный ток часто переводят на английский как alternating current, эти термины не эквивалентны. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: 


Общее понятие о переменном токе[править | править код]
Так как переменный ток в общем случае меняется в электрической цепи не только по величине, но и по направлению, то одно из направлений переменного тока в цепи условно считают положительным, а другое отрицательным. В соответствии с этим и величину мгновенного значения переменного тока в первом случае считают положительной, а во втором случае — отрицательной.
Сила переменного тока — величина скалярная, знак её определяется тем, в каком направлении ток протекает в цепи в рассматриваемый момент времени — в положительном или отрицательном.
Величина переменного тока, соответствующая данному моменту времени, называется мгновенным значением переменного тока.
Максимальное мгновенное значение переменного тока, которого он достигает в процессе своего изменения, называется амплитудой тока 
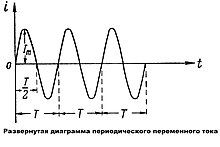
- График зависимости силы переменного тока от времени называется развёрнутой диаграммой переменного тока.
Развёрнутая диаграмма переменного синусоидального тока
На рисунке приведена развёрнутая диаграмма переменного тока, изменяющегося с течением времени по величине и направлению. На горизонтальной оси — оси времени — в определённом масштабе отложены отрезки времени, а по вертикальной оси — сила тока, причём в направлении вверх выбрано положительное направление, а вниз — отрицательное.
В начальный момент времени 





Периодический переменный ток[править | править код]
Развёрнутая диаграмма периодического переменного тока
Периодическим переменным током называется такой электрический ток, который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине.
На представленной диаграмме через равные промежутки времени 
Время 
Величина, обратная периоду, называется частотой переменного тока:
, где:
— частота переменного тока;
— период переменного тока.
Если выразить время 
, то есть размерность частоты переменного тока равна T−1, а в СИ выражается в с−1.
Частота переменного тока численно равна числу периодов по отношению к промежутку времени.
За единицу измерения частоты переменного тока принят 1 герц (Гц) — в честь Генриха Герца. Через основные единицы СИ герц выражается следующим образом: 1 Гц = 1 с−1. Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
Частота переменного тока равна одному герцу, если период тока равен одной секунде (один полный цикл за одну секунду).
Стандарты частоты[править | править код]
В большинстве стран в электротехнике применяются частоты 50 или 60 Гц (вторая из них принята в США и Канаде). В некоторых странах — например, в Японии — используются оба стандарта (см. «Промышленная частота переменного тока»).
Частота 16 ⅔ Гц до сих пор используется в некоторых европейских железнодорожных сетях (Австрия, Германия, Норвегия, Швеция и Швейцария), частота 25 Гц — на старых железнодорожных линиях США (см. статью).
В авиации и военной технике, чтобы снизить массу устройств или повысить частоту вращения электродвигателей переменного тока, применяется частота 400 Гц.
- Число оборотов ротора
синхронного электродвигателя определяется по формуле:

![{displaystyle f [operatorname {s} ^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8271b4a96360786ff30a9fc9c14733cf749d6be)

- Так как минимальное число пар полюсов равно единице, то синхронный электродвигатель, работающий на переменном токе частотой 50 герц, разовьёт 3 000 оборотов в минуту, а электродвигатель, работающий на переменном токе частотой 400 герц, — 24 000 об/мин. Частота вращения ротора асинхронного электродвигателя меньше, чем частота питающего его тока и зависит от нагрузки. Скольжение — разность между частотой вращения вращающегося магнитного поля и частотой вращения ротора.
В технике передачи информации (в частности, в радиотехнике) применяются частоты более высокие — порядка миллионов и миллиардов герц.
Переменный синусоидальный ток[править | править код]
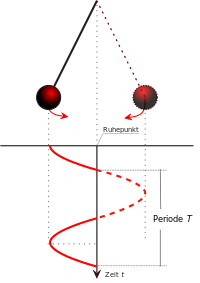
Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по гармоническому закону.
Синусоидальный ток считается элементарным, то есть его невозможно разложить на другие более простые переменные токи[2].
Переменный синусоидальный ток выражается формулой:



Фаза синусоидального тока 

Множитель 

Угловая частота 







Зависимость синусоидального тока от времени

Зависимость синусоидального тока от угла ωt
Периоду 



Исходя из формулы 



Фаза 
- 1 радиан = 57,29° = 57°17′, угол 90° =
радиан, угол 180° =
радиан, угол 270° =
радиан, угол 360° =
радиан,
гдерадиан;
— число «пи», ° — угловой градус и ′ — угловая минута.
Формула 




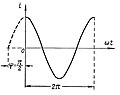
Начальная фаза переменного тока 

Начальная фаза переменного тока 
Если в формуле 




Начальная фаза — это фаза синусоидального тока в момент времени 
Начальная фаза переменного синусоидального тока может быть положительной 




Если начальная фаза 



Если начальная фаза 



Многофазный переменный ток[править | править код]

Два синусоидальных тока совпадают по фазе друг с другом

Синусоидальные токи сдвинуты по фазе на угол 
Два переменных синусоидальных тока совпадают по фазе, если они имеют одинаковые фазы и, следовательно, одновременно достигают своих нулевых и максимальных значений одинакового знака.
На левой иллюстрации представлены развёрнутые диаграммы токов 

Токи 

Два переменных синусоидальных тока сдвинуты по фазе относительно друг друга, если они имеют различные фазы.
На правой иллюстрации токи 



Ток 





Трёхфазный ток[править | править код]

Развёрнутая диаграмма трёхфазного тока. Фаза «A» (или U1), сдвиг по фазе 0° Фаза «B» (или U2), сдвиг по фазе 120° Фаза «C» (или U3), сдвиг по фазе 240°

Трёхфазная электрически связанная система, соединение «звездой» с нейтральным проводом: генератор G слева, нагрузка M справа.

Трёхфазная электрически связанная система, и генератор G и нагрузка M соединены «треугольником».
Среди многофазных систем переменного синусоидального тока наиболее широкое применение получила трёхфазная система электроснабжения.
Трёхфазной системой называется совокупность трёх однофазных электрических цепей, в которых действуют три электродвижущие силы одинаковой частоты, сдвинутые по фазе относительно друг друга на угол 

Статор трёхфазного генератора переменного тока имеет три совершенно одинаковые катушки, размещённые на общем кольцеобразном (тороидальном) магнитопроводе, сдвинутые относительно друг друга на 120°. В обмотках индуктируются синусоидальные электродвижущие силы, сдвинутые по фазе относительно друг друга на 120°.
Если в первой катушке индуктируется электродвижущая сила 
то во второй катушке будет индуктироваться электродвижущая сила 
в третьей катушке — электродвижущая сила 
где 





Если к каждой катушке подключить нагрузку, то в этих цепях будут протекать следующие токи:

где 








Трёхфазная система называется симметричной, если амплитуды электродвижущих сил в отдельных фазах генератора одинаковы по величине, то есть: 
Если в трёхфазной системе отдельные фазы представляют собой совершенно независимые друг от друга электрические цепи, то такая система называется электрически не связанной, имеет мало преимуществ по сравнению с однофазной системой, практического применения не находит.
Трёхфазная система называется электрически связанной, если её отдельные фазы соединены между собой электрически.
Трёхфазная электрически связанная система обладает преимуществами по сравнению с однофазной системой, так как она требует меньшей затраты металла на провода при передаче одной и той же мощности.
Другое преимущество трёхфазной системы — возможность получения вращающегося магнитного поля, с помощью которого осуществляется работа простых по конструкции и удобных в эксплуатации асинхронных двигателей.
Для работы конденсаторных, однофазных и двухфазных асинхронных двигателей также используется вращающееся магнитное поле, однако их характеристики уступают трёхфазным асинхронным двигателям.
Трёхфазные системы как генератора, так и потребителя могут быть соединены «звездой» с нейтральным проводом, «звездой» без нейтрального провода или «треугольником».
- Соединение «звездой» с нейтральным проводом — четырёхпроводное, нейтральный провод обеспечивает независимость работы только одной фазы потребителя от другой фазы, так как при малом падении напряжения в проводах напряжения на фазах потребителя относительно мало изменяются с изменением нагрузки фаз. Применяется при неравномерной нагрузке на фазы.
- Соединение «звездой» без нейтрального провода — трёхпроводное, если результирующий ток в нейтральном проводе равен нулю, то отпадает необходимость в нём, что даёт экономию цветных металлов при передаче одной и той же мощности потребителю. Трёхфазная трёхпроводная система, соединённая «звездой», может применяться там, где нагрузка на фазы равномерна, например, при подключении трёхфазного асинхронного двигателя.
- Если при трёхфазной трёхпроводной системе, соединённой «звездой», нагрузка оказывается неравномерной, то это ведёт к перераспределению напряжений на фазах потребителя в соответствии с их нагрузками и система перестаёт быть симметричной.
- Например, если одну фазу потребителя «закоротить», то есть её напряжение станет равным нулю, то на остальных фазах напряжение возрастёт в
против нормального. Это явление называется «перекос фаз». В бытовых условиях «перекос фаз» происходит, например, когда в домашнем распределительном щите по какой-то причине отсоединяется нулевой провод.
- Соединение «треугольником» — трёхпроводное. Применяется в основном потребителями с целью увеличения крутящего момента трёхфазного асинхронного двигателя, соответственно увеличивается его электрическая мощность при неизменном числе оборотов. Обмотки переключаются с «звезды» на «треугольник».
- Или наоборот, когда необходимо электродвигатель (соединение обмоток «звезда»), рассчитанный, например, на напряжение 380 В включить под напряжение 220 В, в этом случае (обмотки также переключаются с «звезды» на «треугольник») его электрическая мощность и крутящий момент остаются неизменными.
Двухфазный ток[править | править код]

Двухфазным электрическим током называется совокупность двух однофазных токов, сдвинутых по фазе относительно друг друга на угол 
Если две обмотки расположить в пространстве так, чтобы их оси были взаимно перпендикулярны и эти обмотки питать двухфазным синусоидальным током, то в системе возникнут два взаимноперпендикулярных магнитных потока. Вектор суммарного магнитного поля будет вращаться с постоянной угловой скоростью, равной частоте питающего напряжения. При этом возникает вращающееся магнитное поле. Ротор выполненный в виде короткозамкнутого «беличьего колеса» или представляющий собой металлический цилиндр связанный с валом, будет вращаться, производя механическую работу.
Частота вращения двухфазного асинхронного двигателя, как и асинхронного трёхфазного двигателя, будет несколько меньше частоты вращения вращающегося магнитного поля и зависит от нагрузки на валу — при её увеличении скорость вращения двигателя снижается. Разность частот питающего тока и частотой вращения называют частотой скольжения.
Действующее значение переменного синусоидального тока[править | править код]
Если все положительные и отрицательные мгновенные значения переменного синусоидального тока сложить, то их сумма будет равна нулю. Но если алгебраическая сумма всех мгновенных значений за период равна нулю, то и среднее значение этого тока за период также равно нулю: 
- Среднее значение синусоидального тока за период не может служить для измерения этого тока.
Чтобы судить о величине переменного синусоидального тока, переменный ток сравнивают с постоянным током по их тепловому действию.
Закон Джоуля — Ленца
Количество теплоты
, выделяемое в единицу времени
в рассматриваемом участке электрической цепи, пропорционально произведению квадрата силы тока
на этом участке и электрического сопротивления
участка цепи.
Количество теплоты в Джоулях:
;
Количество теплоты в калориях:
, где
— сила тока, Ампер;
— электрическое сопротивление, Ом;
— время в секундах.
- Два тока, один из которых синусоидальный, а другой постоянный, эквивалентны по тепловому действию, если они, протекая по одинаковым сопротивлениям, за одинаковые отрезки времени выделяют одинаковое количество тепла.
- Действующее значение переменного синусоидального тока численно равно току постоянному, эквивалентному данному синусоидальному току, то есть выделяющему порознь с ним в одинаковом сопротивлении за одинаковый отрезок времени одинаковое количество тепла.
Найдено экспериментально, а затем подтверждено теоретически, что величина действующего значения переменного синусоидального тока находится в строго определённой зависимости от амплитуды этого тока: 


Амперметр электромагнитной или электродинамической системы, включенный в цепь переменного синусоидального тока, показывает действующее значение тока.
Аналогично действующему значению переменного синусоидального тока можно говорить о действующем значении переменной синусоидальной электродвижущей силы или переменного синусоидального напряжения.
- Действующее значение напряжения в
меньше его амплитуды:
или
.
Вольтметр электромагнитной или электродинамической системы, включенный в сеть переменного синусоидального тока, показывает действующее значение синусоидального напряжения.
- Например, в электрической розетке электрическое напряжение
, так как это действующее значение, амплитудное напряжение будет
Вольт.
Данные формулы справедливы только для синусоидального тока, если импульсы будут треугольной, пилообразной, прямоугольной или иной формы — требуется другая методика вычисления.
Методом математического анализа можно определить среднее значение переменного синусоидального тока за половину периода, например за положительную полуволну синусоиды.
Среднее значение переменного синусоидального тока за половину периода равно 
Также можно определить отношение 

Генерирование переменного тока[править | править код]
Принцип действия генератора переменного тока основан на законе электромагнитной индукции — индуцировании электродвижущей силы в проволочном контуре (проволочной рамке), находящейся в однородном вращающемся магнитном поле.
Электродвижущая сила 






Частота переменного тока, вырабатываемого генератором, определяется по формуле:




По количеству фаз генераторы переменного тока бывают:
- трёхфазные генераторы — основной тип мощных промышленных генераторов;
См. также трёхфазная система электроснабжения, трёхфазный двигатель, автомобильный генератор трёхфазного переменного тока. - однофазные генераторы, применяются, как правило, на маломощных бензиновых электростанциях, встроены в двигатели внутреннего сгорания мопедов, лёгких мотоциклов, снегоходов, гидроциклов, подвесные лодочные моторы;
См. также конденсаторный двигатель, однофазный двигатель. - двухфазные генераторы, встречаются значительно реже по сравнению с однофазными и трёхфазными.
См. также двухфазная электрическая сеть, двухфазный двигатель.

Инверторы[править | править код]
Постоянный ток может быть преобразован в переменный с помощью инвертора.
Недорогие модели инверторов имеют на выходе переменный ток несинусоидальной формы, обычно прямоугольные импульсы или модифицированная синусоида. Для получения синусоидального тока инвертор должен иметь задающий генератор (как правило, специализированная микросхема, формирующая электрический сигнал синусоидальной формы, который затем управляет работой тиристорных или транзисторных электронных ключей).
Фазорасщепитель[править | править код]
Трёхфазный ток может быть получен из однофазного при помощи фазорасщепителя. Эти электрические машины применяются, в частности, на электровозах, таких как ВЛ60, ВЛ80.
Сети переменного тока[править | править код]

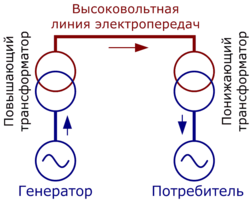

Схема разводки трёхфазной сети в многоквартирных жилых домах.
Производители электроэнергии (ГЭС, ТЭС, ТЭЦ, атомные и другие электростанции) генерируют переменный ток промышленной частоты (в России — 50 Гц), напряжением порядка 10 — 20 кВ.
Затем электрический ток поступает на трансформаторные подстанции, которые находятся рядом с электростанциями, где происходит повышение электрического напряжения.
Переменный ток высокого напряжения передаётся потребителям по линиям электропередачи (ЛЭП). Повышение напряжения необходимо для того, чтобы уменьшить потери в проводах ЛЭП (см. Закон Джоуля — Ленца, при увеличении электрического напряжения уменьшается сила тока в электрической цепи, соответственно уменьшаются тепловые потери).
- Самая высоковольтная в мире ЛЭП Экибастуз-Кокчетав работала под напряжением 1 миллион 150 тысяч вольт.
На другом конце линии электропередачи находится понижающая трансформаторная подстанция, где высоковольтный переменный ток понижается трансформаторами до нужного потребителю значения.
В подавляющем большинстве случаев по линиям электропередачи передаётся трёхфазный ток, однако существуют линии электропередачи постоянного тока, например высоковольтная линия постоянного тока Волгоград-Донбасс, высоковольтная линия постоянного тока Экибастуз-Центр, материковая Южная Корея — остров Чеджудо и другие. Использование постоянного тока позволяет увеличить передаваемую электрическую мощность, передавать электроэнергию между энергосистемами, использующими переменный ток разной частоты, например, 50 и 60 герц, а также не синхронизировать соседние энергосистемы, как это сделано на границе Ленинградской области с Финляндией (см. вставка постоянного тока Выборг — Финляндия).
В России в электрических сетях общего назначения используется трёхфазный ток с межфазным напряжением 380 Вольт.
Качество электрической энергии — её электрическое напряжение и частота должны строго соблюдаться.
К жилым домам (на сельские улицы) подводятся четырёхпроводные (три фазовых провода и один нейтральный (нулевой) провод) линии электропередачи (воздушные или кабельные ЛЭП) с межфазным напряжением 380 вольт (с 2003 года 400 Вольт по ГОСТ 29322-2014). В отдельную квартиру (или в сельский дом) подводится фазовый провод и нулевой провод, электрическое напряжение между «фазой» и «нулём» составляет 220 вольт (с 2003 года 230 Вольт по ГОСТ 29322-2014). Определить, где какой провод можно с помощью индикатора фазы.
- Например, в первую квартиру подводится фаза «A», во вторую квартиру — фаза «B», в третью квартиру — фаза «C» и так далее…
Электрификация железных дорог на переменном токе[править | править код]
В России и в республиках бывшего СССР около половины всех железных дорог электрифицировано на однофазном переменном токе частотой 50 Гц. Напряжение ~ 25 кВ (обычно до 27,5 кВ, с учётом потерь) подаётся на контактный провод, вторым (обратным) проводом служат рельсы. Также проводится электрификация по системе 2 × 25 кВ (два по двадцать пять киловольт), когда на отдельный питающий провод подаётся напряжение ~ 50 кВ (обычно до 55 кВ, с учётом потерь), а на контактный провод от автотрансформаторов подаётся половинное напряжение от 50 кВ (то есть 25 кВ). Электровозы и электропоезда переменного тока при работе на участках 2 × 25 кВ в переделке не нуждаются.
Проводится политика на дальнейшее расширение полигона тяги переменного тока как за счёт вновь электрифицируемых участков, так и за счёт перевода некоторых линий с постоянного тока на переменный ток. Переведены в 1990-е — 2000-е годы:
- на Восточно-Сибирской железной дороге: участок Слюдянка — Иркутск — Зима;
- на Октябрьской железной дороге: участок Лоухи — Мурманск;
- на Приволжской железной дороге: Саратовский и Волгоградский железнодорожные узлы;
- на Северо-Кавказской железной дороге: участки Минеральные Воды — Кисловодск и Бештау — Железноводск.
Также выпускаются двухсистемные электровозы, способные работать как на переменном, так и на постоянном токе (см. ВЛ61Д, ВЛ82 и ВЛ82М, ЭП10, ЭП20).
См. также[править | править код]
- Электрический ток
- Постоянный ток
- Действующее значение переменного тока
- Список параметров напряжения и силы электрического тока
- Трёхфазный ток
- Реактивное сопротивление
- Токи высокой частоты
- Векторная диаграмма
- Стандарты напряжений и частот в разных странах
Примечания[править | править код]
- ↑
Д. Г. Максимов. Курс электротехники. — Издание третье, переработанное. — Москва: Военное издательство Министерства обороны Союза ССР, 1958. — С. 298. — 786 с. - ↑ Теоретическая и практическая важность синусоидального гармонического тока обусловлена тем, что он имеет минимальную ширину спектра. Любой периодический несинусоидальный ток может быть представлен в виде комбинации гармонических составляющих, имеющих соответствующие амплитуды, частоты и фазы. См. Гармонические колебания#Применение, Ряд Фурье.
Ссылки[править | править код]
- Что такое переменный ток и чем он отличается от тока постоянного
- Переменный ток
- Основные понятия и определения о переменном токе
Переменный электрический ток

Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC – Direct Current – постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f – величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота ω – угловая частота, равная количеству периодов за 2π секунд.
ω = 2πf = 2π/T
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ – величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = Iampsin(ωt); u = Uampsin(ωt)
С учётом начальной фазы:
i = Iampsin(ωt + ψ); u = Uampsin(ωt + ψ)
Здесь Iamp и Uamp – амплитудные значения тока и напряжения.
Амплитудное значение – максимальное по модулю мгновенное значение за период.
Iamp = max|i(t)|; Uamp = max|u(t)|
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.
Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой Iamp (Uamp)
среднеквадратичное значение определится из расчёта:

Среднеквадратичное – это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов.
Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода,
что и равный по величине его среднеквадратичному значению постоянный ток.

Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой
амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды – отношение амплитудного значения к среднеквадратичному.

Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы – отношение среднеквадратичного значения к средневыпрямленному.

Для переменного синусоидального тока или напряжения коэффициент формы KФ  ≈ 1.111
≈ 1.111
Для тока и напряжения треугольной или пилообразной формы KФ  ≈ 1.155
≈ 1.155
Для переменного тока и напряжения прямоугольной формы KФ = 1
Замечания и предложения принимаются и приветствуются!
Содержание
- Переменный электрический ток
- Параметры переменного тока и напряжения
- Коэффициент амплитуды и коэффициент формы
- Период и частота переменного тока
- Период и частота переменного тока
- Частота тока
- Общее понятие о переменном токе
- Периодический переменный ток
- Стандарты частоты
- Переменный синусоидальный ток
- Многофазный переменный ток
- Трёхфазный ток
- Двухфазный ток
- Действующее значение синусоидального тока
- Генерирование переменного тока
- Инвертор
- Фазорасщепитель
- Сети переменного тока
- Определение частоты и периода
- Взаимосвязь частоты и работы электрооборудования
- Частотомер
- Токи высокой частоты
- Период пульсаций и частота
- Интенсивность циклов
- Опасность разночастотных зарядов
- Видео
- Период, частота, амплитуда и фаза переменного тока
- Период и частота переменного тока
- Амплитуда переменного тока
- Угловая (циклическая) частота переменного тока.
- Фаза переменного тока.
Переменный электрический ток
Переменный ток (AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC — Direct Current — постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f — величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz)
f = 1 /T
Циклическая частота ω — угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ — величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = I ampsin(ωt); u = U ampsin(ωt)
С учётом начальной фазы:
i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)
Здесь I amp и U amp — амплитудные значения тока и напряжения.
Амплитудное значение — максимальное по модулю мгновенное значение за период.
I amp = max|i(t)|; U amp = max|u(t)|
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.
Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I amp (U amp) среднеквадратичное значение определится из расчёта:

Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.

Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному. 
Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному. 
Для переменного синусоидального тока или напряжения коэффициент формы KФ  ≈ 1.111
≈ 1.111
Для тока и напряжения треугольной или пилообразной формы KФ  ≈ 1.155
≈ 1.155
Для переменного тока и напряжения прямоугольной формы KФ = 1
Замечания и предложения принимаются и приветствуются!
Источник
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10 -3 сек.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами


Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Источник
Период и частота переменного тока
Под этим термином «переменный электрический ток» следовало бы понимать ток, изменяющийся во времени любым образом, соответственно введенному в математику понятию «переменная величина». Однако в электротехнику термин «переменный электрический ток» вошел в значении электрического тока, вменяющегося по направлению (в противовес электрическому току постоянного направления), а следовательно, и по величине, так как физически нельзя представлять себе изменения электрического тока по направлению без соответствующих изменений по величине.
Движение электронов в проводе сначала в одну сторону, а затем в другую называют одним колебанием переменного тока. За первым колебанием следует второе, затем третье и т. д. При колебаниях тока в проводе вокруг него происходит соответствующее колебание магнитного поля.
Время одного колебания называют периодом и обозначают буквой Т. Период выражают в секундах или в единицах, составляющих доли секунды. К ним относятся: тысячная доля секунды — миллисекунда (мс), равная 10 -3 с, миллионная доля секунды — микросекунда (мкс), равная 10 -6 с, и миллиардная доля секунды — наносекунда (нс), равная 10 -9 с.
Важной величиной, характеризующей переменный ток, является частота. Она представляет собой число колебаний или число периодов в секунду и обозначается буквой f или F. Единицей частоты служит герц, названный в честь немецкого ученого Г. Герца и обозначаемый сокращенно буквами Гц (или Hz). Если в одну секунду происходит одно полное колебание, то частота равна одному герцу. Когда в течение секунды совершается десять колебаний, то частота составляет 10 Гц. Частота и период являются обратными величинами:
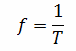
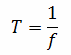
При частоте 10 Гц период равен 0,1 с. А если период равен 0,01 с, то частота составляет 100 Гц.
Частота — важнейшая характеристика переменного тока. Электрические машины и аппараты переменного тока могут нормально работать только на той частоте, на которую они рассчитаны. Параллельная работа электрических генераторов и станций на общую сеть возможна только на одной и той же частоте. Поэтому во всех странах частота переменного тока, производимого электростанциями, стандартизуется законом.
В электрической сети переменного тока частота равна 50 Гц. Ток пятьдесят раз в секунду идет в одну сторону и пятьдесят раз в обратную. Сто раз в секунду он достигает амплитудного значения и сто раз становится равным нулю, т. е. сто раз меняет свое направление при переходе через нулевое значение. Лампы, включенные в сеть, сто раз в секунду притухают и столько же раз вспыхивают ярче, но глаз этого не замечает, благодаря зрительной инерции, т. е. способности сохранять полученные впечатления около 0,1 с.
При расчетах с переменными токами пользуются также угловой частотой, она равна 2пиf или 6,28f. Ее следует выражать не в герцах, а в радианах в секунду.
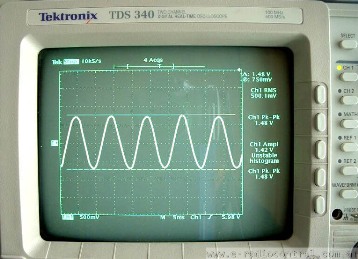
При принятой частоте промышленного тока 50 гц максимально возможное число оборотов генератора — 50 об/сек (р = 1). На такое число оборотов строятся турбогенераторы, т. е. генераторы, приводимые паровыми турбинами. Число оборотов гидротурбин и приводимых ими гидрогенераторов зависит от природных условий (прежде всего от напора) и колеблется в широких пределах, снижаясь иногда до 0,35 — 0,50 об/сек.
Число оборотов оказывает большое влияние на экономические показатели машины — габаритные размеры и вес. Гидрогенераторы с несколькими оборотами в секунду имеют наружный диаметр в 3 — 5 раз больший и вес во много раз больший, чем турбогенераторы той же мощности с n = 50 об/сек. В современных генераторах переменного тока вращается их магнитная система, а проводники, в которых индуктируется э.д.с, размещаются в неподвижной части машины.
Переменные токи принято разделять по частоте. Токи с частотой меньше 10000 Гц называют токами низкой частоты (токами НЧ). У этих токов частота соответствует частоте различных звуков человеческого голоса или музыкальных инструментов, и поэтому они иначе называются токами звуковой частоты (за исключением токов с частотой ниже 20 Гц, которые не соответствуют звуковым частотам). В радиотехнике токи НЧ имеют большое применение, особенно в радиотелефонной передаче.
Однако главную роль в радиосвязи выполняют переменные токи с частотой более 10000 Гц, называемые токами высокой частоты, или радиочастоты (токи ВЧ). Для измерения частоты этих токов применяют единицы: килогерц (кГц), равный тысяче герц, мегагерц (МГц), равный миллиону герц, и гигагерц (ГГц), равный миллиарду герц. Иначе килогерц, мегагерц и гигагерц обозначают kHz, MHz, GHz. Токи частотой в сотни мегагерц и выше называют токами сверхвысокой или ультравысокой частоты (СВЧ и УВЧ).
Радиостанции работают с помощью переменных токов ВЧ, имеющих частоту от сотен килогерц и выше. В современной радиотехнике для специальных целей применяются токи с частотой в миллиарды герц и имеются приборы, позволяющие точно измерять такие сверхвысокие частоты.
Источник
Частота тока
Изобретение электричества поставило человечество на новую грань развития. Технический прогресс опирался на два направления движения с использованием электроэнергии. В одном случае применялся постоянный ток, во втором – переменный. Внедрение источников электричества и электропотребителей вылилось в столетнюю войну между приверженцами двух видов энергии. В конце концов, победу одержали те, кто продвигал идею повсеместного использования её переменного вида.
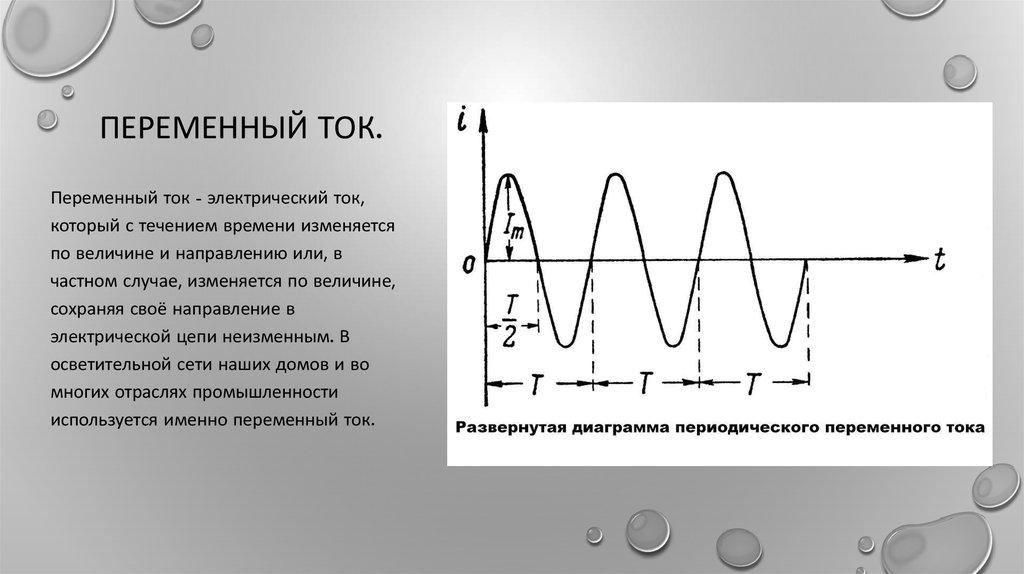
Общее понятие о переменном токе
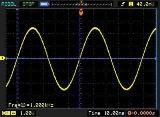
В отличие от постоянного движения электронов в одном направлении, переменный ток меняет как направление, так и значение несколько раз за единицу времени. Изменения происходят по гармоническому закону. Если наблюдать подобный сигнал с помощью осциллографа, можно увидеть картинку в виде синусоиды.
Относительно оси ординат OY ток меняет своё направление с положительного на отрицательное и делает это периодически. Поэтому его мгновенное значение в первой позиции считается положительным, во второй – отрицательным.
Важно! Так как переменный ток – это алгебраическая величина, то говорить о его знаке заряда можно только для конкретного мгновенного значения, смотря, в каком направлении он протекает в этот момент.
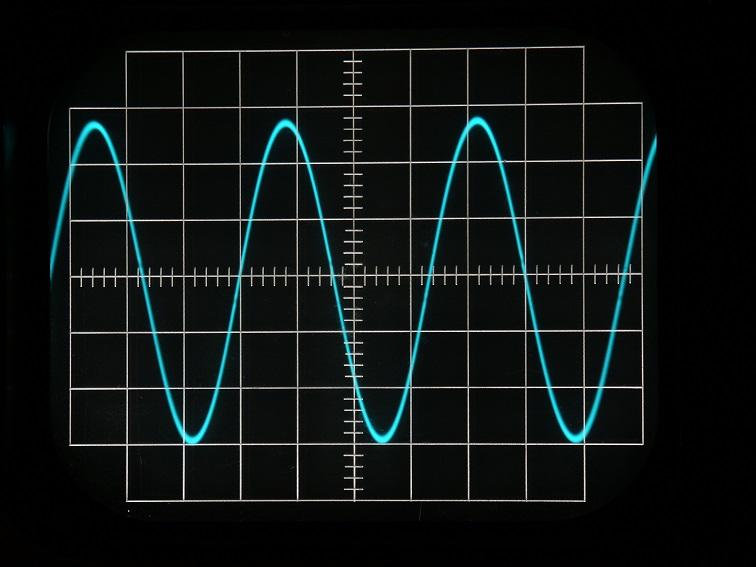
Периодический переменный ток
Тот, который, изменяясь, успевает вернуться к своему исходному значению через одинаковые временные интервалы и при этом проходит весь цикл своих преобразований, называется периодическим. Его можно проследить на синусоиде, изображённой на экране осциллографа.
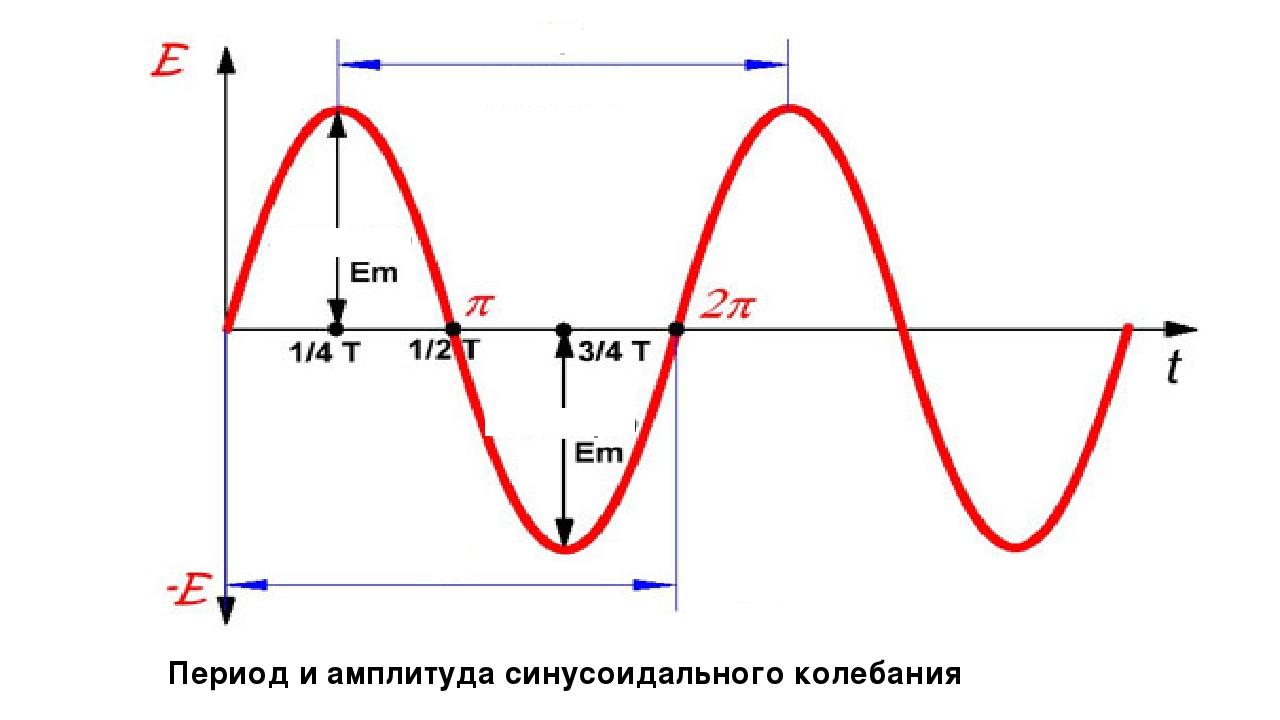
Видно, что через одинаковые интервалы времени график повторяется без перемен. Эти интервалы обозначаются буквой Т и называются периодами. Частота, с которой в единицу времени укладывается определённое количество подобных периодов, – это частота тока переменного значения.
Её можно вычислить по формуле частоты переменного тока:
где:
- f – частота, Гц;
- T – период, с.
Частота равна количеству периодов в секунду и имеет единицу измерения 1 герц (Гц).
Внимание! Единица частоты в системе СИ носит имя Генриха Герца. 1 герц (Гц, Hz) = 1 с-1. К ней применимы кратные и дольные, выраженные стандартными приставками СИ, единицы.
Стандарты частоты
Для того чтобы обеспечить согласование работы источников переменного электричества, систем передач, приём и работу электропотребителей, применяются стандарты частоты. Используемая частота в электротехнике некоторых стран:
- 50 Гц – страны бывшего СССР, Прибалтики, страны Европы, Австралия, КНДР и другие;
- 60 Гц – стандарт, принятый в США, Канаде, Доминиканской республике, Тайвани, на Каймановых островах, Кубе, Коста-Рике, Южной Корее и ещё в некоторых странах.
В Японии используются обе частоты. Восточные регионы (Токио, Сендай, Кавасаки) используют частоту 50 Гц. Западные области (Киото, Хиросима, Нагоя, Окинава) применяют частоту 60 Гц.
К сведению. Железнодорожная инфраструктура Австрии, Норвегии, Германии, Швейцарии и Швеции по сей день применяет частоту 16,6 Гц.
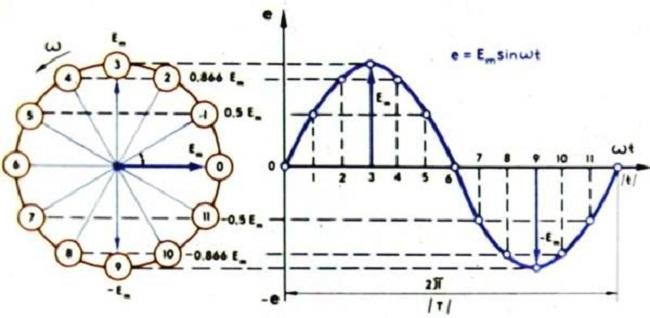
Переменный синусоидальный ток
Это тот ток, который периодически меняется во времени, и его изменения подчиняются закону синусоиды. Это элементарное движение электрических зарядов, потому дальнейшему разложению на простые токи оно не подлежит.
Вид формулы такого переменного тока:
где:
- Im – амплитуда;
- sinωt – фаза синусоидального тока, рад.
Здесь ω = const, называется угловой частотой переменного электричества, причём угол ωt находится в прямой временной зависимости.
Зная частоту f исходного тока, можно вычислить его угловую частоту, применив выражение:
Тут 2π – это выраженное в радианах значение центрального угла окружности:
- Т = 2 π радиан = 3600;
- Т/2 = π = 1800;
- Т/4 = π/2 = 900.
Если выразить 1 рад в градусах, то он будет равен 57°17′.
Многофазный переменный ток
Для запуска и работы многих промышленных устройств и электрооборудования требуется не одна фаза, а несколько. В связи с этим рассматривают такие понятия, как двухфазный и трёхфазный переменные токи.
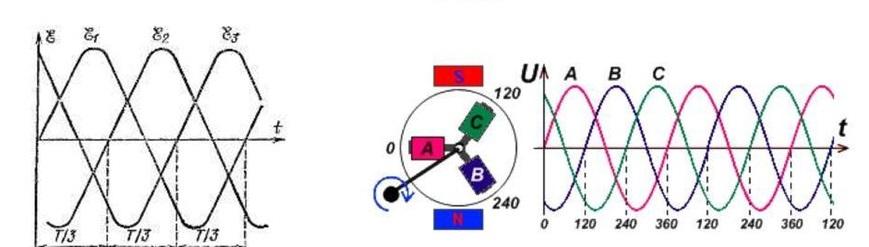
Трёхфазный ток
Этот вид электричества применяют в трёхфазной системе, в которую включены три однофазные цепи. Цепи имеют ЭДС переменной природы одной и той же частоты. Эти ЭДС сдвинуты по фазе относительно друг друга на ϕ = Т/3 = 2π/3. Такую систему называют трёхфазным током, а цепь – фазой.
Выработка, преобразование, доставка и потребление переменного электрического тока в основном происходят по трёхфазной системе электроснабжения.
Двухфазный ток
Ещё в 1888 году Никола Тесла выполнил описание того, как можно на практике применить двухфазную сеть, и предложил разработанную им конструкцию двухфазного двигателя. Такие сети начали применять в начале 20 века. Они состояли из двух контуров.
Там напряжения контуров сдвигались по фазе на 900. Каждая фаза включала в себя два провода, у двухфазных генераторов было по два ротора, также конструктивно развёрнутые на угол 900.
Важно! Такие сети позволяли производить мягкий пуск двухфазных электродвигателей, практически с нулевого момента вращения. В то время как для запуска однофазного асинхронного двигателя требуется дополнительная пусковая обмотка или система запуска.

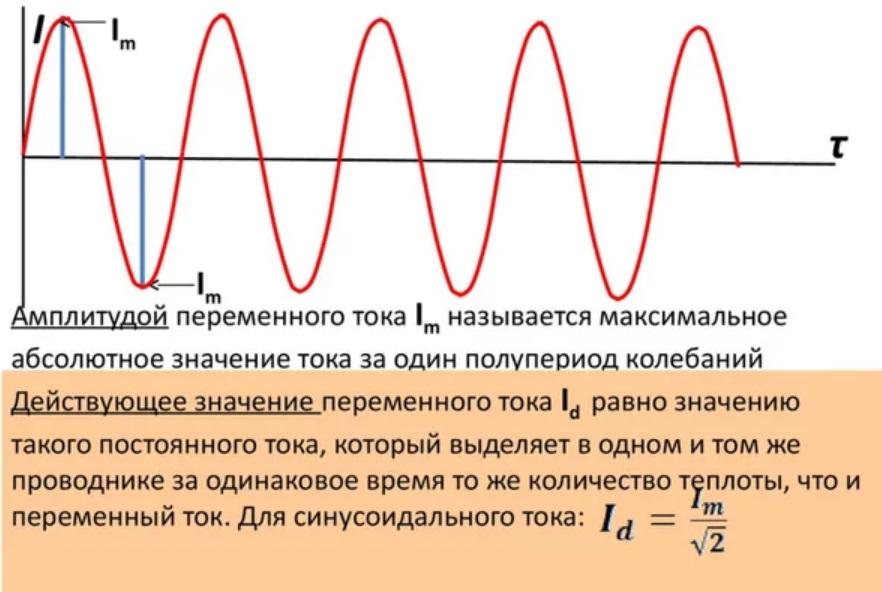
Действующее значение синусоидального тока
Под действующим значением понимают его эффективность. Она равна такому значению постоянного тока, который выполнит ту же работу, что и переменный, за один период времени. Под работой здесь подразумевают его тепловую или электродинамическую направленность. Удобнее всего использовать среднеквадратичное значение переменного электричества.
Тогда действующее значение для синусоидального тока определяют по формуле:
I = * Im ≈ 0,707* Im,
где Im – величина амплитуды тока.
Генерирование переменного тока
Кроме стандартных генераторов, для производства переменного тока применяются инверторы и фазорасщепители.
Инвертор
Это устройство, с помощью которого из постоянного тока получают его переменный вид. В процессе этого величина выходного напряжения тоже меняется. Схема устройства представляет собой электронный генератор синусоидального импульсного напряжения периодического характера. Есть варианты инверторов, работающих с дискретным сигналом. Инверторы применяют для автономного питания оборудования от аккумуляторов постоянного напряжения.

Фазорасщепитель
Ещё один способ получить несколько фаз из какого-либо сигнала – это выполнить его расщепление на несколько фаз. Это делается с помощью фазорасщепителя. Принудительная обработка сигналов цифрового или аналогового формата используется, как в радиоэлектронике, так и в силовой электротехнике.
Для электроснабжения трёхфазных асинхронных двигателей применяют выполненный на их же базе фазорасщепитель. Для этого обмотки трёхфазного двигателя соединяют не «звездой», а иначе. Две катушки присоединяют между собой последовательно, третью – подключают к средней точке второй обмотки. Двигатель запускают, как однофазный, после разгона в его третьей обмотке наводится ЭДС.
Интересно. В случае расщепления фаз подобным методом сдвиг фаз между 2 и 3 обмоткой составляет не 1200, как должно быть в идеале, а 900.
Сети переменного тока
По назначению и применению эти сети можно классифицировать следующим образом:
- общие системы: питание объектов промышленного, транспортного, сельскохозяйственного и бытового назначения;
- автономные сети: снабжение передвижных и стационарных автономных субъектов.
Общие сети переменного трёхфазного тока построены по четырёхпроводной схеме, где три провода – это «фаза», четвёртый – «ноль». Трансформаторные подстанции построены по схеме с глухо заземлённой нейтралью. Передача на дальние расстояния производится при высоком напряжении, которое затем понижается на подстанциях до напряжения 0,4 кВ и раздаётся потребителям.
Бытовые объекты подключаются по однофазной схеме. В этом случае требуются два провода: «фазный» и «нулевой».
Определение частоты и периода
Частота электрического тока – это величина физическая, она определяет количество колебаний за 1 секунду. Время, за которое происходит одно целое колебание, называется периодом.
Взаимосвязь частоты и работы электрооборудования
Частота тока – это один из параметров электроэнергии, который влияет на стабильную работу электроустановок и оборудования. При поставке энергии потребителю этот параметр строго контролируется, так же, как и напряжение.
Нить взаимосвязи выражается формулой номинального количества оборотов в минуту для вращающихся машин. КПД (коэффициент полезного действия) заложен в самой конструкции агрегатов. Он максимален при:
где:
- n – количество об./мин.;
- f – частота;
- p – количество пар полюсов.
Количество оборотов турбины генераторов напрямую связано с частотой вырабатываемого переменного тока, полученная частота отвечает за оптимальный режим вращения электродвигателя потребителя. При снижении частоты в сети обороты машины снижаются автоматически. Происходит перегрузка на валу, и страдает двигатель.
В то же время технологическая линия, в которую он передаёт энергию вращения, также терпит изменения в работе:
- изменяется скорость движения конвейера, что влечёт за собой сбой технологического процесса и брак в итоге;
- снижаются мощность и частота вращения насосов, вентиляторов, что приводит к нестабильной работе систем, в которых они установлены;
- снижение частоты в энергосистеме на 1% приводит к падению общей мощности на нагрузке до 2%.
Для контроля этого важного электрического параметра применяют частотомеры.
Внимание! Снижение частоты на 10-15% вызывает падение производительности механизмов даже на самой электростанции до нуля. При частоте тока в сети 50 Гц (критической величиной являются 45 Гц) происходит лавинный спад.
Частотомер
Это прибор, предназначенный для измерения частоты и отображения полученного результата на экран. Для контроля в электросетях применяют приборы непосредственной оценки синусоидальных колебаний аналоговой конструкции.
Различают по методу установки:
- стационарные;
- щитовые;
- переносные.
Частотомеры в современном исполнении имеют цифровое отображение результатов на электронном дисплее.
Токи высокой частоты
ТВЧ – такова их аббревиатура, используются для плавки металлов, закалки поверхности металлических изделий. ТВЧ – это токи, имеющие частоту более 10 кГц. В индукционных печах используют ТВЧ, помещая проводник внутрь обмотки, через которую пропускают ТВЧ. Под их воздействием возникающие в проводнике вихревые токи разогревают его. Регулируя силу ТВЧ, контролируют температуру и скорость нагрева.
Интересно. Расплавляемый металл может быть подвешен в вакууме с помощью магнитного поля. Для него не нужен тигель (специальный ковш для нагрева). Так получают очень чистые вещества.
Плюсы использования ТВЧ в разных случаях:
- быстрый нагрев при ковке и прокате металла;
- оптимальный температурный режим для пайки или сварки деталей;
- расплав даже очень тугоплавких сплавов;
- приготовление пищи в микроволновых печах;
- дарсонвализация в медицине.
Получают ТВЧ с помощью установок, включающих в свой состав колебательный контур, или электромашинных генераторов. У статора и ротора генераторов на сторонах, обращённых друг другу, нанесены зубцы. Их взаимное движение порождает пульсацию магнитного поля. Частота на выходе тем больше, чем больше произведение числа зубцов ротора на частоту его вращения.
Период пульсаций и частота
Частота переменного тока может иметь другое название – пульсация. Периодом пульсации называют время единичной пульсации.
Интенсивность циклов
Для электросети с частотой 50 Гц период пульсации составит:
При необходимости, зная эту зависимость, можно по времени цикла вычислить частоту.
Опасность разночастотных зарядов
Как постоянный, так и переменный ток при определённых значениях представляет опасность для человека. До 500 В разница в безопасности находится в соотношении 1:3 (42 В постоянного к 120 В переменного).
При значениях выше 500 В это соотношение выравнивается, причём константное электричество вызывает ожоги и электролизацию кожных покровов, изменяющееся – судороги, фибрилляцию и смерть. Тут уже частота пульсации имеет большое значение. Самый опасный интервал частот – от 40 до 60 Гц. Далее с повышением частоты риск поражения уменьшается.

Частота переменного электричества – важный параметр. Она влияет не только на работу электроустановок потребителей, но и на человеческий организм. Изменяя частоту электрических колебаний, можно менять технологические процессы на производстве и качество вырабатываемой энергии.
Видео
Источник
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10 -3 сек.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами


Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2![]() .
.

Рисунок 2. Радиан.
1рад = 360°/2![]()
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2![]() ). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
? = 6,28*f = 2f![]()
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник
Переменный ток, в отличие от тока
постоянного, непрерывно изменяется как
по величине, так и по направлению, причем
изменения эти происходят периодически,
т. е. точно повторяются через равные
промежутки времени.
Чтобы вызвать в цепи такой ток, используются
источники переменного тока, создающие
переменную ЭДС, периодически изменяющуюся
по величине и направлению. Такие
источники называются генераторами
переменного тока.
На рис. 1 показана схема устройства
(модель) простейшего генератора
переменного тока.
Прямоугольная рамка, изготовленная из
медной проволоки, укреплена на оси и
при помощи ременной передачи вращается
в поле магнита.
Концы рамки припаяны к медным контактным
кольцам, которые, вращаясь вместе с
рамкой, скользят по контактным пластинам
(щеткам).
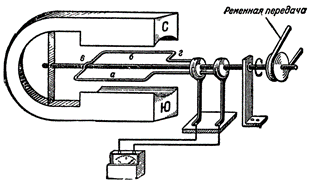
Рисунок 1. Схема простейшего генератора
переменного тока
Такое устройство является источником
переменной ЭДС.
Предположим, что магнит создает между
своими полюсами равномерное
магнитное поле, т. е. такое,
в котором плотность магнитных силовых
линий в любой части поля одинаковая.
Вращаясь, рамка пересекает силовые
линии магнитного поля, и в каждой из ее
сторон а и б индуктируются
ЭДС.
Стороны же в и г рамки — нерабочие,
так как при вращении рамки они не
пересекают силовых линий магнитного
поля и, следовательно, не участвуют в
создании ЭДС.
В любой момент времени ЭДС, возникающая
в стороне а, противоположна по
направлению ЭДС, возникающей в стороне
б, но в рамке обе ЭДС действуют
согласно и в сумме составляют общую
ЭДС, т. е. индуктируемую всей рамкой.
В этом нетрудно убедиться, если
использовать для определения направления
ЭДС известное нам правило правой руки.
Для этого надо ладонь правой руки
расположить так, чтобы она была обращена
в сторону северного полюса магнита, а
большой отогнутый палец совпадал с
направлением движения той стороны
рамки, в которой мы хотим определить
направление ЭДС. Тогда направление ЭДС
в ней укажут вытянутые пальцы руки.
Для какого бы положения рамки мы ни
определяли направление ЭДС в сторонах
а и б, они всегда складываются
и образуют общую ЭДС в рамке. При этом
с каждым оборотом рамки направление
общей ЭДС изменяется в ней на обратное,
так как каждая из рабочих сторон рамки
за один оборот проходит под разными
полюсами магнита.
Величина ЭДС, индуктируемой в рамке,
также изменяется, так как изменяется
скорость, с которой стороны рамки
пересекают силовые линии магнитного
поля. Действительно, в то время, когда
рамка подходит к своему вертикальному
положению и проходит его, скорость
пересечения силовых линий сторонами
рамки бывает наибольшей, и в рамке
индуктируется наибольшая ЭДС. В те
моменты времени, когда рамка проходит
свое горизонтальное положение, ее
стороны как бы скользят вдоль магнитных
силовых линий, не пересекая их, и ЭДС не
индуктируется.
Таким образом, при равномерном вращении
рамки в ней будет индуктироваться ЭДС,
периодически изменяющаяся как по
величине, так и по направлению.
ЭДС, возникающую в рамке, можно измерить
прибором и использовать для создания
тока во внешней цепи.
Используя явление
электромагнитной индукции,
можно получить переменную ЭДС и,
следовательно, переменный ток.
Переменный ток для промышленных
целей и для
освещения вырабатывается
мощными генераторами, приводимыми во
вращение паровыми или водяными турбинами
и двигателями внутреннего сгорания.

Графическое изображение постоянного
и переменного токов
Графический метод дает возможность
наглядно представить процесс изменения
той или иной переменной величины в
зависимости от времени.
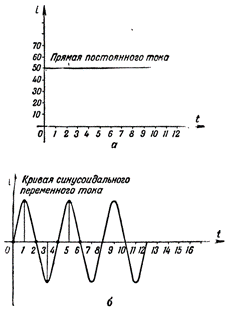
Рисунок 2. Графическое изображение
постоянного и переменного тока
На горизонтальной оси в определенном
масштабе откладывают отрезки времени,
а на вертикальной, также в некотором
масштабе, — значения той величины,
график которой собираются построить
(ЭДС, напряжения или тока).
На рис. 2 графически изображены постоянный
и переменный токи. В данном случае мы
откладываем значения тока, причем вверх
по вертикали от точки пересечения осей
0 откладываются значения тока одного
направления, которое принято называть
положительным, а вниз от этой точки —
противоположного направления, которое
принято называть отрицательным.
Убедиться в правильности построенного
на рис. 2,а графика постоянного тока
величиной 50 мА можно путём проведения
наблюдений.
Так как этот ток постоянный, т. е. не
меняющий с течением времени своей
величины и направления, то различным
моментам времени будут соответствовать
одни и те же значения тока, т. е. 50 мА.
Следовательно, в момент времени, равный
нулю, т. е. в начальный момент нашего
наблюдения за током, он будет равен 50
мА. Отложив по вертикальной оси вверх
отрезок, равный значению тока 50 мА,
получают первую точку графика.
То же самое следует сделать и для
следующего момента времени, соответствующего
точке 1 на оси времени, т. е. отложить от
этой точки вертикально вверх отрезок,
также равный 50 мА. Конец отрезка определит
нам вторую точку графика.
Проделав подобное построение для
нескольких последующих моментов времени,
мы получим ряд точек, соединение которых
даст прямую линию, являющуюся графическим
изображением постоянного тока
величиной 50 мА.

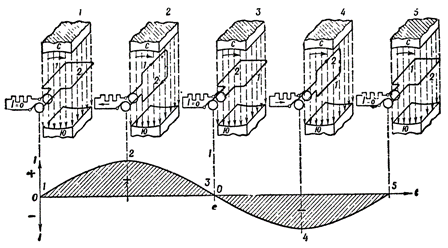
Рисунок 3. Построение графика переменной
ЭДС
Построение графика переменной ЭДС
На рис. 3 в верхней части показана рамка,
вращающаяся в магнитном поле, а внизу
дано графическое изображение возникающей
переменной ЭДС.
При равномерном вращении рамки по
часовой стрелке можно проследить ход
изменения в ней ЭДС, приняв за начальный
момент горизонтальное положение рамки.
В этот начальный момент ЭДС будет равна
нулю, так как стороны рамки не пересекают
магнитных силовых линий. На графике это
нулевое значение ЭДС, соответствующее
моменту t = 0, изобразится
точкой 1.
При дальнейшем вращении рамки в ней
начнет появляться ЭДС и будет возрастать
по величине до тех пор, пока рамка не
достигнет своего вертикального положения.
На графике это возрастание ЭДС изобразится
плавной поднимающейся вверх кривой,
которая достигает своей вершины в точке
2.
По мере приближения рамки к горизонтальному
положению ЭДС в ней будет убывать и
упадет до нуля. На графике это изобразится
спадающей плавной кривой.
Следовательно, за время, соответствующее
половине оборота рамки, ЭДС в ней успела
возрасти от нуля до наибольшей величины
и вновь уменьшиться до нуля в точке 3.
При дальнейшем вращении рамки в ней
вновь возникнет ЭДС и будет постепенно
возрастать по величине, однако направление
ее уже изменится на обратное, в чем можно
убедиться, применив правило правой
руки.
График учитывает изменение направления
ЭДС тем, что кривая, изображающая ЭДС,
пересекает ось времени и располагается
теперь ниже этой оси. ЭДС возрастает
опять-таки до тех пор, пока рамка не
займет вертикальное положение. Затем
начнется убывание ЭДС, и величина ее
станет равной нулю, когда рамка вернется
в свое первоначальное положение, совершив
один полный оборот. На графике это
выразится тем, что кривая ЭДС, достигнув
в обратном направлении своей вершины
в точке 4, встретится затем с осью времени
в точке 5.
На этом заканчивается один цикл изменения
ЭДС, но если продолжать вращение рамки,
тотчас же начинается второй цикл, в
точности повторяющий первый, за которым,
в свою очередь, последует третий, а потом
четвертый, и так до тех пор, пока не
останавливается вращение рамки.
Таким образом, за каждый оборот рамки
ЭДС, возникающая в ней, совершает полный
цикл своего изменения.
Если же рамка будет замкнута на какую-либо
внешнюю цепь, то по цепи потечет переменный
ток, график которого будет по виду таким
же, как и график ЭДС.
Полученная волнообразная кривая
называется синусоидой, а ток, ЭДС
или напряжение, изменяющиеся по такому
закону, называются синусоидальными.
Сама кривая названа синусоидой потому,
что она является графическим изображением
переменной тригонометрической величины,
называемой синусом.
Лекция № 08
Синусоидальный характер изменения
тока — самый распространенный в
электротехнике, поэтому, говоря о
переменном токе, в большинстве случаев
имеют в виду синусоидальный ток.
Для сравнения различных переменных
токов (ЭДС и напряжений) существуют
величины, характеризующие тот или иной
ток. Они называются параметрами
переменного тока.
Период, амплитуда и частота — параметры
переменного тока
Переменный ток характеризуется двумя
параметрами — периодом и амплитудой,
зная которые можно судить, какой это
переменный ток, и построить график тока.
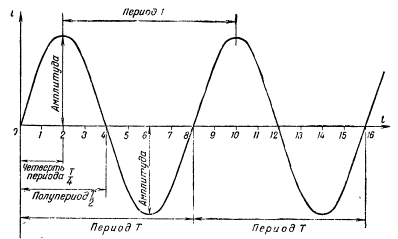
Рисунок 4. Кривая синусоидального тока
Промежуток времени, на протяжении
которого совершается полный цикл
изменения тока, называется периодом.
Период обозначается буквой Т и
измеряется в секундах.
Промежуток времени, на протяжении
которого совершается половина полного
цикла изменения тока, называется
полупериодом. Следовательно, период
изменения тока (ЭДС или напряжения)
состоит из двух полупериодов. Совершенно
очевидно, что все периоды одного и того
же переменного тока равны между собой.
Как видно из графика, в течение одного
периода своего изменения ток достигает
дважды максимального значения.
Максимальное значение переменного
тока (ЭДС или напряжения) называется
его амплитудой или амплитудным значением
тока.
Im, Em и Um — общепринятые обозначения
амплитуд тока, ЭДС и напряжения.
Прежде всего следует обратить внимание
на амплитудное
значение тока, однако, как
это видно из графика, существует
бесчисленное множество промежуточных
его значений, меньших амплитудного.
Значение переменного тока (ЭДС,
напряжения), соответствующее любому
выбранному моменту времени, называется
его мгновенным значением.
i, е и u — общепринятые
обозначения мгновенных значений тока,
ЭДС и напряжения.
Мгновенное значение тока, как и амплитудное
его значение, легко определить с помощью
графика. Для этого из любой точки на
горизонтальной оси, соответствующей
интересующему нас моменту времени,
нужно провести вертикальную линию до
точки пересечения с кривой тока;
полученный отрезок вертикальной прямой
определит значение тока в данный момент,
т. е. мгновенное его значение.
Очевидно, что мгновенное значение тока
по истечении времени Т/2 от начальной
точки графика будет равно нулю, а по
истечении времени – T/4
его амплитудному значению. Ток также
достигает своего амплитудного значения;
но уже в обратном на правлении, по
истечении времени, равного 3/4 Т.
Итак, график показывает, как с течением
времени меняется ток в цепи, и что каждому
моменту времени соответствует только
одно определенное значение как величины,
так и направления тока. При этом значение
тока в данный момент времени в одной
точке цепи будет точно таким же в любой
другой точке этой цепи.
Число полных периодов, совершаемых
током в 1 секунду, называется частотой
переменного тока и обозначается
латинской буквой f.
Чтобы определить частоту переменного
тока, т. е. узнать, сколько периодов
своего изменения ток совершил в течение
1 секунды, необходимо 1 секунду разделить
на время одного периода f
= 1/T. Зная частоту
переменного тока, можно определить
период: T = 1/f.
Частота переменного тока измеряется
единицей, называемой герцем.
Если речь идёт о переменном токе,
частота изменения которого равна 1
герцу, то период такого тока будет равен
1 секунде. И, наоборот, если период
изменения тока равен 1 секунде, то частота
такого тока равна 1 герцу.
Итак, мы определили параметры переменного
тока — период, амплитуду и частоту,
— которые позволяют отличать друг от
друга различные переменные токи, ЭДС и
напряжения и строить, когда это необходимо,
их графики.
При определении сопротивления различных
цепей переменному току использовать
еще одну вспомогательную величину,
характеризующую переменный ток, так
называемую угловую или круговую
частоту.
Круговая частота обозначается
буквой ω и связана с
частотой f соотношением
ω=2πf.
При построении графика переменной ЭДС
можно заметить, что за время одного
полного оборота рамки происходит полный
цикл изменения ЭДС. Иначе говоря, для
того чтобы рамке сделать один оборот,
т. е. повернуться на 360°, необходимо
время, равное одному периоду, т. е. Т
секунд. Тогда за 1 секунду рамка совершает
360°/T оборота. Следовательно, 360°/T
есть угол, на который поворачивается
рамка в 1 секунду, и выражает собой
скорость вращения рамки, которую принято
называть угловой или круговой скоростью.
Но так как период Т связан с частотой
f соотношением f = 1/T, то и круговая
скорость может быть выражена через
частоту и будет равна ω
= 360°f.
Для удобства пользования круговой
частотой при всевозможных расчетах
угол 360°, соответствующий одному обороту,
заменяют его радиальным выражением,
равным 2π радиан,
где π = 3,14. Таким
образом, получается ω
= 2πf. Следовательно,
чтобы определить круговую частоту
переменного тока (ЭДС
или напряжения), надо частоту
в герцах умножить на постоянное число
6,28.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #