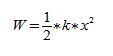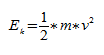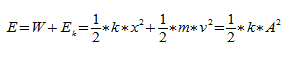|
|
Макеты страниц
При изучении этой темы решают задачи по кинематике и динамике упругих колебаний. Полезно при этом сопоставление упругих колебаний с уже рассмотренными колебаниями маятника для выявления как их общих, так и специфических черт.
Решение задач требует применения второго закона Ньютона, закона Гука и формул кинематики гармонического колебательного движения.
Период упругих гармонических колебаний тела массой 




В задачах о превращениях энергии в колебательном движении в основном рассматривают превращение кинетической энергии в потенциальную. Но для случая затухающих колебаний учитывают также превращение механической энергии во внутреннюю. Кинетическая энергия упругих колебаний

Потенциальная энергия 
Будут ли отличаться и как колебания тел разной массы на одной и той же пружине? Ответ проверьте на опыте.
Ответ. Тело большей массы будет иметь больший период колебаний. Из формулы 
757(э). На пружину подвесили груз и затем поддерживали его так, чтобы пружина не растягивалась. Опишите, как будет двигаться груз, если убрать поддерживающую его опору. Ответ проверьте на опыте.
Решение, Отпустим груз свободно падать вниз. Тогда он растянет пружину на величину 

По закону сохранения энергии при обратном движении вверх груз поднимается на высоту 

Так как 

Рис. 237.
Следовательно, положение, в котором висит груз в состоянии покоя, является центром, около которого совершаются колебания. Этот вывод легко проверить на «мягкой» длинной пружине, например от прибора «ведерко Архимеда».
758. Тело массой 


Рис. 238.
Решение. В крайнем положении вся энергия тела потенциальная, а в среднем — кинетическая. По закону сохранения энергии

Для положения равновесия 


759(э). Определите коэффициент жесткости 

Решение. Для ответа на воррос задачи учащиеся должен иметь резиновую нить, грузик массой 100 в, линейку и секундомер
Подвесив груз на нить, сначала рассчитывают величину 





Измерив по секундомеру время 10—20 полных колебаний груза, убеждаются, что период, найденный расчетами, совпадает с полученным из опыта.
760. Используя решение задач 757 и 758, определите период колебаний вагона на рессорах, если его статическая осадка равна 
Решение. 
Следовательно, 
Мы получили интересную формулу, по которой легко определить период упругих колебаний тела, зная только величину 

761 (э). Используя формулу 
762. Пользуясь формулой 
Решение. Для математического маятника 

763. Используя условие и решение задачи 758, найдите закон, по которому изменяется сила упругости пружины, и запишите уравнения данного гармонического колебательного движения, если в крайнем положении тело обладало энергией 
Решение. 
Примем, что 


Аналогично подставив значение массы, амплитуды и периода в общие формулы смещения, скорости и ускорения, получим:

Формулу ускорения можно было такжеполучить, пользуясь формулои силы 
764. Математический маятник, имеющий массу 




Решение. Найдем сначала период колебания 



Для определения времени 

откуда

По абсолютной величине 

765(a). Изготовьте маятник и проверьте на опыте, как изменяется при увеличении затухания период его колебания. На что расходуется энергия при затухающих колебаниях?
Решение. Для опыта можно использовать затухание колебаний маятника, имеющего кисточку, трущуюся о стол, затухание колебаний маятника (в том числе пружинного), опущенного частично или полностью в воду, и т. д.
В одном из опытов были получены следующие данные. Длина маятника 



замедляют его движение. Механическая энергия маятника превращается во внутреннюю энергию тел (воздуха, воды, нити и др.), которые нагреваются.
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно – кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА
Формулы пружинного маятника в физике
Формулы пружинного маятника
Определение и формулы пружинного маятника
Определение
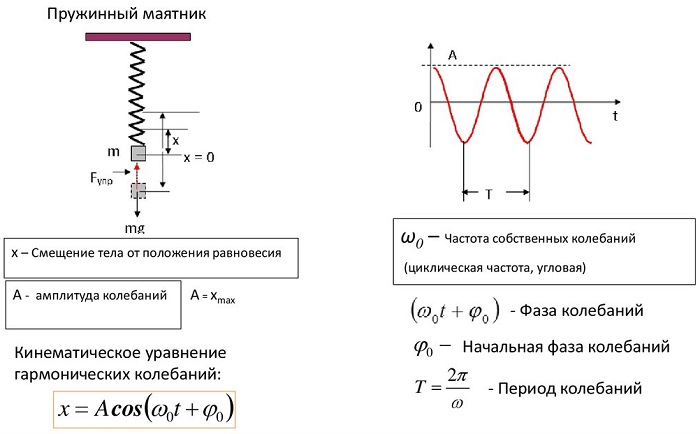
Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.
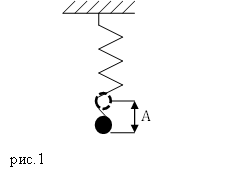
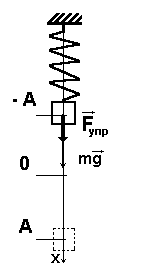
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.
Уравнения колебаний пружинного маятника
Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:
[ddot{x}+{omega }^2_0x=0left(1right),]
где ${щu}^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний.
В экспоненциальном виде колебания пружинного маятника можно записать как:
[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]
Формулы периода и частоты колебаний пружинного маятника
Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:
[T=2pi sqrt{frac{m}{k}}left(4right).]
Так как частота колебаний ($nu $) – величина обратная к периоду, то:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]
Формулы амплитуды и начальной фазы пружинного маятника
Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).
Амплитуду можно найти как:
[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]
начальная фаза при этом:
[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]
где $v_0$ – скорость груза при $t=0 c$, когда координата груза равна $x_0$.
Энергия колебаний пружинного маятника
При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.
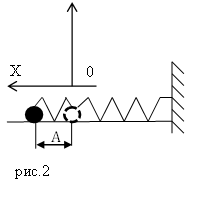
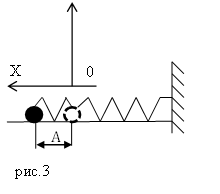
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:
[E_p=-frac{dF}{dx}(8)]
учитывая, что для пружинного маятника $F=-kx$,
тогда потенциальная энергия ($E_p$) пружинного маятника равна:
[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]
Закон сохранения энергии для пружинного маятника запишем как:
[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]
где $dot{x}=v$ – скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ – кинетическая энергия маятника.
Из формулы (10) можно сделать следующие выводы:
- Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
- Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.
Примеры задач с решением
Пример 1
Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac{м}{с}$?
Решение. Сделаем рисунок.
По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:
[E_{pmax}=E_{kmax }left(1.1right),]
где $E_{pmax}$ – потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax }$ – кинетическая энергия шарика, в момент прохождения положения равновесия.
[E_{kmax }=frac{mv^2}{2}left(1.2right).]
Потенциальная энергия равна:
[E_{pmax}=frac{k{x_0}^2}{2}left(1.3right).]
В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:
[frac{mv^2}{2}=frac{k{x_0}^2}{2}left(1.4right).]
Из (1.4) выразим искомую величину:
[x_0=vsqrt{frac{m}{k}}.]
Вычислим начальное (максимальное) смещение груза от положения равновесия:
[x_0=1cdot sqrt{frac{0,36}{1600}}=1,5 cdot {10}^{-3}(м).]
Ответ. $x_0=1,5$ мм
Пример 2
Задание. Пружинный маятник совершает колебания по закону: $x=A{cos left(omega tright), } $где $A$ и $omega $ – постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_{p0}$.
В какой момент времени это произойдет?
Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:
[F=-kx=-kA{cos left(omega tright)left(2.1right). }]
Потенциальную энергию колебаний груза найдем как:
[E_p=frac{kx^2}{2}=frac{kA^2{{cos }^2 left(omega tright) }}{2}left(2.2right).]
В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:
[frac{E_{p0}}{F_0}=-frac{A}{2}{cos left(omega tright) }to t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }.]
Ответ. $t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }$
Читать дальше: формулы равноускоренного прямолинейного движения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Для школьников.
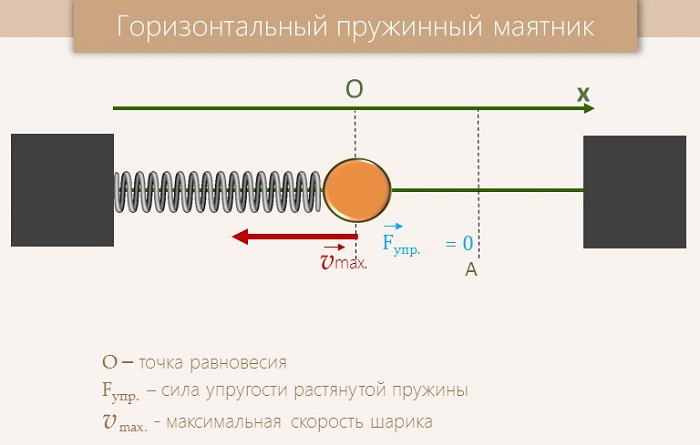
Упругие колебания – такие колебания, когда колеблющаяся система стремится вернуться в состояние устойчивого равновесия под действием возникшей в ней силы упругости.
Например, упругие колебания возникают в пружинном маятнике, представляющем собой тело, подвешенное на пружине.
На рис. а) показано как упругая сила пружины уравновешивает силу тяжести подвешенного тела.
Если пружину оттянуть на расстояние х, то на тело будет действовать большая упругая сила, равная сумме двух сил упругости.
Изменение упругой силы пропорционально смещению х
При отпускании пружины тело станет совершать колебательные движения около точки О.
Сила упругости, вызвавшая колебание, всегда направлена к положению равновесия (в сторону противоположную смещению) – её называют возвращающей силой.
По второму закону Ньютона, эта сила вызывает ускорение тела
Пружинный маятник под действием силы упругости будет совершать гармонические колебания с собственной циклической частотой
Период этих колебаний
При гармонических упругих колебаниях дважды за период происходит переход кинетической энергии груза в потенциальную энергию упругой деформации пружины, и обратно.
Упругие колебания имеют место в любом твёрдом теле, в любой конструкции и характеризуются собственной частотой.
Важным случаем упругих колебаний являются крутильные колебания, при которых тело поворачивается вокруг оси, проходящей через его центр масс.
На рисунке ниже показаны крутильные колебания диска, подвешенного на проволоке.
Если диск повернуть так, чтобы проволока закрутилась, и отпустить, то диск начнёт раскручиваться, затем закручиваться в обратную сторону и т.д., то есть будет совершать крутильные колебания.
При этом два раза за период будет происходить переход кинетической энергии движущегося диска в потенциальную энергию упругой деформации закручивающейся проволоки, и обратно.
Крутильные колебания могут иметь место, например, в валах двигателей и приносить вред при условиях резонанса (о резонансе будет говориться позднее).
Крутильные маятники применяются, например, в ручных механических часах, где нельзя использовать подвесной маятник. Крутильный маятник в ручных часах называют балансиром.
Балансир – это колёсико, к оси которого прикреплена спиральная пружинка. При повороте балансира пружинка закручивается и раскручивается.
Период крутильных колебаний тем больше, чем больше масса колеблющейся системы.
Но при крутильных колебаниях важна не только масса колеблющейся системы, а и её распределение относительно оси вращения. Это можно продемонстрировать на опыте крутильных колебаний гантели.
Опыт показывает, что при раздвигании грузов 1 и 2 частота колебаний уменьшается.
Период крутильных колебаний находится по формуле:
где к – жёсткость колеблющейся системы, а I – её момент инерции.
Момент инерции – это мера инерции при вращательном движении.
Момент инерции характеризуется распределением масс внутри системы.
Для одного груза, который можно принять за материальную точку, момент инерции равен произведению массы груза на квадрат его расстояния до оси вращения:
Для двух грузов (для гантели) момент инерции будет в 2 раза больше.
Задача. Когда груз неподвижно висел на пружине, пружина была растянута на х = 5см. Затем груз оттянули и отпустили. Найти период колебаний груза.
Решение. Период колебаний пружинного маятника находится по формуле:
Когда груз неподвижно висел на пружине, то его сила тяжести уравновешивалась силой упругости пружины
Выразив отсюда коэффициент упругости и подставив его в формулу периода, получим
Ответ: период колебаний груза равен 0,45 с.
Задача
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Нахождение периода колебаний математического маятника.
Следующая запись: Разные задачи на гармонические колебания.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 5 8.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Пружинный маятник – колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.
Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.
В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.
Что такое пружинный маятник
Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.
Приняты следующие обозначения:
-
m – масса тела;
-
k – коэффициент жесткости пружины.
Общий вид маятника:
Особенностями пружинных маятников являются:
-
Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;
-
У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;
-
Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;
-
Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;
-
От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.
Виды пружинных маятников
Существует два типа данной системы:
-
Вертикальный маятник – на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.
-
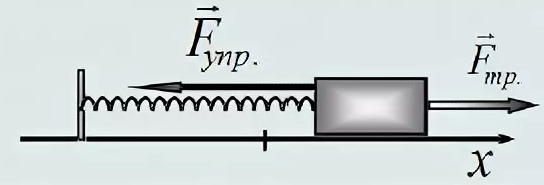
Горизонтальный – в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.
Сила упругости в пружинном маятнике
До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.
Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.
Расчёт силы упругости может быть проведен таким образом:
Fупр = – k*x
где k — коэффициент жесткости пружины (Нм),
x – смещение (м).
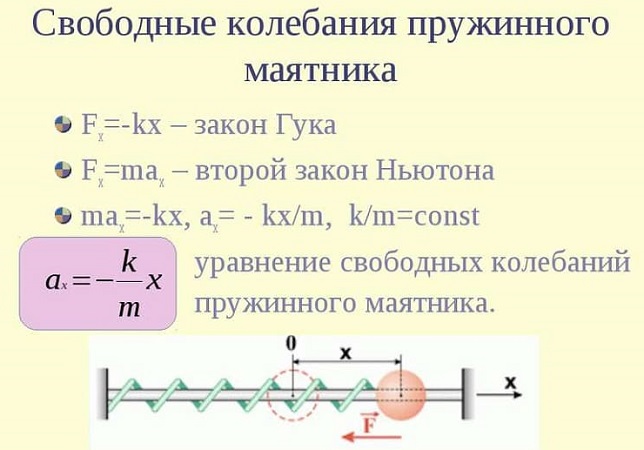
Уравнения колебаний пружинного маятника
Свободные колебания пружинного маятника описываются с помощью гармонического закона.
Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:
F(t) = ma(t) = – mw2x(t),
где w – радиальная частота гармонического колебания.
Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:
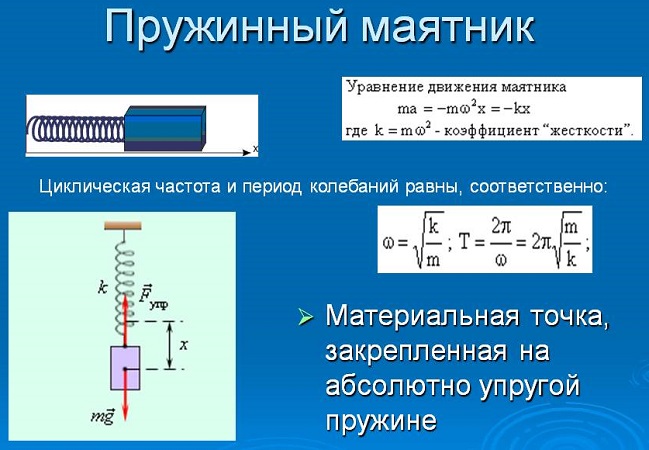
Период и частота свободных колебаний пружинного маятника
При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.
Изменение циклической частоты покажет формула, приведенная на рисунке:
Факторы, от которых зависит частота:
-
Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.
-
Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.
Амплитуда и начальная фаза пружинного маятника
Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.
В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).
Энергия пружинного маятника
При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.
Потенциальная энергия:
Кинетическая энергия:
Полная энергия:
Расчет имеет особенности. При его проведении нужно учитывать несколько условий:
-
Колебания проходят в двух плоскостях: вертикальной и горизонтальной.
-
В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.
-
Влияние силы трения при расчете не учитывают.
Дифференциальное уравнение гармонических колебаний пружинного маятника
Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.
У маятника возвращающая сила обязана своим возникновением силе тяжести. Но для колебаний существенно только само наличие возвращающей силы, т. е. такой силы, которая всегда направлена к положению равновесия и, вообще говоря, увеличивается с удалением от этого положения. Такого рода силы возникают также при деформации твердых тел и представляют собой упругие силы (см. том I, § 58). Следовательно, эти упругие силы тоже могут вызывать колебания. По происхождению возвращающей силы такие колебания называются упругими. Выше мы уже приводили ряд примеров.
Колебания тела, подвешенного на пружине (такое устройство часто называют пружинным маятником), вагона на рессорах, пластинки, зажатой в тиски, колебания камертона, натянутой струны, моста, фундамента, фабричной трубы или высокого здания — все это упругие колебания. В соответствии с иным происхождением возвращающей силы потенциальная энергия упругих колебаний есть энергия деформации упругого тела, а не потенциальная энергия силы тяжести, как у маятника. В остальном динамика упругих колебаний та же, что и у маятника. И здесь мы имеем дважды за период переход кинетической энергии в потенциальную {энергию деформации) и обратно.
Особенно просто проследить все стадии этого процесса, наблюдая тело, например шарик, колеблющееся на пружинах. В этом случае можно считать, что энергия деформации имеется только у пружин, а не у шарика, деформацией которого можно пренебречь. Если же масса тела велика по сравнению с массой пружин, то можно считать, что кинетическая энергия имеется только у тела, а не у пружин, массой которых мы пренебрегаем. Таким образом, переход энергии из кинетической в потенциальную и обратно является вместе с тем переходом энергии от тела к пружинам и обратно.
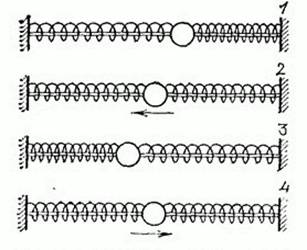
Рис. 17. Колебания тела на пружинах
На рис. 17 показаны четыре положения такой колебательной системы, взятые через каждую четверть периода. В положении 1 тело наиболее сильно отклонено вправо, одна пружина сжата, другая растянута, скорость и кинетическая энергия равны нулю, вся энергия потенциальная. В положении 2 пружины не деформированы, тело с наибольшей скоростью проходит через положение равновесия, вся энергия кинетическая. В положении 3 происходит то же, что и в положении 1. В положении 4 отличие от положения 2 только в направлении скорости.
Взяв при тех же пружинах тело с большей массой, легко убедиться, что частота колебаний уменьшится. С помощью секундомера можно убедиться в том, что четырехкратное увеличение массы тела удлиняет период колебаний (т. е. уменьшает их частоту) в два раза. При массе, увеличенной в девять раз, период увеличится в три раза. Период упругих колебаний пропорционален квадратному корню из массы тела. Этот результат будет получаться на опыте тем точнее, чем лучше выполнены описанные условия, когда можно считать массу сосредоточенной в одной точке (центре тяжести тела) и не принимать во внимание массу пружин. Однако во всех случаях увеличение массы упругой колебательной системы влечет за собой замедление колебаний, увеличение их периода.
Проделаем теперь опыт, оставив тело прежней массы, но заменив пружину более жесткой. Мы тотчас же увидим, что период колебаний уменьшился. Таким образом, период упругих колебаний тем меньше, чем больше жесткость пружины, т.е. чем меньше упругость системы.
Исследование упругих колебаний груза на пружине показывают, что при не слишком больших амплитудах эти колебания являются гармоническими, причем период их выражается формулой математического маятника:
.
Здесь
– масса колеблющегося груза,
– жесткость пружины, т.е. сила, необходимаядля растяжения пружины на единицу длины.