Как найти период увеличения

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

• амплитуда,
• период,
• частота,
• циклическая частота,
• фаза,
• начальная фаза.

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac{1}{c} right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large  displaystyle frac{1}{c} = c^{-1} ).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

[ large boxed{ nu = frac{1}{T} }]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

( large displaystyle omega left( frac{text{рад}}{c} right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

[ large boxed{ omega = 2pi cdot nu }]

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).

(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.

Определим угол (large varphi_{0} ) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text{сек} right)]

Из графика следует, что период T = 4 сек.

• Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):

[large frac{Delta t }{T} = frac{1}{4} ]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

• Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.

• В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

[large varphi_{0} = — frac{pi }{2} ]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

Обозначим их:

( large varphi_{01}) – для первого процесса и,

( large varphi_{02}) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

[large boxed{ Delta varphi = varphi_{01} —  varphi_{02} }]

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

• Связь между периодом, количеством колебаний и общим временем колебательного процесса:

[large boxed{ T cdot N = t }]

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text{шт} right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

• Период и частота колебаний связаны так:

[large boxed{ T = frac{1}{nu} }]

(large nu left( text{Гц} right) ) – частота колебаний.

• Количество и частота колебаний связаны формулой:

[large boxed{ N = nu cdot t}]

• Связь между частотой и циклической частотой колебаний:

[large boxed{ nu cdot 2pi = omega }]

(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.

• Фаза и циклическая частота колебаний связаны так:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

(large varphi_{0} left( text{рад} right) ) — начальная фаза;

(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;

• Между фазой и количеством колебаний связь описана так:

[large boxed{ varphi = N cdot 2pi }]

• Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Когда вы строите графики тригонометрических функций, вы обнаруживаете, что они периодические; то есть они дают результаты, которые повторяются предсказуемо. Чтобы найти период для данной функции, вам нужно немного ознакомиться с каждой из них и узнать, как различия в их использовании влияют на период. Как только вы узнаете, как они работают, вы можете выбрать отдельные функции триггера и без проблем найти период.

TL; DR (слишком долго; не читал)

Период функций синуса и косинуса составляет 2π (pi) радиан или 360 градусов. Для касательной функции период равен π радиан или 180 градусов.

Определено: Период функции

Когда вы наносите их на график, тригонометрические функции создают регулярно повторяющиеся формы волны. Как и любая волна, формы имеют узнаваемые особенности, такие как пики (высокие точки) и впадины (низкие точки). Период указывает на угловое «расстояние» одного полного цикла волны, обычно измеряемое между двумя соседними пиками или впадинами. По этой причине в математике вы измеряете период функции в угловых единицах. Например, начиная с нулевого угла, функция синуса создает плавную кривую, которая увеличивается до максимума 1 при π / 2 радианах (90 градусов), пересекает ноль при π радианах (180 градусов), уменьшается до минимума – 1 при 3π / 2 радиан (270 градусов) и снова достигает нуля при 2π радиан (360 градусов). После этой точки цикл повторяется бесконечно, производя те же характеристики и значения, что и угол, увеличивающийся в положительном направлении x .

Синус и косинус

Функции синуса и косинуса имеют период 2π радиан. Функция косинуса очень похожа на синус, за исключением того, что она «опережает» синус на π / 2 радиана. Функция синуса принимает значение ноль в ноль градусов, где косинус равен 1 в той же точке.

Касательная функция

Вы получаете касательную функцию путем деления синуса на косинус. Его период составляет π радиан или 180 градусов. График тангенса ( x ) равен нулю под углом ноль, изгибается вверх, достигает 1 при π / 4 радианах (45 градусов), затем снова изгибается вверх, где он достигает точки деления на ноль при π / 2 радианах. Затем функция становится отрицательной бесконечностью и отслеживает зеркальное отображение ниже оси y , достигая -1 при 3π / 4 радианах, и пересекает ось y при π радианах. Хотя у него есть значения x, при которых оно становится неопределенным, функция тангенса все еще имеет определенный период.

Секанс, Косекант и Котангенс

Три другие тригональные функции, косеканс, секанс и котангенс, являются взаимными величинами синуса, косинуса и тангенса соответственно. Другими словами, cosecant ( x ) равен 1 / sin ( x ), secant ( x ) = 1 / cos ( x ) и cot ( x ) = 1 / tan ( x ). Хотя их графики имеют неопределенные точки, периоды для каждой из этих функций такие же, как для синуса, косинуса и тангенса.

Множитель периода и другие факторы

Умножая x в тригонометрической функции на константу, вы можете сократить или увеличить его период. Например, для функции sin (2_x_) период равен половине ее нормального значения, поскольку аргумент x удваивается. Он достигает своего первого максимума при π / 4 радианах вместо π / 2 и завершает полный цикл в π радианах. Другие факторы, которые вы обычно видите в функциях триггера, включают изменения фазы и амплитуды, где фаза описывает изменение начальной точки на графике, а амплитуда – это максимальное или минимальное значение функции, игнорируя знак минуса на минимуме. Например, выражение 4 × sin (2_x_ + π) достигает максимума 4 из-за множителя 4 и начинается с изгиба вниз, а не вверх из-за константы π, добавленной к периоду. Обратите внимание, что ни 4, ни π-константы не влияют на период функции, только на ее начальную точку и максимальные и минимальные значения.

Темп роста – это прирост какой-либо изучаемой величины за один временной период (обычно применяется к году).

Темп прироста – это прирост какой либо изучаемой величины за один временной период за вычетом 100%.

Темп роста и темп прироста измеряются в процентах и являются относительными величинами. Темп роста – всегда величина положительная, темп прироста может быть отрицательным. Темп прироста равен темп роста минус 100%.

Теперь рассмотрим расчет темпа роста и темпа прироста более подробно.

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

Расчет темпа роста и прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: темп роста и темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов – формулы расчета темпа роста и прироста.

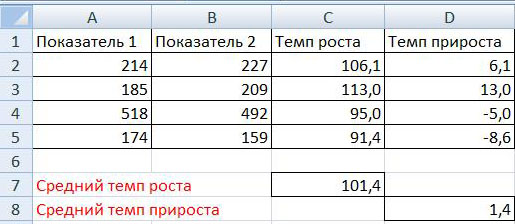
На рисунке представлен пример расчета темпа роста и прироста:

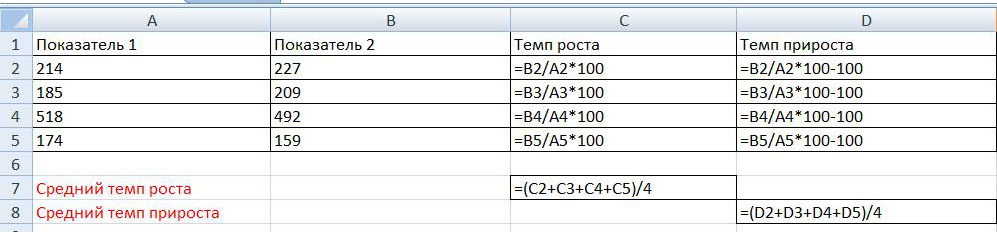
Для наглядности на рисунке ниже приведен этот же пример, только с открытыми формулами:

На рисунке видно, что определение темпа роста осуществляется путем деления Показателя 2 на Показатель 1 и умножения на 100%. При этом темп прироста равен: деление показателя 2 на показатель 1 умножение на 100% и минус 100%, то есть темп прироста равен темп роста минус 100%.

Расчет средних темпов роста и прироста

Так же на рисунках указано как рассчитывается средний темп роста и средний темп прироста. Для определения среднего темпа роста необходимо сложить показатели за все четыре периоды и разделить полученную сумму на количество периодов, то есть на 4. Аналогично рассчитывается средний темп прироста – сумма темпов прироста за все периоды делится на количество периодов.

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

Расчет базисного темпа роста и базисного темпа прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов – формулы расчета темпа роста и прироста.

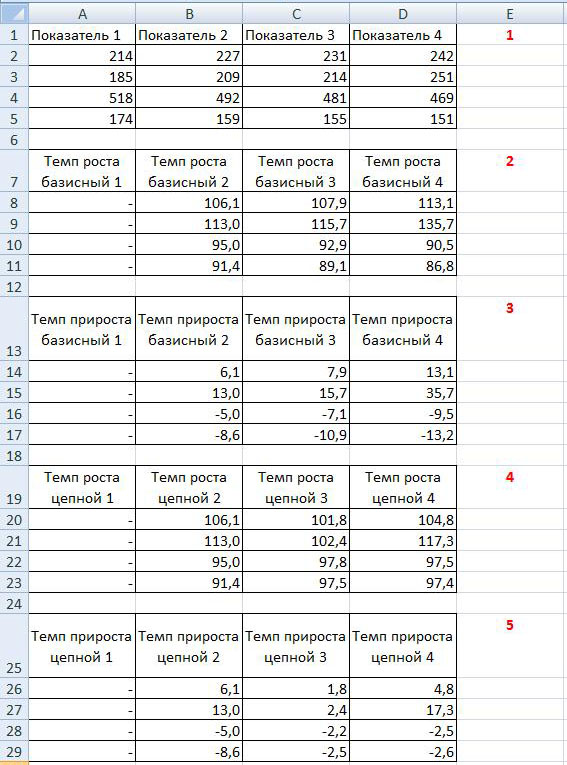
На рисунке ниже представлен расчет базисного темпа роста и прироста (таблицы 2 и 3):

Расчет базисного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя.

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

В примере за базисный показатель принят Показатель 1, поэтому базисный темп роста или базисный темп прироста рассчитывается исходя из этого положения, то есть при расчете базисного темпа роста Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, при расчете базисного темпа прироста из каждого показателя базисного темпа роста вычитаем 100.

Расчет цепного темпа роста и цепного темпа прироста

На рисунке выше представлен расчет базисного темпа роста и прироста (таблицы 4 и 5).

Расчет цепного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя. В отличие от базисного темпа роста или прироста, цепной темп роста или прироста рассчитывается из текущего и предыдущего показателя.

То есть цепной темп роста или цепной темп прироста рассчитывается следующим образом: Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 2 и умножаем на 100, далее Показатель 4 делим на Показатель 3 и умножаем на 100, при расчете цепного темпа прироста из каждого показателя цепного темпа роста вычитаем 100.

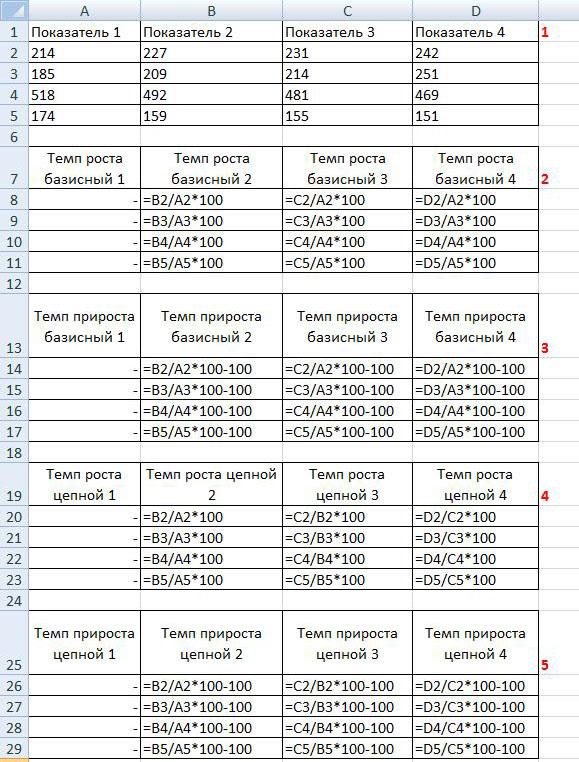
Для того, чтобы закрепить полученную информацию, обратите внимание на рисунок ниже, в котором отражены формулы расчета: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста:

Обратите внимание, что при расчете базисного и цепного показателей, значения базисного и цепного темпов роста и прироста равны, так как при избрании в качестве базисного показателя первого из ряда, они рассчитываются одинаково.

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

---

3.1. Понятие выборки (применительно к исследованию в психологии)

3.2. Не любите проводить социологическое исследование? Вы просто не умеете его готовить!

3.3. Корреляционный анализ по методу Спирмена (ранги Спирмена)

3.4. Дискуссия: Объект и Предмет исследования или наоборот?

3.5. Решение задач по праву. Как решить задачу по Юриспруденции?

3.6. Как рассчитать темп роста и прироста?

3.7. Как выбрать тему дипломной работы?

3.8. Методы исследования в дипломе, пример

Темп прироста является одним из показателей динамики, который в относительном выражении показывает, на сколько процентов увеличился или уменьшился исследуемый признак. Например, прирост ВВП на 2% в 2018 году по сравнению с 2017 годом.

Формула

Формула расчета темпа прироста

tпр=y1−y0y0∗100%t_{text{пр}} = frac {y_1- y_0}{y_0}*100%

где y1y_1 — значение показателя отчетного периода;

y0y_0 — значение показателя базового периода.

В качестве базового показателя может использоваться показатель предыдущего периода, тогда темп прироста будет цепным, а может и другого базового периода, по отношению к которому будут рассчитываться все показатели, тогда темп прироста будет базисным.

Примеры решения задач

Пример 1

В 2016 году прибыль предприятия составила 1200 тыс. руб., а в 2017 году — 1500 тыс. руб. Найти темп прироста прибыли.

Решение

tпр=1500−12001200∗100%=25%t_{text{пр}}=frac{1500-1200}{1200} *100%=25%

То есть прибыть возросла на 25%25%.

Ответ: tпр=25%t_{text{пр}}=25%

Пример 2

В прошлом году сельскохозяйственное предприятие АО «Рассвет» получило урожай картофеля в размер 3500 центнеров, а в этом году — 3200 центнеров. Найдите темп прироста (снижения) урожая картофеля.

Решение

tпр=3200−35003500∗100%=−8,57%t_{text{пр}}=frac{3200-3500}{3500} *100%=-8,57%

Урожай картофеля снизился на 8,57%.
Ответ: tпр=−8,57%t_{text{пр}}=-8,57%

Широкое использование данного показателя обусловлено его простотой расчета, а также ясностью для понимания.

Важнейшим показателем эффективности производства в анализе финансовой ситуации компании является показатель темпа роста. Поговорим об особенностях его расчета.

Как рассчитать темп роста: формула

Что называют снижением темпа роста цен?
Подробнее

Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.

Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.

Как рассчитать темп роста в процентах – формула:

ТР = П_т / П_б х 100%,

где П_к и П_б – показатели значений текущего и базового периодов.

Узнайте, может ли темп роста быть отрицательной величиной.

Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:

1. ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;

2. ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;

3. ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.

Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:

Объем выпуска в тыс. руб.	Расчет (Пт / Пб х 100%)
2017 (Пб)	2018 (Пт)
600	800	133,3%
600	600	100%
600	400	66,7%

Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.

Узнайте, чем отличается темп роста от темпа прироста.

Как рассчитать цепные темпы роста

Рассмотрим пример расчета базисного и цепного темпов роста:

Период	Объем в тыс.руб.	Темп роста в %
базисный	цепной
1 кв.	300	100	–
2 кв.	310	103,3 (310 / 300)	103,3 (310 / 300)
3 кв.	280	93,3 (280 / 300)	90,3 (280 / 310)
4 кв.	360	120 (360 / 300)	128,6 (360 / 280)

Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).

Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.

Как рассчитать темпы прироста

Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:

∆ ТР = (П_тек – П_баз) / П_баз х 100%

Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:

∆ ТР = (П_тек – П_пр.п) / П_{пр. п} х 100%.

Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.

Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:

Период	Темпы прироста
базисные	цепные
1 кв.	–	–
2 кв.	3,3% (103,3 – 100) или ((310 – 300) / 300 х 100)	3,3% (103,3 – 100) или ((310 – 300) / 300 х 100)
3 кв.	– 6,7% (93,3 – 100) или ((280 – 300) / 300 х 100)	-9,7% (90,3 – 100) или ((280 – 310) / 310 х 100)
4 кв.	20% (120 – 100) или (( 360 – 300) / 300 х 100)	28,6% (128,6 – 100) или ((360 – 280) / 280 х 100)

Анализируя результаты вычислений, экономист может сделать вывод:

• Прирост объемов наблюдался во 2-м и 4-м кварталах, причем во 2-м он был наименьшим (3,3%). В 3-м квартале объем выпуска сократился на 6,7% в сравнении с показателями начала года;

• Цепные темпы прироста обнаружили более глубокие колебания: объемы 3-го квартала снизились по отношению к показателям 2-го на 9,7%. Зато выпуск товаров в 4-м квартале вырос почти на треть в сравнении с итогами 3-го квартала. Столь существенные изменения в объемах производства могут свидетельствовать о сезонности выпускаемых продуктов, перебоях в снабжении необходимым сырьем или других причинах, которые исследует аналитик.

Как рассчитать средний темп роста

Средний темп роста – обобщающая характеристика уровня изменений. Расчет средних темпов роста и прироста также разграничивают на базисные и цепные. Для определения среднего темпа роста расчетные показатели по периодам складывают и делят на количество периодов. Таким же образом находят и средние темпы приростов. Вернемся к предыдущему примеру, рассчитав средние значения базисных темпов роста и прироста, а также аналогичных цепных показателей.

Показатель	Значение в %	Расчет
Средний темп роста (базисный)	105,5	(103,3 + 93,3 + 120) / 3
Средний темп прироста (базисный)	5,5	(3,3 – 6,7 + 20) / 3
Средний темп роста (цепной)	107,4	(103,3 + 90,3 + 128,6) / 3
Средний темп прироста (цепной)	7,4	(3,3 – 9,7 + 28,6) / 3

Полученные цифры свидетельствуют о том, что в среднем с начала года объемы выпуска выросли на 5,5%, а в поквартальной привязке рост составил 7,4%.

Читайте также: Экспресс-анализ финансового состояния предприятия

Специализация: Гражданское право – работа с недвижимостью. договорная работа, наследственное право, банкротство.