Как найти период волны по рисунку

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

• амплитуда,
• период,
• частота,
• циклическая частота,
• фаза,
• начальная фаза.

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac{1}{c} right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large  displaystyle frac{1}{c} = c^{-1} ).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

[ large boxed{ nu = frac{1}{T} }]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

( large displaystyle omega left( frac{text{рад}}{c} right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

[ large boxed{ omega = 2pi cdot nu }]

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).

(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.

Определим угол (large varphi_{0} ) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text{сек} right)]

Из графика следует, что период T = 4 сек.

• Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):

[large frac{Delta t }{T} = frac{1}{4} ]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

• Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.

• В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

[large varphi_{0} = — frac{pi }{2} ]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

Обозначим их:

( large varphi_{01}) – для первого процесса и,

( large varphi_{02}) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

[large boxed{ Delta varphi = varphi_{01} —  varphi_{02} }]

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

• Связь между периодом, количеством колебаний и общим временем колебательного процесса:

[large boxed{ T cdot N = t }]

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text{шт} right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

• Период и частота колебаний связаны так:

[large boxed{ T = frac{1}{nu} }]

(large nu left( text{Гц} right) ) – частота колебаний.

• Количество и частота колебаний связаны формулой:

[large boxed{ N = nu cdot t}]

• Связь между частотой и циклической частотой колебаний:

[large boxed{ nu cdot 2pi = omega }]

(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.

• Фаза и циклическая частота колебаний связаны так:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

(large varphi_{0} left( text{рад} right) ) — начальная фаза;

(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;

• Между фазой и количеством колебаний связь описана так:

[large boxed{ varphi = N cdot 2pi }]

• Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Есть много свойств, которые чаще всего используют для описания волн. Они включают в себя амплитуду, частоту, период, длину волны, скорость и фазу.

График волны

При изображении волны при решении какой либо физической или математической задачи на рисунке волна видна, как моментальный снимок. Вертикальная ось в таком случае – это амплитуда волны, в то время как горизонтальная ось может быть расстоянием или временем, зависит от каждой конкретной задачи.
На рисунке ниже можно увидеть, что самая высокая точка на графике волны называется гребнем, а самая низкая точка называется впадиной. Линия, проходящая через центр волны, является положением покоя среды, если волна не проходила.

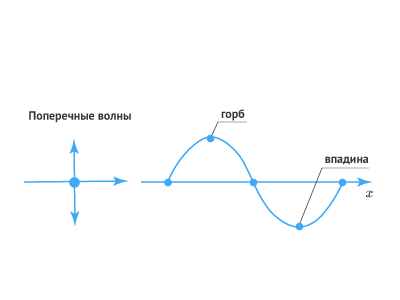
Можно определить ряд волновых свойств из графика.

Амплитуда

Амплитуда волны является мерой смещения волны от ее положения покоя. Амплитуда показана на графике ниже.

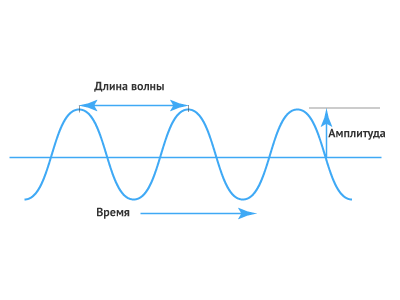
Амплитуда обычно рассчитывается путем просмотра графика волны и измерения высоты волны из положения покоя.

Амплитуда является мерой силы или интенсивности волны.

Например, при взгляде на звуковую волну амплитуда будет измерять громкость звука. Энергия волны также изменяется прямо пропорционально амплитуде волны.

Длина волны

Длина волны

Это расстояние между двумя соответствующими точками в последовательных циклах волны.

Она может быть измерена между двумя гребнями волны или двумя впадинами волны. Длина волны обычно представлена в физике греческой буквой лямбда λλ.

Частота и период

Частота волны

Это количество циклов, которое циклически повторяется.

Частота измеряется в герцах или циклах в секунду. Частота часто представлена строчной буквой ff.

Период волны

Это время между гребнями волны.

Период измеряется в единицах времени, таких как секунды. Период обычно представлен заглавной буквой TT.
Период и частота тесно связаны друг с другом. Период обратно пропорционален частоте и наоборот, как показано в следующей формуле:

T=1/fT = 1 / f

Скорость волны

Другим важным свойством волны является скорость распространения. Скорость механических волн зависит от среды, через которую проходит волна. Например, звук будет распространяться в воде с другой скоростью, чем в воздухе.
Скорость волны обычно обозначается буквой vv. Скорость может быть рассчитана путем умножения частоты на длину волны.

v=f⋅λv = f · λ

Разделяют два вида волн: поперечные и продольные.

Поперечная волна

Движение, при котором все точки волны колеблются по траекториям под прямым углом к направлению движения волны.

Поверхностные волны на воде и электромагнитные (например, радио- и световые волны) представляют собой примеры поперечных волн.

Продольная волна

Волна, состоящая из периодического возмущения или вибрации, которая происходит в том же направлении, что и продвижение волны.

Спиральная пружина, которая сжимается на одном конце, а затем освобождается, испытывает волну сжатия, которая проходит по ее длине с последующим растяжением; точка на любом витке пружины будет двигаться вместе с волной и возвращаться по тому же пути, проходя через нейтральное положение и затем снова изменяя свое движение. Звук, движущийся в воздухе, также сжимает и разжижает газ в направлении движения звуковой волны.

Тест по теме «Волны»

Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной. 

Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

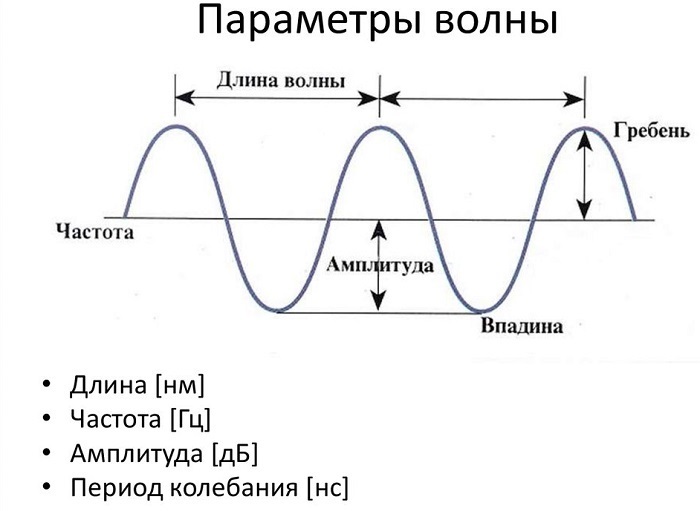
Определение и формула длины волн

Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества. 

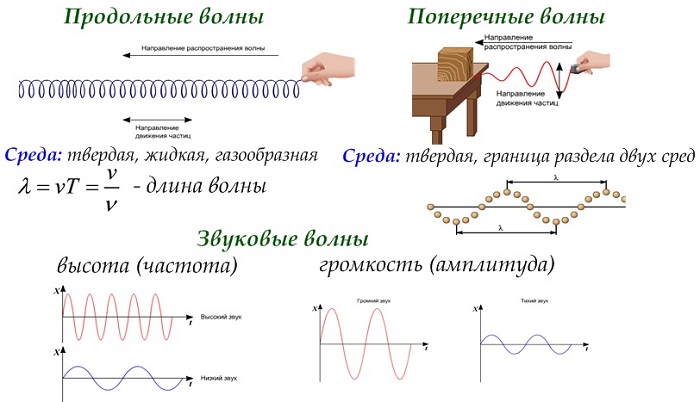
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

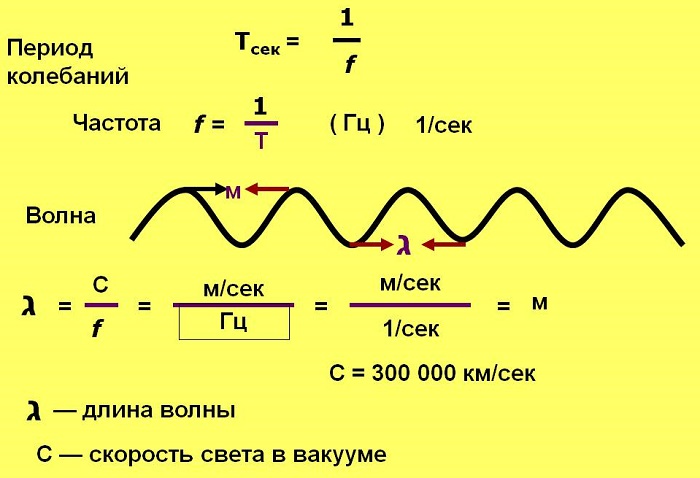
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10⁸ м/с поделить на длину в метрах.

Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

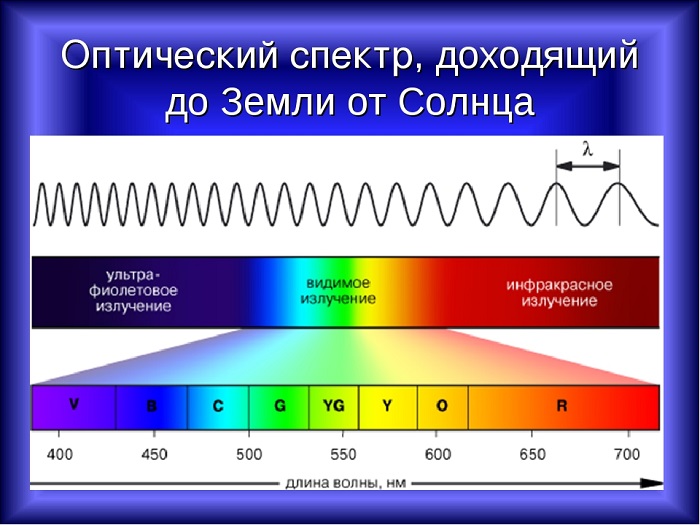
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

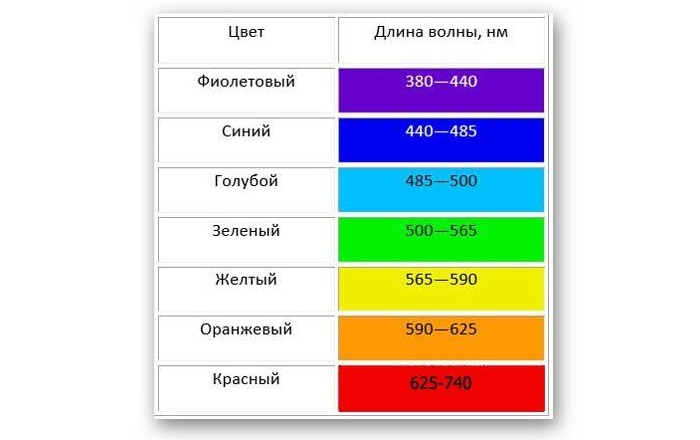
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания. 

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

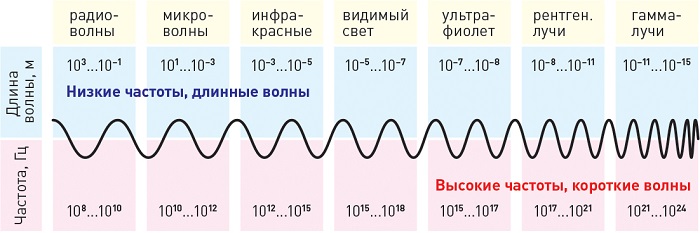
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Gulsina

Профи

(874),
закрыт

7 лет назад

В вакууме в положительном направлении оси 0у распространяется плоская электромагнитная волна. На рисунке приведен график зависимости проекции Вх на ось 0х индукции магнитного поля волны от координаты у в произвольный момент времени t. Период Т волны равен …c.

Волна формально является периодической функцией своего параметра. Функционально волна в однородно параметризованном пространстве–времени t “распространяется” в соответствии с гармоническим уравнением

A = A₀ sin φ = sin2πn, (1)

где A₀ и A – амплитуда и текущее значение “напряженности” волнового поля в конкретной точке пространства,

– текущее значение фазы в этой же точке. Параметр φ выступает в роли универсального параметра состояния. Физический смысл ее – закономерное упорядочение на множестве состояний “фаза” пространства, в чем то эквивалентное физическому времени.

Это наиболее обобщенная форма записи уравнения волны в пространстве. Но в пространстве, которое нам интересно, каждая точка имеет координаты. И первое – это текущее время. С учетом времени уравнение волны записывается так (см. Рисунок 1):

A = A₀ sin(2πω t + φ ᵥ), (2)

Здесь 2 π ω t + ᵥ – текущее значение “фазы” φ волнового поля в момент времени t,

φ ᵥ – начальная фаза волны в начальный момент времени,

ω – “частота” волнового поля. В данной форме записи (2) с множителем 2π она задает количество n волн в единицу времени.

n = Δφj/2 π . (3)

Кстати, эталонные часы, используемые в технике, да и в быту, основаны именно на подсчете количества эталонных периодов волн n специального атомного эталона времени. С появлением данного метода секунда начала соответствовать 9 192 631 770 колебаний электромагнитного излучения, которое возникает в процессе перехода между двумя уровнями сверхтонкой структуры атома цезия-133.

В пространстве, в котором мы существуем, процесс распространения волн связан дополнительно с определенным направлением распространения фронта волны и соответствующими параметрами. Найдем вид функции A(t, r) в случае плоской волны, предполагая, что колебания носят гармонический характер. Для упрощения направим оси координат так, что бы ось x совпадала с направлением распространения волны, а оси y и z перпендикулярны ей. Тогда и волновые поверхности будут перпендикулярны к оси x и, поскольку все точки волновой поверхности колеблются одинаково, напряженность волны A будет зависеть только от x и t:

A = A(t, x). (4)

Пусть колебания точек, лежащих в плоскости x = 0, имеет вид

A(0, t) = Asin2 π ωt. (5)

Найдем вид колебаний частиц в плоскости, соответствующей произвольному значению x. Для того чтобы пройти путь от плоскости x = 0 до плоскости с координатой x, волне потребуется время:

τ = x/c. (6)

c – изотропная скорость распространения фронта волны,

Следовательно, колебания частиц, находящихся в плоскости х, будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т.е. уравнение колебаний точки, находящейся на расстоянии x от источника колебаний будет иметь вид:

A(x, y) = Asin2πω(t – x/c). (7)

Итак, уравнение плоской волны запишется следующим образом:

A = Asin2πω(t – x/c). (8)

Обратите внимание на знак “–” в этом уравнении.

Интересно посмотреть уравнение этой волны при t = const, или t = 0:

A = –Asin2πωx/c. (9)

Это уравнение можно использовать для легализации создания технического эталона длины. Сейчас метр – это расстояние, которое проходит свет в вакууме за 1/299792458-ю долю секунды.

Инварианты уравнения волны

Процесс существования волн сам по себе обладает инвариантными параметрами. В галилеевом пространстве инвариантами являются промежуток времени и расстояние между двумя точками. Если промежуток времени между любыми точками ПВ действительно является инвариантом, то расстояние будет инвариантом только для одновременных точек. Волновое поле добавляет еще один инвариант. Им является фаза j волны в произвольной точке пространства-времени (ПВ), начальная фаза j0 в начале координат. Но эти параметры зависимы от системы координат. Инвариантом, независимым от системы координат, являются разность фаз между любыми точками ПВ и количество волн n между ними. Кстати, эти инварианты является даже более общими инвариантами по сравнению с инвариантом “время” галилеева пространства. Ими можно пользоваться в любом ПВ, не только галилеевом. Разность фаз Δφ непосредственно связана с количеством волн n:

Δ = 2πω ( t – Δx/c) = 2πΔ n. (10)

Физически параметр фазы волны n тесно связан с временем t и частотой w: это количество волн, разделяющих два значения времени – начала и конца отсчета времени.

На основе этой формулы вводится 4–мерное метрическое понятие “интервала” s:

Δs = φ / ω . (11)

Если разность фаз зависит от частоты, то инвариант Δs уже не зависит от частоты используемой волны. Но у нее есть один недостаток – ее значение зависит от направления распространения волны. Поэтому ее можно назвать “линейным” инвариантом. От этого недостатка можно избавиться, направив волну непосредственно между двумя “пробными” точками, и тогда этот инвариант уже будет абсолютным. В этом случае разность фаз между ними примет максимальное значение.

В реальном ПВ для получения этого однозначного результата организуется 4 взаимно ортогональных (т.е. перпендикулярных) волновых поля φ ᵤ , и в качестве волновых координат берутся значения разности фаз этих 4–х полей в конкретной точке ПВ. Одна из этих полей будет представлять часы (2), а остальные три – пространственные значения расстояния между этими точками, как в декартовой системе координат (7), при неизменном времени специальной теории относительности А.Эйнштейна. И “собственное время” движущегося материального объекта определяется через нее. И время в знаменитом парадоксе близнецов – тоже результат применения этого интервала. И система координат в ней определяется именно так. В парадигме времени СТО количество волн, отсчитываемых представленными выше атомными часами и постоянно находящихся рядом с близнецами, отсчитывают “реальное” время их жизни. Вроде бы все логично – время жизни человека определяется количеством колебаний молекул, составляющих его тело, а они строго пропорциональны количеству колебаний атомных часов.

Как видно из вышеизложенного, все очень просто в своей основе.

Если хотите узнать, что обозначает слово или словосочетание, в ОПЕРЕ выделите это слово(сочетание), нажмите правую клавишу мыши и выберите “Искать в …”, далее – “Yandex”. Если это текстовая ссылка – выделите ее, нажмите правую клавишу мыши, выберите “перейти …”. Все! О-ля-ля!

Если вам понравилась статья, то поставьте “лайк” и подпишитесь на канал! Если не понравилась – все равно комментируйте и подписывайтесь. Этим вы поможете каналу.

Ссылка на мою статью Как написать формулы в статье на Дзен?

Мои странички на Дзен: https://zen.yandex.ru/id/5e036c95fc69ab00aecfe6e9