Как найти период вращения маятника

Как найти период вращения маятника

Тип 9 № 450

i

Найти период Т вращения маятника, совершающего круговые движения в горизонтальной плоскости. Длина нити l. Угол, образуемый нитью с вертикалью, альфа .

Спрятать решение

Решение.

Видеорешение: https://youtu.be/az1K1oWOeC8?t=1043

Ответ: T=2 Пи корень из l косинус альфа /g. При малых углах Tapprox 2 Пи корень из l/g.

Источник: Гольд­фарб Н. И. Сбор­ник во­про­сов и задач по фи­зи­ке, М.: «Высш. школа», 1982 (6.30)

Источник



На груз действуют две силы: сила тяжести 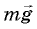Решение к задаче 4. Конический маятник 1 и сила натяжения нити 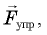Решение к задаче 4. Конический маятник 2 направленная под углом ( к вертикали (рис. 15.4). Поскольку груз движется по окружности, равнодействующая этих сил обеспечивает центростремительное ускорение 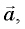Решение к задаче 4. Конический маятник 3 направленное к центру окружности. Радиус окружности обозначим 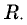Решение к задаче 4. Конический маятник 4 Он связан с длиной нити и углом ее отклонения от вертикали соотношением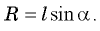 Решение к задаче 4. Конический маятник 5

Согласно второму закону Ньютона, 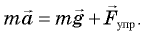Решение к задаче 4. Конический маятник 7 Центростремительное ускорение связано со скоростью соотношением 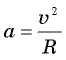Решение к задаче 4. Конический маятник 8 (см. § 4. Криволинейное движение). Поскольку нас интересует период обращения 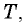Решение к задаче 4. Конический маятник 9 выразим центростремительное ускорение через период, воспользовавшись соотношением 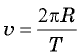Решение к задаче 4. Конический маятник 10 (за время, равное одному периоду, груз совершает один полный оборот). Мы получим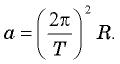 Решение к задаче 4. Конический маятник 11

Запишем уравнение второго закона Ньютона в проекциях на оси координат. Совместим начало координат с положением груза в данный момент, ось 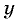Решение к задаче 4. Конический маятник 12 направим вертикально вверх, а ось 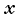Решение к задаче 4. Конический маятник 13 — горизонтально вдоль радиуса к центру окружности. Из уравнения 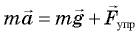Решение к задаче 4. Конический маятник 14 мы получим систему двух уравнений:

Решение к задаче 4. Конический маятник 15

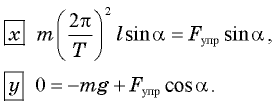
Из второго уравнения 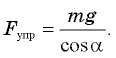Решение к задаче 4. Конический маятник 16 Подставляя это выражение в первое уравнение системы, получаем 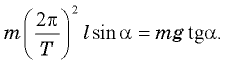Решение к задаче 4. Конический маятник 17 Отсюда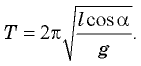 Решение к задаче 4. Конический маятник 18

Заметим, что если угол 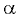Решение к задаче 4. Конический маятник 19 достаточно мал, можно принять 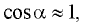Решение к задаче 4. Конический маятник 20 и тогда получим 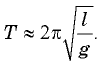Решение к задаче 4. Конический маятник 21 В дальнейшем (см. § 20. Механические колебания) мы увидим, что таков же и период малых колебаний груза, подвешенного на нити.


Механика.
2014

 

Источник

Формула периода колебаний математического маятника

Формула периода колебаний математического маятника

Математический маятник

Определение

Математический маятник – это частный случай физического маятника, масса которого находится в одной точке.

Обычно математическим маятником считают маленький шарик (материальную точку), имеющий большую массу, подвешенный на длинной нерастяжимой нити (подвесе). Это идеализированная система, которая совершает колебания под воздействием силы тяжести. Только для углов порядка 50-100 математический маятник является гармоническим осциллятором, то есть совершает гармонические колебания.

Изучая качание паникадила на длинной цепи Галилей изучал свойства математического маятника. Он понял, что период колебаний данной системы не зависит от амплитуды при малых углах отклонения.

Формула для периода колебаний математического маятника

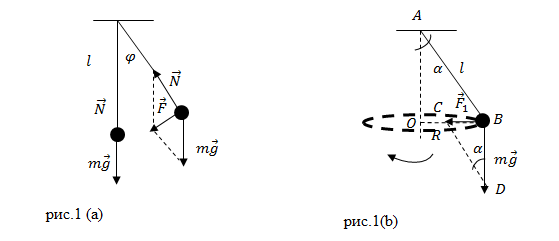
Формула периода колебаний математического маятника, рисунок 1

Пусть точка подвеса маятника неподвижна. Груз, подвешенный к нити маятника, движется по дуге окружности (рис.1(a)) с ускорением, на него действует некоторая возвращающая сила ($overline{F}$). Данная сила изменяется при движении груза. В результате чего расчет движения становится сложным. Введем некоторые упрощения. Пусть маятник совершает колебания не в плоскости, а описывает конус (рис.1 (b)). Груз в этом случае перемещается по окружности. Период интересующих нас колебаний будет совпадать с периодом конического движения груза. Период обращения конического маятника по окружности равен времени, которое тратит груз на один виток по окружности:

[T=frac{L}{v}=frac{2pi R}{v}left(1right),]

где $L$ – длина окружности; $v$ – скорость движения груза. Если углы отклонения нити от вертикали малые (небольшие амплитуды колебаний) то полагают, что возвращающая сила ($F_1$) направлена по радиусу окружности, которую описывает груз. Тогда эта сила равна центростремительной силе:

[F_1=frac{mv^2}{R}left(2right).]

Рассмотрим подобные треугольники: AOB и DBC (рис.1 (b)).

[F_1=mg{sin alpha =mgfrac{R}{l} }left(3right).]

Приравниваем правые части выражений (2) и (3), выражаем скорость движения груза:

[frac{mv^2}{R}=mgfrac{R}{l} to v=Rsqrt{frac{g}{l}}left(4right).]

Полученную скорость подставим в формулу (1), имеем:

[T=frac{2pi R}{Rsqrt{frac{g}{l}}}to ]

[T=2pi sqrt{frac{l}{g}}left(5right).]

Из формулы (5) мы видим, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения. Формулу (5) для периода математического маятника называют формулой Гюйгенса, она выполняется, когда точка подвеса маятника не движется.

Используя зависимость периода колебаний математического маятника от ускорения свободного падения, определяют величину данного ускорения. Для этого измеряют длину маятника, рассматривая большое количество колебаний, находят период $T$, затем вычисляют ускорение свободного падения.

Примеры задач с решением

Пример 1

Задание. Как известно, величина ускорения свободного падения зависит от широты. Каково ускорение свободного падения на широте Москвы, если период колебаний математического маятник длиной $l=2,485cdot {10}^{-1}$м равен T=1 c?textit{}

Решение. За основу решения задачи примем формулу периода математического маятника:

[T=2pi sqrt{frac{l}{g}}left(1.1right).]

Выразим из (1.1) ускорение свободного падения:

[g=lfrac{4{pi }^2}{T^2}.]

Вычислим искомое ускорение:

[g=0,2485cdot frac{4{pi }^2}{1^2}=9,81 (frac{м}{с^2}).]

Ответ. $g=9,81frac{м}{с^2}$

Пример 2

Задание. Каким будет период колебаний математического маятника, если точка его подвеса движется вертикально вниз 1) с постоянной скоростью? 2) с ускорением $a$? Длина нити этого маятника равна $l.$

Решение. Сделаем рисунок.

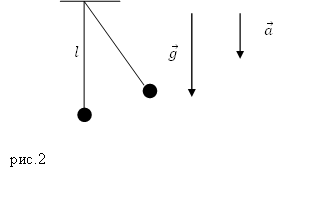
Формула периода колебаний математического маятника, пример 1

1) Период математического маятника, точка подвеса которого движется равномерно, равен периоду маятника с неподвижной точкой подвеса:

[T_1=2pi sqrt{frac{l}{g}}left(2.1right).]

2) Ускорение точки подвеса маятника можно рассматривать как появление дополнительной силы, равной $F=ma$, которая направлена против ускорения. То есть, если ускорение направлено вверх, то дополнительная сила направлена вниз, значит, она складывается с силой тяжести ($mg$). Если точка подвеса движется с ускорением, направленным вниз, то дополнительная сила вычитается из силы тяжести.

Период математического маятника, который совершает колебания и у которого точка подвеса движется с ускорением, найдем как:

[T_2=2pi sqrt{frac{l}{a_p}}left(2.2right),]

где:

[a_p=g-a left(2.3right),]

тогда:

[T_1=2pi sqrt{frac{l}{g-a}}.]

Ответ. 1) $T_1=2pi sqrt{frac{l}{g}}$; 2) $T_1=2pi sqrt{frac{l}{g-a}}$

Читать дальше: формула периода колебаний пружинного маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Период физического маятника — твердое тело, совершающее колебания в гравитационном поле вокруг горизонтальной оси подвеса, расположенной выше его центра тяжести.

Large T=2pi sqrt{frac{J}{mgl}}


Период физического маятника

Давай те выведем формулу для периода физического маятника.

При небольших углах отклонения varphi физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

large F=mgcdot sinvarphi

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла varphi . Так как угол маленький, у нас получается, что F равно:

large F=mgcdot varphi

Для вывода закона движения физического маятников используем основное уравнение динамики вращательного движения:

large J=ml^2

Так как момент силы определить в явном виде нельзя. Надо записать дифференциальное уравнение колебаний физического маятника:

large frac{d^2varphi }{dt^2}+frac{mgl}{J}varphi =0

Сравнивая полученное выражение с уравнением гармонических колебаний:

large a_x(t)+omega ^2 x(t)=0

Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

large omega=sqrt{frac{mgl}{J}}

Тогда период колебаний математического маятника будет равен:

Large T=frac{2pi }{omega } =2pi sqrt{frac{J}{mgl}}

Так же есть:

Период пружинного маятника T=2pi sqrt{frac{m}{k}}

Период математического маятника T=2pi sqrt{frac{L}{g}}

Период крутильного маятника T=2pi sqrt{frac{I}{K}}

В Формуле мы использовали :

T — Период физического маятника

J — Момент силы маятника относительно оси вращения

l — Расстояние от оси вращения до центра масс

m — Масса маятника

g=9.8 — Ускорение свободного падения

Источник

Период.

Период колебаний маятника, близкого по своим свойствам к математическому маятнику, не зависит от массы маятника.

Заставим маятник описывать коническую поверхность. В этом случае шарик маятника двигается по окружности. Определив период обращения маятника, обнаружим, что он равен периоду колебаний этого маятника:

Период обращения конического маятника же равен длине описываемой окружности, деленной на линейную скорость:

На шарик действует центростремительная сила, так как он двигается по окружности. Итак, период математического маятника зависит только от длины маятник l и от ускорения свободного падения g.

Сдвиг фаз

Возьмем два одинаковых маятника и отклоним их в одну и ту же сторону на один и тот же угол от вертикали. Если теперь их отпустить, то мы два гармонических колебания с одинаковыми амплитудами и частотами. Казалось бы, никакого различия между ними быть не может.

Однако стоит нам отпустить маятники не одновременно, и мы сразу увидим разницу: колебания будут сдвинуты по времени.

Про колебания одинаковой частоты, но смещенные по времени, говорят, что они сдвинуты по фазе. Смещение по времени выражается в долях периода, а сдвиг или разность фаз – в угловых единицах.

Если второе колебание запаздывает по сравнению с первым на 1/8 периода, то это значит, что оно отстает по фазе на 360*1/8=45, или сдвинуто по фазе на -45. Если второе колебание опережает первое на 1/8 периода, то говорят, что оно опережает его по фазе на 45, или сдвинуто по фазе +45.

Если колебания происходят без запаздывания, то их называют синфазными, или говорят, что они совершаются в фазе. При запаздывание одного на полпериода говорят, что колебания происходят в противофазе.

Формула периода колебаний математического маятника

Математический маятник

Математический маятник – это частный случай физического маятника, масса которого находится в одной точке.

Обычно математическим маятником считают маленький шарик (материальную точку), имеющий большую массу, подвешенный на длинной нерастяжимой нити (подвесе). Это идеализированная система, которая совершает колебания под воздействием силы тяжести. Только для углов порядка 50-100 математический маятник является гармоническим осциллятором, то есть совершает гармонические колебания.

Изучая качание паникадила на длинной цепи Галилей изучал свойства математического маятника. Он понял, что период колебаний данной системы не зависит от амплитуды при малых углах отклонения.

Формула для периода колебаний математического маятника

Пусть точка подвеса маятника неподвижна. Груз, подвешенный к нити маятника, движется по дуге окружности (рис.1(a)) с ускорением, на него действует некоторая возвращающая сила ($overline$). Данная сила изменяется при движении груза. В результате чего расчет движения становится сложным. Введем некоторые упрощения. Пусть маятник совершает колебания не в плоскости, а описывает конус (рис.1 (b)). Груз в этом случае перемещается по окружности. Период интересующих нас колебаний будет совпадать с периодом конического движения груза. Период обращения конического маятника по окружности равен времени, которое тратит груз на один виток по окружности:

где $L$ – длина окружности; $v$ – скорость движения груза. Если углы отклонения нити от вертикали малые (небольшие амплитуды колебаний) то полагают, что возвращающая сила ($F_1$) направлена по радиусу окружности, которую описывает груз. Тогда эта сила равна центростремительной силе:

Рассмотрим подобные треугольники: AOB и DBC (рис.1 (b)).

Приравниваем правые части выражений (2) и (3), выражаем скорость движения груза:

Полученную скорость подставим в формулу (1), имеем:

Из формулы (5) мы видим, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения. Формулу (5) для периода математического маятника называют формулой Гюйгенса, она выполняется, когда точка подвеса маятника не движется.

Используя зависимость периода колебаний математического маятника от ускорения свободного падения, определяют величину данного ускорения. Для этого измеряют длину маятника, рассматривая большое количество колебаний, находят период $T$, затем вычисляют ускорение свободного падения.

Примеры задач с решением

Задание. Как известно, величина ускорения свободного падения зависит от широты. Каково ускорение свободного падения на широте Москвы, если период колебаний математического маятник длиной $l=2,485cdot <10>^<-1>$м равен T=1 c?textit<>

Решение. За основу решения задачи примем формулу периода математического маятника:

Выразим из (1.1) ускорение свободного падения:

Вычислим искомое ускорение:

Ответ. $g=9,81frac<м><с^2>$

Задание. Каким будет период колебаний математического маятника, если точка его подвеса движется вертикально вниз 1) с постоянной скоростью? 2) с ускорением $a$? Длина нити этого маятника равна $l.$

Решение. Сделаем рисунок.

1) Период математического маятника, точка подвеса которого движется равномерно, равен периоду маятника с неподвижной точкой подвеса:

2) Ускорение точки подвеса маятника можно рассматривать как появление дополнительной силы, равной $F=ma$, которая направлена против ускорения. То есть, если ускорение направлено вверх, то дополнительная сила направлена вниз, значит, она складывается с силой тяжести ($mg$). Если точка подвеса движется с ускорением, направленным вниз, то дополнительная сила вычитается из силы тяжести.

Период математического маятника, который совершает колебания и у которого точка подвеса движется с ускорением, найдем как:

Ответ. 1) $T_1=2pi sqrt<frac>$; 2) $T_1=2pi sqrt<frac>$

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

[spoiler title=”источники:”]

http://www.webmath.ru/poleznoe/fizika/fizika_135_formula_perioda_kolebanij_matematicheskogo_majatnika.php

http://fizmat.by/kursy/kinematika/okruzhnost

[/spoiler]

Источник

Добавить комментарий