Содержание
- Как определить период вращения планеты вокруг своей оси
- Способ 1: Следить за движением звезд на небе
- Способ 2: Использование спутниковых данных
- Способ 3: Измерение силы гравитации
- Способ 4: Использование телескопов и других оптических приборов
- Итог
- Как определить период вращения планеты вокруг своей оси
- 1. Наблюдение
- 2. Определение северно-западного края
- 3. Измерение движения северно-западного края
- 4. Вычисление периода вращения
- 5. Факторы, влияющие на период вращения
- 6. Вывод
- Как определить период вращения планеты вокруг своей оси?
- Методы определения периода вращения
- Метод визуального наблюдения
- Метод использования датчиков световых вспышек
- Метод изучения поверхности планеты
- Общий итог
Как определить период вращения планеты вокруг своей оси

Период вращения планеты — это важная характеристика, которая помогает определить такие параметры, как длина дня, скорость ветра, сила гравитации и т.д. Хотя существует множество методов для определения периода вращения планеты, мы рассмотрим четыре основных способа.
Способ 1: Следить за движением звезд на небе
Один из самых древних способов измерения периода вращения планеты — это наблюдение за движением звезд на небе. Предположим, что мы находимся на одной из полюсных зон планеты и хотим определить ее период вращения вокруг своей оси. Тогда мы можем выбрать некоторую звезду фиксированной яркости, которая находится поблизости от небесного полюса и следить за ее перемещением на небосводе. Если мы начинаем наблюдать за звездой в определенный момент времени и фиксируем момент, когда звезда возвращается в исходное положение, то мы можем определить время, за которое планета совершает один полный оборот вокруг своей оси.
Способ 2: Использование спутниковых данных
Современные технологии спутниковой связи позволяют определять период вращения планеты с большой точностью. Для этого необходимо использовать данные, полученные от спутников, которые вращаются в орбите планеты. При сборе данных спутники фиксируют изменение электромагнитной радиации, которое происходит в зависимости от положения спутника. Затем эта информация анализируется с помощью компьютерных алгоритмов, чтобы определить период вращения планеты.
Способ 3: Измерение силы гравитации

Еще один способ определения периода вращения планеты — это измерение силы гравитации на ее поверхности. Один из инструментов для этого — гравиметр, который измеряет изменение силы притяжения между ним и планетой при изменении расстояния между ними. Информация, полученная с помощью гравиметра, может помочь определить период вращения планеты, так как сила притяжения зависит от расстояния между гравиметром и центром планеты, которое меняется в соответствии с периодом вращения планеты.
Способ 4: Использование телескопов и других оптических приборов
Телескопы и другие оптические приборы также могут использоваться для измерения периода вращения планеты. Например, если мы наблюдаем за планетой через телескоп и фиксируем момент, когда какая-то зона поверхности планеты проходит через центр телескопа, мы можем определить, сколько времени потребуется планете, чтобы выполнить полный оборот вокруг своей оси. Аналогичным способом можно использовать датчики света и тени для измерения периода вращения планеты.
Итог
Таким образом, существует множество способов для определения периода вращения планеты вокруг своей оси. Каждый из них имеет свои преимущества и недостатки и выбор конкретного метода зависит от разных факторов, таких как точность, доступность и исполнение. Независимо от того, какой метод вы выберете, помните, что определение периода вращения планеты — это важный шаг в изучении ее свойств и характеристик.
Как определить период вращения планеты вокруг своей оси
Планеты, как мы знаем, вращаются вокруг своей оси, что определяет период вращения. Наука о планетах и их движении — астрономия — позволяет определить период вращения каждой планеты. В этой статье мы рассмотрим, как это делается.
1. Наблюдение

Первым шагом для определения периода вращения планеты является наблюдение. Существует несколько способов наблюдения:
- Наблюдение через телескоп
- Наблюдение через космические аппараты
- Наблюдение через радиотелескопы
Наблюдение через телескоп может дать наиболее точные результаты, но требует хороших погодных условий и качественного оборудования. Наблюдение через космические аппараты находится на другом уровне, но достаточно дорого и доступно в очень ограниченном круге.
2. Определение северно-западного края

Для определения периода вращения планеты необходимо найти северно-западный край ее поверхности. Планеты изменяют свое положение каждый день относительно солнца и поэтому северно-западный край тоже может изменять свое положение. Чтобы избежать путаницы при определении северно-западного края, следует использовать карту планеты, на которой отмечены контуры поверхности.
3. Измерение движения северно-западного края
После определения северно-западного края планеты необходимо измерить ее движение. Это можно сделать, измерив, сколько времени проходит от одного прохода северно-западного края до следующего прохода. Для определения времени можно использовать специальный секундомер или программу для компьютера.
4. Вычисление периода вращения
После того, как было измерено движение северно-западного края и прошло достаточно времени, можно вычислить период вращения планеты. Для этого можно использовать следующую формулу:
Период вращения = время между проходами / количество проходов
Например, если время между проходами составляет 20 часов, а количество проходов равно 10, то период вращения будет равен 2 часам.
5. Факторы, влияющие на период вращения
Период вращения планеты может быть изменен несколькими факторами, как то:
- Внутренние геологические процессы
- Изменение массы планеты
- Воздействие спутников
- Ряд других факторов
Для точного измерения необходимо учитывать эти факторы. Не смотря на то, что изменение периода вращения может быть небольшим, он может иметь важное значение для исследования планеты и ее движения.
6. Вывод
Определение периода вращения планеты вокруг своей оси является важным фактором для астрономов и других ученых, и позволяет дать более точное представление о движении планеты и ее окружении. Несмотря на то, что измерение периода вращения может быть достаточно сложной задачей, использование современных методов и оборудования делает задачу более простой и точной.
Как определить период вращения планеты вокруг своей оси?
Наблюдая за планетами, мы можем заметить, что они вращаются вокруг своей оси. Это движение мы можем наблюдать, если только планета не имеет очень медленного или, наоборот, очень быстрого вращения. Определение периода вращения планеты может быть простым делом, если использовать различные методы. Найдите ниже описание нескольких простых методов для определения периода вращения планеты.
Методы определения периода вращения
- 1. Метод визуального наблюдения.
- 2. Метод использования датчиков световых вспышек.
- 3. Метод изучения поверхности планеты.
Далее мы рассмотрим каждый из этих методов подробнее.
Метод визуального наблюдения
Метод визуального наблюдения — один из самых простых и доступных методов для определения периода вращения. Для использования этого метода, нужно наблюдать за планетой, используя телескоп. Нежелательно наблюдать за планетой при полном освещении, когда вокруг ярко. Это может сделать наблюдения труднее или вообще невозможными. Лучше всего выбрать момент, когда планета находится в полутени.
Определение периода вращения планеты с помощью визуального наблюдения достаточно просто. Нужно просто зафиксировать время, когда пятна на поверхности планеты возвращаются к исходному положению.
Метод использования датчиков световых вспышек
Датчики световых вспышек могут быть использованы для определения периода вращения планеты. Для этого нужно установить датчик на поверхности планеты и выпустить его на планету.

Когда датчик опускается на поверхность планеты, он будет регистрировать любые световые перепады, которые могут происходить на поверхности планеты во время ее вращения. Эти перепады помогут определить период вращения.
Метод изучения поверхности планеты
Метод изучения поверхности планеты также может быть использован для определения периода вращения. Для этого нужно изучить характеристики поверхности планеты, такие как ее географические особенности и поверхностные отметки. Эти характеристики могут помочь установить, скорее всего, длительность периода вращения планеты. Однако, этот метод может быть сложным, требующим много времени и ресурсов для сбора и анализа данных.
Общий итог

Таким образом, методы определения периода вращения планеты могут быть различными и требуют различных подходов. Выбор подходящего метода может зависеть от доступности ресурсов и инструментов. Однако, любой, даже самый простой метод, может дать важную информацию о планете и ее вращении. Изучая эти методы, мы можем лучше понять нашу вселенную и ее динамику.
Инженер-констриктор
Высший разум
(189516)
11 лет назад
Подобной формулы не существует.
Можно только дать оценку нижней и верхней границ возможных значений.
Период не может быть меньше примерно полутора часов для землеподобных планет и около трёх часов – для газовых гигантов.
А больше – сколько угодно.
P.S. очевидно, что и моменты импульсов тоже ограничены, например, массой исходного протопланетного диска, и поэтому для большинства планет должны быть близки, если считать, что звёзды сбрасывают примерно одинаковые массы оболочек (плюс-минус порядок)
П В
Мыслитель
(6347)
11 лет назад
Чисто визуально это определяется, т. е. по фотоснимкам. Вращение Венеры вообще только радиоволнами “прощупать” смогли, вращение дальних планет Вояджеры показали, при ближайшем пролете…
Трудное детство
Оракул
(70151)
11 лет назад
cвоим вращением вокруг оси планета обязана суммарному моменту количесва движения тех молекул газа и пылинок из которых она образовалась. т. к. скорости молекул и пылинок относительно центра тяжести протопланетного облака и растояния от них до этого центра совершенно хаотические, то невозможно аналитически расчитать каким будет момент количества движения у планеты. приобретя его в процессе формирования, в дальнейшем планета сохраняет его. изменить его может только столкновение с другим небесным телом достаточно большой массы. искомый вами алгоритм не существует.
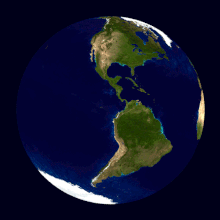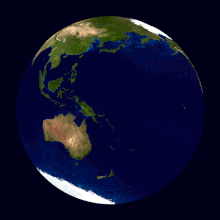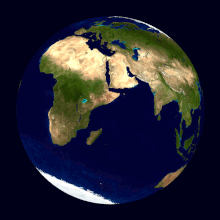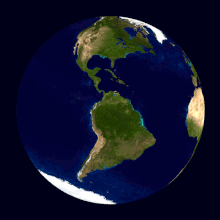
Направление суточного вращения

Фото звёздного неба c Земли при многочасовой экспозиции — иллюстрация вращения Земли вокруг своей оси. Видно северный полюс мира
Су́точное враще́ние Земли́ вокруг своей оси происходит с периодом в одни звёздные сутки. Наблюдаемым проявлением вращения Земли является суточное вращение небесной сферы.
Вращение Земли происходит в том же направлении, что и её движение вокруг Солнца: если смотреть с северной стороны, против часовой стрелки (то есть с запада на восток).
История[править | править код]
История идей о суточном вращении Земли:
Античность[править | править код]
Объяснение суточного вращения небосвода вращением Земли вокруг оси впервые было предложено представителями пифагорейской школы, сиракузянами Гикетом и Экфантом. Согласно некоторым реконструкциям, вращение Земли утверждал также пифагореец Филолай из Кротона[1] (V век до н. э.). Высказывание, которое можно трактовать как указание на вращение Земли, содержится в Платоновском диалоге Тимей[2].
Однако о Гикете и Экфанте практически ничего неизвестно, и даже само их существование иногда подвергается сомнению[3]. Согласно мнению большинства ученых, Земля в системе мира Филолая совершала не вращательное, а поступательное движение вокруг Центрального огня. В других своих произведениях Платон следует традиционному мнению о неподвижности Земли. Однако до нас дошли многочисленные свидетельства, что идею вращения Земли отстаивал философ Гераклид Понтийский (IV век до н. э.)[4]. Вероятно, с гипотезой о вращении Земли вокруг оси связано ещё одно предположение Гераклида: каждая звезда представляет собой мир, включающий землю, воздух, эфир, причем всё это располагается в бесконечном пространстве. Действительно, если суточное вращение неба является отражением вращения Земли, то исчезает предпосылка считать звезды находящимися на одной сфере.
Примерно столетие спустя предположение о вращении Земли стало составной частью первой гелиоцентрической системы мира, предложенной великим астрономом Аристархом Самосским (III век до н. э.)[5]. Аристарха поддержал вавилонянин Селевк (II век до н. э.)[6], также, как и Гераклид Понтийский, считавший Вселенную бесконечной. О том, что идея суточного вращения Земли имела своих сторонников ещё в I веке н. э., свидетельствуют некоторые высказывания философов Сенеки, Деркиллида, астронома Клавдия Птолемея[7]. Подавляющее большинство астрономов и философов, однако, не сомневалось в неподвижности Земли.
Аргументы против идеи движения Земли имеются в произведениях Аристотеля и Птолемея. Так, в своем трактате О Небе Аристотель обосновывает неподвижность Земли тем, что на вращающейся Земле брошенные вертикально вверх тела не могли бы упасть в ту точку, из которой началось их движение: поверхность Земли сдвигалась бы под брошенным телом[8]. Другой довод в пользу неподвижности Земли, приводимый Аристотелем, основан на его физической теории: Земля является тяжелым телом, а для тяжелых тел свойственно движение к центру мира, а не вращение вокруг него.
Одним из доводов Птолемея в пользу неподвижности Земли является вертикальность траекторий падающих тел, как и у Аристотеля. Далее, он отмечает, что при вращении Земли должны наблюдаться явления, которые на самом деле не происходят:
все не закрепленные на ней [Земле] предметы должны совершать одно и то же движение, [по направлению] противоположное земному. Таким образом, мы никогда не могли бы видеть какое-нибудь идущее к востоку облако или брошенное в том же направлении тело, так как Земля в своем движении к востоку опережала бы все тела. Они казались бы нам движущимися к западу и отстающими от движения Земли[9].
Из сочинения Птолемея следует, что сторонники гипотезы вращения Земли на эти доводы отвечали, что и воздух и все земные предметы совершают движение вместе с Землей. По всей видимости, роль воздуха в этом рассуждении принципиально важна, поскольку подразумевается, что именно его движение вместе с Землей скрывает вращение нашей планеты. Птолемей на это возражает, что
находящиеся в воздухе тела всегда будут казаться отстающими… А если бы тела вращались вместе с воздухом как одно целое, то никакое из них не казалось бы опережающим другое или отстающим от него, но оставалось бы на месте, в полете и бросании оно не совершало бы отклонений или движений в другое место вроде тех, которые мы воочию видим совершающимися, и у них вообще не происходило бы замедления или ускорения, оттого что Земля не является неподвижной[10].
Средние века[править | править код]
- Индия
Первым из средневековых авторов, высказавший предположение о вращении Земли вокруг оси, был великий индийский астроном и математик Ариабхата (кон. V — нач. VI вв.). Он формулирует её в нескольких местах своего трактата Ариабхатия, например:
Точно также, как человек на движущемся вперед корабле видит закрепленные объекты движущимися назад, так и наблюдатель… видит неподвижные звезды движущимися по прямой линии на запад[11].
Неизвестно, принадлежит ли эта идея самому Ариабхате или он её заимствовал у древнегреческих астрономов[12].
Ариабхату поддержал только один астроном, Пртхудака (IX век)[13]. Большинство индийских ученых отстаивало неподвижность Земли. Так, астроном Варахамихира (VI в.) утверждал, что на вращающейся Земле летящие в воздухе птицы не могли бы вернуться к своим гнездам, а камни и деревья слетали бы с поверхности Земли. Выдающийся астроном Брахмагупта (VI в.) повторил также старый аргумент, что тело, упавшее с высокой горы, но смогло бы опуститься к её основанию. При этом он, однако, отверг один из доводов Варахамихиры: по его мнению, даже если бы Земля вращалась, предметы не могли бы оторваться от неё вследствие своей тяжести.
- Исламский Восток
Возможность вращения Земли рассматривали многие ученые мусульманского Востока. Так, известный геометр ас-Сиджизи изобрел астролябию, принцип действия которой основан на этом предположении[14]. Некоторые исламские ученые (имена которых до нас не дошли) даже нашли правильный способ опровержения основного довода против вращения Земли: вертикальности траекторий падающих тел. По существу, при этом был высказан принцип суперпозиции движений, согласно которому любое перемещение можно разложить на два или несколько составляющих: по отношению к поверхности вращающейся Земли падающее тело двигается по отвесной линии, но точка, являющаяся проекцией этой линии на поверхность Земли, переносится бы её вращением. Об этом свидетельствует знаменитый ученый-энциклопедист ал-Бируни, который сам, однако, склонялся к неподвижности Земли. По его мнению, если на падающее тело будет действовать какая-то дополнительная сила, то результат её действия на вращающейся Земле приведет к некоторым эффектам, которые на самом деле не наблюдаются[15].
Среди ученых XIII—XVI веков, связанных с Марагинской и Самаркандской обсерваториями, развернулась дискуссия о возможности эмпирического обоснования неподвижности Земли. Так, известный астроном Кутб ад-Дин аш-Ширази (XIII—XIV вв.) полагал, что неподвижность Земли может быть удостоверена экспериментом. С другой стороны, основатель Марагинской обсерватории Насир ад-Дин ат-Туси полагал, что если бы Земля вращалась, то это вращение разделял бы слой воздуха, прилегающий к её поверхности, и все движения вблизи поверхности Земли происходили бы точно также, как если бы Земля была неподвижной. Он это обосновывал с помощью наблюдений комет: согласно Аристотелю, кометы являются метеорологическим явлением в верхних слоях атмосферы; тем не менее, астрономические наблюдения показывают, что кометы принимают участие в суточном вращении небесной сферы. Следовательно, верхние слои воздуха увлекаются вращением небосвода, поэтому и нижние слои также могут увлекаться вращением Земли. Таким образом, эксперимент не может дать ответ на вопрос о том, вращается ли Земля. Однако он оставался сторонником неподвижности Земли, поскольку это соответствовало философии Аристотеля.
Большинство исламских учёных более позднего времени (аль-Урди, аль-Казвини, ан-Найсабури, ал-Джурджани, ал-Бирджанди и другие) были согласны с ат-Туси, что все физические явления на вращающейся и неподвижной Землей проистекали бы одинаково. Однако роль воздуха при этом уже не считалась принципиальной: не только воздух, но и все предметы переносятся вращающейся Землей. Следовательно, для обоснования неподвижности Земли необходимо привлекать учение Аристотеля.
Особую позицию в этих спорах занял третий директор Самаркандской обсерватории Алауддин Али аль-Кушчи (XV в.), отвергавший философию Аристотеля и считавший вращение Земли физически возможным[16]. В XVII веке к аналогичному выводу пришел иранский теолог и ученый-энциклопедист Баха ад-Дин ал-Амили. По его мнению, астрономы и философы не представили достаточных доказательств, опровергающих вращение Земли[17].
- Латинский Запад
Подробное обсуждение возможности движения Земли широко содержится в сочинениях парижских схоластов Жана Буридана[18], Альберта Саксонского[19], и Николая Орема[20] (вторая половина XIV в.). Важнейшим аргументом в пользу вращения Земли, а не неба, приведенным в их работах, является малость Земли по сравнению со Вселенной, что делает приписывание суточного вращения небосвода Вселенной в высшей степени противоестественным.
Однако все эти ученые в конечном итоге отвергли вращение Земли, хотя и на разных основаниях. Так, Альберт Саксонский полагал, что эта гипотеза не способна объяснить наблюдаемые астрономические явления. С этим справедливо не согласились Буридан и Орем, по мнению которых небесные явления должны происходить одинаково независимо от того, что совершает вращение, Земля или Космос. Буридан смог найти только один существенный довод против вращения Земли: стрелы, пускаемые вертикально вверх, падают вниз по отвесной линии, хотя при вращении Земли они, по его мнению, должны были бы отставать от движения Земли и падать к западу от точки выстрела.

Но даже и этот довод был отвергнут Оремом. Если Земля вращается, то стрела летит вертикально вверх и одновременно с этим движется на восток, будучи захваченная воздухом, вращающимся вместе с Землей. Таким образом, стрела должна упасть на то же место, откуда она была выпущена. Хотя здесь снова упоминается об увлекающей роли воздуха, в действительности он не играет особой роли. Об этом говорит следующая аналогия:
Подобным образом, если бы воздух был закрыт в движущемся судне, то человеку, окруженному этим воздухом, показалось бы, что воздух не движется… Если бы человек находился в корабле, движущемся с большой скоростью на восток, не зная об этом движении, и если бы он вытянул руку по прямой линии вдоль мачты корабля, ему бы показалось, что его рука совершает прямолинейное движение; точно так же, согласно этой теории, нам представляется, что такая же вещь происходит со стрелой, когда мы пускаем её вертикально вверх или вертикально вниз. Внутри корабля, движущегося с большой скоростью на восток, могут иметь место все виды движения: продольное, поперечное, вниз, вверх, во всех направлениях — и они кажутся точно такими же, как тогда, когда корабль пребывает неподвижным[21].
Далее Орем приводит формулировку, предвосхищающую принцип относительности:
Я заключаю, следовательно, что с помощью какого бы то ни было опыта невозможно продемонстрировать, что небеса имеют суточное движение и что Земля его не имеет[22].
Тем не менее, окончательный вердикт Орема о возможности вращения Земли был отрицательным. Основанием для такого вывода был текст Библии:
Однако до сих пор все поддерживают и я верю, что они [Небеса], а не Земля движется, ибо «Бог сотворил круг Земли, который не поколеблется», несмотря на все противоположные аргументы[23].
О возможности суточного вращения Земли упоминали и средневековые европейские ученые и философы более позднего времени, однако никаких новых аргументов, не содержавшихся у Буридана и Орема, добавлено не было.
Таким образом, практически никто из средневековых ученых так и не принял гипотезу о вращении Земли. Однако в ходе её обсуждения учеными Востока и Запада было высказано множество глубоких мыслей, которые потом будут повторены учеными Нового времени.
Эпоха Возрождения и Новое время[править | править код]

В первой половине XVI века увидели свет несколько сочинений, утверждавших, что причиной суточного вращения небосвода является вращение Земли вокруг оси. Одним из них был трактат итальянца Челио Кальканьини «О том, что небо неподвижно, а Земля вращается, или о вечном движении Земли» (написан около 1525 г., издан в 1544 г.). Он не произвел большого впечатления на современников, поскольку к тому времени уже был опубликован фундаментальный труд польского астронома Николая Коперника «О вращениях небесных сфер» (1543 г.), где гипотеза суточного вращения Земли у него стала частью гелиоцентрической системы мира, как у Аристарха Самосского. Свои мысли Коперник ранее изложил в небольшом рукописном сочинении Малый Комментарий (не ранее 1515 г.). Два года ранее основного труда Коперника вышло сочинение немецкого астронома Георга Иоахима Ретика Первое повествование (1541 г.), где популярно изложена теория Коперника.
В XVI веке Коперника полностью поддержали астрономы Томас Диггес, Ретик, Кристоф Ротман, Михаэль Мёстлин, физики Джамбатиста Бенедетти, Симон Стевин, философ Джордано Бруно, богослов Диего де Цунига[24]. Некоторые учёные принимали вращение Земли вокруг оси, отвергая её поступательное движение. Такова была позиция немецкого астронома Николаса Реймерса, известного также как Урсус, а также итальянских философов Андреа Чезальпино и Франческо Патрици. Не совсем ясна точка зрения выдающегося физика Вильяма Гильберта, который поддержал осевое вращение Земли, но не высказывался по поводу её поступательного движения. В начале XVII века гелиоцентрическая система мира (включая вращение Земли вокруг оси) получила внушительную поддержку со стороны Галилео Галилея и Иоганна Кеплера. Наиболее влиятельными противниками идеи движения Земли в XVI — начале XVII века были астрономы Тихо Браге и Христофор Клавиус.
- Гипотеза о вращении Земли и становление классической механики
По существу, в XVI—XVII вв. единственным аргументом в пользу осевого вращения Земли было то, что в этом случае отпадает надобность в приписывании звездной сфере огромных скоростей вращения, ведь ещё в античности уже было надежно установлено, что размер Вселенной значительно превышает размер Земли (этот аргумент содержался ещё у Буридана и Орема).
Против этой гипотезы высказывались соображения, основанные на динамических преставлениях того времени. Прежде всего, это вертикальность траекторий падающих тел[25]. Появились и другие доводы, например, равная дальность стрельбы в восточном и западном направлениях. Отвечая на вопрос о ненаблюдаемости эффектов суточного вращения в земных экспериментах, Коперник писал:
Вращается не только Земля с соединенной с ней водной стихией, но также и немалая часть воздуха и все, что каким-либо образом сродно с Землёй, или уже ближайший к Земле воздух пропитанный земной и водной материей, следует тем же самым законам природы, что и Земля, или имеет приобретенное движение, которое сообщается ему прилегающей Землей в постоянном вращении и без всякого сопротивления[26]
Таким образом, главную роль в ненаблюдаемости вращения Земли играет увлечение воздуха её вращением. Такого же мнения придерживались и большинство коперниканцев в XVI веке.
Однако уже у Диггеса и Бруно появились и другие соображения: все земные тела разделяют движение Земли, воздух не играет особой роли. Они это выразили с помощью аналогии с процессами на движущемся корабле: если человек, находящийся на мачте движущегося корабля, бросит вертикально вниз камень, он падет к основанию мачты, как бы быстро корабль ни двигался, лишь бы без качки. Воздух не играет особой роли в этих рассуждениях (необходимо добавить, что такого же рода рассуждения были уже и Орема, ал-Кушчи и других средневековых ученых). При опровержении доводов противников гипотезы о вращении Земли Бруно использовал также теорию импетуса.
Позднее Галилей, рассмотрев много примеров относительности движения, обобщил их и пришел к принципу относительности: движение Земли, корабля или любого другого тела вообще не сказывается на протекающих на них процессах, если это движение равномерное. Пьер Гассенди в 1642 г. выполнил эксперимент по падению тяжести с мачты движущегося корабля и непосредственно убедился в правоте коперниканцев: независимо от скорости движения, груз падал к основанию мачты (возможно, ещё раньше такой эксперимент проделывали Диггес и Галилей)[27].

Однако сам Галилей (руководствуясь, правда, не совсем ясными соображениями) указал, что ввиду сферичности Земли камень, падающий с высокой башни, упадет не точно к основанию и тем более недалеко позади него (как считали противники гипотезы о вращении Земли), но немного впереди основания (то есть к востоку)[28]. В 1679 г. Исаак Ньютон показал с помощью вычислений, что камень действительно должен упасть немного к востоку от основания башни, хотя и ошибся в величине эффекта (точное значение установил только Гаусс в начале XIX века). Он предложил провести такой эксперимент с целью подтверждения или опровержения гипотезы о вращении Земли. Эта идея была реализована только в конце XVIII — начале XIX века, послужив одним из первых экспериментальных свидетельств в пользу вращения Земли вокруг оси.
Другой популярный аргумент против вращения Земли заключался в том, что скорость вращения Земли должна быть настолько велика, что Земля испытывала бы колоссальные центробежные силы, которые разорвали бы её на части, а все находящиеся на её поверхности лёгкие предметы разлетелись бы во все стороны Космоса. Коперник не смог дать на это удовлетворительного ответа, отделавшись замечанием, что этот аргумент ещё более приложим ко Вселенной, «движение которой должно быть во столько раз быстрее, во сколько раз небо больше Земли», и что поскольку вращение Земли происходит «по природе», центробежная сила не угрожает Земле и земным предметам. Галилей, произведя вычисление центробежной силы, заключил, что она бесконечно мала по сравнению с силой тяжести на земной поверхности, так что она практически не сказывается на движении земных тел. Однако его вычисления содержали ошибку, которую устранил только Христиан Гюйгенс (1673 г.), окончательно доказав, что центробежная сила действительно слишком мала, чтобы способствовать распаду Земли или отбрасыванию с её поверхности незакрепленных предметов. Он же предсказал, что из-за действия центробежной силы Земля должна быть сплющена у полюсов.

- Гипотеза о вращении Земли и новая космология
Идея вращения Земли заставила пересмотреть не только механику, но и космологию. В традиционной геоцентрической системе мира обычно предполагалось, что звезды расположены на одной сфере конечного размера. Такого же мнения придерживался и Коперник. Однако если суточное вращение неба является отражением вращения Земли, то исчезает предпосылка считать звезды находящимися на одной сфере. Неудивительно, что многие (хотя и не все) сторонники вращения Земли считали звезды рассеянными по всему пространству и Вселенную — бесконечной[29]. Такой вывод в явном виде был сформулирован выдающимся английским физиком Вильямом Гильбертом, сторонником гипотезы вращающейся Земли. В своем сочинении О магните (1600 г.) он пишет о несовместимости космологии безграничной Вселенной с существованием вращения небосвода:
Невероятно, чтобы высочайшее небо и все это зримое великолепие неподвижных звезд направлялось по этому чрезвычайно быстрому и бесполезному пути[30]… Нет никакого сомнения в том, что также, как планеты находятся на неодинаковом расстоянии от Земли, так и эти обширные и многочисленные светила отстоят от Земли на различные и очень большие расстояния… Каким образом могли бы они сохранять своё положение, подхваченные столь стремительным вращением огромной сферы, состоящей из столь неопределенной субстанции…
Каким же бесконечным должно быть тогда пространство, которое тянется до самых этих отдаленнейших звезд!.. Каким чудовищным было бы тогда совершаемое движение!.. Если им [звездам] присуще движение, то оно будет скорее движением каждой из них вокруг её собственного центра, как это происходит с Землей, либо движением вперед от своего центра по орбите, как это происходит с Луной. Но движение бесконечности и бесконечного тела невозможно и, следовательно, нет суточного обращения Перводвигателя[31].
Сторонниками бесконечности Вселенной в XVI веке были также Томас Диггес, Джордано Бруно, Франческо Патрици — все они поддерживали гипотезу о вращении Земли вокруг оси (а первые двое — также вокруг Солнца). Кристоф Ротман и Галилео Галилей полагали звезды расположенными на разных расстояниях от Земли, хотя явно не высказывались по поводу бесконечности Вселенной. С другой стороны, Иоганн Кеплер отрицал бесконечность Вселенной, хотя и был сторонником вращения Земли.
- Религиозный контекст споров о вращении Земли
Ряд возражений против вращения Земли был связан с её противоречиями тексту Священного Писания. Эти возражения были двух видов. Во-первых, некоторые места в Библии приводились в подтверждение того, что суточное движение совершает именно Солнце, например:
Восходит солнце и заходит солнце, и спешит к месту своему, где оно восходит[32].
В данном случае под удар попадало осевое вращение Земли, поскольку движение Солнца с востока на запад является частью суточного вращения небосвода. Часто в этой связи цитировался отрывок из книги Иисуса Навина:
Иисус воззвал к Господу в тот день, в который предал Господь Аморрея в руки Израилю, когда побил их в Гаваоне, и они побиты были пред лицем сынов Израилевых, и сказал пред Израильтянами: стой, солнце, над Гаваоном, и луна, над долиною Авалонскою[33]!
Поскольку команда остановиться была дана Солнцу, а не Земле, отсюда делался вывод, что суточное движение совершает именно Солнце. Другие отрывки приводились в поддержку неподвижности Земли, например:
Ты поставил землю на твердых основах: не поколеблется она во веки и веки[34].
Эти отрывки считались противоречащими как мнению о вращении Земли вокруг оси, так и обращению вокруг Солнца.
Сторонники вращения Земли (в частности, Джордано Бруно, Иоганн Кеплер[35] и особенно Галилео Галилей[36]) проводили защиту по нескольким направлениям. Во-первых, они указывали, что Библия написана языком, понятным простым людям, и если бы её авторы давали четкие с научной точки зрения формулировки, она не смогла бы выполнять свою основную, религиозную миссию[37]. Так, Бруно писал:
Во многих случаях глупо и нецелесообразно приводить много рассуждений скорее в соответствии с истиной, чем соответственно данному случаю и удобству. Например, если бы вместо слов: «Солнце рождается и поднимается, переваливает через полдень и склоняется к Аквилону» — мудрец сказал: «Земля идет по кругу к востоку и, покидая солнце, которое закатывается, склоняется к двум тропикам, от Рака к Югу, от Козерога к Аквилону», — то слушатели стали бы раздумывать: «Как? Он говорит, что Земля движется? Что это за новости?» В конце концов они его сочли бы за глупца, и он действительно был бы глупцом[38].
Такого рода ответы давались в основном на возражения, касавшиеся суточного движения Солнца. Во-вторых, отмечалось, что некоторые отрывки Библии должны быть трактованы аллегорически (см. статью Библейский аллегоризм). Так, Галилей отмечал, что если Св. Писание целиком понимать буквально, то окажется, что у Бога есть руки, он подвержен эмоциям типа гнева и т. п. В целом, главной мыслью защитников учения о движении Земли было то, что наука и религия имеют разные цели: наука рассматривает явления материального мира, руководствуясь доводами разума, целью религии является моральное усовершенствование человека, его спасение. Галилей в этой связи цитировал кардинала Баронио, что Библия учит тому, как взойти на небеса, а не тому, как устроены небеса.
Эти доводы были сочтены католической церковью неубедительными, и в 1616 г. учение о вращении Земли было запрещено, а в 1631 г. Галилей был осужден судом инквизиции за его защиту. Однако за пределами Италии этот запрет не оказал существенного влияния на развитие науки и способствовал главным образом падению авторитета самой католической церкви.
Необходимо добавить, что религиозные доводы против движения Земли приводили не только церковные деятели, но и ученые (например, Тихо Браге[39]). С другой стороны, католический монах Паоло Фоскарини написал небольшое сочинение «Письмо о воззрениях пифагорейцев и Коперника на подвижность Земли и неподвижность Солнца и о новой пифагорейской системе мироздания» (1615 г.), где высказывал соображения, близкие к галилеевским, а испанский богослов Диего де Цунига даже использовал теорию Коперника для толкования некоторых мест Священного Писания (хотя впоследствии он изменил своё мнение). Таким образом, конфликт между богословием и учением о движении Земли был не столько конфликтом между наукой и религией как таковыми, сколько конфликтом между старыми (к началу XVII века уже устаревшими) и новыми методологическими принципами, полагаемыми в основу науки.
- Значение изучения суточного вращения Земли для развития науки
Осмысление научных проблем, поднимаемых теорией вращающейся Земли, способствовало открытию законов классической механики и созданию новой космологии, в основе которой лежит представление о безграничности Вселенной. Обсуждавшиеся в ходе этого процесса противоречия между этой теорией и буквалистским прочтением Библии способствовали размежеванию естествознания и религии.
Период и скорость вращения[править | править код]

Почему звёздные сутки не равны солнечным. 1-2 — звёздные сутки, 1-3 — солнечные.
где 

- Самолёт, летящий с этой скоростью с востока на запад (на высоте 12 км: 936 км/ч на широте Москвы, 837 км/ч на широте Санкт-Петербурга), в инерциальной системе отсчёта будет покоиться.
- Суперпозиция вращения Земли вокруг оси с периодом в одни звёздные сутки и вокруг Солнца с периодом в один год приводит к неравенству солнечных и звёздных суток: длина средних солнечных суток составляет ровно 24 часа, что на 3 минуты 56 секунд длиннее звёздных суток.
Используемые в России понятия параметров вращения Земли и параметров ориентации Земли несколько отличаются от международных, эти терминологические различия необходимо учитывать при чтении и переводе зарубежной литературы[40].
Физический смысл и экспериментальные подтверждения[править | править код]
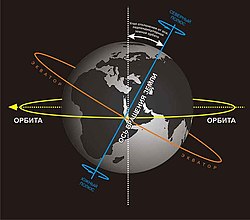
Наклон земной оси по отношению к плоскости эклиптики (плоскости орбиты Земли)
Физический смысл вращения Земли вокруг оси[править | править код]
Поскольку любое движение является относительным, необходимо указывать конкретную систему отсчёта, относительно которой изучается движение того или иного тела. Когда говорят, что Земля вращается вокруг воображаемой оси, имеется в виду, что она совершает вращательное движение относительно любой инерциальной системы отсчёта, причем период этого вращения равен звездным суткам — периоду полного оборота Земли (небесной сферы) относительно небесной сферы (Земли).
Все экспериментальные доказательства вращения Земли вокруг оси сводятся к доказательству того, что система отсчёта, связанная с Землей, является неинерциальной системой отсчёта специального вида — системой отсчёта, совершающей вращательное движение относительно инерциальных систем отсчёта.
В отличие от инерциального движения (то есть равномерного прямолинейного движения относительно инерциальных систем отсчёта), для обнаружения неинерциального движения замкнутой лаборатории не обязательно производить наблюдения над внешними телами, — такое движение обнаруживается с помощью локальных экспериментов (то есть экспериментов, произведенных внутри этой лаборатории). В этом смысле слова неинерциальное движение, включая вращение Земли вокруг оси, может быть названо абсолютным.
Силы инерции[править | править код]

Центробежная сила на вращающейся Земле
В неинерциальных системах отсчёта второй закон Ньютона записывается следующим образом:

где 





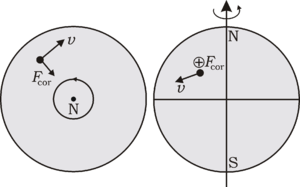
Направление силы Кориолиса на вращающейся Земле
Центробежная сила, действующая на тело массы 

где 



где 


Эффекты центробежной силы[править | править код]
Зависимость ускорения свободного падения от географической широты. Эксперименты показывают, что ускорение свободного падения зависит от географической широты: чем ближе к полюсу, тем оно больше. Это объясняется действием центробежной силы. Во-первых, точки земной поверхности, расположенные на более высоких широтах, ближе к оси вращения и, следовательно, при приближении к полюсу расстояние 
Это явление было открыто в 1672 году, когда французский астроном Жан Рише, находясь в экспедиции в Африке, обнаружил, что у экватора маятниковые часы идут медленнее, чем в Париже. Ньютон вскоре объяснил это тем, что период колебаний маятника обратно пропорционален квадратному корню из ускорения свободного падения, которое уменьшается на экваторе из-за действия центробежной силы.
Сплюснутость Земли. Влияние центробежной силы приводит к сплюснутости Земли у полюсов. Это явление, предсказанное Гюйгенсом и Ньютоном в конце XVII века, было впервые обнаружено Пьером де Мопертюи в конце 1730-х годов в результате обработки данных двух французских экспедиций, специально снаряженных для решения этой проблемы в Перу (под руководством Пьера Бугера и Шарля де ла Кондамина) и Лапландию (под руководством Алексиса Клеро и самого Мопертюи).
Эффекты силы Кориолиса: лабораторные эксперименты[править | править код]

Маятник Фуко на северном полюсе. Ось вращения Земли лежит в плоскости колебаний маятника
Маятник Фуко. Эксперимент, наглядно демонстрирующий вращение Земли, поставил в 1851 году французский физик Леон Фуко. Его смысл наиболее понятен в случае, если маятник закреплен на одном из полюсов Земли. Тогда его плоскость колебаний неизменна относительно инерциальной системы отсчёта, в данном случае относительно неподвижных звёзд. Таким образом, в системе отсчёта, связанной с Землей, плоскость колебаний маятника должна поворачиваться в сторону, противоположную направлению вращения Земли. С точки зрения неинерциальной системы отсчёта, связанной с Землёй, плоскость колебаний маятника Фуко поворачивается под действием силы Кориолиса[42].
Наиболее отчетливо этот эффект должен быть выражен на полюсах, где период полного поворота плоскости маятника равен периоду вращения Земли вокруг оси (звёздным суткам). В общем случае, период обратно пропорционален синусу географической широты[43], на экваторе плоскость колебаний маятника неизменна.
В настоящее время маятник Фуко с успехом демонстрируется в ряде научных музеев и планетариев, в частности, в планетарии Санкт-Петербурга[44], планетарии Волгограда.
Существует ряд других опытов с маятниками, используемых для доказательства вращения Земли[45]. Например, в опыте Браве (1851 г.) использовался конический маятник. Вращение Земли доказывалось тем, что периоды колебаний по и против часовой стрелки различались, поскольку сила Кориолиса в этих двух случаях имела разный знак. В 1853 г. Гаусс предложил использовать не математический маятник, как у Фуко, а физический, что позволило бы уменьшить размеры экспериментальной установки и увеличить точность эксперимента. Эту идею реализовал Камерлинг-Оннес в 1879 г.[уточнить]
Гироскоп — вращающееся тело со значительным моментом инерции сохраняет момент импульса, если нет сильных возмущений. Фуко, которому надоело объяснять, что происходит с маятником Фуко не на полюсе, разработал другую демонстрацию: подвешенный гироскоп сохранял ориентацию, а значит медленно поворачивался относительно наблюдателя[46].
Отклонение снарядов при орудийной стрельбе. Другим наблюдаемым проявлением силы Кориолиса является отклонение траекторий снарядов (в северном полушарии вправо, в южном — влево), выстреливаемых в горизонтальном направлении. С точки зрения инерциальной системы отсчёта, для снарядов, выстреливаемых вдоль меридиана, это связано с зависимостью линейной скорости вращения Земли от географической широты: при движении от экватора к полюсу снаряд сохраняет горизонтальную компоненту скорости неизменной, в то время как линейная скорость вращения точек земной поверхности уменьшается, что приводит к смещению снаряда от меридиана в сторону вращения Земли. Если выстрел был произведён параллельно экватору, то смещение снаряда от параллели связано с тем, что траектория снаряда лежит в одной плоскости с центром Земли, в то время как точки земной поверхности движутся в плоскости, перпендикулярной оси вращения Земли[47]. Этот эффект (для случая стрельбы вдоль меридиана) был предсказан Гримальди в 40-х годах XVII в. и впервые опубликован Риччоли в 1651 г.[48]
Отклонение свободно падающих тел от вертикали.
(подробнее…)
Если скорость движения тела имеет большую вертикальную составляющую, сила Кориолиса направлена к востоку, что приводит к соответствующему отклонению траектории тела, свободно падающего (без начальной скорости) с высокой башни[49]. При рассмотрении в инерциальной системе отсчёта эффект объясняется тем, что вершина башни относительно центра Земли движется быстрее, чем основание[50], благодаря чему траектория тела оказывается узкой параболой, и тело слегка опережает основание башни[51].
Этот эффект был предсказан Борелли в 1667 г. и Ньютоном в 1679 г.[52] Ввиду сложности проведения соответствующих экспериментов эффект удалось подтвердить только в конце XVIII — первой половине XIX века (Гульельмини, 1791; Бенценберг, 1802; Райх, 1831)[53].
Австрийский астроном Иоганн Хаген (1902 г.) осуществил эксперимент, являющийся модификацией этого опыта, где вместо свободно падающих грузов использовалась машина Атвуда. Это позволило снизить ускорение падения, что привело к уменьшению размеров экспериментальной установки и повышению точности измерений[54].
Эффект Этвёша. На низких широтах сила Кориолиса при движении по земной поверхности направлена в вертикальном направлении и её действие приводит к увеличению или уменьшению ускорения свободного падения, в зависимости от того, движется ли тело на запад или восток. Этот эффект назван эффектом Этвёша в честь венгерского физика Лоранда Этвёша, экспериментально обнаружившего его в начале XX века.
Опыты, использующие закон сохранения момента импульса. Некоторые эксперименты основаны на законе сохранения момента импульса: в инерциальной системе отсчёта величина момента импульса (равная произведению момента инерции на угловую скорость вращения) под действием внутренних сил не меняется. Если в некоторый начальный момент времени установка неподвижна относительно Земли, то скорость её вращения относительно инерциальной системы отсчёта равна угловой скорости вращения Земли. Если изменить момент инерции системы, то должна измениться угловая скорость её вращения, то есть начнётся вращение относительно Земли. В неинерциальной системе отсчёта, связанной с Землёй, вращение возникает в результате действия силы Кориолиса. Эта идея была предложена французским учёным Луи Пуансо в 1851 г.
Первый такой эксперимент был поставлен Хагеном в 1910 г.: два груза на гладкой перекладине были установлены неподвижно относительно поверхности Земли. Затем расстояние между грузами было уменьшено. В результате установка пришла во вращение[55]. Ещё более наглядный опыт поставил немецкий учёный Ханс Букка (Hans Bucka) в 1949 г. Стержень длиной примерно 1,5 метра был установлен перпендикулярно прямоугольной рамке. Первоначально стержень был горизонтален, установка была неподвижной относительно Земли. Затем стержень был приведен в вертикальное положение, что привело к изменению момента инерции установки примерно в 104 раз и её быстрому вращению с угловой скоростью, в 104 раз превышающей скорость вращения Земли[56].
Воронка в ванне.
Поскольку сила Кориолиса очень слаба, она оказывает пренебрежимо малое влияние на направление закручивания воды при сливе в раковине или ванне, поэтому в общем случае направление вращения в воронке не связано с вращением Земли. Лишь только в тщательно контролируемых экспериментах можно отделить действие силы Кориолиса от других факторов: в северном полушарии воронка будет закручена против часовой стрелки, в южном — наоборот[57].
Эффекты силы Кориолиса: явления в окружающей природе[править | править код]
Закон Бэра. Как впервые отметил петербургский академик Карл Бэр в 1857 году, реки размывают в северном полушарии правый берег (в южном полушарии — левый), который вследствие этого оказывается более крутым (закон Бэра). Объяснение эффекта аналогично объяснению отклонения снарядов при стрельбе в горизонтальном направлении: под действием силы Кориолиса вода сильнее ударяется в правый берег, что приводит к его размытию, и, наоборот, отступает от левого берега[58]. (См. также Парадокс чайного листа).

Циклон над юго-восточным побережьем Исландии (вид из космоса)
Ветры: пассаты, циклоны, антициклоны. С наличием силы Кориолиса, направленной в северном полушарии вправо и в южном влево, связаны также атмосферные явления: пассаты, циклоны и антициклоны. Явление пассатов вызывается неодинаковостью нагрева нижних слоёв земной атмосферы в приэкваториальной полосе и в средних широтах, приводящему к течению воздуха вдоль меридиана на юг или север в северном и южном полушариях, соответственно. Действие силы Кориолиса приводит к отклонению потоков воздуха: в северном полушарии — в сторону северо-востока (северо-восточный пассат), в южном полушарии — на юго-восток (юго-восточный пассат). (См. также Сила Кориолиса в гидроаэромеханике).
Циклоном называется атмосферный вихрь с пониженным давлением воздуха в центре. Массы воздуха, стремясь к центру циклона, под действием силы Кориолиса закручиваются против часовой стрелки в северном полушарии и по часовой стрелке в южном. Аналогично, в антициклоне, где в центре имеется максимум давления, наличие силы Кориолиса приводит к вихревому движению по часовой стрелке в северном полушарии и против часовой стрелки в южном. В стационарном состоянии направление движения ветра в циклоне или антициклоне таково, что сила Кориолиса уравновешивает градиент давления между центром и периферией вихря (геострофический ветер).
Оптические эксперименты[править | править код]
В основе ряда опытов, демонстрирующих вращение Земли, используется эффект Саньяка: если кольцевой интерферометр совершает вращательное движение, то вследствие релятивистских эффектов[59] во встречных лучах появляется разность фаз
где 


Существует ряд других экспериментальных демонстраций суточного вращения Земли[60].
Неравномерность вращения Земли[править | править код]
Прецессия и нутация[править | править код]
Земля в процессе вращения вокруг своей оси претерпевает прецессию и нутацию, вызванные воздействием Солнца, Луны и планет[40].
Прецессия (позднелат. praecessio — движение впереди, от лат. praecedo — иду впереди, предшествую) — медленное движение вращающегося твёрдого тела, при котором его ось вращения описывает конус. Прецессию Земли открыл во II веке до н. э. древнегреческий учёный Гиппарх[40].
Прецессия Земли называется также предварением равноденствий, так как она вызывает медленное смещение точек весеннего и осеннего равноденствий, обусловленное движением плоскостей эклиптики и небесного экватора (точки равноденствия определяются линией пересечения этих плоскостей). Упрощённо прецессию можно представить как медленное движение оси мира (прямой, параллельной средней оси вращения Земли) по круговому конусу, ось которого перпендикулярна к эклиптике, с периодом полного оборота около 26 000 лет[61].
Прецессия земной оси вызвана в основном действием гравитации Луны и (в меньшей степени) Солнца на экваториальную выпуклость Земли[62][40].
Нутация (от лат. nūtāre лат. nutatio — колебание) — происходящее одновременно с прецессией движение вращающегося твёрдого тела, при котором изменяется угол между осью собственного вращения тела и осью, вокруг которой происходит прецессия; этот угол называется углом нутации (см. Углы Эйлера). В случае Земли нутационные колебания, открытые в 1737 Дж. Брадлеем, обусловлены изменениями притяжения, оказываемого Луной и Солнцем на так называемый экваториальный избыток массы вращающейся Земли (который является следствием сжатия Земли), и называются лунно-солнечной, или вынужденной нутацией[63][40].
Существует также свободная нутация, то есть свободное движение географических полюсов по кривой, близкой к окружности, с периодом 1,2 года, обусловленное тем, что Земля как целое смещается в пространстве относительно оси вращения.
В целом, причиной прецессии и нутации Земли является её несферичность и несовпадение плоскостей экватора и эклиптики. В результате гравитационного притяжения Луной и Солнцем экваториального утолщения Земли возникает момент сил, стремящийся совместить плоскости экватора и эклиптики.
Замедление вращения с течением времени[править | править код]
Скорость вращения Земли медленно снижается[40]. В 1962 году замедление вращения Земли было вычислено по косвенным геологическим факторам[64]. В частности, исследование ископаемых кораллов возрастом 350 млн лет показало, что в тот период год состоял из 385 дней и, следовательно, длительность суток составляла менее 23 часов[65].
Происхождение вращения Земли[править | править код]
Самая распространенная теория объясняет это процессами, происходившими во времена образования планет. Облака космической пыли уплотнялись, образуя зародыши планет, к ним притягивались другие более или менее крупные космические тела. Столкновения с этими телами и могли придать вращение будущим планетам. А дальше планеты продолжали вращаться по инерции[66].
См. также[править | править код]
- Центробежная сила
- Сила Кориолиса
- Сила Кориолиса в гидроаэромеханике
- Маятник Фуко
- Гелиоцентрическая система мира
- Гераклид Понтийский
- Аристарх Самосский
- Ариабхата
- Николай Коперник
- О вращении небесных сфер
- Галилео Галилей
- Эфемеридное время
- Приливное ускорение
- Дельта T
- Сутки
Примечания[править | править код]
- ↑ Веселовский, 1961; Житомирский, 2001.
- ↑ «Земле же, кормилице нашей, он [Демиург] определил вращаться вокруг оси, проходящей через Вселенную» [1] Архивная копия от 9 мая 2008 на Wayback Machine.
- ↑ Иногда их считают персонажами диалогов Гераклида Понтийского.
- ↑ Эти свидетельства собраны в статье Van der Waerden, 1978 Архивная копия от 10 сентября 2010 на Wayback Machine.
- ↑ Свидетельства о суточном вращении Земли у Аристарха: Плутарх, О лике, видимом на диске Луны (отрывок 6)[2] Архивная копия от 6 сентября 2010 на Wayback Machine; Секст Эмпирик, Против ученых [3] Архивная копия от 4 марта 2009 на Wayback Machine; Plutarch, Platonic questions (question VIII) Архивная копия от 26 июня 2009 на Wayback Machine.
- ↑ [https://web.archive.org/web/20090626065257/http://www.gutenberg.org/dirs/etext02/pluta10.txt Архивная копия от 26 июня 2009 на Wayback Machine Об этом свидетельствует Плутарх].
- ↑ Heath 1913, pp. 304, 308; Птолемей, Альмагест, кн. 1, гл.7 (недоступная ссылка).
- ↑ Аристотель, О Небе, кн. II.14.
- ↑ Птолемей, Альмагест, кн. 1, гл.7. (недоступная ссылка)
- ↑ Там же.
- ↑ Chatterjee 1974, p. 51.
- ↑ Согласно мнениям некоторых историков, теория Ариабхаты является переработанной гелиоцентрической теорией греческих астрономов (Van der Waerden, 1987).
- ↑ Chatterjee 1974, p. 54.
- ↑ Розенфельд и др. 1973, с. 94, 152—155.
- ↑ Бируни, Канон Мас’уда, кн.1, гл.1. Дата обращения: 19 июня 2009. Архивировано 9 сентября 2010 года.
- ↑ Ragep, 2001. См. также Джалалов, 1958.
- ↑ The Biographical Encyclopedia of Astronomers, p. 42.
- ↑ Jean Buridan on the diurnal rotation of Earth Архивная копия от 10 декабря 2006 на Wayback Machine; см. также Ланской 1999.
- ↑ Лупандин, Лекция 11. Дата обращения: 19 июня 2009. Архивировано из оригинала 14 июля 2007 года.
- ↑ Nicole Oresme on the Book of the Heavens and the world of Aristotle Архивная копия от 12 июня 2008 на Wayback Machine; см. также Dugas 1955 (p. 62-66), Grant 1974, Ланской 1999 и Лупандин, Лекция 12. Архивная копия от 14 июля 2007 на Wayback Machine
- ↑ Лупандин, Лекция 12. Дата обращения: 19 июня 2009. Архивировано из оригинала 14 июля 2007 года.
- ↑ Grant 1974, p. 506.
- ↑ Ланской 1999, с. 97. Следует отметить, однако, что не все религиозные доводы против вращения Земли Орем считал убедительными (Dugas 1955, p. 64)).
- ↑ В конце жизни Цунига, однако, отверг суточное вращение Земли как «абсурдное предположение». См. Westman 1986, p. 108.
- ↑ Истории этого аргумента и разнообразных попыток его преодоления посвящены многие статьи (Михайлов и Филонович 1990, Koyre 1943, Armitage 1947, Koyre 1955, Ariotti 1972, Massa 1973, Grant 1984).
- ↑ Коперник, О вращениях небесных сфер, русский перевод 1964 г., с. 28.
- ↑ Михайлов и Филонович 1990, Ariotti 1972.
- ↑ Галилей Г. Избранные труды в двух томах. — Т. 1. — С. 333.
- ↑ В древности сторонниками бесконечности Вселенной были Гераклид Понтийский и Селевк, предполагавшие вращение Земли.
- ↑ Имеется в виду суточное вращение небесной сферы.
- ↑ Койре, 2001, с. 46—48.
- ↑ Экклезиаст 1:5.
- ↑ Библия, Книга [[Иисус Навин|Иисуса Навина]], глава 10. Дата обращения: 22 июня 2009. Архивировано 20 сентября 2011 года.
- ↑ Псалом 103:5.
- ↑ Rosen 1975.
- ↑ Этому посвящены его письма к его ученику, священнику Бенедетто Кастелли и Великой герцогине Кристине Лотарингской. Обширные выдержки из них приведены в работе Фантоли 1999.
- ↑ Об этом говорил ещё Орем в XIV веке.
- ↑ Дж. Бруно, Пир на пепле, диалог IV.
- ↑ Howell 1998.
- ↑ 1 2 3 4 5 6 Пасынок, 2016.
- ↑ Пуанкаре, О науке, с. 362—364.
- ↑ Впервые этот эффект наблюдал Винченцо Вивиани (ученик Галилея) ещё в 1661 г. (Граммель 1923, Hagen 1930, Guthrie 1951).
- ↑ Теория маятника Фуко подробно изложена в Общем курсе физики Сивухина (Т. 1, § 68).
- ↑ При советской власти маятник Фуко длиной 98 м демонстрировался в Исаакиевском соборе (Ленинград).
- ↑ Граммель 1923.
- ↑ Kuhn 1957.
- ↑ Подробнее см. Михайлов 1984, с. 26.
- ↑ Graney 2011.
- ↑ Расчет эффекта см. в Общем курсе физики Сивухина (Т. 1, § 67).
- ↑ Угловая скорость основания и вершины одна и та же, но линейная скорость равна произведению угловой скорости на радиус вращения.
- ↑ Несколько иное, но эквивалентное объяснение основано на II законе Кеплера. Секториальная скорость движущегося в поле тяготения тела, пропорциональная произведению радиуса-вектора тела на квадрат угловой скорости, является постоянной величиной. Рассмотрим простейший случай, когда башня расположена на земном экваторе. Когда тело находится на вершине, его радиус-вектор максимален (радиус Земли плюс высота башни) и угловая скорость равна угловой скорости вращения Земли. При падении тела его радиус-вектор уменьшается, что сопровождается увеличением угловой скорости тела. Таким образом, средняя угловая скорость тела оказывается чуть больше угловой скорости вращения Земли.
- ↑ Koyre 1955, Burstyn 1965.
- ↑ Armitage 1947, Михайлов и Филонович 1990.
- ↑ Граммель 1923, с. 362.
- ↑ Граммель 1923, с. 354—356
- ↑ Schiller, Motion Mountain, Архивная копия от 24 сентября 2019 на Wayback Machine pp. 123, 374.
- ↑ Сурдин 2003.
- ↑ Подробное объяснение см. в книге Асламазова и Варламова (1988).
- ↑ Г. Б. Малыкин, «Эффект Саньяка. Корректные и некорректные объяснения», Успехи физических наук, том 170, № 12, 2000. [4] Архивная копия от 4 июня 2009 на Wayback Machine
- ↑ Граммель 1923, Rigge 1913, Compton 1915, Guthrie 1951, Schiller, Motion Mountain Архивная копия от 24 сентября 2019 на Wayback Machine.
- ↑ [bse.sci-lib.com/article092586.html Прецессия] — статья из Большой советской энциклопедии (3-е издание)
- ↑ Астронет > Сферическая астрономия. Дата обращения: 24 октября 2010. Архивировано 19 октября 2012 года.
- ↑ [bse.sci-lib.com/article082842.html Нутация (физич.)] — статья из Большой советской энциклопедии (3-е издание)
- ↑ Ламакин В. В. О возможном значении замедления земного вращения в происхождении Байкальской впадины // Доклады IV совещания по проблемам астрогеологии Географического общества СССР: [Ленинград. 7-12 мая 1962 г.]. Л.: ВГО, 1962. С. 65-67.
- ↑ Чаун, Маркус. Гравитация. Последнее искушение Эйнштейна. Глава «Как замедлить Землю». — СПб.: Питер, 2019. — 336 с. — (New Science). — ISBN 978-5-4461-0724-7.
- ↑ Почему Земля вращается вокруг своей оси, да еще и с постоянной скоростью? :: Сто тысяч”почему”. Почемучка. allforchildren.ru. Дата обращения: 9 апреля 2016. Архивировано 26 марта 2016 года.
Литература[править | править код]
- Л. Г. Асламазов, А. А. Варламов, «Удивительная физика», М.: Наука, 1988. DJVU
- В. А. Бронштэн, Трудная задача, Квант, 1989. № 8. С. 17.
- A. В. Бялко, «Наша планета — Земля», М.: Наука, 1983. DJVU
- И. Н. Веселовский, «Аристарх Самосский — Коперник античного мира», Историко-астрономические исследования, Вып. VII, с.17-70, 1961. Online (недоступная ссылка)
- Р. Граммель, «Механические доказательства движения Земли», УФН, том III, вып. 4, 1923. PDF
- Г. А. Гурев, «Учение Коперника и религия», М.: Изд-во АН СССР, 1961.
- Г. Д. Джалалов, «Некоторые замечательные высказывания астрономов Самаркандской обсерватории», Историко-астрономические исследования, вып. IV, 1958, с. 381—386.
- А. И. Еремеева, «Астрономическая картина мира и её творцы», М.: Наука, 1984.
- С. В. Житомирский, «Античная астрономия и орфизм», М.: Янус-К, 2001.
- И. А. Климишин, «Элементарная астрономия», М.: Наука, 1991.
- А. Койре, «От замкнутого мира к бесконечной Вселенной», М.: Логос, 2001.
- Г. Ю. Ланской, «Жан Буридан и Николай Орем о суточном вращении Земли», Исследования по истории физики и механики 1995—1997, с. 87-98, М.: Наука, 1999.
- А. А. Михайлов, «Земля и её вращение», М.: Наука, 1984. DJVU
- Г. К. Михайлов, С. Р. Филонович. К истории задачи о движении свободно брошенных тел на вращающейся Земле, Исследования по истории физики и механики 1990, с. 93-121, М.: Наука, 1990.
- Е. Мищенко, Ещё раз о трудной задаче, Квант. 1990. № 11. С. 32.
- А. Паннекук, «История астрономии», М.: Наука, 1966. Online
- А. Пуанкаре, «О науке», М.: Наука, 1990. DJVU
- Б. Е. Райков, «Очерки по истории гелиоцентрического мировоззрения в России», М.-Л.: АН СССР, 1937.
- И. Д. Рожанский, «История естествознания в эпоху эллинизма и Римской империи», М.: Наука, 1988.
- Д. В. Сивухин, «Общий курс физики. Т. 1. Механика», М.: Наука, 1989.
- О. Струве, Б. Линдс, Г. Пилланс, «Элементарная астрономия», М.: Наука, 1964.
- В. Г. Сурдин, «Ванна и закон Бэра», Квант, No 3, с. 12-14, 2003. DJVU PDF
- А. Фантоли, «Галилей: в защиту учения Коперника и достоинства Святой Церкви», М.: Мик, 1999.
- P. Ariotti, «From the top to the foot of a mast on a moving ship», Annals of Science, Volume 28, Issue 2, pp. 191—203(13), 1972.
- A. Armitage, «The deviation of falling bodies», Annals of Science, Volume 5, Issue 4, pp. 342-51, 1947.
- Burstyn H. L. The deflecting force of the earth’s rotation from Galileo to Newton // Annals of Science. — 1965. — Vol. 21. — P. 47—80.
- Burstyn H. L. Early explanations of the role of the Earth’s rotation in the circulation of the atmosphere and the ocean // Isis. — 1966. — Vol. 57. — P. 167—187.
- J. W. Campbell, «The Deviations of Falling Bodies», Journal of the Royal Astronomical Society of Canada, Vol. 12, p. 202—209, 1918. Online
- B. Chatterjee, «A glimpse of Aryabhata’s theory of rotation of Earth», Indian J. History Sci., volume 9(1), pp. 51-55, 1974.
- A. H. Compton, «A Determination of Latitude, Azimuth, and the Length of the Day Dependent of Astronomical Observations», Popular Astronomy, vol. 23, pp. 199—207, 1915. Online
- J. L. E. Dreyer, «History of the planetary systems from Thales to Kepler», Cambridge University Press, 1906. PDF
- R. Dugas, «A history of mechanics», Editions du Griffon, Neuchatel, Switzerland, 1955. PDF
- C. M. Graney, «Contra Galileo: Riccioli’s „Coriolis-Force“ Argument on the Earth’s Diurnal Rotation», Physics in Perspective, V. 13, No 4, 387—400, 2011. Online (недоступная ссылка)
- E. Grant, «Late Medieval Thought, Copernicus, and the Scientific Revolution», Journal of the History of Ideas, Vol. 23, No. 2, pp. 197—220, 1962.
- E. Grant, «A Source Book in Medieval Science», Harvard University Press, 1974.
- E. Grant, «In Defense of the Earth’s Centrality and Immobility: Scholastic Reaction to Copernicanism in the Seventeenth Century», Transactions of the American Philosophical Society, New Ser., Vol. 74, No. 4. (1984), pp. 1-69.
- W. G. Guthrie, «The rotation of the Earth», Irish Astronomical Journal, Vol. 1, p. 213, 1951. Online
- J. G. Hagen, «The free-pendulum experiment photographed», Popular Astronomy, Vol. 38, p. 381, 1930. Online
- T. L. Heath, «Aristarchus of Samos, the ancient Copernicus: a history of Greek astronomy to Aristarchus», Oxford: Clarendon, 1913; reprinted New York: Dover, 1981. PDF
- K. J. Howell, «The role of biblical interpretation in the cosmology of Tycho Brahe», Stud. Hist. Phil. Sci., Vol. 29, No. 4, pp. 515—537, 1998.
- A. Koyre, «Galileo and the Scientific Revolution of the Seventeenth Century», The Philosophical Review, Vol. 52, No. 4, pp. 333—348, 1943.
- A. Koyre, «A Documentary History of the Problem of Fall from Kepler to Newton», Transactions of the American Philosophical Society, New Ser., Vol. 45, No. 4., pp. 329—395, 1955.
- T. S. Kuhn, «The Copernican Revolution: planetary astronomy in the development of Western thought», Cambridge: Harvard University Press, 1957. ISBN 0-674-17100-4.
- D. Massa, «Giordano Bruno and the top-sail experiment», Annals of Science, Volume 30, Issue 2, pp. 201—211(11), 1973.
- G. McColley, «The theory of diurnal rotation of the Earth», Isis, volume 26 (1937), pages 392—402.
- F. J. Ragep, «Tusi and Copernicus: The Earth’s Motion in Context», Science in Context 14 (2001) (1-2), p. 145—163.
- W. F. Rigge, «Experimental Proofs of the Earth’s Rotation», Popular Astronomy, vol. 21, pp. 208—216, 267—276, 1913. Part 1 Part 2
- E. Rosen, «Kepler and the Lutheran attitude towards Copernicanism in the context of the struggle between science and religion», Vistas in Astronomy, vol. 18, Issue 1, pp. 317—338, 1975.
- L. Russo, «The forgotten revolution: how science was born in 300 BC and why it had to be reborn», Berlin: Springer 2004.
- C. Schiller, «Motion Mountain», Online edition (Chapter 5. From the rotation of the Earth to the relativity of motion)
- B. L. van der Waerden, «On the motion of the planets according to Heraclides of Pontus», Arch. Internat. Hist. Sci. 28 (103) (1978), 167—182. Русский перевод
- B. L. van der Waerden, «The heliocentric system in Greek, Persian and Hindu astronomy», in «From deferent to equant: A Volume of Studies in the History of Science in the Ancient and Medieval Near East in Honor of E.S. Kennedy», Annals of the New York Academy of Sciences, Volume 500, June 1987, 525—545. Русский перевод (недоступная ссылка)
- R. S. Westman, «The Copernicans and the Churches», God and Nature: Historical Essays on the Encounter between Christianity and Science, ed. by D.C. Lindberg and R.L. Numbers, p. 76-113, Berkeley: University of California Press, 1986.
- Пасынок, Л. Методы и средства определения параметров вращения Земли : [арх. 10 декабря 2020] / ФГУП «ВНИИФТРИ». — Альманах современной метрологии. — 2016. — Т. 3, № 8. — С. 269–323. — УДК 521.3, 521.92(G). — ISSN 2313-8068.
Ссылки[править | править код]
- Ю. А. Кимелев, Т. Л. Полякова. Наука и религия. Глава 3. Коперниканская революция.
- И. В. Лупандин. Лекции по истории натурфилософии: 10. Космология Николая Орема, 12. Космология Альберта Саксонского.
- В. Ф. Майоров. Как узнать, что Земля вращается?
- Г. А. Гурьев. Системы мира от древнейших времён до наших дней
- Опыт Фуко: доказательство вращения Земли (англ.)
- G. Hagen. J. Systems of the Universe (The catholic encyclopedia) (англ.)
- Куда мы движемся? Дата обращения: 6 марта 2013.
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:



Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности, период обращения и частота.
1. Равномерное движение по окружности
Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.
Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.
Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.
Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.
Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.
2. Период вращения и вращающаяся частота
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.
Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.
Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.
При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:  . Итак,
. Итак,
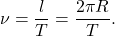
Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:
частота вращения равна количеству полных оборотов за одну секунду.
Частота вращения и период обращения связаны следующим соотношением:
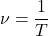
Частоту в СИ измеряют в

3. Вращательное движение
В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.
Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.
Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
ПРОВЕРЬТЕ СЕБЯ
- Приведите два-три примера криволинейного движения.
- Приведите два-три примера равномерного движения по кругу.
- Что такое вращательное движение? Приведите примеры такого движения.
- Как направлена мгновенная скорость при движении по кругу Приведите два-три примера.
1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.
2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением:  Частоту в СИ измеряют в обратных секундах.
Частоту в СИ измеряют в обратных секундах.
3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
[spoiler title=”источники:”]
http://repetitor.org.ua/dvizhenie-po-okruzhnosti-period-obrashheniya-i-chastota
[/spoiler]
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.



Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.


Частота и период взаимосвязаны соотношением


Связь с угловой скоростью


Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.


Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.



Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.


