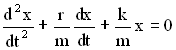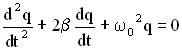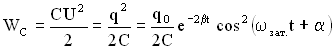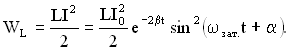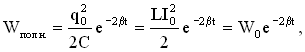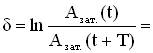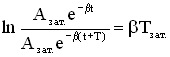1.21.
3АТУХАЮЩИЕ, ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Дифференциальное
уравнение затухающих колебаний и его
решение. Коэффициент затухания.
Логарифмический декремент
затухания. Добротность
колебательной
системы. Апериодический
процесс. Дифференциальное уравнение
вынужденных колебаний и его решение.
Амплитуда
и фаза вынужденных колебаний. Процесс
установления колебаний. Случай резонанса.
Автоколебания.
Затуханием
колебаний называется постепенное
уменьшение амплитуды колебаний с
течением времени, обусловленное потерей
энергии колебательной системой.
Собственные
колебания без затухания – это идеализация.
Причины затухания могут быть разные. В
механической системе к затуханию
колебаний приводит наличие трения.
Когда израсходуется вся энергия,
запасенная в колебательной системе,
колебания прекратятся. Поэтому амплитуда
затухающих
колебаний
уменьшается,
пока не станет равной нулю.
Затухающие колебания,
как и собственные, в системах, разных
по своей природе, можно рассматривать
с единой точки зрения – общих признаков.
Однако, такие характеристики, как
амплитуда и период, требуют переопределения,
а другие – дополнения и уточнения по
сравнению с такими же признаками для
собственных незатухающих колебаний.
Общие признаки и понятия затухающих
колебаний следующие:
-
Дифференциальное
уравнение должно быть получено с учетом
убывания в процессе колебаний
колебательной энергии. -
Уравнение колебаний
– решение дифференциального уравнения. -
Амплитуда затухающих
колебаний зависит от времени. -
Частота и период
зависят от степени затухания колебаний. -
Фаза и начальная
фаза имеют тот же смысл, что и для
незатухающих колебаний.
Механические
затухающие колебания.
Механическая
система:
пружинный маятник с учетом сил трения.
Силы,
действующие на маятник:
Упругая
сила.
,
где k
– коэффициент жесткости пружины, х –
смещение маятника от положения равновесия.
Сила
сопротивления.
Рассмотрим силу сопротивления,
пропорциональную скорости v
движения (такая зависимость характерна
для большого класса сил сопротивления):
.
Знак “минус” показывает, что направление
силы сопротивления противоположно
направлению скорости движения тела.
Коэффициент сопротивления r
численно равен силе сопротивления,
возникающей при единичной скорости
движения тела:
Закон
движения
пружинного
маятника – это второй закон Ньютона:
ma
= Fупр.
+ Fсопр.
Учитывая,
что
и

запишем второй закон Ньютона в виде:

Разделив
все члены уравнения на m,
перенеся их все в правую часть, получим
дифференциальное
уравнение
затухающих колебаний:
Обозначим
,
где β
– коэффициент
затухания,
,
где ω0
– частота незатухающих свободных
колебаний в отсутствии потерь энергии
в колебательной системе.
В новых обозначениях
дифференциальное уравнение затухающих
колебаний имеет вид:

(21.2)
Это линейное
дифференциальное уравнение второго
порядка.
Это
линейное дифференциальное уравнение
решается заменой переменных. Представим
функцию х, зависящую от времени t,
в виде:
.
Найдем
первую и вторую производную этой функции
от времени, учитывая, что функция z
также является функцией времени:
,

Подставим выражения
в дифференциальное уравнение:

Приведем
подобные члены в уравнении и сократим
каждый член на
,
получим уравнение:
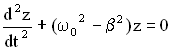
Обозначим
величину
.
Решением
уравнения
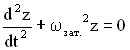
функции
,
.
Возвращаясь к
переменной х, получим формулы уравнений
затухающих колебаний:
.
Таким
образом,
уравнение затухающих колебаний есть
решение дифференциального уравнения
(21.2):
(21.3)
Частота
затухающих колебаний:
(физический
смысл имеет только вещественный корень,
поэтому
).
Период
затухающих колебаний:

Смысл,
который вкладывался в понятие периода
для незатухающих колебаний, не подходит
для затухающих колебаний, так как
колебательная система никогда не
возвращается в исходное состояние из-за
потерь колебательной энергии. При
наличии трения колебания идут медленнее:
.
Периодом
затухающих колебаний
называется минимальный промежуток
времени, за который система проходит
дважды положение равновесия в одном
направлении.
Для механической
системы пружинного маятника имеем:


Амплитуда
затухающих колебаний:
,
для пружинного маятника
.
Амплитуда
затухающих колебаний – величина не
постоянная, а изменяющаяся со временем
тем быстрее, чем больше коэффициент β.
Поэтому определение для амплитуды,
данное ранее для незатухающих свободных
колебаний, для затухающих колебаний
надо изменить.
При
небольших затуханиях амплитудой
затухающих колебаний
называется
наибольшее отклонение от положения
равновесия за период.
Графики
зависимости
смещения от времени
и
амплитуды от времени
представлены
на Рисунках 21.1 и 21.2.
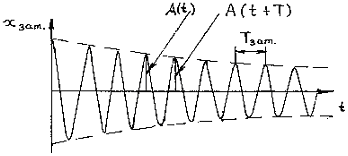
Рисунок
21.1 – Зависимость смещения от времени
для затухающих колебаний.
Рисунок
21.2 – Зависимости амплитуды от времени
для затухающих колебаний
Характеристики
затухающих колебаний.
1.
Коэффициент затухания
β.
Изменение амплитуды
затухающих колебаний происходит по
экспоненциальному закону:
.
Пусть за
время τ
амплитуда колебаний уменьшится в “e
” раз (“е” – основание натурального
логарифма, е ≈ 2,718). Тогда, с одной стороны,
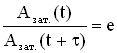
а с другой стороны, расписав амплитуды
Азат.(t)
и Азат.(t+τ),
имеем

Из этих соотношений следует βτ
= 1, отсюда
.
Промежуток
времени τ,
за который амплитуда уменьшается в “е”
раз, называется временем релаксации.
Коэффициент
затухания β
– величина, обратно пропорциональная
времени релаксации.
2.
Логарифмический
декремент затухания δ
–
физическая величина, численно равная
натуральному логарифму отношения двух
последовательных амплитуд, отстоящих
по времени на период .
Если
затухание невелико, т.е. величина β
мала, то амплитуда незначительно
изменяется за период, и логарифмический
декремент можно определить так:
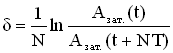
где
Азат.(t)
и Азат.(t+NT)
– амплитуды колебаний в момент времени
е и через N
периодов, т.е.в момент времени (t
+ NT).
3.
Добротность Q
колебательной системы
– безразмерная физическая величина,
равная произведению величины (2π)
νа
отношение энергии W(t)
системы в произвольный момент времени
к убыли энергии за один период затухающих
колебаний:

Так как энергия
пропорциональна квадрату амплитуды,
то

При малых
значениях логарифмического декремента
δ
добротность колебательной системы
равна
,
где Ne
– число колебаний, за которое амплитуда
уменьшается в “е” раз.
Так,
добротность пружинного маятника –

больше добротность колебательной
системы, тем меньше затухание, тем дольше
будет длиться периодический процесс в
такой системе. Добротность
колебательной системы – безразмерная
величина, которая характеризует
диссипацию энергии во времени.
4. При
увеличении коэффициента β,
частота затухающих колебаний уменьшается,
а период увеличивается. При ω0
= β
частота затухающих колебаний становится
равной нулю ωзат.
= 0, а Тзат.
=
∞. При этом колебания теряют периодический
характер и называются апериодическими.
При ω0
= β
параметры системы, ответственные за
убывание колебательной энергии, принимают
значения, называемые критическими.
Для пружинного маятника условие ω0
= β
запишется так: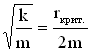
откуда найдем величину критического
коэффициента сопротивления:
.
Рис. 21.3.
Зависимсть амплитуды апериодических
колебаний от времени
Вынужденные
колебания.
Все реальные колебания
являются затухающими. Чтобы реальные
колебания происходили достаточно долго
нужно периодически пополнять энергию
колебательной системы, действуя на нее
внешней периодически изменяющейся
силой
Рассмотрим
явление колебаний, если внешняя
(вынуждающая)
сила изменяется в зависимости от времени
по гармоническому закону. При этом в
системах возникнут колебания, характер
которых в той или иной мере повторит
характер вынуждающей силы. Такие
колебания называются вынужденными.
Общие признаки
вынужденных механических колебаний.
1. Рассмотрим
вынужденные механические колебаний
пружинного маятника, на который действует
внешняя (вынуждающая)
периодическая сила
.
Силы, которые действуют на маятник,
однажды выведенный из положения
равновесия, развиваются в самой
колебательной системе. Это сила упругости
и
сила сопротивления
.
Закон
движения
(второй закон Ньютона) запишется следующим
образом:

Разделим
обе части уравнения на m,
учтем, что
,
и получим дифференциальное
уравнение
вынужденных
колебаний:

Обозначим
(β
– коэффициент
затухания),
(ω0
– частота незатухающих свободных
колебаний),
сила,
действующая на единицу массы. В этих
обозначениях дифференциальное
уравнение
вынужденных колебаний примет вид:

Это дифференциальное
уравнение второго порядка с правой
частью, отличной от нуля. Решение такого
уравнения есть сумма двух решений
.
–
общее
решение однородного дифференциального
уравнения, т.е. дифференциального
уравнения без правой части, когда она
равна нулю. Такое решение нам известно
– это уравнение затухающих колебаний,
записанное с точностью до постоянной,
значение которой определяется начальными
условиями колебательной системы:
,
где
.
Мы обсуждали ранее,
что решение может быть записано через
функции синуса.
Если
рассматривать процесс колебаний маятника
через достаточно большой промежуток
времени Δt
после включения вынуждающей силы
(Рисунок 21.2), то затухающие колебания в
системе практически прекратятся. И
тогда решением дифференциального
уравнения с правой частью будет решение
.
Решение
–
это частное решение неоднородного
дифференциального уравнения, т.е.
уравнения с правой частью. Из теории
дифференциальных уравнений известно,
что при правой части, изменяющейся по
гармоническому закону, решение
будет
гармонической функцией (sin
или cos)
с частотой изменения, соответствующей
частоте Ω
изменения правой части:
, (21.8)
где Аампл.
– амплитуда вынужденных колебаний, φ0
–сдвиг
фаз,
т.е. разность фаз между фазой вынуждающей
силы и фазой вынужденных колебаний. И
амплитуда Аампл.,
и сдвиг фаз φ0
зависят от параметров системы (β,
ω0)
и от частоты вынуждающей силы Ω.
Период
вынужденных колебаний равен
(21.9)
График вынужденных
колебаний на Рисунке 4.1.
Рис.21.3. График
вынужденных колебаний
Установившиеся
вынужденные колебания являются так же
гармоническими.
Зависимости
амплитуды вынужденных колебаний и
сдвига фаз от частоты внешнего воздействия.
Резонанс.
1. Вернемся к
механической системе пружинного
маятника, на который действует внешняя
сила, изменяющаяся по гармоническому
закону. Для такой системы дифференциальное
уравнение и его решение соответственно
имеют вид:

.
Проанализируем
зависимость амплитуды колебаний и
сдвига фаз от частоты внешней вынуждающей
силы, для этого найдем первую и вторую
производную от х и подставим в
дифференциальное уравнение.
,

Воспользуемся
методом векторной диаграммы. Из уравнения
видно, что сумма трех колебаний в левой
части уравнения (Рисунок 4.1) должна быть
равна колебанию в правой части. Векторная
диаграмма выполнена для произвольного
момента времени t.
Из нее можно определить
.
Рисунок
21.4.


Учитывая
значение
,
,
,
получим формулы для φ0
и Аампл.
механической системы:


2. Исследуем
зависимость амплитуды вынужденных
колебаний от частоты вынуждающей силы
и величины силы сопротивления в
колеблющейся механической системе, по
этим данным построим график
.
Результаты исследования отражены в
Рисунке 21.5, по ним видно, что при некоторой
частоте вынуждающей силы
амплитуда
колебаний резко возрастает. И это
возрастание тем больше, чем меньше
коэффициент затухания β.
При
амплитуда
колебаний становится бесконечно большой
.
Явление
резкого возрастания амплитуды
вынужденных
колебаний при частоте вынуждающей силы,
равной
,
называется резонансом.
(21.12)
Кривые
на Рисунке 21.5 отражают зависимость
и
называются амплитудными
резонансными кривыми.
Рисунок
21.5 – Графики зависимости амплитуды
вынужденных колебаний от частоты
вынуждающей силы.
Амплитуда резогансных
колебаний примет вид:
(21.13)
Вынужденные
колебания – это незатухающие
колебания. Неизбежные потери энергии
на трение компенсируются подводом
энергии от внешнего источника периодически
действующей силы. Существуют системы,
в которых незатухающие колебания
возникают не за счет периодического
внешнего воздействия, а в результате
имеющейся у таких систем способности
самой регулировать поступление энергии
от постоянного источника. Такие системы
называются автоколебательными,
а процесс незатухающих колебаний в
таких системах – автоколебаниями.
В автоколебательной
системе можно выделить три характерных
элемента – колебательная система,
источник энергии и устройство обратной
связи между колебательной системой и
источником. В качестве колебательной
системы может быть использована любая
механическая система, способная совершать
собственные затухающие колебания
(например, маятник настенных часов).
Источником
энергии может служить энергия деформация
пружины или потенциальная энергия груза
в поле тяжести. Устройство обратной
связи представляет собой некоторый
механизм, с помощью которого
автоколебательная система регулирует
поступление энергии от источника. На
рис. 21.6 изображена схема взаимодействия
различных элементов автоколебательной
системы.
|
|
|
Рисунок |
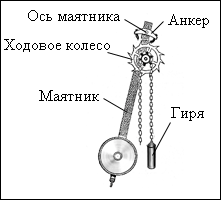
Примером
механической автоколебательной системы
может служить часовой механизм с анкерным
ходом (рис. 21.7.). Ходовое колесо с косыми
зубьями жестко скреплено с зубчатым
барабаном, через который перекинута
цепочка с гирей. На верхнем конце маятника
закреплен анкер (якорек) с двумя
пластинками из твердого материала,
изогнутыми по дуге окружности с центром
на оси маятника. В ручных часах гиря
заменяется пружиной, а маятник –
балансиром – маховичком, скрепленным
со спиральной пружиной.
|
|
|
Рисунок |
Балансир совершает
крутильные колебания вокруг своей оси.
Колебательной системой в часах является
маятник или балансир. Источником энергии
– поднятая вверх гиря или заведенная
пружина. Устройством, с помощью которого
осуществляется обратная связь, является
анкер, позволяющий ходовому колесу
повернуться на один зубец за один
полупериод.
Обратная связь
осуществляется взаимодействием анкера
с ходовым колесом. При каждом колебании
маятника зубец ходового колеса толкает
анкерную вилку в направлении движения
маятника, передавая ему некоторую порцию
энергии, которая компенсирует потери
энергии на трение. Таким образом,
потенциальная энергия гири (или
закрученной пружины) постепенно,
отдельными порциями передается маятнику.
Механические
автоколебательные системы широко
распространены в окружающей нас жизни
и в технике. Автоколебания совершают
паровые машины, двигатели внутреннего
сгорания, электрические звонки, струны
смычковых музыкальных инструментов,
воздушные столбы в трубах духовых
инструментов, голосовые связки при
разговоре или пении и т. д.
13
Соседние файлы в папке физика лекцыи
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для школьников.
Во всех колебательных системах, при выводе их из положения равновесия, кроме возвращающей силы присутствуют силы трения или силы сопротивления, препятствующие их колебательным движениям. Поэтому полная энергия колебательной системы, расходуемая на работу против сил трения (сопротивления), уменьшается, колебания затухают и прекращаются.
На рисунке слева показан график зависимости смещения колеблющейся точки от положения равновесия от времени для затухающего колебания. Пунктирной линией изображено изменение амплитуды затухающего колебания.
Быстрота затухания определяется величиной силы сопротивления. Если сила сопротивления очень большая, то колебания прекращаются после первого прохождения через положение равновесия (нижняя кривая рисунка справа) или даже до первого перехода через положение равновесия (верхняя кривая рисунка справа). Такое движение колеблющегося тела называется апериодическим.
Уравнение, описывающее затухающее колебание, имеет вид:
Здесь
– коэффициент затухания, зависящий от силы сопротивления, которая при малых скоростях пропорциональна скорости.
Выражение для амплитуды затухающих колебаний имеет вид:
где А (с индексом ноль) – амплитуда в начальный момент времени.
Строго затухающее колебание не является периодическим, но если затухание невелико, то можно говорить о периоде.
Период затухающих колебаний зависит от силы сопротивления и определяется формулой:
Здесь буквой “омега”
обозначена круговая частота затухающего колебания, а буквой
круговая частота гармонического колебания.
Чем больше сила сопротивления, тем больше коэффициент затухания, тем быстрее уменьшается амплитуда А и тем больше период затухания Т.
При очень малом трении, когда коэффициент затухания очень мал, период затухающего колебания близок к периоду незатухающего свободного колебания.
На практике быстроту затухания часто характеризуют логарифмическим декрементом затухания, обозначаемым буквой “лямбда”
Логарифмический декремент затухания равен натуральному логарифму отношения двух последовательных амплитуд, отстоящих друг от друга за период времени Т:
Коэффициент затухания и логарифмический декремент затухания связаны между собой зависимостью:
Задача.
Логарифмический декремент затухания маятника равен 0,02. Во сколько раз k уменьшится амплитуда маятника после n = 50 полных колебаний? Считать, что период затухающих колебаний близок к периоду свободных незатухающих колебаний.
Решение. Амплитуда затухающего колебания изменяется по закону:
По условию задачи время 50 колебаний:
Подставив два последних уравнения в уравнение амплитуды затухающего колебания, получим
Тогда амплитуда после n = 50 колебаний уменьшится в k раз:
Здесь е – основание натурального логарифма (е = 2,71828).
Ответ: после совершения 50 колебаний амплитуда уменьшилась в е раз. (Время, в течение которого амплитуда колебаний уменьшается в е раз, называется временем затухания).
На практике в одних случаях надо уменьшать затухание колебаний (например, при работе балансира механических часов), в других случаях, наоборот, увеличивать (например, надо чтобы стрелка электроизмерительных приборов быстро останавливалась).
Для этого в электроизмерительном приборе используется металлическая пластинка, соединённая со стрелкой прибора, в которой при её движении между полюсами электромагнита возникают вихревые токи, тормозящие движение пластинки.
Приведём задачу на затухающие колебания, на переход энергии колеблющейся системы в работу по преодолению сил трения.
Интересен тот факт, что небольшие силы трения мало влияют на период колебаний, тогда как на амплитуду колебаний они влияют гораздо больше. Этот факт используется в работе маятниковых часов.
Ещё Галилеем было сказано о возможности использования маятника в часах. Первые часы с маятником были созданы в 1673 году Гюйгенсом.
Таким образом, все реальные свободные колебания являются затухающими. Но при малых силах трения (сопротивления) колебания в течение достаточно долгого промежутка времени остаются близкими к гармоническим и тогда период затухающих колебаний можно считать равным периоду свободных незатухающих колебаний.
Быстрота затухания характеризуется коэффициентом затухания, логарифмическим декрементом затухания. Коэффициент затухания – это величина, обратная времени, в течении которого амплитуда колебаний уменьшается в е раз.
https://yandex.ru/video/preview/?text=%D0%B4%D0%B5%D0%BC%D0%BE%D0%BD%D1%81%D1%82%D1%80%D0%B0%D1%86%D0%B8%D1%8F%20%D0%B7%D0%B0%D1%82%D1%83%D1%85%D0%B0%D1%8E%D1%89%D0%B8%D0%B5%20%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F&path=wizard&parent-reqid=1638616551229540-1048262997957332495-sas3-0841-245-sas-l7-balancer-8080-BAL-1765&wiz_type=vital&filmId=7663491726844988663
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Сложение гармонических колебаний.
Следующая запись: Вынужденные колебания. Резонанс.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 5 8.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
готово
3.1. Механические затухающие колебания
3.2. Электромагнитные затухающие колебания
3.3. Характеристики затухающих колебаний
Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.
Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:
Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.
Уравнение колебаний – решение дифференциального уравнения.
Амплитуда затухающих колебаний зависит от времени.
Частота и период зависят от степени затухания колебаний.
Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.
3.1. Механические затухающие колебания
Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:
Упругая сила. , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): . Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
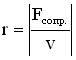
Учитывая, что и
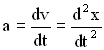
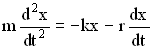
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:
Обозначим , где β – коэффициент затухания,
, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
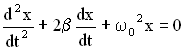
.
В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.
Частота затухающих колебаний:
(физический смысл имеет только вещественный корень, поэтому
).
Период затухающих колебаний: 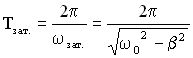
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: .
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Для механической системы пружинного маятника имеем:
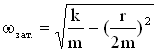
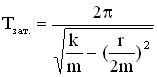
, для пружинного маятника
.
Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.
При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.
Графики зависимости смещения от времени и амплитуды от времени
представлены на Рисунках 3.1 и 3.2.
Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний
Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний
3.2. Электромагнитные затухающие колебания
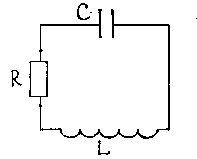
Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).
Рисунок 3.3.
Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:
Падение напряжения:
– на активном сопротивлении: , где I – сила тока в контуре;
– на конденсаторе (С): , где q – величина заряда на одной из обкладок конденсатора.
ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: (закон Фарадея).
Подставим значения UR, UC, в уравнение, отражающее закон Кирхгофа, получим:
.
Сила тока определяется как производная от заряда , тогда
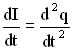
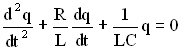
Обозначим ,
, получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:
или
.
Амплитуда затухающих колебаний заряда имеет вид:
, где
.
Частота затухающих колебаний в LCR – контуре:

Период затухающих электромагнитных колебаний:
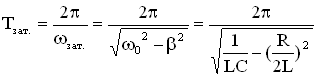
Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так
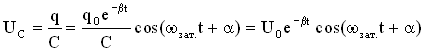
Величина 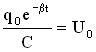
Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение и векторную диаграмму.
Окончательное уравнение для силы тока таково:
,
где 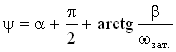
Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.
Энергия колебаний в контуре складывается из энергии электрического поля
и энергии магнитного поля
Полная энергия в любой момент времени:
где W0 – полная энергия контура в момент времени t=0.
1. Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону: .
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 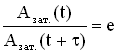
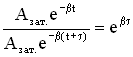
.
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
2. Логарифмический декремент затухания δ – физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
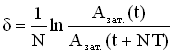
где Азат.(t) и Азат.(t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).
3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
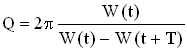
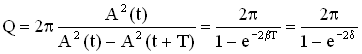
При малых значениях логарифмического декремента δ добротность колебательной системы равна
,
где Ne – число колебаний, за которое амплитуда уменьшается в “е” раз.
Так, добротность электромагнитной системы LCR – контура при малом затухании колебаний равна 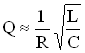
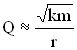
4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω0 = β частота затухающих колебаний становится равной нулю ωзат. = 0, а Тзат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.
При ω0 = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими. Для пружинного маятника условие ω0 = β запишется так: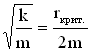
.
Для LCR – контура условие 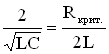
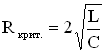
Затухающие колебания, теория и онлайн калькуляторы
Затухающие колебания
Определение затухающих колебаний
Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.
Определение
Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии
колебательной системой.
Уравнение колебаний пружинного маятника с затуханием
Иногда, если тело движется в веществе, силу сопротивления (${overline{F}}_{tr}$), которая действует на рассматриваемое тело, при маленьких скоростях его движения, считают прямо пропорциональной скорости ($overline{v}$):
[{overline{F}}_{tr}=-beta overline{v}left(1right),]
где $beta $ – коэффициент сопротивления.
Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:
[mddot{x}=-kx-beta dot{x}left(2right),]
где $dot{x}=v_x.$ Принимая во внимание равенства:
[{omega }^2_0=frac{k}{m};;2gamma =frac{beta }{m}left(3right),]
(где ${omega }_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $gamma $=0) той же колебательной системы; $gamma $ – коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:
[ddot{x}+2gamma dot{x}+{omega }^2_0x=0 left(4right).]
Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания …) описывают при помощи уравнения формы (4).
Уравнение затухающих колебаний имеет точное решение:
[xleft(tright)=A_0e^{-gamma t}{cos left(omega t+varphi right)left(5right), }]
где $omega =sqrt{{omega }^2_0-{gamma }^2}$; $A_0$ – начальная амплитуда колебаний, задаваемая начальными условиями; $varphi $ – постоянная из начальных условий. При $gamma ll {omega }_0$, $omega approx {omega }_0$, параметр $A_0e^{-gamma t}$ можно считать медленно изменяющейся во времени амплитудой колебаний.
Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.
Диссипация энергии при затухающих колебаниях
Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.
Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:
[frac{dE}{dt}=-frac{2beta }{m}leftlangle E_krightrangle left(6right),]
где $frac{dE}{dt}$ – скорость изменения энергии колебаний; $leftlangle E_krightrangle $ – средняя величина кинетической энергии за период колебаний. Уравнение (6) не применяют для промежутков времени, которые меньше периода колебаний.
Так как мы считаем затухание малым, то $leftlangle E_krightrangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:
[leftlangle E_krightrangle =frac{E}{2}left(7right).]
В таком случае уравнение (6) можно записать в виде:
[frac{dE}{dt}=-2gamma E left(8right).]
Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:
[Eleft(tright)=E_0e^{left(-2gamma tright)}left(9right),]
где $E_0$ – величина энергии колебательной системы в начальный момент времени.
Так как энергия колебаний пропорциональна квадрату амплитуды ($Esim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:
[A=A_0e^{-gamma t}left(10right),]
$A_0$ – начальная амплитуда колебаний.
Время жизни колебаний. Период затухающих колебаний. Декремент затухания
Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $tau =frac{1}{gamma }$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($tau gg T$). За время жизни происходит много колебательных движений.
Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.
Период затухающих колебаний считают равным:
[T=frac{2pi }{sqrt{{omega }^2_0-{gamma }^2}}left(11right).]
Пусть $Aleft(tright) и A(t+T)$ – амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:
[frac{Aleft(tright)}{A(t+T)}=e^{gamma T}(12)]
называют декрементом затухания. Натуральный логарифм декремента затухания ($theta $):
[theta ={ln left(frac{Aleft(tright)}{Aleft(t+Tright)}right) }=gamma T=frac{T}{tau }=frac{1}{N_e}(13)]
называют логарифмическим декрементом затухания. Для колебательной системы $theta $ постоянная величина.
Примеры задач с решением
Пример 1
Задание. Каков коэффициент затухания маятника ($gamma $), если за $Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?
Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:
[xleft(tright)=A_0e^{-gamma t}{cos left(omega t+varphi right)left(1.1right), }]
По условию задачи имеем:
[frac{A_1}{A_2}=n.]
С другой стороны:
[A_1left(t_1right)=A_0e^{-gamma t_1};;A_2left(t_2right)=A_0e^{-gamma t_2} to frac{A_1}{A_2}=frac{A_0e^{-gamma t_1}}{A_0e^{-gamma t_2}}=e^{gamma Delta t}left(1.2right),]
где $t_2-t_1=Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:
[{ln left(frac{A_1}{A_2}right) }=gamma Delta tleft(1.3right).]
Выразим $gamma $ из (1.3) учтем, что $frac{A_1}{A_2}=n$:
[gamma =frac{{ln left(frac{A_1}{A_2}right) }}{Delta t}=gamma =frac{{ln n }}{Delta t}.]
Ответ. $gamma =frac{{ln n }}{Delta t}$
Пример 2
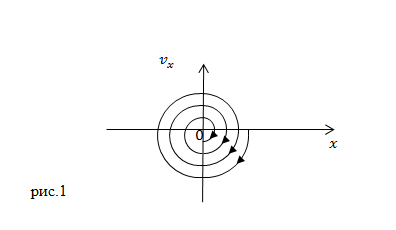
Задание. Что представляет собой фазовая траектория затухающего колебания?
Решение. Фазовой траекторией называют траекторию движения в плоскости $left(x;;vright).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $left(x,vright),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:
[v=vleft(xright)left(2.1right).]
Фазовая траектория затухающего колебания, если
[{overline{F}}_{tr}=-beta overline{v}left(2.2right),]
представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.
Читать дальше: линейная скорость.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Уравнение затухающих колебаний
Затухание колебаний
Свободные колебания в реальных условиях не могут длиться вечно. Для механических систем всегда имеет место сопротивление среды, в результате чего энергия движения объекта рассеивается трением. В электромагнитных цепях колебания затухают из-за сопротивления проводников.
График затухания
Затухающее уравнение
Уравнение затухающих колебаний описывает движение реальных колебательных систем. В дифференциальной форме он записывается следующим образом:
Из этого выражения вы можете получить другую каноническую форму:
либо
Здесь x и t – координаты пространства и времени, A – начальная амплитуда. – коэффициент затухания, который зависит от сопротивления среды r и массы осциллирующего объекта m:
Чем больше сопротивление среды, тем больше энергии рассеивается вязким трением. И наоборот – чем больше масса (и, следовательно, инерция) тела, тем дольше он будет продолжать двигаться.
Циклическая частота свободных колебаний (той же системы, но без трения) учитывает упругую силу в системе (например, жесткость пружины k):
Строго говоря, в случае затухающих колебаний невозможно говорить о периоде – время между повторяющимися движениями системы постоянно увеличивается. Однако, если колебания медленно исчезают, для них с достаточной точностью вы можете определить период T:
Циклическая частота затухающих колебаний
Другой характеристикой затухающих колебаний является циклическая частота:
Время релаксации – это коэффициент, указывающий, как долго амплитуда колебаний уменьшается в e раз:
Отношение амплитуды переменной в два последовательных периода называется коэффициентом затухания:
Такая же характеристика в расчетах часто представляется как логарифм:
Коэффициент качества Q характеризует, насколько упругие силы системы превышают силы сопротивления среды, предотвращая диссипацию энергии:
Примеры решения проблем
ПРИМЕР 1
После того, как груз был подвешен к весне, он растянулся на 9,8 см. Весна колеблется в вертикальном направлении .Определите период колебаний.
Поскольку весна растягивается под весом, на ней действует гравитация:
Сила тяжести противодействует пружинной силе:
Из двух выражений получаем коэффициент упругости:
Замените коэффициент упругости в формуле для периода затухающих колебаний:
Зная, что декремент логарифмического демпфирования , из него выражаем неизвестную величину
, подставляем в знаменатель формулы и выражаем T:
Т = 0,7 с
ПРИМЕР 2
Затухающие колебания характеризуются следующими параметрами: периодом T = 4 с, логарифмическим декрементом демпфирования . В начальный момент не было фазового отклонения. Когда система прошла четверть периода, отклонение точки составляло 4,5 см. Получите уравнение этого колебания, а также график.
Используйте уравнение для затухающих колебаний в канонической форме:
Поскольку при t = 0 не было фазового отклонения, второй член в аргументе косинуса равен нулю.
Определите циклическую частоту:
Найти коэффициент затухания:
Подставим найденные параметры, а также отклонение точки в момент времени в каноническое уравнение:
Тогда уравнение для этих колебаний примет окончательный вид:
В соответствии с этим мы вычисляем значения x для моментов времени до t = 3T = 12 c включительно и строим график.
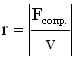











 3
3