ВИДЕО УРОК
Периодические функции.
Функцию у = f(х), х ∈ Х, называют периодической,
если существует такое отличное от нуля число
Т, что для любого х из области определения функции справедливо
равенство:
f(х + Т) = f(х) = f(х – Т).
Число Т называют периодом функции у = f(х).
Из этого
определения сразу следует, что если Т –
период функции
у = f(х), то
2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т
– также периоды
функций. Значит у периодической функции бесконечно много периодов.
Если Т – период функции, то число вида kТ,
где k – любое целое
число, также является периодом функции.
Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.
График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.
График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)
Графики
периодических функций обладают следующей особенностью. Если Т – основной период функции у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси х длиной
Т, а затем осуществить параллельный перенос этой ветви по
оси х на
± Т, ±
2Т, ± 3Т, …
Чаще всего в
качестве такого промежутка длиной Т выбирают промежуток с концами в точках
(–Т/2; 0) и (Т/2; 0) или
(0; 0) и (Т; 0).
ПРИМЕР:
Рассмотрим функцию
у = х – [х], где [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:
f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).
Следовательно, при любом
значении х
f(x + 1) = f(x).
А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.
График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.
Периодичность тригонометрических функций.
Возьмём произвольный угол α и построим
подвижной радиус ОМ единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.
Если мы к углу прибавим
2π или 360° (то есть полный
оборот), то углу α + 2π или α + 360° будет соответствовать то же положение
подвижного радиуса ОМ, что для угла α.
Так как синус и косинус угла,
составленного с осью Ох подвижным радиусом ОМ единичной
окружности, по сути соответственно ордината
у и
абсцисса х точки М, то
sin (α + 2π) = sin α или
sin (α + 360°) = sin α
и
cos (α + 2π)
= cos α или
cos (α + 360°) = cos α.
Таким образом, функции sin α и cos α от
прибавления к аргументу α одного
полного оборота (2π или 360°) не меняют своих значений.
Точно так же, прибавляя к
углу α любое целое
число полных оборотов, мы не изменим положения подвижного радиуса ОМ, а потому:
sin (α + 2kπ) = sin α или
sin (α + 360°k) = sin α
и
cos (α + 2kπ) = cos α или
cos (α + 360°k) = cos α,
где k – любое целое
число.
Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.
Периодом функции sin α и cos α
является 2π или 360°.
Функции tg α и сtg α также
периодические и их периодом является число
π или 180°.
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным
радиусом ОМ единичной окружности.
Построим точку М‘,
симметричную точке М относительно
начала координат. Один из углов, образованных с осью Ох подвижным
радиусом ОМ‘, будет равен α + π.
Если х и у – координаты точки
М, то точки М‘ будут –х и –у. Поэтому
sin α = у, cos α = х,
sin (α + π) = –у,
cos (α + π) = –х.
Отсюда
и, следовательно,
tg (α + π) = tg α,
сtg (α + π)
= сtg α.
отсюда следует, что значения tg α и сtg α не
изменяются, если к углу α прибавить любое число полуоборотов:
tg (α + kπ) = tg α,
сtg (α + kπ) = сtg α.
где k – любое целое
число.
Периоды функций
y = A sin (ωx + φ) и
y = A cos (ωx + φ)
вычисляются по формуле
T = 2π/ω,
а период функции
y = A tg (ωx + φ)
по формуле
T = π/ω.
Если период функции y = f(x) равен T1, а период функции y = g(x) равен T2, то период функций
y = f(x) + g(x) и
y = f(x) – g(x)
равен наименьшему числу, при делении которого
на T1 и T2 получаются целые числа.
ПРИМЕР:
Найти
период функции
y = 3 sin (x – 2) + 7 соs πx.
РЕШЕНИЕ:
Период
функции
y = 3 sin (x – 2)
равен
T1 = 2π/1 = 2π.
Период
функции
y = 7 соs πx
равен
T2 = 2π/π = 2.
Периода
у функции
y = 3 sin (x – 2) + 7 соs πx
не
существует, так как такого числа, при делении которого на 2π и
на 2 получались бы целые числа, нет.
ОТВЕТ:
Периода
не существует.
ПРИМЕР:
Доказать
следующее утверждение:
tg
3850° = tg 250°.
РЕШЕНИЕ:
Так как тангенс – периодическая функция с минимальным
периодом 20 ∙ 180°, то получим:
tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.
ПРИМЕР:
Доказать
следующее утверждение:
сos (–13π) = –1.
РЕШЕНИЕ:
Так как косинус – чётная и периодическая функция с
минимальным периодом 2π, то получим:
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
ПРИМЕР:
Доказать
следующее утверждение:
sin (–7210°) = – sin 10°.
РЕШЕНИЕ:
Так как синус – нечётная и периодическая функция с
минимальным периодом 20 ∙ 360°, то получим:
sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.
ПРИМЕР:
Найти основной период функции
sin 7х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
sin 7х = sin 7(х + t) = sin (7х + 7t)
так как 2πk период синуса, то получим:
sin (7х + 7t) = sin (7х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти основной период функции
соs 0,3х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)
так как 2πk период косинуса, то получим:
соs (0,3х + 0,3t) = соs (0,3х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти период функции:
y = 5sin 2x + 2ctg 3х.
РЕШЕНИЕ:
Период функции
y = 5sin 2x
равен Т1 = 2𝜋/2 = π,
а период функции
y = 2ctg 3х
равен Т2 = 𝜋/3.
Наименьшее число, при делении которого на
Т1 = π и Т2 = 𝜋/3
– получаются целые числа будет число π.
Следовательно, период заданной функции равен Т = π.
ПРИМЕР:
Найти период функции:
y = 9sin (5x + π/3) – 4cоs (7х + 2).
РЕШЕНИЕ:
Находим периоды слагаемых. Период функции
y = 9sin (5x + π/3)
равен Т1 = 2𝜋/5,
а период функции
y = 4cоs (7х + 2)
равен Т2 = 2𝜋/7.
Очевидно, что период заданной функции равен
Т = 2π.
ПРИМЕР:
Найти период функции:
y = 3sin πx + 8tg (х + 5).
РЕШЕНИЕ:
Период функции
y = 3sin πx
равен Т1 = 2π/π = 2,
а период функции
y = 8tg (х + 5)
равен Т2 = 𝜋/1 = π.
Периода у заданной функции не существует, так как нет
такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
ПРИМЕР:
Найти период функции:
y = sin 3x + соs 5х.
РЕШЕНИЕ:
Период функции
y = sin 3x
равен Т1 = 2π/3,
а период функции
y = соs 5х
равен Т2 = 2π/5.
Приведём к общему знаменателю периоды:
Т1 = 10π/15, Т2 = 6π/15.
Тогда наименьшее общее кратное (НОК) будет:
НОК (10π; 6π)
= 30π.
Теперь найдём период заданной функции:
Т = 30π/15 = 2π.
Задания к уроку 5
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
Содержание:
Рассматривая произвольное действительное число
Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Определение функция y=sin x
Определение:
Зависимость, при которой каждому действительному числу 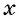
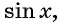
Рассмотрим свойства функции 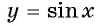
Область определения функции y=sin x
Областью определения функции 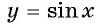
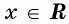
Графически это означает, что для любой абсциссы найдется точка графика функции
Множеством значений функции y=sin x
Множеством значений функции 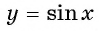
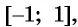
Графически это означает, что график функции 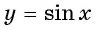
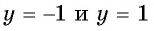
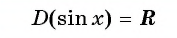
Периодичность функции y=sin x
Периодичность функции 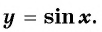
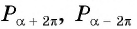
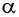
Говорят, что число 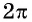
Определение:
Функция 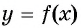
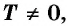
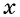
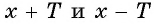
Чтобы определить, является ли функция периодической с периодом 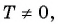
- принадлежат ли области определения функции числа
если
принадлежит области определения функции;
- выполняется ли равенство
Определим, верно ли, что число 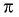
- Числа
принадлежат области определения функции, так как
- Проверим, выполняется ли равенство
для всех
Пусть
Значит, число 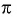
Периодом функции 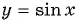
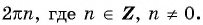
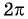
Функция 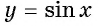
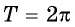
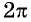
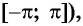
Четность (нечетность) функции y=sin x
Четность (нечетность) функции y=sin x 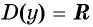
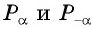
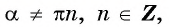
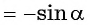
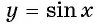
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.
Нули функции y=sin x
Нули функции. Ординаты точек 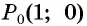
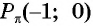
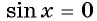
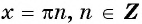
Промежутки знакопостоянства функции y=sin x
На промежутках 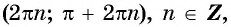
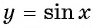
На промежутках 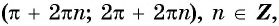
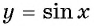
Монотонность функции y=sin x
Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 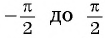
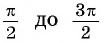
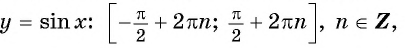
Функции 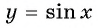
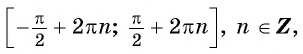
Наибольшее значение функции 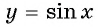
Наименьшее значение функции 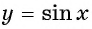
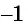
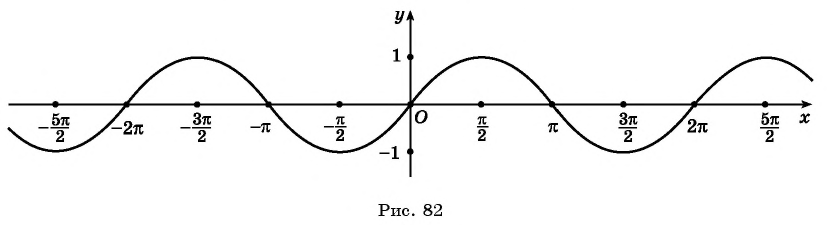
На основании проведенного исследования построим график функции 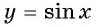
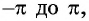
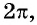
На этом периоде функция
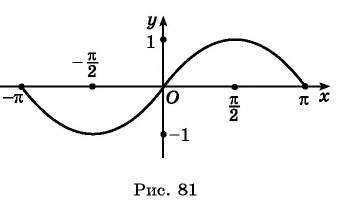
На рисунке 81 изображена часть графика функции 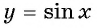
Перенесем эту часть на другие периоды и получим график функции 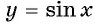
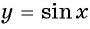
Примеры заданий и их решения
Пример №1
Определите, принадлежит ли графику функции 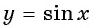
Решение:
а) Подставим в формулу 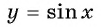
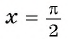
Полученное значение функции равно ординате точки 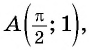
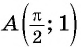
б) При 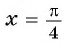
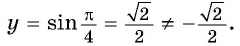
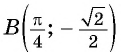
в) При 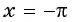
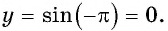
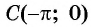
г) При 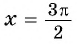
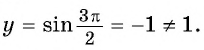
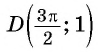
Пример №2
Найдите область определения и множество значений функции:
Решение:
а) Так как область определения функции 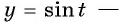
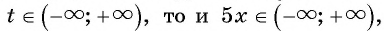
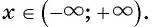
Множеством значений функции 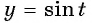
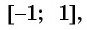
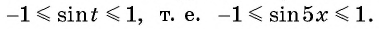
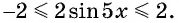
б) 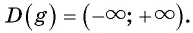
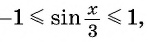
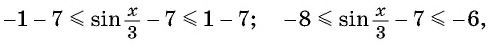
Пример №3
Найдите наибольшее значение функции
Решение:
Так как 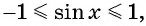
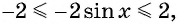
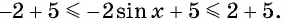
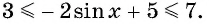
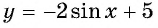
- Заказать решение задач по высшей математике
Пример №4
Найдите значение выражения, используя свойство периодичности функции
Решение:
Так как число 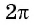
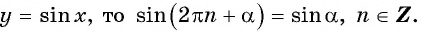
Пример №5
Найдите значение выражения, используя свойство нечетности функции
Решение:
Так как функция 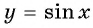
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
a) 
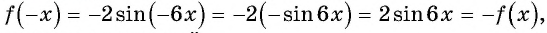
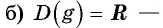
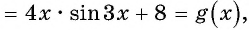
Пример №7
Найдите нули функции:
Решение:
а) Пусть 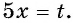
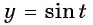
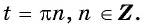
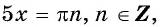
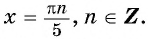
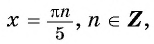
б) Пусть 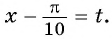
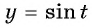
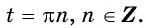
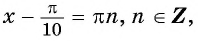
Таким образом, числа 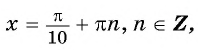
Пример №8
Определите знак произведения
Решение:
Так как 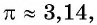
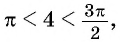
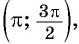
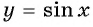
Углы 2 радиана и 1 радиан принадлежат промежутку 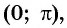
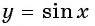
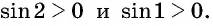
Пример №9
Что больше: 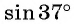
Решение. Так как функция 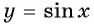
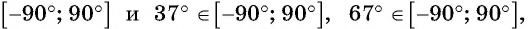
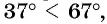
Пример №10
Постройте график функции:
Решение:
а) График функции 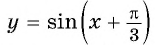
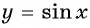
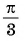
б) График функции 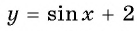
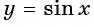
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x – их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Единичная окружность – в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
Как определить периодичность функции
По школьным урокам математики каждый помнит график синуса, равномерными волнами уходящий вдаль. Аналогичным свойством — повторяться через определенный промежуток — обладают и многие другие функции. Они называются периодическими. Периодичность — очень важное свойство функции, часто встречающееся в различных задачах. Поэтому полезно уметь определять, является ли функция периодической.
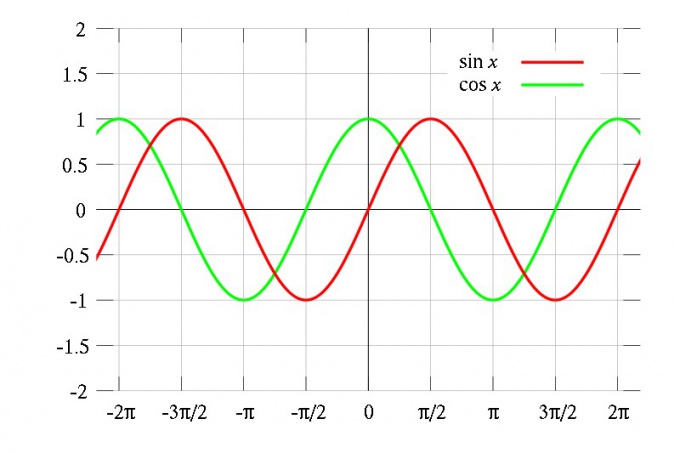
Инструкция
Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.
Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.
Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.
Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.
Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.
Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.
Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.
Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете график функции по горизонтали именно в столько раз
Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.
Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.
Однако если соотношение периодов иррационально, то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.
Источники:
- Теоретические сведения о функциях
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Тема урока, введение
Периодичность функций, наличие периода – специфика тригонометрических функций. Какова причина его появления?
Причины возникновения периода
Во-первых, это определение синуса, косинуса, тангенса и котангенса.
Во-вторых, – специфика отображения аргумента на числовой оси или числовой окружности.
Рассмотрим подробнее. Пусть аргумент откладывается на координатной прямой. Вспомним, что необходимо сделать, чтобы из обычной прямой получить координатную.
1. Отметить начальную точку.
2. Задать положительное направление.
3. Определить масштаб.
На координатной прямой существует взаимно-однозначное соответствие между точкой и действительным числом. Каждому действительному числу соответствует своя точка на прямой и наоборот, каждой точке прямой соответствует одно действительное число (рис. 1).
На числовой окружности числу соответствует единственная точка M. Но длина окружности радиуса 1 равна
Число
тоже попадет в точку M. Точка M соответствует бесчисленному множеству чисел вида
.
У точки M единственная пара координат, т.е. единственные значения синуса и косинуса (рис. 2).
Еще раз посмотрим, какое существует взаимоотношение между числовой прямой и числовой окружностью. Представим себе, что бесконечная тонкая нить наматывается на тонкий обод радиуса 1. Тогда все точки попадут в одну точку окружности. В этом и причина периодичности.
Определение периодичной функции, наименьший положительный период функций y=sint, y=cost
Дадим строгое определение периодичности.
Определение: Функцию называют периодической, если существует такое отличное от нуля число T, что для любого t выполняется равенство
Число T называется периодом функции
Функции имеют много различных периодов. Докажем, что
наименьший положительный период.
Доказательство:
Число является периодом функций
Осталось доказать, что меньшего положительного периода не существует.
Пусть T – произвольный период. Тогда для всех
в частности для
(рис. 3).
Наименьшим положительным периодом вида является
.
Особенности исследования периодических функций y=sint, y=cost
Заменим аргумент t на x и обсудим исследование периодических функций и
Так как наименьший положительный период, то необходимо сделать следующее:
1) Построить график и исследовать функцию на любом отрезке длиной
2) Продолжить график и сформулировать свойства на всей области определения,
При этом необходимо учесть нечетность функции и четность функции
В соответствии с изложенной схемой рассмотрим функции и
Функция – периодическая, период
В силу нечетности достаточно исследовать её на участке
и симметрично отобразить график относительно начала координат (рис. 4).
Рассмотрим функцию Учтём, что она четная, график симметричен относительно оси y.
Мы можем построить график на участке и симметрично отобразить относительно оси y (рис. 5).
Наличие периода позволяет решать многочисленные задачи.
Решение задач
Задача 1. Вычислить
a)
b)
Решение:
a)
Ответ: 1.
b)
Ответ:
Задача 2. Доказать тождество
Доказательство:
верно для любого x.
Тождество доказано.
Задача 3. Решить уравнение
Решение:
Рис. 7.
На рисунке видно, что значению косинуса соответствуют углы
Ответ:
Вывод, заключение
Мы выяснили причины периодичности тригонометрических функций, установили, что синус и косинус имеют много периодов – все числа вида
наименьший положительный период для функций
Наличие периода мы использовали для исследования функций и решения типовых задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 16.15, 16.18.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции 
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции 
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции 
. Это можно записать так:
.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции


Синус — нечетная функция: 
Синус — периодическая функция с наименьшим положительным периодом :

вид графика функции

, а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение
. Тогда соответствующее значение
, то есть график функции
проходит через начало координат.
На оси значение

, при которых


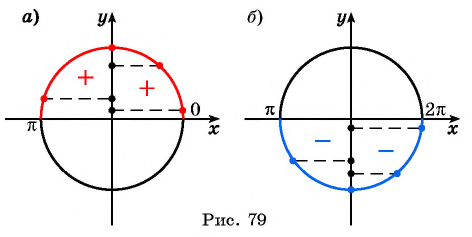
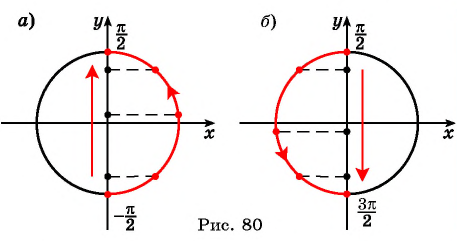
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 


Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 

Промежутки возрастания и убывания. Учитывая периодичность функции 



Если 




Рис.2 Рис.3
Если 




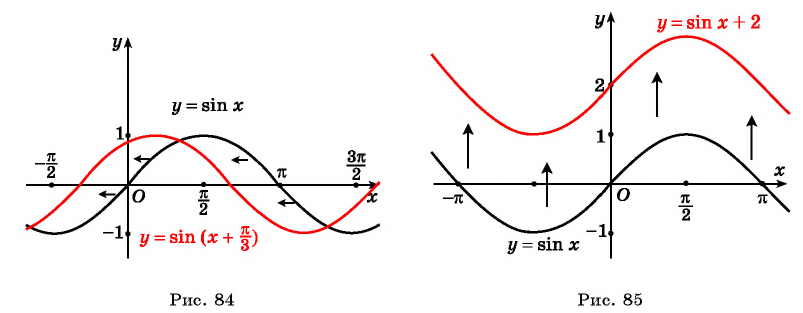
Проведенное исследование позволяет обоснованно построить график функции 







Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной 


на

Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
График функции 

. Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой

колебания, 


СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число)
.
- Область значений:
-
Функция четная:
(график симметричен относительно оси
).
- Функция периодическая с периодом
:
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции 

Рис.7
Для точек единичной окружности абсциссы находятся в промежутке 

точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции 

Как видим, наибольшее значение функции 

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при 
Косинус — четная функция: 

Косинус — периодическая функция с наименьшим положительным периодом 



Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 







Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 


Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому 
Промежутки возрастания и убывания. Учитывая периодичность функции 


Если 





Если 





Рис.8 Рис.9
Проведенное исследование позволяет построить график функции 
. Но график функции


Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки 
абсциссы и ординаты этих точек. Так как 
прямоугольника 



Укажем также формулы, которые нам понадобятся далее:
Тогда,
Таким образом, 
Учитывая, что 

его параллельным переносом вдоль оси


Рис.11
Рис.12
СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции 
Свойства функции 
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
СВОЙСТВО ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.











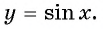
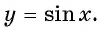
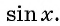
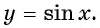
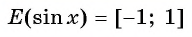
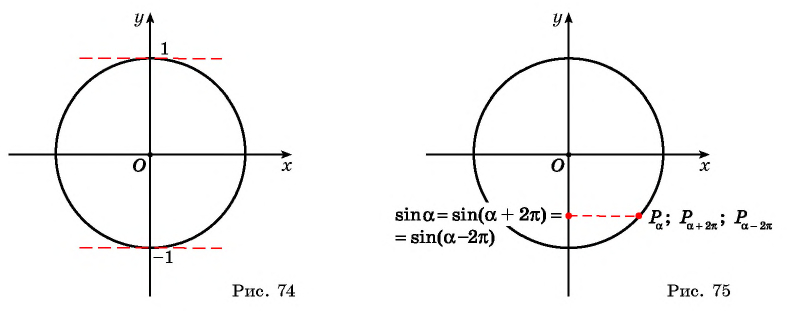
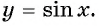
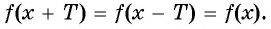
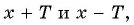 если
если 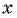 принадлежит области определения функции;
принадлежит области определения функции;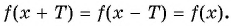
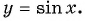
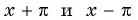 принадлежат области определения функции, так как
принадлежат области определения функции, так как 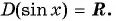
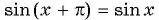 для всех
для всех 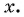
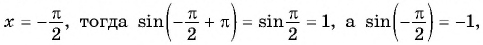
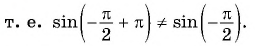
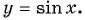
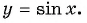
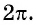
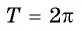
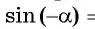
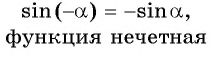
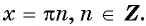
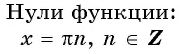
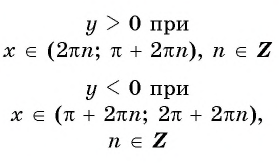
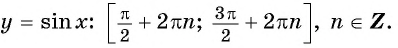
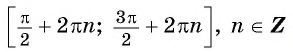
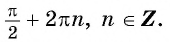
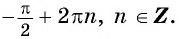
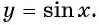
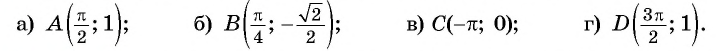
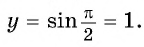
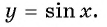
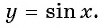
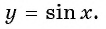
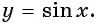
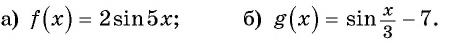
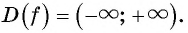
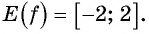
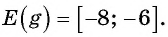
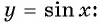
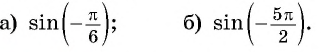
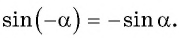
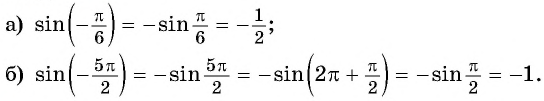
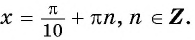
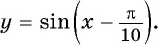
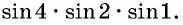
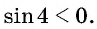
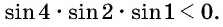
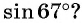
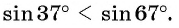








![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)

![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)