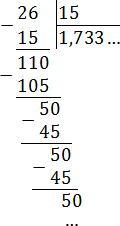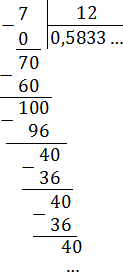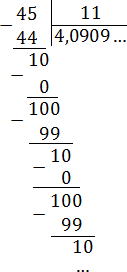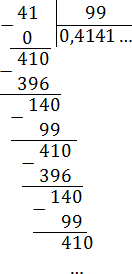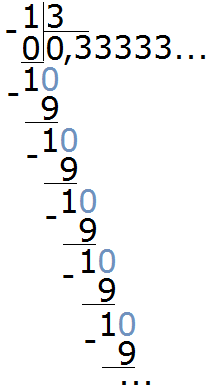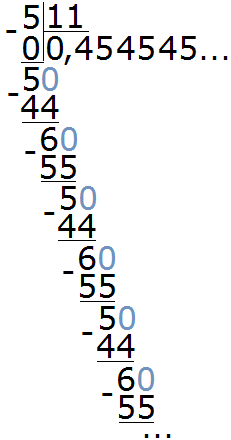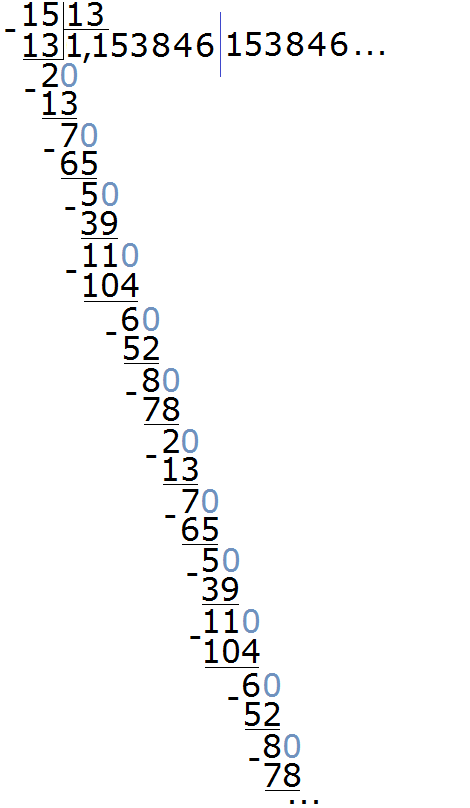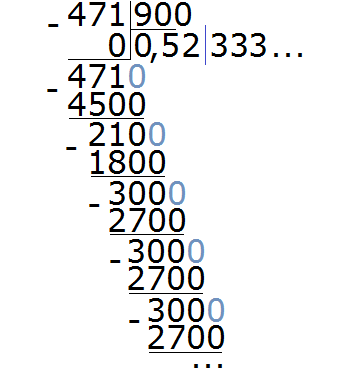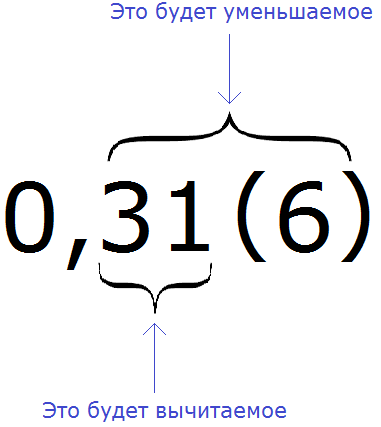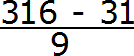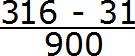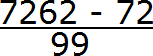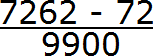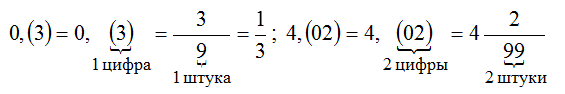Как найти периоды чисел - Сайт, где вы сможете решить свои вопросы

Это очень просто

Время на прочтение
2 мин

Количество просмотров 19K

Рассмотрим следующую задачу. Найти период дроби 1/81. Уверяю, что для решения не потребуется ни калькулятор, ни деление столбиком. Для начала вспомним чему равно 81*(Период). Пусть длина периода n, тогда исходная дробь запишется как:

$frac{1}p=frac{Период}{10^n}+frac{Период}{10^{2n}}+frac{Период}{10^{3n}}+...$

Перепишем данное представление в следующем виде:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotleft(frac{Период}{10^{n}}+frac{Период}{10^{2n}}+..right)$

Последнее выражение можно представить так:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotfrac{1}p$

Ну а теперь то соотношение, которое мы искали:

Для нашего случая это тождество будет следующим:

Разделим левую и правую часть на 9, получим:

Первое число, составленное из одних единиц, которое делится на 9 равно 111111111, это следует из признака делимости на 9. Делить будем через сумму цифр исходного числа. Двигаемся слева направо, складываем цифры делимого и на каждом шаге записываем полученную сумму. Результат работы данного алгоритма — число 12345678,9999… Здесь надо пояснить, что когда мы достигаем крайней правой цифры, то ставим запятую и полученную сумму цифр исходного числа дублируем как бесконечную десятичную дробь. Вспоминаем, что 0,999…=1 и получаем ответ, который мы искали 12345679. Если рассмотреть более общую задачу нахождения периода дроби $frac{1}{9^n}$ , то окажется, что период такой дроби имеет длину ${9^{n-1}}$ и если известен период для случая n-1, то следующий равен произведению данного периода на число вида 11111… (повторяется ${9^{n-1}}$ раз)22222… (повторяется ${9^{n-1}}$ раз)33333… (повторяется ${9^{n-1}}$ раз). Самая правая секция будет иметь вид 8888..889. Последняя цифра девятка.
И еще одно наблюдение, теперь для дробей вида $frac{1}{11^{n}}$ . В этом случае длина периода равна $2cdot{11^{n-1}}$ . И если известен период для случая n-1, то следующий период равен произведению данного периода на число, составленное из 10 блоков, где длина каждого блока $2cdot{11^{n-2}}$ . Блоки имеют следующую структуру:
09090909…
18181818…
27272727…
36363636…
…
последний блок 90909091. Для $frac{1}{11}$ период 09, для $frac{1}{11^{2}}$ период будет 09182736455463728191*9=0082644628099173553719.
Проверил формулу для $frac{1}{11^{3}}$ . Получил

75131480090157776108189331329827197595792637114951164537941397445529676934635612
32156273478587528174305033809166040570999248685199098422238918106686701728024042
0736288504883546205860255447032306536438767843726521412471825694966190833959429,

что совпадает с периодом без ведущих нулей.

Приведу код процедур, которые я использовал для проверки своих выводов.

Function GreatestCommonDivisor(x,y)

    if x=y then
        return x;
    endif;  

    a=min(x,y);
    if a=1 then
        return 1;
    endif;  
    b=x+y-a;

    while TRUE do
     c=b%a; 
     if c=0 then
         return a;
     endif;  
     b=a;
     a=c;
    enddo;

EndFunction

Function NumeratorFractionPeriod(numerator,denumerator)

    // дробь a/b

    a=numerator;
    b=denumerator;

    while b%2=0 do
        b=b/2;
        a=a*5;
    enddo;  

    while b%5=0 do
        b=b/5;
        a=a*2;
    enddo;  
    //наибольший общий делитель
    c=GreatestCommonDivisor(a,b);
    a=a/c;
    b=b/c;

    if b=1 then
        Period=string(a);
        return Period;
    endif;

    if a>b then
        Period=string((a-a%b)/b);
        a=a%b;
        if a=0 then
            return Period;
        endif;  
        Period=Period+"(";
    else
        Period="(";
    endif;      

    while a%10=0 do
        a=a/10;
    enddo;  

    i=a;
    while TRUE do
        j=0;
        while i<b do
            i=i*10;
            j=j+1;
            if j>1 then
             Period=Period+"0";
            endif; 
        enddo;  

        check=i-a;
        if (check%b)=0 then
            Period=Period+(check)/b;
            break;
        else
            j=i%b;
            Period=Period+(i-j)/b;
            i=j;
        endif;    
    enddo;

    return Period+")";
EndFunction

Источник

Периодические десятичные дроби

10 февраля 2012

Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.

Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.

Периодическая десятичная дробь — это любая десятичная дробь, у которой:

Значащая часть состоит из бесконечного количества цифр;

Через определенные интервалы цифры в значащей части повторяются.

Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:

Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:

В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.

Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».

При этом будет происходить следующее:

Сначала разделится целая часть, если она есть;
Возможно, будет несколько чисел после десятичной точки;
Через некоторое время цифры начнут повторяться.

Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.

Задача. Переведите обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:

Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 … = 1,7(3).

В итоге получается дробь: 0,5833 … = 0,58(3).

Записываем в нормальном виде: 4,0909 … = 4,(09).

Получаем дробь: 0,4141 … = 0,(41).

Переход от периодической десятичной дроби к обыкновенной

Рассмотрим периодическую десятичную дробь X = abc(a₁b₁c₁). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:

Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
Найдите значение выражения X · 10^k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.

Задача. Приведите к обыкновенной неправильной дроби числа:

9,(6);

32,(39);

0,30(5);

0,(2475).

Работаем с первой дробью: X = 9,(6) = 9,666 …

В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10^k = 10¹ = 10. Имеем:

10X = 10 · 9,6666 … = 96,666 …

Вычитаем исходную дробь и решаем уравнение:

10X − X = 96,666 … − 9,666 … = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.

Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 …

Период k = 2, поэтому умножаем все на 10^k = 10² = 100:

100X = 100 · 32,393939 … = 3239,3939 …

Снова вычитаем исходную дробь и решаем уравнение:

100X − X = 3239,3939 … − 32,3939 … = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.

Приступаем к третьей дроби: X = 0,30(5) = 0,30555 … Схема та же самая, поэтому я просто приведу выкладки:

Период k = 1 ⇒ умножаем все на 10^k = 10¹ = 10;

10X = 10 · 0,30555 … = 3,05555 …
10X − X = 3,0555 … − 0,305555 … = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.

Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 … Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:

k = 4 ⇒ 10^k = 10⁴ = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 …
10 000X − X = 2475,2475 … − 0,2475 2475 … = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.

Смотрите также:

Сравнение дробей
Тест к уроку «Десятичные дроби» (2 вариант)
Четырехугольная пирамида в задаче C2
Как сдать ЕГЭ по математике
Задача B5: площадь сектора
Задача B4: тарифы на сотовую связь

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 января 2022 года; проверки требуют 4 правки.

Периодическая последовательность — это последовательность, для которой те же самые элементы повторяются снова и снова:

${displaystyle a_{1},a_{2},dots ,a_{p},,a_{1},a_{2},dots ,a_{p},,a_{1},a_{2},dots ,a_{p},dots }$

Число p повторяющихся элементов называется периодом^[1].

Определение[править | править код]

Периодическая последовательность (с периодом p) или p-периодическая последовательность — это последовательность ${displaystyle a_{1},a_{2},a_{3},dots }$ , удовлетворяющая соотношению ${displaystyle a_{n+p}=a_{n}}$ для всех значений n^[1]^[2]^[3]^[4]^[5]. Если последовательность рассматривается как функция, областью определения которой является множество натуральных чисел, то периодическая последовательность — это просто специальный вид периодической функции. Наименьшее p, для которой периодическая последовательность p-периодична, называется её наименьшим периодом^[1]^[6].

Примеры[править | править код]

Любая постоянная функция 1-периодична^[4].

Последовательность периодична с наименьшим периодом 2^[2].

Последовательность цифр в десятичном представлении 1/7 является периодической последовательностью с периодом 6:

${displaystyle {frac {1}{7}}=0{,}142857,142857,142857,ldots }$

Вообще, последовательность цифр в десятичном представлении любого рационального числа является, в конечном счёте, периодической (см. ниже)^[7].

Последовательность степеней −1 периодична с периодом два:

Вообще, последовательность степеней любого корня из единицы периодична. То же выполняется для степеней любого элемента конечного порядка в группе.

Периодическая точка для функции f : X → X — это точка x, орбита^[en] которой

${displaystyle x,,f(x),,f(f(x)),,f^{3}(x),,f^{4}(x),,ldots }$

является периодической последовательностью. Здесь $f^{n}(x)$ означает n-кратную композицию функции f, применённую к x^[6]. Периодические точки играют важную роль в теории динамических систем. Любая функция из конечного множества на себя имеет периодическую точку. Нахождение цикла является алгоритмической задачей поиска такой точки.

Тождества[править | править код]

Частичные суммы[править | править код]

${displaystyle sum _{n=1}^{kp+m}a_{n}=kcdot sum _{n=1}^{p}a_{n}+sum _{n=1}^{m}a_{n}}$

Где k и m<p являются натуральными числами.

Частичные произведения[править | править код]

${displaystyle prod _{n=1}^{kp+m}a_{n}=({prod _{n=1}^{p}a_{n}})^{k}cdot prod _{n=1}^{m}a_{n}}$

Где k и m<p являются натуральными числами.

Периодические 0, 1 последовательности[править | править код]

Любую периодическую последовательность можно построить поэлементным сложением, вычитанием, умножением и делением периодических последовательностей, состоящих из нулей и единиц. Периодические последовательности из нулей и единиц можно выразить через суммы тригонометрических функций:

${displaystyle sum _{k=1}^{1}cos(-pi {frac {n(k-1)}{1}})/1=1,1,1,1,1,1,1,1,1...}$

${displaystyle sum _{k=1}^{2}cos(2pi {frac {n(k-1)}{2}})/2=0,1,0,1,0,1,0,1,0...}$

${displaystyle sum _{k=1}^{3}cos(2pi {frac {n(k-1)}{3}})/3=0,0,1,0,0,1,0,0,1,0,0,1,0,0,1...}$

${displaystyle sum _{k=1}^{N}cos(2pi {frac {n(k-1)}{N}})/N=0,0,0...,1}$

последовательность с периодом N

Обобщения[править | править код]

Последовательность в конечном итоге периодическая, если её можно сделать периодической путём отбрасывания некоторого конечного набора членов с начала. Например, последовательность цифр в десятичном представлении числа 1/56 в конечном итоге периодична:

1 / 56 = 0,017 857142 857142 857142 …^[1].

Последовательность асимптотически периодична, если её члены стремятся к периодической последовательности. То есть, последовательность ${displaystyle x_{1},x_{2},x_{3},dots }$ асимптотически периодична, если существует периодическая последовательность ${displaystyle a_{1},a_{2},a_{3},dots }$ , для которой

${displaystyle lim _{nrightarrow infty }x_{n}-a_{n}=0.}$

^[4]^[8]^[9]

Например, последовательность

1 / 3, 2 / 3, 1 / 4, 3 / 4, 1 / 5, 4 / 5, …

асимптотически периодична, поскольку её члены стремятся к периодической последовательности 0, 1, 0, 1, 0, 1, …

Примечания[править | править код]

↑ ¹ ² ³ ⁴ Ultimately periodic sequence – Encyclopedia of Mathematics. encyclopediaofmath.org (7 февраля 2011). Дата обращения: 13 августа 2021. Архивировано 11 декабря 2021 года.
↑ ¹ ² Weisstein, Eric W. Periodic Sequence (англ.). mathworld.wolfram.com. Дата обращения: 13 августа 2021. Архивировано 13 августа 2021 года.
↑ Bosma, Wieb Complexity of Periodic Sequences. www.math.ru.nl. Дата обращения: 13 августа 2021. Архивировано 17 февраля 2022 года.
↑ ¹ ² ³ Janglajew, Schmeidel, 2012, с. 195.
↑ Menezes, van Oorschot, Vanstone, 2018.
↑ ¹ ² Weisstein, Eric W. Least Period (англ.). mathworld.wolfram.com. Дата обращения: 13 августа 2021. Архивировано 13 августа 2021 года.
↑ Hosch, William L. Rational number (англ.). Encyclopedia Britannica (1 июня 2018). Дата обращения: 13 августа 2021. Архивировано 11 декабря 2021 года.
↑ Cheng, 2017.
↑ Shlezinger, Todros, 2019, с. 260–271.

Литература[править | править код]

Klara Janglajew, Ewa Schmeidel. Periodicity of solutions of nonhomogeneous linear difference equations // Advances in Difference Equations. — 2012. — Ноябрь (т. 2012, вып. 1). — ISSN 1687-1847. — doi:10.1186/1687-1847-2012-195.
Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone. Handbook of Applied Cryptography. — CRC Press, 2018. — ISBN 978-0-429-88132-9.
SuiSun Cheng. New Developments in Difference Equations and Applications: Proceedings of the Third International Conference on Difference Equations. — Routledge, 2017. — ISBN 978-1-351-42880-4.
Nir Shlezinger, Koby Todros. Performance analysis of LMS filters with non-Gaussian cyclostationary signals // Signal Processing. — 2019. — Январь (т. 154). — ISSN 0165-1684. — doi:10.1016/j.sigpro.2018.08.008. — arXiv:1708.00635.

Источник

Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:

0,66666666666666…

0,33333333333333…

0,68181818181818…

Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.

Получаем периодическую дробь

Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.

Итак, делим 1 на 3

23111

Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.

Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.

В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).

В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:

0, (3)

Читается как «ноль целых и три в периоде»

Пример 2. Разделить 5 на 11

23112

Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:

0, (45)

Читается как «ноль целых и сорок пять в периоде»

Пример 3. Разделить 15 на 13

23113

Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:

1, (153846)

Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».

Пример 4. Разделить 471 на 900

23114

В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:

0, 52 (3)

Читается как: «ноль целых пятьдесят две сотых и три в периоде».

Виды периодических дробей

Периодические дроби бывают двух видов: чистые и смéшанные.

Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:

0, (3)

0, (6)

0, (5)

Видно, что в этих дробях период начинается сразу после запятой.

Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:

0,52 (3)

0,16 (5)

0,31 (6)

Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.

Избавляемся от хвоста

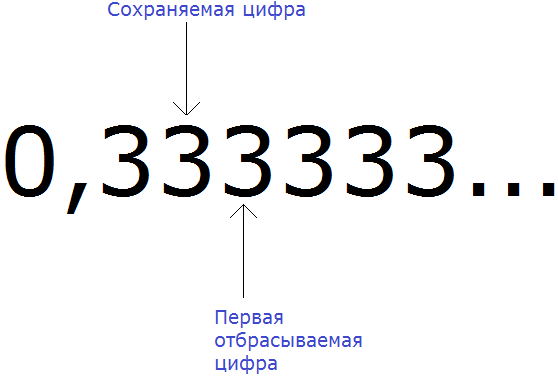
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.

Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:

23115

Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33

0, (3) ≈ 0,33

Округлим периодическую дробь 6,31 (6) до разряда тысячных.

Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:

23116

Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317

6,31 (6) ≈ 6,317

Перевод чистой периодической дроби в обыкновенную дробь

Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.

Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.

Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.

В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.

Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.

Итак, записываем в числителе период дроби 0, (3) то есть тройку:

А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).

В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:

Полученную дробь можно сократить на 3, тогда получим следующее:

Получили обыкновенную дробь .

Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается

Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.

Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:

А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).

В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:

Полученную дробь можно сократить эту дробь на 9, тогда получим следующее:

Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается

Перевод смешанной периодической дроби в обыкновенную дробь

Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.

В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.

Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:

23411

Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)

В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:

23413

Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

23414

Получили выражение, которое вычисляется легко:

Получили ответ

Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается

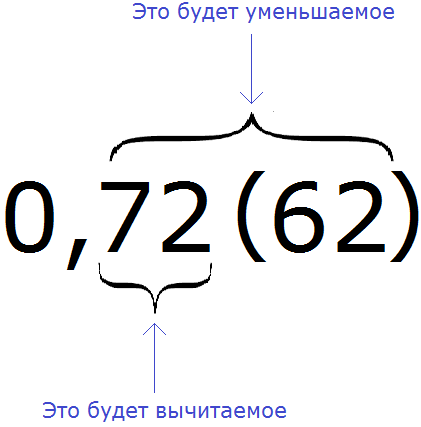
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь

23511

Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)

В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:

23513

В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

23514

Получили выражение, которое вычисляется легко:

Получили ответ

Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Определение

Бесконечная десятичная дробь, у которой одна или несколько цифр повторяются в одной и той же
последовательности, называется периодической десятичной дробью.

Например. $0,1234444444 ldots ; 12,453737373737 ldots$

Повторяющиеся цифры – период – для сокращения записи пишут в круглых скобках.

Например. $0,12344444444 ldots=0,123(4)$ ;
$12,453737373737 ldots=12,45(37)$

Определение

Чистой периодической дробью называется периодическая дробь, у которой период начинается сразу после запятой.

Например. $2,4949 ldots=2,(49)$

Определение

Смешанной периодической дробью называется такая десятичная дробь, у которой между запятой и
периодом есть не менее одной неповторяющейся бесконечное число раз цифры.

Например. $0,11232323 ldots=0,11(23)$ ;
$1,54444 . .=1,5(4)$

Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период,
а в знаменателе записать столько девяток, сколько цифр в периоде.

Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго
периода вычесть число, стоящее до первого периода, результат записать в
числителе; в
знаменатель записать
число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между
запятой и периодом.

Например. Запишем дробь $2,34(2)$ в виде обыкновенной

Читать первую тему – понятие дроби и виды дробей,
раздела дроби.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Это очень просто

Периодические десятичные дроби

Переход к периодической десятичной дроби

Переход от периодической десятичной дроби к обыкновенной

Определение[править | править код]

Примеры[править | править код]

Тождества[править | править код]

Частичные суммы[править | править код]

Частичные произведения[править | править код]

Периодические 0, 1 последовательности[править | править код]

Обобщения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Получаем периодическую дробь

Виды периодических дробей

Избавляемся от хвоста

Перевод чистой периодической дроби в обыкновенную дробь

Перевод смешанной периодической дроби в обыкновенную дробь

Вам также может понравиться

Как найти площадь с разными значениями

Системная ошибка 5 отказано в доступе windows 10 командная строка как исправить

Как можно найти денег на счет

Добавить комментарий Отменить ответ