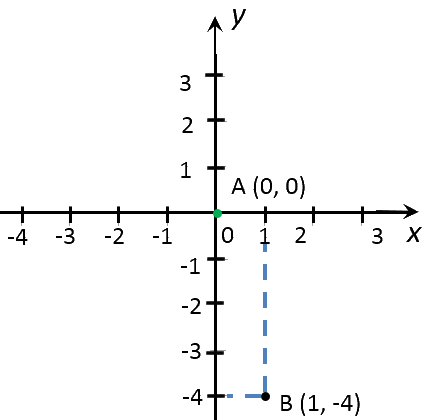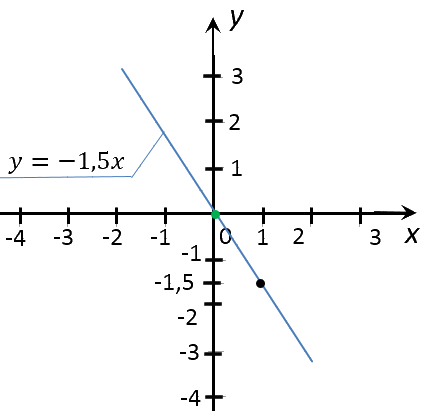Как найти перпендикуляр к графику

Вывод уравнения нормали к графику функции

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Замечание 1

Нормаль — это прямая, которая образует с касательной к графику функции угол в $90°$.

Рисунок 1. Нормальный перпендикуляр к графику касательной. Автор24 — интернет-биржа студенческих работ

В связи с тем, что нормаль перпендикулярна к касательной, её угловой коэффициент будет величиной, обратной к угловому коэффициенту касательной:

$k_{норм}=- frac{1}{k_{к}}= -1 frac{1}{f’(x_0)}$.

Пользуясь полученным выводом, запишем уравнение нормали к графику функции:

$y – y_0 = – frac{1}{f’(x_0)} cdot (x – x_0) left(1right) $, здесь $x_0$ и $y_0$ — координаты точки для которой строится искомая линия, при этом производная в этой точке $f’(x_0) ≠ 0$.

Порядок действий при поиске уравнения нормальной прямой если задана координата $x_0$:

1. Вычисляется, чему равен нулевой игрек $y(x_0)$ для функции.
2. Затем нужно определить производную.
3. Нужно высчитать затем, чему равен $f’(x)$ в точке $x_0$, найденное значение — коэффициент касательной.
4. Все найденные значения подставляются в формулу $(1)$.

Напомним также как выглядит само уравнение касательной:

$y – y_0 = f’(x_0) cdot (x – x_0)$.

Пример 1

Найдите уравнение нормали для функции $y=x^2$ в точке $x_0=2$.

Решение:

Производная данной функции составит $y’(x) = 2x$, затем найдём, чему равен наш подопытный кролик-функция в заданной точке $y_0= x^2 = 2^2 = 4$.

Теперь нужно высчитать производную функции в точке $x_0$: $y’(2) = 2 x = 2 cdot 2= 4$.

Все полученные значения расставляем по своим местам в формулу $(1)$:

$y-4=-frac{1}{4} cdot (x – 2)$

Уравнение нормали найдено.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

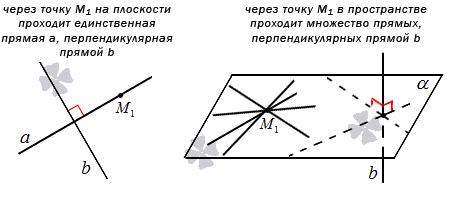
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М1 перпендикулярно к заданной прямой b, то прямые, лежащие  в этой плоскости, в том числе и проходящая через М1 являются перпендикулярными заданной прямой b.

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат Охуz имеем прямую b, то ей соответствует уравнение прямой на плоскости, задается точка с координатами M1(x1, y1), а необходимо составить уравнение прямой a, которая проходит через точку М1 , причем перпендикулярно прямой b.

По условию имеем координаты точки М1. Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a, или координаты нормального вектора прямой a, или угловой коэффициент прямой a.

Необходимо получить данные из заданного уравнения прямой b. По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a. Отсюда получим, что угловые коэффициенты обозначаются как kb и ka. Они связаны при помощи соотношения kb·ka=-1.

Получили, что направляющий вектор  прямой b имеет вид b→=(bx, by), отсюда нормальный вектор – na→=(A2, B2), где значения A2=bx, B2=by. Тогда запишем общее уравнение прямой, проходящее через точку с координатами M1(x1, y1), имеющее нормальный вектор na→=(A2, B2), имеющее вид A2·(x-x1)+B2·(y-y1)=0.

Нормальный вектор прямой b определен и имеет вид nb→=(A1, B1), тогда направляющий вектор прямой a является вектором a→=(ax, ay), где значения ax=A1, ay=B1. Значит осталось составить каноническое или параметрическое уравнение прямой a, проходящее через точку с координатами M1(x1, y1) с направляющим вектором a→=(ax, ay), имеющее вид x-x1ax=y-y1ay или x=x1+ax·λy=y1+ay·λ соответственно.

После нахождения углового коэффициента kb прямой b можно высчитать угловой коэффициент прямой a. Он будет равен -1kb. Отсюда следует, что можно записать уравнение прямой a, проходящей через M1(x1, y1) с угловым коэффициентом -1kb в виде y-y1=-1kb·(x-x1).

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Функция «y = kx» — это первый тип функции, который изучается в математике.

Другими словами, можно сказать, что «y = kx» — это семейство всевозможных функций, где вместо
«k» стоит число.

Примеры функций вида «y = kx».

• y = 4x
• y = −1,5x
• y = x

Давайте определим для каждой из функций выше, чему в них равен числовый коэффициент
«k».

Функция	Коэффициент «k»
y = 4x	k = 4
y = −1,5x	k = −1,5
y = 1 2 x	k = 1 2

Как построить график функции «y = kx»

Из геометрии вспомним аксиому (утверждение, которое не требует доказательства),
что через любые две точки можно провести прямую и притом только одну.

Исходя из этой аксиомы, что
чтобы построить график функции вида «у = kx» нам будет достаточно найти всего
две точки.

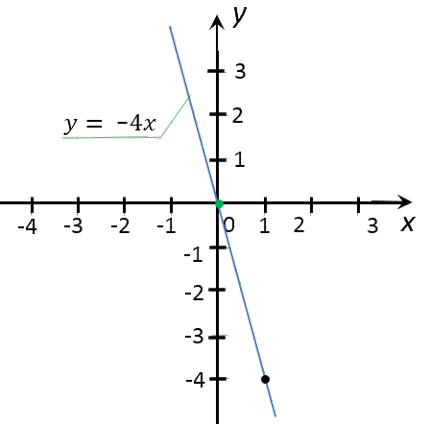
Для примера построим график функции «y = −4x».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

x	Расчет «y»
0	y(0) = −4 · 0 = 0
1	y(1) = −4 · 1 = −4

Полученные значения «x» и «y» — это координаты точек графика

функции «y = −4x».

Запишем полученные координаты точек «y = −4x» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	0
(·)B	1	−4

Отметим полученные точки на системе координат.

Теперь проведем прямую через отмеченные точки. Эта прямая и будет
являться графиком функции «y = −4x».

После построения не забудьте подписать график функции.

Как решать задачи на функцию «y = kx»

Рассмотрим задачу.

---

Построить график функции «y = −1,5x». Найти по графику:

1. значение «y» соответствующее значению «x» равному 1; 0; 2; 3;
2. значение «x», если значение «y» равно
   −3; 4,5; 6;
3. несколько целых значений «x», при которых значения
   «y» положительны (отрицательны).

---

Вначале построим график функции «y = −1,5x».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = −1,5x» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 = 0
(·)B	1	y(1) = −1,5 · 1 = −1,5

Отметим полученные точки на прямоугольной системе координат.

Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = −1,5x».

---

Теперь работаем с построенным графиком функции «y = −1,5x».

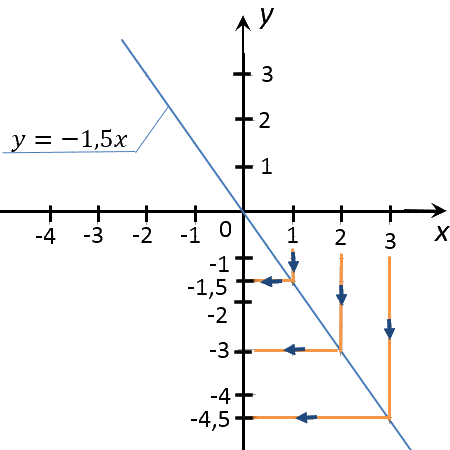
Требуется найти значение «y»,
соответствующее значению «x» равному 1; 0; 2; 3.

---

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

По правилам выше найдем на построенном ранее графике функции «y = −1,5x»
необходимые значения функции «y» для
«x» равным 1; 0; 2; 3.

Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
0	0
1	−1,5
2	−3
3	−4,5

---

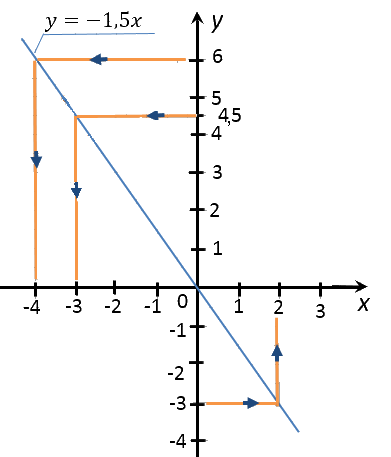
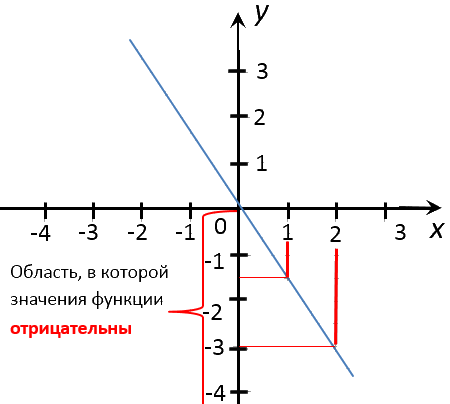
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно −3; 4,5; 6.

---

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры
от оси «Oy».

Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−3	2
4,5	−3
6	−4

---

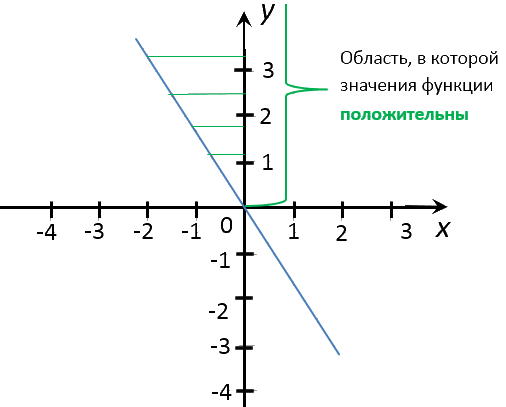
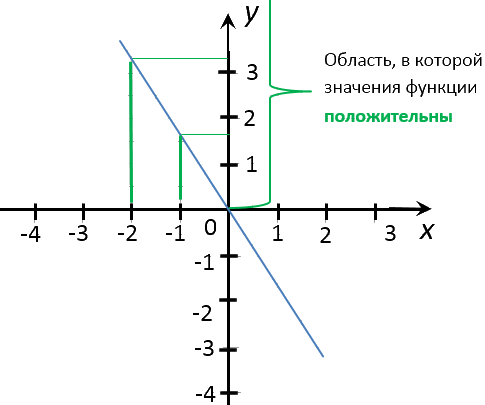
Перейдем к последнему заданию. Нас просят найти несколько целых значений «x»,
при которых значения «y» положительны (отрицательны).

Для решения этой задачи необходимо внимательно изучить
график функции
«y = −1,5x».

Отметим область на оси
«Oy», где значения «y» для графика функции «y = −1,5x»
положительны.

Из этой области проведем от графика функции несколько перпендикуляров
к оси «Ox».

Помните, что по заданию, нас просят найти несколько «целых» значений «x».
Поэтому перпендикуляры мы будем проводить к оси «Ox» в целые числовые значения.

Запишем ответ. При x = −2; x = −1 значения
y > 0.

---

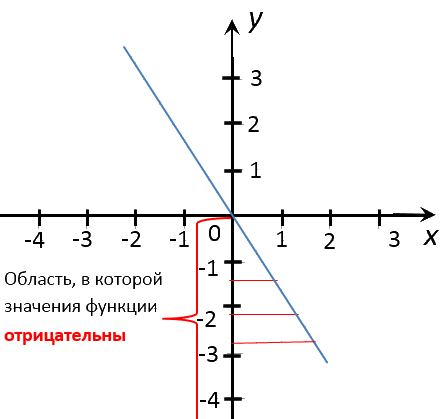
Теперь найдем при каких «x», значения
«y» отрицательны.
Отметим область на оси «Oy», где значения
«y» на графике функции отрицательны.

Проведем перпендикуляры из отмеченной области к оси «Ox» в
целые числовые значения «x».

Запишем ответ. При x = 1; x = 2 значения
y < 0.

---

Рассмотрим другую задачу.

Какие из точек A(5; −3), D(2; 1)
принадлежат графику функции, заданной
формулой
«y = x»?

---

Подробный разбор задачи «Как проверить, что точка принадлежит графику функции» мы приводили в уроке
«Как решать задачи на функцию».

В этом уроке мы вспомним только основные моменты решения подобных задач.

Подставим в функцию
«y = x»
координаты точки (·)A(5; −3).

−3 = · 5

              
−3 = (неверно)

Это означает, что точка (·)А(5; −3)
не принадлежит графику функции «y = x»

Проверим точку (·)D(2; 1).
Также подставим её координаты в функцию «y = x».

1 = ·2

1 =

            
1 = 1(верно)

Это означает, что точка (·)D(2; 1)
принадлежит графику функции «y = x».

---

Ваши комментарии

Оставить комментарий:

---

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k₁x+b₁ — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

   

Если эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b.

Примеры.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Решение:

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

   

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

   

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

   

откуда b=1.

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

   

Ответ: y= -0,2x+1.

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Решение:

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

Ответ: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Решение:

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.

Ответ: x=7.