Геометрия, 10 класс
Урок №10. Перпендикуляр и наклонные
Перечень вопросов, рассматриваемых в теме.
- Определение перпендикуляра, наклонной и проекции наклонной на плоскость;
- Доказательство теоремы о трех перпендикулярах;
- Определение угла между прямой и плоскостью.
Глоссарий по теме
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Основная литература:
Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Дополнительная литература:
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
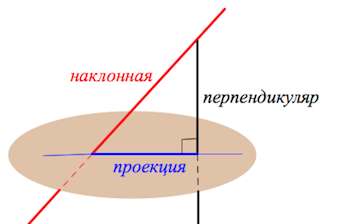
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.
(Рис. 1)
Рассмотрим прямоугольный треугольник АМН. Сторона АН — катет, а сторона AM — гипотенуза, поэтому АН < AM. Поэтому перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.
Следовательно, из всех расстояний от точки А до различных точек плоскости α наименьшим является расстояние до точки Н. Это расстояние, т. е. длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.
Стоит отметить, что в случае двух параллельных плоскостей, расстоянием между ними будет расстояние от произвольной точки одной плоскости до другой плоскости. Например, все точки потолка находятся на одинаковом расстоянии от пола. Если же прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью. Например, все точки прямой b равноудалены от потолка комнаты.
Если мы имеем дело со скрещивающимися прямыми, то расстоянием между ними будет расстояние между одной из этих прямых и плоскостью, проходящей через другую прямую параллельно первой.
Сформулируем теорему о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
(Рис. 2)
На рисунке 2: АН — перпендикуляр к плоскости α, AM — наклонная, а — прямая, проведенная в плоскости α через точку М перпендикулярно к проекции наклонной НМ. Докажем, что прямая а перпендикулярна наклонной AM.
Рассмотрим плоскость АМН. Прямая а перпендикулярна к НМ по условию. Так как прямая а, лежит в плоскости α, а эта плоскость перпендикулярна отрезку AH, то прямая а перпендикулярна к этой плоскости. Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности прямая а перпендикулярна отрезку АМ. Теорема доказана.
Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АН, НМ и AM.
Справедлива также обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Введем теперь понятие проекции произвольной фигуры на плоскость. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
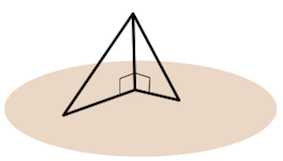
Обозначим буквой F какую-нибудь фигуру в пространстве. Если мы построим проекции всех точек этой фигуры на данную плоскость, то получим фигуру F1, которая называется проекцией фигуры F на данную плоскость (рис. 3).
(Рис. 3)
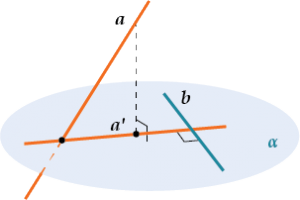
Докажем теперь, что проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая (рис. 4).
Данную плоскость обозначим буквой α. Произвольную прямую, не перпендикулярную к плоскости, обозначим буквой а. Из какой-нибудь точки М прямой а проведем перпендикуляр МН к плоскости α и рассмотрим плоскость β, проходящую через прямую a и перпендикуляр МН. Плоскости α и β пересекаются по некоторой прямой а1.
Докажем, что эта прямая и является проекцией прямой а на плоскость α. В самом деле, возьмем произвольную точку М1 прямой а и проведем в плоскости β прямую М1Н1, параллельную прямой МН.
Так как отрезок MH перпендикуляр к плоскости α и отрезок MH параллелен М1Н1, то отрезок М1Н1 тоже перпендикулярен плоскости α.
Этим мы доказали, что проекция произвольной точки прямой а лежит на прямой а1.
Аналогично доказывается, что любая точка прямой а1 является проекцией некоторой точки прямой а. Следовательно, прямая а1 — проекция прямой а на плоскость α. Что и требовалось доказать.
(Рис. 4)
Теперь введем понятие угла между прямой и плоскостью.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Докажем, что угол между φ0 между данной прямой AM и плоскостью α является наименьшим из всех углов φ, которые данная прямая образует с прямыми, проведенными в плоскости α через точку А.
(Рис. 5)
Обозначим буквой Н основание перпендикуляра (рис. 5), проведенного из точки М к плоскости α.
Рассмотрим произвольную прямую р в плоскости α, проходящую через точку А и отличную от прямой АН.
Угол между прямыми AM и р обозначим через φ.
Докажем, что φ больше чем φ0.
Из точки М проведем перпендикуляр MN к прямой р. Если точка N совпадает с точкой А, то φ равняется 90 градусам и поэтому φ больше чем φ 0. Рассмотрим случай, когда точки А и N не совпадают. Отрезок AM — общая гипотенуза прямоугольных
треугольников ANM и АНМ, поэтому
sinφ=MN/AM
Так как наклонная MN больше, чем перпендикуляр МН, то синус угла φ больше, чем синус угла φ0. Поэтому угол φ больше, чем угол φ0. Что и требовалось доказать.
Тестовый вопрос №7. Прямая AM перпендикулярна плоскости равностороннего треугольника ABC, точка H середина стороны BC. Найдите угол между прямой MH и плоскостью ABC, если AM = a, HB = a.
Решение. Искомый угол – MHA.
Рассмотрим треугольник ABC. Он равносторонний. Это означает, что его медиана так же является высотой и биссектрисой. Так как HB = a, следовательно, любая сторона треугольника имеет длину 2a. Рассмотрим треугольник AHB. Он прямоугольный, т.к. AH медиана и высота. По теореме Пифагора вычислим длину стороны AH: 
Далее рассмотрим треугольник MHA, он прямоугольный, т.к. MA перпендикулярна плоскости ABC. Зная это мы можем выразить тангенс искомого угла: 
Ответ: ∠MHA = 30˚.
Тестовый вопрос №8. Из точки O к плоскости α проведена наклонная, длина которой равна 17 см, проекция наклонной равна 15 см. На каком расстоянии от плоскости находится точка O?
Решение. Нарисуем рисунок. OH – перпендикуляр, OM – наклонная, длина которой 17 см, MH – проекция наклонной, длина которой 15 см.
Треугольник OHM – прямоугольный, т.к. OH – перпендикуляр. Поэтому OH – искомое расстояние. Найдем его по теореме Пифагора: 
Ответ: 8 сантиметров.
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
AB – перпендикуляр к плоскости α. AC – наклонная, CB – проекция. С – основание наклонной, B – основание перпендикуляра.
У равных наклонных, проведенных к плоскости из одной точки, проекции равны.
Из двух наклонных, проведенных к плоскости из одной точки, больше та, у которой проекция больше.
Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
Обратная теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Прямая a, не лежащая в плоскости α, перпендикулярна прямой b, лежащей в плоскости α, тогда и только тогда, когда проекция a‘ прямой a перпендикулярна прямой b.
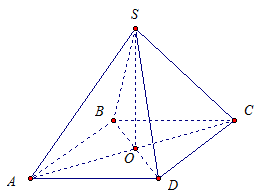
Пример. Отрезок SО – перпендикуляр к плоскости квадрата АВСD, где точка О – центр квадрата. Доказать: (BD perp SC).
Доказательство:
Первый способ.
Имеем квадрат, центр квадрата точка – О, SО – перпендикуляр. Значит, для наклонной SC отрезок ОС есть проекция.
Прямая ВD перпендикулярна прямой ОС, которая является проекцией наклонной SC, значит, по теореме о трех перпендикулярах, прямая ВD перпендикулярна наклонной SC.
Второй способ.
Прямая SО перпендикулярна плоскости АВС, а значит – и прямой ВD, лежащей в ней.
Прямая ВD перпендикулярна SО и прямая ВD перпендикулярна прямой АС по свойству квадрата.
Получаем, что прямая ВD перпендикулярна двум пересекающимся прямым плоскости SОС, значит, она перпендикулярна ко всей плоскости SОС, а значит – и к прямой SC, лежащей в этой плоскости.
Расстояние от точки до плоскости есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ.
- Если прямая параллельна плоскости, то расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
- Если две плоскости параллельны, то расстояние от произвольной точки одной из плоскостей до другой называется расстоянием между данными плоскостями.
- Если две прямые скрещиваются, то расстояние между одной из этих прямых и плоскостью, проведенной через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
Перпендикуляр и наклонная к прямой
СОДЕРЖАНИЕ
- 1 Перпендикуляр и наклонная к прямой
- 1.1 1. Проекция отрезка на прямую.
- 1.2 2. Свойства перпендикуляра и наклонных.
- 2 Наклонная к прямой
- 3 Математика
- 4 Перпендикуляр и наклонная
- 5 Перпендикулярность геометрических элементов
- 6 1. Теорема о проецировании прямого угла
- 7 2. Главные линии плоскости
- 8 3 Прямая, перпендикулярная к плоскости
- 9 4. Перпендикулярные плоскости
- 10 6.5 Перпендикулярные прямые
- 11 Построение перпендикуляра к базовой линии
- 12 Построение направления,параллельного базовой линии
- 13 Перпендикуляр и наклонная
- 13.1 Теорема о трех перпендикулярах
- 14 Пересекающиеся прямые
- 15 Перпендикуляр и наклонная
- 16 Определение перпендикуляра и наклонной
- 17 Перпендикуляр к наклонной линии
1. Проекция отрезка на прямую.
Если через какую-нибудь точку, взятую вне прямой, провести прямую, перпендикулярную к ней, то отрезок от данной точки до прямой для краткости называют одним словом перпендикуляр.
Отрезок СО — перпендикуляр к прямой АВ. Точка О называется основанием перпендикуляра СО (рис).
Если прямая, проведённая через данную точку, пересекает другую прямую, но не перпендикулярна к ней, то отрезок её от данной точки до точки пересечения с другой прямой называют наклонной к этой прямой.
Отрезок ВС — наклонная к прямой АО. Точка С называется основанием наклонной (рис.).
Если из концов какого-нибудь отрезка опустим перпендикуляры на произвольную прямую, то отрезок прямой, заключённый между основаниями перпендикуляров, называется проекцией отрезка на эту прямую.
Отрезок А’В’ — проекция отрезка АВ на ЕС. Отрезок ОМ’ — также называется проекцией отрезка ОМ на ЕС.
Проекцией отрезка КР, перпендикулярного к ЕС, будет точка К’ (рис.).
2. Свойства перпендикуляра и наклонных.
Теорема 1. Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой.
Отрезок АС (рис.) является перпендикуляром к прямой ОВ, а АМ — одна из наклонных, проведённых из точки А к прямой ОВ. Требуется доказать, что АМ > АС.
В ΔМАС отрезок АМ является гипотенузой, а гипотенуза больше каждого из катетов этого треугольника. Следовательно, АМ > АС. Так как наклонная АМ взята нами произвольно, то можно утверждать, что всякая наклонная к прямой больше перпендикуляра к этой прямой (а перпендикуляр короче всякой наклонной), если они проведены к ней из одной и той же точки.
Верно и обратное утверждение, а именно: если отрезок АС (рис.) меньше всякого другого отрезка, соединяющего точку АС любой точкой прямой ОВ, то он является перпендикуляром к ОВ. В самом деле, отрезок АС не может быть наклонной к ОВ, так как тогда он не был бы самым коротким из отрезков, соединяющих точку А с точками прямой ОВ. Значит, он может быть только перпендикуляром к ОВ.
Длина перпендикуляра, опущенного из данной точки на прямую, принимается за расстояние от данной точки до этой прямой.
Теорема 2. Если две наклонные, проведённые к прямой из одной и той же точки, равны, то равны и их проекции .
Пусть ВА и ВС — наклонные, проведённые из точки В к прямой АС (рис.), причём АВ = ВС. Нужно доказать, что равны и их проекции.
Для доказательства опустим из точки В перпендикуляр ВО на АС. Тогда АО и ОС будут проекции наклонных АВ и ВС на прямую АС. Треугольник АВС равнобедренный по условию теоремы. ВО — высота этого треугольника. Но высота в равнобедренном треугольнике, проведённая к основанию, является в то же время и медианой этого треугольника.
Теорема 3 (обратная). Если две наклонные, проведённые к прямой из одной и той же точки, имеют равные проекции, то они равны между собой.
Пусть АС и СВ — наклонные к прямой АВ (рис.). СО ⊥ АВ и АО = ОВ.
Требуется доказать, что АС = ВС.
В прямоугольных треугольниках АОС и ВОС катеты АО и ОВ равны. СО — общий катет этих треугольников. Следовательно, ΔAOС = ΔВОС. Из равенcтва треугольников вытекает, что АС = ВС.
Теорема 4. Если из одной и той же точки проведены к прямой две наклонные, то та из них больше, которая имеет большую проекцию на эту прямую.
Пусть АВ и ВС — наклонные к прямой АО; ВО ⊥ АО и АО>СО. Требуется доказать, что АВ > ВС.
1) Наклонные расположены по одну сторону перпендикуляра.
Угол АСЕ внешний по отношению к прямоугольному треугольнику СОВ (рис.), а поэтому ∠АСВ > ∠СОВ, т. е. он тупой. Отсюда следует, что АВ > СВ.
2) Наклонные расположены по обе стороны перпендикуляра. Для доказательства отложим на АО от точки О отрезок ОК = ОС и соединим точку К с точкой В (рис.). Тогда по теореме 3 имеем: ВК = ВС, но АВ > ВК, следовательно, АВ > ВС, т. е. теорема справедлива и в этом случае.
Теорема 5 (обратная). Если из одной и той же точки проведены к прямой две наклонные, то большая наклонная имеет и большую проекцию на эту прямую.
Пусть КС и ВС — наклонные к прямой КВ (рис.), СО ⊥ КВ и КС > ВС. Требуется доказать, что КО > ОВ.
Между отрезками КО и ОВ может быть только одно из трёх соотношений:
КО не может быть меньше ОВ, так как тогда по теореме 4 наклонная КС была бы меньше наклонной ВС, а это противоречит условию теоремы.
Точно так же КО не может равняться ОВ, так как в этом случае по теореме 3 КС = ВС, что также противоречит условию теоремы.
Следовательно, остаётся верным только последнее соотношение, а именно, что КО > ОВ.
Наклонная к прямой
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
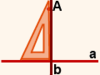
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
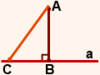
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.
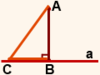
На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
Математика
Теорема 11. Из точки, лежащей вне прямой, на данную прямую можно опустить только один перпендикуляр.
Дана линия AB и внешняя точка C (чер. 29).
Требуется доказать, что можно опустить только одни перпендикуляр.
Доказательство. Предположим, что из точки C опущены на прямую AB два перпендикуляра CD и CE. Продолжим линию CD и отложим на ней точку F на расстоянии DF равном CD и соединим точку F с E.
Перегнем около линии AB верхнюю часть чертежа, тогда
a) линия CD пойдет по направлению линии DF, ибо углы CDE и EDF равны как прямые.
b) точка C совпадает с точкой F, ибо CD = DF по построению, и
c) линия CE совпадет с линией EF, следовательно, угол α = углу β.
Угол α прямой, следовательно, и угол β тоже прямой.
Сумма углов α + β = 2d, следовательно, по теореме 6, две стороны CE и EF составляют одну прямую CEF. Таким образом между двумя точками C и F проведены две не совпадающие прямые CDF и CEF. Это невозможно, следовательно, из точки C на линию AB дух перпендикуляров провести нельзя.
Кроме перпендикуляра всякая линия CE, идущая от точки C до прямой, называется наклонной или косвенной.
Теорема 12 . Перпендикуляр короче наклонной.
Д а ны перпендикуляр CD и наклонная CE (чер. 29).
Требуется доказать, что CD
Доказательство . Из предыдущего построения видно, что
Прямая менее ломаной, следовательно,
Так как CE = EF, CD = DF, то
Расстояние DE называется расстоянием наклонной от перпендикуляра. Это расстояние есть расстояние подошвы перпендикуляра от подошвы наклонной.
Так как перпендикуляр короче всякой наклонной, то длина его выражает собой кратчайшее расстояние от точки до прямой линии.
Отсюда вытекает следующее заключение . Кратчайшее расстояние точки от прямой равно длине перпендикуляра, опущенного из точки на прямую линию.
Теорема 13 . Наклонные, равноотстоящая от перпендикуляра, равны.
Даны линии CD ⊥ AB (чер. 30) и две наклонные DM и DN, находящиеся на равных расстояниях CM и CN (CM = CN).
Требуется доказать, что DM = DN.
Доказательство . Повернем левую часть чертежа около линии CD, как около оси, тогда a) линия CA пойдет по линии CB, ибо углы при C прямые, b) точка M совпадет с N, ибо CM = CN по условию, и линия DM совпадет с линией DN всеми своими точками, следовательно
Теорема 14 . На большем расстоянии от перпендикуляра находится большая наклонная.
Даны DC ⊥ AB и две наклонные DF и DE, находящиеся на расстоянии CF и CE, из которых CF > CE (чер. 31).
Требуется доказать, что DF > DE.
Доказательство . a) Продолжим линию DC и отложим линию CG = CD.
Соединим точки E и F с точкой G. Повернув верхнюю часть чертежа около линии AB, как около ос, увидим, что линия DC пойдет по линии CG, ибо углы при точке C прямые, точка D совпадет с точкою G, линия DE совпадет с линией EG, а DF с FG, следовательно,
b) Внешняя ломаная больше внутренней, следовательно,
DF + FG > DE + EG или 2DF > 2DE
Сократив на 2, имеем:
Теорема 15 (обратная 14). Большая наклонная более удалена от перпендикуляра.
Даны DC ⊥ AB и две наклонные DF и DE, из которых DF > DE (чер. 32).
Требуется доказать, что CF > CE.
Доказательство . Тут могут быть три случая: CF > CE, CF = CE и CF
a) Если бы линия CF была меньше CE, то по теореме 14 линия DF тоже была бы
b) Если бы CF = CE, по теореме 13 было бы DF = DE, что также противоречит условию, следовательно, CF > CE (ЧТД).
Теорема 16 (обратная 13). Равные наклонные находятся на равном расстоянии от перпендикуляра.
Даны равные наклонные DM и DN (черт. 30) (DM = DN).
Требуется доказать, что CN = CM.
Доказательство . Здесь могут быть три случая: CN > CM, CN
a) Если бы было CN > CM, по теореме 14 было бы DN > DM, что противоречит условию.
b) Если бы было CN
Теорема 17 . Каждая точка перпендикуляра, восставленного из середины отрезка, находится на равных расстояниях от его концов.
Дано. Точка C есть середина отрезка AB, следовательно, AC = CB и линия CD ⊥ AB (черт. 33).
Требуется доказать, что DA = DB.
Доказательство . Наклонные DA и DB, находящиеся на равных расстояниях CA и CB, равны, следовательно, DA = DB (ЧТД).
Теорема 18 . Все точки вне перпендикуляра не находятся на равных расстояниях от его концов.
Дана точка E вне перпендикуляра CD (чер. 34).
Требуется доказать, что ее расстояния до концов отрезка AB не равны.
Доказательство . Соединим G, точку пересечения линий AE и CD с концом B, тогда AG = GB.
Ломаная EGB больше EB или
Заменив BG равной линией AG (т. 17), имеем:
Перпендикуляр и наклонная
Теорема. Если из одной точки вне плоскости проведены перпендикуляр и наклонные, то:
1) наклонные, имеющие равные проекции, равны;
2) из двух наклонных больше та, проекция которой больше;
3) равные наклонные имеют равные проекции;
4) из двух проекций больше та, которая соответствует большей наклонной.
Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной (рис. 12.3).
Теорема о площади ортогональной проекции многоугольника на плоскость. Площадь ортогональной проекции многоугольника на плоскость равна произведению площади многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
Пример 1. Через данную точку провести прямую, параллельную данной плоскости.
Решение. Анализ. Предположим, что прямая построена (рис. 12.4). Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в плоскости (по признаку параллельности прямой и плоскости). Две параллельные прямые лежат в одной плоскости. Значит, построив плоскость, проходящую через данную точку и произвольную прямую в данной плоскости, можно будет построить параллельную прямую.
1. На плоскости проводим прямую а.
2. Прямая а и точка А задают плоскость. Построим плоскость .
3. В плоскости через точку А проведем прямую b, параллельную прямой а.
4. Построена прямая b, параллельная плоскости .
Доказательство. По признаку параллельности прямой и плоскости прямая b параллельна плоскости , так как она параллельна прямой а, принадлежащей плоскости .
Исследование. Задача имеет бесконечное множество решений, так как прямая а в плоскости выбирается произвольно.
Пример 2. Определите, на каком расстоянии от плоскости находится точка А, если прямая АВ пересекает плоскость под углом 45º, расстояние от точки А до точки В, принадлежащей плоскости, равно см.
Решение.Сделаем рисунок (рис. 12.5):
АС – перпендикуляр к плоскости , АВ – наклонная, угол АВС – угол между прямой АВ и плоскостью . Треугольник АВС – прямоугольный, так какАС – перпендикуляр. Искомое расстояние от точки А до плоскости – это катет АС прямоугольного треугольника. Зная угол и гипотенузу найдем катетАС:
В ответе получаем: АС = 3 см.
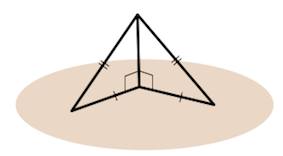
Пример 3. Определите, на каком расстоянии от плоскости равнобедренного треугольника находится точка, удаленная от каждой из вершин треугольника на 13 см, если основание и высота треугольника равны по 8 см.
Решение. Сделаем рисунок (рис. 12.6). Точка S удалена от точек А, В и С на одинаковое расстояние. Значит, наклонные SA, SB и SC равные, SO – общий перпендикуляр этих наклонных. По теореме о наклонных и проекциях АО = ВО = СО.
Точка О – центр окружности, описанной около треугольника АВС. Найдем ее радиус:
где ВС – основание; AD – высота данного равнобедренного треугольника.
Находим стороны треугольника АВС из прямоугольного треугольника ABD по теореме Пифагора:
Теперь находим ОВ:
Рассмотрим треугольник SOB: SB = 13 см, ОВ = 5 см. Находим длину перпендикуляра SO по теореме Пифагора:
В ответе получаем: SO = 12 см.
Пример 4. Даны параллельные плоскости и . Через точку М, не принадлежащую ни одной из них, проведены прямые а и b, которые пересекают плоскость в точках А1 и В1, а плоскость – в точках А2 и В2. Найти А1В1, если известно, что МА1 = 8 см, А1А2 = 12 см, А2В2 = 25 см.
Решение. Так как в условии не сказано, как расположена относительно обеих плоскостей точка М, то возможны два варианта: (рис. 12.7, а, б). Рассмотрим каждый из них. Две пересекающиеся прямые а и b задают плоскость. Эта плоскость пересекает две параллельные плоскости и по параллельным прямым А1В1 и А2В2 согласно теореме 5 о параллельных прямых и параллельных плоскостях.
Отсюда
Получаем ответ: 10 см и 50 см.
Пример 5. Через точку А плоскости проведена прямая АВ, образующая с плоскостью угол . Через прямую АВ проведена плоскость , образующая с плоскостью угол . Найти угол между проекцией прямой АВ на плоскость и плоскостью .
Решение. Сделаем рисунок (рис. 12.8). Из точки В опустим перпендикуляр на плоскость . Линейный угол двугранного угла между плоскостями и – это угол ПрямаяAD перпендикулярна плоскости треугольника DBC, по признаку перпендикулярности прямой и плоскости, так как иПо признаку перпендикулярности плоскостей плоскость перпендикулярна плоскости треугольника DBC, так как она проходит через прямую AD. Искомый угол построим, опустив перпендикуляр из точки С на плоскость , обозначим его Найдем синус этого угла прямоугольного треугольникаСАМ. Введем вспомогательный отрезок ВС = а. Из треугольника АВС: Из треугольникаВМС ( ) найдем:
Тогда искомый угол
Перпендикулярность геометрических элементов
1. Теорема о проецировании прямого угла
2. Главные линии плоскости
3. Прямая, перпендикулярная к плоскости
4. Перпендикулярные плоскости
5. Перпендикулярные прямые
1. Теорема о проецировании прямого угла
Возможны три случая проецирования прямого угла:
1. Если обе стороны прямого угла прямые общего положения, то прямой угол проецируется искаженно на все три плоскости проекций.
2. Если обе стороны прямого угла параллельны какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину.
3. Если одна сторона прямого угла параллельна какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину, рис. 64. Это основная теорема о проецировании прямого угла.
Дано: ÐАВС = 90°; ВСúú Н. Необходимо доказать: ÐА ¢В ¢С ¢ = 90°.
ВС ^АВ , следовательно ВС ^ВВ ¢ — по свойству ортогонального проецирования
4. В ¢С ¢^А ¢В ¢ — что и требовалось доказать
2. Главные линии плоскости
Линии уровня плоскости
Кроме прямых линий общего положения, в плоскости отмечают три главные линии: горизонтальную (горизонталь), фронтальную (фронталь) и линию наибольшего наклона. Эти линии применяют как вспомогательные: они упрощают решение задач. Две из них — горизонтальная и фронтальная — уже рассматривались.
Необходимо добавить, что все горизонтальные линии плоскости параллельны между собой, а их горизонтальные проекции параллельны горизонтальному следу плоскости (рис. 65). Горизонтальный след плоскости — одна из горизонталей.
Рис. 64
Рис. 65
Все фронтальные линии плоскости параллельны между собой, а их фронтальные проекции параллельны фронтальному следу плоскости. Фронтальный след плоскости — одна из фронтальных линий (рис. 66).
Линии наибольшего наклона плоскости
Прямые плоскости, перпендикулярные к прямым уровня этой плоскости, называются линией наибольшего наклона (ЛНН) данной плоскости к соответствующей плоскости проекций.
Линии наибольшего наклона плоскости перпендикулярны к ее следам или к линиям уровня (либо к ее горизонталям, либо к фронталям, либо к ее профильным прямым) (рис. 67).
В случае перпендикулярности к горизонтали определяется наклон к плоскости проекций H (при этом ЛНН называют линией наибольшего ската ), перпендикулярности к фронтали — наклон к плоскости проекций V, перпендикулярности к профильной прямой — наклон к плоскости проекций W.
На рис. 67, 68 дано изображение плоскости (а ||b ), для которой требуется построить линию наибольшего наклона к горизонтальной плоскости проекций H.
Проведем в данной плоскости горизонталь h (рис. 68). Прямая n , перпендикулярная к прямой h , перпендикулярна и к следу плоскости H (KL ^H) (рис. 69).
Угол наклона прямой n к плоскости H определяется как угол между прямой и ее проекцией на плоскость H. Строим KK ¢^H (рис. 69). Тогда угол j — искомый угол наклона прямой n к плоскости H.
На рис. 68 построена линия наибольшего наклона плоскости к горизонтальной плоскости проекций — прямая n . Угол наклона плоскости к плоскости H получают при определении натуральной величины отрезка KM при построении прямоугольного треугольника по проекциям K ¢M ‘ и
3 Прямая, перпендикулярная к плоскости
Прямая, перпендикулярная к плоскости, если перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. На основании теоремы о проецировании прямого угла в качестве прямых плоскости общего положения удобнее всего использовать ее линии уровня.
Поэтому, проводя перпендикуляр к плоскости, необходимо брать в этой плоскости две такие прямые: горизонталь и фронталь.
Проекции прямой, перпендикулярной к плоскости, на комплексном чертеже перпендикулярны к соответствующим проекциям ее линий уровня, т.е. если прямая линия перпендикулярна плоскости, то ее горизонтальная проекция должна быть перпендикулярна горизонтальной проекции горизонтали, а ее фронтальная проекция — фронтальной проекции фронтали (рис. 70) или соответствующим следам плоскости (рис. 71).
Рис. 70
Рис. 71
На рис. 72 изображена плоскость общего положения (a ||b ), к которой к которой требуется провести перпендикулярную прямую.
Проводим в данной плоскости горизонталь h (через точки 1,3) и фронталь v (через точки 1,4) (рис. 72).
Затем из точки 1 проводим прямую n перпендикулярно к горизонтали и фронтали плоскости следующим образом:
Построенная прямая n (n’ , n» ) является искомым перпендикуляром к плоскости .
4. Перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную данной плоскости. Построение таких плоскостей может быть выполнено двумя путями:
1) плоскость проводится через перпендикуляр к другой;
2) плоскость проводится перпендикулярно прямой, принадлежащей другой плоскости.
На рис. 73 изображены прямая общего положения
Для решения задачи необходимо через какую-нибудь точку данной прямой, например, точку М, провести перпендикуляр к плоскости , заданной пересекающимися прямыми a и b.
Проводим в плоскости горизонталь h и фронталь v (рис. 73).
Далее из точки М , взятой на прямой
6.5 Перпендикулярные прямые
Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.
На рис. 74 изображена прямая
Через точку А прямой
Любая прямая, лежащая в плоскости будет также перпендикулярна к данной прямой
Соединив точки А и В , лежащие в плоскости, получим прямую n , перпендикулярную к данной прямой
Построение перпендикуляра к базовой линии
Пусть АВ есть базовая линия, точки которой недоступны для установки теодолита, и к этой линии необходимо построить перпендикуляр с точки Г, где установлен теодолит (рис. 15.5).
Задача сводится к отысканию основания перпендикуляра (точка Т°), опущенного с точки стояния теодолита на базовую линию. Для этого на базовой линии
Рис. 15.5. Построение перпендикуляра к базовой линии
выбирают на некотором удалении друг от друга две точки 1 и 2. Рулеткой измеряют расстояние между этими точками, а также измеряют расстояние S от точки 2 до оси вращения теодолита. Кроме того, измеряется угол /? в точке стояния прибора.
Найдя отрезки х и у, находят положение точки V на базовой линии построением этих отрезков соответственно от точек 2 или 1. Очевидно, что х + у = Ь.
Кроме того, следует проконтролировать выполнение условия у + /?’ = 90°, для чего необходимо измерить угол /У’.
Построение направления,параллельного базовой линии
В протяжённых направляющих со сложным креплением с большими пролётами (для подкрановых путей) выверку параллельности производят от двух параллельных створов. При исполнительной съёмке конструкций, установленных но монтажной оси, также возникает задача построения створа, параллельного оси, с целью производства съёмки методом бокового нивелирования. Часто в таких случаях створ задаётся коллимационной плоскостью теодолита, ориентированного параллельно базовой линии.
Ориентировать визирную плоскость теодолита параллельно базовой линии можно несколькими способами.
На рисунке 15.6, а) приведён способ построения параллельного направления путём введения поправки в отсчёт по горизонтальному кругу теодолита, труба которого ориентирована приблизительно параллельно базовой линии.
Теодолит устанавливают в точке Т на некотором удалении от базовой линии, заданной точками А и В. К базовой линии в точках А и В последовательно прикладывается измерительная линейка (нивелирная шашечная рейка) и производятся отсчёты а и b. Если разность отсчётов Д = b — а не равна нулю, то трубу теодолита следует повернуть на угол Да, значение которого вычисляют по формуле
где SI и S2 — расстояния от теодолита до точек базовой линии. Для контроля отложения угла Да целесообразно вычислить по рейкам отсчёт а(), соответствующий параллельному положению коллимационной плоскости теодолита заданной базовой линии:
Задача может быть решена без линейных измерений, а с использованием лишь нивелирных шашечных рейек, устанавливаемых горизонтально в исходных точках А и В базовой линии.
Установив теодолит в точку Т на некотором удалении от базовой линии (рис. 15.6, b), приводят его в рабочее положение, и зрительную трубу визуально ориентируют по направлению Тх, так, чтобы её коллимационная плоскость в перспективе пересеклась с направлением базовой линии. В этом положении зрительной трубы производят отсчёты по рейке а, и а2, последовательно устанавливаемой в исходных точках А и В.
При следующем положении зрительной трубы, когда её ось ориентирована по направлению Тх2 на удаление от базовой линии, по рейкам, установленным в тех
Построение направления, параллельного базовой линии
же точках, последовательно читают отсчёты а, и а4. Далее вычисляется отсчёт но рейке ап = а2 + z, соответствующий параллельному положению визирной плоскости базовой линии. Здесь z вычисляют по формуле
Вычислив отсчёт а0 , устанавливают рейку на одну из исходных точек (естественно, на дальнюю) и, наведя крест сетки нитей на этот отсчёт, закрепляют трубу. Контролируют построенное направление но другим точкам, задающим базовую линию.
Перпендикуляр и наклонная
Перпендикуляр короче любой наклонной, проведенной к плоскости из той же точки
У равных наклонных, проведенных к плоскости из одной точки, проекции равны. Верно и обратное. Если равны проекции наклонных к плоскости, проведенных из одной точки, то равны и наклонные.
Из двух наклонных, проведенных к плоскости из одной точки, больше та, у которой проекция больше.
Верно и обратное.
Теорема о трех перпендикулярах
Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.
Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Заметим, что, вообще говоря, теорема о трех перпендикулярах верна и в более общем случае:
Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. И наоборот.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Пересекающиеся прямые
Если две прямые имеют общую точку, то говорят, что эти прямые пересекаются. Такие прямые называют пересекающимися прямыми:
Говорят: прямые a и b пересекаются в точке O . Точка O лежит и на прямой a, и на прямой b . Точка O является точкой пересечения прямых a и b .
Точка пересечения – это точка, общая для двух или более геометрических фигур.
Перпендикуляр и наклонная
При пересечении вертикальной и горизонтальной прямой линии образуется четыре прямых угла. Такие линии, относительно друг к другу, называются перпендикулярными линиями или просто перпендикулярами:
Прямые a и b взаимно перпендикулярны. Перпендикулярность обозначается символом ⊥, то есть a ⊥ b или b ⊥ a. Каждая из этих прямых называется перпендикуляром относительно другой прямой: a – перпендикуляр к b, и b – перпендикуляр к a.
Даже если прямые не являются вертикальной и горизонтальной линиями, но при пересечении образуют четыре прямых угла, то они всё равно являются перпендикулярными:
Если прямая линия пересекает другую не под прямым углом, то такая линия называется наклонной к прямой, которую она пересекает. При этом образуется четыре угла: два из них будут острыми и два тупыми:
Образованные острые углы равны и относительно друг друга будут называться вертикальными углами. То же самое можно сказать и об образованных тупых углах – они равные и вертикальные.
Определение перпендикуляра и наклонной
1) Определение перпендикуляра и наклонной.
Пусть дана плоскость и не лежащая на ней точка.
· Отрезок прямой, перпендикулярной плоскости, соединяющий данную точку с точкой на плоскости называется перпендикуляром из данной точки к данной плоскости.
· Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
· Любой отрезок, соединяющий данную точку с точкой на плоскости и не являющийся перпендикуляром к плоскости, называется наклонной.
· Конец отрезка, лежащий в плоскости, называется основанием наклонной.
На рисунке из точки А проведены к плоскости α перпендикуляр АВ и наклонная АС. Точка В — основание перпендикуляра, точка С — основание наклонной, ВС — проекция наклонной АС на плоскость α.
2) Доказательство того, что перпендикуляр корочек наклонной
На рисунке 2 изображена плоскость α, перпендикуляр к ней AO, наклонная AB, а также показан отрезок BO, соединяющий основания наклонной и перпендикуляра. Отрезки AO, BO и AB образуют ΔAOB.
Рассмотрим ΔAOB, из определения перпендикуляра следует, что он прямоугольный. Перпендикуляр AO является катетом этого треугольника, а наклонная AB – его гипотенузой. Катет прямоугольного треугольника всегда меньше его гипотенузы (по теореме Пифагора), следовательно, перпендикуляр всегда короче наклонной.
3) Определение проекции
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
Отрезок BO на рисунке 2 – является проекцией наклонной AB.
4) Теорема о сравнительной длине наклонных и их проекций
А) Любая наклонная больше своей проекции.
Вновь рассмотрим ΔAOB, изображенный на рис. 2, из определения перпендикуляра следует, что он прямоугольный. Проекция BO является катетом этого треугольника, а наклонная AB – его гипотенузой, т. к. катет прямоугольного треугольника всегда меньше его гипотенузы, следовательно, проекция наклонной на плоскость всегда короче самой наклонной.
Б) Равные наклонные имеют равные проекции
Доказательство: Рассмотрим треугольники AOB и AOD, они равны, т. к. равны их гипотенузы AB и AD, и углы AOB и AOD (они прямые), а сторона AO у них общая. Из равенства треугольников следует и равенство их сторон BO = OD, что и требовалось доказать.
В) Если проекции наклонных равны, то и наклонные равны. Доказывается аналогично утверждению Б.
Г) Большей наклонной соответствует большая проекция.
Рассмотрим прямоугольные треугольники AOB и AOD, AB > AD.
=
=
Но так как AB > AD => AB2 > AD2 => > =>
=> BO > DO. Что и требовалось доказать.
Д) Из двух наклонных больше та, у которой проекция больше. Доказывается аналогично Г.
Перпендикуляр к наклонной линии
Задачи, в которых определяются натуральные величины отрезков прямых, плоских фигур, углов и т.д., называются метрическими. В основе решения любой метрической задачи лежат свойства конгруэнтности и теорема о проецировании прямого угла (см. тему 1).
6.1. Определение натуральной величины отрезка прямой линии общего положения методом прямоугольного треугольника
Рис. 6.1. Натуральная величина отрезка определяется гипотенузой прямоугольного треугольника у которого катеты равны разности координат начала и конца.
Аналитически длина отрезка вычисляется (на языке программирования) по формуле:
s = sqrt ((xA-xB)*(xA-xB)+(xA-xB)*(xA-xB)+(xA-xB)*(xA-xB)),
где
xA-xB — разность широт начальной и конечной точек отрезка;
yA-yB — разность глубин начальной и конечной точек отрезка;
zA-zB — разность высот начальной и конечной точек отрезка;
6.2. Перпендикулярность прямой и плоскости
Для того, чтобы прямая была перпендикулярна плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекции перпендикулярна фронтальной проекции фронтали (рис. 6.4,а).
а) б) в)
Рис. 6.2. Прямая перпендикулярная плоскости (ее фронтали и горизонтали).
Если плоскость задана следами, то прямая, перпендикулярная к ней, будет изображаться прямой линией, перпендикулярной к одноименным следам плоскости (имеем горизонтальный след — это горизонталь и фронтальный след — фронталь плоскости) (рис. 6.2,б).
Если прямая перпендикулярна к проецирующей плоскости, то она будет являться линией уровня (рис. 6.2,в).
Прямая а перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в плоскости (на рис. плоскость задана следами, а две пересекающиеся прямые f и h выбраны фронталью и горизонталью, которые параллельны следам плоскости).
6.3. Перпендикулярность двух плоскостей
На рис. 6.4, а показано построение плоскости Q (n пересекается с m), проходящей через точку К, перпендикулярной плоскости треугольника АВС и параллельной заданной прямой l (последнее дополнительное условие определяет единственное решение задачи).
Рис.6.4. Плоскость проходящая через перпендикуляр к другой плоскости перпендикулярна ей.
Решение задачи состоит в следующем: вначале, опускаем из точки К перпендикуляр n на плоскость треугольника АВС, для чего проводим горизонталь h и фронталь f в плоскости треугольника, и затем строим n’ перпендикулярно h’ и n» перпендикулярно f», и через точку К проводим прямую m, параллельную прямой l. Две пересекающиеся прямые m и n определяют искомую плоскость, перпендикулярную заданной плоскости.
Аналогично решаются задачи о построении перпендикулярной плоскости к плоскости, заданной следами. На рис. показана такая задача. Кроме того, плоскость Р проведена перпендикулярно и плоскости Н.
Рис. 6.5. Плоскость Q (ее след перепендикулярен P) явно видно, что перпендикулярна P.
По определению: плоскость перпендикулярно другой плоскости, если она перпендикулярно двум пересекающимся прямым этой плоскости.
Если плоскость перпендикулярна горизонтальной линии (горизонтали), то она перпендикулярна горизонтальной плоскости проекций Н
6.4. Линия ската и углы наклона плоскости к плоскостям проекций
Линией наибольшего ската (уклона) называется прямая плоскости, перпендикулярная к горизонтальному следу или горизонталям этой плоскости. (рис. 6.7, а,б, а также см. тему 3). При помощи линий ската определяется угол наклона данной плоскости к плоскости H.
Натуральная величина наклона плоскости (в частности, линий ската) может быть на ортогональном чертеже определена с помощью прямоугольного треугольника.
а) б)
Рис. 6.7. а) Прямая плоскости перпендикулярная ее горизонтали называется линией ската, б) прямая плоскости перпендикулярная горизонтальному следу плоскости является линией ската.
Аналогично могут быть определены углы наклона плоскости и к плоскостям V и W. Для этого используются прямые наибольшего уклона данной плоскости к соответствующим плоскостям проекций.
Прямые наибольшего уклона, перпендикулярные фронталям плоскости, образуют наибольший угол с фронтальной плоскостью;
прямые наибольшего уклона, перпендикулярные профильным прямым плоскости, образуют наибольший угол с профильной плоскостью проекций.
Угол, образованный между прямой наибольшего уклона и ее проекцией на выбранную плоскость проекций, определяют угол наклона плоскости общего положения к плоскостям проекций. На эпюре данный угол может быть определен из метода прямоугольного треугольника.
Что такое перпендикуляр к прямой? Как построить перпендикуляр к прямой? Сколько перпендикуляров можно провести из точки к прямой? Что такое наклонная? Что называется проекцией наклонной? Об этом — ниже.
Определение.
Перпендикуляр, опущенный из точки A на прямую a — это отрезок, лежащий на прямой, перпендикулярной прямой a, один конец которого — точка A, второй — точка пересечения этих двух прямых.
Как построить перпендикуляр к прямой?
рисунок 1
На рисунке 1 изображены прямая a и точка A, не лежащая на прямой a.
Чтобы построить перпендикуляр, воспользуемся угольником.
рисунок 2
Угольник располагаем так,
чтобы одна сторона прямого угла проходила вдоль прямой a,
а вторая — через точку A.
рисунок 3
Если провести через точку A вдоль стороны угольника прямую,
то получим прямую b, перпендикулярную данной прямой a.
Нам нужно построить перпендикуляр, то есть отрезок — часть этой прямой.
рисунок 4
Соединим точку A с точкой на пересечении прямых a и b
(назовем вторую точку B).
Отрезок AB — перпендикуляр, проведенный из точки A к прямой a.
Точка B называется основанием перпендикуляра.
Расстояние от точки до прямой измеряется длиной перпендикуляра.
Расстояние от точки A до прямой a (рисунок 4) равно длине отрезка AB.
Из данной точки к данной прямой можно провести только один перпендикуляр.
Любой другой отрезок, который соединяет точку A с точкой на прямой a, называется наклонной.
Определение.
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
рисунок 5
На рисунке 5 AC — наклонная, проведенная из точки A к прямой a.
Точка C называется основанием наклонной AC.
Определение.
Отрезок, который соединяет основание перпендикуляра с основанием данной наклонной, называется проекцией этой наклонной на прямую.
рисунок 6
На рисунке 6 BC — проекция наклонной AC на прямую a.
Перпендикуляр часто встречается при решении задач, связанных с треугольниками. В частности, определение высоты треугольника опирается на перпендикуляр.
В следующий раз рассмотрим свойства перпендикуляра и наклонной.
Перпендикулярные прямые. Перпендикуляр и наклонная. Расстояние от точки до прямой
Прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком ⊥. Запись а ⊥ b читается: прямая аперпендикулярна прямой b.
Теорема. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Перпендикуляр к прямой – это отрезок, проведенный из заданной точки к прямой под прямым углом.
Расстояние от точки до прямой – это длина перпендикуляра, проведенного к прямой из данной точки.
Наклонной, проведенной из данной точки к данной прямой, называется любой отрезок, соединяющий данную точку с точкой прямой, не являющийся перпендикуляром к прямой. Конец отрезка, лежащий на прямой, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
Последнее изменение: Воскресенье, 29 Январь 2017, 17:44
Назад