Задача.
Расстояние от точки О до сторон квадрата равно 13 см. Найдите расстояние от точки О до плоскости квадрата, если сторона квадрата равна 10 см.
Решение.
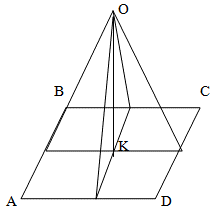
Точка О, которая равноудалена от каждой из сторон квадрата будет проецироваться в точку пересечения его диагоналей (центр). Докажем это.
Опустим из точки О на плоскость квадрата перпендикуляр, который коснется плоскости квадрата в точке К. Теперь докажем равенство образовавшихся прямоугольных треугольников треугольников. Поскольку их гипотенузы равны по условию задачи, а один из катетов – общий, то вторые катеты также равны как следствие из теоремы Пифагора. Таким образом, точка К равноудалена от сторон квадрата и является его центром.
Поскольку сторона квадрата равна 10 см, то точка К удалена от каждой из них на 10/2 = 5 см . Из имеющегося прямоугольного треугольника с катетом 5 см и гипотенузой 13 см, найдем его катет (который и является расстоянием от точки О до плоскости квадрата.
OK 2 = 132 – 5 2
OK = 12
Ответ: 12 см
0
Параллелограмм и плоскость |
Описание курса
| Перпендикуляр к плоскости прямоугольного треугольника
|
Как решить задачу по геометрии (найти расстояние)…?Bttn kkot 8 лет назад
КВ-перпендикуляр к плоскости квадрата ABCD. Постройте расстояние от точки К до прямой AD
RIOLIt 8 лет назад Даже, без чертежа, наглядно представляется себе, прямоугольный треугольник АВК, где один катет КБ,- заданный по условию, перпендикуляр. Второй катет АВ,- сторона, заданного квадрата( заданной плоскости), гипотенуза- АК и должна быть искомым расстоянием до стороны ( прямой АД). модератор выбрал этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить bezdelnik 8 лет назад Если отвечать на вопрос, принимая за расстояние от точки К до прямой АД кратчайшее расстояние, то для построения этого расстояния надо соединить прямой линией точку К с точкой А. В общем случае можно построить бесчисленное количество расстояний от точки К до прямой АД, соединяя точку К с любой точкой прямой АД. Отрезок КА – кратчайшее расстояние, отрезок КД – наибольшее расстояние от точки К до прямой КД.
в избранное
ссылка
отблагодарить Rafail Расстоянием от точки до прямой называется КРАТЧАЙШЕЕ РАССТОЯНИЕ, т.е. длина ПЕРПЕНДИКУЛЯРА, опущенного из заданной точки (вне прямой) на заданную прямую. Конкретно, в данной задаче, РАССТОЯНИЕМ ОТ ТОЧКИ К ДО ПРЯМОЙ, содержащей отрезок AD (прямая – бесконечна, а AD – конечный отрезок на бесконечной прямой, прямой AD не бывает.), является ТОЛЬКО отрезок КА – гипотенуза треугольника ABK.
bezdelnik Вы непоследовательны:”Расстоянием от точки до прямой называется КРАТЧАЙШЕЕ РАССТОЯНИЕ, т.е. длина ПЕРПЕНДИКУЛЯРА, опущенного из заданной точки (вне прямой) на заданную прямую. Конкретно, в данной задаче, РАССТОЯНИЕМ ОТ ТОЧКИ К ДО ПРЯМОЙ, содержащей отрезок AD (прямая – бесконечна, а AD – конечный отрезок на бесконечной прямой, прямой AD не бывает.), является ТОЛЬКО отрезок КА – ГИПОТЕНУЗА треугольника ABK.” Последнее верно, а “т.е. длина ПЕРПЕНДИКУЛЯРА” неверно. То что отрезок КА – кратчайшее расстояние у меня написано, но это не значит, что не может быть других расстояний.
Rafail Вы что, не согласны, что KB перпендикулярно AD?. Основную мысль Вы не поняли. Не бывает других (нескольких) РАССТОЯНИЙ от точки до прямой, оно ЕДИНСТВЕННОЕ, и равно длине ПЕРПЕНДИКУЛЯРА, проведенного от точки (К) к прямой, т.е. КА. А длины отрезков, соединяющих точку К с ЛЮБОЙ точкой на прямой, содержащей отрезок AD, всего лишь длины соответствующих отрезков, но они не являются РАССТОЯНИЕМ от точки К до прямой, содержащей отрезок AD.
bezdelnik КВ и АД лежат в разных плоскостях, поэтому КВ не пересекается с АД.
Rafail Я ошибся, конечно нужно было написать не КВ, а КА, ведь и разногласия у нас с Вами возникли по поводу перпендикулярности КА и AD.
все комментарии (еще 5) Знаете ответ? |
Смотрите также: Объём куба равен 72. Как найти объём четырёхугольной пирамиды внутри куба? Как найти площадь прямоугольной трапеции с меньшими сторонами 6 см и ∠135°? Как найти площадь трапеции АВСD с основаниями АВ и СD, если (см.)? Стороны треугольника 16 и 22 см, высота 11 см. Как найти другую высоту? Как решить: а – основание, h – высота, S – площадь треугольника? Как найти стороны прямоугольника, если его площадь равна 250 см², (см)? В трапеции АВСD диагональ АС перпендикулярна СD, периметр 20. Как найти АD? Диагональ АC квадрата АВСD равна 18,4 см. Как решить? Как решить: Основания прямоугольной трапеции равны а и b, один из углов α? Как найти углы В и D трапеции АВСD с основаниями AD и ВС, если ∠А=36°, ∠С=? |
Пусть SA – данный перпендикуляр. Тогда SB = SD = а (так как равные наклонные имеют равные проекции). АВ ⊥ ВС (стороны квадрата). SB ⊥ ВС (по теореме о трех перпендикулярах).
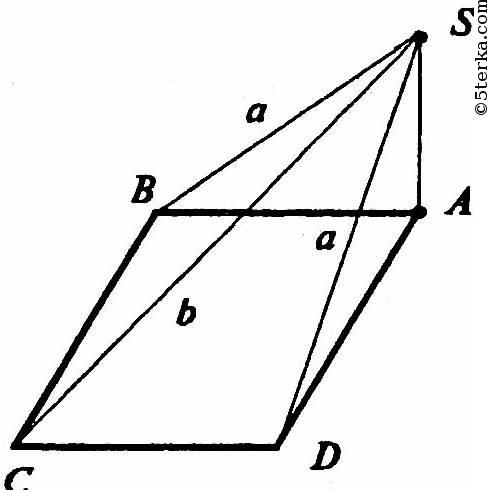
Значит, ΔSBC — прямоугольный, поэтому по теореме Пифагора: ВС2 = SC2 – SB2 = b2 – а2, так что
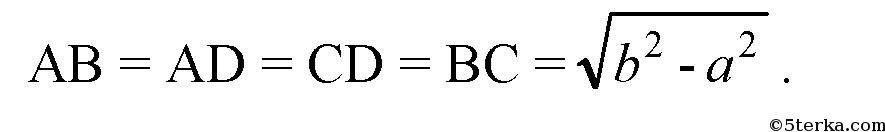
SA ⊥ AB (по условию), так что
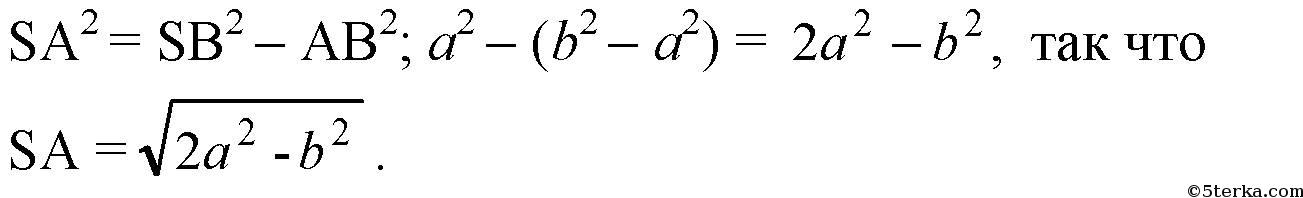
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
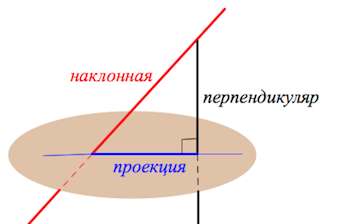
AB – перпендикуляр к плоскости α. AC – наклонная, CB – проекция. С – основание наклонной, B – основание перпендикуляра.
У равных наклонных, проведенных к плоскости из одной точки, проекции равны.
Из двух наклонных, проведенных к плоскости из одной точки, больше та, у которой проекция больше.
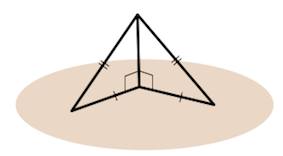
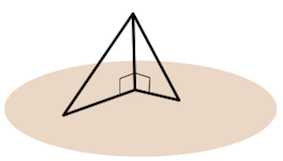
Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
Обратная теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
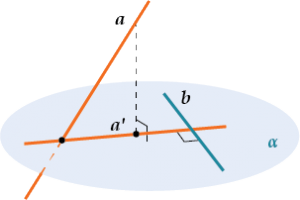
Прямая a, не лежащая в плоскости α, перпендикулярна прямой b, лежащей в плоскости α, тогда и только тогда, когда проекция a‘ прямой a перпендикулярна прямой b.
Пример. Отрезок SО – перпендикуляр к плоскости квадрата АВСD, где точка О – центр квадрата. Доказать: (BD perp SC).
Доказательство:
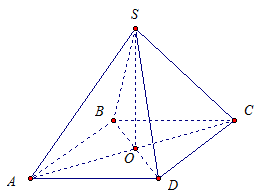
Первый способ.
Имеем квадрат, центр квадрата точка – О, SО – перпендикуляр. Значит, для наклонной SC отрезок ОС есть проекция.
Прямая ВD перпендикулярна прямой ОС, которая является проекцией наклонной SC, значит, по теореме о трех перпендикулярах, прямая ВD перпендикулярна наклонной SC.
Второй способ.
Прямая SО перпендикулярна плоскости АВС, а значит – и прямой ВD, лежащей в ней.
Прямая ВD перпендикулярна SО и прямая ВD перпендикулярна прямой АС по свойству квадрата.
Получаем, что прямая ВD перпендикулярна двум пересекающимся прямым плоскости SОС, значит, она перпендикулярна ко всей плоскости SОС, а значит – и к прямой SC, лежащей в этой плоскости.
Расстояние от точки до плоскости есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ.
- Если прямая параллельна плоскости, то расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
- Если две плоскости параллельны, то расстояние от произвольной точки одной из плоскостей до другой называется расстоянием между данными плоскостями.
- Если две прямые скрещиваются, то расстояние между одной из этих прямых и плоскостью, проведенной через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
