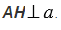Как найти перпендикуляр от линии - Сайт, где вы сможете решить свои вопросы

This is a vectorized Matlab function for finding pairwise projections of m points onto n line segments. Here xp and yp are m by 1 vectors holding coordinates of m different points, and x1, y1, x2 and y2 are n by 1 vectors holding coordinates of start and end points of n different line segments.
It returns m by n matrices, x and y, where x(i, j) and y(i, j) are coordinates of projection of i-th point onto j-th line.

The actual work is done in first few lines and the rest of the function runs a self-test demo, just in case where it is called with no parameters. It’s relatively fast, I managed to find projections of 2k points onto 2k line segments in less than 0.05s.

function [x, y] = projectPointLine(xp, yp, x1, y1, x2, y2)
if nargin > 0
        xd = (x2-x1)';
    yd = (y2-y1)';
    dAB = xd.*xd + yd.*yd;
    u = bsxfun(@rdivide, bsxfun(@times, bsxfun(@minus, xp, x1'), xd) + ...
        bsxfun(@times, bsxfun(@minus, yp, y1'), yd), dAB);
    x = bsxfun(@plus, x1', bsxfun(@times, u, xd));
    y = bsxfun(@plus, y1', bsxfun(@times, u, yd));
else
    nLine = 3;
    nPoint = 2;
    xp = rand(nPoint, 1) * 2 -1;
    yp = rand(nPoint, 1) * 2 -1;
    x1 = rand(nLine, 1) * 2 -1;
    y1 = rand(nLine, 1) * 2 -1;
    x2 = rand(nLine, 1) * 2 -1;
    y2 = rand(nLine, 1) * 2 -1;
    tic;
    [x, y] = projectPointLine(xp, yp, x1, y1, x2, y2);
    toc
    close all;
    plot([x1'; x2'], [y1'; y2'], '.-', 'linewidth', 2, 'markersize', 20);
    axis equal;
    hold on
    C = lines(nPoint + nLine);
    for i=1:nPoint
        scatter(x(i, :), y(i, :), 100, C(i+nLine, :), 'x', 'linewidth', 2);
        scatter(xp(i), yp(i), 100, C(i+nLine, :), 'x', 'linewidth', 2);
    end
    for i=1:nLine
        scatter(x(:, i)', y(:, i)', 100, C(i, :), 'o', 'linewidth', 2);
    end
end
end

Источник

Как сделать перпендикулярную прямую?

Построение перпендикулярных прямых

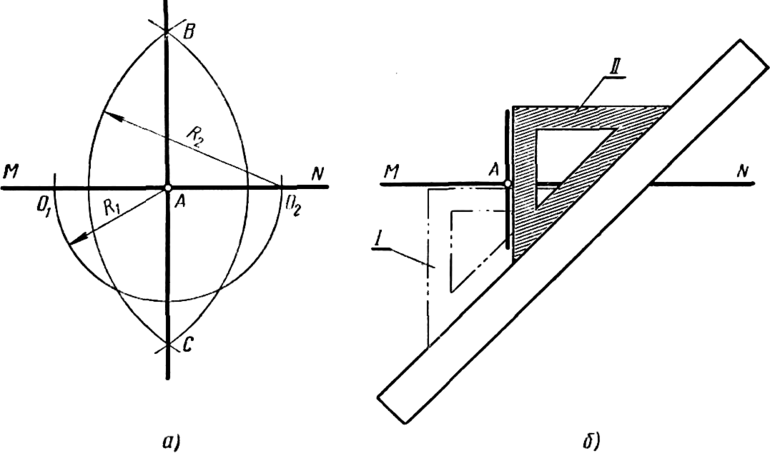
На рисунке 1 построим окружность с центром в точке и произвольным радиусом , большим, чем расстояние от точки до прямой . …
Построим окружность с центром в точке радиусом и окружность с центром в точке радиусом . …
Проведём отрезок , это и есть перпендикуляр к прямой .

Как построить перпендикуляр?

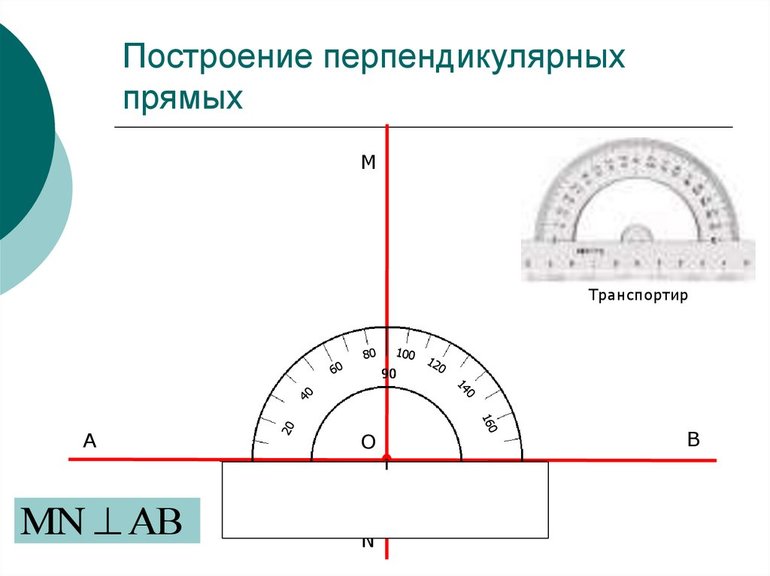
Таким образом, чтобы провести перпендикуляр, нужно отложить угол в 90°. Соедините точку на отрезке с точкой, которую вы поставили у деления «90». Для этого воспользуйтесь линейкой транспортира. Получившийся отрезок является перпендикуляром к данному отрезку и проходит через заданную точку на отрезке.

Как провести перпендикуляр к линии?

Re: Как построить перпендикуляр к прямой в AutoCAD 1. Берешь и рисуешь две окружности с центрами, расположенными на этой прямой и с условием, что эти окружности друг с другом пересекаются. Затем точки пересечения окружностей соединяешь прямой. Перпендикуляр готов!

Какие линии являются перпендикулярными?

Перпендикулярные прямые Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

Как построить перпендикуляр с помощью угольника?

Чтобы построить перпендикуляр к прямой через заданную точку с помощью рейсшины, необходимо переместить ее ниже заданной прямой. К рейсшине приложить угольник так, как показано на рис. 59, совместив положение стороны угольника с заданной точкой. Затем провести прямую, которая будет перпендикулярна заданной.

Как определить перпендикулярную прямую?

1. Перпендикулярность прямой и плоскости

Две прямые называются перпендикулярными, если угол между ними равен 90°.
Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна этой прямой.

Как построить перпендикуляр из точки на плоскость?

Для этого сначала проводим горизонталь и фронталь в плоскости. Затем из фронтальной проекции точки К проводим перпендикуляр к фронтальной проекции фронтали, а из горизонтальной проекции точки – перпендикуляр к горизонтальной проекции горизонтали.

Как построить перпендикуляр в треугольнике?

0:486:38Рекомендуемый клип · 58 сек.Серединный перпендикуляр к стороне треугольника. Построение.YouTube

Как обозначают знак перпендикулярно?

Перпендикулярность прямых обозначают специальным символом — , т. е. для рис. 1, а можно записать АВ СD (читается: «прямая АВ перпендикулярна прямой СD), а для рис.

Что такое параллельно и перпендикулярно?

Параллельными называются прямые, которые не пересекаются, сколько бы мы их не продолжали. На рисунке a и b. Определение 2. Перпендикулярными называются прямые, которые пересекаются под прямым углом.

Как обозначают перпендикулярные прямые?

Перпендикулярность прямых обозначают специальным символом — , т. е. для рис. 1, а можно записать АВ СD (читается: «прямая АВ перпендикулярна прямой СD), а для рис.

Как построить серединный перпендикуляр к стороне треугольника?

0:486:38Рекомендуемый клип · 60 сек.Серединный перпендикуляр к стороне треугольника. Построение.YouTube

Как доказать что прямая перпендикулярна прямой?

1. Перпендикулярность прямой и плоскости

Две прямые называются перпендикулярными, если угол между ними равен 90°.
Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна этой прямой.

Как доказать что прямая перпендикулярна?

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90º. Прямая называется перпендикулярной к плоскости, если она перпендикулярная к любой прямой, лежащей в этой плоскости.

Как провести перпендикуляр от прямой к плоскости?

Для этого сначала проводим горизонталь и фронталь в плоскости. Затем из фронтальной проекции точки К проводим перпендикуляр к фронтальной проекции фронтали, а из горизонтальной проекции точки – перпендикуляр к горизонтальной проекции горизонтали.

Что такое перпендикуляр из точки к плоскости?

Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. AC — перпендикуляр; C — основание перпендикуляра.

Как найти серединный перпендикуляр треугольника?

Серединный перпендикуляр — это прямая, перпендикулярная отрезку и делящая его пополам. Чтобы найти серединный перпендикуляр отрезка по его двум точкам, нужно найти точку, являющуюся серединой отрезка, и угловой коэффициент перпендикуляра и подставить найденные значения в линейное уравнение.

Источник

Использование транспортира

Одним из наиболее простых способов построения перпендикуляра к прямой является чертеж при помощи специального инструмента, который называется транспортир. Чтобы правильно начертить отрезок, необходимо по пунктам выполнить следующие действия:

Выбранную точку на отрезке необходимо соединить с нулевым значением транспортира (оно находится непосредственно посередине нижней линейки инструмента).
На угломерной шкале нужно поставить точку у деления 90°. Поскольку перпендикуляр образовывает прямой угол, то отложить нужно именно 90°.
На завершающем этапе точку, отмеченную на отрезке, следует соединить с той, которая была отмечена по угломерной шкале.

Этот способ широко используется на уроках геометрии. Его преимущество заключается в быстром и простом построении. Для выполнения требуется только транспортир и простой карандаш.

Циркуль и линейка

Перпендикулярный луч можно опустить на отрезок при помощи еще одного незамысловатого способа. Для этого необходимы простой карандаш, линейка и циркуль. Построить прямой угол можно, выполнив следующие действия:

На отрезке от заданной точки необходимо, используя циркуль, провести две одинаковые дуги. Чтобы расстояние было идентичным с каждой стороны, нужно иглу циркуля поставить в отмеченную точку и при помощи линейки раствор циркуля отодвинуть на какое-то расстояние (это индивидуальный показатель). Таким образом нужно начертить две дуги.
Затем необходимо увеличить раствор циркуля и сделать так, чтобы карандаш находился посередине между точкой справа (слева) и исходной.
Так нужно нарисовать две дуги: одну над прямой, а другую — под ней.
Потом необходимо нарисовать вторую такую дугу. При этом раствор циркуля изменять не требуется. Отметку пересечения двух дуг (правой и левой) нужно обозначить.
Точку пересечения этих двух дуг нужно состыковать с точкой на исходном отрезке. Соединять и проводить линию лучше с использованием линейки. Так рисунок получится ровным и аккуратным.

В результате этих действий должен получиться перпендикуляр, составляющий с прямой линией угол в 90°. Метод более сложный, если сравнивать его с первым. Его целесообразно использовать в том случае, если под рукой не оказалось транспортира.

Теорема Пифагора

Чтобы построить перпендикуляр по этому способу, мало знать одного определения, поскольку потребуется теорема Пифагора и ее доказательство. Наиболее распространенный вариант — свойство египетского треугольника со сторонами 5, 4 и 3.

От основной точки А необходимо отмерить и отметить отрезок, равный 3. В результате получается точка В. Далее необходимо построить две одинаковые окружности. При этом центр первой будет располагаться в А, а центр второй — в В. Отметка пересечения этих окружностей обозначается как С. Значит, искомый перпендикуляр — это линия, соединяющая две точки (А и С). Конечно, этот способ лучше посмотреть наглядно на картинке или показать в виде чертежа.

Эту тему проходят на геометрии в 7 классе. Школьники должны дать определение перпендикуляра к прямой. А на его основании построить линию его под углом 90°.

Источник

Загрузить PDF

Перпендикуляр — это прямая, которая пересекает другую прямую под углом 90°. Перпендикуляры часто используются в геометрии, поэтому важно знать, как их строить. Чтобы быстро провести перпендикуляр, воспользуйтесь транспортиром. Также построить перпендикуляр можно с помощью циркуля и линейки.

1
Приложите линейку (прямую сторону) транспортира к данному отрезку. Нулевое деление транспортира совместите с точкой на отрезке. Совместите линейку транспортира с данным отрезком.
- Нулевое деление находится в центре линейки транспортира.
- Угломерная шкала находится на полукруглой стороне транспортира и служит для измерения углов (от 0° до 180°).
2

Поставьте точку у деления «90» на угломерной шкале. Это деление находится сверху на полукруглой стороне транспортира. Помните, что две перпендикулярные прямые образуют угол в 90°.^[1] Таким образом, чтобы провести перпендикуляр, нужно отложить угол в 90°.
3

Соедините точку на отрезке с точкой, которую вы поставили у деления «90». Для этого воспользуйтесь линейкой транспортира. Получившийся отрезок является перпендикуляром к данному отрезку и проходит через заданную точку на отрезке.

Реклама

1
Проведите дуги с двух сторон от заданной точки. Для этого поставьте иглу циркуля в заданную точку на прямой. Затем проведите две дуги с обеих сторон от заданной точки. Дуги должны пересекать прямую.^[2] Отметьте точки пересечения дуг с прямой.
- На данном этапе раствор циркуля может быть любым.
- Например, на прямой дана точка A. С помощью циркуля поставьте на прямой точку P (слева) и точку Q (справа).
2
Увеличьте раствор циркуля. Поставьте его иглу в точку слева от исходной точки. Теперь сделайте раствор циркуля таким, чтобы карандаш циркуля находился примерно посередине между исходной точкой и точкой справа от исходной.^[3]
- Например, поставьте иглу циркуля в точку P, а затем увеличьте раствор так, чтобы карандаш находился примерно посередине между точками A и Q.
3
Нарисуйте дугу над или под прямой. Сделайте это, когда циркуль стоит в точке слева от исходной.^[4]
- Например, если игла циркуля находится в точке P, проведите дугу над или под прямой.
4
Нарисуйте вторую дугу, пересекающую первую. Раствор циркуля не меняйте. Иглу циркуля поставьте в точке справа от исходной, а затем проведите вторую дугу над или под прямой; вторая дуга должна пересечь первую. ^[5] Отметьте точку пересечения двух дуг.
- Например, поставьте иглу циркуля в точку Q. Нарисуйте дугу, которая пересечет первую дугу в точке T.
5
Соедините точку пересечения дуг с исходной точкой. Для этого воспользуйтесь линейкой. Получившийся отрезок является перпендикуляром к данной прямой и проходит через заданную точку.^[6]
- Например, проведите отрезок, соединяющий точки A и T.
6

Готово.

Реклама

Об этой статье

Эту страницу просматривали 36 870 раз.

Была ли эта статья полезной?

Источник

Как найти длину перпендикуляра

Даны точка и прямая представленная уравнением (1) § 161. Требуется найти расстояние от точки до прямой т. е. длину перпендикуляра (см. рис. 175), опущенного из точки на прямую .

Можно сначала найти основание К перпендикуляра (§ 161, пример), затем длину отрезка Проще применить формулу (при обозначениях § 161)

т. е. в векторной форме

Числитель выражения (1а) есть площадь параллелограмма (§ 111) , а знаменатель — длина основания Следовательно, дробь равна высоте параллелограмма.

Расстояние от точки до прямой

Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.

Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.

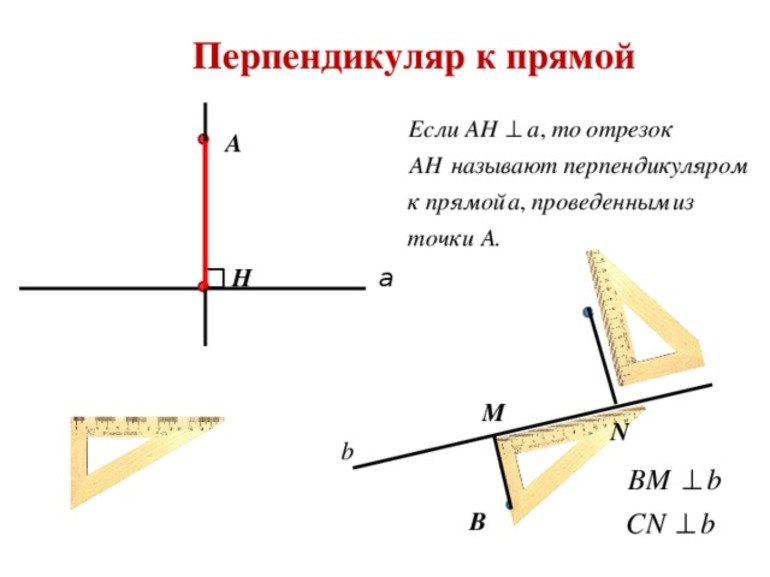
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.

Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.

№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

Дано: A∉a,

BC и BD — их проекции, BC=2 см, BD=7 см

1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

$[A{C^2} = A{B^2} + B{C^2},]$

$[A{B^2} = A{C^2} - B{C^2}]$

$[A{B^2} = {(2k)^2} - {2^2}]$

$[underline {A{B^2} = 4{k^2} - 4} ]$

3) Аналогично, из треугольника ABD

$[A{B^2} = A{D^2} - B{D^2}]$

$[A{B^2} = {(3k)^2} - {7^2}]$

$[underline {A{B^2} = 9{k^2} - 49} ]$

4) Приравниваем правые части полученных равенств и находим k:

$[4{k^2} - 4 = 9{k^2} - 49]$

$[5{k^2} = 45]$

$[{k^2} = 9]$

5) Зная k, найдем AB:

$[A{B^2} = 4 cdot {3^2} - 4 = 32]$

№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

Дано: A∉a,

AC и AD — наклонные, AC=13 см, AD=15 см,

BC и BD — их проекции, BD-BC=4 см

1) Пусть BC=x см, тогда BD=x+4 см.

$[A{C^2} = A{B^2} + B{C^2},]$

$[A{B^2} = A{C^2} - B{C^2}]$

$[underline {A{B^2} = {{13}^2} - {x^2}} ]$

3) Аналогично, из треугольника ABD

$[A{B^2} = A{D^2} - B{D^2}]$

$[underline {A{B^2} = {{15}^2} - {{(x + 4)}^2}} ]$

4) Приравниваем правые части полученных равенств и находим x:

$[{13^2} - {x^2} = {15^2} - {(x + 4)^2}]$

$[169 - {x^2} = 225 - {x^2} - 8x - 16]$

5) Зная x, найдем AB:

$[A{B^2} = {13^2} - {5^2} = 169 - 25 = 144]$

№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Дано: A∉a,

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.

Основные сведения о перпендикуляре к прямой — что это такое, как находить

Каким будет определение положения прямой и плоскости, зависит от наличия общих точек. Если их больше одной, то прямая лежит на данной плоскости, если одна — то она ее пересекает. Если прямая не имеет с плоскостью точек пересечения, то прямая и плоскость параллельны.

Пересечение прямой линии и плоскости может происходить под разными углами. Если при пересечении между прямой и плоскостью образуется прямой угол, то такая прямая является к плоскости перпендикуляром. При этом она перпендикулярна всем прямым линиям, принадлежащим данной плоскости. Из этого свойства вытекает следующее определение.

Перпендикулярной к плоскости называется прямая линия, которая перпендикулярна всем без исключения прямым, лежащим в выбранной плоскости.

Следствием из данного определения является свойство плоскости, для которой установлено наличие перпендикуляра. Оно формулируется следующим образом: «Если плоскость перпендикулярна некоторой прямой, то она является также перпендикулярной для всех прямых, параллельных данной прямой».

В решении задач на построение перпендикуляров к плоскости в конкретной точке существует только одно решение, поскольку через определенную точку можно провести только одну прямую, занимающую по отношению к плоскости перпендикулярное положение.

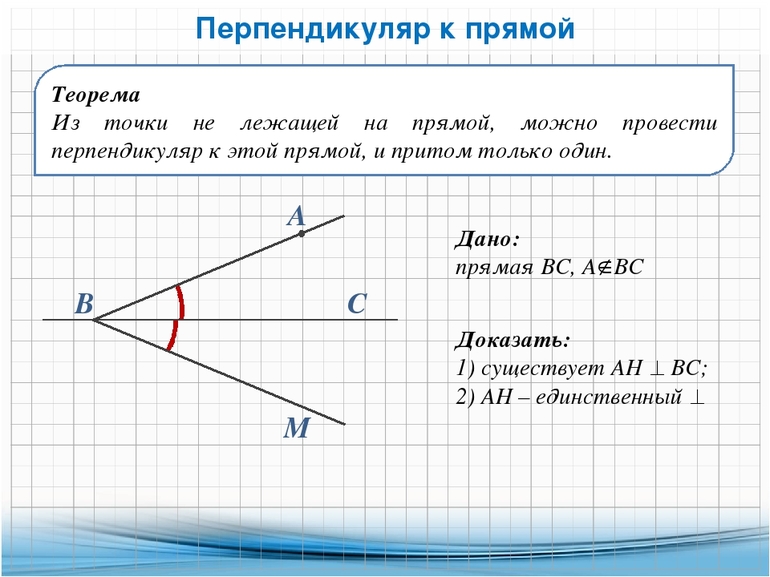
О единственности такой прямой в геометрии существует доказательство.

Проведение перпендикуляра из точки к прямой

В жизни с перпендикуляром можно столкнуться часто. Например, если по двум параллельным направляющим движутся тела, то кратчайшее расстояние между ними будет лежать именно по перпендикуляру.

Допустим, на уроке ученикам дали задание построить перпендикуляр к имеющейся площади. Особым условием является то, что проходить этот перпендикуляр должен через выбранную точку. Технически задача проста. Для ее исполнения нужен чертежный треугольник, один угол у которого является прямым, то есть составляет 90°.

Приложив его к прямой таким образом, что одна из сторон, образующих прямой угол, лежит на прямой, а другая — проходит через точку с определенными координатами, необходимо соединить эту точку и прямую.

Такой отрезок будет кратчайшим соединением точки с прямой линией (и выбранной плоскостью).

Взаимное положение такого перпендикуляра и прямой обозначается специальным знаком.

Для перпендикуляра, проведенного из выбранной точки к прямой, можно определить длину. Она равна расстоянию от этой точки до точки пересечения с прямой плоскостью.

Как построить перпендикуляр к прямой

Построить перпендикуляр к прямой можно несколькими способами:

1. С помощью циркуля.

Из выбранной точки P проводим полуокружность, которая пересекается с прямой в точках A и B.

Затем тем же радиусом строим две окружности, центры которых совпадают с точками A и B. При этом окружности проходят через точку P.

Следующим шагом будет соединение точек P и Q.

На данном рисунке перпендикуляр к прямой AB — отрезок PQ.

2. Вторым способом построения перпендикуляра является использование транспортира. Чтобы провести перпендикуляр, внимательно откладываем 90° от выбранной точки на прямой, используя при этом линейку транспортира. Отрезок, соединяющий эту точку и деление 90°, является перпендикуляром к прямой в заданной точке.

3. Третий способ был описан выше. Он основан на применении чертежного треугольника и линейки. С помощью линейки проводим прямую. Прикладываем к ней прямым углом треугольник и очерчиваем этот угол с двух сторон. Один отрезок совпадает с имеющейся прямой, а второй является перпендикуляром к ней.

Пояснение на примерах

В конспектах по геометрии присутствует понятие высоты, представляющей собой перпендикуляр к одной из сторон геометрической фигуры (например, треугольника).

Высотой треугольника называется перпендикуляр, который выходит из вершины треугольника и следует к противоположной стороне (либо к продолжению этой стороны, если треугольник тупоугольный).

В данном определении содержится отличие от основной характеристики биссектрисы, которая, опускаясь на противолежащую углу сторону, не является перпендикуляром к ней.

Аналогичная ситуация с определением медианы — линии, исходящей из угла треугольника и делящей противоположную сторону на две равные части.

Высоту треугольника можно провести из любого его угла, поэтому у каждого треугольника имеется три высоты.

Существует теорема, что все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.

Используя свойство высоты треугольника о пересечении одной из его сторон под прямым углом, можно через высоту выразить формулу площади треугольника:

Уравнение для расчета высоты через площадь:

Найти через длины сторон:

h a = 2 p p — a p — b p — c a

где p — это полупериметр треугольника, который рассчитывается так:

p = a + b + c 2
Можно дать краткую характеристику еще двум способам выразить высоту треугольника:

Источник

Как сделать перпендикулярную прямую?

Как построить перпендикуляр?

Как провести перпендикуляр к линии?

Какие линии являются перпендикулярными?

Как построить перпендикуляр с помощью угольника?

Как определить перпендикулярную прямую?

Как построить перпендикуляр из точки на плоскость?

Как построить перпендикуляр в треугольнике?

Как обозначают знак перпендикулярно?

Что такое параллельно и перпендикулярно?

Как обозначают перпендикулярные прямые?

Как построить серединный перпендикуляр к стороне треугольника?

Как доказать что прямая перпендикулярна прямой?

Как доказать что прямая перпендикулярна?

Как провести перпендикуляр от прямой к плоскости?

Что такое перпендикуляр из точки к плоскости?

Как найти серединный перпендикуляр треугольника?

Использование транспортира

Циркуль и линейка

Теорема Пифагора

Об этой статье

Была ли эта статья полезной?

Как найти длину перпендикуляра

Расстояние от точки до прямой

Основные сведения о перпендикуляре к прямой — что это такое, как находить

Проведение перпендикуляра из точки к прямой

Как построить перпендикуляр к прямой

Пояснение на примерах

Вам также может понравиться

Как найти скорость звука стали

Домохозяйка как найти друзей

Как найти телефон через интернет видео

Добавить комментарий Отменить ответ