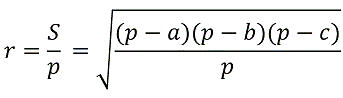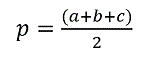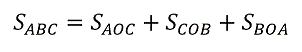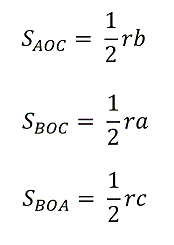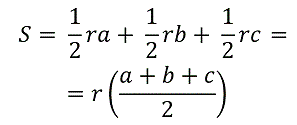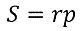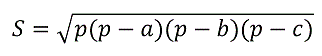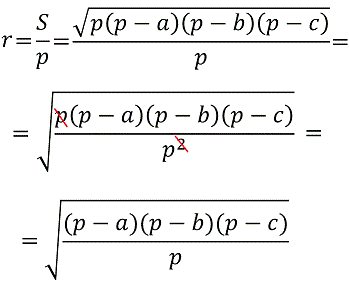Как найти перпендикуляр вписанной окружности

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

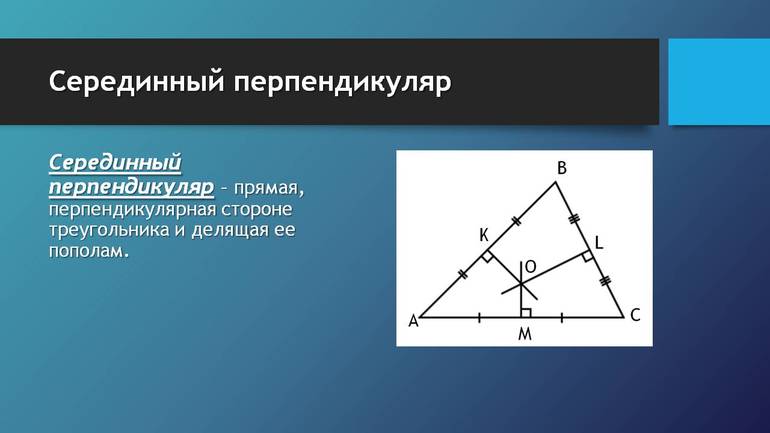
Серединный перпендикуляр к отрезку

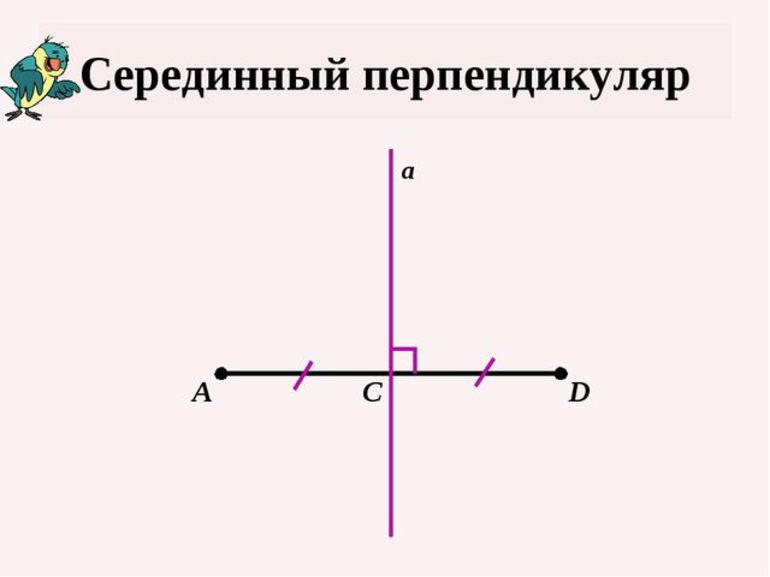
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

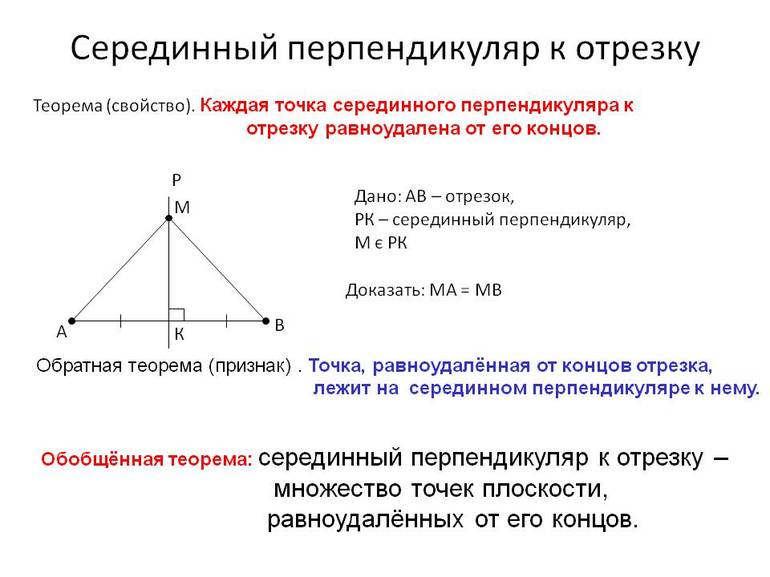
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

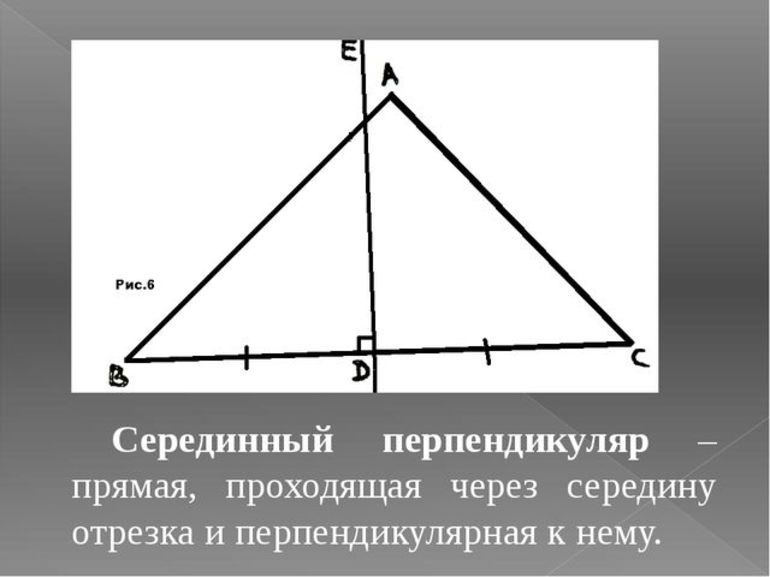
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности	Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Площадь треугольника
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

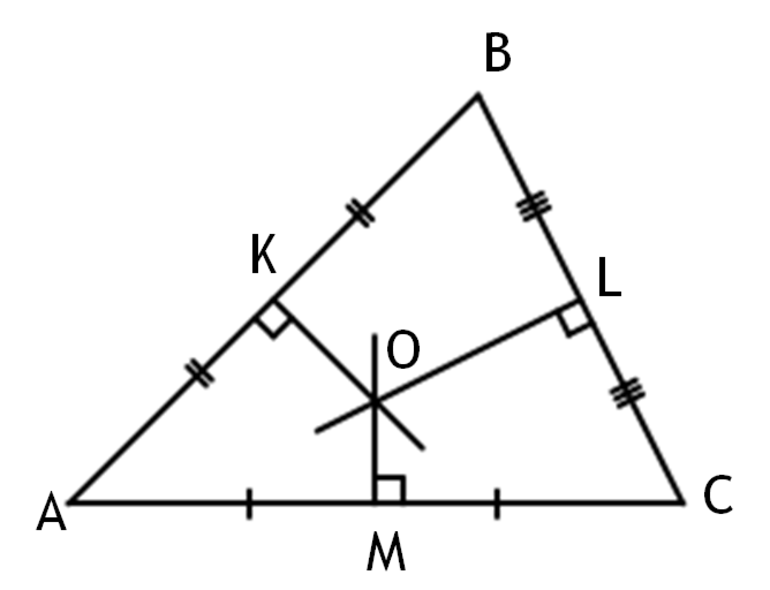
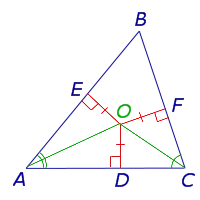
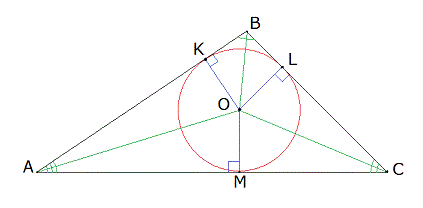
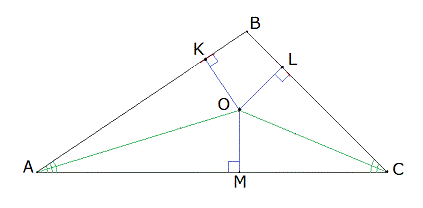
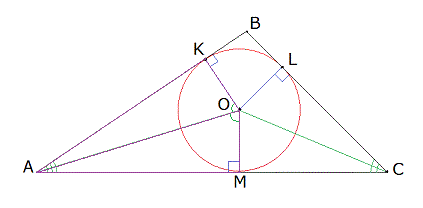
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Серединный перпендикуляр – определение, свойства и формулы

Общие сведения

Серединным перпендикуляром отрезка называют прямую, которая проходит под прямым углом через среднюю точку, т. е. середину отрезка. Для полного понимания материала следует остановиться на базовых элементах геометрии.

Точка — единица, при помощи которой строятся прямые, отрезки, лучи и фигуры. Прямая — простая фигура в форме бесконечной линии, состоящей из множества точек, лежащих в одной плоскости. Луч — базовая геометрическая фигура в виде бесконечной линии с одной стороны и точки-ограничителя — с другой. Иными словами, луч имеет начало, но не имеет конца. Отрезок — некоторая часть прямой (луча или другого отрезка), ограниченная двумя точками.

Кроме того, в геометрии серединный перпендикуляр встречается в треугольниках. Из определения можно сделать вывод, что им может быть прямая, отрезок и даже луч.

Аксиомы геометрии Евклида

Евклидовой геометрией называется наука о фигурах на плоскости, основанная на аксиомах и теоремах. Аксиома — базовое утверждение, не требующее доказательства. Оно используется для доказательства каких-либо теорем. Математики выделяют пять аксиом:

1. Принадлежности.
2. Порядка.
3. Конгруэнтности.
4. Параллельности прямых.
5. Непрерывности.

Формулировка первой имеет такой вид: если существует в геометрическом пространстве плоскость, состоящая из множества точек, то через любые из них можно провести только одну прямую. Иными словами, можно взять произвольные две точки и провести через них одну прямую. Чтобы начертить еще одну прямую, следует взять две другие точки.

Следующее утверждение называется аксиомой порядка. Она гласит, что существует точка, которая лежит между двумя другими на прямой. Значение слова “конгруэнтность” не совсем понятно для новичка, однако нужно постепенно привыкать к терминологии. Оно обозначает “равенство”. Третий геометрический факт формулируется таким образом: когда два отрезка или угла конгруэнтны третьему, тогда они равны между собой. Аксиома касается только отрезков и углов.

Чтобы убедиться в ее правильности, нужно разобрать следующий пример: длина первого отрезка составляет 10 см, второго — тоже, а третий равен первому. Необходимо доказать, что они равны между собой. Это делается очень просто:

• Вводятся обозначения: первый — MN, второй — OP и третий — RS.
• Устанавливаются значения по условию: MN = 10 см, ОР = 10 см, а RS = MN.
• Доказательство строится таким образом: MN = RS = 10 (см). Следовательно, отрезки равны, поскольку MN = ОР = RS = 10 (см).

Следует отметить, что данные действия оказались лишними — было потрачено время на понимание простой “истины”. Параллельность прямых является также аксиомой и формулируется таким образом: если существует некоторая прямая на плоскости и точка, не лежащая на ней, то через последнюю можно провести только одну параллельную ей прямую.

И последняя аксиома называется Архимедовой. Ее формулировка имеет такой вид: для произвольных отрезков, лежащих на одной прямой, существует некоторая последовательность базовых элементов (точек), лежащих на одном и другом отрезках, таких, что заданные их части равны между собой. Иными словами, на одной прямой могут быть расположены равные между собой отрезки.

Информация о треугольниках

Треугольником является любая фигура, состоящая из трех вершин (точек) соединенных отрезками (сторонами), причем точки не лежат на одной прямой в одной плоскости. Они классифицируются по такому типу:

В первом случае фигуры делятся на остроугольные, тупоугольные и прямоугольные. Остроугольным называется треугольник, у которого все углы острые (меньше 90 градусов). У тупоугольного — один угол тупой (> 90), а в прямоугольном — один из углов равен 90 градусам. Следует отметить, что сумма градусных мер углов любого треугольника эквивалентна 180.

Когда стороны у треугольника неравны между собой, тогда его называют разносторонним. При равенстве двух боковых сторон он считается равнобедренным, у которого третья сторона — основание. Если все стороны равны, то значит, фигура является равносторонней или правильной.

У треугольника есть еще и другие параметры. Их называют медианой, биссектрисой и высотой. Первый параметр является отрезком, который проводится из любой вершины на среднюю точку стороны. Высота — часть прямой, которая проводится из произвольной вершины и перпендикулярна противоположной стороне. Биссектрисой называется прямая, делящая угол на две равные части.

Медиана, высота и биссектриса, проведенные из вершины к основанию, совпадают и эквивалентны серединному перпендикуляру в треугольниках равнобедренного и равностороннего типов. Это очень важно при решении задач. Еще одним признаком, по которому выполняется классификация — подобность треугольников. У них могут быть равными только углы и некоторые стороны. Они отличаются между собой по определенному параметру, который называется коэффициентом подобия. Последний влияет только на размерность сторон. Говорят, что фигуры подобны по определенному признаку (их всего три).

Основные теоремы

Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.

Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:

• Прямая.
• Обратная.
• Пересечение в треугольнике.

Первая теорема называется прямой о СП. Она показывает, каким свойством обладают точки серединного перпендикуляра. Ее формулировка следующая: произвольная точка, которая взятая на перпендикуляре, удалена на равные расстояния от конечных точек отрезка, ограничивающих его на плоскости.

Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.

Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.

Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.

Важные свойства

Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:

1. Центр описанной окружности вокруг треугольника соответствует точке их пересечения.
2. Точка, взятая на СП, равноудалена от конечных точек отрезка и образует равнобедренный или равносторонний треугольник.
3. В треугольниках равнобедренного и равностороннего типов им является высота, медиана и биссектриса.

В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.

Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:

1. а: Pa = (2 * а * S) / (a^2 + b^2 – c^2).
2. b: Pb = (2 * b * S) / (a^2 + b^2 – c^2).
3. c: Pc = (2 * c * S) / (a^2 – b^2 + c^2).

Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:

1. Основание и высоту, проведенную к нему: S = (1/2) * a * Ha = (1/2) * b * Hb = (1/2) * c * Hc.
2. Через радиус вписанной окружности: S = (1/2) * r * (a + b + c).
3. Формулу Герона через полупериметр (р) и без него: S = [p * (p – a) * (p – b) * (p – c)]^(1/2) и S = 1/4 * [(a + b + c) * (b + c – a) * (а + c – b) * (a + b – c)]^(1/2).

В основном по таким соотношениям и нужно определить площадь. Полупериметр вычисляется таким образом: р = (а + b + с) / 2.

Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.

Пример решения задачи

В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:

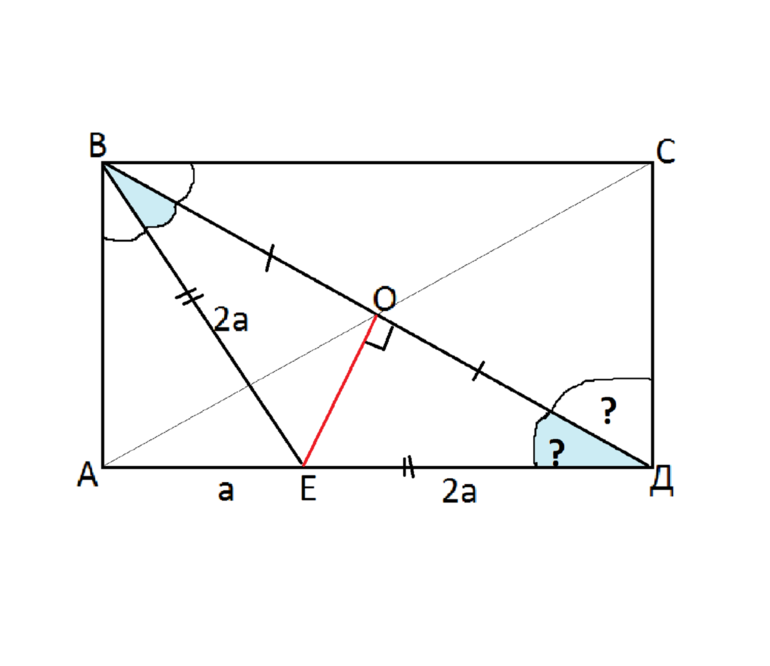
1. Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
2. Серединный перпендикуляр, проведенный к диагонали прямоугольника.
3. Точка Е делит сторону на отрезки а и 2а.

Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении

Рисунок 1. Чертеж для решения задачи.

Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:

1. Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
2. Необходимо найти угол ЕВО. Сделать это проблемно. Рекомендуется обратить внимание на треугольник АВЕ.
3. При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
4. Угол СВЕ вычисляется следующим образом: 90 – 30 = 60 (градусов).
5. Следовательно, искомый угол равен 30, поскольку 90 – 30 – 30 = 30.
6. В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).

Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой “х”. Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = [4a^2 + a^2]^(1/2) = a * [5]^(1/2). Следовательно, АВ = a * [5]^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 – d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 – (d^2) / 4]^(1/2).

Таким образом, нахождение серединного перпендикуляра позволяет значительно уменьшить объемы вычислений. Однако для этого нужно знать не только основные теоремы, но и его свойства.

Серединный перпендикуляр

Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?

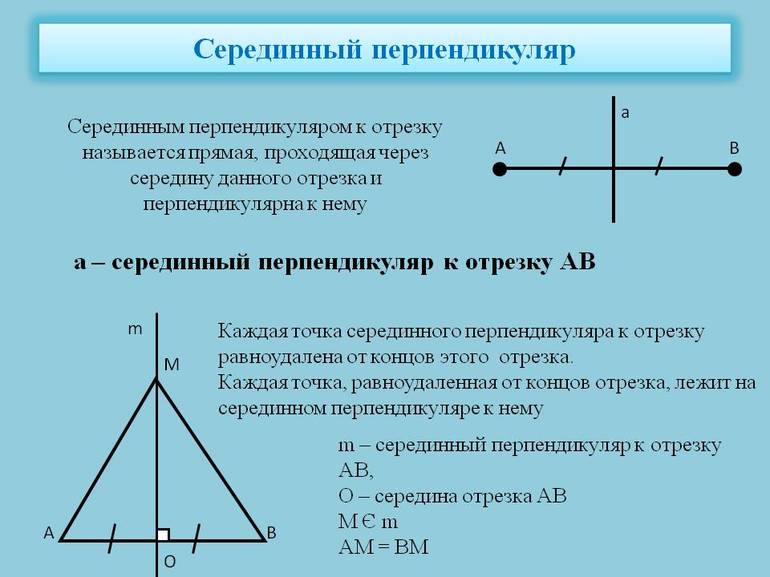
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

m — серединный перпендикуляр к отрезку AB, если

точка C — середина отрезка AB,

Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:

1) найти середину отрезка;

2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):

Свойства серединного перпендикуляра.

1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.

Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).

2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.

3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

[spoiler title=”источники:”]

http://nauka.club/matematika/geometriya/seredinnyi-perpendikulyar.html

[/spoiler]

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

---

Свойства вписанной окружности

В треугольник

1.  В любой треугольник может быть вписана окружность, причем только один раз.
2.  Центр вписанной окружности — точка пересечения биссектрис треугольника.
3.  Вписанная окружность касается всех сторон треугольника.
4.  Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

   [ S = frac{1}{2}(a+b+c) cdot r = pr ]

   p —  полупериметр четырехугольника.
   r — радиус вписанной окружности четырехугольника.

5.  Центр окружности вписанной в треугольник равноудален от всех сторон.
6.  Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон треугольника.
7.  От центра вписанной окружности можно провести
   перпендикуляры к любой точке касания.
8.  Вписанная в треугольник окружность делит стороны
   треугольника на 3 пары равных отрезков.
9.  Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
   Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

   [ с = sqrt{R^2 — 2Rr} ]

   с — расстояние между центрами вписанной и описанной окружностей треугольника.
   R — радиус описанной около треугольника.
   r — радиус вписанной окружности треугольника.

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих
   сторон равны, то окружность, может быть, вписана (Теорема Пито).
3. Центр вписанной окружности и середины двух
   диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается
   окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

   [ S = frac{1}{2}(a+b+c+d)cdot r = pr ]

   p —  полупериметр четырехугольника.
   r — радиус вписанной окружности четырехугольника.

7. Точка касания вписанной окружности, которая лежит на любой из сторон,
   равноудалены от этой конца и начала этой стороны, то есть от его вершин.

---

Примеры вписанной окружности

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

---

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

---

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

---

Центральный угол вписанной окружности – это угол, вершина
которого лежит в центре вписанной окружности.

Вписанный угол вписанной окружности – это угол,
вершина которого лежит на вписанной окружности.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Так-же читайте статью про треугольник вписанный в окружность.

План урока:

Точка пересечения биссектрис в треугольнике

Серединный перпендикуляр

Точка пересечения высот треугольника

Вписанная окружность

Описанная окружность

Построение вписанной и описанной окружности

Точка пересечения биссектрис в треугольнике

Напомним, что для каждой прямой и точки можно вычислить расстояние между ними. Оно представляет собой длину перпендикуляра, который из точки проведен к этой прямой.

Если есть пара прямых и одна точка, то можно определить расстояние от точки до каждой из прямых. В случае, когда эти расстояния одинаковы, точку называют равноудаленной от обеих прямых.

Например, на этом рисунке длины AВ и ВС одинаковы, а потому точка А – равноудаленная от прямых m и n.

Сформулируем важную теорему.

Для доказательства опустим из произвольно выбранной точки М, принадлежащей биссектрисе ∠AВС, расстояния МК и МL на AВ и ВС:

Сравним ∆ВКМ и ∆ВМL. Это два прямоугольных треуг-ка, у которых общая гипотенуза ВМ, а также одинаковы острые углы ∠МВL и ∠KBM (они одинаковы, ведь биссектриса по определению разбивает угол пополам). Тогда ∆BKM и ∆BLM равны, и отрезки КM и МС также одинаковы, ч. т. д.

Верно и обратное утверждение.

Для доказательства можно использовать тот же рисунок. Пусть точка М находится на одинаковом расстоянии от ВК и ВL. То есть КМ = МL. Тогда ∆ВКМ и ∆ВМL снова оказываются равными, но уже как прямоугольные треуг-ки с одинаковыми катетом и гипотенузой. Из равенства треуг-ков вытекает, что

Действительно, если в ∆AВС построить биссектрисы ∠А и ∠В, то они должны будут пересечься в какой-нибудь точке О:

Опустим из О перпендикуляры на все стороны треуг-ка. Так как О принадлежит биссектрисе ∠А, то она находится на одинаковом расстоянии от АС и AВ, то есть

Из него следует, что О также находится на одном расстоянии от АС и ВС и потому принадлежит биссектрисе ∠С. Получается, что О – общая точка для всех трех биссектрис ∆AВС.

Серединный перпендикуляр

Введем новое понятие – серединный перпендикуляр.

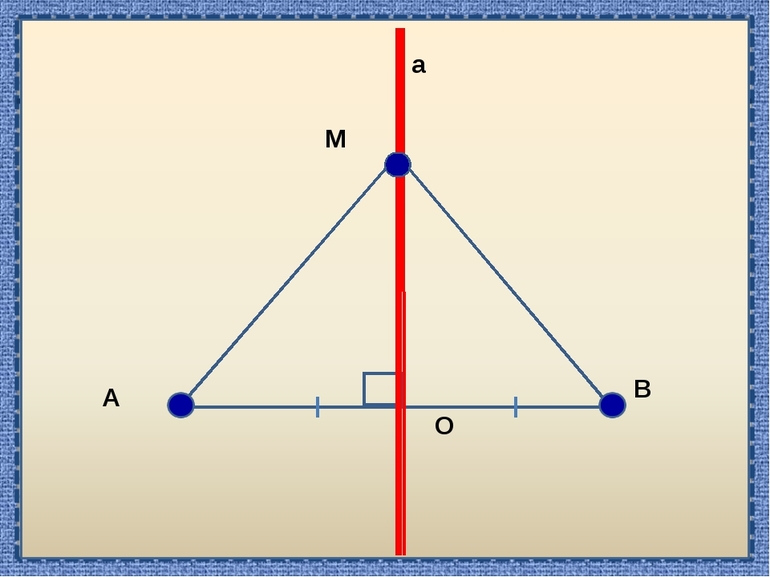
На рисунке О – это середина AВ. Через нее проведена прямая m, образующая прямой угол с AВ. Тогда по определению m – это серединный перпендикуляр:

Рассмотрим две теоремы, которые связаны с серединным перпендикуляром и являются обратными друг для друга.

Сначала рассмотрим первое утверждение. Пусть точка М находится на серединном перпендикуляре, проведенному к AВ. Нам надо

Изучим∆АОМ и ∆ВОМ. Они прямоугольные, имеют одинаковые катеты АО и ОВ (ведь О – середина AВ) и общий катетОМ. Получается, что ∆АОМ и ∆ВОМ равны. Значит, одинаковы и отрезки АМ и МВ, ч. т. д.

Во второй теореме уже изначально известно, что

AM = MB

Надо доказать, что М принадлежит серединному перпендикуляру. Изучим∆АМВ, он равнобедренный, ведь АМ = МВ. Теперь из М опустим медиану МО на AВ. ∆АМВ – равнобедренный, поэтому эта медиана окажется также и высотой. Получается, что отрезок ОМ перпендикулярен AВ и одновременно делит его пополам. Значит, ОМ – это серединный перпендикуляр.

Из этих двух теорем вытекает важное утверждение:

Действительно, в ∆AВС проведем серединные перпендикуляры к сторонам треугольника AВ и АС:

Здесь N и K – середины сторон AN и AC, а О – точка пересечения серединных перпендикуляров в треугольнике. Так как О лежит на серединном перпендикуляре, проведенному к AВ, то справедливо равенство

AO = OB

Аналогично О равноудаленная от вершин А и С, ведь она лежит на серединном перпендикуляре, проведенному к АС:

AO = OC

В итоге можно составить двойное равенство:

OC = AO = OB

Оно показывает, что О также расположена на одном расстоянии от В и С. Отсюда вытекает, что она должна принадлежать серединному перпендикуляру, проведенному к ВС, ч. т. д.

Точка пересечения высот треугольника

Следующая теорема касается высот треуг-ка.

Для доказательства выполним такое построение – через вершины ∆AВС проведем прямые, которые будут параллельны сторонам ∆АВС. Они образуют новый ∆А₁В₁С₁:

Из условий AВ||A₁В₁ и АС||А₁С₁ вытекает, что четырехуг-к АСА₁В – это параллелограмм. Значит, у него одинаковы противоположные стороны:

Аналогично можно показать, что четырехуг-ки AВСВ₁ и АСВС₁ – также параллелограммы, откуда вытекают равенства:

Теперь обозначим на рисунке все отрезки, равные AВ, одной черточкой, отрезки, равные ВС – двумя чертами, в тремя черточками отметим те отрезки, равные АС:

Получается, что А, В и С являются серединами сторон А₁В₁, А₁С₁ и В₁С₁. Построим в ∆А₁В₁С₁ серединные перпендикуляры. Они по определению будут проходить через середины А, В и С и при этом будут иметь общую точку О:

Заметим, что проведенные перпендикуляры будут также перпендикулярны сторонам исходного ∆AВС. Например, ОВ⊥А₁С₁ и А₁С₁|| АС, значит, ОВ⊥АС (прямая, перпендикулярная одной из двух параллельных прямых, будет перпендикулярна и второй прямой). Аналогично можно продемонстрировать, что АО⊥ВС, а СО⊥AВ. Другими словами, прямые АО, ВО и СО оказываются высотами, и при этом они пересеклись точке О. Так как ∆AВС был выбран произвольно, то получается, что в любом треуг-ке высоты пересекутся в одной точке, ч. т. д.

Ранее, изучая подобие треуг-ков, мы уже выяснили, что и медианы треуг-ка будут пересекаться в одной точке. В итоге можно сформулировать следующее утверждение:

Задание. На рисунке ∠MKN = 66°. Вычислите величину ∠FNO.

Решение. Судя по рисунку, в точке О пересекаются высоты MF и KE. Но тогда и прямая ON также должна быть высотой. Достроим рисунок с учетом этого факта:

Теперь на рисунке множество прямоугольных треуг-ков. Напомним, что у каждого из них острые углы в сумме составляют 90°. Например, в ∆MKF

Ответ: 24°.

Задание. В ∆AВС биссектрисы АА₁ и ВВ₁ пересеклись в точке М, причем ∠АМВ = 128°. Вычислите ∠МСВ₁.

Решение. Изучим ∆АМВ. В сумме его углы должны составлять 180°:

Ясно, что МС – это биссектриса ∠АСВ, ведь она проходит через общую точку двух других биссектрис ∆AВС. То есть МС делит ∠АСВ пополам:

Задание. На рисунке RO = 20. Вычислите длину OK:

Решение. На рисунке видно, что OM и ON – это серединные перпендикуляры. Отсюда вытекает, что точка О равноудалена от ОР и OR:

OP = OR = 20

Теперь можно рассмотреть ∆РОК. Он прямоугольный, и в нем есть ∠30°. Напомним, что катет, лежащий против такого угла, вдвое короче гипотенузы:

OK = OP/2 = 20/2 = 10

Ответ: 10.

Вписанная окружность

Иногда в многоугольник можно вписать окруж-ть. Это значит, что возможно построить такую окруж-ть (ее именуют вписанной окружностью), которая будет касаться каждой стороны многоуг-ка (его в таком случае называют описанным около окружности многоуг-ком).

Для того чтобы, построить вписанную в многоуг-к окруж-ть, надо сначала определить, возможно ли вообще это сделать. Оказывается, что в треуг-к окруж-ть можно вписать всегда.

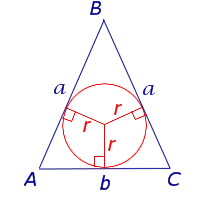
Действительно, построим произвольный ∆AВС и биссектрисы в нем. Они пересекутся в какой-нибудь точке О. Далее из О проведем перпендикуляры на стороны ∆AВС.

Эти перпендикуляры являются, по сути, расстояниями от О до сторон углов ∠А, ∠В и ∠С. По свойству биссектрисы они окажутся одинаковыми. Теперь проведем окруж-ть с центром в О, радиус которой будет равен длине этих перпендикуляров.

r = OK = OL = OM

Ясно, что точки M, L и K будут принадлежать окруж-ти, ведь они находятся на расстоянии R от ее центра. При этом отрезки OK, OM, OL будут радиусами. Заметим, что прямая AВ перпендикулярна радиусу OK, а потому является касательной. По той же причине ВС и АС также окажутся касательными. В итоге окруж-ть оказывается вписанной, ч. т. д.

В данном доказательстве мы не просто доказали, что для каждого треуг-ка существует вписанная окруж-ть, но и показали, как ее построить. Надо сначала провести биссектрисы углов, найти точку их пересечения (это и будет центр вписанной окруж-ти), после чего из этой точки надо опустить перпендикуляр на одну из сторон треуг-ка. Осталось лишь построить окруж-ть, радиус которой будет этот перпендикуляр. Заметим, что так как в треуг-ке есть только одна точка пересечения биссектрис, то и окруж-ть в треуг-к можно вписать лишь одну.

Ещё раз посмотрим на окружность, вписанную в треугольник:

Заметим, что радиусы OK, ОМ и ОL одновременно являются и высотами в ∆AВО, ∆АОС и ∆ВОС. Тогда через радиус можно выразить площади этих треуг-ков:

Сумма сторон AВ, АС и ВС – это периметр ∆AВС (его обозначают буквой Р), а потому можно записать, что

Эту формулу часто используют не для вычисления площади треуг-ка, а для нахождения радиуса вписанной окружности.

Задание. Найдите радиус окруж-ти, вписанной в равнобедренный треуг-к, основание которого имеет длину 20, а боковая сторона – 26.

Теперь надо найти его площадь. Для этого опустим на основание MN высоту KH, которая одновременно будет и медианой:

Отрезок HN будет вдвое короче MN:

Зная в ∆MKN высоту и основание, к которой она проведена, сможем найти его площадь:

Теперь запишем формулу площади, содержащую радиус вписанной окруж-ти, и найдем из нее этот радиус:

Ответ: 20/3.

Задание. В прямоугольный треуг-к, длина гипотенузы которого составляет 52, вписана окруж-ть радиусом 8. Вычислите периметр этого треуг-ка.

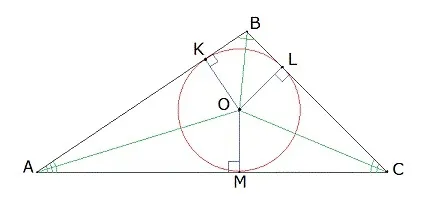
Решение. Проведем радиусы ОМ и ОК из центра окруж-ти к катетам:

Буквой N обозначим точку касания окруж-ти и гипотенузы. Сначала изучим четырехуг-к МОКС. В нем∠С – прямой, ведь ∆AВС – прямоугольный, а ∠ОМС и ∠ОКС также составляют 90°, так как образованы радиусом и касательной. Тогда и ∠МОК тоже должен быть прямым. Значит, МОКС – это квадрат, и его стороны одинаковы:

MO = OK = CK = MC

Заметим, что отрезки AN и AM одинаковы, ведь они представляют собой отрезки касательных, которые построены из одной точки:

AN = AM

Аналогично одинаковы ВК и BN:

BK = BN

Тогда периметр можно записать так:

Ответ: 120.

Задание. Вписанная в ∆AВС окруж-ть касается его сторон AВ, ВС и АС в точках Е, М и F. Известно, что АЕ = 4, СF = 6, МВ = 10. Определите периметр ∆AВС.

Решение. Заметим, отрезки касательных, проведенных к окруж-ти из одной точки, одинаковы, поэтому

Это позволяет найти каждую из сторон ∆AВС:

Ответ: 40.

В многоугольники, имеющие 4 и более вершины, вписать окруж-ть можно лишь в отдельных случаях. В частности, четырехуг-к должен для этого обладать особым свойством.

Действительно, пусть в четырехуг-к AВСD вписана окруж-ть. Тогда отрезки касательных, которые построены из точек А, В, С и D, будут одинаковыми.

Обозначим их маленькими буквами a, b, cи d:

Тогда стороны четырехуг-ка будут вычисляться так:

Действительно, пусть есть четырехуг-к AВСD, у которого

AD + BC = CD + AB (1)

Проведем биссектрисы ∠Aи ∠B, они пересекутся в некоторой точке О. Эта точка окажется равноудаленной от сторон AD, AB и ВС, то есть можно построить окруж-ть, которая коснется этих трех прямых. Докажем, что она также коснется и CD. Возможны три варианта:

1) СD вообще не пересекается с окруж-тью;

2) CD – секущая, и пересекается с окруж-тью в 2 точках;

3) CD – касательная.

Сначала рассмотрим первый вариант, когда СD и окруж-ть не имеют общих точек. Тогда можно провести касательную С’D’, параллельную CD:

Мы видим, что существует описанный четырехуг-к AВС’D’, а значит, суммы его противоположных сторон будут одинаковыми:

Мы получили, что в четырехуг-ке С’D’DC сторона CD равна сумме трех других сторон. Это невозможно, то есть мы получили противоречие. Значит, принятое нами предположение о том, что CD не имеет общих точек с окруж-тью, является ошибочным. С помощью аналогичных утверждений можно отбросить и вариант, согласно которому CD – это секущая. Остается один вариант, по которому СD – касательная, ч. т. д.

Задание. В четырехуг-к MCЕА вписана окруж-ть, причем МС = 5, СЕ = 10, АЕ = 8. Какова длина АМ?

Решение. Если в четырехуг-к можно вписать окруж-ть, то суммы его противоположных сторон одинаковы:

Рассмотрим частные случаи четырехуг-ков. Очевидно, что в ромб и квадрат вписать окруж-ть можно, ведь у них одинаковы все стороны, значит, одинаковы и суммы противоположных сторон. С другой стороны, если параллелограмм НЕ является ромбом, то есть его смежные стороны различны, то вписать в него окруж-ть не получится. Также ее нельзя вписать и в прямоугольник, если он НЕ является квадратом:

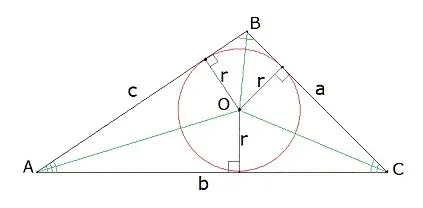
Ранее мы составили формулу, которая связывала периметр треуг-ка с его площадью и радиусом вписанной окруж-ти. Оказывается, она справедлива и для четырехуг-ка. Действительно, пусть есть произвольный описанный четырехуг-к AВСD. Соединим центр вписанной окруж-ти с вершинами, а также проведем из нее радиусы к точкам касания:

В результате мы разбили AВСD на ∆АОD, ∆DOC, ∆COВ и ∆АОВ, причем высотой для каждого из них являются радиусы длиной r. Тогда площади этих треуг-ков можно вычислить так:

Аналогичным образом эту формулу можно доказать и для пятиугольника, и для шестиугольника, и т. д.

Задание. В четырехуг-к AВСD, у которого стороны AB и CD соответственно составляют 13 и 8, вписана окруж-ть радиусом 5. Какова площадь AВСD?

Решение.

Мы можем найти сумму сторон AВ и CD:

AB + CD = 13 + 8 = 21

Так как в четырехуг-к вписана окруж-ть, то и сумма двух других сторон, AD и BC, будет такой же:

AD + BC = AB + CD = 21

Теперь можно вычислить и периметр AВСD:

 P = AB + CD + AD + BC = 21 + 21 = 42

Осталось только применить формулу и рассчитать площадь:

Ответ: 105.

Задание. В квадрат вписана окруж-ть с радиусом 6. Какова площадь квадрата?

Решение. Проведем в окруж-ти радиусы, которые коснутся противоположных сторон квадрата:

В результате получится прямоугольник ВСНК. КН – диаметр окруж-ти, поэтому он вдвое длиннее радиуса:

KH = 6*2 = 12

В прямоугольнике противоположные стороны одинаковы, поэтому

BC = KH = 12

Но ВС – это сторона квадрата, площадь которого и надо найти. Для этого ВС надо возвести в квадрат:

S = BC² = 12² = 144

Ответ: 144.

Описанная окружность

Возможна и ситуация, при которой не окруж-ть вписана в многоуг-к, а наоборот, многоуг-к в окруж-ть. В таком случае все его вершины будут лежать на окруж-ти.

Есть несколько важных теорем, касающихся описанных окружностей.

Для доказательства построим в произвольном ∆AВС серединные перпендикуляры. Они пересекутся в некоторой точке О:

Каждая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка, к которому этот перпендикуляр проведен. Значит, и точка О равноудалена от вершин ∆AВС:

OA = OB = OC

Но тогда из О можно провести окруж-ть, на которой будут лежать точки А, В и С. Она как раз и окажется окружностью, описанной около треугольника. Так как серединные перпендикуляры пересекаются только в одной точке, то и окруж-ть около треуг-ка можно описать лишь одну.

Из теоремы следует важный вывод:

Действительно, три точки, не лежащие на прямой, образуют на плоскости треуг-к.Окруж-ть, проведенная через его вершины, по определению и будет описанной окруж-тью.

Задание. Около равнобедренного треуг-ка с основанием длиной 6 описана окруж-ть радиусом 5. Какова длина боковых сторон этого треуг-ка?

Решение: Проведем радиусы ОА, ОВ и ОС к вершинам вписанного треуг-ка, а на основание ВС опустим перпендикуляр:

Стоит обратить внимание, что точки А, О и Н лежат на одной прямой. Это высота, проведенная к основанию. Она же, по свойству равнобедренного треуг-ка, является медианой, то есть Н – середина ВС. Тогда ОН оказывается серединным перпендикуляром.

Сначала найдем ВН, он равен половине ВС:

BH = BC:2 = 6:2 = 3

Далее изучим ∆ОНВ. Он прямоугольный, то есть для него верна теорема Пифагора:

Задание. Выведите формулу, которая связывает длину стороны равностороннего треуг-ка с радиусом описанной окружности.

Решение. Обозначим буквой a сторону треуг-ка, а буквой R – радиус описанной окруж-ти. Также проведем один серединный перпендикуляр:

Так как ∆AВС – равносторонний, то все его углы, в частности, ∠AВС, составляют 60°.

Заметим, что ∆ВОС и ∆АОВ равны по трем одинаковым сторонам, поэтому

В четырехуг-к окруж-ть удается вписать не всегда. Для этого должно соблюдаться одно условие:

Действительно, пусть около четырехуг-ка ABCD описана окруж-ть:

Тогда вся окруж-ть может быть разбита на две дуги: ⋃ВАD и ⋃ВСD. Их сумма составляет 360°:

Аналогично доказывается утверждение и для другой пары противоположных углов, ∠ADC и ∠ABC.

Обратное утверждение также справедливо:

Докажем эту теорему методом от «противного». Пусть есть четырехуг-к AВСD, у которого сумма противоположных углов составляет 180°, но вокруг него нельзя описать окруж-ть. Тогда проведем окруж-ть через любые три его вершины. Четвертая вершина (пусть это будет D) не может оказаться на окруж-ти. То есть она находится либо внутри окруж-ти, либо вне ее. Сначала рассмотрим случай, когда точка оказывается внутри окруж-ти:

Продолжим прямые AD и CD до пересечения окруж-ти в точках А’ и C’, а потом выберем произвольную точку D’ на окруж-ти между ними.

Теперь сравним ∆АСD и ∆АСD’. У обоих сумма углов одинакова и составляет 180°:

Получается, что ∠D и ∠D’ должны быть равны, но ранее мы показали, что ∠D больше. Это противоречие означает, что точка D не может быть внутри окруж-ти. Аналогичным образом рассматривается второй случай, когда D лежит вне окруж-ти:

Здесь, рассматривая ∆АСD и АСD’, можно показать, что ∠D меньше, чем ∠D’. Однако они должны быть равны друг другу, ведь в сумме с∠В должны давать 180°.             

Задание. В окруж-ть вписан четырехуг-к AВСD, причем∠А составляет 110°, а ∠В – 62°. Найдите два других угла четырехуг-ка.

Решение. 

Здесь надо просто использовать тот факт, что противоположные углы в AВСD должны давать в сумме 180°:

Задание. Докажите, что если трапеция вписана в окруж-ть, то она равнобедренная.

Решение.

Пусть в окруж-ть вписана трапеция AВСD, причем AD и ВС– ее основания. Тогда∠А и ∠В – это односторонние углы при параллельных прямых ВС и AD и секущей AВ, и в сумме они дают 180°. Но так как AВСD вписана в окруж-ть, то и ее противоположные углы, ∠А и ∠С, также должны составлять в сумме 180°:

∠А + ∠B = 180°

∠А + ∠C = 180°

Естественно, эти равенства могут одновременно справедливыми только в том случае, если∠В и ∠С одинаковы. Они являются углами при основании трапеции. Если они одинаковы, то трапеция – равнобедренная (это признак равнобедренной трапеции).

Построение вписанной и описанной окружности

Дополнительно уточним, как выполнить построение вписанной окружности либо описанной окруж-ти. Мы уже говорили, в центр вписанной окружности в треуг-ке – это центр пересечения его биссектрис, ведь он равноудален от сторон. То же самое относится и к многоуг-кам. Вписанная окруж-ть равноудалена от его сторон, поэтому будет лежать на биссектрисе каждого из углов многоуг-ка. При этом строить биссектрисы всех углов не нужно, достаточно выбрать любые два из них. Найдя таким способом центр вписанной окруж-ти, из нее надо опустить перпендикуляр на любую сторону – он и будет радиусом окруж-ти:

При построении описанной окружности нужно помнить, что ее центр описанной окруж-ти находится уже в той точке, где пересекаются серединные перпендикуляры. Снова достаточно провести только два перпендикуляра:

Итак, мы узнали про вписанные и описанные окруж-ти, как определять их центры, и какими свойствами обладают вписанные и описанные многоуг-ки. Это поможет решить ряд задач на экзаменах, в том числе и на ЕГЭ.

Доказательства. Противоположные углы α и β вписаны. Они лежат на дугах, которые дополняют друг друга в круге. Круг содержит 360°. Окружной угол равен половине дуги, на которой он лежит, поэтому сумма углов α и β равна 180°.

Вписанная окружность

Круг — это окружность, вписанная в геометрическую форму и касательная ко всем ее сторонам.

Круг можно записать в виде точной геометрической фигуры — четырехугольника.

В четырехугольниках окружность можно начертить только в том случае, если сумма длин противоположных сторон равна.

Во всех вышеперечисленных схемах круг может быть зарегистрирован только один раз.

Невозможно написать круги на прямоугольниках и прямоугольники на кругах. Это происходит потому, что круг не соприкасается со всеми краями этих фигур.

Геометрическая фигура, в которую вписана окружность, называется кругом.

Акроцикл — это треугольник, он является периметром, и три его стороны соприкасаются с окружностью.

Эндоцикл — это четырехугольник, проведенный вокруг окружности, четыре стороны которого соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

В четырехугольник

1. Не во всякий четырехугольник можно вписать окружность.
2. Если у четырехугольника суммы длин его противолежащих сторон равны, то окружность, может быть, вписана ( Теорема Пито ).
3. Центр вписанной окружности и середины двух диагоналей лежат на одной прямой ( Теорема Ньютона, прямая Ньютона ).
4. Точка пересечения биссектрис — это центр вписанной окружности.
5. Точка касания — это точка, в которой соприкасается окружность и любая из сторон четырехугольника.
6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной в четырехугольник вычисляется по одной и той же формуле. Верное утверждение .
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение .
3. В любой четырехугольник можно вписать окружность. Неверное утверждение .
4. В любой ромб можно вписать окружность. Верное утверждение .
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение .
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение .
7. Угол вписанный в окружность равен соответствующему центральному углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен половине разности суммы катетов и гипотенузы. Верное утверждение .
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение .
10. Вписанная окружность в треугольник имеет в общем три общие точки со всеми сторонами треугольника. Верное утверждение .

Контур, вписанный в угол, — это окружность, проведенная внутри этого угла и соприкасающаяся с его сторонами.

Центр окружности, вписанной в угол, является биссектрисой этого угла.

К центру окружности, вписанной в угол, проведены два перпендикуляра.

Центральный угол окружности — это угол, вершина которого находится в центре окружности.

Диаметр, радиус, строка и длина дуги окружности измеряются в км, м, см, мм и других единицах.

Если окружность радиуса r вписана в многоугольник площадью S и ее полуокружность равна p, то справедлива причина: площадь вписанного круга равна произведению полуокружности и радиуса эндоцикла.

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла

Определение 1. Биссектриса угла — это радиус, который делит угол на две равные части.

Теорема 1 (Основные свойства биссектрисы угла). Каждая точка биссектрисы угла находится на одинаковом расстоянии от стороны угла (рис. 1).

Доказательство Рассмотрим любую точку D на биссектрисе угла BAC и проведем перпендикулярные прямые DE и DF из D к ребру угла (рис. 1). Прямоугольные треугольники ADF и ADE равны, так как острые углы DAF и DAE равны, а косая сторона AD общая. Следовательно.

Доказательство.

Теорема 2 (обратная теорема теоремы 1). Если точки находятся на одинаковом расстоянии от сторон угла, то он лежит на биссектрисе угла (рис. 2).

Доказательство Рассмотрим любую точку D, которая лежит внутри угла BAC и находится на одинаковом расстоянии от края угла. Пусть DE и DF — перпендикуляры, проведенные из D к ребру угла (рис. 2). Прямоугольные треугольники ADF и ADE равны, так как перпендикулярные линии DF и DE равны, а косая сторона AD общая. Следовательно.

Доказательство.

Определение 2. Окружность называется вписанной в угол, если она является касательной к сторонам угла.

Теорема 3. Если окружность вписана в диагональ, то расстояние от вершины угла до точки касания окружности со стороной угла равно.

Доказательство Пусть D — центр окружности, вписанной в угол BAC, а E и F — точки касания окружности с боковыми линиями (рис. 3).

Прямоугольные треугольники ADF и ADE равны, так как кривые DF и DE равны (потому что радиус окружности — это радиус круга), а косая сторона AD — общая. Поэтому.

Доказательство.

Заявление. Теорему 3 можно сформулировать и по-другому. Отрезки касательной, проведенной по окружности из точки, равны.

Определение 3. Биссектриса треугольника — это часть биссектрисы угла треугольника, соединяющая вершины треугольника с противоположными точками.

Теорема 4. В каждом треугольнике все три биссектрисы пересекаются в одной точке.

Доказательство Рассмотрите две биссектрисы A и C ABC и покажите их пересечение в точке O (рис. 4).

Из точки O оставьте перпендикуляры OD, OE и OF на сторонах треугольника. Так как O лежит на биссектрисе угла BAC, уравнение следует из Теоремы 1.

Согласно Теореме 1, если точка C лежит на биссектрисе угла ACB, то из уравнения следует.

Следовательно, уравнение верно.

Формулы для радиуса окружности, вписанной в треугольник

Уравнение для нахождения радиуса окружности, вписанной в треугольник, удобно приводить в виде следующей таблицы.

a, b, c — стороны треугольника, S — площадь, r — радиус конечной окружности, p — полусфера.

α — сторона равностороннего треугольника, r — радиус внутренней окружности.

где α, β и γ — стороны треугольника, S — площадь, r — радиус эндоцикла и p — полусфера.

Где α, β и γ — стороны треугольника, r — радиус эндоцикла, а p — полусфера.

Где α — сторона равностороннего треугольника, r — радиус эндоцикла.

Произвольный треугольник

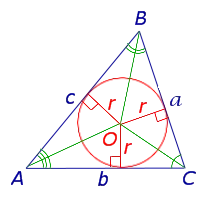где α, β и γ — стороны треугольника, S — площадь, r — радиус эндоцикла и p — полусфера.

Где α, β и γ — стороны треугольника, r — радиус эндоцикла, а p — полусфера.

Где α — сторона равностороннего треугольника, r — радиус эндоцикла.

Вывод формул для радиуса окружности, вписанной в треугольник

Теорема 5. Для любого треугольника

где a, b и c — стороны треугольника, а r — радиус эндоцикла, т.е. гемицикла (рис. 6).

Теорема 6. Для равнобедренных треугольников применимо следующее уравнение

где α — сторона равнобедренного треугольника, β — основание, а r — радиус эндоцикла (рис. 7).

Далее, для равнобедренных треугольников имеем

Теорема 7. Для равнобедренных треугольников применимо следующее уравнение

где α — сторона равнобедренного треугольника, а r — радиус эндоцикла (рис. 8).

Далее, в случае равносторонних треугольников, уравнение имеет следующий вид

описано в следующем разделе. В качестве упражнения читателю предлагается непосредственно вывести формулу радиуса окружности, вписанной в равносторонний треугольник. То есть не используйте общую формулу для радиуса окружности, вписанной в любой треугольник или равнобедренный треугольник.

Теорема 8. Для правильных треугольников уравнение

Доказательство Рассмотрим рисунок 9.

Четырехугольник CDOF является правильным треугольником с равными сторонами DO и OF, поэтому этот четырехугольник является четырехугольным квадратом. Поэтому.

Исходя из теоремы 3, экв.

Таким образом, также принимая во внимание теорему Пифагора, мы имеем

Заявление. В качестве упражнения читателю предлагается вывести, используя общую формулу для радиуса окружности, вписанной в любой треугольник, формулу для радиуса окружности, вписанной в прямоугольный треугольник.

Заявление. В качестве упражнения читателю предлагается вывести, используя общую формулу для радиуса окружности, вписанной в любой треугольник, формулу для радиуса окружности, вписанной в прямоугольный треугольник.

Формулы вычисления радиуса вписанной окружности

Параметры окружности, вписанной в геометрическую фигуру с тремя углами, можно вычислить по стандартным формулам. Радиус окружности определяется в зависимости от типа треугольника.

Произвольный треугольник

Радиус окружности, вписанной в треугольник, можно определить как площадь треугольника, деленную на его периметр.

В данном случае α, β и γ — стороны геометрической фигуры с тремя углами, а S — ее площадь.

Прямоугольный треугольник

Радиус окружности, вписанной в прямоугольный треугольник, равен дроби, числитель которой равен сумме перпендикуляров минус количество виртуальных знаменателей2.

Уравнения a и b — катеты, а c — гипотенуза треугольника.

Равнобедренный треугольник

Радиус окружности, вписанной в равнобедренный треугольник, определяется по формуле

В данном случае a — это сторона, а b — основание треугольника.

Равносторонний треугольник

Расчет радиуса окружности, вписанной в равносторонний или правильный треугольник, производится по следующей формуле

где α — сторона геометрической фигуры с тремя углами.

Как найти через высоту или стороны, примеры решения

Имеется геометрическая фигура с тремя углами, стороны которой равны 5, 7 и 10 см. Вам нужно определить радиус окружности, вписанной в этот треугольник.

Первое, что вам нужно сделать, это определить площадь треугольника. Для этого можно воспользоваться формулой Герона.

Затем примените формулу для расчета радиуса окружности.

ОТВЕТ: радиус окружности равен приблизительно 1,48 см.

Вам нужно вычислить радиус окружности, вписанной в равнобедренный треугольник. Стороны геометрической фигуры равны 16 см, а основание — 7 см.

Вам необходимо вычислить радиус, подставив известные значения в соответствующую формулу.

Доказательства.. Соедините центр внутренней окружности с вершиной треугольника, стороны которого равны α, β и γ. Получите три треугольника, радиусы которых являются высотами радиусов конечных циклов, выполненных в точках контакта. Площадь треугольника равна сумме площадей этих треугольников:.

Как вписывать окружность в треугольник

9 класс Оптическая геометрия. Ссылка 2 Круглые и внутренние круглые круги

Можно сформировать круг вокруг любого треугольника. Она проходит через все вершины треугольника. Вы уже знаете, что точки пересечения середин равноудалены от вершин треугольника. Он является центром региона.

Окружность может быть вписана в любой треугольник. Он касается всех сторон треугольника. Вы также знаете, что пересечение биссектрис треугольника равноудалено от сторон треугольника. Центр круга.

Но можно ли нарисовать круг вокруг произвольного прямоугольника? Если вы попытаетесь это сделать, то обнаружите, что нарисовать круг вокруг прямоугольника можно только в том случае, если прямоугольник Вы узнаете о свойствах вписанных и описанных четырехугольников и свойствах, позволяющих определить, можно ли описать область вокруг определенного четырехугольника и можно ли вписать в него окружность.

Кроме того, вы узнаете ключевую формулу для площади треугольника S =pr.

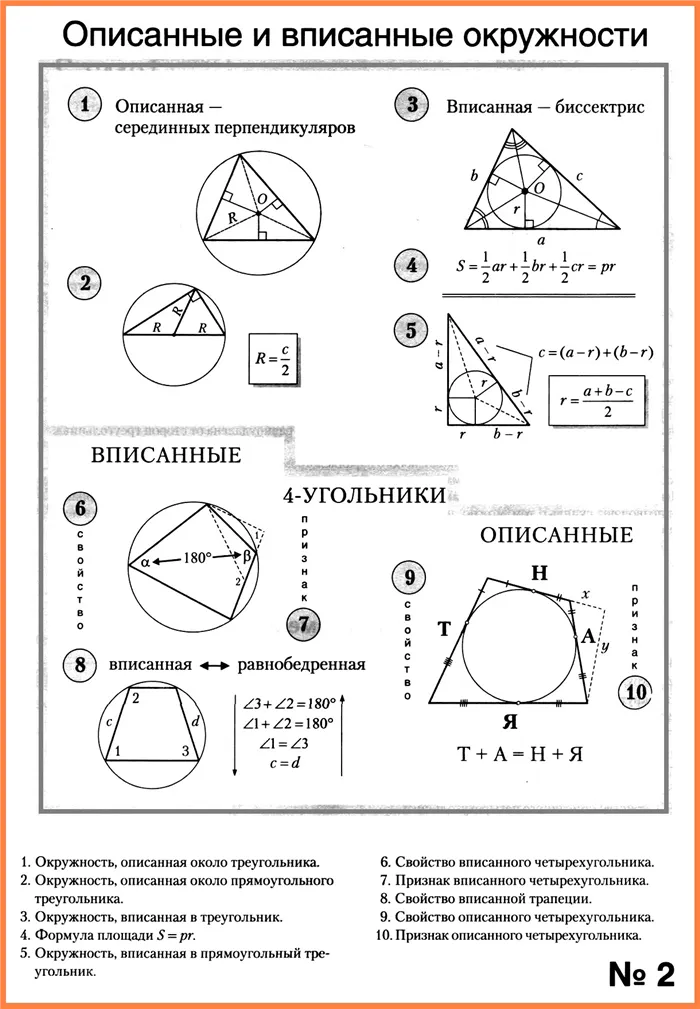
ТАБЛИЦА «Описанные и вписанные окружности»

1. Окружность, описанная около треугольника.

Если окружность проходит через все вершины, она называется очерченной вокруг треугольника.

Теорема. Круг можно нарисовать вокруг любого треугольника, но только одного. Его центр лежит на пересечении перпендикулярных линий сторон треугольника.

Доказательства.. Точка пересечения средних перпендикуляров сторон треугольника равноудалена от его вершины (доказано в седьмой степени). Поэтому точка является центром окружности, а расстояние от нее до любой вершины равно ее радиусу.

Если существует еще один круг, то его центр равноудален от трех вершин, поэтому он совпадает с пересечением перпендикулярных линий, а его радиус совпадает с радиусом первого круга. Круги совпадают.

2. Окружность, описанная около прямоугольного треугольника.

Теорема. Периферийный центр окружности, проведенной вокруг прямоугольного треугольника, находится в середине гипотенузы, а радиус окружности равен половине гипотенузы.

Доказательства.. Мы знаем, что медиана прямоугольного треугольника, образованного из вершин прямого угла, равна половине гипотенузы (это было доказано в 7 классе). Поэтому середина гипотенузы является центром окружности, а ее радиус равен половине гипотенузы. То есть, R = c/2.

3. Окружность, вписанная в треугольник.

Считается, что окружность вписана в треугольник, если она является касательной ко всем сторонам треугольника.

Теорема. В любом треугольнике можно нарисовать окружность, имеющую только один Его центр лежит на пересечении биссектрис треугольника.

Доказательства.. Пересечение биссектрис треугольника равноудалено от сторон треугольника (доказано в классе 7). Если из этой точки провести перпендикуляр к стороне и очертить окружность радиусом, равным перпендикуляру, то сторона треугольника касается окружности в точке касания.

Если существует еще один эндоцикл, то его центр равноудален от всех трех сторон, поэтому он совпадает с пересечением биссектрис, а его радиус совпадает с радиусом первой окружности. Круги совпадают.

4. Формула площади S = рr.

Теорема. Площадь треугольника S = p r, где p — полуокружность треугольника, а r — радиус вписанной окружности.

Доказательства.. Соедините центр внутренней окружности с вершиной треугольника, стороны которого равны α, β и γ. Получите три треугольника, радиусы которых являются высотами радиусов конечных циклов, выполненных в точках контакта. Площадь треугольника равна сумме площадей этих треугольников:.

где p — полуокружность треугольника.

Это уравнение применимо ко всем многоугольникам, которые могут быть вписаны в окружность, то есть ко всем окружностям. Доказательство аналогично.

5. Окружность, вписанная в прямоугольный треугольник.

Теорема. Радиус окружности, вписанной в правильный треугольник, находится по уравнению r = (a + b —c)/2.

Свойства вписанной в треугольник окружности

В этой статье Вы сможете найти свойства вписанной в треугольник окружности, а также их доказательства.

Вписанная в треугольник окружность – это такая окружность, которая находится внутри треугольника и при этом касается всех его сторон (то есть все стороны треугольника являются касательными к окружности). Стоит отметить, что в этом случае сам треугольник является описанным вокруг данной окружности.

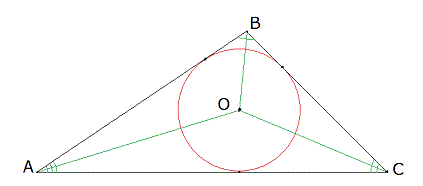
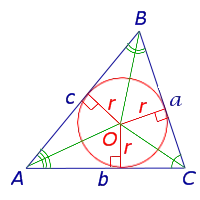
Рисунок 1

Свойства вписанной в треугольник окружности

1. Центр вписанной в треугольник окружности (на рис. 1 – точка О) лежит на пересечении биссектрис треугольника (на рис.1 – АО, ВО и СО).
2. В любой треугольник вписывается окружность и притом только одна.
3. Радиус вписанной в треугольник окружности равен:

   

   Где S – это площадь треугольника,
   
   p – полупериметр треугольника,
   
   a, b, c – стороны треугольника.

Доказательства свойств

Первое свойство

Доказать, что центр вписанной в треугольник окружности находится на пересечении биссектрис.

Доказательство.

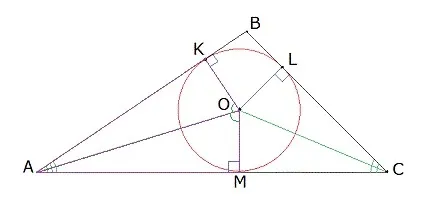
1. Опустим из центра окружности перпендикуляры (OL, OK и OM) к каждой из сторон треугольника ABC (рис. 2). Также из каждого угла проведем прямую к центру окружности (OA, OC и OB).

   

   Рисунок 2

2. Рассмотрим 2 треугольника AOM и AOK. Они являются прямоугольными, т.к. OM и OK – перпендикуляры к сторонам AC и AB. Гипотенуза OA является общей для обоих треугольников.
3. Поскольку касательная к окружности перпендикулярна радиусу, проведенному в точку касания (свойство касательной к окружности), то катеты OМ и OК являются радиусами окружности и, следовательно, равны.
4. Из вышесказанного следует, что прямоугольные треугольники AOМ и AOК равны по гипотенузе и катету. Т.к. треугольники равны, то углы OAМ и OAК тоже равны, отсюда следует, что OA – биссектриса угла BAC.
5. Аналогичным образом доказывается, что OC – биссектриса угла ACB, а OB – биссектриса угла ABC.
6. То есть биссектрисы треугольника пересекаются в одной точке и этой точкой является центр вписанной окружности.

Что и требовалось доказать.

Второе свойство

Доказать, что в любой треугольник можно вписать окружность и притом только одну.

Доказательство

1. В треугольник можно вписать окружность только в том случае, если найдется точка равноудаленная от его сторон.
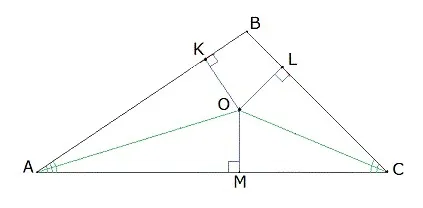
2. Проведем 2 биссектрисы OA и OC. Опустим из точки их пресечения перпендикуляры (OK, OL и OM) ко всем трем сторонам треугольника ABC (рис. 3).

   

   Рисунок 3

3. Рассмотрим треугольники AOK и AOM.
4. У них общая гипотенуза AO. Углы OAK и OAM равны (т.к. OA – биссектриса угла KAM). Углы OKA и OMA прямые (т.е. тоже равны), т.к. OK и OM – перпендикуляры к сторонам AB и AC соответственно.
5. Поскольку 2 пары углов равны, то и 3-я пара (AOM и AOK) также является равной.
6. Из вышенаписанного следует, что треугольники AOK и AOM равны по стороне (AO) и 2-м прилежащим к ней углам (рис. 4).

   

   Рисунок 4

7. Отсюда следует, что стороны OM и OK равны, т.е. равноудалены от сторон треугольника AC и AB соответственно.
8. Аналогичным образом доказывается, что OM и OL равны, т.е. они равноудалены от сторон треугольника AC и BC соответственно.
9. Из вышенаписанного следует, что точка O равноудалена от сторон треугольника, т.е. является центром вписанной окружности.
10. Аналогичным образом можно найти точку внутри любого треугольника, которая будет равноудалена от его сторон, то есть будет центром вписанной в этот треугольник окружности.
11. Из вышенаписанного следует, что в любой треугольник можно вписать окружность.
12. Следует отметить, что центр данной окружности лежит на пересечении биссектрис треугольника.
13. Допустим, что в треугольник можно вписать две (или более) окружности.
14. Проведя 3 отрезка из вершин треугольника к центру этой окружности и, опустив перпендикуляры из этого центра к каждой из сторон треугольника, мы сможем доказать, что эта окружность лежит на пересечении биссектрис треугольника (см. доказательство первого свойства).
15. То есть центр этой окружности совпадает с центром первой окружности, уже вписанной в треугольник, а ее радиус равен перпендикуляру, опущенному на сторону треугольника (как и в первом случае). Это говорит о том, что данные окружности совпадают.
16. Аналогичным образом можно доказать, что любая новая вписанная окружность совпадает с первой, которую мы впишем.
17. То есть вписать в треугольник можно только одну окружность.

Что и требовалось доказать.

Третье свойство

Доказать, что радиус вписанной окружности r равен отношению площади треугольника S к полупериметру p.

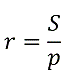
А также равенство:

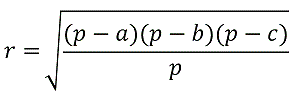
Доказательство.

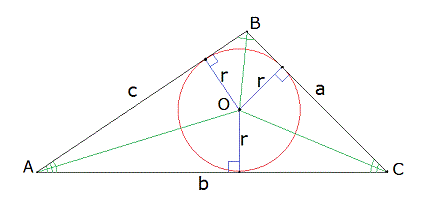
Рисунок 5

1. Рассмотрим произвольный треугольник ABC со сторонами a, b и c (рис 5). Полупериметр данного треугольника p рассчитывается по формуле:

   

2. Центр нашей окружности (точка O на рис. 5) находиться на пересечении биссектрис треугольника. Отрезки OA, OB и OC, соединяющие O с вершинами треугольника АВС, делят треугольник на три: AOC, COB, BOA. Площадь треугольника ABC можно найти как сумму площадей этих трех треугольников.

   

3. Поскольку площадь любого треугольника равна половине произведения его основания на высоту, а высота треугольников AOC, COB, BOA равна радиусу окружности r, то площади треугольников AOC, COB и BOA можно найти как:

   

4. Выразим площадь S треугольника ABC через сумму площадей этих трех треугольников:

   

5. Заметив, что второй множитель – это полупериметр треугольника ABC, можно представить наше равенство в виде:

   

   Или

   

6. Итак, мы доказали, что радиус вписанной окружности равен отношению площади треугольника к полупериметру.
7. Вспомним формулу Герона, которая в нашем случае будет иметь вид:

   

8. Теперь радиус можно выразить как:

   

Что и требовалось доказать.