Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
При условии значения угла между двумя ненулевыми векторами равным 90°( π2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Скалярное произведение двух ненулевых векторов a→ и b→ равном нулю для выполнения равенства a→, b→=0 достаточно для их перпендикулярности.
Пусть заданные векторы a→ и b→ перпендикулярны, тогда выполним доказательство равенства a⇀, b→=0.
Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на косинус угла между ними. По условию a→ и b→ перпендикулярны, а, значит, исходя из определения, угол между ними 90°. Тогда имеем a→, b→=a→·b→·cos(a→, b→^)=a→·b→·cos90°=0.
Вторая часть доказательства
При условии, когда a⇀, b→=0 доказать перпендикулярность a→ и b→.
По сути доказательство является обратным предыдущему. Известно, что a→ и b→ ненулевые, значит, из равенстваa⇀, b→=a→·b→·cos(a→, b→)^ найдем косинус. Тогда получим cos(a→, b→)^=(a→,b→)a→·b→=0a→·b→=0. Так как косинус равен нулю, можем сделать вывод, что угол a→, b→^ векторов a→ и b→ равен 90°. По определению это и есть необходимое и достаточное свойство.
Условие перпендикулярности на координатной плоскости
Раздел скалярного произведения в координатах демонстрирует неравенство (a→, b→)=ax·bx+ay·by, справедливое для векторов с координатами a→=(ax, ay) и b→=(bx, by), на плоскости и (a→,b→)=ax·bx+ay·by для векторов a→=(ax, ay, az) и b→=(bx, by, bz) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид ax·bx+ay·by=0, для трехмерного пространства ax·bx+ay·by+az·bz=0.
Применим на практике и рассмотрим на примерах.
Проверить свойство перпендикулярности двух векторов a→=(2, -3), b→=(-6, -4).
Решение
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
(a→, b→)=ax·bx+ay·by=2·(-6)+(-3)·(-4)=0. Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Ответ: да, заданные векторы a→ и b→ перпендикулярны.
Даны координатные векторы i→, j→, k→. Проверить, могут ли векторы i→-j→ и i→+2·j→+2·k→ быть перпендикулярными.
Решение
Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i→-j→ и i→+2·j→+2·k→ имеются соответствующие координаты (1,-1, 0) и (1, 2, 2). Подставляем числовые значения и получаем: i→+2·j→+2·k→, i→-j→=1·1+(-1)·2+0·2=-1.
Выражение не равно нулю, (i→+2·j→+2·k→, i→-j→)≠0, а это означает, что векторы i→-j→ и i→+2·j→+2·k→ не перпендикулярны, так как условие не выполнилось.
Ответ: нет, векторы i→-j→ и i→+2·j→+2·k→ не перпендикулярны.
Даны векторы a→=(1,0,-2) и b→=(λ, 5, 1). Найти значение λ, при котором данные векторы перпендикулярны.
Решение
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
ax·bx+ay·by+az·bz=0 ⇔1·λ+0·5+(-2)·1=0 ⇔λ=2
Ответ: векторы перпендикулярны при значении λ=2.
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
Дан треугольник АВС со сторонами АВ=8, АС=6, ВС=10 см. проверить на перпендикулярность векторы AB→ и AC→.
Решение
При перпендикулярности векторов AB→ и AC→ треугольник ABC считается прямоугольным. Тогда применим теорему Пифагора, где ВС – гипотенуза треугольника. Равенство BC2=AB2+AC2 должно выполниться. Отсюда следует, что 102=82+62⇔100=100. Значит, АВ и АС являются катетами треугольника АВС, следовательно, AB→ и AC→ перпендикулярны.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
Ненулевой вектор a→ может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.
Задан ненулевой вектор a→, лежащий на прямой а. Тогда заданный b→, расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным иa→. Если вектору i→ перпендикулярен вектор j→ или любой из векторов λ·j→при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b→, перпендикулярному a→=(ax, ay), сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a→=(ax, ay). Для этого необходимо записать условие перпендикулярности векторов в такой форме ax·bx+ay·by=0. Имеем bx и by , являющиеся искомыми координатами перпендикулярного вектора. Когда ax≠0, значение by является ненулевым, а bx вычислим из неравенства ax·bx+ay·by=0 ⇔bx=-ay·byax. При ax=0 и ay≠0 присваиваем bx любое значение кроме нуля, а by находим из выражения by=-ax·bxay.
Дан вектор с координатами a→=(-2, 2). Найти перпендикулярный данному вектор.
Решение
Обозначим искомый вектор как b→(bx, by). Найти его координаты можно из условия перпендикулярности векторов a→ и b→. Тогда получим: (a→, b→)=ax·bx+ay·by=-2·bx+2·by=0. Присвоим by=1 и подставим: -2·bx+2·by=0⇔-2·bx+2=0. Отсюда из формулы получим bx=-2-2=12. Значит, вектор b→=(12, 1) является вектором, перпендикулярным a→.
Ответ: b→=(12, 1).
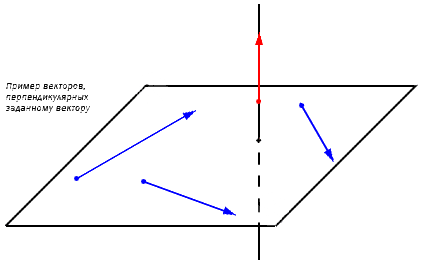
Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a→=(ax, ay, az) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a→ , лежащая на прямой a. Перпендикулярную прямой a плоскость обозначаем α. В этом случае любой ненулевой вектор b→ из плоскости α перпендикулярен a→.
Необходимо найти координаты b→, перпендикулярного ненулевому вектору a→=(ax, ay, az).
Пусть задан b→ с координатами bx, by и bz. Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство ax·bx+ay·by+az·bz=0 должно выполняться. Из условия a→ – ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что ax≠0, ( ay≠0 или az≠0). Следовательно, имеем право разделить на эту координату все неравенство ax·bx+ay·by+az·bz=0, получим выражениеbx+ay·by+az·bzax=0⇔bx=-ay·by+az·bzax. Присваиваем координатам by и bx любое значение, вычисляем значение bx, исходя из формулы, bx=-ay·by+az·bzax. Искомый перпендикулярный вектор будет иметь значение a→=(ax, ay, az).
Рассмотрим доказательство на примере.
Дан вектор с координатами a→=(1, 2, 3) . Найти вектор, перпендикулярный данному.
Решение
Обозначим искомый вектор за b→=(bx, by, bz). Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.
a⇀, b⇀=0⇔ax·bx+ay·by+az·bz=0⇔1·bx+2·by+3·bz=0⇔bx=-(2·by+3·bz)
Если значение by=1, bz=1, тогда bx=-2·by-3·bz=-(2·1+3·1)=-5. Отсюда следует, что координаты вектора b→(-5, 1, 1). Вектор b→ является одним из перпендикулярных векторов заданному.
Ответ: b→=(-5, 1, 1).
Нахождение координат вектора, перпендикулярного двум заданным векторам
Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторамa→(ax, ay, az) и b→=(bx, by, bz). При условии коллинеарности векторов a→ и b→ в задаче достаточно будет найти вектор, перпендикулярный a→ или b→.
При решении применяется понятие векторного произведения векторов.
Векторным произведением векторов a→ и b→ называют вектор, одновременно перпендикулярный и a→ и b→. Для решения данной задачи применяется векторное произведение a→×b→. Для трехмерного пространства имеет вид a→×b→=a→j→k→axayazbxbybz
Разберем подробнее векторное произведение на примере задачи.
Заданы векторы b→=(0, 2, 3) и a→=(2, 1, 0). Найти координаты любого перпендикулярного вектора данным одновременно.
Решение
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
a→×b→=i→j→k→210023=i→·1·3+j→·0·0+k→·2·2-k→·1·0-j→·2·3-i→·0·2=3·i→+(-6)·j→+4·k→
Ответ: (3, -6, 4) – координаты вектора, одновременно перпендикулярного заданным a→ и b→.
Перпендикулярность векторов
Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.
Координаты вектора на плоскости, равного по модулю и перпендикулярного данному
Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.
Алгоритм получения координат перпендикулярных векторов
Вектор на плоскости xOy, перпендикулярный данному вектору получают так:
- Поменять местами координатные числа «x» и «y».
- Заменить знак у одной из координат на противоположный.
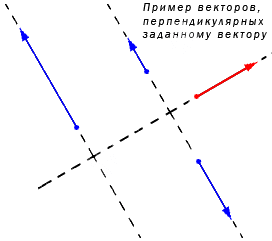
Графический пример
Рассмотрим небольшой графический пример (рис. 1).
Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом
На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec{a}) и (vec{b}).
[ vec{a} = left{ 4 ; 3 right} ]
[ vec{b} = left{ -3 ; 4 right} ]
Из рисунка видно, что векторы (vec{a}) и (vec{b}) перпендикулярны: ( vec{a} perp vec{b} ).
Вектор ( -vec{b} = left{ 3 ; -4 right} ), также будет перпендикулярным вектору ( vec{a} ): ( vec{a} perp vec{(-b)} )
Векторы, изображенные черным цветом, перпендикулярны красному вектору.
Длины векторов ( vec{a} ), ( vec{b} ) и ( vec{(-b)} ) равны.
Условие перпендикулярности векторов
Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.
Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.
Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.
[ large boxed { begin{cases} vec{a} = left{ a_{x} ; a_{y} ; a_{z} right} \ vec{b} = left{ b_{x} ; b_{y} ; b_{z} right} \ |vec{a}| ne 0 \ |vec{b}| ne 0 end{cases}}]
Запишем условие перпендикулярности векторов.
Для двумерного случая:
[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} = 0 }]
Для трехмерного случая:
[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} + a_{z} cdot b_{z} = 0 }]
Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.
При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.
Примечание:
Есть такое правило: Количество неизвестных должно равняться количеству уравнений.
Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.
Перпендикулярные векторы в физике
В физике перпендикулярность некоторых векторов достаточно важна.
Вот несколько примеров:
- Если угол между вектором скорости тела и вектором силы, действующей на тело, будет прямым, то такая сила работу по перемещению тела совершать не будет.
- На проводник с током магнитное поле действует максимальной силой, когда вектор магнитной индукции и вектор тока в проводнике перпендикулярны.
- Когда угол между вращающей силой и, расстоянием между точкой приложения силы и осью вращения, будет прямым, вращательный момент будет максимальным.
- Между линейной скоростью точки колеса и расстоянием от этой точки до оси вращения, угол прямой (радиус и касательная перпендикулярны).
- На вращающееся тело действует центростремительная сила. Угол прямой между этой силой и линейной скоростью точки тела (радиус и касательная перпендикулярны).
Оценка статьи:
Загрузка…
Как найти вектор перпендикулярный вектору
ФОРМУЛА
Чтобы вектор ( overline{a}) был перпендикулярен вектору ( overline{b}) , необходимо, чтобы его скалярное произведение было равно нулю, т.е.
(
(overline{a}, overline{b})=0
)
Если векторы задаются на плоскости своими координатами (
overline{a}=left(a_{x} ; a_{y}right)
) и (
overline{b}=left(b_{x} ; b_{y}right)
), то условие их перпендикулярности принимает вид:
(
(overline{a}, overline{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}=0
)
Если векторы заданы в пространстве и имеют координаты (
overline{a}=left(a_{x} ; a_{y} ; a_{z}right)
) и (
overline{b}=left(b_{x} ; b_{y} ; b_{z}right)
), то перпендикулярное условие записывается в виде:
(
(overline{a}, overline{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}=0
)
ПРИМЕРЫ РАСПОЛОЖЕНИЯ ПЕРПЕНДИКУЛЯРНОГО ВЕКТОРА
ПРИМЕР
overline{a}=(2 ;-1)
) и (
overline{b}=(-3 ; m)
) . При каком значении (
m
) эти векторы будут перпендикулярны?
overline{a}
) и (
overline{b}
) были перпендикулярны, необходимо, чтобы их скалярное произведение было равно нулю, то есть условие выполняется:
(
(overline{a}, overline{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}=0
)
Подставляем координаты указанных векторов в это выражение и из полученного равенства находим (
m
):
(
2 cdot(-3)+(-1) cdot m=0
)
(
-6-m=0
)
(
m=-6
)
overline{a}
) и (
overline{b}
) будут перпендикулярны (
m=-6
)
ПРИМЕР
overline{a}=(3 ;-2 ; m)
) и (
overline{b}=(-1 ; m ; 1)
) даны. При каком значении (
m
) эти векторы будут перпендикулярны?
(
(overline{a}, overline{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}=0
)
Подставив в него указанные координаты векторов, мы получим:
(
3 cdot(-1)+(-2) cdot m+m cdot 1=0
)
(
3-2 cdot m+m=0
)
Из полученного уравнения находим (
m=-6
):
(
3-m=0 Rightarrow m=-3
)
m=-3
)
Как найти перпендикулярный вектор
Перпендикулярными называются вектора, угол между которыми составляет 90º. Перпендикулярные вектора строятся при помощи чертежных инструментов. Если известны их координаты, то проверить или найти перпендикулярность векторов можно аналитическими методами.

Вам понадобится
- – транспортир;
- – циркуль;
- – линейка.
Инструкция
Постройте вектор перпендикулярный данному. Для этого в точке, которая является началом вектора, восстановите к нему перпендикуляр. Это можно сделать при помощи транспортира, отложив угол 90º. Если транспортира нет, сделайте это циркулем.
Установите его в точку начала вектора. Проведите окружность произвольным радиусом. Затем постройте две окружности с центрами в точках, где первая окружность пересекла прямую, на которой лежит вектор. Радиусы этих окружностей должны быть равны между собой и больше радиуса первой построенной окружности. На точках пересечения окружностей постройте прямую, которая будет перпендикулярна исходному вектору в точке его начала, и отложите на ней вектор, перпендикулярный данному.
Определите перпендикулярность двух произвольных векторов. Для этого с помощью параллельного переноса постройте их так, чтобы они исходили из одной точки. Измерьте угол между ними, при помощи транспортира. Если он равен 90º, то вектора перпендикулярны.
Найдите вектор, перпендикулярный тому, координаты которого известны и равны (x;y). Для этого найдите такую пару чисел (x1;y1), которая удовлетворяла бы равенству x•x1+y•y1=0. В этом случае вектор с координатами (x1;y1) будет перпендикулярен вектору с координатами (x;y).
ПримерНайдите вектор, перпендикулярный вектору с координатами (3;4). Используйте свойство перпендикулярных векторов. Подставив в него координаты вектора, получите выражение 3•x1+4•y1=0. Подберите пары чисел, которые делают это тождество верным. Например, пара чисел x1=-4; y1=3 делает тождество верным. Значит, вектор с координатами (-4;3) будет перпендикулярен данному. Таких пар чисел можно подобрать бесконечное множество, а потому и векторов тоже бесконечно много.
Проверяйте перпендикулярность векторов при помощи тождества x•x1+y•y1=0, где (x;y) и (x1;y1) координаты двух векторов. Например, вектора с координатами (3;1) и (-3;9) перпендикулярны, так как 3•(-3)+1•9=0.
Источники:
- перпендикулярные векторы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Понятие вектора и перпендикулярности векторов
Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Определение 1
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Определение 2
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Определение 3
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
Обозначение: $overline{AB}$ – вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $overline{a}$ (рис. 1).
Определение 4
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Обозначение: $overline{0}$.
Введем теперь, непосредственно, определение коллинеарных векторов.
Определение 5
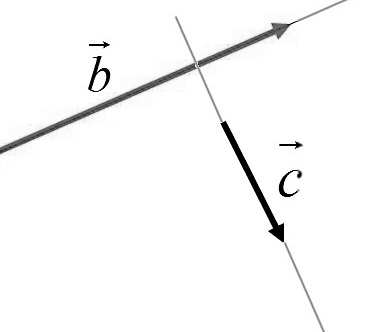
Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).
«Как найти вектор, перпендикулярный вектору» 👇
Также введем определение скалярного произведения, которое будет нам необходимо далее.
Определение 6
Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$overline{α}overline{β}=|overline{α}||overline{β}|cos∠(overline{α},overline{β})$
Скалярное произведение также можно найти с помощью координат векторов следующим образом
$overline{α}overline{β}=α_1 β_1+α_2 β_2+α_3 β_3$
Признак перпендикулярности через пропорциональность
Теорема 1
Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.
Доказательство.
Необходимость: Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство
$overline{α}cdot overline{β}=0$
Так как векторы $overline{α}$ и $overline{β}$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.
$overline{α}cdot overline{β}=|overline{α}||overline{β}|cos90^circ =|overline{α}||overline{β}|cdot 0=0$
Достаточность: Пусть верно равенство $overline{α}cdot overline{β}=0$. Докажем, что векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.
По определению 6, будет верно равенство
$|overline{α}||overline{β}|cos∠(overline{α},overline{β})=0$
$cos∠(overline{α},overline{β})=0$
$∠(overline{α},overline{β})=90^circ$
Следовательно, векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.
Теорема доказана.
Пример 1
Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.
Доказательство.
Найдем скалярное произведение для этих векторов через формулу, данную выше
$overline{α}cdot overline{β}=1cdot 2+(-5)cdot 1+2cdot frac{3}{2}=2cdot 5+3=0$
Значит, по теореме 1, эти вектор перпендикулярны.
Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение
Введем вначале понятие векторного произведения.
Определение 7
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $overline{α}хoverline{β}$.
Чтобы найти векторное произведение, будем пользоваться формулой
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$
Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.
Пример 2
Найти вектор, перпендикулярный к векторам с координатами $overline{α}=(1,2,3)$ и $overline{β}=(-1,0,3)$
Решение.
Найдем векторное произведение данных векторов.
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\1&2&3\-1&0&3end{vmatrix}=(6-0)overline{i}-(3+3)overline{j}+(0+2)overline{k}=6overline{i}-6overline{j}+2overline{k}=(6,6,2)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме