Перпендикулярность векторов
Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.
Координаты вектора на плоскости, равного по модулю и перпендикулярного данному
Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.
Алгоритм получения координат перпендикулярных векторов
Вектор на плоскости xOy, перпендикулярный данному вектору получают так:
- Поменять местами координатные числа «x» и «y».
- Заменить знак у одной из координат на противоположный.
Графический пример
Рассмотрим небольшой графический пример (рис. 1).

Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом
На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec{a}) и (vec{b}).
[ vec{a} = left{ 4 ; 3 right} ]
[ vec{b} = left{ -3 ; 4 right} ]
Из рисунка видно, что векторы (vec{a}) и (vec{b}) перпендикулярны: ( vec{a} perp vec{b} ).
Вектор ( -vec{b} = left{ 3 ; -4 right} ), также будет перпендикулярным вектору ( vec{a} ): ( vec{a} perp vec{(-b)} )
Векторы, изображенные черным цветом, перпендикулярны красному вектору.
Длины векторов ( vec{a} ), ( vec{b} ) и ( vec{(-b)} ) равны.
Условие перпендикулярности векторов
Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.
Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.
Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.
[ large boxed { begin{cases} vec{a} = left{ a_{x} ; a_{y} ; a_{z} right} \ vec{b} = left{ b_{x} ; b_{y} ; b_{z} right} \ |vec{a}| ne 0 \ |vec{b}| ne 0 end{cases}}]
Запишем условие перпендикулярности векторов.
Для двумерного случая:
[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} = 0 }]
Для трехмерного случая:
[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} + a_{z} cdot b_{z} = 0 }]
Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.
При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.
Примечание:
Есть такое правило: Количество неизвестных должно равняться количеству уравнений.
Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.
Перпендикулярные векторы в физике
В физике перпендикулярность некоторых векторов достаточно важна.
Вот несколько примеров:
- Если угол между вектором скорости тела и вектором силы, действующей на тело, будет прямым, то такая сила работу по перемещению тела совершать не будет.
- На проводник с током магнитное поле действует максимальной силой, когда вектор магнитной индукции и вектор тока в проводнике перпендикулярны.
- Когда угол между вращающей силой и, расстоянием между точкой приложения силы и осью вращения, будет прямым, вращательный момент будет максимальным.
- Между линейной скоростью точки колеса и расстоянием от этой точки до оси вращения, угол прямой (радиус и касательная перпендикулярны).
- На вращающееся тело действует центростремительная сила. Угол прямой между этой силой и линейной скоростью точки тела (радиус и касательная перпендикулярны).
Оценка статьи:
![]() Загрузка…
Загрузка…
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Понятие вектора и перпендикулярности векторов
Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Определение 1
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Определение 2
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Определение 3
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Обозначение: $overline{AB}$ – вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $overline{a}$ (рис. 1).
Определение 4
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Обозначение: $overline{0}$.
Введем теперь, непосредственно, определение коллинеарных векторов.
Определение 5
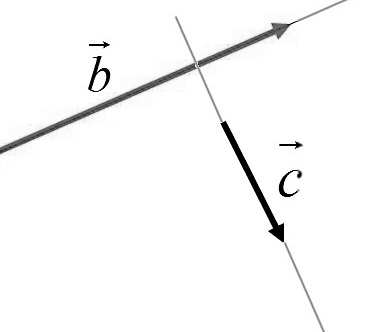
Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).
«Как найти вектор, перпендикулярный вектору» 👇
Также введем определение скалярного произведения, которое будет нам необходимо далее.
Определение 6
Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$overline{α}overline{β}=|overline{α}||overline{β}|cos∠(overline{α},overline{β})$
Скалярное произведение также можно найти с помощью координат векторов следующим образом
$overline{α}overline{β}=α_1 β_1+α_2 β_2+α_3 β_3$
Признак перпендикулярности через пропорциональность
Теорема 1
Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.
Доказательство.
Необходимость: Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство
$overline{α}cdot overline{β}=0$
Так как векторы $overline{α}$ и $overline{β}$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.
$overline{α}cdot overline{β}=|overline{α}||overline{β}|cos90^circ =|overline{α}||overline{β}|cdot 0=0$
Достаточность: Пусть верно равенство $overline{α}cdot overline{β}=0$. Докажем, что векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.
По определению 6, будет верно равенство
$|overline{α}||overline{β}|cos∠(overline{α},overline{β})=0$
$cos∠(overline{α},overline{β})=0$
$∠(overline{α},overline{β})=90^circ$
Следовательно, векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.
Теорема доказана.
Пример 1
Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.
Доказательство.
Найдем скалярное произведение для этих векторов через формулу, данную выше
$overline{α}cdot overline{β}=1cdot 2+(-5)cdot 1+2cdot frac{3}{2}=2cdot 5+3=0$
Значит, по теореме 1, эти вектор перпендикулярны.
Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение
Введем вначале понятие векторного произведения.
Определение 7
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $overline{α}хoverline{β}$.
Чтобы найти векторное произведение, будем пользоваться формулой
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$
Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.
Пример 2
Найти вектор, перпендикулярный к векторам с координатами $overline{α}=(1,2,3)$ и $overline{β}=(-1,0,3)$
Решение.
Найдем векторное произведение данных векторов.
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\1&2&3\-1&0&3end{vmatrix}=(6-0)overline{i}-(3+3)overline{j}+(0+2)overline{k}=6overline{i}-6overline{j}+2overline{k}=(6,6,2)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
������������������ ��������
�������� �����:
������������������, ������ �����, ��������������, ������, ������������ �������, ����������
������� ������������������ ��������
- ������� �������� ����������������� ����� � ������ �����, ����� �� ��������� ������������ ����� ����.
- ���� ��� ������� $$vec a(x_{a}; y_{a})$$ � $$vec b(x_{b}; y_{b})$$. ��� ������� ����� ���������������, ���� ��������� xaxb + yayb = 0.
������� �������������� ��������
- ������� �����������, ���� �������� ������� ������� ��������� �
�������� ������� ��� ��, ��� �������� ������� — � �������� �������. - ���� ��� ������� $$vec a(x_{a}; y_{a})$$ � $$vec b(x_{b}; y_{b})$$. ��� ������� �����������, ���� xa = $$lambda$$ xb � ya = $$lambda$$ yb, ��� $$lambda in R$$.

��. �����:
���� �� ���������,
���������� �������
Прежде чем приступить к понятию того, как найти перпендикулярные векторы, сначала нам нужно узнать о векторах. Физические величины, имеющие как величину, так и направление, называются векторами.
Чтобы проиллюстрировать концепцию вектора, сначала нам нужно принять во внимание векторную величину. Например, сила является вектором. Предположим, что вес тела равен 5 Н, это означает, что величина веса равна 5 Н и он действует в направлении вниз. Если говорить о двух векторах, то при выполнении условия, что их скалярное произведение равно нулю, можно сказать, что они перпендикулярны друг другу.
Например, если мы рассмотрим скалярное произведение векторов A и B, то
AB= AB cos х
Здесь x определяется как угол между двумя векторами A и B. Если мы возьмем x = 90 градусов, то значение скалярного произведения A и B равно ABcos90=0 (поскольку cos90=0). И наоборот, если скалярное произведение двух векторов равно 0, то можно сказать, что они перпендикулярны друг другу.
АВ=0
АВ, потому что х=0
потому что х=0
потому что х = потому что 90
х = 90
Концепция перпендикулярных векторов может быть проиллюстрирована некоторыми численными задачами, написанными ниже:
Пример
Значения двух векторов A и B равны (5i+3j-8k) и (i+j+k) соответственно. Эти два вектора перпендикулярны или нет?
AB
=(5i+3j-8k).(i+j+k)
=5i.i+3j.j-8k.k [при ii=1,jj=1 и kk=1]
=5+3-8
= 8-8
=0
Согласно полученному ранее правилу, когда скалярное произведение двух векторов равно нулю, говорят, что они перпендикулярны друг другу. Следовательно, векторы А и В перпендикулярны друг другу.
Два вектора (3i+7j+7k) и (-7i-aj+7k) перпендикулярны друг другу. Найдите значение а.
Сначала нам нужно вычислить скалярное произведение этих двух векторов.
(3i+7j+7k).(-7i-aj+7k)
=(-21-7а+49)
Как мы знаем, в случае перпендикулярных векторов скалярное произведение двух векторов должно быть равно 0. Итак –
(-21-7а+49)=0
Или -7а+28=0
Или 7а=28
Или а=28/7
Или а=4
Подобная концепция не используется ни в какой рабочей силе. Безработная сила – это сила, действующая перпендикулярно направлению перемещения тела.
Вт=ФС
= FScosx
Здесь W = выполненная работа
F= сила
S = смещение
х=90 градусов
W= ФС cos90
=0
Здесь совершенная работа равна 0, что означает, что сила не совершает никакой работы. Следовательно, это называется отсутствием рабочей силы.
Пример
Человек идет по горизонтальной поверхности с грузом на голове. Здесь совершенная работа равна 0, так как сила тяжести и его перемещение на земле перпендикулярны друг другу.
Как найти вектор, перпендикулярный двум векторам?
Здесь применяется условие, что оба вектора, на которых перпендикулярен третий вектор, должны быть непараллельными векторами. Вычислив векторное произведение двух непараллельных векторов, мы сможем получить вектор, перпендикулярный обоим из них по отдельности. Например, A и B – два непараллельных вектора, где A= (a1i+a2j+a3k) и B= (b1i+b2j+b3k), тогда их перпендикулярный вектор будет = перекрестное произведение A и B

p = (a1i+a2j+a3k)*(b1i+b2j+b3k)
Or, p = (a1b2k-a1b3j-a2b1k+a2b3i+a3b1j-a3b2i)
[Поскольку i*i=0,i*j=k,i*k=-j,j*j=0,j*k=i,j*i=-k,k*k=0,k*i= j,k*j=-i]
Or, p= i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)
Таким образом, искомый перпендикулярный вектор равен i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)
Теперь, если мы хотим перепроверить, перпендикулярен вектор или нет, нам нужно рассмотреть отдельные скалярные произведения pA и pB.
Now, p.A= { i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}.(a1i+a2j+a3k)
= a1a2b3-a1b2a3+b1a2a3-a1a2b3+a1b2a3-b1a2a3
= 0
And p.B= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}. (b1i+b2j+b3k)
= b1a2b3-b1b2a3+b1b2a3-a1b2b3+a1b2b3-b1a2b3
= 0
Таким образом, из приведенных выше вычислений видно, что перпендикулярный вектор p перпендикулярен обоим векторам A и B по отдельности. Отсюда доказано, что перекрестное произведение двух непараллельных векторов дает перпендикулярный к ним вектор.
Как найти блок вектор перпендикуляр в два векторы?
Возьмем два вектора X и Y.
Компания перекрестное произведение X и Y = X * Y
Величина X и Y равна = |X*Y|
Таким образом, требуемый единичный вектор, перпендикулярный и X, и Y, равен =( X*Y)/ |X*Y|
Пример
A и B — два вектора, где A= (5i+5j+7k) и B= (i+j+k). Найдите единичный вектор, который перпендикулярен и А, и В.
А*В=(5i+5j+7k)*(i+j+k)
= 5k-5j-5k+5i+7j-7i
=-2i+2j
=2(-i+j)
|А*В|=[(-2)^2+(2)^2]^(½)
=2.(2)^(½)
Следовательно, единичный вектор, перпендикулярный A и B = 2(-i+j)/2.(2)^(½)
=(-i+j)/(2)^(½)
Как определить, перпендикулярны ли два вектора?
Чтобы определить, перпендикулярны ли два вектора друг другу или нет, мы должны сначала вычислить их скалярное произведение. По результату мы сможем сделать вывод, перпендикулярны векторы или нет. Значение 0 скалярного произведения означает, что векторы перпендикулярны друг другу, тогда как ненулевое значение означает, что векторы не перпендикулярны друг другу.
Пример
Вес автомобиля F=3i+3j+3k действует вниз. Его перемещение в горизонтальной плоскости равно D=-3i+3j. Что можно сказать о проделанной работе по машине?
Проделанная работа = ФД
=(3i+3j+3k).(-3i+3j+0k)
= -9 + 9
= 0
Здесь в приведенной выше задаче скалярное произведение равно 0. Таким образом, можно сделать вывод, что F и D перпендикулярны друг другу.
Как найти равнодействующую двух перпендикулярных векторов?

А+В=Р
Пусть есть два вектора А и В, между которыми есть угол С. Если их результирующая равна R, то величина R будет равна
R = (A ^ 2 + B ^ 2-2ABcosC) ^ (½)
Пример
На тело действуют две силы F1 и F2, причем величина F1 равна 8 Н, а величина F2 равна 6 Н, и они взаимно перпендикулярны. Чему будет равна результирующая сила?
F1=8 Н
F2=6 Н
С= 90 градусов
R= (F1^2+F2^2-2F1F2cosC)^(½)
={(8)^2+(6)^2-2.8.6.cos 90}^(½)
={64+36-0}^(½)
=100^(½)
= 10 Н
Как найти вектор, перпендикулярный трем векторам?
Возьмем три различные точки, лежащие в одной плоскости, но не на одной прямой. Эти точки имеют три разных вектора положения, равные x, y, z соответственно. Пусть r будет вектором положения другой точки на той же плоскости, где лежат остальные три точки. Таким образом, векторы (rx), (yx) и (z-x) компланарны.. Используя формулу для компланарных векторов, можно сказать, что
(рх). (ух)* (zх)=0
Или (rx).(x*y+y*z+z*x)=0
Следовательно, (x*y+y*z+z*x) перпендикулярно (rx) и, следовательно, перпендикулярно плоскости трех различных точек.
Как найти перпендикулярное расстояние между двумя векторами?
Перпендикулярное расстояние — это кратчайшее расстояние между двумя векторами. Формула кратчайшего расстояния между двумя векторами:
Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|
Пример
r1=(i+j+k)+k1(ijk)
r2=(2i+2j+2k)+k2(2i-2j-2k)
а1=я+j+к
a2=2i+2j+2k
b1=ijk
b2=2i-2j-2k
a2-a1=(2i+2j+2k)-(i+j+k)
=2i+2j+2k-ijk
=я+у+к
b1*b2=(i-j-k)*(2i-2j-2k)
=-2k+2j+2k+2i+2j-2i
= 4j
Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|
=|4j.(i+j+k)/4|
=|1|
=1 единица
Как найти параллельные и перпендикулярные векторы?
Мы можем использовать следующую формулу, чтобы найти параллельные векторы:
ка=б
Здесь k — константа, а a и b — два вектора.
Пример
Есть два вектора a и b, значения которых равны (3i+6j) и (4i+8j) соответственно. Эти два вектора параллельны друг другу или нет?
По формуле, написанной выше ka=b
к.(3 6)=(4 8)
3к=4 6к=8
Or, k=4/3 or,k=8/6=4/3
Поскольку значения k одинаковы в обоих случаях, векторы a и b параллельны друг другу.
Точно так же мы можем определить, перпендикулярны ли какие-либо два вектора, вычислив их наклоны. Если значение произведения этих наклонов равно -1, то можно сказать, что векторы являются перпендикулярными или ортогональными векторами.
Есть два вектора (3i-5j) и (5i+3j). Определите, перпендикулярны они или нет?
Пусть а=(3i-5j)
и b=(5i+3j)
Следовательно, наклон a=ma=- 5/3 и наклон b=mb= ⅗
Здесь ma.mb=(-5/3)*(⅗)
= -1
Итак, векторы а и b перпендикулярны.
Как найти перпендикулярные векторы в 3D?
Давайте возьмем пример, чтобы получить ответ.
p=(1 2 -2) и q=(-2 2 1). Эти два трехмерных вектора перпендикулярны или нет?
pq= (-2+4-2)
=0
Следовательно, p и q — два перпендикулярных трехмерных вектора.
Прежде чем начать понятие перпендикулярных векторов, сначала нам нужно узнать о векторах. Физические величины, имеющие как величину, так и направление, называются векторами.
Чтобы проиллюстрировать концепцию вектора, сначала нам нужно принять во внимание векторную величину. Например, сила является вектором. Предположим, что вес тела равен 5 Н, это означает, что величина веса равна 5 Н и он действует в направлении вниз. Если говорить о двух векторах, то при выполнении условия, что их скалярное произведение равно нулю, можно сказать, что они перпендикулярны друг другу. Например, если мы рассмотрим скалярное произведение векторов A и B, то
AB= AB cos х
Здесь x определяется как угол между двумя векторами A и B. Если мы возьмем x = 90 градусов, то значение скалярного произведения A и B равно ABcos90=0 (поскольку cos90=0). И наоборот, если скалярное произведение двух векторов равно 0, то можно сказать, что они перпендикулярны друг другу.
АВ=0
АВ, потому что х=0
потому что х=0
потому что х = потому что 90
х = 90
Концепция перпендикулярных векторов может быть проиллюстрирована некоторыми численными задачами, написанными ниже:
Пример
Значения двух векторов A и B равны (5i+3j-8k) и (i+j+k) соответственно. Эти два вектора перпендикулярны или нет?
AB
=(5i+3j-8k).(i+j+k)
=5i.i+3j.j-8k.k [при ii=1,jj=1 и kk=1]
=5+3-8
= 8-8
=0
Согласно полученному ранее правилу, когда скалярное произведение двух векторов равно нулю, говорят, что они перпендикулярны друг другу. Следовательно, векторы А и В перпендикулярны друг другу.
2) Два вектора (3i+7j+7k) и (-7i-aj+7k) перпендикулярны друг другу. Найдите значение а.
Сначала нам нужно вычислить скалярное произведение этих двух векторов.
(3i+7j+7k).(-7i-aj+7k)
=(-21-7а+49)
Как мы знаем, в случае перпендикулярных векторов скалярное произведение двух векторов должно быть равно 0. Итак –
(-21-7а+49)=0
Или -7а+28=0
Или 7а=28
Или а=28/7
Или а=4
Подобная концепция не используется ни в какой рабочей силе. Безработная сила – это сила, действующая перпендикулярно направлению перемещения тела.
Вт=ФС
= FScosx
Здесь W = выполненная работа
F= сила
S = смещение
х=90 градусов
W= ФС cos90
=0
Здесь совершенная работа равна 0, что означает, что сила не совершает никакой работы. Следовательно, это называется отсутствием рабочей силы.
Пример
Человек идет по горизонтальной поверхности с грузом на голове. Здесь совершенная работа равна 0, так как сила тяжести и его перемещение на земле перпендикулярны друг другу.
Как найти вектор, перпендикулярный двум векторам?
Здесь применяется условие, что оба вектора, на которых перпендикулярен третий вектор, должны быть непараллельными векторами. Вычислив векторное произведение двух непараллельных векторов, мы сможем получить вектор, перпендикулярный обоим из них по отдельности.
Например, A и B – два непараллельных вектора, где A= (a1i+a2j+a3k) и B= (b1i+b2j+b3k), тогда их перпендикулярный вектор будет = перекрестное произведение A и B
p = (a1i+a2j+a3k)*(b1i+b2j+b3k)
Or, p = (a1b2k-a1b3j-a2b1k+a2b3i+a3b1j-a3b2i)
[Поскольку i*i=0,i*j=k,i*k=-j,j*j=0,j*k=i,j*i=-k,k*k=0,k*i= j,k*j=-i]
Or, p= i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)
Таким образом, искомый перпендикулярный вектор равен i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)
Теперь, если мы хотим перепроверить, перпендикулярен вектор или нет, нам нужно рассмотреть отдельные скалярные произведения pA и pB.
Now, p.A= { i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}.(a1i+a2j+a3k)
= a1a2b3-a1b2a3+b1a2a3-a1a2b3+a1b2a3-b1a2a3
= 0
And p.B= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}. (b1i+b2j+b3k)
= b1a2b3-b1b2a3+b1b2a3-a1b2b3+a1b2b3-b1a2b3
= 0
Таким образом, из приведенных выше вычислений видно, что перпендикулярный вектор p перпендикулярен обоим векторам A и B по отдельности. Отсюда доказано, что перекрестное произведение двух непараллельных векторов дает перпендикулярный к ним вектор.
Как найти единичный вектор, перпендикулярный двум векторам?
Возьмем два вектора X и Y.
Перекрестное произведение X и Y равно X*Y
Величина X и Y равна = |X*Y|
Таким образом, требуемый единичный вектор, перпендикулярный и X, и Y, равен =( X*Y)/ |X*Y|
Пример
A и B — два вектора, где A= (5i+5j+7k) и B= (i+j+k). Найдите единичный вектор, который перпендикулярен и А, и В.
А*В=(5i+5j+7k)*(i+j+k)
= 5k-5j-5k+5i+7j-7i
=-2i+2j
=2(-i+j)
|А*В|=[(-2)^2+(2)^2]^(½)
=2.(2)^(½)
Следовательно, единичный вектор, перпендикулярный A и B = 2(-i+j)/2.(2)^(½)
=(-i+j)/(2)^(½)
Как определить, перпендикулярны ли два вектора?
Чтобы определить, перпендикулярны ли два вектора друг другу или нет, мы должны сначала вычислить их скалярное произведение. По результату мы сможем сделать вывод, перпендикулярны векторы или нет. Значение 0 скалярного произведения означает, что векторы перпендикулярны друг другу, тогда как ненулевое значение означает, что векторы не перпендикулярны друг другу.
Пример
Вес автомобиля F=3i+3j+3k действует вниз. Его перемещение в горизонтальной плоскости равно D=-3i+3j. Что можно сказать о проделанной работе по машине?
Проделанная работа = ФД
=(3i+3j+3k).(-3i+3j+0k)
= -9 + 9
= 0
Здесь в приведенной выше задаче скалярное произведение равно 0. Таким образом, можно сделать вывод, что F и D перпендикулярны друг другу.
Как найти равнодействующую двух перпендикулярных векторов?
Пусть есть два вектора А и В, между которыми есть угол С. Если их результирующая равна R, то величина R будет равна
R = (A ^ 2 + B ^ 2-2ABcosC) ^ (½)
Пример
На тело действуют две силы F1 и F2, причем величина F1 равна 8 Н, а величина F2 равна 6 Н, и они взаимно перпендикулярны. Чему будет равна результирующая сила?
F1=8 Н
F2=6 Н
С= 90 градусов
R= (F1^2+F2^2-2F1F2cosC)^(½)
={(8)^2+(6)^2-2.8.6.cos 90}^(½)
={64+36-0}^(½)
=100^(½)
= 10 Н
Как найти вектор, перпендикулярный трем векторам?
Возьмем три различные точки, лежащие в одной плоскости, но не на одной прямой. Эти точки имеют три разных вектора положения, равные x, y, z соответственно. Пусть r будет вектором положения другой точки на той же плоскости, где лежат остальные три точки.
Таким образом, векторы (rx), (yx) и (z-x) компланарны. Используя формулу для компланарных векторов, можно сказать, что
(рх). (ух)* (zх)=0
Или (rx).(x*y+y*z+z*x)=0
Следовательно, (x*y+y*z+z*x) перпендикулярно (rx) и, следовательно, перпендикулярно плоскости трех различных точек.
Как найти перпендикулярное расстояние между двумя векторами?
Перпендикулярное расстояние — это кратчайшее расстояние между двумя векторами. Формула кратчайшего расстояния между двумя векторами:
Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|
Пример
r1=(i+j+k)+k1(ijk)
r2=(2i+2j+2k)+k2(2i-2j-2k)
а1=я+j+к
a2=2i+2j+2k
b1=ijk
b2=2i-2j-2k
a2-a1=(2i+2j+2k)-(i+j+k)
=2i+2j+2k-ijk
=я+у+к
b1*b2=(i-j-k)*(2i-2j-2k)
=-2k+2j+2k+2i+2j-2i
= 4j
Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|
=|4j.(i+j+k)/4|
=|1|
=1 единица
Как найти параллельные и перпендикулярные векторы?
Мы можем использовать следующую формулу, чтобы найти параллельные векторы:
ка=б
Здесь k — константа, а a и b — два вектора.
Пример
Есть два вектора a и b, значения которых равны (3i+6j) и (4i+8j) соответственно. Эти два вектора параллельны друг другу или нет?
По формуле, написанной выше ka=b
к.(3 6)=(4 8)
3к=4 6к=8
Or, k=4/3 or,k=8/6=4/3
Поскольку значения k одинаковы в обоих случаях, векторы a и b параллельны друг другу.
Точно так же мы можем определить, перпендикулярны ли какие-либо два вектора, вычислив их наклоны. Если значение произведения этих наклонов равно -1, то можно сказать, что векторы являются перпендикулярными или ортогональными векторами.
Пример
Есть два вектора (3i-5j) и (5i+3j). Определите, перпендикулярны они или нет?
Пусть а=(3i-5j)
и b=(5i+3j)
Следовательно, наклон a=ma=- 5/3 и наклон b=mb= ⅗
Здесь ma.mb=(-5/3)*(⅗)
= -1
Итак, векторы а и b перпендикулярны.
Как найти перпендикулярные векторы в 3D?
Давайте возьмем пример, чтобы получить ответ.
p=(1 2 -2) и q=(-2 2 1). Эти два трехмерных вектора перпендикулярны или нет??
pq= (-2+4-2)
=0
Следовательно, p и q — два перпендикулярных трехмерных вектора.
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = {ax; ay} и b = {bx; by}, условие ортогональности запишется следующим образом:
a · b = ax · bx + ay · by = 0
Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 – 2 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 – 5 = 16
Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = {ax; ay; az} и b = {bx; by; bz}, условие ортогональности запишется следующим образом:
a · b = ax · bx + ay · by + az · bz = 0
Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 – 2 + 0 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 – 8 = 2n – 4
2n – 4 = 0
2n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.