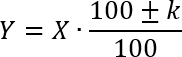Формула простого процента: как найти исходное значение
13 ноября 2013
В этом коротком видеоуроке мы научимся решать задачи на проценты с помощью специальной формулы, которая так и называется: формула простого процента. Давайте оформим эту формулу в виде теоремы.
Теорема о простом проценте. Предположим, что есть некая исходная величина x, которая затем меняется на k%, и получается новая величина y. Тогда все три числа связаны формулой:
Плюс или минус перед коэффициентом k ставится в зависимости от условия задачи. Если по условию величина x возрастает, то перед k стоит плюс. Если же величина уменьшается, то перед коэффициентом k стоит минус.
Несмотря на кажущуюся мудреность этой формулы, многие задачи с ее помощью решаются очень быстро и красиво. Давайте попробуем.
Задача. Цена на товар была повышена на 10% и составила 2970 рублей. Сколько рублей стоил товар до повышения цены?
Чтобы решить эту задачу с помощью формулы простых процентов, нам необходимы три числа: исходное значение x, проценты k и итоговое значение y. Из всех трех чисел нам известны проценты k = 10 и итоговое значение y = 2970. Обратите внимание: 2970 — это именно итоговая цена, т.е. y. Потому что по условию задачи исходная цена на товар неизвестна (ее как раз требуется найти). Но затем она была повышена, и только тогда составила 2970 рублей.
Итак, нам нужно найти x, т.е. исходное значение. Что ж, подставляем наши числа в формулу и получаем:
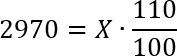
Складываем числа в числителе и получаем:
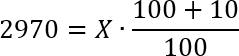
Сокращаем по одному нулю в числителе и знаменателе, а затем умножаем обе части уравнения на 10. Получим:
11x = 29 700
Чтобы найти x из этого простейшего линейного уравнения, нужно разделить обе стороны на 11:
x = 29 700 : 11 = 2700
Как видите, это довольно большие числа, поэтому в уме такие вычисления не провести. В случае, если такая задача встретится вам на ЕГЭ, придется делить уголком. При этом все разделилось без остатка, и мы получили значение x:
x = 2700
Именно столько стоил товар до повышения цены. И именно это число нам требовалось найти по условию задачи. Поэтому все: задача решена. Причем решена не «напролом», а с помощью формулы простого процента — быстро, красиво и наглядно.
Разумеется, эту задачу можно было решать по-другому. Например, через пропорции. Или экзотическим методом коэффициентов. Но будет гораздо лучше и надежнее, если у вас на вооружении будет несколько приемов для решения любой задачи на проценты. Так что обязательно попрактикуйтесь в использовании данной формулы.
А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Смотрите также:
- Процент: неизвестно начальное значение (метод пропорции)

- Формула простого процента: неизвестно конечное значение

- Решение ЕГЭ-2011: вариант 1, часть B

- Метод коэффициентов, часть 1

- Деление многочленов уголком

- Сфера, вписанная в куб

Вычисление исходного числа по известному проценту от числа
Формула вычисления числа по его проценту.
Если дано число B которое составляет P процентов от числа A и необходимо найти значение числа A, то
Для вывода этого соотношения используем методику решения задач с процентами через пропорции
“все“”часть” =100%”часть в %“ =>
“все” = “часть” · “100%“часть в %
Примеры вычисления исходного числа по известному проценту от числа
Пример 1.
Найти исходное число, если 5% от этого числа равно 40.
Решение:
Ответ: 800.
Пример 2.
На заводе работает 270 женщины. Это 30% от всех работников. Сколько человек работает на заводе?
Решение:
Ответ: На заводе работает 900.
Пример 3.
Какую сумму нужно положить на депозит под 10% годовых, чтобы через год получить прибыль 1000 рублей.
Решение:
Ответ: на депозит необходимо положить 10000 рублей.
При изучении процентов вам также будут полезны:
Найти число к которому был прибавлен процент
Онлайн калькулятор вычисляет исходное число по итоговому числу и проценту. Процент от разницы.
Задано число А, к которому прибавили определенный процент, и получили число В. Необходимо найти число А а разница между числом А и B будет размер процента в единичном выражении.
Типичным примером такой задачи является нахождение суммы до прибавления процента НДС в бухгалтерском учете.
Пример: Сумма, сданная кассиром в конце рабочего дня, составляет 100 000 рублей. Найти сумму без НДС и процент НДС в денежном выражении, если он составляет 20% на данную категорию товаров.
Решение: 100 000 рублей составляет 100%+20%=120%. Тогда 1%=100 000/120 = 833.33 рубля. 20% НДС найдем, умножив полученный 1% на 20:833.33×20 = 16 666.6 рублей – процент от разницы а исходное число без НДС 83333.4 рубля.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Как рассчитать от какой суммы был взят процент?
Василий Васильев
Знаток
(309),
закрыт
7 лет назад
Если известны:
1)какой был взят процент от числа и 2)какое число получилось в результате,
то как узнать от какого изначального числа взят процент. Какова формула расчета?
Дополнен 7 лет назад
как узнать 4250 это 15% от какого числа (знаю, что 5000, но как это вычислить 🙂 )
Дополнен 7 лет назад
*да, прошу прощения, 85%, спасибо
Ёжка
Высший разум
(269811)
7 лет назад
4250 – это 85% от 5000, а не 15.
Решать лучше пропорцией, чтобы понять смысл.
Нужно найти то число, которое 100%.
4250 – 85%
Х – 100%
Пропорция решается “крестиком”:
Х=4250*100:85=5000
——————————————-
Если что не понятно, не вопрос дополняйте, а нажимайте под ответом “Комментировать”))
Калькулятор «Обратный процент» поможет найти исходное число до того, как от него отняли известный процент.
Зачастую такие задачи приходится решать в финансовой сфере: к примеру, если необходимо определить размер заработной платы до того, как был вычтен налог на доход физических лиц (НДФЛ).
Вычисления могут понадобиться также, чтобы узнать стоимость товара до распродажи и в других случаях.
Сложность подсчета заключается в том, что проценты, которые вычли из исходной суммы, относились именно к исходной сумме, а не к известному итоговому числу.
Чтобы найти исходное число, необходимо определить, сколько процентов от него составляет известное число. Далее исходное число делим на то количество процентов, что оно составляет, и полученный результат умножаем на 100.
Рассмотрим на примере
Менеджер Роберт получил зарплату — 26 100, после чего решил перейти на другое место работы. Новый работодатель попросил указать размер заработной платы на прошлой работе до вычета налога (НДФЛ 13 %).
Каков был полный доход менеджера на прошлой работе?
26 100 — именно столько получал на руки менеджер.
Это сумма после вычета налога 13 %, следовательно его доход составлял 100-13=87,87% от дохода до вычета НДФЛ.
26100/87=300, 300*100=30 000 руб.
Ответ: доход менеджера до вычета налогов составлял 30 000 рублей.