Перейти к содержанию
Правильная и неправильная дроби
Опубликовано 04.06.2021
Дадим определение правильной и неправильной дроби. Эти понятия часто используются в математике. Как понять – какая дробь правильная, а какая неправильная – даем определения. Пример правильной дроби и пример неправильной дроби – в этом материале.
Правильная дробь
Определение правильной дроби:
Дробь, в которой числитель меньше знаменателя, называется правильной. Например,
– правильная дробь.
Неправильная дробь
Определение неправильной дроби:

Дробь, в которой числитель равен знаменателю или больше его, называется неправильной дробью. Например,
,
– неправильные дроби.
Обращение числа с целой и дробной частями в неправильную дробь
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Например, ![]() .
.
![]() .
.
Вообще, чтобы записать число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к произведению прибавить числитель дробной части. Полученная сумма будет числителем дроби, а знаменателем будет знаменатель дробной части.

Как выделить целую часть из неправильной дроби
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления будет целой частью числа, остаток – числителем, а делитель – знаменателем. Например, .

( 8 оценок, среднее 4.25 из 5 )
На этом уроке мы вспомним, что такое обыкновенная дробь.
Рассмотрим, какие виды обыкновенных дробей существуют и выясним, какую дробь считают правильной, а какую неправильной и научимся сравнивать их.
Эта информация доступна зарегистрированным пользователям
Определим месторасположение правильной и не правильной дроби на координатном луче.
Разберем несколько задач на нахождение части целого и целого по его части, в которых часть представлена в виде обыкновенной неправильной дроби.
Вам уже известно, что дробь представляет собой часть некоторой величины.
Эта информация доступна зарегистрированным пользователям
Обыкновенная дробь записывается двумя числами, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).
Число, стоящее над дробной чертой, называют числителем.
Числитель показывает, сколько долей взяли от целого.
Число, стоящее под дробной чертой, называют знаменателем.
Знаменатель показывает, на сколько всего равных долей разделили целое.
Дробь можно получить следующим образом: разделить целое на равные части и взять несколько из этих частей.
В качестве примера рассмотрим такую ситуацию.
Эта информация доступна зарегистрированным пользователям
Плитку молочного шоколада разделили на 8 равных долек и из них взяли и съели 4.
Восемь долек шоколадки- это одна целая плитка шоколада.
Одна долька этой шоколадки представляет собой 1/8 всей плитки.
Четыре дольки из восьми можно записать дробью, получим дробь 4/8 (четыре восьмых).
Эта информация доступна зарегистрированным пользователям
Дробь 4/8 указывает на то, что целое разделили на восемь равных частей и из них взяли четыре.
8 (общее количество долей)- знаменатель дроби 4/8.
4 (количество долей, которые взяли)- числитель дроби 4/8.
Обратим внимание на члены этой дроби (числитель и знаменатель).
4 и 8– это два натуральных числа, причем если их сравнить, то мы можем заметить, что число 4 меньше 8, т.е. числитель меньше знаменателя.
Обыкновенная дробь, в которой числитель меньше знаменателя, называется правильной дробью.
Давайте выясним являются ли дроби 5/8, 6/8, 7/8 правильными.
- Дробь 5/8 (пять восьмых) показывает (для нашего примера) часть шоколадной плитки, которую съели (пять долек из восьми).
Эта информация доступна зарегистрированным пользователям
Для данной дроби 5– это числитель, 8– это знаменатель.
Сравним числитель со знаменателем: 5 < 8.
Числитель меньше знаменателя, следовательно, дробь пять восьмых является правильной.
- Дробь 6/8 (шесть восьмых) показывает часть шоколадной плитки, которую съели (шесть долек из восьми).
Эта информация доступна зарегистрированным пользователям
Для данной дроби 6– это числитель, 8– это знаменатель.
Сравним числитель со знаменателем: 6 < 8.
Числитель меньше знаменателя, следовательно, дробь шесть восьмых является правильной.
- Дробь 7/8 (семь восьмых) показывает (для нашего примера) часть шоколадной плитки, которую съели (семь долек из восьми).
Эта информация доступна зарегистрированным пользователям
Для данной дроби 7– это числитель, 8– это знаменатель.
Сравним числитель со знаменателем: 7 < 8.
Числитель меньше знаменателя, следовательно, дробь семь восьмых является правильной.
Все дроби, рассмотренные нами, представляют собой некоторую часть одного целого (часть единицы).
Правильная дробь по сути своей- это некоторая часть от целого, а целое подразумевает единицу чего-либо.
В задаче про плитку шоколада за единицу принимается целая плитка шоколада.
Когда мы брали от всей шоколадки 4, 5, 6 или 7 долек, то в результате можно было съесть только лишь часть всей шоколадки, а часть- это всегда меньше, чем целое.
Правило: любая правильная дробь меньше единицы.
Эта информация доступна зарегистрированным пользователям
Выясним, какую дробь называют неправильной на следующем примере:
На праздник купили один большой торт и разрезали его на девять одинаковых частей (9 долей).
Каждый гость съел по кусочку этого торта, в результате торта больше не осталось.
Эта информация доступна зарегистрированным пользователям
Получается, что гости съели девять кусочков торта из девяти возможных.
В таком случае дробь (mathbf{frac{9}{9}}) будет показывать, что целое (весь торт) разделили на 9 долей и потом все эти 9 частей взяли, т.е. съели весь торт.
В данной дроби 9 (общее количество долей)- знаменатель дроби (mathbf{frac{9}{9}}).
9 (количество долей, которые взяли)- числитель дроби (mathbf{frac{9}{9}}).
Очевидно, что дробь (mathbf{frac{9}{9}}) будет равна единице.
Любая дробь, в которой числитель равен знаменателю, равна единице.
Дробь (mathbf{frac{m}{n}}), где n = m, всегда равна единице.
Например, (mathbf{frac{20}{20} = 1}), (mathbf{frac{100}{100} = 1}), (mathbf{frac{1543}{1543} = 1}), (mathbf{frac{1}{1} = 1}) и т.д.
Давайте выясним может ли обыкновенная дробь больше единицы.
Рассмотрим еще одну ситуацию.
Допустим, на праздник купили два одинаковых торта.
Каждый торт разрезали на девять равных частей.
За все время праздника гости съели 13 кусочков торта.
От второго торта осталось 5 несъеденных куска.
Когда разделили оба торта на 9 равных частей, в итоге получили 18 одинаковых кусочков (равных долей), они составляют два целых торта.
Эта информация доступна зарегистрированным пользователям
(mathbf{frac{9}{9}})– первый торт.
(mathbf{frac{9}{9}})– второй торт.
Получается из этих 18 кусочков съели 13, т.е. 1 целый торт и еще 4 кусочка.
Эта информация доступна зарегистрированным пользователям
Четыре кусочка от второго торта будут выражаться дробью (mathbf{frac{4}{9}}).
В таком случае получаем (mathbf{frac{9}{9}}) (один целый торт), да еще (mathbf{frac{4}{9}}) второго торта- это часть кусочков торта, которые съели.
9 долей первого торта + 4 доли второго торта = (mathbf{frac{13}{9}}) торта съели на празднике.
Так как каждый торт был разрезан на 9 частей, то в знаменателе дроби (mathbf{frac{13}{9}}) стоит цифра 9.
Осталось пять частей торта, т.е. (mathbf{frac{5}{9}}) торта- часть второго торта.
Обратите внимание на дроби (mathbf{frac{9}{9}}) и (mathbf{frac{13}{9}}).
В дроби (mathbf{frac{9}{9}}) знаменатель равен 9 (общее количество долей), числитель равен 9 (количество долей, которые взяли).
Сравним числитель и знаменатель дроби (mathbf{frac{9}{9}}) .
9 = 9- числитель равен знаменателю.
В дроби (mathbf{frac{13}{9}}) знаменатель равен 13 (общее количество долей), числитель равен 9 (количество долей, которые взяли).
Сравним числитель и знаменатель дроби (mathbf{frac{13}{9}}) .
13 > 9– числитель больше знаменателя.
Обыкновенную дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.
Из нашего примера видно, что дробь (mathbf{frac{13}{9}}) – это больше, чем один торт (целый торт и еще часть второго).
Правило: Любая неправильная дробь больше единицы или равна ей.
Эта информация доступна зарегистрированным пользователям
Любое натуральное число можно представить в виде неправильной дроби, данная запись будет выглядеть так:
Эта информация доступна зарегистрированным пользователям
Дробь с числителем а, где а– любое натуральное число, и знаменателем, равным единице- это еще одна верная форма записи натурального числа а.
Пример.
Натуральное число 3 = (mathbf{frac{3}{1}})
(mathbf{frac{3}{1}})- неправильная дробь, так как числитель (3) больше знаменателя (1).
Натуральное число (mathbf{24 = frac{24}{1}})
(mathbf{frac{24}{1}})- неправильная дробь, так как числитель (24) больше знаменателя (1).
Натуральное число (mathbf{1245 = frac{1245}{1}})
(mathbf{frac{1245}{1}})- неправильная дробь, так как числитель (1245) больше знаменателя (1).
Сравнивая правильную и неправильную дробь, можно однозначно сказать, что любая неправильная дробь больше правильной.
Эта информация доступна зарегистрированным пользователям
Пример.
Определите какая из дробей (mathbf{frac{7}{8}}) и (mathbf{frac{8}{7}}) больше, какая меньше.
(mathbf{frac{7}{8}})– правильная дробь (числитель меньше знаменателя), а (mathbf{frac{8}{7}})– неправильная дробь (числитель больше знаменателя), следовательно (mathbf{frac{7}{8} < frac{8}{7}}).
Определите какая из дробей (mathbf{frac{15}{1}}) и (mathbf{frac{1}{15}}) больше, какая меньше.
(mathbf{frac{1}{15}})– правильная дробь (числитель меньше знаменателя), а (mathbf{frac{15}{1}})– неправильная дробь (числитель больше знаменателя), следовательно (mathbf{frac{1}{15} < frac{15}{1}}).
Эта информация доступна зарегистрированным пользователям
Выясним, где на координатном луче изображают правильные и неправильные дроби.
Любому дробному числу соответствует конкретное место на координатном луче.
Чтобы обозначить на координатном луче точку с координатой (mathbf{frac{m}{n}}), необходимо от начала координат отложить m отрезков, длина каждого такого отрезка должна составлять (mathbf{frac{1}{n}}) от единичного отрезка.
Чтобы найти число (mathbf{frac{1}{n}}), нужно единичный отрезок разделить на n равных частей.
Рассмотрим поясняющий пример.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Определим расположение точек A((mathbf{frac{2}{6}})), B((mathbf{frac{11}{6}})), D((mathbf{frac{6}{6}})) на координатном луче.
Эта информация доступна зарегистрированным пользователям
Так как знаменатель каждой данной дроби равен шести, то разобьем единичный отрезок ОЕ на шесть равных частей-отрезков, каждая часть будет равна (mathbf{frac{1}{6}}) ОЕ.
Правильная дробь (mathbf{frac{2}{6}}) представляет собой две части (доли) из шести.
Следовательно, точка А((mathbf{frac{2}{6}})) удалена от начала координат на расстояние двух отрезков, равных одной доле единичного отрезка- (mathbf{frac{1}{6}}) ОЕ.
Отметим тот факт, что (mathbf{frac{2}{6}}) правильная дробь, а это значит она меньше единицы.
На координатном луче данная точка располагается между числами 0 и 1, т.е. левее точки E(1).
Выясним, где на координатном луче будет располагаться точка D ((mathbf{frac{6}{6}})).
Известно, что дробь, у которой числитель равен знаменателю, представляет собой неправильную дробь, равную единице.
Дробь (mathbf{frac{6}{6}}) означает шесть частей из шести- это единица.
Отметим точку D ((mathbf{frac{6}{6}})) на координатном луче, для этого отсчитаем 6 отрезков от начала координат, в результате попадаем в точку Е(1).
Точка с координатой (mathbf{frac{6}{6}}) совпадает с точкой Е(1), в результате получаем сам единичный отрезок ОЕ.
Обозначим на координатном луче точку В с координатой (mathbf{frac{11}{6}}).
Дробь (mathbf{frac{11}{6}}) означает шесть частей (т.е. один единичный отрезок ОЕ) и еще пять таких частей.
Отложим от начала координат один единичный отрезок и от него отсчитаем еще пять делений, каждый из которых равен (mathbf{frac{1}{6}}) единичного отрезка (в общем говоря, нам необходимо отсчитать от начала координат 11 делений, равных (mathbf{frac{1}{6}}) ОЕ).
Нам несложно заметить, что неправильная дробь, у которого числитель больше знаменателя, лежит на координатном луче правее единицы.
На самом деле, такая неправильная дробь выражает некоторую целую часть, да еще часть целого.
Эта информация доступна зарегистрированным пользователям
Задачи с неправильными дробями решаются по тем же правилам, что и задачи с правильными дробями.
Разберем решение нескольких задач с неправильными дробями.
Задача №1.
Эта информация доступна зарегистрированным пользователям
В первый день спортсмен на тренировке пробежал 20 километров.
Во второй день спортсмен пробежал 3/2 от того расстояния, которое он преодолел в первый день.
Сколько километров пробежал спортсмен во второй день?
За известное целое примем путь, который спортсмен пробежал в первый день.
Необходимо найти часть от известной целой величины.
Нам известно правило нахождения части от целого, применим его к этой задаче.
Пусть:
В– неизвестная часть, выраженная дробью (mathbf{frac{m}{n}}).
А– известная целая величина.
m– числитель дроби (mathbf{frac{m}{n}}).
n– знаменатель дроби (mathbf{frac{m}{n}}).
Чтобы найти часть В (выраженную дробью (mathbf{frac{m}{n}})) от числа А, необходимо это число разделить на знаменатель (n) и умножить на числитель (m) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
Задача №2.
Эта информация доступна зарегистрированным пользователям
Дима за два дня собрал несколько килограммов ягод.
В первый день он собрал 10 килограммов ягод, что составило 5/3 килограммов ягод, собранных во второй день.
Сколько килограммов ягод собрал Дима во второй день?
Неизвестна целая величина (количество ягод, собранных во второй день), известна только некоторая ее часть, таким образом необходимо найти целое по части.
Нам уже известно правило нахождения целого по части, применим его к данной задаче.
Пусть:
В– известная часть числа А, выраженная дробью (mathbf{frac{m}{n}}).
А– неизвестная целая величина.
m– числитель дроби (mathbf{frac{m}{n}}) .
n– знаменатель дроби (mathbf{frac{m}{n}}).
Чтобы найти целое число А, необходимо число В, соответствующее части числа А, разделить на числитель (m) и полученный результат умножить на знаменатель (n) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
Читайте также
Правильная дробь


4.6
Средняя оценка: 4.6
Всего получено оценок: 70.
4.6
Средняя оценка: 4.6
Всего получено оценок: 70.
Понятие правильной дроби часто пугает учеников. Дело в том, что это понятие часто путают с обыкновенной дробью. Что такое правильная дробь и можно ли называть ее обыкновенной, разберемся вместе.
Что такое дробь?
При первоначальном ознакомлении с темой, ученикам рассказывают, что дробь это число, обозначающая часть целого. И в общих чертах, это правильное обозначение. Именно оно появилось при первом использовании дробных чисел в Древней Греции. Тогда торговались четвертью монеты и половиной ведра пшеницы – это было нормой древнего мира.
Сегодня в математике принято немного другое определение: дробью называют незавершенную операцию деления. В расчетах часто возникают ситуации, когда точно посчитать результат деления не получается, даже при делении в столбик. Специально для того, чтобы не терять точность в промежуточных расчетах и были придуманы дроби.
Любую дробь, записанную с помощью дробной черты, можно заменить операцией деления, где числитель станет делимым, а знаменатель делителем.
Правильная и неправильная дробь
Дроби бывают следующих видов:
- Обыкновенная дробь, в которой числитель меньше знаменателя
- Неправильная, в которой числитель больше знаменателя
- Смешанная, где помимо целой части есть еще и дробная.
- Десятичная, то есть дробь, которая записывается в строку с помощью разделительной запятой. Знаменателем такой дроби является степень числа 10. Для того, чтобы узнать, какая именно степень числа 10 в знаменателе, нужно посчитать количество знаков после запятой.
Возникает вопрос, где же среди всех этих дробей спряталась правильная дробь?
На самом деле правильной дробью называют обыкновенную дробь.
Откуда взялось название правильной и неправильной дроби? Дело в том, что результат дробных примеров принято записывать в виде правильной дроби, соответственно запись неправильной дроби в ответе – ошибка. Если в примере получилась неправильная дробь, то в конечном ответе нужно записать смешанное, максимально сокращенное число.
Вот и весь секрет: правильной и обыкновенной дробью называют одинаковые числа. При этом правильную дробь можно записать в десятичном виде. Например, число 0,67 это пример правильной дробь, записанной в десятичном виде.
Поговорим о том, как перевести правильную дробь в десятичную. Нужно вспомнить, что дробь это незавершенная операция деления. Чтобы перевести обычную дробь в десятичную, нужно числитель поделить на знаменатель без остатка. Неправильную дробь перевести в десятичные нельзя, так как при делении числителя на знаменатель целая часть выделится сама по себе и получится смешанная десятичная дробь.

Что мы узнали?
Мы вспомнили, что такое дробь. Выделили виды дробей и рассказали о том, чем отличается правильная дробь от обыкновенной. Поговорили о возникновении понятия правильной и неправильной дроби.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 70.
А какая ваша оценка?
В этом уроке мы коснёмся тех моментов, о которых не упоминали при изучении дробей, посчитав что на первых порах они создают трудности для обучения.
Правильные и неправильные дроби
В самом начале своего пути при изучении дробей мы узнали, что правильная дробь — это та дробь, у которой числитель меньше знаменателя.
В школьной литературе можно встретить другое определение правильной дроби. Выглядит оно следующим образом:
Правильная дробь всегда меньше единицы.
Как понять данное определение? Дробь сама по себе указывает на то, что какой-либо объект разделен на несколько частей. И это всегда один единственный объект. Под единицей именно это и подразумевается.
Например, пусть у нас имеется одна пицца:
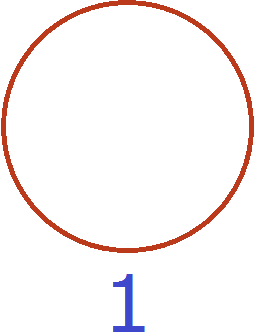
В данном случае она и является единицей.
Если мы отрежем от этой пиццы половину, то есть ![]() (одну вторую пиццы), то наш кусок будет меньше, чем вся целая пицца:
(одну вторую пиццы), то наш кусок будет меньше, чем вся целая пицца:

В этом и заключается суть фразы «правильная дробь всегда меньше единицы».
Наша половинка пиццы является дробью ![]() и она меньше одной целой пиццы, то есть меньше единицы:
и она меньше одной целой пиццы, то есть меньше единицы:
![]()
Это выражение можно доказать. Если мы вычислим дробь ![]() , то получим десятичную дробь 0,5. А это рациональное число меньше единицы:
, то получим десятичную дробь 0,5. А это рациональное число меньше единицы:
![]()
На координатной прямой можно увидеть, как располагаются эти числа:

Видно, что рациональное число 0,5 располагается левее, чем 1. А мы помним, что чем левее число располагается на координатной прямой, тем оно меньше.
С неправильными дробями всё было наоборот. Неправильной дробью мы назвали ту дробь, у которой числитель больше знаменателя.
Но в школьной литературе можно встретить другое определение неправильной дроби. Выглядит оно следующим образом:
Неправильная дробь всегда больше единицы или равна ей.
Например, рассмотрим неправильную дробь ![]() . Выделим в этой дроби целую часть, получим
. Выделим в этой дроби целую часть, получим . Изобразим эту смешанную дробь в виде одной целой пиццы и ещё половинки пиццы:
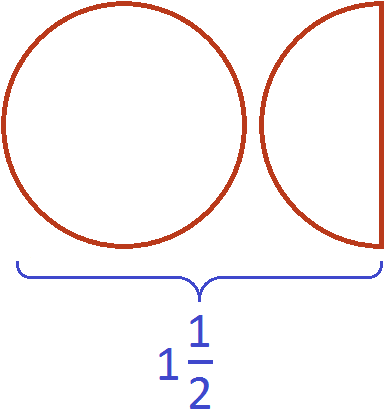
Вместе одна целая пицца и ещё половина пиццы больше, чем просто одна целая пицца
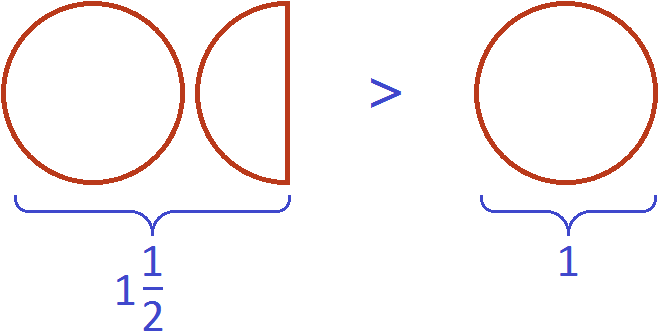
В этом и заключается суть фразы «неправильная дробь всегда больше единицы».
Одна целая пицца и ещё половина пиццы описывается смешанной дробью и эта смешанная дробь больше единицы:
![]()
Переведём смешанную дробь обратно в неправильную дробь, чтобы не противоречить правилу. Ведь речь в данном случае идёт о неправильных дробях:
![]()
что схематически будет выглядеть так:
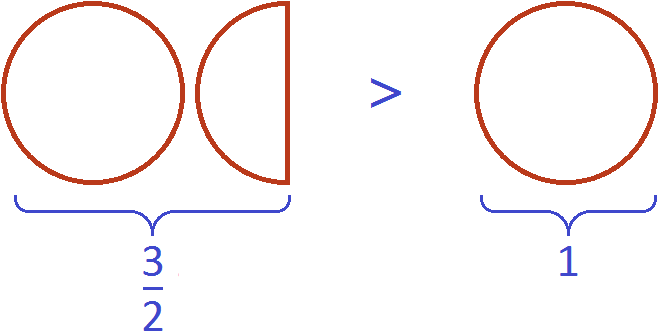
Выражение ![]() можно доказать. Если мы вычислим дробь
можно доказать. Если мы вычислим дробь ![]() , то получим десятичную дробь 1,5. А это рациональное число больше единицы:
, то получим десятичную дробь 1,5. А это рациональное число больше единицы:
![]()
На координатной прямой можно увидеть, как располагаются эти числа:

Видно, что рациональное число 1,5 располагается правее, чем 1. А мы помним, что чем правее число располагается на координатной прямой, тем оно больше.
Неправильной также называется дробь равная единице. Речь в данном случае идет о тех дробях, у которых числитель и знаменатель равны.
Рассмотрим дробь ![]() . Изобразим её в виде двух одинаковых кусочков пиццы:
. Изобразим её в виде двух одинаковых кусочков пиццы:
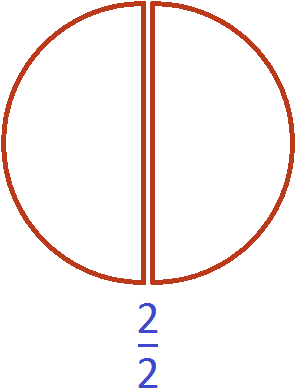
Фактически речь идёт не о дроби, а об одной целой пицце:
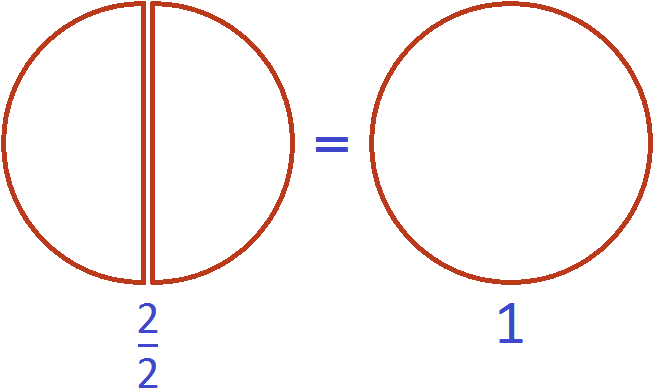
В этом и заключается суть фразы «неправильная дробь может равняться единице».
![]()
Любое целое число отличное от нуля (не равное нулю) можно представить в виде неправильной дроби со знаменателем 1. Например, числа 3, 5, 9, 12 можно представить в виде неправильных дробей со знаменателем 1
![]()
Представление объекта в виде единицы позволяет проще решать задачи. Рассмотрим примеры.
Пример 1. Куплен один шоколадный батончик. От него отрезали треть. Сколько батончика осталось?
Осталось две трети батончика. Сам батончик можно описать цифрой 1, далее из этой единицы вычесть треть:
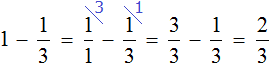
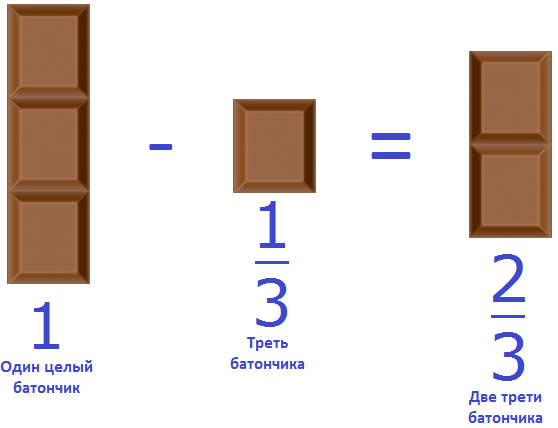
Не приводя на бумаге никаких вычислений, можно ответить на вопрос подобной задачи. Сказано «отрезали треть» — значит сразу нужно обратить внимание на то, что знаменатель равен 3.
Если отрезали одну часть из трёх, то сколько частей должно остаться? Верно, две части. Поэтому и ответ «две части из трёх» или «две трети».
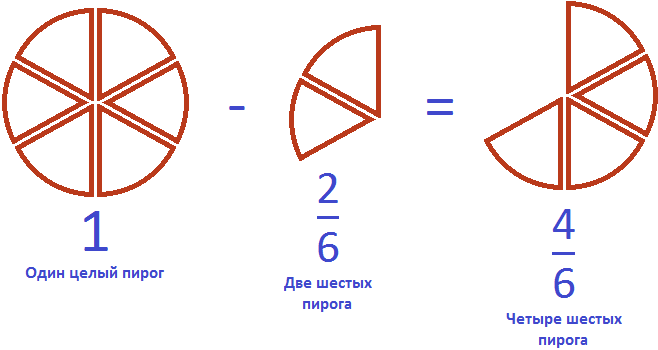
Пример 2. Куплен один пирог. От него отрезали две шестых. Сколько пирога осталось?
Осталось четыре шестых пирога. Сам пирог можно описать цифрой 1, далее из этой единицы вычесть две шестых:
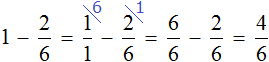
Приведение дробей к общему знаменателю
Чтобы привести дроби к общему знаменателю, мы находили НОК (наименьшее общее кратное) знаменателей этих дробей. Затем делили найденный НОК на знаменатель первой дроби и получали дополнительный множитель для первой дроби.
То же самое мы делали и для второй дроби — делили НОК на знаменатель второй дроби и получали дополнительный множитель для второй дроби.
Затем дроби умножались на свои дополнительные множители. В результате они обращались в дроби, у которых одинаковые знаменатели. К примеру, выражение ![]() вычисляется следующим образом:
вычисляется следующим образом:
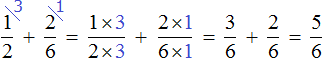
Но есть и другой способ приведения дробей к общему знаменателю. Этим способом часто пользуются школьники и ленивые студенты. Суть этого способа заключается в том, что роль дополнительных множителей берут на себя знаменатели обеих дробей, причем происходит это «крест-накрест» — знаменатель первой дроби становится дополнительным множителем второй дроби, а знаменатель второй дроби становится дополнительным множителем первой дроби.
Вычислим предыдущее выражение ![]() этим способом. Знаменатель первой дроби 2 становится дополнительным множителем второй дроби, а знаменатель второй дроби 6 становится дополнительным множителем первой дроби:
этим способом. Знаменатель первой дроби 2 становится дополнительным множителем второй дроби, а знаменатель второй дроби 6 становится дополнительным множителем первой дроби:
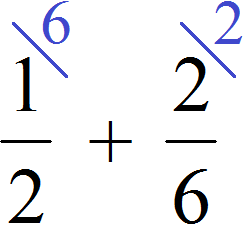
Далее числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель и вычисляем:
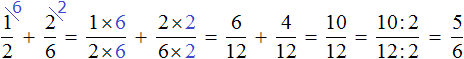
Преимущество данного способа в том, что не нужно находить НОК знаменателей обеих дробей. В процессе вычисления всё выравнивается само. Единственный недостаток заключается в том, что выражение становится более длинным и корявым.
Сравните выражения, которые мы вычислили сначала первым способом, а затем вторым:
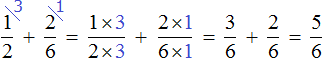
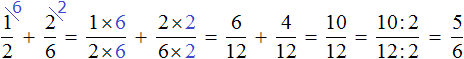
Выражение, вычисленное первым способом, намного аккуратнее и короче, нежели второе.
Вторым способом мы будем пользоваться при изучении алгебры. В алгебре работать с буквенными выражениями приходиться чаще, чем с числовыми.
К примеру, если перед нами будет стоять задача привести буквенное выражение ![]() к общему знаменателю, то у нас не будет другого выхода, кроме как воспользоваться методом «крест-накрест», то есть использовать второй способ, который мы сейчас рассмотрели:
к общему знаменателю, то у нас не будет другого выхода, кроме как воспользоваться методом «крест-накрест», то есть использовать второй способ, который мы сейчас рассмотрели:
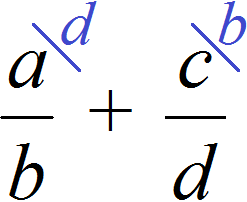
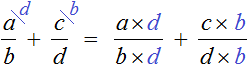
Нахождение дроби от числа
Чтобы найти дробь от числа, мы делим это число на знаменатель искомой дроби и полученный результат умножаем на числитель искомой дроби.
Например, чтобы найти ![]() от 10 сантиметров, нужно 10 разделить на 5, и полученный результат умножить на 2
от 10 сантиметров, нужно 10 разделить на 5, и полученный результат умножить на 2
10 : 5 = 2
2 × 2 = 4
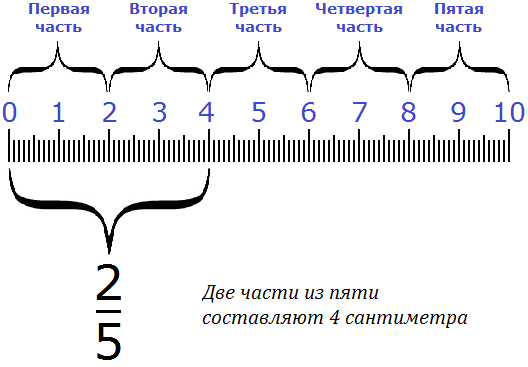
Получили ответ 4. Значит ![]() от десяти сантиметров составляют 4 сантиметра. Схематически это выглядит примерно так:
от десяти сантиметров составляют 4 сантиметра. Схематически это выглядит примерно так:
Но есть и второй вариант решения. Для нахождения ![]() от десяти сантиметров, достаточно умножить 10 на
от десяти сантиметров, достаточно умножить 10 на ![]() . Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:
. Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:
![]()
Поэтому можно взять на заметку следующее правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число умножить на искомую дробь.
Пример 2. Найти от двух часов.
Два часа это 120 минут. Чтобы найти от 120 минут, нужно 120 умножить на дробь
![]()
Значит от двух часов составляют 80 минут.
Нахождение числа по дроби
Чтобы найти всё число по его дроби, мы делили это число на числитель имеющейся дроби и полученный результат умножали на знаменатель имеющейся дроби.
Например, зная что рулетки составляет 12 см, мы можем найти длину всей рулетки. Для этого 12 нужно разделить на 2, и полученный результат умножить на 3
12 : 2 = 6
6 × 3 = 18
Получили 18. Значит длина всей рулетки равна 18 см.
Но есть и второй вариант решения. Для нахождения длины всей рулетки, достаточно 12 разделить на дробь . Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:
![]()
Поэтому можно взять на заметку следующее правило нахождения числа по дроби:
Чтобы найти число по дроби, нужно это число разделить на данную дробь.
Пример 2. ![]() всего пути составляет 6 км. Найти длину всего пути.
всего пути составляет 6 км. Найти длину всего пути.
Чтобы найти длину всего пути, достаточно 6 разделить на дробь ![]()
![]()
Получили ответ 15. Значит длина всего пути составляет 15 километров.
Десятичная точка в дробях
Запятую в десятичной дроби, которая отделяет целую часть от дробной, по-другому называют десятичной точкой.
Дело в том, что в некоторых источниках целая часть от дробной отделяется именно точкой, а не запятой. Например:
2.5 (две целых пять десятых)
15.65 (пятнадцать целых шестьдесят пять сотых)
Точка часто используется для записи десятичных дробей на компьютере — в программировании и при работе в математических пакетах. В остальных случаях: на письме и при подготовке документов, в десятичных дробях чаще используется запятая, а не точка.
Мы используем в десятичных дробях запятую, а не точку, поэтому разумнее называть эту запятую десятичной запятой.
Но десятичную запятую большинство людей тоже называют десятичной точкой. Что в принципе не является ошибкой, потому как речь всё равно идёт о разделителе, котором отделяет целую часть от дробной.
Давайте и мы будем называть свою запятую в десятичных дробях десятичной точкой. Это словосочетание проговаривается легче и приятнее на слух.
Десятичная точка используется для увеличения или уменьшения дроби в 10, 100, 1000 и более раз. При увеличении десятичной дроби, десятичная точка передвигается вправо, а при уменьшении — влево. Чтобы быстро запомнить это, можно воспользоваться фразами «чем правее, тем больше» и «чем левее, тем меньше».
Пример 1. Увеличить десятичную дробь 6,3 в десять раз.
Чтобы увеличить десятичную дробь 6,3 в десять раз, достаточно передвинуть десятичную точку вправо на одну цифру, получим 63.
Пример 2. Уменьшить десятичную дробь 6,3 в десять раз.
Для уменьшения дроби 6,3 в десять раз достаточно передвинуть десятичную точку влево на одну цифру, получим 0,63
На вопрос «как узнать на сколько цифр передвигать десятичную точку?», нужно смотреть во сколько увеличивается (или уменьшается) десятичная дробь. Если дробь нужно увеличить (или уменьшить) в десять раз, то десятичная точка сдвигается на одну цифру.
Если дробь нужно увеличить (или уменьшить) в сто раз, то десятичная точка сдвигается на две цифры.
Если дробь нужно увеличить (или уменьшить) в тысячу раз, то десятичная точка сдвигается на три цифры. В общем, всё зависит от количества нулей во множителе.
Например, увеличить дробь в десять раз означает умножить её на 10. Мы помним, что для того чтобы умножить десятичную дробь на 10, нужно в этой дроби передвинуть запятую вправо на одну цифру (поскольку в числе 10 один ноль). Теперь можно не заучивать подобные правила. Такое умножение можно легко выполнить, передвинув десятичную точку.
Пример 3. Увеличить десятичную дробь 6,3 в тысячу раз.
Чтобы увеличить десятичную дробь 6,3 в тысячу раз, достаточно передвинуть десятичную точку вправо на три цифры, получим 6300. Если после запятой не хватает цифр, то вместо недостающих цифр записывают нули, что мы и сделали.
Пример 4. Уменьшить десятичную дробь 12,5 в сто раз.
Для уменьшения дроби 12,5 в сто раз, достаточно передвинуть десятичную точку влево на две цифры, получим 0,125
Десятичную точку можно использовать не только в десятичных дробях. Её можно использовать для увеличения (уменьшения) и других чисел в 10, 100 или в 1000 раз.
Возьмём к примеру целое число 325 и поставим в конце точку, получим 325 с точкой. Воспользуемся в этот раз точкой, так как её легче изобразить на рисунке:
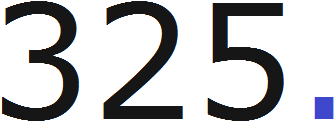
Попробуем уменьшить это число в десять раз. Для этого достаточно будет передвинуть точку влево на одну цифру, получим 32.5

Попробуем увеличить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры вправо, получим 123000.
Попробуем уменьшить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,123
Попробуем уменьшить число 65 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,065
Попробуем увеличить число 65 в сто раз. Для этого достаточно передвинуть десятичную точку на две цифры вправо, получим 6500.
Составные выражения
Встречаются задачи, в которых требуется вычислить выражение составленное из нескольких дробей. Например,
![]()
Такое выражение вычисляется согласно порядку действий. В данном случае вычисление будет выполнено последовательно слева направо:
![]()
Если из ![]() пиццы вычесть
пиццы вычесть ![]() пиццы, затем прибавить
пиццы, затем прибавить ![]() пиццы, затем вычесть
пиццы, затем вычесть ![]() пиццы, то останется
пиццы, то останется ![]() пиццы
пиццы
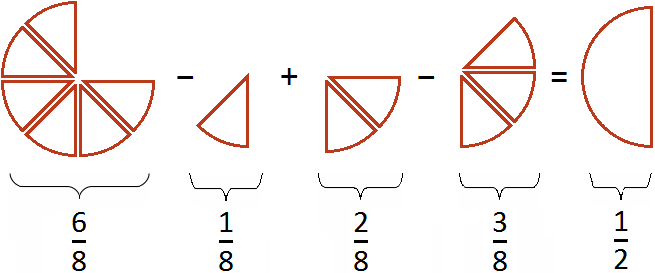
Если вам тяжело понять данный пример, попробуйте самостоятельно решить его на бумаге, делая соответствующие рисунки к каждой дроби.
Пример 2. Найти значение выражения ![]()
В данном примере сначала необходимо выполнить умножение затем сложение и вычитание
![]()
![]()
Если ![]() пиццы увеличить в два раза, то получится одна целая пицца
пиццы увеличить в два раза, то получится одна целая пицца
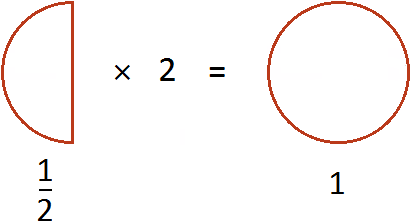
Затем если к ![]() пиццы прибавить эту целую пиццу, а затем из полученного результата вычесть
пиццы прибавить эту целую пиццу, а затем из полученного результата вычесть ![]() пиццы, то получится
пиццы, то получится пиццы
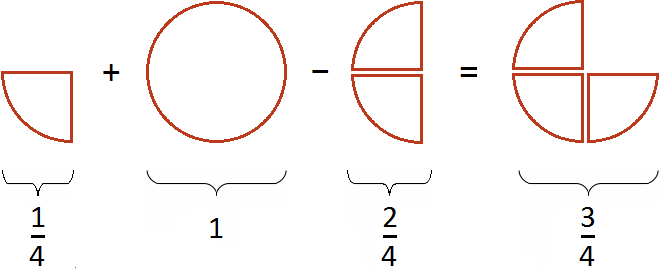
Пример 3. Найти значение выражения ![]()
Сначала желательно вычислить выражения, находящиеся в числителях обеих дробей, а именно выражения 2−1 и 1+1,
![]()
Дальнейшее вычисление не составляет особого труда ![]() плюс
плюс ![]() равно
равно
![]()
Конечно, можно было записать в одном числителе выражения, находящиеся в числителях обеих дробях. От этого ответ не изменился бы:
![]()
Но в некоторых случаях возможны подвохи, особенно если из одной дроби вычитается другая. Следующий пример демонстрирует это.
Пример 4. Найти значение выражения ![]()
Вычислим выражения, находящиеся в числителях обеих дробей, а именно выражения 2+1 и 2−1
![]()
Ну и нетрудно догадаться, что ![]() равно
равно ![]() или
или ![]() (при условии, что дробь
(при условии, что дробь ![]() будет сокращена на 2)
будет сокращена на 2)
![]()
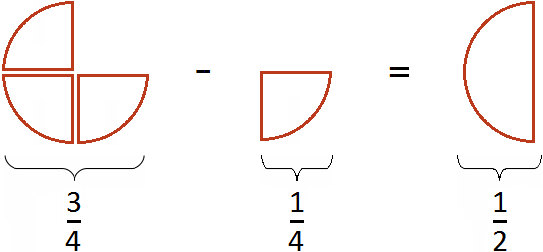
Все логично. Если из пиццы вычесть
![]() пиццы, то получится
пиццы, то получится ![]() пиццы.
пиццы.
Теперь попробуем решить данный пример, записав в одном числителе оба выражения, находящиеся в числителях обеих дробей:
![]()
Получается совсем другой ответ. Этот ответ не является правильным. Давайте посмотрим, что представляет собой выражение ![]() .
.
Для начала запишем его следующим образом:
![]()
Теперь попробуем проследить весь процесс вычисления этого выражения. Предположим, что имелось ![]() пиццы
пиццы

К ней добавили еще ![]() пиццы
пиццы
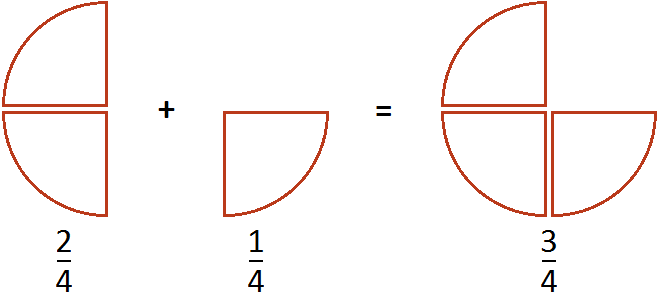
Затем из получившейся пиццы вычитается
![]()
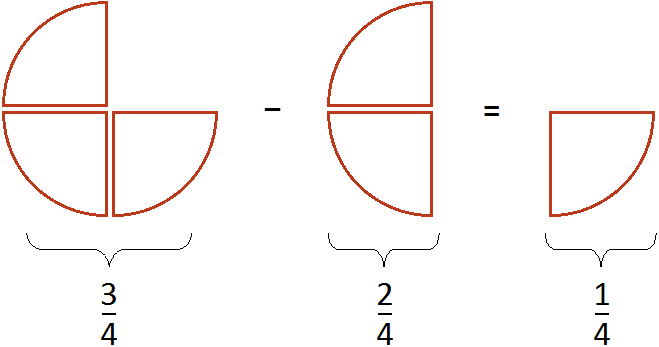
Затем из получавшейся ![]() пиццы вычитают еще
пиццы вычитают еще ![]() пиццы
пиццы
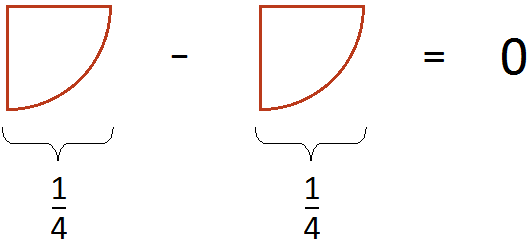
Получился 0, то есть пицца исчезла. Но мы знаем, что должно было остаться ![]() пиццы. Поэтому при вычислении дробных выражений следует быть внимательным, особенно при вычитании выражений, содержащих в числителе другие выражения.
пиццы. Поэтому при вычислении дробных выражений следует быть внимательным, особенно при вычитании выражений, содержащих в числителе другие выражения.
Если хочется сэкономить время и записать в числителе оба выражения, находящиеся в числителях обеих дробей, то второй числитель нужно взять в скобки. Это спасёт от ошибки:
![]()
Пример 5. Найти выражения ![]()
Вычислим выражения, находящиеся в числителях обеих дробей:
![]()
Приведем полученные дроби к общему знаменателю и как обычно вычислим полученное выражение:
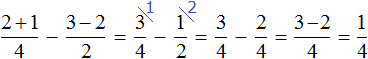
Если из вычесть
![]() пиццы, то получится
пиццы, то получится ![]() пиццы
пиццы
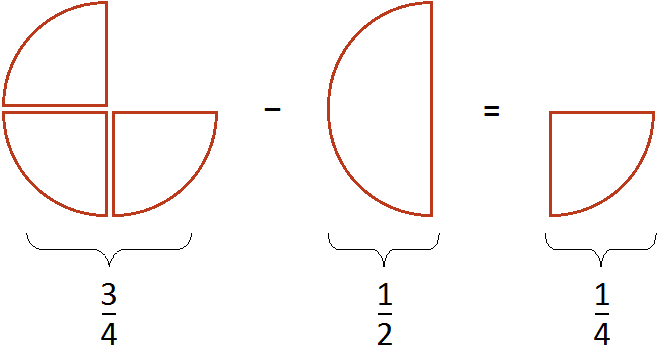
Пример 6. Найти значение выражения ![]()
В первую очередь необходимо выполнить умножение:
![]()
Далее выполняется сложение:
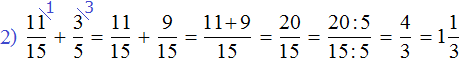
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Содержание:
- Правильные и неправильные дроби
- Смешанные дроби
Правильные и неправильные дроби
Например. Дробь $frac{11}{23}$ является правильной,
так как ее числитель, равный 11, меньше, чем знаменатель, который равен 23: 11
Определение
Дробь называется неправильной, если ее числитель больше знаменателя или равен ему.
Например. Дробь $frac{23}{11}$ – неправильная,
так как 23 > 11 . Дробь $frac{3}{3}$ – неправильная, так как числитель дроби равен ее знаменателю.
Смешанные дроби
Определение
Числа, в состав которых входит целое число и правильная дробь, называются смешанными числами.
Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа.
Например. Для смешанной дроби $3 frac{11}{23}=3+frac{11}{23}$
число 3 – целая часть, $frac{11}{23}$ – дробная.
Неправильную дробь можно записать в виде смешанного числа, для этого нужно
числитель поделить на
знаменатель.
Полученное неполное частное будет целой частью смешанной дроби, остаток – числителем дробной части, а знаменатель
исходной неправильной дроби – знаменателем дробной части.
Пример
Задание. Записать неправильную дробь
$frac{20}{3}$ в виде смешанной.
Решение. Поделим числитель дроби – 20 на ее знаменатель – 3 (то есть выделим целую часть):
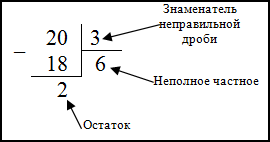
Итак, получаем, что $frac{20}{3}=20 : 3=$ 6 (остаток 2).
А тогда искомая смешанная дробь
$frac{20}{3}=6 frac{2}{3}$
Ответ. $frac{20}{3}=6 frac{2}{3}$
Чтобы смешанное число записать в виде неправильной дроби, надо целую часть умножить на знаменатель
дробной части, к полученному числу прибавить числитель дробной части и записать эту сумму в числитель,
а знаменатель дробной части оставить без изменений.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Смешанное число
8$frac{2}{3}$ записать в виде неправильной дроби.
Решение. $8 frac{2}{3}=frac{8 cdot 3+2}{3}=frac{26}{3}$
Ответ. $8 frac{2}{3}=frac{26}{3}$
Читать следующую тему: сравнение дробей.
