Это слайд-шоу требует JavaScript.
Сущность простых процентов состоит в том, что процент по кредиту все время начисляется на первоначальную сумму кредита в течение всего срока действия кредита.
Например, если банк выдал клиенту в кредит 100 000 рублей на 2 года по ставке 10% годовых, то процент по кредиту и в первый и во второй год, при расчёте по формуле простого процента, составит 10 000 рублей (10 000*0,1).
К наращению простыми процентами прибегают при выдаче кредита сроком до 1 года или когда проценты не присоединяются к основной сумме долга, а периодически выплачиваются.
Для записи формулы простых процентов примем следующие обозначения:
I — сумма денежных средств, начисленных на первоначальную сумму по процентам за весь период (сумма с процентами — первоначальная сумма)
P — первоначальная сумма долга
S — сумма в конце срока (первоначальная сумма + сумма денежных средств по процентам)
i — процентная ставка, десятичная дробь. Например, если процентная ставка 20%, то в расчетах необходимо использовать 0,2 =20%/100
n — срок кредита в годах
Формула начисленных за весь срок процентов
I=Pni (I)
Формула простых процентов
S=P+I=P+Pni=P(1+ni) (II)
Вычисление первоначальной суммы долга по формуле простого процента
P=S/(1+ni) или P=S/(1+ni/100), если i измеряется в % (III)
Вычисление годовой процентной ставки по формуле простого процента
i=(S/P-1)/n или i=(S/P-1)/n*100, если необходимо получить процентную ставку (IV)
Вычисление срока кредита по формуле простого процента
n=(S/P-1)/i (V)
ПРАКТИКУМ
-
ВЫЧИСЛЕНИЕ СУММЫ НАКОПЛЕННОГО ДОЛГА ПО ФОРМУЛЕ ПРОСТЫХ ПРОЦЕНТОВ
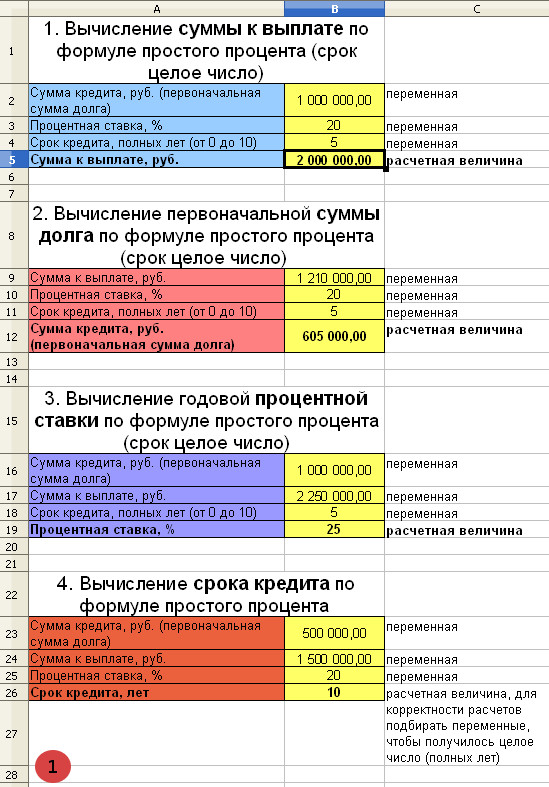
Банком выдан кредит в размере 1 000 000 рублей на 5 лет под 20% годовых. Необходимо определить сумму к погашению по кредиту по формуле простых процентов.
Первоначальная сумма кредита равна 1 000 000 рублей, P=1 000 000
Процентная ставка 20%, т.е. i=0,2
Срок кредита 5 лет, n=5
Сумма начисленных процентов за 5 лет по формуле простых процентов
I=Pni=1 000 000 * 5 *0,2=1 000 000
Сумма к выплате по кредиту
S=P+I=1 000 000 + 1 000 000=2 000 000 рублей
или
S=1 000 000(1+5*0,2)=2 000 000 рублей
-
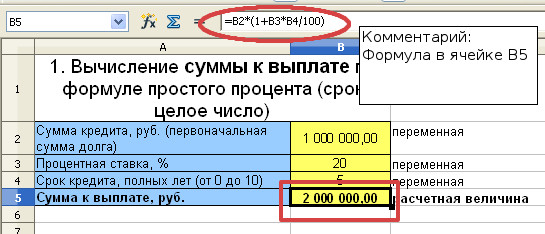
ВЫЧИСЛЕНИЕ ПЕРВОНАЧАЛЬНОЙ СУММЫ ДОЛГА ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА
Клиент выплатил банку 1 210 000 рублей за кредит, который он взял на 5 лет назад под 20% годовых. Кредит рассчитывался по формуле простых процентов. Определить первоначальную сумму долга.
Сумма, выплаченная банку равна 1210 000 рублей, S=1 210 000
Процентная ставка 20%, т.е. i=0,2
Срок кредита 5 лет, n=5
Для расчёта первоначальной суммы кредита воспользуемся формулой (III)
P=S/(1+ni)=1 210 000/(1+5*0,2)=605 000 рублей
Пять лет назад банк выдал клиенту кредит в размере 605 000 рублей.
-
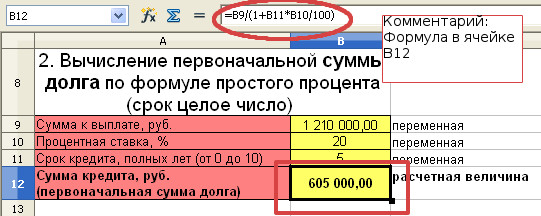
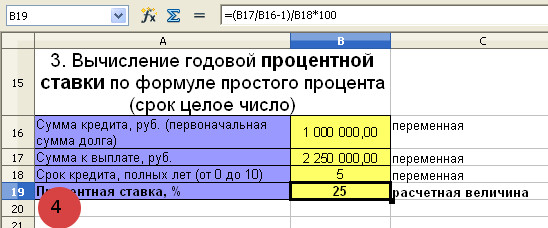
ВЫЧИСЛЕНИЕ ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА
Банк выдал клиенту кредит в размере 1 000 000 рублей на 5 лет. Клиент вернул в банк 2 250 000 рублей. Определить годовую процентную ставку. В течение 5 лет процент начислялся на 1 000 000 рублей.
Первоначальная сумма кредита равна 1 000 000 рублей, P=1 000 000
Сумма, выплаченная банку равна 2 250 000 рублей, S=2 250 000
Срок кредита 5 лет, n=5
Для расчёта годовой процентной ставки по кредиту воспользуемся формулой (IV)
i=(S/P-1)/n=(2 250 000/1 000 000 – 1)/5=0,25 или 25%
Банк выдал кредит клиенту по ставке 25% годовых.
-
ВЫЧИСЛЕНИЕ СРОКА КРЕДИТА ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА
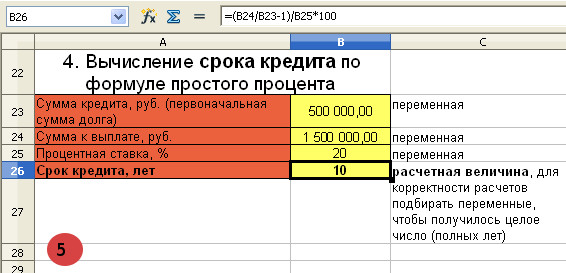
Банк выдал клиенту кредит в размере 500 000 рублей под 20% годовых. Клиент обязался вернуть кредит, когда сумма с процентами достигнет 1 500 000 рублей. Через сколько лет клиенту нужно отдать кредит, рассчитанный по формуле простого процента?
Первоначальная сумма кредита равна 500 000 рублей, P=500 000
Сумма, выплаченная банку равна 1 500 000 рублей, S=1 500 000
Процентная ставка 20%, т.е. i=0,2
Для вычисления срока кредита воспользуемся формулой (V)
n=(S/P-1)/i=(1 500 000/500 000-1)/0,2=10 лет
Клиент должен заплатить банку 1 500 000 рублей через 10 лет.
Сделаем вычисления в OpenOffice Calc по формуле простого процента.
OpenOffice Calc
- Исходная таблица с расчетами простого процента
- Дополнительные настройки
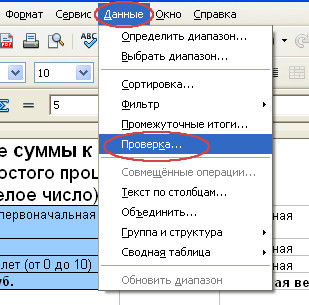
- Для корректности расчетов установим некоторые ограничения на вводимые в ячейку значения.
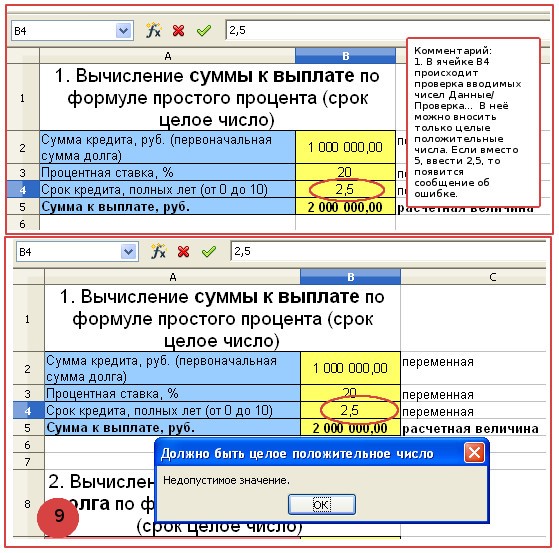
Например, сделаем так, чтобы в ячейку B4 можно было вводить только целые положительные числа. Для этого выделим ячейку B4 и вызовем диалоговое окно “Проверка вводимых значений”, последовательно выбрав Данные/Проверка…
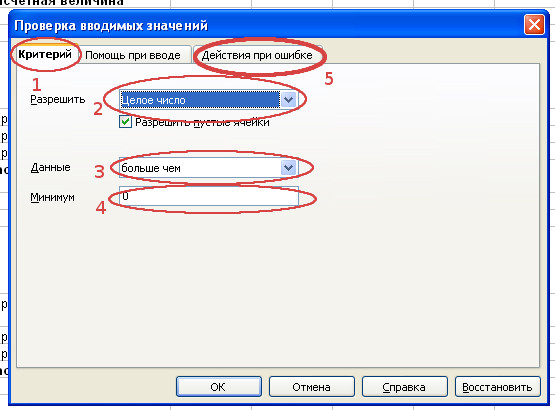
- Последовательно заполним все пункты диалогового окна “Проверка вводимых значений” в соответствии с примером.
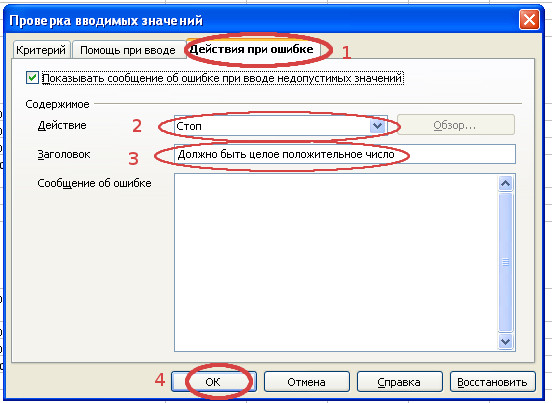
- Проверим, как работают данные ограничения. Теперь при вводе в ячейку B4 неправильных значений, например, 2,5 вместо 5, появляется сообщение об ошибке и возвращается исходное значение 5.
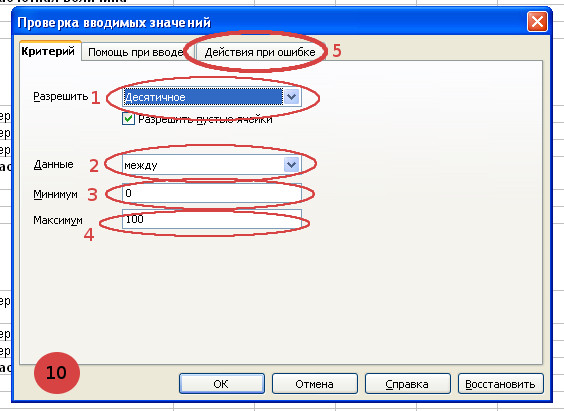
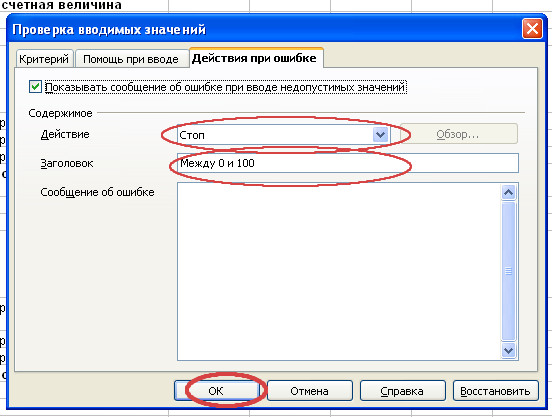
- Установим ограничения на вводимые значения для ячейки B3. Теперь в ячейку должны вводиться десятичные положительные значения в диапазоне от 0 до 100.
Задача №283 (расчет суммы кредита и дисконта)
На основе значений показателей, приведенных в таблице, рассчитать, какую сумму получил заемщик и чему равен дисконт.
Исходные данные:
- Срок кредитного договора – 9 месяцев.
- Годовая ставка кредита – 60%.
- Сумма возвращения кредита – 300 тыс. грн.
Решение задачи:
Сумма кредита, подлежащая уплате банку-кредитору, рассчитывается по формуле:
Кн=Ко*(1+p*n),
где Кн – наращенная сумма долга;
Ко – первоначальная сумма кредита;
p – годовая процентная ставка, выраженная десятичной дробью;
n – срок кредита, лет.
Нам необходимо найти первоначальную сумму кредита, для этого преобразуем формулу следующим образом:
Ко=Кн/(1+p*n).
Таким образом, первоначальная сумма кредита составляет:
Ко=Кн/(1+p*n)=300/(1+0,6*9/12)=300/1,45=206,9 тыс. грн.
Сумма дисконта равна разнице между наращенной суммой долга и первоначальной суммой кредита:
Д=Кн-Ко=300-206,9=93,1 тыс. грн.
Первоначальная сумма Наращение Наращенная сумма
 n
n
Процентная ставка (Возвращаемая сумма)
n
Дисконтирование
 Современная
Современная
стоимость
(Возвращаемая сумма)
Процентная ставка
Рис. 6. Логика
финансовых операций
Математическое дисконтирование
Математическое
дисконтирование представляет собой
формальное решение задачи, обратной
наращению первоначальной суммы ссуды.
Задача в этом случае формулируется так:
какую первоначальную сумму ссуды надо
выдать в долг, чтобы получить в конце
срока сумму S
при условии, что на долг начисляются
проценты по ставке i
? Решив уравнение
(1)
относительно P,
находим:
![]() (12)
(12)
Установленная
таким путем величина P
является современной величиной суммы
S,
которая будет выплачена через n
лет. Выражение 1/(1 + n∙i)
называется дисконтным
множителем,
который показывает современную стоимость
одной денежной единицы.
Разность (S
– P)
можно рассматривать не только как
проценты, начисляемые на P,
но и как дисконт суммы S.
Обозначим последний через D.
Дисконт, как скидка с конечной суммы
долга необязательно определяется через
процентную ставку, он может быть
установлен по соглашению сторон и в
виде абсолютной величины для всего
срока.
Рассмотрим примеры.
Пример 8.
Через год владелец
векселя, выданного коммерческим банком,
должен получить по нему 220 тыс. руб. Какая
сумма была внесена в банк в момент
приобретения векселя, если годовая
ставка составляет 12%?
Д ано:
ано:
Решение:
S
= 220 т.р. Представим
задачу графически
i
= 12%
n
= 1 год

Р
– ?
i
= 12%; n
= 1 г.




P
=
?
S
=
120т.р.
дисконтирование
0
1 2
И спользуя
спользуя
выражение(12)
получим:
![]() тыс. руб.
тыс. руб.
Пример 9.
Ссуда должна быть
погашена через год в сумме 200 тыс. руб.
Кредитор попросил погасить ссуду через
270 дней после выдачи под 10% годовых. Какую
сумму получит кредитор? К
= 365 дн.
Д ано: Решение:
ано: Решение:
S
= 200 тыс. руб. Изобразим
задачу графически:
I
= 10%
n
= 1г.
n 1
1
= 270 дн.
Р
– ?


i
= 10%
n
= 365-270


P
=
?
S
=
200т.р.
дисконтирование
0
1
n1
=
270
n0
= 95 дн.
n
= 365
Находим
количество дней, оставшихся до погашения
ссуды:
n0
= n
– n1
= 365 – 270 = 95 (дн.)
Используя
выражение (12)
находим:
 (тыс. руб.)
(тыс. руб.)
Банковский или коммерческий учет (учет векселей)
При учете векселя
применяется банковский учет. Согласно
этому методу проценты за использование
ссуды в виде дисконта начисляются на
сумму, подлежащую уплате в конце срока.
При этом применяется учетная
ставка d.
(рис. 7)



 Р
Р
дисконтирование
(учет) S
d, n

n
Рис. 7
Дисконтирование с использованием простой учетной ставки
Расчетная формула для
вычисления этих процентов выводится
на основе следующих рассуждений.
Пусть с 1 руб. берется
годовая учетная (дисконтная, авансовая)
ставка d,
тогда должник получает на руки сумму
(1-d)
и по истечении срока должен вернуть 1
руб. То есть, если 1 руб. – это возвращаемая
сумма S,
то первоначальная сумма будет равна: P
= S
– d
(при условии что срок равен одному году),
или в нашем случае, P
= 1 – d.
Если значение S,
Р
и n
– произвольны, то
P
= S
– S
∙
n
∙
d
= S
∙
(1 – n
∙
d), (13)
где S∙n∙d
– величина дисконта, а n
– срок от момента учета до даты погашения
векселя. Величина (1 – n∙d)
называется дисконтным
множителем при
использовании учетной процентной
ставки. Учет посредством учетной ставки
осуществляется чаще всего при временной
базе K
= 360 дней, число дней ссуды берется точное
(обыкновенные проценты с точным числом
дней ссуды).
Для уяснения практического
приложения рассмотрим дисконтный
вексель. Используя номинал векселя (S),
учетную ставку (d),
время, оставшееся до срока погашения
(t),
вычитают дисконт (D)
– скидку с номинала, т.е. разницу между
S
и Р.
![]()
Затем рассчитывают
выкупную (фактурную) стоимость векселя
до срока погашения
![]() (13а)
(13а)
Рассмотрим пример:
Пример 10.
Владелец векселя
номиналом 100 тыс. руб. и периодом обращения
105 дн., за 15 дн. до наступления срока
платежа учитывает его в банке по учетной
ставке 20%. Определить сумму, полученную
владельцем векселя.
Д
 ано: Решение:
ано: Решение:
S
= 100 тыс. руб. Изобразим
задачу графически:
Пер.
обращение – 105 дн.
n
= 15 дн.
d
= 20%

Р
– ?
Р
– ? S
= 100
n
= 15 дн.


d
= 20%
105
дн.
Используя выражение
(13а)
получим:
![]() (тыс. руб.)
(тыс. руб.)
В отдельных случаях
может возникнуть ситуация, когда
совмещается начисление процентов по
ставке наращения i
и дисконтирование по учетной ставке d.
В этом случае, полученная при учете
сумма определиться как:
P `
`
= P
∙
(1 + n
∙
i)
∙
(1 – n`
∙
d) (14)
S`
где P(S)
– номинальная сумма; n
– общий срок платежного обязательства;
n`
– срок от момента учета до даты погашения
платежа; Р`
– сумма, полученная при учете обязательства.
Пример 11.
Долговое обязательство,
предусматривающее уплату 400 тыс. руб. с
начисленными на них 12% годовых, подлежит
погашению через 90 дн. Владелец обязательства
(кредитор) учел его в банке за 15 дн. до
наступления срока по учетной ставке
13,5%. Полученная сумма после учета
составила:
Д
 ано:
ано:
Решение:
S
= 400 тыс. руб. В
этой задаче номинальная стоимость
n
= 90 дн. (возвращаемая
сумма) принимается за
n`
= 15 дн. первоначальную:
S
= P (см.
график).
d
= 13,5%
i
= 12%
Р `
`
– ?
P(S)=400
т.р. S`



i
= 12%; n
= 90 дн.


d
= 13,5%; n`
= 15дн.
дисконтирование
P`-?
1.
Вначале определяем наращенную сумму
обязательства S`,
принимая его номинальную стоимость за
первоначальную сумму:
![]() (тыс. руб.)
(тыс. руб.)
2.
Находим полученную после учета сумму:
![]() (тыс. руб.)
(тыс. руб.)
3.
Используя выражение (14)
получаем ту же сумму:
![]() (тыс. руб.)
(тыс. руб.)
Необходимость
использования простой учетной ставки
для расчета наращенной суммы возникает
в случае определения номинальной
стоимости векселя при выдаче ссуды. В
этом случае сумма долга, проставленная
в векселе, будет равна
![]() (15)
(15)
Величина
1/(1-n∙d)
в этом случае является множителем
наращения при
использовании простой учетной ставки.
Пример 12.
Предприниматель
обратился в банк за ссудой в размере
200 тыс. руб. на срок 55 дней. Банк согласен
выдать указанную сумму при условии
начисления процентов по
простой учетной
ставке, равной 20%. Найти возвращаемую
сумму.
Дано: Решение:

Р
= 200 тыс. руб. В
этой задаче наращение производится
n
= 55 дн. по простой
учетной ставке.
d
= 20%
S
– ?
Р
= 200
S
– ?
наращение



d
= 20; n
= 55 дн.
Используя
выражение (15)
получим:
 тыс.
тыс.
руб.
Если
бы сумма выдавалась под простую процентную
ставку (i),
то наращенная сумма была бы равна
![]() тыс.руб.
тыс.руб.
, т.е. наращение
по учетной ставке идет быстрее и она
менее выгодна должнику 206,111 < 206,304 т.е.
возвращаемая сумма в первом случае
будет больше.
Определение
срока ссуды при использовании учетной
ставки производится по формулам:
![]() , (16)
, (16)
![]() , (17)
, (17)
где n
– срок
ссуды в годах; t
– срок ссуды в днях; k
– временная база.
Рассмотрим пример:
П ример
ример
13.
Фирме необходим
кредит в 500 тыс. руб. Банк согласен на
выдачу кредита при условии, что он будет
возвращен в размере 600 тыс. руб. Учетная
ставка 21% годовых. На какой срок банк
предоставит кредит фирме? К
= 365 дней
Д ано:
ано:
Решение:
S
= 600 тыс. руб.
Графическая иллюстрация задачи
Р
= 500 тыс. руб.
d
= 21%
n
– ?
Р
= 500 т.р. S
= 600 т.р.

d
= 20%; n
– ?


0 n
дисконтирование
При
решении подобного рода задач проще
воспользоваться выражением (17),
тогда срок кредита сразу получится в
днях (при использовании выражения (16)
срок будет выражен в
долях года):
![]() (дн.)
(дн.)
Величина
учетной ставки рассчитывается по
формулам:
![]() , (18)
, (18)
![]() . (19)
. (19)
Пример 14.
Контракт на получение
ссуды в 500 тыс. руб. предусматривает
возврат долга через 300 дней в сумме 600
тыс. руб. Определим примененную банком
учетную ставку. К
= 365 дней.
Д
 ано:
ано:
Решение:
Р
= 500 тыс. руб.
S
= 600 тыс. руб.
t
= 300 дней

i
– ?
Р
= 500 т.р. дисконтирование
S
= 600 т.р.



d
= ? t
= 300 дн.
0 t
По
формуле (19)
получим:
![]() илиd
илиd
= 20,27%
При
операциях с дисконтными финансовыми
инструментами учетная ставка иногда
может задаваться неявно: в виде общей
относительной доли уменьшения номинала
![]() или как отношение дисконтированной
или как отношение дисконтированной
суммы к номиналу![]() ;
;
тогдаd
находится как
![]() или
или
![]() (20)
(20)
где
d`
– процент скидки; t
– срок до учета (срок векселя).
Пример
15.
Размер
удерживаемых процентов при выдаче
полугодовой ссуды составляет 20% суммы
ссуды. Определим заложенную учетную
ставку процентов (дисконтную ставку).
К
= 365
Д ано:
ано:
Решение:
d`
= 20%
t
= 0,5 г.(180 дн.)
К
= 365 дн.
d
– ?
![]()
Пример 16.

Государственные
краткосрочные трехмесячные векселя
котируются по курсу 90. Вычислим учетную
ставку. К=360.
Д ано: Решение:
ано: Решение:
P
/ S
= 0,9 скидка в нашем
случае: 1 – 0,9 = 0,1
d
– ? тогда:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Если нравится – подписывайтесь на телеграм-канал Бробанк.ру и не пропускайте новости
Эксперт в области финансовой грамотности и инвестиций. Образование высшее экономическое. Опыт работы в банке – более 15 лет. Регулярно повышает квалификацию и проходит курсы по финансам и инвестициям, что подтверждено сертификатами Банка России, Ассоциации Развития Финансовой Грамотности, Нетологии и других образовательных платформ. Сотрудничает со Сравни.ру, Тинькофф Инвестиции, ГПБ Инвестиции и другими финансовыми изданиями. treskova@brobank.ru
Открыть профиль
Всем им нужно узнать, от чего зависит ежемесячный платеж по кредиту и можно ли его вычислить самостоятельно.Бробанк расскажет, как рассчитывается кредит, какие методики использовать для подсчета ежемесячных процентов и итоговой суммы переплаты. В статье собраны формулы, которые расписаны на конкретном примере, чтобы стало понятно, как был получен тот или иной результат.
-
Что входит в ежемесячный платеж
-
Виды ежемесячных выплат по кредитам
-
Что берут за основу при расчете ежемесячного платежа
-
Как рассчитать ежемесячную сумму платежа
-
Самостоятельный подсчет при аннуитетных платежах
-
График расчетов для аннуитетной схемы
-
Самостоятельный подсчет при дифференцированных платежах
-
График расчетов при дифференцированных выплатах
-
Какой из вариантов выгоднее заемщику
-
Какую схему начисления процентов выбрать
Проц. ставка
7.9% годовых
Платеж в месяц
9 964.29 ₽
Сумма выплат
358 714 ₽
Переплата
58 714 ₽
График платежей
| №, Месяц |
Сумма платежа Платеж |
Проценты + долг | Остаток долга |
|---|---|---|---|
| 1. 10.04.2019 |
61 811.94 3 000.00 + 58 811.94 |
3 000.00 + 58 811.94 | 241 188.06 |
| 1. 10.04.2019 |
61 811.94 3 000.00 + 58 811.94 |
3 000.00 + 58 811.94 | 241 188.06 |
График платежей
Что входит в ежемесячный платеж
Банки выдают на руки график погашения при оформлении кредита. Сумма ежемесячной выплаты может быть указана одним числом или несколькими. Вид графика погашения зависит от того, какая форма предоставления данных принята в банке. Некоторые кредиторы расписывают данные в двух колонках:
- основной долг, иногда его называют тело;
- начисленные проценты.
Другие банки указывают только общую сумму к выплате в указанную дату.
Если заемщик отклоняется от графика и допускает просрочки, то к основной сумме добавляют штрафы, пени, комиссии или неустойки. Каждый банк самостоятельно устанавливает очередность удержания накопленных штрафных санкций из последующих поступлений. Какой порядок предусмотрен у компании, прописано в кредитном договоре. Например, из суммы очередного поступления списывания происходят в такой очередности:
- Проценты на просроченные проценты.
- Проценты за заемные средства, которые были просрочены по выплате.
- Погашение просроченной задолженности.
- Проценты по текущей задолженности.
- Погашение текущей задолженности.

Банки применяют и другие схемы, но такой вариант считается наиболее распространенным в банковской практике.
Виды ежемесячных выплат по кредитам
Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.
Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.
В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.
Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.
Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.
Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.
Что берут за основу при расчете ежемесячного платежа
Для самостоятельного подсчета суммы ежемесячного платежа по кредиту нужны такие данные:
- общая сумма кредита;
- процентная ставка;
- период кредитования.
Но часто в итоговую сумму выплат включают и другие суммы. Например, страховка по кредиту, услуги смс-информирования или другие платные сервисы от банка. Кроме того сумма будет немного отличаться в зависимости от способа поступления средств. Так, некоторые банки берут комиссию за зачисление наличными.
Дополнительные расходы возникают и при пересылке суммы из другого банка: процент от суммы могут брать как в банке-отправителе, так и банке-получателе. Такие моменты желательно выяснять заранее, чтобы отправленной сумму хватило на ежемесячный платеж, и какая-то его часть не вышла на просрочку.
Как рассчитать ежемесячную сумму платежа
Для расчета ежемесячной суммы платежа по кредиту используют:
- кредитный калькулятор;
- помощь сотрудника банка;
- самостоятельный расчет по формулам
- таблицы в Excel/
Кредитный калькулятор. Такие сервисы размещают в интернете или на сайте банка, который предлагает выдать кредит.
Кредитные калькуляторы позволяют не только рассчитать сумму ежемесячного платежа, но и показывают график выплат. Понадобится внести: сумму, срок и ставку, а также указать, какой тип выплат аннуитетный или дифференцированный. Но данные не всегда будут полностью совпадать с реальными. Потому что платеж может быть внесен не через 30 дней, а через 25, либо равными долями дважды в месяц. Кроме того калькуляторы не учитывают дополнительные платные услуги банка.
Помощь специалиста в отделении банка. Каждый потенциальный заемщик вправе обратиться к менеджеру или позвонить по горячей линии до того, как оформит кредит. Сотрудники банка подскажут диапазон процентной ставки. Затем на основе суммы и срока могут дать информацию по ежемесячному платежу. Но эти сведения предварительные.

После рассмотрения заявки, изучения кредитной истории и платежеспособности, банк установит индивидуальные условия кредитования. В договоре будет указана точная сумма и график платежей.
Самостоятельный расчет по готовым формулам. Ежемесячные платежи можно вычислить самому, если знать все входные данные. Для этого разработаны специальные формулы, куда понадобится подставить свои значения.
Таблицы в Excel. Для вычисления ежемесячного платежа по кредиту понадобятся встроенные функции программы. Подсчитать аннуитетные платежи поможет функция ПЛТ, она же PMT, если искать в латинской версии.
В строке подсчета ежемесячного платежа понадобится вписать такую формулу: =ПЛТ(18%/12;24;-500000). Где 18%/12 — это процентная ставка по кредиту, 24 — количество выплат, а 500 000 — сумма долга. Аннуитетный платеж при таких цифрах будет равен 24 962,05 рублей в месяц.
Какой из вариантов выбрать, зависит от вас. Некоторые предпочитают делать расчеты в онлайн-калькуляторах, другим удобнее один раз внести свои данные в таблицу в Excel и потом только менять параметры.
Самостоятельный подсчет при аннуитетных платежах
Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:
- Процентная ставка — 18%.
- Период кредитования — 24 месяца.
- Сумма кредита — 500000 рублей.
Классическая формула для расчета аннуитетного платежа выглядит так:
Разовый аннуитетный платеж = Сумма кредита * Ка
где Ка — это коэффициент аннуитета.
Ка = ((ЕПС* (1 + ЕПС)n)/( (1 + ЕПС)n -1)
где ЕПС — ежемесячная процентная ставка.
Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.
Итоговый расчет примет вид:
500 000 * (0,015 * (1 + 0,015)24)/((1 + 0,015)24 -1) = 24 962,05 рублей в месяц.
Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.
Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:
24 962,05 * 24 = 599 089,24 рублей.
Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.
График расчетов для аннуитетной схемы
| Дата | Сумма платежа | Проценты | Тело | Остаток платежа |
| 02.04.2020 | 0 | 0 | 0 | 500 000.00 |
| 02.05.2020 | 24 962.05 | 7 500.00 | 17 462.05 | 482 537.95 |
| 02.06.2020 | 24 962.05 | 7 238.07 | 17 723.98 | 464 813.97 |
| 02.07.2020 | 24 962.05 | 6 972.21 | 17 989.84 | 446 824.13 |
| 02.08.2020 | 24 962.05 | 6 702.36 | 18 259.69 | 428 564.44 |
| 02.09.2020 | 24 962.05 | 6 428.47 | 18 533.58 | 410 030.86 |
| 02.10.2020 | 24 962.05 | 6 150.46 | 18 811.59 | 391 219.27 |
| 02.11.2020 | 24 962.05 | 5 868.29 | 19 093.76 | 372 125.51 |
| 02.12.2020 | 24 962.05 | 5 581.88 | 19 380.17 | 352 745.34 |
| 02.01.2021 | 24 962.05 | 5 291.18 | 19 670.87 | 333 074.47 |
| 02.02.2021 | 24 962.05 | 4 996.12 | 19 965.93 | 313 108.54 |
| 02.03.2021 | 24 962.05 | 4 696.63 | 20 265.42 | 292 843.12 |
| 02.04.2021 | 24 962.05 | 4 392.65 | 20 569.40 | 272 273.72 |
| 02.05.2021 | 24 962.05 | 4 084.11 | 20 877.94 | 251 395.78 |
| 02.06.2021 | 24 962.05 | 3 770.94 | 21 191.11 | 230 204.67 |
| 02.07.2021 | 24 962.05 | 3 453.07 | 21 508.98 | 208 695.69 |
| 02.08.2021 | 24 962.05 | 3 130.44 | 21 831.61 | 186 864.08 |
| 02.09.2021 | 24 962.05 | 2 802.96 | 22 159.09 | 164 704.99 |
| 02.10.2021 | 24 962.05 | 2 470.57 | 22 491.48 | 142 213.51 |
| 02.11.2021 | 24 962.05 | 2 133.20 | 22 828.85 | 119 384.66 |
| 02.12.2021 | 24 962.05 | 1 790.77 | 23 171.28 | 96 213.38 |
| 02.01.2022 | 24 962.05 | 1 443.20 | 23 518.85 | 72 694.53 |
| 02.02.2022 | 24 962.05 | 1 090.42 | 23 871.63 | 48 822.90 |
| 02.03.2022 | 24 962.05 | 732.34 | 24 229.71 | 24 593.19 |
| 02.04.2022 | 24 962.09 | 368.90 | 24 593.19 | 0 |
| Всего выплат | 599 089.24 | 99 089.24 | 500 000.00 | 0 |
Самостоятельный подсчет при дифференцированных платежах

Дифференцированный платеж изменяется каждый месяц. Сумма уменьшается, и клиент меньше переплачивает. Формула подсчета выглядит так:
Ежемесячный дифференцированный платеж = ЧОД + Сумма процентов
ЧОД — это часть основного долга, фиксированная величина при дифференцированных выплатах кредита, если будет соблюден график выплат с точностью до дня. Для ее вычисления потребуется сумму кредита поделить на его срок. С данными из примера это выглядит так:
ЧОД = 500000/24 = 20 833,33 рубля
Сумма процентов постоянно уменьшается, так как уменьшается общая итоговая задолженность по кредиту. Банки используют разные формулы для подсчета этой величины, но наиболее распространена такая:
Сумма процентов = ОстЗ * ПСГ * КД/365 или 366 дней в году
ОстЗ — остаток задолженности,
ПСГ — процентная ставка за год,
КД — количество календарных дней, за которые были начислены проценты.
Расширим входящие данные в примере. Предположим, что кредит взят в 2020 году, он високосный, но будет выплачиваться два года, поэтому в 2021 году в формуле будет 365, а не 366 дней. Дополнительные вводные данные: деньги получены 02.04.2020 года, а первый платеж предстоит 02.05.2020 года. Между этими платежами 30 календарных дней. Подставленные в формулу данные будут выглядеть так:
Сумма процентов = 500 000 * 18% * 30/366 = 7377,05 рублей.
Дифференцированный платеж за первый месяц = 20 833,33 + 7 377,05 = 28 210,38 рублей.
Остаток долга к следующему месяцу уменьшится, поэтому:
500 000 — 20 833,33 = 479 166,67 рублей
Следовательно, и сумма начисленных процентов будет меньше. Кроме того в мае 31 день, поэтому формула примет вид:
Сумма процентов во втором месяце = 479 166,67 * 18% * 31/366 = 7 305,33 рублей.
Дифференцированный платеж за второй месяц = 20 833,33 + 7 305,33 = 28 138,66 рублей.
По этой методике подсчитаем все выплаты за 24 месяца пользования кредитом. Итоговая сумма переплаты составит 93 712,98 рублей. При условии, что платежи буду внесены день в день по графику.
График расчетов при дифференцированных выплатах
| Дата | Сумма платежа | Проценты | Тело | Остаток платежа |
| 02.04.2020 | 0 | 0 | 0 | 500 000.00 |
| 02.05.2020 | 28 210.38 | 7 377.05 | 20 833.33 | 479 166.67 |
| 02.06.2020 | 28 138.66 | 7 305.33 | 20 833.33 | 458 333.34 |
| 02.07.2020 | 27 595.63 | 6 762.30 | 20 833.33 | 437 500.01 |
| 02.08.2020 | 27 503.41 | 6 670.08 | 20 833.33 | 416 666.68 |
| 02.09.2020 | 27 185.79 | 6 352.46 | 20 833.33 | 395 833.35 |
| 02.10.2020 | 26 673.49 | 5 840.16 | 20 833.33 | 375 000.02 |
| 02.11.2020 | 26 558.23 | 5 724.90 | 20 833.33 | 354 166.69 |
| 02.12.2020 | 26 058.74 | 5 225.41 | 20 833.33 | 333 333.36 |
| 02.01.2021 | 25 915.30 | 5 081.97 | 20 833.33 | 312 500.03 |
| 02.02.2021 | 25 610.73 | 4 777.40 | 20 833.33 | 291 666.70 |
| 02.03.2021 | 24 860.73 | 4 027.40 | 20 833.33 | 270 833.37 |
| 02.04.2021 | 24 968.18 | 4 134.85 | 20 833.33 | 250 000.04 |
| 02.05.2021 | 24 531.96 | 3 698.63 | 20 833.33 | 229 166.71 |
| 02.06.2021 | 24 336.76 | 3 503.43 | 20 833.33 | 208 333.38 |
| 02.07.2021 | 23 915.52 | 3 082.19 | 20 833.33 | 187 500.05 |
| 02.08.2021 | 23 699.77 | 2 866.44 | 20 833.33 | 166 666.72 |
| 02.09.2021 | 23 381.28 | 2 547.95 | 20 833.33 | 145 833.39 |
| 02.10.2021 | 22 990.87 | 2 157.54 | 20 833.33 | 125 000.06 |
| 02.11.2021 | 22 746.86 | 1 913.53 | 20 833.33 | 104 166.73 |
| 02.12.2021 | 22 374.43 | 1 541.10 | 20 833.33 | 83 333.40 |
| 02.01.2022 | 22 107.30 | 1 273.97 | 20 833.33 | 62 500.07 |
| 02.02.2022 | 21 788.81 | 955.48 | 20 833.33 | 41 666.74 |
| 02.03.2022 | 21 408.67 | 575.34 | 20 833.33 | 20 833.41 |
| 02.04.2022 | 21 151.48 | 318.07 | 20 833.41 | 0 |
| Всего выплат | 593 712.98 | 93 712.98 | 500 000.00 | 0 |
Какой из вариантов выгоднее заемщику
Если ориентироваться исключительно на сумму переплаты, то однозначно дифференцированный способ начисления и выплаты процентов выгоднее для заемщика. Логично, что при аннуитетных платежах, больше выгод у банка. Но не у всех заемщиков получится соблюдать повышенную нагрузку по дифференциальной схеме, когда первоначальные ежемесячные платежи значительно выше. В приведенном примере выплаты в первый месяц при разных способах отличались на 3,2 тысячи рублей. Но при длительном периоде кредитования и большой сумме этот разрыв значительно выше.
Например, если заемная сумма по ипотеке 5 млн рублей, ставка 10% и срок кредитования 15 лет, данные приобретут такой вид:
| Суммы | Аннуитетный платеж | Дифференцированный платеж |
| Первый ежемесячный платеж | 53 730,26 | 70 070,59 |
| Итоговая сумма переплаты | 4 761 445,18 | 3 771 213,11 |
Не каждый заемщик осилит первоначальную разницу в 17 тысяч рублей, хотя итоговая сумма переплаты представлена наглядно.
Какую схему начисления процентов выбрать
Таблица поможет определить, какая из схем начисления процентов подойдет больше в разных ситуациях:
| Условие | Аннуитетная схема | Дифференцированная схема |
| Равные суммы платежей на протяжении всего срока | Да, но можно вносить больше, главное оповестить банк, чтобы досрочное погашение было оформлено своевременно. | Нет, суммы постепенно уменьшаются. Но если есть возможность и желание можно платить еще больше, чем предложено по графику. В этом случае следует оповестить банк-кредитор о своем желании. |
| Сумма итоговой переплаты по кредиту | Больше | Меньше |
| Методика самостоятельного подсчета | Проще | Сложнее, но можно использовать онлайн-калькуляторы |
| Кому подходит больше | Тем, у кого фиксированная и стабильная заработная плата с понятными ожиданиями на длительную перспективу. | Тем, у кого высокие доходы в ближайшем будущем, но более отдаленные перспективы менее поняты. Например, проектным работникам. |

Чтобы уменьшить переплату при аннуитетной схеме, погашайте кредит досрочно. Если удастся досрочно вносить такие же суммы, как предусмотрены в графике дифференцированных платежей, то итоговая переплата почти такая же, как в дифференцированной схеме.
В этом случае самое главное условие предупреждать сотрудников банка, зачем вы вносите на счет сумму большие, чем предусмотрены в вашем графике выплат. О том, как и когда надо уведомлять банк, пишут в кредитном договоре. В некоторых компаниях допускают уведомление на горячую линию, в других через сообщения в интернет-банке, в третьих — через личное заявление у офисе.
Оценивайте свои финансовые возможности до подписания договора. Не берите взаймы больше, чем способны погасить, и тогда вы сохраните свою кредитную историю и сможете своевременно выплатить долги.
Комментарии: 3
Для выбора кредита нужно учитывать не только базовую процентную ставку за пользование заемными средствами, но и учитывать полную стоимость данного кредита (займа).
Что такое полная стоимость кредита?
Полная стоимость кредита (ПСК) – это сумма, которую клиент фактически заплатит банку за пользование средствами, реальная цена кредита.
Практики раскрытия настоящей цены банковской ссуды появилась в России не сразу, но после нескольких лет возмущенного непонимания между кредитными учреждениями и заемщиками. Психологически цена кредита под 11% годовых на 15 лет кажется привлекательной, но по итогу, за весь период погашения, придется заплатить вдвое больше, чем было взято. Еще более усложнялось дело обилием комиссий, в процентах и с фиксированной величиной. Некоторые проценты исчислялись от суммы остатка, а другие от первоначальной суммы кредита. В такой ситуации определить реальную стоимость банковской ссуды без сложных вычислений невозможно.
Полная стоимость кредита должна быть рассчитана еще до его получения, т.к. условия кредитования заранее известны.
Важно учитывать, что список расходов, включаемых в ПСК не бесконечен. Он не может быть расширен по аналогии, по мнению одной из сторон сделки или решением каких-либо еще лиц и организаций.
Центральный банк РФ в рамках закона «О потребительском кредите (займе)» обязал рассчитывать и указывать данную величину на первой странице кредитного договора, а именно:
«Полная стоимость
потребительского кредита (займа) определяется как в процентах годовых, так и в
денежном выражении и рассчитывается в порядке, установленном настоящим
Федеральным законом. Полная стоимость потребительского кредита (займа)
размещается в квадратных рамках в правом верхнем углу первой страницы договора
потребительского кредита (займа) перед таблицей, содержащей индивидуальные
условия договора потребительского кредита (займа), и наносится цифрами и
прописными буквами черного цвета на белом фоне четким, хорошо читаемым шрифтом
максимального размера из используемых на этой странице размеров шрифта. Полная
стоимость потребительского кредита (займа) в денежном выражении размещается
справа от полной стоимости потребительского кредита (займа), определяемой в
процентах годовых. Площадь каждой квадратной рамки должна составлять не менее
чем 5 процентов площади первой страницы договора потребительского кредита
(займа) (часть 1 в ред. Федерального закона от 05.12.2017 N 378-ФЗ)
Из этого следует, что полная стоимость кредита не обязательно равна сумме, которую заемщик реально заплатит кредитору. Т.к. в процессе погашения возможны:
- Задержки платежей или досрочное погашение. За первое начисляется пеня, второе обещает пересчет процентов и уменьшение общей стоимости кредита или штрафные санкции, если это предусмотрено договором.
- Изменения условий возврата ссуды. Такая возможность часто прописывается в договоре, но ее наступление увязывается с внешними обстоятельствами.
Эти и другие обстоятельства могут повлиять на фактически уплачиваемую заемщиком сумму. Но если изменения в момент получения ссуды не известны, или их наступление зависит не от кредитора, то включать их в общую стоимость кредита не будут.
Важно чтобы полная стоимость кредита была известна заранее, еще до его получения. Если банк скроет информацию об этом, то сделка должна быть признана недействительной, договор кредитования расторгнут, а потраченные клиентом средства возвращены ему.
Для получателей банковских ссуд именно значение полной стоимости кредита, а не процентная ставка, должна быть критерием оценки и сравнения разных кредитных продуктов.
Что входит в расчет ПСК?
В расчет ПСК включаются следующие платежи:
- сумма основного долга;
- проценты на эту сумму;
- различные платежи в пользу кредитора, если они указаны в договоре;
- плата за выпуск и обслуживание электронного средства платежа (пластиковой карты), с помощью которого вы будете погашать кредит;
- различные платежи в пользу третьих лиц (например, страховых компаний, застройщиков, нотариусов и т. д.);
- сумма страховой премии;
- сумма страховой премии по договору добровольного страхования, если в зависимости от его заключения банк предлагает иные условия по кредиту (например, когда изменяется срок возврата, ПСК, процентная ставка, другие платежи и комиссии).
Данные платежи и являются затратами кредитополучателя.
Платежи не входящие в расчет ПСК:
- штрафы за несоблюдение условий договора;
- обязательные виды страхования (КАСКО или страхование квартиры);
- комиссии за валютные операции;
- пени по договору;
- комиссия за приостановление операций;
- плата за безналичный перевод денег;
- плата за получение (погашение) кредита наличными (расчетно-кассовое обслуживание);
- комиссия за пользование онлайн- или мобильным банком, СМС-оповещение.
Как рассчитать полную стоимость кредита?
Процесс вычисления реальной цены кредита происходит по сложным формулам, учить которые для рядового потребителя долго и не обязательно. Однако понимать, как происходит такой расчет полезно.
Прежде всего, уточним – все платежи в рамках кредита вычисляются по собственным формулам. Отдельно рассчитывается основной процент, отдельно комиссии и прочие платежи (в зависимости от условий договора – на первоначальную сумму или от невыплаченного остатка). Затем все полученные цифры суммируются и составляют общую цену ссуды.
Порядок расчета ПСК
Порядок расчета полной стоимости потребительского кредита (займа) приведен во 2 части Федерального закона от 21.07.2014 N 229-ФЗ.
ПСК, определяемая в процентах годовых, рассчитывается по формуле:
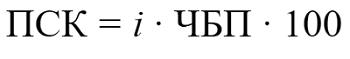
где:
- ПСК – полная стоимость кредита (займа);
- i – процентная ставка базового периода, выраженная в десятичной форме;
- ЧБП – число базовых периодов в календарном году.
Это уравнение приведено в тексте закона «О потребительском кредите (займе)» и применяется всеми банками.
Процентная ставка базового периода (i) определяется как наименьшее положительное решение уравнения:
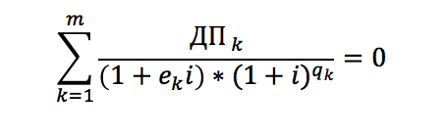
где:
- ДПk – сумма k-го платежа;
- qk– количество полных базовых периодов с момента выдачи кредита до даты k-го платежа;
- ek– срок, выраженный в долях базового периода, с момента завершения qk-го базового периода до даты k-го платежа;
- m – количество платежей;
- i – процентная ставка базового периода, выраженная в десятичной форме.

Упрощенный расчет
Сделать самостоятельный расчет поможет упрощенная формула расчета стоимости кредита:
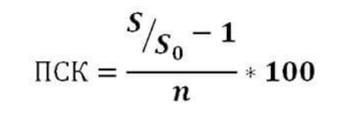
Расчет по ней происходит так:
- сумма всех кредитных платежей (S) делится на полученную от банка сумму (S0);
- из результата деления вычитается единица;
- полученное число делится на n – количество лет погашения ссуды, и умножается на 100.
Итоговую величину стоимости кредита представляют в процентах годовых. Ее можно сравнить с основной процентной ставкой и узнать размер дополнительной переплаты.
Важно: в государственных нормативных актах данной формулы нет. С помощью данной формулы вы можете сами выяснить реальную полную стоимость кредита.
Пример расчета ПСК и ставки базового периода
Рассчитаем ПСК для займа в 20 000 рублей на 5 дней под 0.8% в день. Займ погашается в конце срока единым платежом.
Рассчитаем процентную ставку базового периода (i):

- Сумма займа = 20 000 рублей;
- Срок пользования займом = 5 дней;
- Дневная процентная ставка = 0.8%;
- q1=0– количество полных базовых периодов с момента выдачи займа до даты первого платежа (выдача займа);
- q2=1– количество полных базовых периодов с момента выдачи займа до даты второго платежа (возврат займа);
- e2=0– срок, с момента завершения первого (т.к. q2=1) базового периода до даты второго денежного потока (дата второго денежного потока и дата завершения базового периода в данном примере совпали).
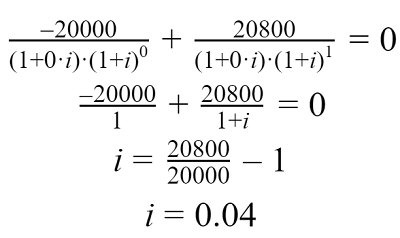
Полная стоимость данного кредита (займа) составит:
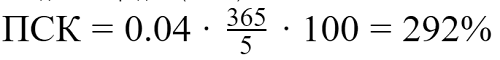
Полная стоимость кредита (займа) составить 292% годовых.
Сравнение условий по кредитам – главная задача заемщика, который хочет получить максимальную выгоду, и для их упрощения рекомендуем пользоваться калькулятором займа.
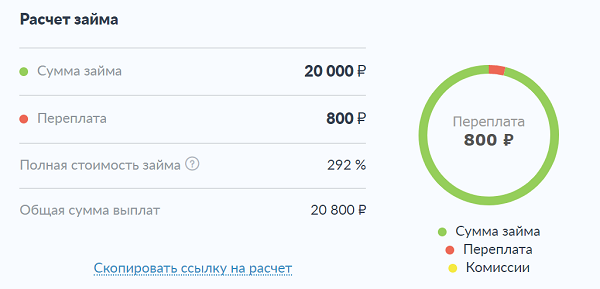
Результат расчета кулькулятором займа
Пример расчета ПСК калькулятором
Вычислим полную стоимость кредита в 1 миллион рублей на 2 года, под 10% годовых и с дополнительной комиссией в 12 тысяч в год. Тип платежей – аннуитетный, т.е. равными долями во все периоды.
|
период |
ежемесячный платеж |
по основной сумме |
процентные платежи |
комиссия |
невыплаченный остаток |
|
1 |
47 144,93 |
37 811.59 |
8 333,33 |
1 000,00 |
962 188,41 |
|
2 |
47 144,93 |
38 126.69 |
8 018,24 |
1 000,00 |
924 061,72 |
|
3 |
47 144,93 |
38 444.41 |
7 700,51 |
1 000,00 |
885 617,31 |
|
4 |
47 144,93 |
38 764.78 |
7 380,14 |
1 000,00 |
846 852,52 |
|
5 |
47 144,93 |
39 087.82 |
7 057,10 |
1 000,00 |
807 764,70 |
|
6 |
47 144,93 |
39 413.55 |
6 731,37 |
1 000,00 |
768 351,15 |
|
7 |
47 144,93 |
39 742.00 |
6 402,93 |
1 000,00 |
728 609,15 |
|
8 |
47 144,93 |
40 073.18 |
6 071,74 |
1 000,00 |
688 535,96 |
|
9 |
47 144,93 |
40 407.13 |
5 737,80 |
1 000,00 |
648 128,84 |
|
10 |
47 144,93 |
40 743.85 |
5 401,07 |
1 000,00 |
607 384,98 |
|
11 |
47 144,93 |
41 083.38 |
5 061,54 |
1 000,00 |
566 301,60 |
|
12 |
47 144,93 |
41 425.75 |
4 719,18 |
1 000,00 |
524 875,85 |
|
13 |
47 144,93 |
41 770.96 |
4 373,97 |
1 000,00 |
483 104,89 |
|
14 |
47 144,93 |
42 119.05 |
4 025,87 |
1 000,00 |
440 985,84 |
|
15 |
47 144,93 |
42 470.04 |
3 674,88 |
1 000,00 |
398 515,80 |
|
16 |
47 144,93 |
42 823.96 |
3 320,96 |
1 000,00 |
355 691,83 |
|
17 |
47 144,93 |
43 180.83 |
2 964,10 |
1 000,00 |
312 511,01 |
|
18 |
47 144,93 |
43 540.67 |
2 604,26 |
1 000,00 |
268 970,34 |
|
19 |
47 144,93 |
43 903.51 |
2 241,42 |
1 000,00 |
225 066,83 |
|
20 |
47 144,93 |
44 269.37 |
1 875,56 |
1 000,00 |
180 797,46 |
|
21 |
47 144,93 |
44 638.28 |
1 506,65 |
1 000,00 |
136 159,18 |
|
22 |
47 144,93 |
45 010.27 |
1 134,66 |
1 000,00 |
91 148,92 |
|
23 |
47 144,93 |
45 385.35 |
759,57 |
1 000,00 |
45 763,56 |
|
24 |
47 144,93 |
45 763,56 |
381,36 |
1 000,00 |
0 |
|
Итого |
1 131 478,32 |
999 999,98 |
107 478,21 |
24 000,00 |
Общая выплата по кредиту составляет 1 миллион 131 тысячу 478 рублей 32 копейки. Вставим эту цифру в упрошенную формулу:
((1 131 478,32/1 000 000)-1)/2*100 = 6,57%
Общая стоимость кредита составила чуть более 6 с половиной процентов в год, т.е. 13,15% за два года.
Почему это не похоже на заявленную ставку в 10% годовых?
Потому, что проценты начислялись только на сумму невыплаченного остатка, но действовала комиссия, начисляемая от первоначальной суммы кредита.
Этот простой пример показывает, как сильно отличается реальность от того, что кажется понятным до расчета.
Как рассчитать стоимость кредита онлайн?
Расчет полной стоимости кредита, по общей (а не упрощенной) формуле, ручным способом, может стать весьма долгим упражнением в математике. Трата времени здесь гарантирована, а риск ошибок весьма велик. Но, к радости пользователей, интернет предлагает немало кредитных калькуляторов – программ, в которых уже есть все нужные для расчета формулы, и остается только поставить в соответствующие формы свои данные.
В практике поиска кредита будут особенно полезны калькуляторы с возможностью подбора кредита удовлетворяющего заданным параметрам, с функцией поиска кредита на нужную сумму и с подходящей процентной ставкой. Вот хороший пример такого калькулятора.
После ввода данных и подбора кредитных продуктов по заданным критериям, можно узнать полную стоимость выбранного кредита. Для быстрого поиска и сравнения банковских ссуд будет полезна «Таблица подбора кредитов». Это можно сделать сортировкой по 3 параметрам:
- годовой ставке%;
- среднемесячному платежу;
- сумме переплаты за год.
Переход по клику «Получить кредит» не означает подачи заявки на данный конкретный продукт, но только переносит клиента на соответствующую страницу банка с подробной информацией о выбранном варианте.
Не лишним будет еще раз напомнить, что банки, по действующему законодательству, обязаны письменно сообщать заемщику полную стоимость кредита.
Кредиты с онлайн-заявкой | Подобрать кредитную карту | Сделать вклад
Теперь взять кредит или кредитную карту онлайн стало еще проще. Скачайте и установите мобильное приложение Bankiros.ru в Google Play.В приложении вы можете быстро и бесплатно подобрать кредит или кредитную карту среди самых выгодных предложений, оставить заявку в выбранные банки или отправить единую анкету во все банки в пару кликов.
Обнаружили ошибку? Выделите ее и нажмите Ctrl + Enter.
