Как найти первоначальный объем точечная эластичность

Задача №1. Определение изменения дохода при увеличении проданной продукции на одну единицу

Фирма имеет кривую спроса:

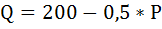
Зная, что P=100, определить изменение дохода при увеличении проданной продукции на одну единицу.

Решение:

Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой (MR — marginal revenue).

Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.

Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).

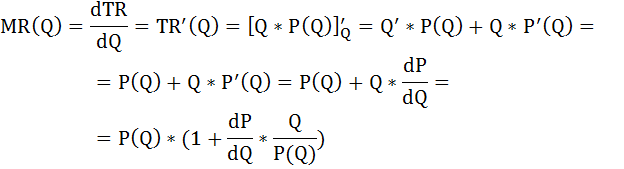
Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:

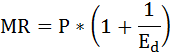
Определим эластичность спроса по цене:

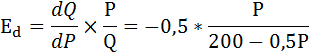
При P=100

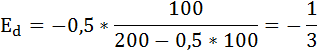
Тогда:

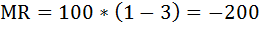
Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.

Задача №2. Коэффициент точечной эластичности

Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.

а) Как изменилась выручка фирмы?

б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.

Решение:

а) Выручка фирмы рассчитывается по формуле:

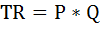
Соответственно изменение выручки фирмы в процентном выражении рассчитаем по формуле:

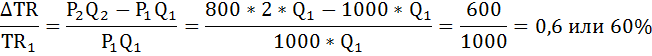
Таким образом, выручка фирмы увеличилась на 60 %.

б) Коэффициент точечной эластичности рассчитаем по формуле, используемой в определении:

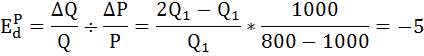
Коэффициент эластичности по абсолютной величине больше 1, следовательно спрос эластичен.

Задача №3. Эластичность спроса по цене

Функция задана уравнением

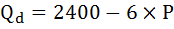
а) Выведите формулу эластичности этого спроса.

б) При какой цене эластичность спроса по цене составит – 0,5?      

в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?

Решение:

а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.

В точке (P₀,Q₀) точечная эластичность вычисляется как

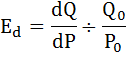
Где

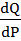
  – производная функции спроса в этой точке.

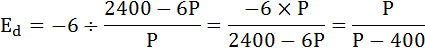
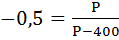
б) 

Отсюда:

Р = 133,33

в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.

Задача №4. Функция суммарного спроса

а) Определить функцию суммарного спроса на основании данных об индивидуальном спросе:

Q(1) = 100 – 5 P при P≤ 20 и 0 при Р > 20,

Q(2) = 50 – 8 P при P≤ 10 и 0 при Р > 10,

Q(3) = 56 – 4 P при P≤ 14 и 0 при Р > 14.

б) Найти эластичность спроса в точке P = 12.

Решение:

а) Для определения функции суммарного спроса при каждом возможном уровне цены необходимо сложить величины индивидуальных спросов отдельных покупателей.

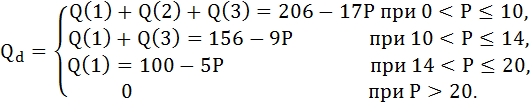
б) Так как точка P=12 находится в промежутке [10;14], то эластичность спроса в этой точке найдём для функции

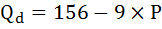
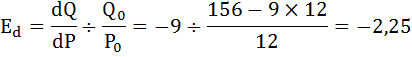
Так как абсолютное значение коэффициента эластичности больше единицы, следовательно спрос эластичен.

Задача №5. Функция суммарного спроса

Известны данные об индивидуальном спросе:

Q(1) = 80 – 8 P при P ≤ 10 и 0 при Р > 10,

Q(2) = 50 – 10 P при P ≤ 5 и 0 при Р > 5,

Q(3) = 32 – 4 P при P ≤ 8 и 0 при Р > 8.

а) Выведите уравнение кривой спроса аналитически.

б) Получите формулу эластичности по абсолютной величине в зависимости от цены.

Решение:

а) Для определения функции суммарного спроса при каждом возможном уровне цены необходимо сложить величины функций индивидуального спроса отдельных покупателей.

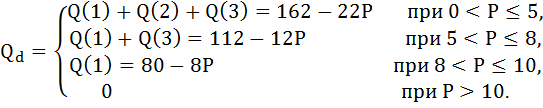
Формула эластичности для непрерывной функции выглядит следующим образом:

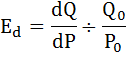
Тогда эластичность для каждой функции спроса по абсолютной величине будет равна:

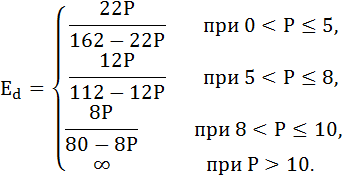
Задача №6. Расчёт дуговой эластичности

Является ли спрос на товар эластичным, если известно:

Цена, руб.	Объём спроса
3500	500
4000	440

Решение:

При значительных колебаниях цены (более 10%) рекомендуется использовать коэффициент дуговой эластичности:

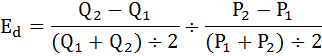
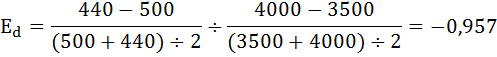
Так как:

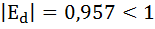
значит спрос на товар не эластичен.

Задача №7. Расчёт дуговой эластичности

Является ли спрос на товар эластичным, если известно:

Цена, руб.	Величина спроса	Объём продаж
500	300	150
700	240	220

Решение:

Чтобы ответить на вопрос задачи необходимо рассчитать коэффициент дуговой эластичности по формуле:

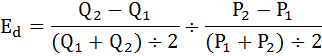
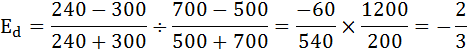
Так как:

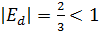
следовательно спрос на товар не эластичен.

Задача №8. Расчёт точечной эластичности

Определить точечную эластичность спроса, если при снижении цены на 10 % выручка увеличилась на 8 %.

Решение:

Пусть P– первоначальная цена до её снижения, а Q– величина спроса до снижения цены.

Тогда выручка будет равна:

PQ.

Из условия задачи известно, что цена снизилась на 10%, запишем это как:

ΔP / P = -0,1

А выручка увеличилась на 8%, то есть стала равна:

1,08PQ

По-другому выручку после изменения можно записать как:

0,9P(Q + ΔQ)

Приравняв два последних выражения, получим уравнение:

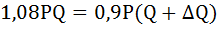
Разделим обе части уравнения на PQ

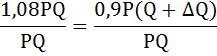
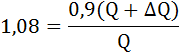
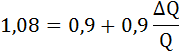
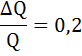
Рассчитаем точечную эластичность спроса по формуле

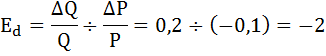
Так как коэффициент точечной эластичности по абсолютной величине больше единицы, следовательно спрос эластичен.

Задача №9. Расчёт точечной эластичности

Определить точечную эластичность спроса на товар, если уменьшение цены на 5 % привело к снижению выручки на 2 %.

Решение:

Пусть P– первоначальная цена до её уменьшения,

а Q– величина спроса до уменьшения цены.

Тогда выручка будет равна PQ.

Из условия задачи известно, что цена снизилась на 5%, запишем это как:

ΔP / P = -0,05

А выручка снизилась на 2%, то есть стала равна:

0,98PQ

По-другому выручку после изменения можно записать как:

0,95P(Q+ΔQ)

Приравняв два последних выражения, получим уравнение:

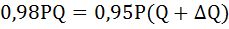
Разделим обе части уравнения на PQ

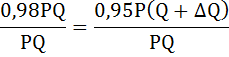
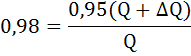
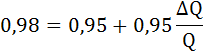
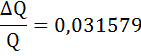
Рассчитаем точечную эластичность спроса по формуле:

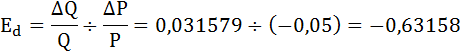
Так как коэффициент точечной эластичности спроса по абсолютной величине меньше единицы, следовательно, спрос неэластичен.

Задача №10. Расчёт первоначального объёма рыночного спроса

Цена за товар выросла с 30 до 33 рублей. Точечная эластичность спроса на него при цене 30 руб. равна (-2). Каков был первоначальный объём рыночного спроса на этот товар, если после повышения цены он составил 1200 единиц.

Решение:

Точечная эластичность спроса рассчитывается по формуле:

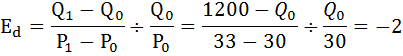
Отсюда:

.

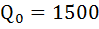
Примеры решений задач: спрос и предложение

В этом разделе вы найдете подробно решенные задачи на тему спроса, предложения, рыночного равновесия и его колебаний, эластичности и т.п.

Эластичность: задачи с решениями

Задача 1. Доход мистера Z увеличился на 3%, а величина спроса при той же цене выросла на 9%. Определить эластичность спроса по доходу.

Задача 2. Оценка спроса тремя покупателями А, Б и В выражается следующими данными:
Покупатель Цена единицы товара, ден. ед.
1000 1100 1200 1300 1400 1500
А 15 15 14 14 13 13
Б 10 10 9 8 5 0
В 12 10 8 6 4 2
Определить коэффициент эластичности рыночного спроса по цене в интервале от 1300 до 1400. Эластичен ли спрос?

Задача 3. Цена на товар выросла с 20 до 23 ден. ед. Коэффициент точечной эластичности спроса по цене равен (-2). Найти первоначальный объем рыночного спроса на товар, если после повышения цены он составлял 1200 штук.

Задача 4. К какой категории относят товар, если известно, что при среднем доходе покупателя 2300 ден. ед. объем индивидуального спроса на товар 5 ед., а при доходе 2500 ден. ед. – 6 ед.?

Задача 5. Коэффициент эластичности спроса по цене равен 1,5. Объем спроса на начало периода составляет 200 тыс. ед., цена за единицу товара равна 50 руб. Определите, насколько изменится объем спроса и объем выручки фирмы, если:
А) цена снизится на 5%;
Б) цена возрастет на 12%.
Определите тип эластичности спроса.

Задача 6. Вы знаете, что кривая спроса линейна. По текущей цене 3 за единицу товара вы продаете 60 000 единиц товара в год. Ваш начальник предлагает увеличить цену до 3.2. Вы знаете, что эластичность спроса по цене в этой точке = –2.5. Сколько товаров вы продадите по новой цене? Если ваша маржа была 1, а станет при новой цене 1.2, целесообразно ли повышать цену?

Задача 7. Компания решила снизить цену на 10%. Без учета реакции конкурентов ожидается, что объем продаж вырастет на 25%. Но компания ожидает, что после такого снижения цены конкурент снизит цену на 5%. Из-за этого компания потеряет 3,5% ожидаемого по новой цене объема продаж. Рассчитайте ожидаемое увеличение объема продаж и показатели, перечисленные ниже.
Собственная эластичность =
Эластичность реакции конкурентов =
Перекрестная эластичность =
Остаточная эластичность =
Ожидаемый рост объема продаж =

Задача 8. При цене продукта Р1 = 50 денежных единиц объем его предложения составил 100 единиц. При снижении цены до Р2 = 40 денежных единиц объем предложения сократился до 80 единиц. Рассчитайте коэффициент эластичности предложения.

Задача 9. Для функции спроса $QD=200 – 4P$ определить:
а) ценовую эластичность спроса при цене P=10;
б) ценовую эластичность спроса при росте цены с 10 до 12;
в) при какой цене эластичность данной функции спроса равна –4

Задача 10. Эластичность спроса по цене на картофель – 0,3, на кефир – 1,0, на мебель – 1,2. Кто больше пострадает от введения косвенного налога: производители или потребители? Ответ проиллюстрировать графиком.

Задача 11. Функция спроса задаётся формулой $C=45 D^{0,3}P^{-0,1}$, где $C$ – товар, $D$ – доход, $Р$ – цена товара.
Найти:
a) Предельный спрос по доходу и цене при D=70, Р=25.
b) Коэффициенты эластичности спроса по доходу и цене и объяснить их экономический смысл для полученных значений.

Задача 12. Дана функция спроса в виде $Y=10.130 e^{-3.130p}$. Цена товара $p_0=0.2$ ден. ед. Предполагается увеличить цену до $p_1 = 0.25$ ден. ед. Рассчитать абсолютные и относительные приращения результата и фактора, средние и мгновенные скорости изменения объёма продаж, эластичность. Дать экономическую интерпретацию каждой рассчитанной характеристике, а также записать их размерности (считаем, что объём продаж измеряется в тыс. шт.).

Задача 13. Вычислить дуговую эластичность предложения по двум точкам: величина предложения увеличивается со 120 до 160 штук при росте цены с 4 до 10 ден. ед.

Равновесная цена: задачи с решениями

Задача 14. Закон спроса на йогурт описывается формулой $Qd = 400 – Р$, закон предложения – формулой $Qs = 2Р – 200$. Как изменится рыночное равновесие и выручка производителей йогурта, если государство станет субсидировать производителей из расчета 30 ден. ед. за штуку?

Задача 15. Спрос и предложение на муку описываются уравнениями: $Qd = 2500 – 100Р$, $Qs = -1000 + 250Р$. В целях социальной защиты мэрия установила цену 6 ден. ед. за килограмм муки. Охарактеризуйте последствия данного решения для рынка. Изобразите графически первоначальное и последующее состояния рынка.

Задача 16. Кривая рыночного спроса на сахар описывается уравнением $Qd = 200 – 4Р$, кривая предложения – уравнением $Qs = Р – 150$. На сколько процентов вырастет рыночная цена, если величина спроса на сахар при любом уровне цены увеличится на 40 тонн?

Задача 17. Р – рыночная цена товара. Функции спроса и предложения заданы аналитически: Qs = 1500+2.4P ; Qd=35000-2.9P
Определить условия рыночного равновесия

Задача 18. Ситуация на рынке такова, что при цене в 10 ден. ед. покупатели готовы были купить 40 штук гвоздик, а продавцы согласны были продать 10 штук гвоздик; по цене 20 ден. ед. — соответственно 30 и 20 штук; по цене 30 ден. ед. — 20 и 30 штук и, наконец, по цене в 40 ден. ед. – 10 и 40 штук. Определить равновесную цену и объем продаж.

Задача 19. Спрос и предложение на рынке товара X описываются уравнениями $q = 200 – 2р$, $q = -10 + р$. На каком уровне установится равновесная цена товара X, если будет введена дотация производителям X в размере 90 руб. за каждую проданную единицу товара? Чему равен объем дотационных выплат из бюджета? Дать графическую иллюстрацию.

Задача 20. На рынке две группы покупателей с функциями спроса $P_{D1} = 20 – Q$, $P_{D2} = 4 -Q/4$. Определить равновесную цену и количество товара и проиллюстрировать решение графически, если предложение задано уравнением $Q_S = 4P$.

Задача 21. Функции спроса и предложения на рынке $QD = 600 – 25P$, $QS= 100 + 100P$. Пусть введен потоварный налог, уплачиваемый производителем, в 2,5 денежных единицы на единицу товара. Определить
равновесную цену и равновесное количество товара после введения налога,
изменение излишков потребителя и производителя,
сумму налоговых выплат, получаемую государством и чистые потери общества.
Какую часть налога производитель будет перекладывать на потребителя? Решение проиллюстрировать графиком.

Задача 22. Функция спроса и предложения на рюкзаки в месяц следующие: $Qd = 600-2Р$, $Qs=300+4Р$
1. Каковы равновесная цена и равновесный объем продаж?
2. Предположим, что установлен потолок цены рюкзака 10 рублей. Какая ситуация будет на рынке? Подсчитайте сумму дефицита или излишки.
3. Представьте графически данную ситуацию.

Задача 23. Опытным путем установлены функции спроса q(p) и предложения q, S – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени: p – цена товара. Построить на одном чертеже графики q(p) и S(p).
Найти: а) равновесную цену, т.е. цену, при которой спрос и предложение уравновешиваются; б) эластичность спроса и предложения для этой цены; в) изменение дохода при увеличении цены на 5 % от равновесной.

$$q = frac{p+10}{p+3}, S=p+0,4.$$

Спрос и предложение в таблицах: задачи с решениями

Задача 24. В таблице представлены данные об объеме спроса и предложения на рынке данного товара при различных ценах.
Объем, ед. Цена, р.
5 10 15 20 25 30 35
Спроса 68 53 42 34 27 22 19
Предложения 15 29 42 52 59 64 68
Ответьте на следующие вопросы:
а) чему равна равновесная цена на рынке данного товара?
б) каково равновесное количество продукта на рынке?
в) что изменится на рынке, если цена установится на уровне 5 р.?
г) какие изменения произойдут при цене 30 р.?

Задача 25. Условия: в таблице представлены данные по рынку консервированного зеленого горошка.
Цена (рубли) Объем спроса (млн. банок в год) Объем предложения (млн. банок в год)
8 70 10
16 60 30
24 50 50
32 40 70
40 30 90
Найти и выполнить:
1) по табличным данным построить кривые спроса и предложения
2) определить условие равновесия рынка.
3) Дать качественную и количественную характеристики рынка при:
– рыночной цене =8 руб.?
– рыночной цене =32 руб.?
4) Потребление зеленого горошка повысилось на 15 млн. банок в год при каждом уровне цен. О чем это свидетельствует и каковы будут условия равновесия рынка?

Задача 26. На рынке действуют три потребителя X,Y,Z, поведение которых охарактеризовано в таблице.
Цена (руб.) Количественный объем покупок (шт.)
Потребитель X Потребитель Y Потребитель Z
10 0 0 0
9 0 3 1
8 0 5 5
7 1 7 8
6 2 9 11
5 4 12 12
4 6 15 15
3 10 18 18
2 15 21 20
1 21 24 23
0 25 25 25
1) Построить индивидуальные графики спроса.
2) Построить общую кривую спроса.
3) Рассчитать динамику общего и предельного дохода на рынке.
4) Построить новую общую кривую спроса, предположив, что количественный объем спроса на товар со стороны потребителей Х и Y удвоится при любом уровне цен, а сторон потребителя Z одновременно сократится вдвое.
5) Рассчитать все параметры рыночного спроса при новых условиях. Построить индивидуальные графики спроса.
6) Построить общую кривую спроса.
7) Рассчитать динамику общего и предельного дохода на рынке.

Задача 27. Условия: рынок перфораторов характеризуется следующими данными:
Цена (руб.)
1000 2000 3000 4000 5000 6000 7000
Объем тыс. шт.
Спроса 32 28 24 20 16 12 8
Предложения 4 6 10 13 16 19 22
Задание:
1) построить графики кривых спроса и предложения, используя табличные данные;
2) Определить равновесную цену на рынке перфораторов;
3) Каков равновесный объем купли/продажи перфораторов;
4) Состояние рынка при цене перфоратора 3000 руб.;
5) Состояние рынка при цене перфоратора 6000 руб

Может быть интересно:

Точечная и дуговая эластичность спроса

Существуют два
метода вычисления коэффициента
эластичности: 1)
определение точечной и 2) дуговой
эластичности.

Точечная эластичность–
эластичность, измеренная в одной точке
кривой спроса или предложения; является
постоянной величиной повсюду, вдоль
линии спроса и предложения. Точечная
эластичность – точный показатель
чувствительности спроса или предложения
к изменению цен, доходов и т.д.

Точечная эластичность применяется при
малых приращениях (обычно до 5%) или в
абстрактных задачах, где задаются
непрерывные функции спроса:

Точечная эластичность (point elasticity) может
быть определена, если провести касательную
к кривой спроса. Наклон кривой спроса
в любой своей точке, как известно,
определяется значением тангенса угла
касательной с осью X (рис. 1).

Рис. 6. Точечная эластичность

Значение точечной эластичности обратно
пропорционально тангенсу угла наклона.

Дуговая эластичность(arc
elasticity) – примерная степень реакции
спроса или предложения на изменение
цены, дохода и других факторов.

Дуговая эластичность спроса –  показатель
средней реакции спроса на изменение
цены товара, выраженной кривой спроса
на некотором отрезке : 

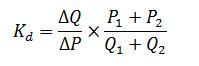
Рис. 7. Дуговая эластичность

Дуговая эластичность спроса используется
в случаях с относительно большими
изменениями цен, доходов и других
факторов (более 5%), а также, если у нас
недостаточно данных и удалось, например,
замерить две более или менее близкие
точки на кривой спроса.

Коэффициент дуговой эластичности всегда
лежит где-то (но не всегда посередине)
между двумя показателями точечной
эластичности для низкой и высокой цен.

Полезность

Потребление благ
приносит потребителю определенную
полезность.

Полезность
– это общее удовлетворение, которое
получает потребитель от потребления
данного количества блага в определенный
промежуток времени.

Каждый потребитель
имеет большой круг потребностей, но его
средства всегда ограничены. Т.е. это
бюджетное ограничение, которое
определяется величиной денежного дохода
потребителя и ценами благ. Распределение
дохода должно обеспечивать максимальную
полезность. Таким образом, потребительский
выбор – это принятие потребителем
решения о таком распределении его
бюджета, при котором структура и
количество купленных благ обеспечивали
бы ему максимальную полезность.

первый
закон Госсена.

Закон убывающей
предельной полезности говорит о том,
что при фиксированном потребительском
наборе с увеличением потребления одного
из входящих в такой набор благ предельная
полезность каждой следующей потребляемой
единицы этого блага убывает, а общая
полезность возрастает убывающими
темпами.

Это означает, что
максимальная полезность от покупки
достигается потребителем тогда, когда
имеет место равенство отношений между
предельными полезностями

(MU)
и ценами покупаемых благ (Р) покупаемых
благ:

MU(X)/Px
= MU(Y)/Py = … =
MU(Z)/Pz

Кривые безразличия

Данное
равенство (MU(X)/Px
= MU(Y)/Py
= … = MU(Z)/Pz)
является вторым
законом Госсена,
который гласит, что при оптимальном
распределении ограниченного дохода
уровень полезности, получаемый
потребителем от расходования последней
денежной единицы, одинаков для всех
покупаемых благ вне зависимости от
того, на покупку какого из благ она будет
истрачен

Кривая
безразличия (indifference
curve) показывает
различные комбинации двух экономических
благ, имеющих одинаковую полезность
для потребителя.

Кривые безразличия широко
используются неоклассической
школойпри
исследовании многих микроэкономических
процессов, связанных с проблемой выбора.
При помощи кривых безразличия можно
показатьравновесие
потребителя.

Рис.8. Кривая безразличия

На графике на одной оси
отложено число единиц товара X,
на другой — число единиц товара Y.
Соединив точки А, В, С, D получим
кривую U₁,
каждая точка которой показывает возможные
комбинации единиц товара X и
товара Y,
дающие одинаковое удовлетворение.
Кривая U₁ называется
кривой безразличия, которая указывает,
что потребитель безразличен к этим трем
наборам продуктов, т.е. потребитель не
чувствует себя ни лучше, ни хуже,
отказавшись от 2 единиц товара X и
получив 1 единицу товара Y при
перемещении от набора А к
набору В.
Точно так же потребитель одинаково
ранжирует А и D.

Кривые безразличия обладают следующими
свойствами.

1. Кривая безразличия,
   расположенная справа и выше другой
   кривой, является более предпочтительной
   для потребителя.

1. Кривые безразличия
   всегда имеют отрицательный наклон, ибо
   рационально действующие потребители
   будут предпочитать большее количество
   любого набора меньшему.

1. Кривые
   безразличия имеют вогнутую форму,
   обусловленную уменьшающимися предельными
   нормами замещения.

2. Кривые безразличия
   никогда не пересекаются и обычно
   показывают уменьшающиеся предельные
   нормы замещения одного блага на другое.

3. Наборы благ на
   кривых, более удаленных от начала
   координат, предпочтительнее наборам
   благ, расположенным на менее удаленных
   от координат кривых.

Набор кривых безразличия
образуюткарту
кривых безразличия,которая используется для
описания предпочтения человека по всем
наборам товаров.

Совокупность точек оптимума
потребителя, построенных для изменяющегося
дохода и неизменных цен называется кривой
доход-потребление.

Рис.9 Кривые безразличия

Данная кривая позволяет построить
графическое изображение зависимости
реального потребления (спроса) от дохода
потребителя.

Аналогичным образом можно проанализировать
влияние изменения цен на оптимальный
выбор потребителя, предположив
неизменность дохода и цены одного из
товаров.

Эффект
замены –
это реакция потребителя на изменение
цены блага, выражающаяся в изменении
потребительского набора путем замещение
в нем блага, относительная цена на
которое выросла, благом, относительная
цена которого снизилась. Увеличение
спроса на благо Х является следствием
перераспределения расходов потребителя
в пользу этого блага за счет сокращения
расходов на покупку блага У, в чем и
суть замены.

Эффект
дохода –
это реакция потребителя на изменение
цены блага, выражающаяся в изменении
спроса на него , которое вызвано
изменением реального дохода потребителя.

Этот эффект
возникает в силу того, что изменение
цены блага приводит к изменению
бюджетного поля потребителя, расширяя
возможности выбора при снижении цены
и сокращая при ее росте.

В
редких случаях величина эффекта дохода
может превышать величину эффекта замены.
Кривая спроса на такое благо имеет
положительный наклон. Закон спроса в
таком случае не действует, так как при
росте цены блага наблюдается увеличение
спроса на него. Благо, характеризующееся
такой особенностью, определяют как
товар Гиффена.

Издержки

Постоянные
издержки
не зависят от объема производства. Они
определяются тем, что стоимость
оборудования должна быть оплачена даже
если предприятие остановится. К постоянным
издержкам относятся плата по облигационным
займам, рентные платежи, часть отчисления
на амортизацию зданий, страховые взносы,
зарплату управленческому персоналу,
оплата охраны и т.д.

Переменные
издержки
непосредственно зависят от количества
произведенной продукции. К ним относятся
затраты на сырье, материалы, электроэнергию
зарплата работникам, транспортные
расходы и т.д. Сумма постоянных и
переменных издержек составляет валовые
издержки. Средние
издержки –
это величина издержек на единицу
продукции. Средние
переменные
и средние
постоянные.
Предельные
издержки
– это издержки на производство каждой
дополнительной единицы продукции
относительно объема производства.

Трансакционные
издержки –
это издержки, связанные с обменом и
защитой правомочий.

Увеличение
издержек, связанных с приведением в
действие институтов, развитием
организаций, расширением многообразия
форм и правомочий реализации собственности,
выявило проблему трансакционных
издержек.

В узком смысле
под трансакционными издержками
подразумевают время и усилия, затрачиваемые
на совершение сделки. Величина издержек
зависит от числа участников, их
месторасположения относительно друга.
В эк. литературе часто их определяют
так:

Это издержки сбора
и обработки информации, издержки
проведения переговоров и принятия
решений, издержки контроля и юридической
защиты выполнения контрактов. Общим
для всех определения является то, что
это издержки, прямо не связанные с
процессом производства.

Делятся на:

– издержки поиска
информации

– издержки ведения
переговоров

– издержки измерения
количества и качества вступающих в
обмен товаров и услуг

– издержки
спецификации и защиты прав собственности

Издержки защиты
от оппортунистического поведения
(недобросовестное поведение, направленное
на получение односторонних выгод).

В условиях
трансформации учитывают трансакционные
издержки, направленные на ликвидацию
старых институтов и создание новых.

Прибыль

Это превышение
доходов от продажи товаров и услуг над
затратами на производство и продажу
этих товаров. Это один из наиболее важных
показателей финансовых результатов
хозяйственной деятельности предприятия
и предпринимателей. Прибыль исчисляется
как разность между выручкой от реализации
и суммой затрат факторов производства
на эту деятельность в денежном выражении.

Выручка

Денежные средства,
полученные (вырученные) предприятием,
фирмой, предпринимателем от продажи
товаров и услуг, выручка от реализации.
(Если продано 5 единиц товара по цене 5
рублей, то выручка равняется 5х5=25 рублей)

Типы рыночных
структур

Конкуренция –
это борьба предпринимателей за наиболее
выгодные условия производства и сбыта
товаров в целях получения максимальной
прибыли. Конкуренция – это способ
эффективного распределения ограниченных
ресурсов общества. Конкуренция выполняет
стимулирующую функцию. Посредством
конкуренции происходит распределение
доходов в соответствии с вкладом и
эффективностью использования факторов
производства.

Методы конкурентной борьбы:

–  ценовая
– соперничество
при помощи маневрирования ценами (война
цен, лидерство в ценах, ценовые льготы
оплаты);

–  неценовая
– повышение
технического уровня качества продукции,
овладение передовыми технологиями,
послепродажное обслуживание, реклама).

Конкуренция выполняет
следующие функции:

1)  Регулирующая
функция –
проявляется в воздействии на производство
товаров, чтобы оно осуществлялось в
соответствии со спросом, а также в
ограничении рыночной власти.

2)  Инновационная
функция – необходимость
инновации как средство повышения
экономической эффективности.

В зависимости от соотношения конкуренции
различают два типа рынка: совершенной
и несовершенной конкуренции.

Совершенная конкуренция
– вид
конкуренции, осуществляемой между
множеством продавцов однородной
продукции при свободном ценообразовании.

Основные черты рынка совершенной
конкуренции:

–  значительное число продавцов и
покупателей на конкретном рынке;

–  объемы производства и предложения
отдельного производителя составляет
незначительную долю, поэтому отдельная
фирма не может повлиять на цену;

–  продукция однородная, стандартная;

–  все участники рынка обладают
одинаковой информацией о положении цен
на рынке;

–  фирмы могут свободно выходить из
одной отрасли и входить в другую;

Совершенная конкуренция была характерна
для экономики развитых стран XIX в., в
настоящее время это явление редкое. В
наибольшей степени к такому рынку можно
отнести рынки сельскохозяйственных
продуктов, биржи, валютные, фондовые
рынки (рынок зерна, ценных бумаг, валюты).

Несовершенная конкуренция
– это
экономическая ситуация, в которой не
соблюдается хотя бы один из признаков
совершенной конкуренции, фирма в условиях
несовершенной конкуренции обладает
определенной властью над ценой. К ней
относятся следующие модели рынка: чистая
монополия, монополистическая конкуренция,
олигополия.

Рынок, на котором
отсутствует хотя бы один признак
совершенной конкуренции, называется
рынком несовершенной конкуренции. На
таком рынке подавляющая часть продукции
предлагается ограниченным числом фирм,
которые, занимая господствующее положение
на рынке, могут влиять на условия
реализации продукции и, прежде всего,
на цены.

    Существует три
основные структуры (модели) рынка
несовершенной конкуренции:
– чистая
монополия;
– олигополия;
– монополистическая
конкуренция.
    Чистая
монополия –
это рынок, на котором функционирует
один продавец. В условиях чистой монополии
отрасль состоит из одной фирмы, т.е.
понятие фирма и отрасль совпадают.
Вхождение в отрасль для других фирм
блокировано. Препятствием для вхождения
в отрасль могут быть:
– низкие
издержки  производства крупной
фирмы,  монополизировавшей рынок
(эффект масштаба);
– наличие
государственных патентов и
лицензий;
– исключительные права
на важнейшие источники сырья;
– предоставление
правительством одной фирме статуса
единственного продавца (транспортные
услуги, связь, газоснабжение).
   
Условием существования чистой монополии
является уникальность предлагаемой
продукции, отсутствие близких заменителей.
Чистая монополия в масштабах национального
хозяйства – явление редкое, однако она
достаточно широко представлена на
местных рынках. Практически в любом
городе один продавец продает электроэнергию,
обеспечивает водоснабжение, оказывает
телеграфные услуги, обеспечивает
транспортные перевозки и т.д. В связи с
тем, что чистая монополия не просто
ограничивает, а фактически ликвидирует
конкуренцию, государство в отношении
чистых монополий проводит антимонопольную
политику.
  Существуют различные
показатели, с помощью которых можно
измерить силу рыночных факторов
(монопольной власти): Коэффициент
концентрации; Индекс четырех фирм;
Индекс Херфиндаля – Хиршмана; Индекс
Линда; Индекс Лернера .

L=
P-MC
/ P

Один из способов определения
монопольной власти был предложен в 1934
г. А. Лернером и получил название показателя
монопольной власти Лернера (L).
Он вычисляется по формуле, представленной
на рисунке 1. Здесь P –
цена, MC –
предельные издержки. Численное значение
коэффициента Лернера всегда находится
между 0 и 1. Для совершенно конкурентной
фирмы Р=МСи L=0.
Чем больше L,
тем больше монопольная власть.

HHI
= S²₁
+S²₂
+S²₃
+… + S²
_n

Еще один метод оценки степени
монопольной власти связан с использованием
«индекса концентрации рынка», названного
по имени его авторов «индексом
Херфиндаля – Хиршмана».
Индекс Херфиндаля – Хиршмана ННI определяется
как сумма квадратов долей всех фирм,
действующих на рынке, где S1 –
доля рынка фирмы, обеспечивающей
наибольший объем поставок, S2 –
доля рынка следующей по величине фирмы 

  Олигополия (от
греческого олиго — немногие и полео –
продаю) – это рынок, на котором доминирует
несколько крупных фирм. (Так, например,
в США имеется 9 фирм-продавцов жевательной
резинки, на долю которых приходится 95%
годовых продаж.) Четкого количественного
критерия олигополии в виде числа фирм
нет, но обычно оно колеблется от трех
до десяти. Олигополия, состоящая из 3-4
фирм, называется “жесткой”; состоящая
из 4—9 фирм, на долю которых приходится
70-80% рынка, называется “аморфной”.
Олигополия может существовать на рынке
стандарти-зированной продукции (нефть,
цемент) или на рынке дифференцированной
продукции (автомобили, бытовая
техника).
Различают олигополию
сбалансированную (несколько фирм
одинакового размера) и асимметричную
(один продавец-лидер и ряд небольших
продавцов).
Фирмы, функционирующие на
олигополистическом рынке, получают
высокие прибыли потому что, как и в
случае чистой монополии, вхождение в
отрасль для фирм-аутсайдеров затруднено.
Характерной особенностью олигополистического
рынка является взаимозависимость фирм
– любой из олигополистов находится под
существенным воздействием поведения
остальных фирм и вынужден учитывать
эту зависимость.

    Результаты
функционирования фирмы-олигополиста
зависят не только от ее собствен¬ной
политики, но и от решений ее конкурентов.
Если одна фирма (“Кока-кола”) снизит
цену на свою продукцию, то другая фирма,
функционирующая в этой отрасли
(“Пепси-кола”), будет вынуждена
также снизить цену своей продукции.
Ценовая конкуренция среди олигополистов
носит разорительный характер, поэтому
фирмы стремятся к соглашению о ценах,
смещая конкуренцию в направлении
качества, рекламы, индивидуализации
продукции.
    Монополистическая
конкуренция.
На рынке такого типа имеется множество
продавцов, продающих однотипную, но
дифференцированную продукцию (например,
джинсы, зубная паста), в отношении которой
продавец ведет себя как монополист.
Продавцы самостоятельно определяют
цену на свои товары, объемы продаж. Но
поскольку продавцов аналогичной
продукции много и объем продаж отдельной
фирмой относительно невелик, постольку
контроль фирмы над ценами ограничен.
Основные методы конкуренции – товарные
знаки, реклама, выделяющие различия
товаров. Вход на рынок монополистической
конкуренции относительно свободен.
   
Внешне монополистическая конкуренция
схожа с совершенной конкуренцией, но
наличие хотя ограниченной, но монопольной
власти ведет к тому, что производство,
осуществляется с издержками более
высокими, чем в условиях совершенной
конкуренции. Однако широкий выбор марок,
видов, стилей, качества продукции
позволяет лучше удовлетворять
разнообразные потребности покупателей,
компенсируя тем самым потери общества
от более высоких издержек производства.

Рынок труда и
заработная плата

Рынок
труда —
сфера формирования спроса и предложения
на рабочую силу. Через него осуществляется
продажа рабочей силы на определенный
срок.

Точечная эластичность спроса – это отношение процентного изменения количества потребляемого товара к процентному изменению его цены, рассчитанному в определенной точке кривой спроса.

Точечная эластичность спроса на самом деле не является новым типом эластичности. Это всего лишь один из двух методов расчета эластичности, другой из которых является дуговой эластичностью спроса.

Все основные показатели эластичности, то есть (ценовая) эластичность предложения, эластичность дохода, перекрестная эластичность спроса/предложения, имеют свои варианты точечной эластичности и дуговой эластичности, хотя метод точечной эластичности является более простым и популярным методом.

Пример

Чтобы понять разницу между точечной эластичностью и дуговой эластичностью, давайте рассмотрим гипотетический рынок общественного транспорта.

Предположим, что если стоимость поездки изменяется от $2 (P₀) до $3 (P₁), то спрос на пассажиров в день падает с 0,5 млн (Q₀) до 0,4 млн (Q₁).

Эластичность спроса определяется как процентное изменение количества потребляемых товаров, деленное на процентное изменение цены:

E_d = ΔQ% / ΔP%

Процентные соотношения чаще всего определяются по отношению к P₀ и Q₀, и это дает нам ценовую эластичность спроса на общественный транспорт -0,4:

E_d = ΔQ% / ΔP% = [(0.5 – 0.4) / 0.5] / [($2 – $3) / $2] =

-0.1 × ($2 / 0.5) = -0.4

Теперь представьте себе, что движение цены противоположно, то есть если цена снижается с $3 до $2, а спрос на пассажиров увеличивается. В этом случае расчет эластичности спроса будет выглядеть следующим образом:

E_d = ΔQ% / ΔP% = [(0.5 – 0.4) / 0.4] / [($2 – $3) / $3] =

-0.1 × ($3 / 0.4) = -0.75

Просто использование другой отправной точки для движения цены привело к примерно 100 % – ному увеличению эластичности, что звучит неправильно.

Сама формула ценовой эластичности показывает, что эластичность спроса в точке кривой зависит от отношения изменения количества спроса к изменению цены и от отношения начальной цены и количества в точке кривой, по которой мы хотим рассчитать эластичность.

Если разница между P₀ и P₁ или Q₀ и Q₁ высока, то наша оценка ценовой эластичности не будет точной.

Упругость дуги

Одним из способов решения проблемы чувствительности точечной эластичности к начальной цене и количеству является расчет эластичности дуги.

Дуговая эластичность спроса рассчитывается путем нахождения процента, основанного на среднем значении начальной и конечной цен и количеств. Средняя ценовая эластичность спроса на общественный транспорт на рынке составит -0,55:

E_d = {(Q₁ – Q₀) / [(Q₁ + Q₀)/2]} / {(P₁ – P₀) / [(P₁ + P₀)/2]} =

{(0.4 – 0.5) / [(0.4 + 0.5)/2]} / {($3 – $2) / [($3 + $2)/2]} =

(-0.1 / 0.45) / ($1 / $2.5) = -0.55

Метод расчета упругости дуги также называется методом средней точки.

Там, где изменение цены или требуемого количества является большим, метод дуговой эластичности является улучшением точечного метода расчета. Однако там, где изменение невелико, предпочтительна точечная эластичность спроса.

Точечная эластичность спроса также может быть рассчитана для любой точки на кривой спроса с помощью небольшого вычисления следующим образом:

Ed = (dQ/dP) × (P/Q),

где dQ/dP – первая производная кривой спроса/функции.

Уравнение измеряет изменение количества, необходимого для очень малого изменения цены при цене P. Поскольку значение dQ/dP может быть вычислено в точной точке кривой, приведенное выше уравнение дает лучшую оценку эластичности.

Точечная эластичность

Данный вид эластичности является одним из методов расчета эластичности. Такой расчет предполагает, что на графике спрос имеет вид прямой под влиянием цены. А это значит, что спрос будет изменяться пропорционально ценам на какое-либо благо.

Такая величина измеряется в одной конкретной точке. Данный показатель является более точным, а величина постоянна в конкретной точке.

В задачах такой вариант используется тогда, когда нужно узнать чувствительность спроса к цене на каком-то определенном участке спроса при конкретной цене или объеме спроса. В таком случае принимается точный показатель, который рассчитывается с помощью точечного варианта эластичности. В таком случае часто сама функция спроса не дается или неизвестна.

Формула для исчисления следующая:

производная функции спроса • (цена / объем спроса)

или:

изменение спроса / изменение цены • (цена / объем спроса)

Дуговая эластичность

Данный расчет является приблизительным, так как в расчете используются средние значения. От первого вида расчета расчет дуговой эластичности отличается тем, что результат вычислений будет являться относительным к среднему. При этом кривая спроса примет вид дуги.

Данный метод расчета необходим в том случае, если нужно найти приближенную эластичность в целом за период без учета локальных изменений. Например, найти, как изменялся спрос, если цены в начальном периоде были 20 условных единиц, а стали 10. Иногда нужно определить не точную величину в данной точке, а величину в среднем выражении к ценам в периоде.

«Точечная и дуговая эластичность спроса» 👇

Это происходит потому, что при больших изменениях начального и конечного значения параметра сложно найти взаимосвязь, поэтому используются средние и приближенная величина эластичности, рассчитанная с помощью дуговой эластичности.

Формула для исчисления следующая:

((новый объем спроса – предыдущий объем спроса) / (новая цена – предыдущая цена)) • ((новая цена + предыдущая цена) / (новый объем спроса + предыдущий объем спроса))

В таком случае, если индикатор эластичности находится на уровне больше 1, то спрос эластичный ( то есть чувствительный к изменению цен), а если индикатор от 0 до 1, то спрос буде неэластичным.

Примеры расчетов

Рассмотрим пример задачи на точечную эластичность. Допустим, экономистами фирмы выявлена следующая функция спроса на рынке: $Q(p) = 100 – 2P$. Найдем ту эластичность, которая образуется при установлении цены в 20 рублей.

Тогда для решения найдем производную от функции: $-2$.

Видно, что знак отрицательный, а это говорит о выполнении закона спроса.

Далее для решения найдем второе значение спроса при значении цены в 20 рублей. То есть подставляем значение 20 в функцию спроса. Итак, $Q(20) = 60$.

Далее получившиеся данные нужно поставить в формулу точечной эластичности.

Тогда получим следующее: -220 / 60 = -0,66 или -2/3

Так как значение рассматривается по модулю (так как нужно определить не наклон направления изменения), то рассмотрим абсолютное значение. Так как по модулю значение меньше единицы, то считается, что спрос неэластичен.