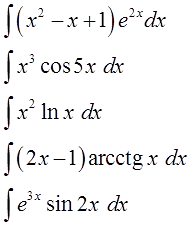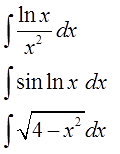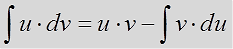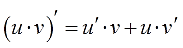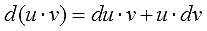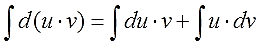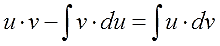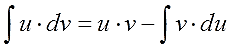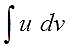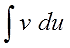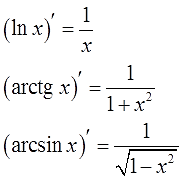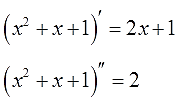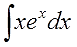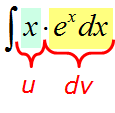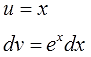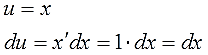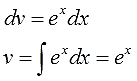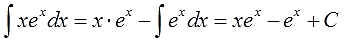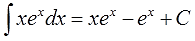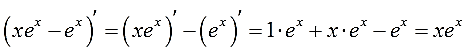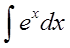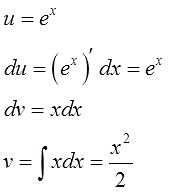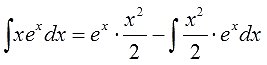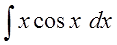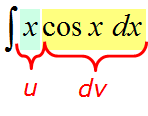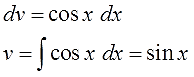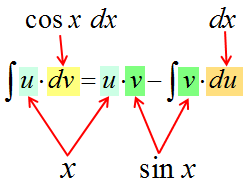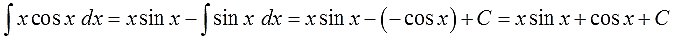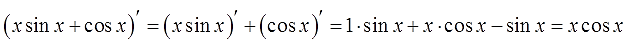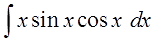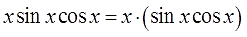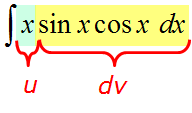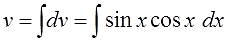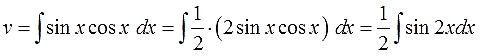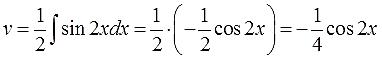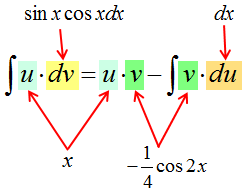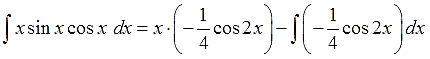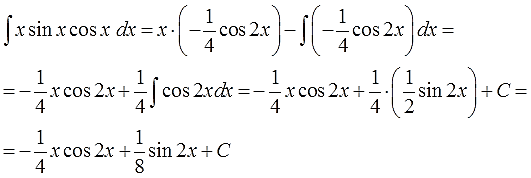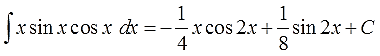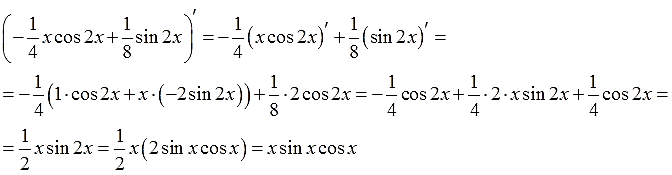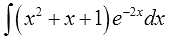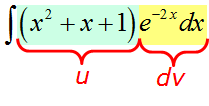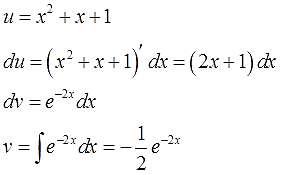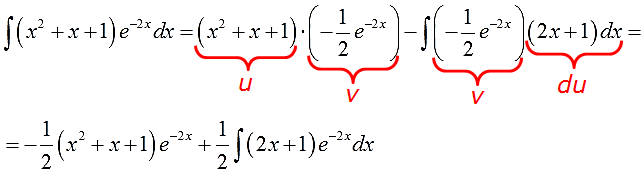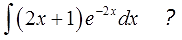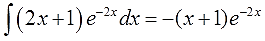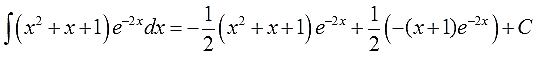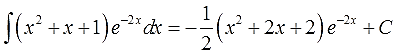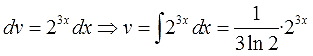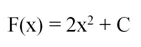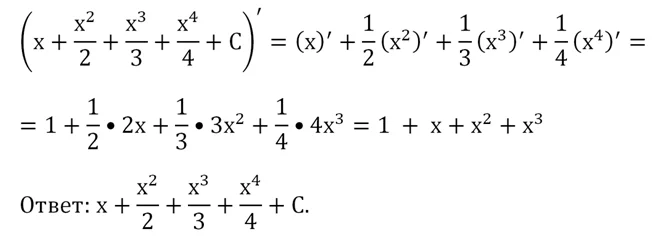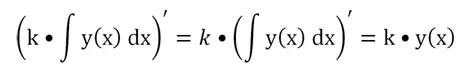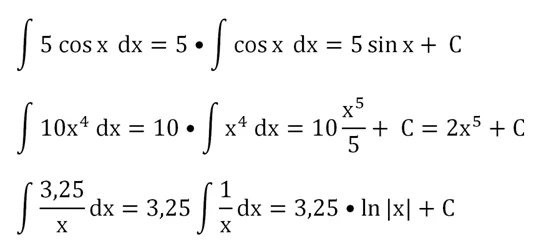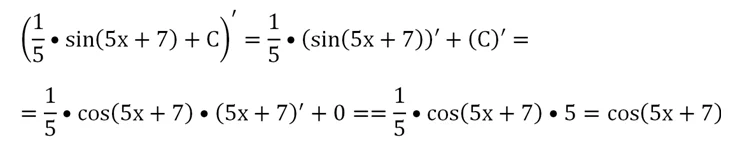Как найти первообразную частного

Первообразная функции и общий вид

20 июля 2015

Этот урок — первый из серии видео, посвященных интегрированию. В нём мы разберём, что такое первообразная функции, а также изучим элементарные приёмы вычисления этих самых первообразных.

На самом деле здесь нет ничего сложного: по существу всё сводится к понятию производной, с которым вы уже должны знакомы.:)

Сразу отмечу, что, поскольку это самый первый урок в нашей новой теме, сегодня не будет никаких сложных вычислений и формул, но то, что мы изучим сегодня, ляжет в основу гораздо более сложных выкладок и конструкций при вычислении сложных интегралов и площадей.

Кроме того, приступая к изучению интегрирования и интегралов в частности, мы неявно предполагаем, что ученик уже, как минимум, знаком к понятиям производной и имеет хотя бы элементарные навыки их вычисления. Без четкого понимания этого, делать в интегрировании совершенно нечего.

Однако здесь же кроется одна из самых частых и коварных проблем. Дело в том, что, начиная вычислять свои первые первообразные, многие ученики путают их с производными. В результате на экзаменах и самостоятельных работах допускаются глупые и обидные ошибки.

Поэтому сейчас я не буду давать четкого определения первообразной. А взамен предлагаю вам посмотреть, как она считается на простом конкретном примере.

Что такое первообразная и как она считается

Допустим, нам необходимо посчитать следующую производную:

[fleft( x right)={{x}^{3}}]

Мы знаем такую формулу:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

Считается эта производная элементарно:

[{f}’left( x right)={{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}}]

Посмотрим внимательно на полученное выражение и выразим ${{x}^{2}}$:

[{{x}^{2}}=frac{{{left( {{x}^{3}} right)}^{prime }}}{3}]

Но мы можем записать и так, согласно определению производной:

[{{x}^{2}}={{left( frac{{{x}^{3}}}{3} right)}^{prime }}]

А теперь внимание: то, что мы только что записали и есть определением первообразной. Но, чтобы записать ее правильно, нужно написать следующее:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

Аналогично запишем и такое выражение:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

Если мы обобщим это правило, то сможем вывести такую формулу:

[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]

Теперь мы можем сформулировать четкое определение.

Первообразной функции называется такая функция, производная которой равна исходной функции.

Вопросы о первообразной функции

Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:

1. Допустим, хорошо, эта формула верна. Однако в этом случае при $n=1$ у нас возникают проблемы: в знаменателе появляется «ноль», а на «ноль» делить нельзя.
2. Формула ограничивается только степенями. Как считать первообразную, например, синуса, косинуса и любой другой тригонометрии, а также констант.
3. Экзистенциальный вопрос: а всегда ли вообще можно найти первообразную? Если да, то как быть с первообразной суммы, разности, произведения и т.д.?

На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.

Решение задач со степенными функциями

Давайте попробуем посчитать такое выражение:

[{{x}^{-1}}to frac{{{x}^{-1+1}}}{-1+1}=frac{1}{0}]

Как видим, данная формула для ${{x}^{-1}}$ не работает. Возникает вопрос: а что тогда работает? Неужели мы не можем посчитать ${{x}^{-1}}$? Конечно, можем. Только давайте для начала вспомним такое:

[{{x}^{-1}}=frac{1}{x}]

Теперь подумаем: производная какой функции равна $frac{1}{x}$. Очевидно, что любой ученик, который хоть немного занимался этой темой, вспомнит, что этому выражению равна производная натурального логарифма:

[{{left( ln x right)}^{prime }}=frac{1}{x}]

Поэтому мы с уверенностью можем записать следующее:

[frac{1}{x}={{x}^{-1}}to ln x]

Эту формулу нужно знать, точно так же, как и производную степенной функции.

Итак, что нам известно на данный момент:

• Для степенной функции — ${{x}^{n}}to frac{{{x}^{n+1}}}{n+1}$
• Для константы — $=constto cdot x$
• Частный случай степенной функции — $frac{1}{x}to ln x$

Идем далее. Что нам еще может потребоваться? Конечно же, правило вычисления первообразных от суммы и от разности. Запишем так:

[fleft( x right)to Fleft( x right)]

[gleft( x right)to Gleft( x right)]

[f+gto F+G]

[f-g=F-G]

[ccdot fto ccdot Fleft( c=const right)]

А если простейшие функции мы начнем умножать и делить, как тогда посчитать первообразную произведения или частного. К сожалению, аналогии с производной произведения или частного здесь не работают. Какой-либо стандартной формулы не существует. Для некоторых случаев существуют хитрые специальные формулы — с ними мы познакомимся на будущих видеоуроках.

Однако запомните: общей формулы, аналогичной формуле для вычисления производной частного и произведения, не существует.

Решение реальных задач

Задача № 1

[fleft( x right)={{x}^{2}}+5{{x}^{4}}]

Давайте каждую из степенных функций посчитаем отдельно:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[5{{x}^{4}}to 5cdot frac{{{x}^{5}}}{5}={{x}^{5}}]

Возвращаясь к нашему выражению, мы запишем общую конструкцию:

[Fleft( x right)=frac{{{x}^{3}}}{3}+{{x}^{5}}]

Задача № 2

[fleft( x right)=frac{x+1}{x}]

Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:

[fleft( x right)=frac{x}{x}+frac{1}{x}=1+frac{1}{x}]

Мы разбили дробь на сумму двух дробей.

Посчитаем:

[Fleft( x right)=1cdot x+ln x]

[Fleft( x right)=x+ln x]

Хорошая новость состоит в том, что зная формулы вычисления первообразных, вы уже способны считать более сложные конструкции. Однако давайте пойдем дальше и расширим наши знания еще чуть-чуть. Дело в том, что многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к ${{x}^{n}}$, могут быть представлены в виде степени с рациональным показателем, а именно:

[sqrt{x}={{x}^{frac{1}{2}}}]

[sqrt[n]{x}={{x}^{frac{1}{n}}}]

[frac{1}{{{x}^{n}}}={{x}^{-n}}]

Все эти приемы можно и нужно комбинировать. Степенные выражения можно

• умножать (степени складываются);
• делить (степени вычитаются);
• умножать на константу;
• и т.д.

Решение выражений со степенью с рациональным показателем

Пример № 1

[fleft( x right)=7sqrt{x}+sqrt[4]{x}]

Посчитаем каждый корень отдельно:

[]

[sqrt{x}={{x}^{frac{1}{2}}}to frac{{{x}^{frac{1}{2}+1}}}{frac{1}{2}+1}=frac{{{x}^{frac{3}{2}}}}{frac{3}{2}}=frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[sqrt[4]{x}={{x}^{frac{1}{4}}}to frac{{{x}^{frac{1}{4}}}}{frac{1}{4}+1}=frac{{{x}^{frac{5}{4}}}}{frac{5}{4}}=frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Итого всю нашу конструкцию можно записать следующим образом:

[Fleft( x right)=7cdot frac{2cdot {{x}^{frac{3}{2}}}}{3}+frac{5cdot {{x}^{frac{5}{4}}}}{4}=frac{14cdot {{x}^{frac{3}{2}}}}{3}+frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Пример № 2

[fleft( x right)=frac{1}{sqrt{x}}-frac{1}{{{x}^{3}}}]

Запишем:

[frac{1}{sqrt{x}}={{left( sqrt{x} right)}^{-1}}={{left( {{x}^{frac{1}{2}}} right)}^{-1}}={{x}^{-frac{1}{2}}}]

Следовательно, мы получим:

[Fleft( x right)=frac{{{x}^{-frac{1}{2}+1}}}{-frac{1}{2}+1}=frac{{{x}^{frac{1}{2}}}}{frac{1}{2}}=2{{x}^{frac{1}{2}}}=2sqrt{x}]

[frac{1}{{{x}^{3}}}={{x}^{-3}}to frac{{{x}^{-3+1}}}{-3+1}=frac{{{x}^{-2}}}{-2}=-frac{1}{2{{x}^{2}}}]

Итого, собирая все в одно выражение, можно записать:

[Fleft( x right)=2sqrt{x}+frac{1}{2{{x}^{2}}}]

Пример № 3

[fleft( x right)=sqrt[4]{x}-xsqrt{x}+1]

Для начала заметим, что $sqrt[4]{x}$ мы уже считали:

[sqrt[4]{x}to frac{4{{x}^{frac{5}{4}}}}{5}]

[xsqrt{x}={{x}^{1}}cdot {{x}^{frac{1}{2}}}={{x}^{frac{3}{2}}}]

[{{x}^{frac{3}{2}}}to frac{{{x}^{frac{3}{2}+1}}}{frac{3}{2}+1}=frac{2cdot {{x}^{frac{5}{2}}}}{5}]

[1to x]

Перепишем:

[Fleft( x right)=frac{4{{x}^{frac{5}{4}}}}{5}-frac{2{{x}^{frac{5}{2}}}}{5}+x]

Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.

Решение более сложных примеров

Задача № 1

[fleft( x right)={{left( sqrt[3]{x}-2 right)}^{2}}]

Вспомним формулу квадрата разности:

[{{left( a-b right)}^{2}}={{a}^{2}}-ab+{{b}^{2}}]

Давайте перепишем нашу функцию:

[fleft( x right)=left( sqrt[3]{x} right)-2cdot sqrt[3]{x}cdot 2+4]

[fleft( x right)={{x}^{frac{2}{3}}}-4{{x}^{frac{1}{3}}}+4]

Первообразную такой функции нам сейчас предстоит найти:

[{{x}^{frac{2}{3}}}to frac{3cdot {{x}^{frac{5}{3}}}}{5}]

[{{x}^{frac{1}{3}}}to frac{3cdot {{x}^{frac{4}{3}}}}{4}]

[4to 4x]

Собираем все в общую конструкцию:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x]

Задача № 2

[fleft( x right)={{left( frac{1}{x}-2 right)}^{3}}]

В этом случае нам нужно раскрыть куб разности. Вспомним:

[{{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}cdot b+3acdot {{b}^{2}}-{{b}^{3}}]

С учетом этого факта можно записать так:

[fleft( x right)=frac{1}{{{x}^{3}}}-3cdot frac{1}{{{x}^{2}}}cdot 2+3cdot frac{1}{x}cdot 4-8]

Давайте немного преобразуем нашу функцию:

[fleft( x right)={{x}^{-3}}-6{{x}^{-2}}+12cdot {{x}^{-1}}-8]

Считаем как всегда — по каждому слагаемому отдельно:

[{{x}^{-3}}to frac{{{x}^{-2}}}{-2}]

[{{x}^{-2}}to frac{{{x}^{-1}}}{-1}]

[{{x}^{-1}}to ln x]

[8to 8x]

Запишем полученную конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x-8x]

Задача № 3

[fleft( x right)=frac{{{left( x+sqrt{x} right)}^{2}}}{x}]

Сверху у нас стоит квадрат суммы, давайте его раскроем:

[frac{{{left( x+sqrt{x} right)}^{2}}}{x}=frac{{{x}^{2}}+2xcdot sqrt{x}+{{left( sqrt{x} right)}^{2}}}{x}=]

[=frac{{{x}^{2}}}{x}+frac{2xsqrt{x}}{x}+frac{x}{x}=x+2{{x}^{frac{1}{2}}}+1]

Далее все легко:

[xto frac{{{x}^{2}}}{2}]

[{{x}^{frac{1}{2}}}to frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[1to x]

Давайте напишем итоговое решение:

[Fleft( x right)=frac{{{x}^{2}}}{x}+frac{4{{x}^{frac{3}{2}}}}{3}+x]

А теперь внимание! Очень важная вещь, с которой связана львиная доля ошибок и недопониманий. Дело в том, что до сих пор считая первообразные с помощью производных, приводя преобразования, мы не задумывались о том, чему равна производная константы. А ведь производная константы равна «нулю». А это означает, что можно записать такие варианты:

1. ${{x}^{2}}to frac{{{x}^{3}}}{3}$
2. ${{x}^{2}}to frac{{{x}^{3}}}{3}+1$
3. ${{x}^{2}}to frac{{{x}^{3}}}{3}+C$

Вот это очень важно понимать: если производная функции всегда одна и та же, то первообразных у одной и той же функции бесконечно много. Просто к нашим первообразным мы можем дописывать любые числа-константы и получать новые.

Неслучайно, в пояснении к тем задачам, которые мы только что решали, было написано «Запишите общий вид первообразных». Т.е. уже заранее предполагается, что их не одна, а целое множество. Но, на самом деле, они отличаются лишь константой $C$ в конце. Потому в наших задачах мы исправим то, что мы не дописали.

Еще раз переписываем наши конструкции:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x+C]

В таких случаях следует дописывать, что $C$ — константа — $C=const$.

Во второй нашей функции мы получим следующую конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x+C]

И последняя:

[Fleft( x right)=frac{{{x}^{2}}}{2}+frac{4{{x}^{frac{3}{2}}}}{3}+x+C]

И вот теперь мы действительно получили то, что от нас требовалось в исходном условии задачи.

Решение задач на нахождение первообразных с заданной точкой

Сейчас, когда мы знаем о константах и об особенностях записи первообразных, вполне логично возникает следующий тип задач, когда из множества всех первообразных требуется найти одну-единственную такую, которая проходила бы через заданную точку. В чем состоит эта задача?

Дело в том, что все первообразные данной функции отличаются лишь тем, что они сдвинуты по вертикали на какое-то число. А это значит, что какую бы точку на координатной плоскости мы не взяли, обязательно пройдет одна первообразная, и, причем, только одна.

Итак, задачи, которые сейчас мы будем решать, сформулированы следующем образом: не просто найти первообразную, зная формулу исходной функции, а выбрать именно такую из них, которая проходит через заданную точку, координаты которой будут даны в условии задачи.

Пример № 1

[fleft( x right)=5{{x}^{4}}+6{{x}^{3}}-2x+6]

[M=left( -1;4 right)]

Для начала просто посчитаем каждое слагаемое:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

[{{x}^{3}}to frac{{{x}^{4}}}{4}]

[xto frac{{{x}^{2}}}{2}]

[6to 6x]

Теперь подставляем эти выражения в нашу конструкцию:

[Fleft( x right)=5cdot frac{{{x}^{5}}}{5}+6cdot frac{{{x}^{4}}}{4}-2cdot frac{{{x}^{2}}}{2}+6x+C]

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+C]

Эта функция должна проходить через точку $Mleft( -1;4 right)$. Что значит, что она проходит через точку? Это значит, что если вместо $x$ поставить везде $-1$, а вместо $Fleft( x right)$ — $-4$, то мы должны получить верное числовое равенство. Давайте так и сделаем:

[4={{left( -1 right)}^{5}}+frac{3cdot {{left( -1 right)}^{4}}}{2}-{{left( -1 right)}^{2}}+6cdot left( -1 right)+C]

Мы видим, что у нас получилось уравнение относительно $C$, поэтому давайте попробуем его решить:

[4=-1+frac{3}{2}-1-6+C]

[C=4+6+2-frac{3}{2}=10,5]

Давайте запишем то самое решение, которое мы искали:

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+10,5]

Пример № 2

[fleft( x right)={{left( x-3 right)}^{2}}]

[M=left( 2;-1 right)]

В первую очередь необходимо раскрыть квадрат разности по формуле сокращенного умножения:

[fleft( x right)={{x}^{2}}-6x+9]

Считаем:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[xto frac{{{x}^{2}}}{2}]

[9to 9x]

Исходная конструкция запишется следующим образом:

[Fleft( x right)=frac{{{x}^{3}}}{3}-6cdot frac{{{x}^{2}}}{2}+9x+C]

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x+C]

Теперь давайте найдем $C$: подставим координаты точки $M$:

[-1=frac{8}{3}-12+18+C]

Выражаем $C$:

[C=-1-6-2frac{2}{3}=-9frac{2}{3}]

Осталось отобразить итоговое выражение:

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x-9frac{2}{3}]

Решение тригонометрических задач

В качестве финального аккорда к тому, что мы только что разобрали, предлагаю рассмотреть две более сложные задачи, в которых содержится тригонометрия. В них точно так же потребуется найти первообразные для всех функций, затем выбрать из этого множества одну-единственную, которая проходит через точку $M$ на координатной плоскости.

Забегая наперед, хотел бы отметить, что тот прием, который мы сейчас будем использовать для нахождения первообразных от тригонометрических функций, на самом деле, является универсальным приемом для самопроверки.

Задача № 1

[fleft( x right)=frac{1}{{{cos }^{2}}x}]

[M=left( frac{text{ }!!pi!!text{ }}{text{4}};-1 right)]

Вспомним следующую формулу:

[{{left( text{tg}x right)}^{prime }}=frac{1}{{{cos }^{2}}x}]

Исходя из этого, мы можем записать:

[Fleft( x right)=text{tg}x+C]

Давайте подставим координаты точки $M$ в наше выражение:

[-1=text{tg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[-1=1+C]

[C=-2]

Перепишем выражение с учетом этого факта:

[Fleft( x right)=text{tg}x-2]

Задача № 2

[fleft( x right)=frac{1}{{{sin }^{2}}x}]

[M=left( -frac{text{ }!!pi!!text{ }}{text{4}};2 right)]

Тут будет чуть сложнее. Сейчас увидите, почему.

Вспомним такую формулу:

[{{left( text{ctg}x right)}^{prime }}=-frac{1}{{{sin }^{2}}x}]

Чтобы избавится от «минуса», необходимо сделать следующее:

[{{left( -text{ctg}x right)}^{prime }}=frac{1}{{{sin }^{2}}x}]

Вот наша конструкция

[Fleft( x right)=-text{ctg}x+C]

Подставим координаты точки $M$:

[2=-text{ctg}left( -frac{text{ }!!pi!!text{ }}{4} right)+C]

[2=text{ctg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[2=1+C]

[C=1]

Итого запишем окончательную конструкцию:

[Fleft( x right)=-text{ctg}x+1]

Вот и все, о чем я хотел сегодня вам рассказать. Мы изучили сам термин первообразных, как считать их от элементарных функций, а также как находить первообразную, проходящую через конкретную точку на координатной плоскости.

Надеюсь, этот урок хоть немного поможет вам разобраться в этой сложной теме. В любом случае, именно на первообразных строятся неопределенные и неопределенные интегралы, поэтому считать их совершенно необходимо. На этом у меня все. До новых встреч!

Смотрите также:

1. Таблица первообразных
2. Интегрирование по частям
3. Решение задач B12: №448—455
4. Что такое ЕГЭ по математике 2011 и как его сдавать
5. Задача B4: случай с неизвестным количеством товара
6. Задача B15: что делать с квадратичной функцией

ВИДЕО УРОК

Что такое первообразная и как она считается ?

ПРИМЕР:

Найдём производную:

f(x) = x³.

Находим её, пользуясь формулой:

Откуда

Это и есть определение
первообразной.

Аналогично запишем и
такое выражение:

Обобщим это правило и
выведем следующую формулу:

При   n = –1 
первообразная функция определяется следующим образом:
Учитывая,
что

а производная

Первообразной функции называется такая функция, производная которой равна
исходной функции.

Функция

y = F(x)

называется первообразной функции

y = f(x)

на промежутке  Х, если для любого  х ∈ Х  выполняется равенство:

F(x) = f(x).

Таблица первообразных
функций.

К каждому выражению в правой части таблицы необходимо прибавить константу.

Правила нахождения первообразных функций.

1. Первообразная функция суммы (разности) равна сумме (разности)
первообразных функций.

F(x + у) = F(x) + F(у),

F(x – у) = F(x) – F(у).

ПРИМЕР:

Найти первообразную для функции

у
= 4х³ + cos x.

РЕШЕНИЕ:

Первообразная суммы равна сумме
первообразных, тогда надо найти первообразную для каждой из представленных
функций.

f(x) = 4x³,  F(x)
= x⁴.

f(x) = cos x,  F(x) = sin x.

Тогда первообразная исходной
функции будет

у
= х⁴ + sin x

или любая функция вида

у
= х⁴ + sin x + C.

2. Если  F(x) –
первообразная для  f(x), то

k F(x)–
первообразная для функции  k f(x).

(Коэффициент можно выносить за функцию).

ПРИМЕР:

Найти первообразную для функции

у
= 8 sin x.

РЕШЕНИЕ:

Первообразной для  sin x  служит
минус  cos x.
Тогда первообразная исходной функции примет вид:

у
= –8 cos x.

ПРИМЕР:

Найти первообразную для функции

у
= 3x² + 4х + 5.

РЕШЕНИЕ:

Первообразной для  x²  служит

Первообразной для  x  служит

Первообразной для  1  служит  x.

Тогда первообразная исходной
функции примет вид:

у
= x³ + 2x² + 5 x.

3. Если  y = F(x) – первообразная для функции

y = f(x),

то первообразная для функции

y = f(kx + m)

служит функция

y = ¹/_k F(kx + m).

ПРИМЕР:

Найти первообразную для функции

у
= cos (7x).

РЕШЕНИЕ:

Первообразной для  cos x  служит  sin x. Тогда первообразная для функции

cos (7x)

будет функция

ПРИМЕР:

Найти первообразную для функции

у
= sin ^x/₂.

РЕШЕНИЕ:

Первообразной для  sin x  служит минус  cos x. Тогда первообразная для функции

у
= sin ^x/₂

будет функция

ПРИМЕР:

Найти первообразную для функции

у
= (–2х + 3)³.

РЕШЕНИЕ:

Первообразной для  x³  служит

Тогда первообразная для исходной
функции

у
= (–2х + 3)³.

будет функция

ПРИМЕР:

Первообра́зная. Красивое слово.) Для начала немного русского
языка. Произносится это слово именно так, а не “первоОбразная”,
как может показаться. Первообразная – базовое понятие всего интегрального
исчисления. Любые интегралы — неопределённые, определённые (с ними вы
познакомитесь уже в этом семестре), а также двойные, тройные, криволинейные,
поверхностные (а это уже главные герои второго курса) — строятся на этом
ключевом понятии. Имеет полный смысл освоить. Поехали.)

        Прежде чем знакомиться
с понятием первообразной, давайте в самых общих чертах вспомним самую
обычную производную. Не углубляясь в занудную теорию пределов,
приращений аргумента и прочего, можно сказать, что нахождение производной
(или дифференцирование) — это просто математическая операция
над функцией. И всё. Берётся любая функция (допустим, f(x)
= x²) и по определённым
правилам преобразовывается, превращаясь в новую функцию. И
вот эта самая новая функция и называется производной.

        В нашем случае, до дифференцирования
была функция f(x) = x²,
а после дифференцирования стала уже другая функция f’(x) =
2x.

        Производная —
потому, что наша новая функция f’(x) = 2x произошла от
функции f(x) = x². В
результате операции дифференцирования. И причём именно от неё, а не от какой-то
другой функции (x³,
например).

        Грубо говоря, f(x) = x² —
это мама, а f’(x) = 2x — её любимая дочка.) Это понятно. Идём
дальше.

        Математики — народ
неугомонный. На каждое своё действие стремятся найти противодействие. 🙂 Есть
сложение — есть и вычитание. Есть умножение — есть и деление.
Возведение в степень — извлечение корня. Синус — арксинус. Точно
также есть дифференцирование – значит, есть и… интегрирование.)

        А теперь поставим такую
интересную задачу. Есть у нас, допустим, такая простенькая функция f(x)
= 1. И нам надо ответить на такой вопрос:

        Производная КАКОЙ функции даёт нам
функцию f(x) = 1?

        Иными словами, видя дочку, с помощью
анализа ДНК, вычислить, кто же её мамаша. 🙂 Так от какой же исходной функции
(назовём её F(x)) произошла наша производная функция f(x) = 1?
Или, в математической форме, для какой функции F(x)
выполняется равенство: 

        F’(x) = f(x) = 1?

        Пример элементарный. Я
старался.) Просто подбираем функцию F(x) так, чтобы равенство сработало. 🙂 Ну
как, подобрали? Да, конечно! F(x) = x. Потому, что:

        F’(x) = x’ = 1 = f(x).

        Разумеется, найденную
мамочку F(x) = x надо как-то назвать, да.) Знакомьтесь!

        Первообразной
для функции f(x) называется такая функция F(x), производная которой
равна f(x), т.е. для которой справедливо равенство F’(x) = f(x).

        Вот и всё. Больше
никаких научных хитростей. В строгом определении добавляется ещё дополнительная
фраза “на промежутке Х”. Но мы пока в эти тонкости
углубляться не будем, ибо наша первоочередная задача — научиться находить
эти самые первообразные.

        В нашем случае как раз и получается,
что функция F(x) = x является первообразной для
функции f(x) = 1.

        Почему? Потому что F’(x) =
f(x) = 1. Производная икса есть единица. Возражений нет.)

        Термин “первообразная”
по-обывательски означает “родоначальница”, “родитель”,
“предок”. Сразу же вспоминаем самого родного и близкого человека.) А
сам поиск первообразной — это восстановление исходной функции по
известной её производной. Иными словами, это действие, обратное
дифференцированию. И всё! Сам же этот увлекательный процесс тоже называется
вполне научно — интегрирование. Но об интегралах —
позже. Терпение, друзья!)

        Запоминаем: 

        Интегрирование —
это математическая операция над функцией (как и дифференцирование).

        Интегрирование — операция,
обратная дифференцированию.

        Первообразная — результат
интегрирования.

        А теперь усложним задачу. Найдём
теперь первообразную для функции f(x) = x. То есть, найдём такую
функцию F(x), чтобы её производная равнялась
бы иксу:

        F’(x) = x

        Кто дружит с производными, тому, возможно,
на ум придёт что-то типа:

        (x²)’
= 2x.

        Что ж, респект и уважуха тем, кто
помнит таблицу производных!) Верно. Но есть одна проблемка. Наша исходная
функция f(x) = x, а (x²)’
= 2x. Два икс. А у нас
после дифференцирования должен получиться просто икс. Не катит. Но…

        Мы с вами народ учёный. Аттестаты
получили.) И со школы знаем, что обе части любого равенства можно умножать и
делить на одно и то же число (кроме нуля, разумеется)! Так уж тождественные
преобразования устроены. Вот и реализуем
эту возможность себе во благо.)

        Мы ведь хотим, чтобы справа
остался чистый икс, верно? А двойка мешает… Вот и берём соотношение
для производной (x²)’ = 2x и
делим обе его части на эту самую двойку:

        Так, уже кое-чего проясняется. Идём
дальше. Мы знаем, что любую константу можно вынести за знак
производной. Вот так:

        Все формулы в математике работают как
слева направо, так и наоборот — справа налево. Это значит, что, с тем
же успехом, любую константу можно и внести под знак производной:

        В нашем случае спрячем двойку в
знаменателе (или, что то же самое, коэффициент 1/2) под знак производной:

        А теперь внимательно присмотримся
к нашей записи. Что мы видим? Мы видим равенство, гласящее, что производная
от чего-то (это что-то — в скобочках)
равняется иксу.         

        Полученное равенство как раз и
означает, что искомой первообразной для функции f(x) = x служит
функция F(x) = x²/2.
Та, что стоит в скобочках под штрихом. Прямо по смыслу первообразной.) Что ж,
проверим результат. Найдём производную:

        

        Отлично! Получена исходная
функция f(x) = x. От чего плясали, к тому и вернулись. Это значит,
что наша первообразная найдена верно.)

        А если f(x) = x²?
Чему равна её первообразная? Не вопрос! Мы с вами знаем (опять же, из правил дифференцирования),
что:

        3x² =
(x³)’

        И, стало
быть,

        

        Уловили? Теперь мы, незаметно для
себя, научились считать первообразные для любой степенной функции
f(x)=xⁿ. В уме.) Берём исходный
показатель n, увеличиваем его на единичку, а в качестве компенсации
делим всю конструкцию на n+1:

        Полученная формулка, между прочим,
справедлива не только для натурального показателя степени n,
но и для любого другого — отрицательного, дробного. Это позволяет легко
находить первообразные от простеньких дробей и корней.

        Например:

        

        

        Естественно, n ≠ -1 ,
иначе в знаменателе формулы получается ноль, и формула теряет смысл.) Про
этот особый случай n = -1 чуть позже.)

Что такое неопределённый
интеграл? Таблица интегралов.

        Идём дальше. Те студенты, которые хотя
бы мало-мальски “шарят” в производных, — люди грамотные. И,
возможно, уже приготовили мне убойный вопрос. 🙂

        Скажем, чему равна производная для
функции F(x) = x? Ну, единица, единица — слышу
недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже
будет равна единице:

        

        Также производная будет равна единице
и для функции x+1234, и для функции x-10, и
для любой другой функции вида x+C, где С —
любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания
нуля никому ни холодно ни жарко.)

        Получается неоднозначность. Выходит,
что для функции f(x) = 1 первообразной служит не
только функция F(x) = x, но и функция  F₁(x)
= x+1234 и функция F₂(x)
= x-10 и так далее!

        Да. Именно так.) У всякой (непрерывной
на промежутке) функции существует не какая-то одна первообразная,
а бесконечно много – целое семейство! Не одна мама или
папа, а целая родословная, ага.)

        Но! Всех наших
родственников-первообразных объединяет одно важное свойство. На то они и
родственники.) Свойство настолько важное, что в процессе разбора приёмов
интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё
долго.) 

        Вот оно, это свойство:

        Любые две
первообразные F₁(x)
и F₂(x) от
одной и той же функции f(x) отличаются на константу:

        F₁(x)
– F₂(x) = С.

        Кому интересно доказательство —
штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу.
Благо доказательство тут элементарное, в одно действие. Берём равенство

        F₁(x)
– F₂(x) = С

        и дифференцируем
обе его части. То есть, просто тупо ставим штрихи:

        Вот и всё. Как говорится, ЧТД. 🙂

        О чём говорит это свойство? А о том,
что две различные первообразные от одной и той же функции f(x) не
могут отличаться на какое-то выражение с иксом . Только
строго на константу! Иными словами, если у нас есть график какой-то одной
из первообразных (пусть это будет F(x)), то графики всех
остальных наших первообразных строятся параллельным переносом графика
F(x) вдоль оси игреков.

        Посмотрим, как это выглядит на примере
функции f(x) = x. Все её первообразные, как нам уже известно, имеют
общий вид F(x) = x²/2+C.
На картинке это выглядит как бесконечное множество парабол,
получаемых из “основной” параболы y = x²/2 сдвигом
вдоль оси OY вверх или вниз в зависимости от значения константы С.

        Помните школьное построение графика
функции y=f(x)+a сдвигом графика y=f(x) на
“а” единиц вдоль оси игреков?) Вот и тут то же самое.)

        Причём, обратите внимание: наши
параболы нигде не пересекаются! Оно и естественно. Ведь две
различные функции y₁(x) и y₂(x)
неизбежно будут соответствовать двум различным значениям константы — С₁ и С₂.

        Поэтому уравнение y₁(x)
= y₂(x) никогда не имеет решений:

С₁ =
С₂

x ∊ ∅,
так как С₁ ≠
С2

        А теперь мы плавненько подходим ко
второму краеугольному понятию интегрального исчисления. Как мы только что
установили, у всякой функции f(x) существует бесконечное множество
первообразных F(x) + C, отличающихся друг от друга на константу. Это самое
бесконечное множество тоже имеет своё специальное название.) Что ж, прошу
любить и жаловать!

        Что такое
неопределённый интеграл?

        Множество
всех первообразных для функции f(x) называется неопределённым
интегралом от функции f(x).

        Вот и всё
определение.)

        “Неопределённый” –
потому, что множество всех первообразных для одной и той же функции бесконечно.
Слишком много различных вариантов.)

        “Интеграл” —
с подробной расшифровкой этого зверского слова мы познакомимся в следующем
большом разделе, посвящённом определённым интегралам. А пока, в
грубой форме, будем считать интегралом нечто общее, единое, целое.
А интегрированием — объединение, обобщение, в
данном случае переход от частного (производной) к общему (первообразным). Вот,
как-то так.

        Обозначается неопределённый интеграл
вот так:

        Читается так же, как и пишется: интеграл
эф от икс дэ икс. Или интеграл от эф от икс дэ
икс. Ну, вы поняли.)

        Теперь разберёмся с обозначениями.

        ∫ — значок
интеграла. Смысл тот же, что и штрих для производной.)

        d — значок дифференциала. Не
пугаемся! Зачем он там нужен — чуть ниже.

        f(x) — подынтегральная
функция (через “ы”).

        f(x)dx — подынтегральное
выражение. Или, грубо говоря, “начинка” интеграла.

        Согласно смыслу неопределённого
интеграла,

        Здесь F(x) — та
самая первообразная для функции f(x), которую мы
так или иначе нашли сами. Как именно нашли — не
суть. Например, мы установили, что F(x) = x²/2 для f(x)=x.

        “С” – произвольная
постоянная. Или, более научно, интегральная константа.
Или константа интегрирования. Всё едино.)

        А теперь вернёмся к нашим самым первым
примерам на поиск первообразной. В терминах неопределённого интеграла можно
теперь смело записать:

        

        

        

        

        

        И так далее.) Идея понятна, думаю. Ни
в коем случае не забываем приплюсовывать константу С!

Что такое интегральная константа
и зачем она нужна?

        Вопрос очень интересный. И очень
(ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества
первообразных выделяет ту линию, которая проходит через заданную точку.

         В чём суть.
Из исходного бесконечного множества первообразных (т.е. неопределённого
интеграла) надо выделить ту кривую, которая будет проходить через
заданную точку. С какими-то конкретными координатами. Такое
задание всегда и везде встречается при начальном знакомстве с интегралами.
Как в школе, так и в ВУЗЕ.

         Типичная задачка:

         Среди множества всех
первообразных функции f=x выделить ту, которая проходит через точку (2;2).

         Начинаем
думать головой… Множество всех первоообразных  — это значит,
сначала надо проинтегрировать нашу исходную функцию. То
есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:

         

         А теперь разбираемся, что именно
мы получили. Мы получили не одну функцию, а целое семейство функций. Каких
именно? Вида y=x²/2+C. Зависящее
от значения константы С. И вот это значение константы нам и предстоит
теперь “отловить”.) Ну что, займёмся ловлей?)

         Удочка наша — семейство
кривых (парабол) y=x²/2+C. 

         Константы — это
рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)

         А что же
служит приманкой? Правильно! Наша точка (-2;2).

         Вот и
подставляем координаты нашей точки в общий вид первообразных! Получим:

         

         y(2) = 2

         

         Отсюда уже легко ищется C
= 0.         

         Что сиё означает? Это значит,
что из всего бесконечного множества парабол вида y=x²/2+C только парабола
с константой С=0 нам подходит! А именно: y=x²/2. И
только она. Только эта парабола будет проходить через нужную
нам точку (-2; 2). А все остальные параболы из нашего
семейства проходить через эту
точку уже не будут. Через какие-то другие точки
плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?

         Для наглядности вот вам две
картинки — всё семейство парабол (т.е. неопределённый интеграл) и
какая-то конкретная парабола, соответствующая конкретному
значению константы и проходящая через конкретную точку:

        Видите, насколько важно учитывать
константу С при интегрировании! Так что не пренебрегаем этой
буковкой “С” и не забываем приписывать к окончательному ответу.

        А теперь разберёмся, зачем же внутри
интегралов везде тусуется символ dx. Забывают про него
студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё
дело в том, что интегрирование — операция, обратная дифференцированию. А
что именно является результатом дифференцирования? Производная?
Верно, но не совсем. Дифференциал!

        В нашем случае, для функции f(x) дифференциал её
первообразной F(x), будет:

        

        Кому непонятна данная цепочка —
срочно повторить определение и смысл дифференциала и то, как именно он
раскрывается! Иначе в интегралах будете тормозить нещадно….

        Напомню, в самой грубой обывательской
форме, что дифференциал любой функции f(x) – это просто произведение f’(x)dx.
И всё! Взять производную и помножить её на дифференциал аргумента (т.е.
dx). То есть, любой дифференциал, по сути, сводится к вычислению обычной производной.

        Поэтому, строго говоря, интеграл
“берётся” не от функции f(x), как принято
считать, а от дифференциала f(x)dx! Но, в
упрощённом варианте, принято говорить, что “интеграл берётся от
функции”. Или: “Интегрируется функция f(x)“. Это
одно и то же. И мы будем говорить точно так же. Но про значок dx при
этом забывать не будем! 🙂

        И сейчас я подскажу, как его не забыть
при записи. Представьте себе сначала, что вы вычисляете обычную производную по
переменной икс. Как вы обычно её пишете?

        Вот так: f’(x), y’(x), у’_x.
Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам
показывают, что производная берётся именно по иксу. А не по “игреку”,
“тэ” или какой-то там другой переменной.)

        Так же и в интегралах. Запись ∫f(x)dx нам
тоже как бы показывает, что интегрирование проводится
именно по переменной икс. Конечно, это всё очень упрощённо и
грубо, но зато понятно, я надеюсь. И шансы забыть приписать
вездесущее dx резко снижаются.)

        Итак, что такое же неопределённый
интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые
неопределённые интегралы вычислять. Или, попросту говоря,
“брать”. 🙂 И вот тут студентов поджидает две новости — хорошая
и не очень. Пока начнём с хорошей.)

         Новость хорошая. Для интегралов,
так же как и для производных, существует своя табличка. И все интегралы,
которые нам будут встречаться по пути, даже самые страшные и навороченные,
мы по определённым правилам будем так или иначе сводить к этим
самым табличным.)

        Итак, вот она, таблица
интегралов!

        Вот такая вот красивая табличка
интегралов от самых-самых популярных функций. Рекомендую обратить отдельное
внимание на группу формул 1-2 (константа и степенная функция). Это — самые
употребительные формулы в интегралах!

        Третья группа формул (тригонометрия),
как можно догадаться, получена простым обращением соответствующих формул для
производных.

        Например:

         
 

        C четвёртой группой формул
(показательная функция) — всё аналогично.

        А вот четыре последние группы формул
(5-8) для нас новые. Откуда же они взялись и за какие такие
заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных
интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?

        Так уж сложилось исторически в
процессе развития методов интегрирования. Когда мы будем
тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что
интегралы от перечисленных в таблице функций встречаются очень и очень часто.
Настолько часто, что математики отнесли их к табличным.) Через них выражаются
очень многие другие интегралы, от более сложных конструкций.

        Ради интереса можно взять какую-нибудь
из этих жутких формул и продифференцировать. 🙂 Например, самую зверскую 7-ю
формулу.

        

        

        Всё нормально. Не обманули математики.
🙂

        Таблицу интегралов, как и таблицу
производных, желательно знать наизусть. Во всяком случае, первые четыре группы
формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть
последние четыре группы (с дробями и корнями) пока не стоит.
Всё равно поначалу будете путаться, где логарифм писать, где арктангенс,
где арксинус, где 1/а, где 1/2а … Выход тут один – решать побольше примеров.
Тогда таблица сама собой постепенно и запомнится, а сомнения грызть
перестанут.)

        Особо любознательные лица,
присмотревшись к таблице, могут спросить: а где же в таблице интегралы от
других элементарных “школьных” функций — тангенса, логарифма,
“арков”? Скажем, почему в таблице ЕСТЬ интеграл от синуса, но при
этом НЕТУ, скажем, интеграла от тангенса tg x? Или нету интеграла
от логарифма ln x? От арксинуса arcsin x? Чем они хуже?
Но зато полно каких-то “левых” функций – с корнями, дробями,
квадратами…

        Ответ. Ничем не хуже.) Просто
вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не
являются табличными. И встречаются на практике значительно реже, нежели
те, что представлены в таблице. Поэтому знать наизусть, чему они
равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)

        Что, кому-то всё-таки невтерпёж? Так
уж и быть, специально для вас!

        Ну как, будете заучивать? 🙂 Не
будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно
найдём. В соответствующих уроках. 🙂

        Что ж, теперь переходим к свойствам
неопределённого интеграла. Да-да, ничего не поделать! Вводится новое
понятие — тут же и какие-то его свойства рассматриваются.

Свойства неопределённого
интеграла.

        Теперь не очень хорошая новость.

        В отличие от дифференцирования, общих
стандартных правил интегрирования, справедливых на все случаи жизни,
в математике нету. Это фантастика!

        Например, вы все прекрасно знаете
(надеюсь!), что любое произведение любых двух
функций f(x)·g(x) дифференцируется вот так:

(f(x)·g(x))’ = f’(x)·g(x) +
f(x)·g’(x).

        Любое частное
дифференцируется вот так:

        А любая сложная функция, какой бы накрученной
она ни была, дифференцируется вот так:

        И какие бы функции ни скрывались под
буквами f и g, общие правила всё равно сработают и производная, так или иначе,
будет найдена.

        А вот с интегралами такой номер уже не
пройдёт: для произведения, частного (дроби), а также сложной функции общих
формул интегрирования не существует! Нету никаких
стандартных правил! Вернее, они есть. Это я зря математику обидел.)
Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А
во-вторых, большинство методов интегрирования, о которых мы будем разговаривать
в следующих уроках, очень и очень специфические. И справедливы лишь для
определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных
функций. Или каких-то ещё.

        А какие-то интегралы, хоть и
существуют в природе, но вообще никак не выражаются через элементарные
“школьные” функции! Да-да, и таких интегралов полно! 🙂

        Именно поэтому интегрирование —
гораздо более трудоёмкое и кропотливое занятие, чем дифференцирование. Но в
этом есть и своя изюминка. Занятие это творческое и очень увлекательное.) И,
если вы хорошо усвоите таблицу интегралов и освоите хотя бы два базовых приёма,
о которых мы поговорим далее (замена
переменной и интегрирование
по частям), то интегрирование вам очень понравится. 🙂

        А теперь познакомимся, собственно, со
свойствами неопределённого интеграла. Их всего ничего. Вот они.

        Первые два свойства полностью
аналогичны таким же свойствам для производных и называются свойствами
линейности неопределённого интеграла. Тут всё просто и логично:
интеграл от суммы/разности равен сумме/разности интегралов, а постоянный
множитель можно вынести за знак интеграла.

        А вот следующие три свойства для нас
принципиально новые. Разберём их поподробнее. Звучат по-русски они следующим
образом.

        Третье свойство

        Производная
от интеграла равна подынтегральной функции

        Всё просто, как в сказке. Если
проинтегрировать функцию, а потом обратно найти производную от результата, то…
получится исходная подынтегральная функция. 🙂 Этим свойством всегда можно (и
нужно) пользоваться для проверки окончательного результата интегрирования.
Вычислили интеграл – продифференцируйте ответ! Получили подынтегральную
функцию — ОК. Не получили — значит, где-то накосячили. Ищите ошибку.)

        Конечно же, в ответе могут получаться
настолько зверские и громоздкие функции, что и обратно дифференцировать их
неохота, да. Но лучше, по возможности, стараться себя проверять. Хотя бы в тех
примерах, где это несложно.)

        Идём дальше, по порядочку.

        Четвёртое свойство

        Дифференциал
от интеграла равен подынтегральному выражению.

        Тут ничего особенного. Суть та же
самая, только dx на конце появляется. Согласно предыдущему свойству и правилам
раскрытия дифференциала.

        Пятое свойство

        Интеграл
от дифференциала некоторой функции равен сумме этой функции и произвольной
постоянной.

        Тоже очень простое свойство. Им мы
тоже будем регулярно пользоваться в процессе решения интегралов.
Особенно — в методе
подведения функции под знак дифференциала и замены
переменной.

        Вот такие вот полезные свойства.
Занудствовать с их строгими доказательствами я здесь не собираюсь. Желающим
предлагаю это сделать самостоятельно. Прямо по смыслу производной и
дифференциала. Докажу лишь последнее, пятое свойство, ибо оно менее очевидно.

        Итак, у нас есть утверждение:

           

        Вытаскиваем
“начинку” нашего интеграла и раскрываем, согласно определению
дифференциала:

           

        На всякий случай, напоминаю, что,
согласно нашим обозначениям производной и первообразной, F’(x)
= f(x).

        Вставляем теперь наш результат обратно
внутрь интеграла:

           

        Получено в точности определение
неопределённого интеграла (да простит меня русский язык)! 🙂

        Вот и всё.)

Метод интегрирования по частям.

        Продолжаем осваивать базовые приёмы интегрирования. В предыдущих уроках мы рассмотрели три таких приёма – непосредственное интегрирование (то бишь, по таблице), метод подведения функции под знак дифференциала и метод замены переменной. Три ножки для стула. Сидеть уже можно, но… как-то неудобно.)

        Сегодняшний наш урок будет началом изучения ещё одной обширной темы интегрального исчисления. Последней, четвёртой ножки для нашего стула.) А именно – метода интегрирования по частям. Великого и могучего. Фраза “интегрируем по частям” вселяет уверенность и так же обнадёживает студентов, как и фраза “решаем через дискриминант” у школьников. 🙂

        В чём же заключается столь сильная мощь данного метода и почему именно он так популярен при вычислении львиной доли неопределённых интегралов? А дело вот в чём.

        Ключевой момент №1

        Как мы уже знаем, в отличие от производных, в матанализе не существует стандартных правил для интегралов от произведения, частного и сложной функции. Но в процессе интегрирования такие операции с функциями встречаются сплошь и рядом. И очень часто именно метод интегрирования по частям позволяет свести вычисление интеграла от навороченной функции к совсем простенькому выражению, проинтегрировать которое не составит труда. Если таблицу знать, конечно.

        Ключевой момент №2

        Нередко под интегралом могут стоять всякие нехорошие трансцендентные конструкции — логарифмы, арксинусы, арктангенсы и прочие ужасы. Таблица интегралов не катит: нету в ней ни логарифмов, ни арков. И замена не годится тоже.

        И в таких случаях тоже надо уметь как-то выкручиваться, да…

        Какие же именно интегралы берутся по частям?

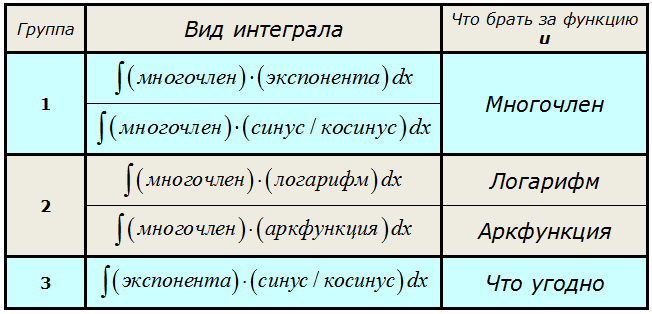
        Вот типовые схемы подынтегральных функций:

        

        Например, что-то в таком духе:

        

        Что общего во всех таких интегралах? А общее то, что подынтегральная функция представляет собой произведение (а в ряде случаев и частное) “разнородных” функций. Многочлена и логарифма, синуса и экспоненты и так далее… Или же под интегралом тусуются всякие там арксинусы, арктангенсы и прочая жесть.

        Под последним шестым пунктом стоит слово “прочие”. Это такие функции, которые не относятся к предыдущим пяти типам, но которые также вполне можно проинтегрировать по частям (а иногда и только по частям). Как правило, сочетая в себе и другие способы интегрирования — замену переменной, подведение под дифференциал и т.п. Это всякие сложные экзотические функции, а также некоторые дроби и функции с корнями.

        Например:

        

        И тому подобные примеры. Их разберём в соответствующем уроке.

        Ну вот. Про таинственный метод упомянули, какие именно интегралы с его помощью вычисляются — тоже. Пора бы уже начать более близкое знакомство. Знакомимся? Поехали!

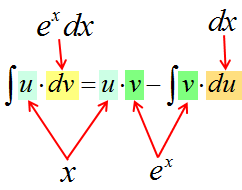
Формула интегрирования по частям — вывод и смысл.

        Итак, прошу любить и жаловать:

        Это и есть формула интегрирования по частям собственной персоной.)

        Откуда же она берётся и почему так называется? Она берётся из обычного правила дифференцирования произведения.

        Все вы (надеюсь) его хорошо помните ещё со школы:

        

        Или почти то же самое, только по-взрослому, через дифференциалы:

       

        Все формулы в матанализе, если слева и справа стоят функции или их производные (или дифференциалы), можно почленно интегрировать. Вот и проинтегрируем левую и правую части нашего правила. Имеем полное право!

        Подвешиваем на крючки левую и правую части и получаем:

        

        Осталось сообразить, что значок интеграла всегда “съедает” значок дифференциала (согласно соответствующему свойству). Стало быть, слева останется просто произведение u∙v. А справа приведём первый интеграл к приличному виду и отправим его влево к u·v (со сменой знака, разумеется). Получим:

        

        И, наконец, финальный бросок. Меняем местами левую и правую части и получаем:

        

        Всё! Больше никаких научных хитростей.)

        Собственно, формула производной произведения и формула интегрирования по частям — это две взаимно обратных формулы. 🙂 Так же, как и операции дифференцирования сложной функции и подведения функции под знак дифференциала. Вот и вся суть.

        Запоминается формула на удивление легко и просто. Чаще всего, в виде секретного заклинания:

        Интеграл у-дэ-вэ равен у на вэ минус интеграл вэ-дэ-у. 🙂

        Итак, будем считать, что с происхождением формулы разобрались. Теперь разбираемся с названием – что ещё там за части какие-то. 🙂

        Смотрим на формулу ещё разок:

        В чём основная суть? Исходное подынтегральное выражение (то, что слева) разбивается на два кусочка. Или две части.) Причём только с помощью умножения! Именно поэтому в общей формуле я отдельно и выделяю знаки умножения.

        Первая часть (первый множитель) — это некоторая функция u. Функция как функция. Выражаемая какой-то формулой.

        Вторая часть (второй множитель) — это не функция, а дифференциал некоторой другой функции v. То есть, dv.

        Что это за таинственные u и v? Об этом дальше подробненько будет. Никаких тайн.)

        Что же происходит при применении формулы? С точки зрения математики ничего особенного не происходит:

        1. Первый множитель — u — дифференцируется. Было u, а становится du.

        2. Второй множитель – dv – наоборот, интегрируется. Было dv, а после интегрирования стало просто v.

        Зато с точки зрения наших хотелок происходит оч-чень много полезного! Исходный интеграл:

        

        который, по каким-то причинам, нам не очень нравится, заменяется на другой интеграл

       

        вычисление которого должно оказаться проще исходного.

        Вот и всё. Вот и вся ключевая идея применения формулы!

        Что брать за u, а что за dv?  

        Вопрос хороший! Этот момент – стратегически самый важный при применении формулы. Давайте разбираться. В самых общих чертах.) Выпишем ещё раз формулу:

        Как видно из формулы, нам надо интегрировать новое выражение v∙du. И оно должно оказаться проще старого подынтегрального выражения u∙dv. Вот такая ключевая идея — упростить исходное подынтегральное выражение!

        Поскольку в новом подынтегральном выражении стоит дифференциал du, то за функцию u всегда принимается функция, упрощающаяся при дифференцировании.

        И какие же функции упрощаются при дифференцировании? Как правило, это всякие ужасы типа логарифмов или “арков”. Почему же они упрощаются при дифференцировании? А потому, что их производные — гораздо более простые функции! Рациональные дроби или, в худшем случае, выражения с корнями (для арксинуса/арккосинуса). Вспоминаем нашу старую добрую таблицу производных:

        

        И так далее. С дробью 1/х всяко проще работать в процессе интегрирования, чем с логарифмом, правда?  И с арками та же история.

        Точно так же упрощаются при дифференцировании и многочлены, степень которых после каждого дифференцирования понижается на единичку:

        

        В общем, принцип выбора функции u предельно ясен — упрощение после дифференцирования. А что же со вторым множителем dv?

        Поскольку множитель dv нам придётся интегрировать, то за dv всегда берётся конструкция, не усложняющаяся при интегрировании!

        Например, это вполне может быть экспонента. Или же тригонометрическая функция — синус там или косинус… Или степенная функция или многочлен. Эти функции никак не усложняются при интегрировании! Почему? Вспоминаем теперь уже таблицу интегралов (первообразных): экспонента при интегрировании превращается сама в себя, синус/косинус — друг в друга (с точностью до знака), а любой многочлен степени n — также в многочлен, но степени n+1.

        Запоминаем:

        За функцию u всегда принимаем выражение, упрощающееся при дифференцировании.

        За dv принимаем выражение, не усложняющееся при интегрировании.

        Разумеется, сразу увидеть и сообразить в уме, что упростится/усложнится после дифференцирования/интегрирования, не всегда возможно. Всё от конкретного примера и от опыта зависит. Не всегда с первого раза получается. Бывает.)

        Но для некоторых типовых схем я всё же приведу небольшую сводную табличку. Пользуйтесь на здоровье! 🙂

        Что ж, думаю, хватит грузной теории, давайте перейдём к конкретным примерам — всё станет куда понятнее.) В этом уроке рассмотрим интегралы из группы №1.

Произведение многочлена и показательной/тригонометрической функции.

        Это интегралы из первой группы нашей сводной таблички.

        Общий рецепт здесь следующий:

        Если под интегралом стоит произведение многочлена и показательной/тригонометрической функции, то за функцию u всегда берётся МНОГОЧЛЕН.

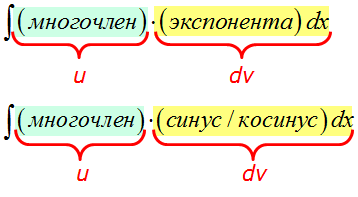
        А что берётся за dv?  А за dv всегда берётся оставшаяся часть подынтегрального выражения вместе с dx! Что уж там осталось, то и берётся, так уж формула интегрирования по частям устроена: всё подынтегральное выражение надо по кусочкам распределить между u и dv.

        Вот так:

        

        Ну что, посмотрим на формулу интегрирования по частям в действии?)

        Например, пусть надо найти вот такой интересный интеграл:

Пример 1

        Казалось бы, всё просто. Под знаком интеграла стоит произведение знакомых табличных функций — икса и e^x. Вроде, всё хорошо. Но есть одна проблемка: общей стандартной формулы для интеграла от произведения не существует! По отдельности каждая функция интегрируется без проблем, а вот произведение — уже проблема, да…) Как быть?

        Как-как… Надо разделить разные типы функций!

        Вот и разбиваем наше подынтегральное выражение на кусочки! Наша задача представить конструкцию

        xe^xdx

        в виде произведения функции u и дифференциала другой функции dv.

        Определяемся, что выбираем за u и за dv!

        Работаем прямо по правилу для группы №1. В роли показательной функции у нас, очевидно, e^x. А множитель х служит как раз тем самым многочленом, который целесообразно брать в качестве функции u. Не так очевидно, что это многочлен, но это именно он.) Состоящий всего из одного члена — икса. Бывает.)

        А вот к dv мы должны отнести то, что осталось — выражение e^xdx.

        Так и пишем:

        

        Да-да, именно так и выделяем, прямо в тетрадке!

        Итак, выбор u и dv сделан. Вот он:

        

        Теперь следующим шагом мы начинаем операцию, которую я условно называю “миграция дифференциала”: функцию u мы будем дифференцировать и превращать в du, а dv — наоборот интегрировать и превращать в v. Таким образом, под дифференциалом вместо функции v окажется функция u. Вспоминаем нашу картинку с пляшущими человечками.)

        Поехали!

        Дифференцируем функцию u, считаем du:

        

        Интегрируем множитель dv и ищем функцию v:

        

        Внимание! Не прибавляем константу С после отыскания функции v! Ведь в качестве функции v нам нужна только какая-то одна конкретная первообразная! А не всё бесконечное множество, да…) Самая простая такая первообразная — очевидно, с константой С, равной нулю (С=0). Именно поэтому я и пишу

        v = e^x,

        а не

        v = e^x + C.

        А теперь берём формулу интегрирования по частям

        

        и аккуратно подставляем все исходные данные на свои места:

        

        И считаем:

        

        Вот и все дела.)

        Ответ:

        

        Как всегда, для пущей уверенности, дифференцируем результат:

        

        Ура! Совпало! 🙂

        Что у нас произошло после применения формулы интегрирования по частям? А произошло то, что мешающий нам множитель х исчез из примера, и исходный интеграл от нехорошего произведения

       

        свёлся к табличному (!) интегралу от безобидной экспоненты

       

        Берущемуся в уме. Если таблицу знать.) Здорово, правда?

        Именно так и работает формула интегрирования по частям. Разделяет разнотипные функции и превращает ужасный на вид интеграл в белый и пушистый. Вот и вся суть метода интегрирования по частям.)

        А что будет, если поступить наоборот –  за u принять e^x, а за dv — xdx?

        Не вопрос, давайте посмотрим:

        

        Тогда, подставляя всё в формулу, получим:

        

        Хм… И что нам с таким интегралом делать?! Даже ещё хуже стало, чем было…

        Да! При таком выборе u и dv новый интеграл не упрощается, а, наоборот, усложняется! Экспоненте-то всё равно, что с ней делают — дифференцируют/интегрируют. У неё ко всем воздействиям врождённый иммунитет.) В отличие от многочлена, который при таком раскладе не понижает свою степень, а повышает. Что никак не делает пример проще, да…)

        Собственно в этом-то и кроется причина выбора именно многочлена в качестве функции u для интегралов первой группы — понизить его степень.

        А для общего развития запоминаем:

        Если после применения формулы новый интеграл получился сложнее исходного, то, скорее всего, неудачно сделан выбор u и dv. Не падаем духом и пробуем другую комбинацию.

        Эта рекомендация относится не только к этому уроку, на примеры из первой группы, а ко всему интегрированию по частям вообще.

        Но самое надёжное — не бездумно расчленять подынтегральное выражение и комбинировать кусочки, задумчиво глядя на пример, а понимать общий смысл формулы и принцип выбора u и dv для конкретного типа интеграла. Уметь заранее просчитывать ситуацию и оценивать последствия того или иного выбора. Такой опыт только с практикой приходит. Прорешаете хотя бы 20-30 примеров — и проблема выбора u и dv отпадёт сама собой.)

        Ну вот. Первый пример разобран по косточкам. Разумеется, так подробно расписывать следующие примеры я уже не буду. Это чисто для знакомства сделано. Чтобы общую идею уловить.)

        А теперь можно записать и общий алгоритм вычисления неопределённых интегралов по частям.

        Алгоритм вычисления неопределённых интегралов по частям.

        1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

        2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

        3. Дифференцируем функцию u и считаем дифференциал du.

        4. Интегрируем дифференциал dv и ищем саму функцию v.

        5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

        6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.

        Ну что, потренируемся в применении алгоритма?)

        Пример 2

       

        И опять под интегралом стоит произведение функций разной природы — икса и косинуса. Значит, разделяем разнородные функции и интегрируем по частям: у нас просто нет других вариантов!

        Работаем строго по пунктам.

        1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

        Очевидно, это интеграл из первой группы — типа “многочлен на синус/косинус”. Переходим к пункту 2.

        2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

        Наше правило для первой группы гласит, что за функцию u следует принимать многочлен — то есть, просто множитель x.

        Ну, а за dv, ясен перец, принимаем то что осталось, т.е. cos x dx.

        Вот так:

        

        Итак, выбор сделан. Переходим к пунктам 3 и 4. Тут всё просто, без фокусов:

        3. Дифференцируем функцию u и считаем дифференциал du.

       

        4. Интегрируем дифференциал dv и ищем саму функцию v.

       

        5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

        Итак, все исходные данные для применения формулы подготовлены. Подставляем:

        

        6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.

Вперёд!

Ответ:

        Готово дело.)

        Проверяем ответ дифференцированием:

        

        Всё путём.)

        Мы видим, что новый интеграл опять оказался табличным и берущимся в уме! От синуса. Халява! 🙂 Но далеко не всегда выпадает такое счастье. Иногда при поиске функции v надо дополнительно потрудиться. Поэтому теперь решим что-нибудь посложнее. Чтобы в ступор не впасть, в случае чего…

        Пример 3

       

        Чем-то похоже на предыдущий пример, правда? Только синус ещё затесался, в качестве третьего множителя. Поскольку перед нами снова произведение разнородных функций — икса и тригонометрии, то такой интеграл можно попробовать взять только по частям. Но под интегралом произведение трёх функций, а не двух, как обычно! Что делать?

        Что-что… Не бояться, вот что! Ибо из трёх множителей всегда можно сделать два. Нас спасут… скобочки! Вот так:

        

        А дальше опять по алгоритму. Поехали!

        1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.

        Всё ясно. Это первая группа, т.к. под интегралом произведение многочлена (икса) и тригонометрии (sinx∙cosx).

        2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.

        И здесь вопросов нет. Икс — это u. То, что осталось (т.е. sinx∙cosxdx) — это dv.

        Итого имеем следующее:

        

        3. Дифференцируем функцию u и считаем дифференциал du.

       

        4. Интегрируем дифференциал dv и ищем саму функцию v.

        А вот здесь начинается самое интересное.) Для поиска v нам надо проинтегрировать выражение sinx∙cosxdx.

        Вот так:

        

        Вот тут уже с ходу, в уме, этот интеграл не возьмёшь. В одно действие. Подумать надо.)

        Варианта два. Можно внести косинус (или синус) под знак дифференциала и старым добрым способом, но в данном случае гораздо выгоднее искусственно выделить под интегралом синус двойного угла:

        

        А проинтегрировать синус двойного угла уже никакого труда не составляет. В уме интегрируется. Как это делается, смотрим этот урок. Самое главное — не забываем про дополнительные коэффициенты и про знаки.

        

        Всё. Функцию v мы нашли. Идём дальше по алгоритму.

        5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.

        

        6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.

        

        И снова мы видим, что новый интеграл, от косинуса двойного угла, много проще старого интеграла от сборной солянки x∙sinx∙cosx. Интегрируем косинус двойного угла, “причёсываем” ответ и добиваем наш злой пример.

        Пишу подробно, со всеми знаками и коэффициентами, поскольку именно в них народ и косячит на 99%:

        

        Ответ:

        

        Вот и все дела.) Кому не нравятся двойные углы, те могут перейти обратно к одинарным по соответствующим формулам, но в таком виде ответ выглядит гораздо компактнее.

        Что, сомнения нахлынули? Не ленимся, дифференцируем:

        

        Нет, всё честно.)

        Всё бы ничего, но… могут случаться и такие сюрпризы, когда по частям приходится интегрировать несколько раз. Разберём ещё один пример.

        Пример 4

        

        Надеюсь, общий алгоритм интегрирования по частям уже запомнился? Можно не расписывать подробно в четвёртый раз?)

        В этот раз на экспоненту умножается не одинокий икс, а вполне себе полноценный многочлен. Но схема выбора u и dv та же самая.

        

        Действуем в соответствии с алгоритмом:

        

        Отлично. Функции u и v, а также их дифференциалы du и dv найдены. Пора приступать к интегрированию по частям. Снова прямо по формуле вставляем все исходные данные, упрощаем что упрощается и получаем:

        

        А вот и обещанный сюрприз! Что делать с новым интегралом

       

        В таблице такого и близко нет, обычными преобразованиями с подынтегральной функцией тоже ничего не сделаешь… Но! Можно заметить, что под новым интегралом у нас опять произведение многочлена и экспоненты! Поэтому… снова интегрируем по частям (да-да!). Утешает то, что новый многочлен (2х+1) стал уже линейным (а не квадратичным, как был изначально)! Казалось бы, мелочь, но очень существенная: новый интеграл в целом проще старого! Как и должно быть.)

        Если мы сейчас отдельно возьмём этот интеграл по частям и упростим до упора, то получим такой результат:

        

        Что, у вас не так получилось? А за знаками следили? А за коэффициентами? Не забываем, что е^-2х — сложная функция! Со всеми вытекающими.)

        Вот практически и всё. Возвращаемся к исходному примеру, вставляем результат промежуточного интегрирования по частям на своё место и константу не забываем.)

        Получим:

        

        В принципе, интеграл мы уже нашли. Если требуются дальнейшие упрощения и наведение марафета, то, раскрыв скобки и приведя подобные, окончательно получим:

        Ответ:

        

        Вот такой ответ. Проверочное обратное дифференцирование предлагаю провести самостоятельно.)

        Чем поучителен этот пример? Как видите, здесь нам пришлось интегрировать по частям два раза! Почему? Всему виной является вторая степень нашего многочлена x²+x+1. Проблема в том, что после каждого применения формулы (т.е. взятии дифференциала du) степень многочлена понижается лишь на единичку. Как и при любом дифференцировании, да.

        Например, если бы под интегралом стоял многочлен 10-й степени (да даже хотя бы простое произведение x¹⁰e^x), то последовательно интегрировать по частям пришлось бы (о, ужас!) десять раз! Это огорчает. Но зато при каждом новом интегрировании степень многочлена будет становиться всё ниже. Пускай на единичку, но — ниже. Это радует.)

        Запоминаем:

        Интегрировать по частям требуется столько раз, какова степень многочлена.

        Между прочим, в качестве показательной функции совершенно не обязательно должна стоять именно экспонента (e^x, е^2х и тому подобные конструкции). Запросто может оказаться вообще не “е”, а что-то типа 2^3х и т. п. Не надо пугаться. Принцип интегрирования тот же самый. Отличие состоит лишь в том, что при вычислении функции v будут всплывать дополнительные коэффициенты с логарифмами, которые ни в коем случае нельзя терять.

        Например:

        

        И так далее…

        Итак, с первой группой интегралов, берущихся по частям, поработали. Переходим ко второй группе — логарифмам, аркам и прочим питомцам нашего зоопарка элементарных функций. В следующей теме.)

План урока:

Понятие первообразной

Бесконечное количество первообразных

Неопределенный интеграл

Таблица первообразных

Правила вычисления интегралов

Физический смысл неопределенного интеграла

Понятие первообразной

Ранее мы познакомились с важнейшим понятием математического анализа – производной. Она имеет большое практическое значение, в частности, с ее помощью можно определить скорость тела, если известен закон его передвижения. Например, если путь, пройденный автомобилем, можно вычислить с помощью функции S = t², то его скорость в любой момент времени может быть рассчитана по формуле

Однако на практике значительно чаще встречается прямо противоположная задача. Известно, как меняется скорость тела, и найти требуется путь, пройденный им. В таком случае необходимо по производной определить ту функцию, которая «подверглась» дифференцированию.

Задание. Известна производная функции у(х):

В этом примере мы выполнили операцию, обратную дифференцированию. В математическом анализе он называется интегрированием. Если интегрируют некоторую произвольную функцию f(х), то в итоге получают новую функцию, которую чаще всего обозначают как F(x). Её называют первообразной функции f(x).

Приведем несколько примеров первообразной:

Последний пример показывает, что иногда первообразная может и совпадать с исходной функцией.

Задание. Докажите, что функция

Первообразные встречаются и в ряде практических задач, особенно в тех, где рассматривается движение тел.

Задание. Автомобиль Buggati Veyron разгоняется от 0 до 40 м/с за 4 секунды. Какое расстояние проедет эта машина за эти 4 секунды, если разгон осуществляется равномерно?

Решение: Если за 4 секунды машина разгоняется до 30 м/с, то за одну секунду она увеличивает скорость на

Примечание – в будущем мы научимся более строго решать такие задачи, и «угадывать» подходящую первообразную не придётся.

Бесконечное количество первообразных

Рассмотрим функцию

Оказывается, что g₁ также является первообразной для у. То есть у одной функции у = 4х³ есть сразу две первообразных:g = x⁴и g = x⁴ + 1! Более того, можно доказать, что у любой функции есть бесконечное количество первообразных!

Действительно, рассмотрим сразу все функции

где С – некоторая константа, то есть параметр. В данном случае можно сказать, что мы рассматриваем не одну функцию, а семейство функций. Продифференцируем g:

Мы видим, что у всех функций из этого семейства, независимо от значения параметра С, производная одинакова. Здесь С может принимать любое действительное значение. Так как действительных чисел бесконечно много, то и количество функций, образующих семейство, также бесконечно. И все они являются первообразными для у = 4х³.

Данная особенность операции интегрирования может быть сформулирована в виде следующей теоремы:

Можно дать и графическую иллюстрацию этого правила. Построим произвольный график g = F(x). Далее построим ещё один график

Очевидно, что он может быть получен параллельным переносом первого графика на С единиц вверх:

Теперь в какой-нибудь точке х₀ проведем касательные к обоим графикам первообразных. Очевидно, что они будут иметь одинаковый угол наклона, так как по сути тоже могут быть получены параллельным переносом:

Если же углы наклона касательных совпадают, то и производные в этих точках также равны.

В связи с наличием у каждой функции бесконечного количества первообразных их часто записывают в общем виде. Например, пусть надо записать первообразную для

Однако 2х² – это лишь одна из бесконечного множества первообразных. Все вместе они образуют семейство, которое записывается так:

Неопределенный интеграл

Каждая математическая операция имеет какое-то особое обозначение. Например, чтобы показать, что мы дифференцируем некоторую функцию, мы ставим после неё штрих (и при необходимости берем в скобки):

Напомним, что операция нахождения первообразной называется интегрированием. Для ее обозначения используется особый знак – интеграл. Например, мы знаем, что первообразная для у = х² – это семейство функций вида

Рассмотрим элементы записанного нами равенства:

Исходная функция – это та самая функция, для которой необходимо найти первообразную, то есть интегрируемая функция. Справа от знака «равно» как раз записывается первообразная. Сразу после первообразной надо писать «+ С». Тем самым мы показываем, что у интегрируемой функции есть бесконечное количество первообразных.

После интегрируемой функции стоит так называемый дифференциал dх (читается как «дэ икс»). В данном случае он указывает, что именно буквой х мы обозначаем переменную в интегрируемой функции. Его значение мы разберем несколько позже. Пока что надо запомнить, что после интегрируемой функции необходимо писать «dx». В целом вся запись

читается так: «интеграл от два икс по дэ икс равен икс в квадрате плюс цэ».

В чем разница между первообразной и интегралом? Первообразная – это функция, при дифференцировании которой получается исходная функция. Интеграл же – это не функция, а целое семейство функций (или их множество), которое включает в себя сразу все первообразные интегрируемой функции.

Так как интегрирование – это действие, обратное дифференцированию, то мы можем проверить результат своих вычислений. Пусть мы записали, что

Получили подынтегральное выражение. Значит, мы всё сделали правильно.

Здесь важно заметить, что в математике существует сразу несколько видов интегралов, каждый из которых имеет разное определение. Здесь описан так называемый «неопределенный интеграл». Несложно догадаться, что существует ещё и «определенный интеграл», который мы рассмотрим на следующих уроках. Теперь можно дать следующее определение:

Задание. Найдите неопределенный интеграл

Решение. Вспомним таблицу производных элементарных функций. Производная синуса равна косинусу:

Заметим, что непосредственно из определения следует важное свойство неопределенного интеграла – производная интеграла равна его подынтегральному выражению:

Грубо говоря, операции интегрирования дифференцирования «сокращают» друг друга.

Задание. Вычислите производную:

Таблица первообразных

Как же вычислять интегралы? Проще всего начать с тех функций, которые уже есть в таблице производных. Напомним, как она выглядит:

Из определения первообразной следует, что для тех функций, которые указаны во втором столбце таблицы, одной из первообразных является соответствующая функция из первого столбца. То есть можно составить такую таблицу первообразных:

Обратите внимание на третью строку снизу. Здесь произошло небольшое изменение – вместо первообразной lnx мы записали ln |x|, то есть использовали модуль числа. Дело в том, что функция

определена при любом значении аргумента, кроме нуля. В то же время функция

не определена при отрицательных значениях х, так как под знаком логарифма не может стоять отрицательное число. Однако области определения интегрируемой функции и ее первообразной должны совпадать. Использование модуля обеспечивает выполнение этого условия.

Полученная нами таблица интегралов не совсем удобна. Предположим, нам надо проинтегрировать функцию

отличающуюся от интересующей нас функции лишь множителем перед х⁵.

Однако можно догадаться, что в качестве подходящей первообразной можно взять функцию

В связи с этим есть смысл немного подкорректировать таблицу первообразных таким образом, чтобы в первом столбце стояли стандартные функции без неудобных множителей. В результате таблица примет следующий вид:

Можно доказать, что каждое равенство в третьем столбце является справедливым. Возьмем, например, равенство

Получили подынтегральное выражение, а это значит, что равенство справедливо. Таким же образом можно доказать и все остальные равенства в таблице.

Задание. Вычислите неопределенный интеграл:

Решение. Этот интеграл присутствует в таблице (7-ая строка), а потому мы просто переписываем равенство из неё:

Задание. Найдите первообразную функции

Правила вычисления интегралов

Что делать в том случае, если надо вычислить интеграл, которого нет в таблице? Существует три несложных правила интегрирования, которые могут помочь в такой ситуации.

Докажем это правило. Для этого просто продифференцируем правую часть равенства:

Получили именно то выражение, которое стоит под знаком интеграла в левой части равенства. Это значит, что формула справедлива.

Рассмотрим пример использования этого правила. Пусть надо найти первообразную функции

Здесь мы представили исходный интеграл как сумму двух более простых интегралов, которые являются табличными

Обратите внимание, что мы не стали складывать константы интегрирования С как подобные слагаемые и писать 2С. Дело в том, что С – это некоторое произвольное число. Но если сложить два произвольных числа, то в итоге получится третье произвольное число, которое также будет обозначаться как С! Поэтому обычно константу С просто дописывают в самом конце решаемого примера.

Естественно, что правило сложения интегралов работает и в случае суммы не двух, а большего количества слагаемых.

Задание. Вычислите неопределенный интеграл

Возможна ситуация, когда мы не уверены в правильности полученного решения. В таком случае можно легко проверить себя, просто продифференцировав получившийся интеграл. В итоге мы должны получить исходную функцию (подынтегральное выражение):

Следующее правило позволяет выносить множитель из-под знака интеграла.

Для доказательства тождества снова продифференцируем его левую часть:

Получили как раз то выражение, которое стоит под интегралом справа. Следовательно, формула верна.

Рассмотрим несколько простейших примеров использования этого метода интегрирования неопределенных интегралов:

Естественно, что правила 1 и 2 можно комбинировать друг с другом, решая более сложные примеры.

Задание. Вычислите неопределенный интеграл от квадратичной функции

Первые два правила достаточно просты и напоминают аналогичные правила дифференцирования. А вот третий метод вычисления неопределенного интеграла более сложный.

Проиллюстрируем его на примере. Пусть надо найти первообразную для функции

Но в нашем случае под знаком косинуса стоит не х, а выражение 5х + 7, являющееся линейной функцией. Поэтому, согласно правилу, мы должны написать впервообразной не sinx, а sin (5x + 7), то есть изменить аргумент. Также надо добавить перед синусом «поправочный множитель», равный 1/k, то есть в нашем случае 1/5:

Проверим себя. Продифференцируем получившуюся первообразную. При этом мы используем правило дифференцирования сложной функции:

Получили ту самую функцию, которую и надо было проинтегрировать.

Приведем ещё несколько примеров использования правила 3:

Напомним, что при изучении производной мы познакомились также с правилами дифференцирования произведения, дроби и сложной функции. Используя их, мы могли найти производную для почти любой функции, которую только могли записать. С решением неопределенных интегралов ситуация значительно сложнее. С помощью приведенных трех правил не получится вычислить такие интегралы, как

Более того, в записанной нами таблице интегралов отсутствует ряд элементарных функций, поэтому мы не сможем даже проинтегрировать такую простую функцию, как

Дело в том, что задача интегрирования является значительно более сложной, чем задача дифференцирования. Отметим три момента. Во-первых, в нашей школьной таблице интегралов, содержащей всего 11 формул, указаны лишь самые простые элементарные функции. Существуют справочники, где в качестве табличных указаны интегралы десятков, а то и сотен функций. Во-вторых, есть и более сложные правила интегрирования, которые изучаются уже в институте. В-третьих, существуют такие элементарные функции, первообразную которых в принципе невозможно записать, используя элементарные функции (синус, косинус, логарифм и т.п.). В связи с этим приходится вводить в рассмотрение новые специальные функции, а также использовать приближенные методы вычислений.

Физический смысл неопределенного интеграла

Напомним физический смысл производной – если известен закон движения материальной точки, то есть некоторая функция S(t), то производная этого закона будет выражать скорость тела в момент времени t:

Отсюда прямо вытекает физический смысл первообразной. Если известен закон изменения скорости v(t), то его первообразная будет являться законом движения S(t). Точнее говоря, законом движения будет являться только одна из первообразных, так как их существует бесконечно много.

Задача. Скорость тела в произвольный момент времени t может быть вычислена по закону

Найдите закон движения материальной точки S(t). Известно, что в начальный момент времени тело находилось в точке с координатой 1,5, то есть S(0) = 1,5.

Решение. Нам надо просто проинтегрировать функцию v(t):

Интеграл вычислен, но это ещё не закон движения, ведь в нем присутствует константа интегрирования. Как от неё избавиться? Надо использовать условие, согласно которому S(0) = 1,5. В общем виде закон движения имеет вид

Мы нашли конкретное значение константы интегрирования. С учетом этого закон движения (1) примет вид: