Алгебра и начала математического анализа, 11 класс
Урок №21. Первообразная.
Перечень вопросов, рассматриваемых в теме
1) Нахождение первообразной
2) Определение первообразной, график которой проходит через заданную точку
3) Решение задач, обратных задаче нахождения закона изменения скорости материальной точки по закону ее движения
Глоссарий по теме
Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для 
Таблица первообразных:
|
Функция f(x) |
Первообразная F(x) |
|
0 |
C = const |
|
1 |
x + C |
|
|
|
|
|
|
|
cos x |
sin x + C |
|
sin x |
-cos x + C |
|
|
|
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Сегодня мы познакомимся с новым математическим понятием – первообразной. Что это такое?
Для начала обратимся к задаче, которая поможет сформулировать определение первообразной.
С точки зрения механики скорость прямолинейного движения определяется как производная пути по времени. Если некоторая точка прошла путь S(t), то ее мгновенная скорость 

Итак, функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для х 
Как следует из определения, операция нахождения первообразной – обратна нахождению производной функции
Примеры и разбор решения заданий тренировочного модуля
№1.Материальная точка движется прямолинейно со скоростью v(t)=8t–4. Найдите закон движения точки, если в момент времени t=2c пройденный путь составил 4 м.
Решение:
Воспользуемся определением первообразной, т.к. S(t)=v0t+at2/2
S’(t) = v(t).
Найдем все первообразные S(t)= -4t+4t2 +c.
Подставим t=2c и пройденный путь S=4 м.
4= -8+16+с
С= -4.
Следовательно, закон движения будет выглядеть следующим образом:
s(t)=4t2–4t–4
Ответ: s(t)=4t2–4t–4
№2. По графику первообразной функции y = F(x) определите количество точек, в которых функция y = f(x) равна нулю.
Решение:
Так как F'(x) = f(x) -по определению первообразной, то точки, в которых функция f(x) (производная функции F(x)) – это точки экстремума функции F(x). А таких точек на графике 4.
Ответ: 4.
№3. По графику первообразной функции y = F(x) определите числовые промежутки, на которых функция y = f(x) имеет отрицательный знак.
Решение:
Так как F’(x) = f(x)- по определению первообразной, то числовые промежутки, на которых функция f(x) (производная функции F(x)) имеет отрицательный знак – это промежутки убывания функции F(x). Таких промежутков на данном графике 2. Это (-2; 1) и (2; 5).
Ответ: (-2; 1); (2; 5).
№4. Докажите, что функция y = F(x) является первообразной для функции y = f(x).
Решение:
Доказательство.
F'(x)=(х2-е2х+2)’=2х-2е2х
По определению первообразной, F'(x)=f(x), следовательно, F'(x) и есть первообразная для функции f(x)
№5. Для функции f(x) = х 2 найти первообразную, график которой проходит через точку (-3; 10).
Решение:
Найдем все первообразные функции f(x) :
Найдем число С, такое, чтобы график функции f(x) = х 2 проходил через точку (-3; 10). Подставим х = – 3, y = 10, получим:
10 = (-3)3/3 +с
С=19
Следовательно,
Ответ:
На чтение 2 мин. Просмотров 20.1k.
Вспомним определения:
1. Дифференцируемая функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство:
F′(x)=f (x).
2. Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом.
Как можно представить себе неопределенный интеграл
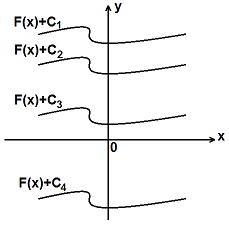
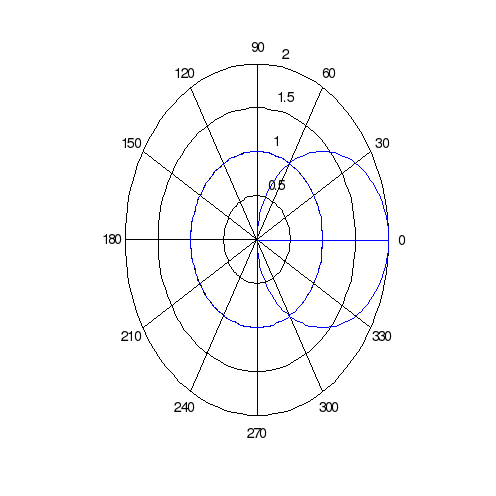
Если в данном примере или задаче не даются начальные условия для нахождения величины С, то мы получаем неоднозначную функцию F (x)+С – семейство интегральных кривых. Графики этих кривых можно совместить с помощью параллельного переноса. Из семейства этих кривых нам нужно уметь выделять ту, которая проходит через данную точку.
Пример 1
Найти для функции f (x)=1-2x первообразную, график которой проходит через точку М(3; 2).
Решение.
F (x)=∫(1-2x) dx=∫dx-2∫xdx=x-x²+C.
Так как F (3)=2 по условию, то получаем равенство:
2=3-3²+С;
2=3-9+С;
2=-6+С → С=8.
Тогда F (x)=x-x²+8.
Пример 2
Найти ∫(sinx-cosx) dx, если при π/2 первообразная равна 6.
Решение.
∫(sinx-cosx) dx=∫sinxdx-∫cosxdx=-cosx-sinx+C.
По условию F (π/2)=6. Получаем равенство: -cos (π/2) -sin (π/2)+C=6;
0-1+C=6 → C=6+1; C=7.
Искомая функция F (x)=-cosx-sinx+7.
Пример 3
Найти первообразную для функции
принимает значение, равное нулю.
Решение.
( 4 оценки, среднее 4.5 из 5 )
Севастопольский
национальный университет ядерной
энергии и промышленности
Расчётно-графическая
работа
по
вычислительной математике
на
тему:
«Неопределенный
и определенный интеграл»
Вариант
№10
Выполнил:
студент 211
класса
Долгорука
Николая
Проверила:
Деркач С. И.
Севастополь
2011
Задание
№1
Найти
первообразную для функции

проходящую через точку

построить ее график.
>>
syms x C
>>
y=sin(2*x);
>>
%найдем все первообразные данной функции
>>
I=int(y,x)+C
I
=
sin(x)^2
+ C
– 1/2
>>
C=solve(‘sin(x)^2
+ C
– 1/2=y’,’C’)
C
=
–
sin(x)^2
+ y
+ 1/2
>>%найдем
первообразную проходящею через точку
с координатами (0;2)
>>
x=0;y=2;
>>
C=-sin(x)^2
+ y
+ 1/2
C
=
2.5000
>>уравнение
прямой в точке М(0;2) имеет вид:
y=
sin(x)^2+2
>>%
построим первообразную заданную
уравнением
>>
syms x
>>
y1=sin(x)^2 + 2.5000 – 1/2
y1
=
sin(x)^2
+ 2
>>
ezplot(y1)
>>
grid on
Задание
№2
Вычислить
неопределённый интеграл

Построить семейство первообразных при
изменении произвольной постоянной от
-10 до 10.
>>
syms x C
>>
y=(x-2)/(x^2-4*x+7)+x^2*2^(x^3)+log(x)/x*sqrt(10+(log(x))^2)+4*x/sqrt(4-x^2)
y
=
2^(x^3)*x^2
+ (x – 2)/(x^2 – 4*x + 7) + (4*x)/(4 – x^2)^(1/2) + (log(x)*(log(x)^2
+ 10)^(1/2))/x
>>%
вычислим неопределённый интеграл
>>
I=int(y,x)+C
I
=
C
+ log(x^2 – 4*x + 7)/2 + (log(x)^2 + 10)^(3/2)/3 + 2^(x^3)/(3*log(2))
– 4*(4 – x^2)^(1/2)
%
построим семейство первообразных
>>
for
C=-10:10
syms
x C
y=C
+ log(x^2 – 4*x + 7)/2 + (log(x)^2 + 10)^(3/2)/3 + 2^(x^3)/(3*log(2))
– 4*(4 – x^2)^(1/2);
ezplot(y)
hold
on
end
>>
grid on
Задание
№3
Найти
интеграл методом подстановки
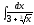

>>%
решим интеграл относительно t
>>
syms t C
>>
y=3*t^2/(3+t)
y
=
(3*t^2)/(t
+ 3)
>>
I=int(y,t)+ C
I
=
C
– 9*t + 27*log(t + 3) + (3*t^2)/2
>>%
обратная
подстановка
>>
syms x C
>>
t=(x)^(1/3);
>>
I =
9*t
+ 27*log(t + 3) + (3*t^2)/2 -C
>>
I=C – 9*t + 27*log(t + 3) + (3*t^2)/2
I
=
27*log(x^(1/3)
+ 3) – 9*x^(1/3) + (3*x^(2/3))/2 +C
Задание
№4
Найти
интеграл, используя формулу интегрирования
по частям
Формула
интегрирования по частям имеет вид:
>>%
зададим
и
>>
syms x C
>>
u=(cos(x))^2;v=int(2*x,x);
>>%
найдем интеграл, используя формулу
>>
I=u*v-int(v*diff(u,x),x)+C
I
=
(x*sin(2*x))/2
+ (x^2*(2*sin(x)^2 – 1))/2 – sin(x)^2/2 + x^2*cos(x)^2 +C
Задание
№5
Вычислить площадь
криволинейной трапеции, ограниченной
линиями

с основанием на оси

построить и закрасить криволинейную
трапецию, подобрать масштаб.
>>
syms x
>>
y=exp(2*x)/(exp(2*x)-1)
y
=
exp(2*x)/(exp(2*x)
– 1)
>>%
построим функцию и прямые, заданные
уравнением х= log(2),
х= log(3)и
у=0
>>
ezplot(y)
>>
grid on
>>
hold on
>>
ezplot(‘y*0+x-log(2)=0’)
>>
ezplot(‘y*0+x-log(3)=0’)
>>
ezplot(‘y+x*0=0’)
>>%Подберьом
маштаб воспользовавшысь функцией axis
>>
axis ([-5 5 -5 5])
>>закрашиваем
криволинейную трапецию
>>
a=log(2);b=log(3);
>>
x1=[a:0.01:b];
>>
y1=subs(exp(2*x)/(exp(2*x)-1),x,x1);
>>
patch([a x1 b],[0 y1 0],[0 0 1])
>>%
найдем площадь криволинейной трапеции
>>
syms x
>>
S=int(1/sqrt(x^2+2*x+4),x,-2,0)
S
=
log(3)
>>
S=int(exp(2*x)/(exp(2*x)-1),x,log(2),log(3))
S
=
log(exp(2473854946935173/1125899906842624)
– 1)/2 – log(exp(6243314768165359/4503599627370496) – 1)/2
>>
S=vpa(S,4)
S
=
0.4904
S
=0.4904(кв. ед)
Задание
№6
Исследовать на
сходимость интеграл

>>
syms
x
>>
y=1/(x^2+2);
>>%
найдём интеграл от функции у с пределами
>>
I=int(y,x,-inf,inf)
I
=
(pi*2^(1/2))/2
>>%Интеграл
сходится, поскольку равен числу.
Задание
№7
Вычислить площадь
фигуры, ограниченной линиями



>>
phi=0:pi/100:2*pi;
>>%
задам
и строим
заданные
линии
>>
ro=2*cos(phi);
>>
polar(phi,ro)
>>
hold on
>>
ro=1+phi*0;
>>
polar(phi,ro)
>>
hold on
>>
polar([0 0],[0 2])
>>
syms phi
>>%
Вычисляем
площадь фигуры с приделами интегрирования
от 0 до pi/3
>>
S=1/2*2*int(((2*cos(phi))^2-1^2),phi,0,pi/3)
S
=
pi/3
+ 3^(1/2)/2
>>
vpa(S,4)
ans
=
1.913
S=1.913(кв.
ед)
Задание
№8
Найти площадь
поверхности, образованной вращением
кривых

вокруг оси

>>%
зададим функции
построим их
график
.
>>
syms x
>>
y=x^2/2
y
=
x^2/2
>>
ezplot(y)
>>
hold on
>>
ezplot(‘3/2’)
>>
syms
y
>>
x=sqrt(2*y)
x
=
2^(1/2)*y^(1/2)
>>%
т. к. график вращаэм симметрична
относительно оси OУ,
то площадь получившегося тела будет
равен S=
с пределами интегрирования от 0 до
3/2.
>>
S=2*pi*int(x*sqrt(1+(diff(x,y))^2),y,0,3/2)
S
=
(14*pi)/3
>>
vpa(S,4)
ans
=
14.66
S
=14.66(кв.
ед)
Соседние файлы в папке опр инт
- #
- #
- #
- #
- #
- #
Первообразная. Неопределенный интеграл и его свойства
- Понятие первообразной
- Основное свойство первообразной. Неопределенный интеграл
- Таблица неопределенных интегралов
- Правила нахождения первообразных
- Свойства неопределенных интегралов
- Примеры
п.1. Понятие первообразной
Функция (F(x)) называется первообразной для функции (f(x)) на промежутке (X), если для всех (xin X) выполняется равенство (F'(x)=f(x)).
На практике промежутком (X) считают облать определения функции (F(x)).
Например:
1) Функция (F(x)=x^2) является первообразной для (f(x)=2x), т.к. для любого (x) производная (F'(x)=f(x)).
2) Функция (F(x)=cosx) является первообразной для (f(x)=sinx), т.к. для любого (x) производная (F'(x)=f(x)).
Поиск производной данной функции называют дифференцированием.
Поиск первообразной данной функции называют интегрированием.
Дифференцирование и интегрирование являются взаимно обратными операциями.
п.2. Основное свойство первообразной. Неопределенный интеграл
Каждая первообразная для функции (f(x)) имеет вид (F(x)+C), где (F(x)) – одна из этих первообразных, (C) – произвольная постоянная.
Действительно, по правилу нахождения производной суммы: $$ (F(x)+C)’=F'(x)+C’=f(x)+0=f(x) $$ Т.е. первообразная определена с точностью до константы.
Например:
Для (f(x)=sinx)
Первообразными будут begin{gather*} F(x)=cosx, F(x)=cosx+1, \ F(x)=cosx-2, F(x)=cosx+0,100500 end{gather*} и т.д.
Множество всех первообразных функции (f(x)) называют неопределенным интегралом этой функции: $$ int f(x)dx=F(x)+C $$
Например: $$ int x^2 dx=frac{x^3}{3}+C, int frac{dx}{sqrt{x}}=2sqrt{x}+C $$
п.3. Таблица неопределенных интегралов
Пользуясь результатами, полученными для производных (см. Главу 8 данного справочника), можем составить таблицу неопределенных интегралов.
Таблица неопределенных интегралов
(f(x))
(int f(x)dx=F(x)+C)
(x)
(frac{x^2}{2}+C)
(x^q, qne -1)
(frac{x^{q+1}}{q-1}+C)
(frac1x)
(ln |x|+C)
(frac{1}{cos^2x})
(tgx+C)
(frac{1}{sin^2x})
(-ctgx+C)
(a^x)
(frac{a^x}{ln a})
Если взять производную от функции в правом столбце, мы получаем функцию в левом столбце. В этом легко убедиться самостоятельно.
п.4. Правила нахождения первообразных
Первообразная суммы равна сумме первообразных.
Если (F(x)) и (G(x)) являются первообразными для функций (f(x)) и (g(x)),
то (F(x)+G(x)) – первообразная для функции (f(x)+g(x)).
Действительно $$ begin{cases} F'(x)=f(x)\ G'(x)=g(x) end{cases} Rightarrow left(F(x)+G(x)right)’=F'(x)+G'(x)=f(x)+g(x) $$
Например:
Найдем первообразную функции (y=x^5+sinx)
Это сумма двух функций (f_1(x)=x^5, f_2(x)=sinx).
Соответствующие первообразные (F_1(x)=frac{x^6}{3}, F_2(x)=-cosx)
Общая первообразная с учетом постоянного слагаемого:
(F(x)=frac{x^6}{3}-cosx+C)
Постоянный множитель функции является постоянным множителем первообразной.
Если (F(x)) является первообразной для (f(x)),
то (kF(x)) – первообразная для (kf(x)).
Действительно $$ left(kF(x)right)’=kF'(x)=kf(x) $$
Например:
Найдем первообразную функции (y=5sinx+2=5cdot sinx+2cdot 1)
Первообразная для синуса (F_1(x)=-cosx), первообразная для единицы (F_2(x)=x)
Общая первообразная
(F(x)=-5cosx+2x)
Линейное преобразование аргумента функции.
Если (F(x)) является первообразной для (f(x)),
то для функции с аргументом (f(kx+b)) – первообразной будет (frac1k F(kx+b)).
Действительно
Для (x) получаем цепочку отображений: (xrightarrow kx+brightarrow F(kx+b))
По правилу дифференцирования сложной функции (см. §45 данного справочника) begin{gather*} left(frac1k F(kx+b)right)’=frac1kcdot F'(kx+b)cdot (kx+b)’=frac1kcdot F'(kx+b)cdot k=F'(kx+b)=\ =f(kx+b) end{gather*}
Например:
Найдем первообразную функции (y=sin(5x+2) )
Нам известно, что первообразная для (f(x)=sinx, F=-cosx)
При преобразовании аргумента (xrightarrow 5x+2) у новой первообразной будет новый аргумент и множитель (frac1k=frac15). Получаем:
(F(x)=-frac15 cos(5x+2))
п.5. Свойства неопределенных интегралов
Свойства неопределенных интегралов являются прямыми следствиями свойств первообразных.
Интеграл суммы равен сумме интегралов: $$ int(f(x)+g(x))dx=int f(x)dx+int g(x)dx $$
Постоянный множитель перед функцией можно вынести за знак интеграла: $$ int kf(x)dx=kint f(x)dx $$
Линейное преобразование аргумента подынтегральной функции: $$ int f(xk+b)dx=frac1k F(kx+b)+C $$ где (F(x)) – первообразная для (f(x), kne 0)
Например:
Найдем интеграл (int left(xsqrt{x}+frac{1}{cos^2(2x+1)}right)dx)
Подынтегральное выражение – это сумма двух функций, первообразные для которых: begin{gather*} F_1(x)=frac{x^{frac32+1}}{frac32+1}=frac{x^{frac52}}{frac52}=frac25x^2sqrt{x}\ F_2(x)=frac12cdot tg(2x-1) end{gather*} Получаем: begin{gather*} intleft(xsqrt{x}+frac{1}{cos^2(2x-1)}right)dx=frac25x^2sqrt{x}+frac12 tg(2x-1)+C end{gather*} Поверим результат интегрирования дифференцированием: begin{gather*} left(frac25x^2sqrt{x}+frac12 tg(2x-1)+Cright)’=frac25cdotfrac52 x^{frac52-1}+frac12cdotfrac{1}{cos^2(2x-1)}cdot (2x-1)’+0=\ =xsqrt{x}+frac{1}{cos^2(2x-1)} end{gather*} Мы получили исходную подынтегральную функцию. Результат интегрирования верный.
п.6. Примеры
Пример 1. Докажите, что функция (F(x)) является первообразной для (f(x)), если:
a) (F(x)=x^2sqrt{x}+14sin3x)
(f(x)=frac52 xsqrt{x}+42cos 3x)
Найдем производную (F'(x)) $$ F'(x)=frac52cdot x^{frac52-1}+14cdot cos3xcdot (3x)’=frac52 xsqrt{x}+42cos3x=f(x) $$ Что и требовалось доказать.
б) (F(x)=tg5x-4e^x)
(f(x)=frac{5}{cos^2 5x}-4e^x) $$ F'(x)=frac{1}{cos^2 5x}cdot (5x)’-4e^x=frac{5}{cos^2 5x}-4e^x=f(x) $$ Что и требовалось доказать.
Пример 2. Найдите первообразную функции, которая проходит через данную точку:
a) (y=sinx, Aleft(fracpi 3;frac14right))
Общий вид первообразных для синуса: $$ F(x)=-cosx+C $$ Чтобы найти ту первообразную, которая проходит через данную точку, нужно подставить координаты этой точки: $$ frac14=-cosfracpi 3+CRightarrow C=frac14+cosfracpi 3=frac14+frac12=frac34 $$ Искомая первообразная: $$ F(x)=-cosx+frac34 $$
б) (y=(x+2)(3x-1), A(0;4))
Получаем квадратный трехчлен: (y=3x^2+5x-6)
Общий вид первообразной: $$ F(x)=3cdotfrac{x^3}{3}+5cdotfrac{x^2}{2}-6cdot x+C=x^3+2,5x^2-x+C $$ Первообразная, которая проходит через данную точку: $$ 4=0^3+2,5cdot 0^2-0+CRightarrow C=4 $$ Искомая первообразная: $$ F(x)=x^3+2,5x^2-x+4 $$
в*) (y=frac{x}{x+3}, A(-2;1))
Выделим целую часть: (y=frac{x}{x+3}=frac{(x+3)-3}{x+3}=1-frac{3}{x+3})
Общий вид первообразной: $$ F(x)=x-3cdotln(x+3)+C $$ Первообразная, которая проходит через данную точку: $$ 1=-2-3cdotln(-2+3)+C=-2-3cdot 0+C=-2+CRightarrow C=3 $$ Искомая первообразная: $$ F(x)=x-3ln(x+3)+3 $$
г*) (y=frac{cos2x}{cos^2x}, Aleft(fracpi 4;fracpi 2right))
Преобразуем тригонометрическое выражение: (y=frac{cos2x}{cos^2x}=frac{2cos^2x-1}{cos^2x}=2-frac{1}{cos^2x})
Общий вид первообразной: $$ F(x)=2x-tgx+C $$ Первообразная, которая проходит через данную точку: $$ fracpi 2=2cdotfracpi 4-tgfracpi 4+C=fracpi 2-1+CRightarrow C=1 $$ Искомая первообразная: $$ F(x)=2x-tgx+1 $$
Пример 3. Найдите неопределенный интеграл и результат проверьте дифференцированием:
a) $$ intleft(e^x+frac1xright)dx=e^x+ln|x|+C $$ Проверка: $$ (e^x+ln|x|+C)’=e^x+frac1x+0=e^x+frac1x $$ Получили подынтегральную функцию. Ответ верный.
б) $$ intleft(frac1x-frac{4}{x^2}-frac{3}{sin^2x}right)dx=ln|x|-4cdotfrac{x^{-2+1}}{-2+1}+3cdot ctgx+C=ln|x|+frac4x+3ctgx+C $$ Проверка: $$ (ln|x|+frac4x+3ctgx+C)’=frac14+4cdotleft(-frac{1}{x^2}right)+3cdotleft(-frac{1}{sin^2x}right)+0=frac1x-frac{4}{x^2}-frac{3}{sin^2x} $$ Получили подынтегральную функцию. Ответ верный.
в*) begin{gather*} intfrac{pi^x-1}{pi^x-pi^{2x}}dx=-intfrac{pi^x-1}{pi^{2x}-pi^x}dx=-intfrac{pi^x-1}{pi^x(pi^x-1)}dx=-intpi^{-x}dx=\ =-(-2)frac{pi^x}{lnpi}+C=frac{pi^{-x}}{lnpi}+C end{gather*} Проверка: begin{gather*} left(frac{pi^{-x}}{lnpi}+Cright)’=frac{pi^{-x}lnpicdot(-x)’}{lnpi}+0=pi^{-x}=-frac{1}{pi^x}=-frac{pi^x-1}{pi^x(pi^x-1)}=\ =-frac{pi^x-1}{pi^{2x}-pi^x}=frac{pi^x-1}{pi^x-pi^{2x}} end{gather*} Получили подынтегральную функцию. Ответ верный.
г*) begin{gather*} intfrac{4}{1-cosx}dx=intfrac{4}{2sin^2frac x2}dx=2intfrac{dx}{sin^2frac x2}=-2cdot 2ctgfrac x2+C=-4ctgfrac x2+C end{gather*} Проверка: begin{gather*} left(-4ctgfrac x2+Cright)’=-4cdotleft(-frac{1}{sin^2frac x2}right)cdotleft(frac x2right)’+0=frac{4}{2sin^2frac x2}=frac{4}{1-cosx} end{gather*} Получили подынтегральную функцию. Ответ верный.
Пример 4*. Найдите ту первообразную для функции (f(x)=3x^3-4), для графика которой касательной является прямая (y=-x+2)
Общий вид первообразной: (F(x)=3cdotfrac{x^4}{4}-4cdot x+C=frac34 x^4-4x+C)
Уравнение касательной (см. §47 данного справочника) к первообразной: $$ y=underbrace{F'(x_0)}_{=f(x_0)}(x-x_0)+F(x_0)=f(x_0)cdot x+(F(x_0)-f(x_0)cdot x_0) $$ По условию ( y=-x+2Rightarrow begin{cases} f(x_0)=-1\ F(x_0)-f(x_0)cdot x_0=2 end{cases} )
Из первого уравнения найдем абсциссу точки касания: $$ 3x_0^3-4=-1Rightarrow 3x_0^3=3Rightarrow x_0^3=1Rightarrow x_0=1 $$ Тогда из второго уравнения: $$ F(x_0)=f(x_0)x_0+2=-1cdot 1+2=1 $$ Получаем: $$ 1=frac34cdot 1^4-4cdot 1+C=-3frac14+CRightarrow C=1+3frac14=4frac14 $$ Искомая первообразная: $$ F(x)=frac34x^4-4x+4frac14 $$
Сегодня на уроке мы введём понятие первообразной функции. Познакомимся
с основным свойством первообразных.
Перейдём к рассмотрению новой темы. прямой. Закон движения точки задан
функцией . Тогда
мгновенная скорость равна производной
функции , то есть
верно равенство . Об этом мы
с вами говорили на одном из предыдущих занятий.
На практике встречается обратная задача, где по заданной
скорости движения точки надо найти
закон движения, то есть найти такую функцию , производная
которой равна .
Функцию , такую что
, называют первообразной
функции .
Приведём пример. Пусть , где
– заданное
число. Тогда функция является первообразной
функции , так как
.
Сформулируем определение. Функция называется первообразной
функции на некотором
промежутке, если для любого из этого
промежутка .
Например, функция – первообразная функции
, так как
.
Функция – первообразная функции
, так как
.
Давайте докажем, что функции ,
,
являются
первообразными функции .
Обозначим .
Тогда .
Вторую функцию обозначим как .
Найдём .
Третью функцию обозначим как .
Найдём .
Получается, что производные всех трёх функций равны. Становится
понятно, что эти функции не являются единственными первообразными функции . Вообще,
любая функция вида , где
–
постоянная, является первообразной функции . Это следует
из того, что производная постоянной равна нулю. Рассмотренный пример
показывает, что для заданной функции её производная определяется неоднозначно.
Пусть и
– две
первообразные функции . Тогда
и
. Обозначим
функцией .
Найдём производную этой разности:
.
Мы знаем, что если производная функции равна 0 на
некотором промежутке, то касательная к графику функции параллельна
оси в каждой
точке этого промежутка. Поэтому графиком функции является
прямая, параллельная оси , то есть
, где
– некоторая
постоянная.
Тогда . Откуда
следует, что .
Итак, основное свойство первообразных заключается в
следующем: каждая первообразная функции на некотором
промежутке может быть записана в виде , где
– одна из
этих первообразных функции на том же
промежутке, а –
произвольная постоянная.
Основному свойству первообразных можно придать геометрический
смысл. Если – одна из
первообразных функции , то любая
первообразная этой функции получается прибавлением к некоторой
постоянной: .
Так, из графика функции получаются
графики функций сдвигом
вдоль оси Oy. Получается, что выбором постоянной C можно добиться того, чтобы
график первообразной проходил через заданную точку.
Прежде чем приступить к выполнению заданий, давайте докажем, что
для любого действительного функция
является
первообразной функции на
промежутке .
А теперь выполним несколько заданий.
Задание первое. Покажите, что функция является
первообразной функции на множестве
:
а) ,
; б)
,
.
Решение.
Задание второе. Найдите все
первообразные функций:
а) ; б)
.
Решение.
Задание третье. Для функции найдите
первообразную, график которой проходит через точку .
Решение.