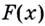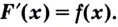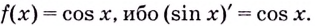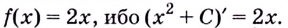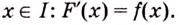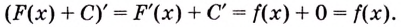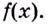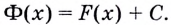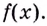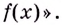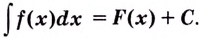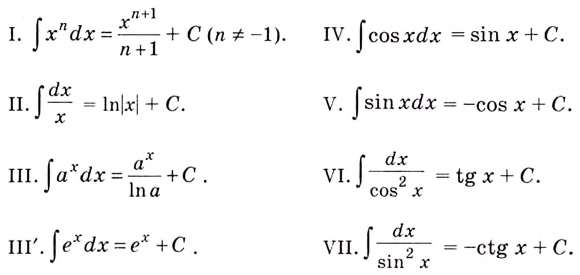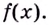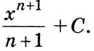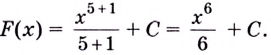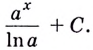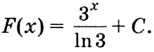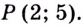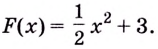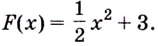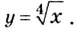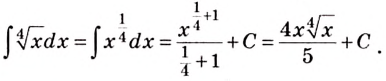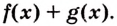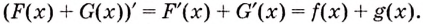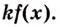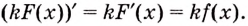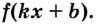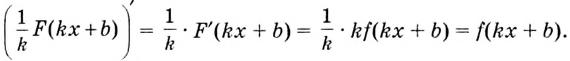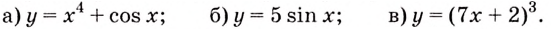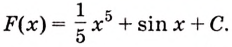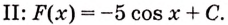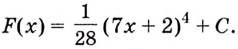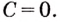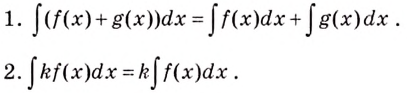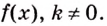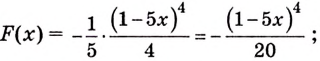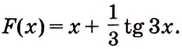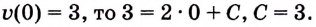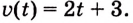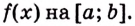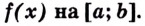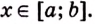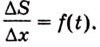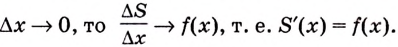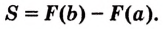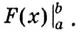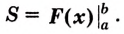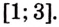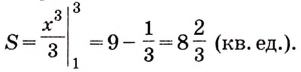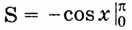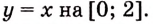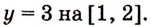На этой странице вы узнаете:
- Родственные связи первообразной. Как первообразная связана с производной?
- Одна функция, но много ее первообразных. Как такое происходит?
Понятие первообрвообразной
Легко догадаться, что термин “первоОбразная” происходит от двух слов: первый и образ. Первым образом у автомобиля была повозка, а у пюре — картофель.
Вернемся к математике.
Ранее мы уже рассматривали, что такое Производная и как найти её. Давайте быстро вспомним, что нахождение производной или дифференцирование — это совершение математической операции над функцией. То есть, следуя определенным правилам, любая функция может быть преобразована в новую функцию, которая и будет производной.
В обычной жизни, совершая несколько действий, мы можем преобразовать муку в тесто, а затем и в пирожки. Но разобрать готовый пирожок на муку у нас уже не получится. Зато в математике всегда можно вернуться на шаг назад: сложили два числа — вычтем обратно, возвели в степень — извлечем корень.
Похожим образом мы можем поступить с функцией.
Возьмем любую функцию, например, f(x) = x2 и найдем для нее производную f'(x) = 2x — получилась новая функция. Теперь для того, чтобы вернуться на шаг назад, нам нужно найти первообразную от новой функции (f'(x) = 2x).
Первообразной для функции f(x) называется такая функция F(x), для которой выполняется равенство: F'(x) = f(x).
То есть, если взять производную от первообразной какой-либо функции, получится сама эта функция. Процесс нахождения множества первообразных называется интегрированием.
F'(x) = f(x)
Связь первообразной и функции можно рассмотреть на примере родственных связей. Мама является предшественником дочери, а первообразная — предшественник функции.
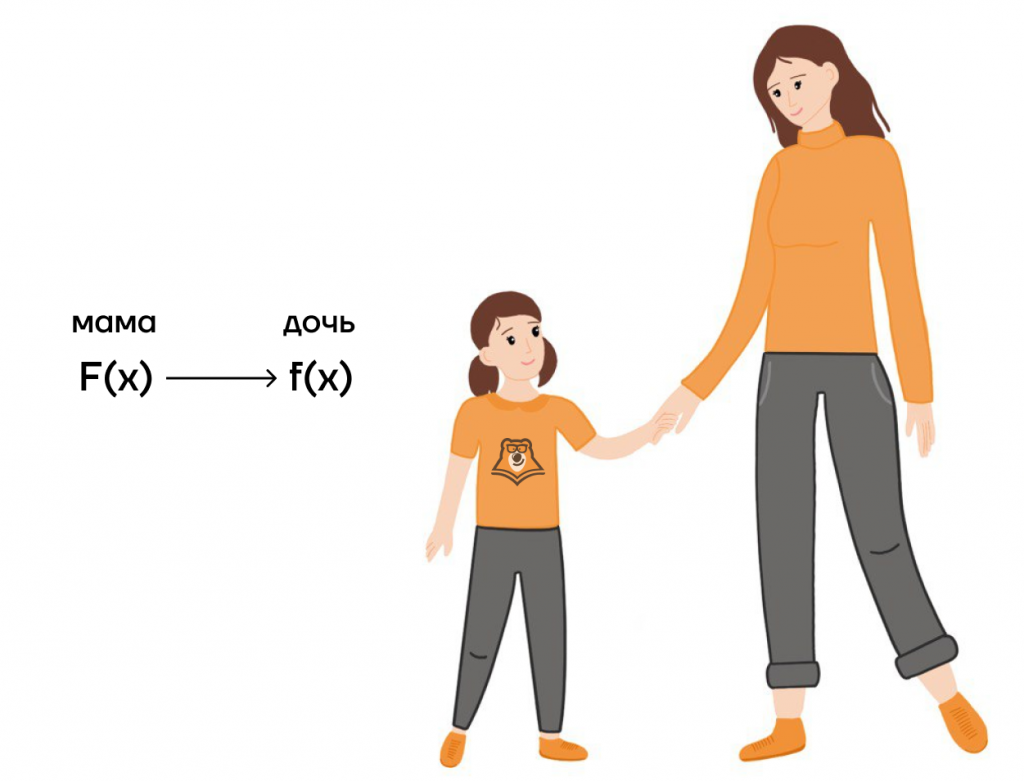
Для нахождения первообразных существует специальная таблица. В ней приведены первообразные для каждой функции. А чтобы убедиться в этом, можно найти производную от первообразной и сравнить с функцией. Они будут одинаковые.
Таблица первообразных

Где С — произвольное число
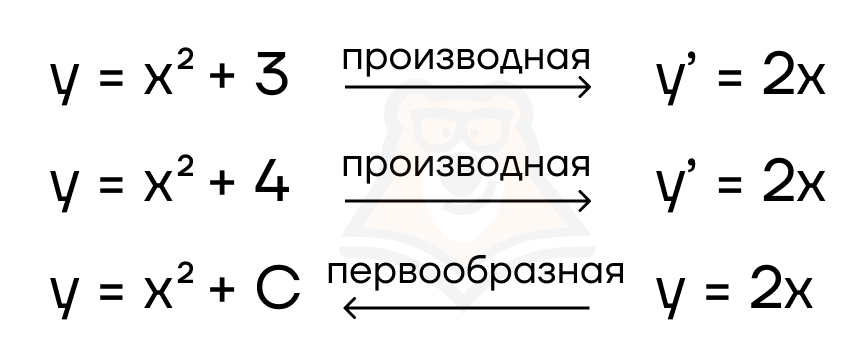
Так как нахождение первообразной — это обратное действие нахождению производной, а производная от константы всегда равна нулю, первообразная для множества функций с разными константами будет одинаковой.
Важно: F(x) первообразная f(x) только на том промежутке, где F(x) и f(x) существуют. То есть, (F(x) = frac{1}{2} * ln (2x) + C) первообразная (f(x) = frac{1}{2}x) на промежутке 2х > 0 (rightarrow) x > 0
Рассмотрим нахождение первообразной от следующей функции
y = 2x3
Применим правило интегрирования для степенной функции из таблицы первообразных
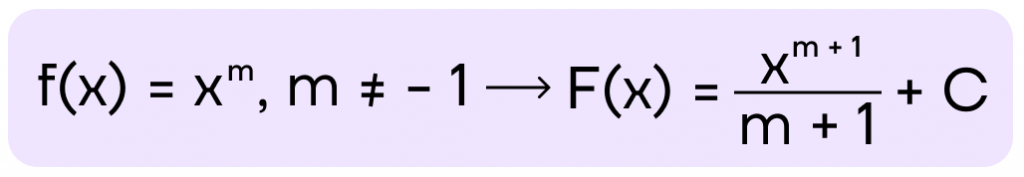
(F(x) = frac{2x^4}{4} + C)
(F(x) = frac{1}{2} x^4 + C)
Правила нахождения первообразных:
- Если нужно найти первообразную от произведения числа на функцию, то первообразной выражения будет произведение этого числа на первообразную функции.
a*f(x) (rightarrow) a*F(x)
Пример:
f(x) = 4x (rightarrow F(x) = 4 * frac{x^2}{2} = 2x^2)
- Если нужно найти первообразную от суммы/разности двух функций, то первообразной выражения будет сумма/разность первообразных этих двух функций.
g(x) (pm) f(x) (rightarrow) G(x) (pm) F(x)
Пример:
f(x) = x2 + 2 (rightarrow F(x) = frac{x^3}{3} + 2x)
Фактчек
- Первообразной для функции f(x) называется такая функция F(x), для которой выполняется равенство: F'(x) = f(x)
- Для нахождения первообразных существует специальная таблица первообразных
- Правила нахождения первообразных:
a*f(x) (rightarrow) a*F(x)
g(x) (pm) f(x) (rightarrow) G(x) (pm) F(x)
Проверь себя
Задание 1.
Найдите первообразную функции y = 4x5
- F(x) = 20x4
- (F(x) = frac{1}{3}x^6)
- (F(x) = frac{1}{3}x^5)
- (F(x) = frac{2}{3}x^6)
Задание 2.
Найдите первообразную функции y = 4
- F(x) = 4x
- F(x) = x
- (F(x) = frac{1}{2}x^2)
- (F(x) = frac{1}{2}x)
Задание 3.
Найдите первообразную функции (y = 2sin x)
- F(x)= x
- (F(x) = -2cos x)
- (F(x) = frac{1}{2}cos x)
- (F(x) = -2sin x)
Задание 4.
Найдите первообразную функции y = 2x
- (F(x) = frac{2^x}{ln2})
- F(x) = ln2
- F(x) = 2
- F(x) = x2
Ответы: 1. — 4; 2. — 1; 3. — 2; 4. -1
Первообразная функции и общий вид
20 июля 2015
Этот урок — первый из серии видео, посвященных интегрированию. В нём мы разберём, что такое первообразная функции, а также изучим элементарные приёмы вычисления этих самых первообразных.
На самом деле здесь нет ничего сложного: по существу всё сводится к понятию производной, с которым вы уже должны знакомы.:)
Сразу отмечу, что, поскольку это самый первый урок в нашей новой теме, сегодня не будет никаких сложных вычислений и формул, но то, что мы изучим сегодня, ляжет в основу гораздо более сложных выкладок и конструкций при вычислении сложных интегралов и площадей.
Кроме того, приступая к изучению интегрирования и интегралов в частности, мы неявно предполагаем, что ученик уже, как минимум, знаком к понятиям производной и имеет хотя бы элементарные навыки их вычисления. Без четкого понимания этого, делать в интегрировании совершенно нечего.
Однако здесь же кроется одна из самых частых и коварных проблем. Дело в том, что, начиная вычислять свои первые первообразные, многие ученики путают их с производными. В результате на экзаменах и самостоятельных работах допускаются глупые и обидные ошибки.
Поэтому сейчас я не буду давать четкого определения первообразной. А взамен предлагаю вам посмотреть, как она считается на простом конкретном примере.
Что такое первообразная и как она считается
Допустим, нам необходимо посчитать следующую производную:
[fleft( x right)={{x}^{3}}]
Мы знаем такую формулу:
[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]
Считается эта производная элементарно:
[{f}’left( x right)={{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}}]
Посмотрим внимательно на полученное выражение и выразим ${{x}^{2}}$:
[{{x}^{2}}=frac{{{left( {{x}^{3}} right)}^{prime }}}{3}]
Но мы можем записать и так, согласно определению производной:
[{{x}^{2}}={{left( frac{{{x}^{3}}}{3} right)}^{prime }}]
А теперь внимание: то, что мы только что записали и есть определением первообразной. Но, чтобы записать ее правильно, нужно написать следующее:
[{{x}^{2}}to frac{{{x}^{3}}}{3}]
Аналогично запишем и такое выражение:
[{{x}^{4}}to frac{{{x}^{5}}}{5}]
Если мы обобщим это правило, то сможем вывести такую формулу:
[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]
Теперь мы можем сформулировать четкое определение.
Первообразной функции называется такая функция, производная которой равна исходной функции.
Вопросы о первообразной функции
Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:
- Допустим, хорошо, эта формула верна. Однако в этом случае при $n=1$ у нас возникают проблемы: в знаменателе появляется «ноль», а на «ноль» делить нельзя.
- Формула ограничивается только степенями. Как считать первообразную, например, синуса, косинуса и любой другой тригонометрии, а также констант.
- Экзистенциальный вопрос: а всегда ли вообще можно найти первообразную? Если да, то как быть с первообразной суммы, разности, произведения и т.д.?
На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.
Решение задач со степенными функциями
Давайте попробуем посчитать такое выражение:
[{{x}^{-1}}to frac{{{x}^{-1+1}}}{-1+1}=frac{1}{0}]
Как видим, данная формула для ${{x}^{-1}}$ не работает. Возникает вопрос: а что тогда работает? Неужели мы не можем посчитать ${{x}^{-1}}$? Конечно, можем. Только давайте для начала вспомним такое:
[{{x}^{-1}}=frac{1}{x}]
Теперь подумаем: производная какой функции равна $frac{1}{x}$. Очевидно, что любой ученик, который хоть немного занимался этой темой, вспомнит, что этому выражению равна производная натурального логарифма:
[{{left( ln x right)}^{prime }}=frac{1}{x}]
Поэтому мы с уверенностью можем записать следующее:
[frac{1}{x}={{x}^{-1}}to ln x]
Эту формулу нужно знать, точно так же, как и производную степенной функции.
Итак, что нам известно на данный момент:
- Для степенной функции — ${{x}^{n}}to frac{{{x}^{n+1}}}{n+1}$
- Для константы — $=constto cdot x$
- Частный случай степенной функции — $frac{1}{x}to ln x$
Идем далее. Что нам еще может потребоваться? Конечно же, правило вычисления первообразных от суммы и от разности. Запишем так:
[fleft( x right)to Fleft( x right)]
[gleft( x right)to Gleft( x right)]
[f+gto F+G]
[f-g=F-G]
[ccdot fto ccdot Fleft( c=const right)]
А если простейшие функции мы начнем умножать и делить, как тогда посчитать первообразную произведения или частного. К сожалению, аналогии с производной произведения или частного здесь не работают. Какой-либо стандартной формулы не существует. Для некоторых случаев существуют хитрые специальные формулы — с ними мы познакомимся на будущих видеоуроках.
Однако запомните: общей формулы, аналогичной формуле для вычисления производной частного и произведения, не существует.
Решение реальных задач
Задача № 1
[fleft( x right)={{x}^{2}}+5{{x}^{4}}]
Давайте каждую из степенных функций посчитаем отдельно:
[{{x}^{2}}to frac{{{x}^{3}}}{3}]
[5{{x}^{4}}to 5cdot frac{{{x}^{5}}}{5}={{x}^{5}}]
Возвращаясь к нашему выражению, мы запишем общую конструкцию:
[Fleft( x right)=frac{{{x}^{3}}}{3}+{{x}^{5}}]
Задача № 2
[fleft( x right)=frac{x+1}{x}]
Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:
[fleft( x right)=frac{x}{x}+frac{1}{x}=1+frac{1}{x}]
Мы разбили дробь на сумму двух дробей.
Посчитаем:
[Fleft( x right)=1cdot x+ln x]
[Fleft( x right)=x+ln x]
Хорошая новость состоит в том, что зная формулы вычисления первообразных, вы уже способны считать более сложные конструкции. Однако давайте пойдем дальше и расширим наши знания еще чуть-чуть. Дело в том, что многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к ${{x}^{n}}$, могут быть представлены в виде степени с рациональным показателем, а именно:
[sqrt{x}={{x}^{frac{1}{2}}}]
[sqrt[n]{x}={{x}^{frac{1}{n}}}]
[frac{1}{{{x}^{n}}}={{x}^{-n}}]
Все эти приемы можно и нужно комбинировать. Степенные выражения можно
- умножать (степени складываются);
- делить (степени вычитаются);
- умножать на константу;
- и т.д.
Решение выражений со степенью с рациональным показателем
Пример № 1
[fleft( x right)=7sqrt{x}+sqrt[4]{x}]
Посчитаем каждый корень отдельно:
[]
[sqrt{x}={{x}^{frac{1}{2}}}to frac{{{x}^{frac{1}{2}+1}}}{frac{1}{2}+1}=frac{{{x}^{frac{3}{2}}}}{frac{3}{2}}=frac{2cdot {{x}^{frac{3}{2}}}}{3}]
[sqrt[4]{x}={{x}^{frac{1}{4}}}to frac{{{x}^{frac{1}{4}}}}{frac{1}{4}+1}=frac{{{x}^{frac{5}{4}}}}{frac{5}{4}}=frac{4cdot {{x}^{frac{5}{4}}}}{5}]
Итого всю нашу конструкцию можно записать следующим образом:
[Fleft( x right)=7cdot frac{2cdot {{x}^{frac{3}{2}}}}{3}+frac{5cdot {{x}^{frac{5}{4}}}}{4}=frac{14cdot {{x}^{frac{3}{2}}}}{3}+frac{4cdot {{x}^{frac{5}{4}}}}{5}]
Пример № 2
[fleft( x right)=frac{1}{sqrt{x}}-frac{1}{{{x}^{3}}}]
Запишем:
[frac{1}{sqrt{x}}={{left( sqrt{x} right)}^{-1}}={{left( {{x}^{frac{1}{2}}} right)}^{-1}}={{x}^{-frac{1}{2}}}]
Следовательно, мы получим:
[Fleft( x right)=frac{{{x}^{-frac{1}{2}+1}}}{-frac{1}{2}+1}=frac{{{x}^{frac{1}{2}}}}{frac{1}{2}}=2{{x}^{frac{1}{2}}}=2sqrt{x}]
[frac{1}{{{x}^{3}}}={{x}^{-3}}to frac{{{x}^{-3+1}}}{-3+1}=frac{{{x}^{-2}}}{-2}=-frac{1}{2{{x}^{2}}}]
Итого, собирая все в одно выражение, можно записать:
[Fleft( x right)=2sqrt{x}+frac{1}{2{{x}^{2}}}]
Пример № 3
[fleft( x right)=sqrt[4]{x}-xsqrt{x}+1]
Для начала заметим, что $sqrt[4]{x}$ мы уже считали:
[sqrt[4]{x}to frac{4{{x}^{frac{5}{4}}}}{5}]
[xsqrt{x}={{x}^{1}}cdot {{x}^{frac{1}{2}}}={{x}^{frac{3}{2}}}]
[{{x}^{frac{3}{2}}}to frac{{{x}^{frac{3}{2}+1}}}{frac{3}{2}+1}=frac{2cdot {{x}^{frac{5}{2}}}}{5}]
[1to x]
Перепишем:
[Fleft( x right)=frac{4{{x}^{frac{5}{4}}}}{5}-frac{2{{x}^{frac{5}{2}}}}{5}+x]
Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.
Решение более сложных примеров
Задача № 1
[fleft( x right)={{left( sqrt[3]{x}-2 right)}^{2}}]
Вспомним формулу квадрата разности:
[{{left( a-b right)}^{2}}={{a}^{2}}-ab+{{b}^{2}}]
Давайте перепишем нашу функцию:
[fleft( x right)=left( sqrt[3]{x} right)-2cdot sqrt[3]{x}cdot 2+4]
[fleft( x right)={{x}^{frac{2}{3}}}-4{{x}^{frac{1}{3}}}+4]
Первообразную такой функции нам сейчас предстоит найти:
[{{x}^{frac{2}{3}}}to frac{3cdot {{x}^{frac{5}{3}}}}{5}]
[{{x}^{frac{1}{3}}}to frac{3cdot {{x}^{frac{4}{3}}}}{4}]
[4to 4x]
Собираем все в общую конструкцию:
[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x]
Задача № 2
[fleft( x right)={{left( frac{1}{x}-2 right)}^{3}}]
В этом случае нам нужно раскрыть куб разности. Вспомним:
[{{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}cdot b+3acdot {{b}^{2}}-{{b}^{3}}]
С учетом этого факта можно записать так:
[fleft( x right)=frac{1}{{{x}^{3}}}-3cdot frac{1}{{{x}^{2}}}cdot 2+3cdot frac{1}{x}cdot 4-8]
Давайте немного преобразуем нашу функцию:
[fleft( x right)={{x}^{-3}}-6{{x}^{-2}}+12cdot {{x}^{-1}}-8]
Считаем как всегда — по каждому слагаемому отдельно:
[{{x}^{-3}}to frac{{{x}^{-2}}}{-2}]
[{{x}^{-2}}to frac{{{x}^{-1}}}{-1}]
[{{x}^{-1}}to ln x]
[8to 8x]
Запишем полученную конструкцию:
[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x-8x]
Задача № 3
[fleft( x right)=frac{{{left( x+sqrt{x} right)}^{2}}}{x}]
Сверху у нас стоит квадрат суммы, давайте его раскроем:
[frac{{{left( x+sqrt{x} right)}^{2}}}{x}=frac{{{x}^{2}}+2xcdot sqrt{x}+{{left( sqrt{x} right)}^{2}}}{x}=]
[=frac{{{x}^{2}}}{x}+frac{2xsqrt{x}}{x}+frac{x}{x}=x+2{{x}^{frac{1}{2}}}+1]
Далее все легко:
[xto frac{{{x}^{2}}}{2}]
[{{x}^{frac{1}{2}}}to frac{2cdot {{x}^{frac{3}{2}}}}{3}]
[1to x]
Давайте напишем итоговое решение:
[Fleft( x right)=frac{{{x}^{2}}}{x}+frac{4{{x}^{frac{3}{2}}}}{3}+x]
А теперь внимание! Очень важная вещь, с которой связана львиная доля ошибок и недопониманий. Дело в том, что до сих пор считая первообразные с помощью производных, приводя преобразования, мы не задумывались о том, чему равна производная константы. А ведь производная константы равна «нулю». А это означает, что можно записать такие варианты:
- ${{x}^{2}}to frac{{{x}^{3}}}{3}$
- ${{x}^{2}}to frac{{{x}^{3}}}{3}+1$
- ${{x}^{2}}to frac{{{x}^{3}}}{3}+C$
Вот это очень важно понимать: если производная функции всегда одна и та же, то первообразных у одной и той же функции бесконечно много. Просто к нашим первообразным мы можем дописывать любые числа-константы и получать новые.
Неслучайно, в пояснении к тем задачам, которые мы только что решали, было написано «Запишите общий вид первообразных». Т.е. уже заранее предполагается, что их не одна, а целое множество. Но, на самом деле, они отличаются лишь константой $C$ в конце. Потому в наших задачах мы исправим то, что мы не дописали.
Еще раз переписываем наши конструкции:
[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x+C]
В таких случаях следует дописывать, что $C$ — константа — $C=const$.
Во второй нашей функции мы получим следующую конструкцию:
[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x+C]
И последняя:
[Fleft( x right)=frac{{{x}^{2}}}{2}+frac{4{{x}^{frac{3}{2}}}}{3}+x+C]
И вот теперь мы действительно получили то, что от нас требовалось в исходном условии задачи.
Решение задач на нахождение первообразных с заданной точкой
Сейчас, когда мы знаем о константах и об особенностях записи первообразных, вполне логично возникает следующий тип задач, когда из множества всех первообразных требуется найти одну-единственную такую, которая проходила бы через заданную точку. В чем состоит эта задача?
Дело в том, что все первообразные данной функции отличаются лишь тем, что они сдвинуты по вертикали на какое-то число. А это значит, что какую бы точку на координатной плоскости мы не взяли, обязательно пройдет одна первообразная, и, причем, только одна.
Итак, задачи, которые сейчас мы будем решать, сформулированы следующем образом: не просто найти первообразную, зная формулу исходной функции, а выбрать именно такую из них, которая проходит через заданную точку, координаты которой будут даны в условии задачи.
Пример № 1
[fleft( x right)=5{{x}^{4}}+6{{x}^{3}}-2x+6]
[M=left( -1;4 right)]
Для начала просто посчитаем каждое слагаемое:
[{{x}^{4}}to frac{{{x}^{5}}}{5}]
[{{x}^{3}}to frac{{{x}^{4}}}{4}]
[xto frac{{{x}^{2}}}{2}]
[6to 6x]
Теперь подставляем эти выражения в нашу конструкцию:
[Fleft( x right)=5cdot frac{{{x}^{5}}}{5}+6cdot frac{{{x}^{4}}}{4}-2cdot frac{{{x}^{2}}}{2}+6x+C]
[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+C]
Эта функция должна проходить через точку $Mleft( -1;4 right)$. Что значит, что она проходит через точку? Это значит, что если вместо $x$ поставить везде $-1$, а вместо $Fleft( x right)$ — $-4$, то мы должны получить верное числовое равенство. Давайте так и сделаем:
[4={{left( -1 right)}^{5}}+frac{3cdot {{left( -1 right)}^{4}}}{2}-{{left( -1 right)}^{2}}+6cdot left( -1 right)+C]
Мы видим, что у нас получилось уравнение относительно $C$, поэтому давайте попробуем его решить:
[4=-1+frac{3}{2}-1-6+C]
[C=4+6+2-frac{3}{2}=10,5]
Давайте запишем то самое решение, которое мы искали:
[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+10,5]
Пример № 2
[fleft( x right)={{left( x-3 right)}^{2}}]
[M=left( 2;-1 right)]
В первую очередь необходимо раскрыть квадрат разности по формуле сокращенного умножения:
[fleft( x right)={{x}^{2}}-6x+9]
Считаем:
[{{x}^{2}}to frac{{{x}^{3}}}{3}]
[xto frac{{{x}^{2}}}{2}]
[9to 9x]
Исходная конструкция запишется следующим образом:
[Fleft( x right)=frac{{{x}^{3}}}{3}-6cdot frac{{{x}^{2}}}{2}+9x+C]
[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x+C]
Теперь давайте найдем $C$: подставим координаты точки $M$:
[-1=frac{8}{3}-12+18+C]
Выражаем $C$:
[C=-1-6-2frac{2}{3}=-9frac{2}{3}]
Осталось отобразить итоговое выражение:
[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x-9frac{2}{3}]
Решение тригонометрических задач
В качестве финального аккорда к тому, что мы только что разобрали, предлагаю рассмотреть две более сложные задачи, в которых содержится тригонометрия. В них точно так же потребуется найти первообразные для всех функций, затем выбрать из этого множества одну-единственную, которая проходит через точку $M$ на координатной плоскости.
Забегая наперед, хотел бы отметить, что тот прием, который мы сейчас будем использовать для нахождения первообразных от тригонометрических функций, на самом деле, является универсальным приемом для самопроверки.
Задача № 1
[fleft( x right)=frac{1}{{{cos }^{2}}x}]
[M=left( frac{text{ }!!pi!!text{ }}{text{4}};-1 right)]
Вспомним следующую формулу:
[{{left( text{tg}x right)}^{prime }}=frac{1}{{{cos }^{2}}x}]
Исходя из этого, мы можем записать:
[Fleft( x right)=text{tg}x+C]
Давайте подставим координаты точки $M$ в наше выражение:
[-1=text{tg}frac{text{ }!!pi!!text{ }}{text{4}}+C]
[-1=1+C]
[C=-2]
Перепишем выражение с учетом этого факта:
[Fleft( x right)=text{tg}x-2]
Задача № 2
[fleft( x right)=frac{1}{{{sin }^{2}}x}]
[M=left( -frac{text{ }!!pi!!text{ }}{text{4}};2 right)]
Тут будет чуть сложнее. Сейчас увидите, почему.
Вспомним такую формулу:
[{{left( text{ctg}x right)}^{prime }}=-frac{1}{{{sin }^{2}}x}]
Чтобы избавится от «минуса», необходимо сделать следующее:
[{{left( -text{ctg}x right)}^{prime }}=frac{1}{{{sin }^{2}}x}]
Вот наша конструкция
[Fleft( x right)=-text{ctg}x+C]
Подставим координаты точки $M$:
[2=-text{ctg}left( -frac{text{ }!!pi!!text{ }}{4} right)+C]
[2=text{ctg}frac{text{ }!!pi!!text{ }}{text{4}}+C]
[2=1+C]
[C=1]
Итого запишем окончательную конструкцию:
[Fleft( x right)=-text{ctg}x+1]
Вот и все, о чем я хотел сегодня вам рассказать. Мы изучили сам термин первообразных, как считать их от элементарных функций, а также как находить первообразную, проходящую через конкретную точку на координатной плоскости.
Надеюсь, этот урок хоть немного поможет вам разобраться в этой сложной теме. В любом случае, именно на первообразных строятся неопределенные и неопределенные интегралы, поэтому считать их совершенно необходимо. На этом у меня все. До новых встреч!
Смотрите также:
- Таблица первообразных
- Интегрирование по частям
- Решение задач B12: №448—455
- Что такое ЕГЭ по математике 2011 и как его сдавать
- Задача B4: случай с неизвестным количеством товара
- Задача B15: что делать с квадратичной функцией
ВИДЕО УРОК
Что такое первообразная и как она считается ?
ПРИМЕР:
Найдём производную:
f(x) = x3.
Находим её, пользуясь формулой:
Откуда
Это и есть определение
первообразной.
Аналогично запишем и
такое выражение:
Обобщим это правило и
выведем следующую формулу:
При n = –1
первообразная функция определяется следующим образом:
Учитывая,
что
а производная
Первообразной функции называется такая функция, производная которой равна
исходной функции.
Функция
y = F(x)
называется первообразной функции
y = f(x)
на промежутке Х, если для любого х ∈ Х выполняется равенство:
F(x) = f(x).
Таблица первообразных
функций.
К каждому выражению в правой части таблицы необходимо прибавить константу.
Правила нахождения первообразных функций.
1. Первообразная функция суммы (разности) равна сумме (разности)
первообразных функций.
F(x + у) = F(x) + F(у),
F(x – у) = F(x) – F(у).
ПРИМЕР:
Найти первообразную для функции
у
= 4х3 + cos x.
РЕШЕНИЕ:
Первообразная суммы равна сумме
первообразных, тогда надо найти первообразную для каждой из представленных
функций.
f(x) = 4x3, F(x)
= x4.
f(x) = cos x, F(x) = sin x.
Тогда первообразная исходной
функции будет
у
= х4 + sin x
или любая функция вида
у
= х4 + sin x + C.
2. Если F(x) –
первообразная для f(x), то
k F(x)–
первообразная для функции k f(x).
(Коэффициент можно выносить за функцию).
ПРИМЕР:
Найти первообразную для функции
у
= 8 sin x.
РЕШЕНИЕ:
Первообразной для sin x служит
минус cos x.
Тогда первообразная исходной функции примет вид:
у
= –8 cos x.
ПРИМЕР:
Найти первообразную для функции
у
= 3x2 + 4х + 5.
РЕШЕНИЕ:
Первообразной для x2 служит
Первообразной для x служит
Первообразной для 1 служит x.
Тогда первообразная исходной
функции примет вид:
у
= x3 + 2x2 + 5 x.
3. Если y = F(x) – первообразная для функции
y = f(x),
то первообразная для функции
y = f(kx + m)
служит функция
y = 1/k F(kx + m).
ПРИМЕР:
Найти первообразную для функции
у
= cos (7x).
РЕШЕНИЕ:
Первообразной для cos x служит sin x. Тогда первообразная для функции
cos (7x)
будет функция
ПРИМЕР:
Найти первообразную для функции
у
= sin x/2.
РЕШЕНИЕ:
Первообразной для sin x служит минус cos x. Тогда первообразная для функции
у
= sin x/2
будет функция
ПРИМЕР:
Найти первообразную для функции
у
= (–2х + 3)3.
РЕШЕНИЕ:
Первообразной для x3 служит
Тогда первообразная для исходной
функции
у
= (–2х + 3)3.
будет функция
ПРИМЕР:
Найти первообразную для функции
РЕШЕНИЕ:
Сначала упростим выражение в степени:
Первообразной экспоненциальной
функции является сама экспоненциальная функция. Первообразной исходной функции
будет:
Если y = F(x) –
первообразная для функции
y = f(x) на
промежутке Х, то у функции y = f(x) бесконечно много первообразных, и все они
имеют вид:
y = F(x) + С.
Если во всех примерах, которые были рассмотрены выше, потребовалось бы
найти множество всех первообразных, то везде следовало бы прибавить
константу С.
Для функции у = cos (7x) все первообразные имеют вид:
Для функции
у = (–2х +
3)3 все
первообразные имеют вид:
ПРИМЕР:
По заданному закону изменения
скорости тела от времени
v = –3sin 4t
найти закон движения
S = S(t),
если в начальный момент времени
тело имело координату равную
1,75.
РЕШЕНИЕ:
Так как v =
S‘(t), нам надо найти первообразную для заданной скорости.
S = –3 1/4 (–cos 4t) + C
= 3/4 cos 4t + C.
В этой задаче дано
дополнительное условие – начальный момент времени. Это значит, что t = 0.
S(0)= 3/4 (–cos 4∙ 0) + C = 7/4,
3/4 cos 0 + C = 7/4,
3/4 ∙1 + C = 7/4,
C = 1.
Тогда закон движения
описывается формулой:
S = 3/4 cos 4t + 1.
Формул для нахождения частного и произведения первообразной функции не
существует.
ПРИМЕР:
Найти первообразную для функции
РЕШЕНИЕ:
Так как формул для нахождения частного и
произведения первообразной функции не существует, то поступаем следующим
образом. Разобьём дробь на сумму двух дробей.
Найдём первообразные каждого
слагаемого и их сумму.
F(x) = 1∙ х + ln x = х + ln x.
Решение выражений со степенью с рациональным показателем.
Многие конструкции и
выражения, которые, на первый взгляд, не имеют никакого отношения к
могут быть представлены в виде степени с
рациональным показателем, а именно:
ПРИМЕР:
Найти первообразную для функции
РЕШЕНИЕ:
Посчитаем каждый корень отдельно:
Итого:
Решение задач на нахождение первообразных с заданной точкой.
Иногда необходимо из множества всех первообразных найти одну-единственную
такую, которая проходила бы через заданную точку.
Все первообразные данной функции отличаются лишь тем, что они сдвинуты по
вертикали на какое-то число. А это значит, что какую бы точку на координатной
плоскости мы не взяли, обязательно пройдёт одна первообразная, и причём, только
одна.
Поэтому примеры, приведённые ниже, сформулированы следующим образом:
Надо не просто найти первообразную, зная формулу исходной функции, а
выбрать именно такую из них, которая проходит через заданную точку, координаты
которой будут даны в условии задачи.
ПРИМЕР:
Найти первообразную для функции
f(x) = 5x4 + 6x3 – 2x + 6
в точке М (–1; 4).
РЕШЕНИЕ:
Посчитаем каждое слагаемое:
Найдём первообразную:
Эта функция должна проходить через точку
М (–1; 4). Что значит, что она проходит через точку ? Это значит, что если вместо х
поставить –1, а вместо F(x) – 4, то получится верное числовое равенство:
Получилось уравнение
относительно С. Найдём С.
Подставим в общее решение С =
10,5 и получим ответ:
ПРИМЕР:
Найти первообразную для функции
f(x) = (x – 3)2
в точке М (2; –1).
РЕШЕНИЕ:
В
первую очередь необходимо раскрыть квадрат разности по формуле сокращённого
умножения.
f(x) = x2 – 6x + 9.
Посчитаем каждое слагаемое:
Найдём первообразную:
Найдём С, подставив координаты
точки М.
Осталось отобразить
итоговое выражение.
Решение тригонометрических задач.
ПРИМЕР:
Найти первообразную для функции
в точке М (π/4; –1).
РЕШЕНИЕ:
Воспользуемся формулой:
Тогда
F(x)
= tg x +
C,
Подставляем
координаты точки М
–1 = tg π/4 + C,
–1 = 1 + C,
C = –2.
Осталось отобразить итоговое
выражение.
F(x)
= tg x –
2.
ПРИМЕР:
Найти первообразную для функции
в точке М (π/4; 2).
РЕШЕНИЕ:
Воспользуемся формулой:
Или
Тогда
F(x)
= –ctg x +
C,
Подставляем
координаты точки М
2 = –сtg (–π/4) + C,
2 = сtg π/4 + C,
2 = 1 + C
C = 1.
Осталось отобразить итоговое
выражение.
F(x) = –сtg x + 1.
Задания к уроку 4
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Предел функции
- Урок 2. Определение производной функции
- Урок 3. Дифференцирование функции
- Урок 5. Неопределённый интеграл
- Урок 6. Определённый интеграл
- Урок 7. Применение производной при исследовании функций
- Урок 8. Применение определённого интеграла для решения геометрических задач
Содержание:
Первообразная и интеграл
Ранее вы ознакомились с операцией дифференцирования: нахождения производной по данной функции. Не менее важна и обратная ей операция — интегрирование: нахождение функции по её производной.
Пусть дано функцию
Функция 
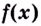
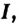
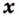
Например, на всей числовой оси (т. е. на 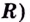
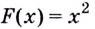
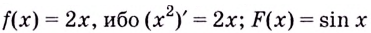
Функция 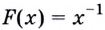
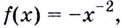
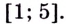
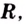
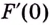
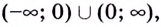
Одна ли функция 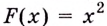
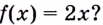
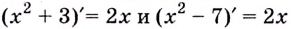
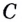
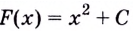
Существуют ли другие функции, отличные от 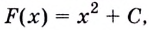
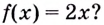
Теорема. (Основное свойство первообразных.) Каждая первообразная для функции 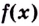
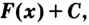
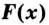
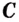
Доказательство 1. Пусть 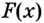
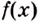
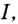
По правилу нахождения производной суммы
Этим доказано, что какая бы ни была постоянная 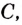
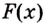
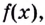
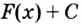
2. Пусть 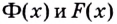
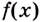
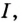
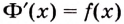
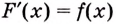
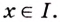
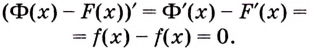
Как видим, функция 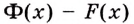
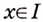
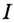
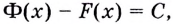
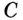
Этим доказано, что если 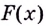
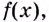
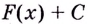
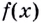
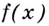
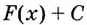
Каждая первообразная рассматривается на некотором промежутке. Если же для краткости его не указывают, то имеют в виду промежуток максимально возможной длины. В частности, если функция 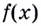
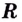
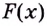
Операцию нахождения производной данной функции называют дифференцированием. Обратная ей операция — нахождение первообразной — называется интегрированием.
Используя формулы дифференцирования (с. 218), составим таблицу первообразных. Советуем запомнить её.
Обосновать эту таблицу можно дифференцированием функции из её второй строки. Пользуясь таблицей, можно сразу писать, что, например, для функции 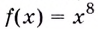
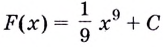
Множество всех первообразных функции 
Выражение «проинтегрировать функцию 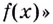
То есть, если 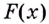
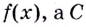
Слово интеграл в переводе с латинского языка означает целый. Почему его так назвали, вы поймёте, когда ознакомитесь с определённым интегралом (см. с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении 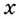
Таблицу первообразных, с помощью символа неопредёленного интеграла можно записать так:
Пример №577
Докажите, что функция 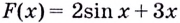
Доказательство:
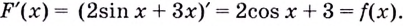
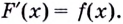
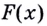
Пример №578
Найдите первообразную для функции:
Решение:
Воспользуемся таблицей первообразных.
а) Первообразной для функции 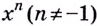
Для функции 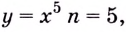
б) Первообразной для функции 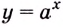
Для функции 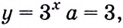
Пример №579
Найдите для функции 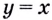
Решение:
Пользуясь таблицей, найдём общий вид первообразных: 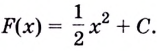
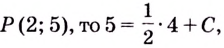
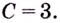
Ответ.
Пример №580
Проинтегрируйте функцию
Решение:
Нахождение первообразных
Выведем несколько правил, подобных правилам дифференцирования, которые облегчают нахождение первообразных.
I. Если 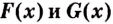
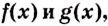
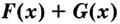
Действительно, если 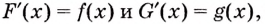
II. Если 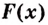
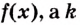
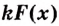
Ведь
III. Если 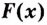
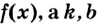
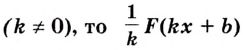
Ведь
Пример №581
Найдите первообразную для функции:
Решение:
а) Для функций 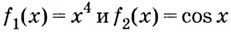
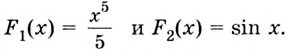
б) По правилу
в) Одной из первообразных для функции 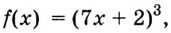
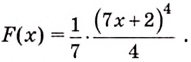
К нахождению первообразных сводятся прежде всего задачи, обратные тем, которые решаются с помощью производной. Рассмотрим пример.
Если известен закон прямолинейного движения тела 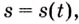
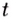
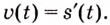
Пример №582
Точка движется прямолинейно с переменной скоростью 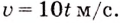
Решение:
Искомый закон движения выражается такой функцией 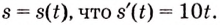
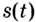
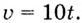
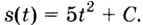
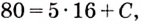
Ответ. Искомый закон движения точки 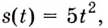
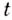
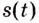
Примеры других применений первообразной рассмотрим в следующих параграфах.
С помощью неопределённого интеграла правила интегрирования записываются так:
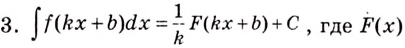
Пример №583
Найдите одну из первообразных для функции:
Решение:
а) Для функции 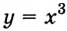
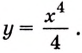
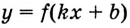
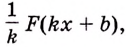
б) преобразуем сначала формулу, задающую функцию:
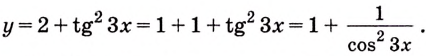
Пример №584
Тело движется прямолинейно с ускорением 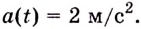
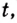
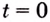
Решение:
Ускорение — производная скорости. Поэтому если 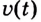
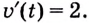
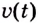
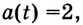
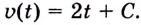
Ответ.
Первообразная и площадь криволинейной трапеции
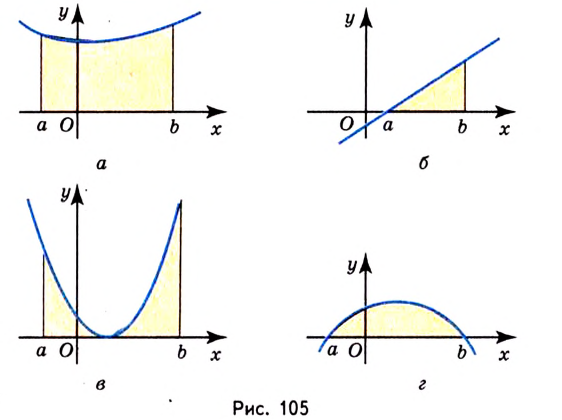
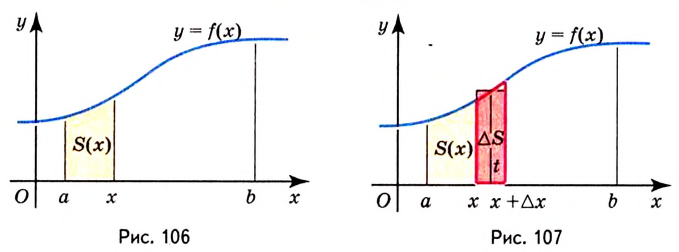
Пусть на координатной плоскости задан график непрерывной функции 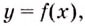
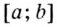
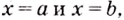
Криволинейную трапецию называют также подграфиком функции
Несколько криволинейных трапеций изображено на рисунке 105.
Каждая криволинейная трапеция имеет определённую площадь (это доказано в строгих курсах математического анализа). Эти площади можно находить с помощью первообразных.
Теорема. Площадь криволинейной трапеции, образованной графиком функции 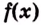
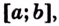
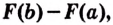
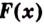
Доказательство. Рассмотрим произвольную криволинейную трапецию, образованную графиком функции 
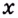
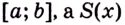
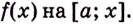
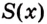
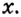
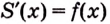
Дадим переменной 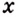
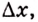
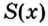
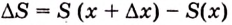
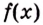
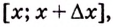
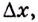
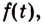
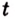
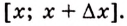
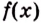
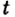
Следовательно, 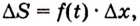
Если 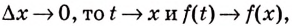
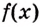
Как видим, функция 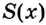

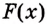
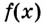
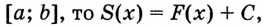
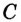
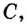
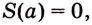
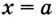
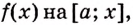
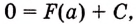
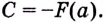
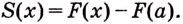
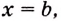
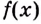
Значение выражения 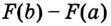
Итак, формула (1) приобретает вид:
- Заказать решение задач по высшей математике
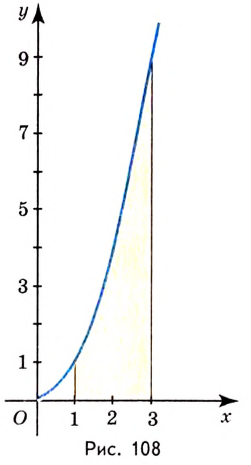
Пример №585
Найдите площадь криволинейной трапеции, образованной графиком функции 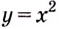
Решение:
На рисунке 108 изображена фигура, площадь которой нужно найти. Для функции 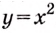
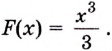
Пример №586
Найдите площадь фигуры, ограниченной одной аркой синусоиды и осью абсцисс (рис. 109).
Решение:
Надо найти площадь криволинейной трапеции, образованной графиком функции 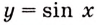
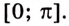
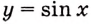
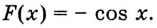
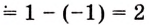
Пользуясь термином «криволинейная трапеция», следует иметь в виду, что «криволинейная трапеция» не всегда является трапецией (рис. 109) и не всегда она криволинейная (рис. 105, б). А вообще она — не геометрическая фигура в научном понимании. Любое движение отображает каждую фигуру на равную ей фигуру такого же вида. А если «криволинейную трапецию», например, изображенную на рисунке 108, повернуть на 90°, она отображается на фигуру, которая не является криволинейной трапецией. Поэтому вместо «криволинейная трапеция» говорят и пишут «подграфик функции».
Пример №587
Найдите площадь криволинейной трапеции, образованной графиком функции
Решение:
Данная криволинейная трапеция — прямоугольный треугольник с катетами 2 и 2 (рис. 110). Его площадь 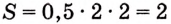
Ответ. 2 кв. ед.
Пример №588
Найдите площадь криволинейной трапеции, образованной графиком функции
Решение:
Заданная криволинейная трапеция — прямоугольник с измерениями 1 и 3 (рис. 111). Его площадь 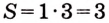
Пример №589
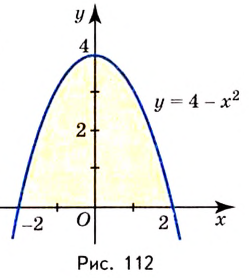
Найдите площадь фигуры, ограниченной графиком функции 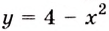
Решение:
Найдем абсциссы точек пересечения графика данной функции с осью 
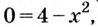
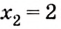
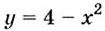
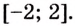
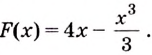
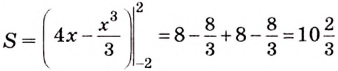
Ответ. 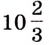
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
- Уравнение
- Метод математической индукции
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Интеграл и его применение
Первообразная и неопределенный интеграл.
Функция $F(x)$ называется первообразной функции $f(x),$ заданной на некотором множестве $X,$ если $F'(x)=f(x)$ для всх $xin X.$ Если $F(x -)$ первообразная функции $f(x),$ то $Phi(x)$ является первообразной той же функции в том и только в том случае, когда $Phi(x)=F(x)+C,$ где $C$ – некоторая постоянная. Совокупность всех первообразных функции $f(x)$ называется неопределенным интегралом от этой функции и обозначается символом $$int f(x),dx.$$ Таким образом, по определению $$int f(x),dx=F(x)+C,$$ где $F(x)$ одна из первообразных функции $f(x)$ а постоянная $C$ принимает действительные значения.
Свойства неопределенного интеграла.
1. $left(int f(x),dxright)’=f(x).$
2. $int f'(x)dx=f(x)+C.$
3. $int af(x)dx=aint f(x) dx.,,,,,,aneq 0.$
4. $int (f_1(x)+f_2(x))dx=int f_1(x),dx+int f_2(x), dx.$
Таблица основных неопределенных интегралов.
1. $int dx=x+C$
2. $int x^{alpha}dx=frac{x^{alpha+1}}{alpha+1}+C$
3. $int {dx}{x}=ln |x|+C$
4. $int a^x dx=frac{a^x}{ln a}+C$
5. $int e^x dx=e^x+C$
6. $int sin x dx=-cos x+C$
7. $int cos x dx=sin x+C$
8. $int frac{dx}{cos^2 x}=tg x+C$
9. $int frac{dx}{sin^2 x}=-ctg x+C$
10. $int frac{dx}{sqrt{a^2-x^2}}=arcsinfrac{x}{a}+C$
11. $int frac{dx}{sqrt{x^2 pm a^2}}=lnleft|x+sqrt{x^2pm a^2}right|+C$
12. $int frac{dx}{x^2+a^2}=frac{1}{a}arctgfrac{x}{a}+C$
13. $int frac{dx}{x^2 -a^2}=frac{1}{2a}lnleft|frac{x-a}{x+a}right|+C$
14. $int sh x dx = ch x+C$
15. $int ch x dx = sh x+C$
16. $int frac{dx}{ch^2 x} = th x+C$
17. $int frac{dx}{sh^2 x} = -cth x+C$
Примеры.
Найти первообразные следующих функций:
6.1. $2x^7.$
Решение.
Из определения первообразной следует, что нам необходимо найти такую функцию $F(x),$ что $F'(x)=2x^7.$
$$(x^8)’=8x^7Rightarrow (frac{1}{4}x^8)’=2x^7.$$
Таким образом, $F(x)=0,25 x^8,$ а все первообразные заданной функции имеют вид $0,25x^8+c.$
Ответ: $0,25x^8+c.$
6.4.$frac{x^3+5x^2-1}{x}.$
Решение.
Из определения первообразной следует, что нам необходимо найти такую функцию $F(x),$ что $F'(x)=frac{x^3+5x^2-1}{x}=x^2+5x-frac{1}{x}.$
$$(x^3)’=3x^2Rightarrow (frac{1}{3}x^3)’=x^2;$$
$$(x^2)’=2xRightarrow (frac{5}{2}x^2)’=5x;$$
$$(ln |x|)’=frac{1}{x}.$$
Отсюда находим, $$F(x)=frac{1}{3} x^3+frac{5}{2}x^2-ln |x|,$$ а все первообразные заданной функции имеют вид $frac{1}{3} x^3+frac{5}{2}x^2-ln |x|+c.$
Ответ: $frac{1}{3} x^3+frac{5}{2}x^2-ln |x|+c.$
6.7.$frac{1}{sqrt{a+bx}}.$
Решение.
Из определения первообразной следует, что нам необходимо найти такую функцию $F(x),$ что $F'(x)=frac{1}{sqrt{a+bx}}.$
$$(sqrt{a+bx})’=frac{1}{2sqrt{a+bx}}(a+bx)’=frac{b}{2sqrt{a+bx}}Rightarrow$$ $$Rightarrow (frac{2}{b}sqrt{a+bx})’=frac{1}{sqrt{a+bx}}.$$
Таким образом, $$F(x)=frac{2}{b}sqrt{a+bx},$$ а все первообразные заданной функции имеют вид $frac{2}{b}sqrt{a+bx}+c.$
Ответ: $frac{2}{b}sqrt{a+bx}+c.$
6.10.$frac{1}{cos^2{4x}}.$
Решение.
Из определения первообразной следует, что нам необходимо найти такую функцию $F(x),$ что $F'(x)=frac{1}{cos^2{4x}}.$
$$(tg 4x)’=frac{1}{cos^2{4x}}(4x)’=frac{4}{cos^2{4x}}Rightarrow (frac{1}{4}tg 4x)’=frac{1}{cos^2 4x}.$$
Таким образом, $$F(x)=frac{1}{4 }tg 4x,$$ а все первообразные заданной функции имеют вид $0,25 tg 4x+c.$
Ответ: $0,25 tg 4x+c.$
Используя таблицу основных интегралов, найти следующие интегралы:
6.15.$intleft(3x^2+2x+frac{1}{x}right), dx.$
Решение.
$$intleft(3x^2+2x+frac{1}{x}right), dx=3int x^2 dx+2int xdx+intfrac{1}{x}dx=$$ $$=3frac{x^3}{3}+2frac{x^2}{2}+ln |x|+c=x^3+x^2+ln|x|+c.$$
Ответ: $x^3+x^2+ln|x|+c.$
6.17.$intsqrt{mx},dx.$
Решение.
$$intsqrt{mx}, dx=sqrt mint x^{frac{1}{2}},dx=sqrt mfrac{x^{1/2+1}}{1/2+1}+c=sqrt mfrac{x^{frac{3}{2}}}{frac{3}{2}}+c=$$ $$=frac{2sqrt {mx^3}}{3}+c.$$
Ответ: $frac{2sqrt{mx^3}}{3}+c.$
6.19.$intleft(frac{1}{sqrt[3]{x^2}}-frac{x+1}{sqrt[4]{x^3}}right),dx.$
Решение.
$$intleft(frac{1}{sqrt[3]{x^2}}-frac{x+1}{sqrt[4]{x^3}}right),dx=int x^{-2/3}dx-intfrac{x}{x^{3/4}},dx-intfrac{1}{x^{3/4}}dx=$$ $$=int x^{-2/3}dx-int{x^{1/4}},dx-int{x^{-3/4}}dx=$$ $$=frac{x^{-2/3+1}}{-2/3+1}-frac{x^{1/4+1}}{1/4+1}-frac{x^{-3/4+1}}{-3/4+1}+c=$$ $$=3x^{1/3}-frac{4x^{5/4}}{5}-4{x^{1/4}}+c=$$
Ответ: $3sqrt[3]x-frac{4}{5}xsqrt[4]{x}-4sqrt[4]{x}+c.$
6.22.$int 2^xe^x, dx.$
Решение.
$$int 2^xe^x,dx=int (2e)^x,dx=frac{(2e)^x}{ln (2e)}+c=frac{(2e)^x}{ln2+1}+c$$
Ответ: $frac{(2e)^x}{ln 2+1}+c.$
6.24.$int(2x+3cos x),dx.$
Решение.
$$int (2x+3cos x),dx=2int x,dx+3intcos x,dx=2frac{x^2}{2}+3sin x+c=$$ $$=x^2+3sin x+c$$
Ответ: $x^2+3sin x+c.$
6.28.$intsin^2frac{x}{2},dx.$
Решение.
$$int sin^2frac{x}{2},dx=int frac{1-cos x}{2},dx=frac{1}{2}int,dx-frac{1}{2}intcos x,dx=$$ $$=0,5 x-0,5sin x+c.$$
Ответ: $0,5 x-0,5sin x+c.$
6.42.$intfrac{dx}{sqrt{x^2-7}}.$
Решение.
$$int frac{dx}{sqrt{x^2-7}}=ln|x+sqrt{x^2-7}|+c.$$
Ответ: $ln|x+sqrt{x^2-7}|+c.$