Как найти первообразную для сложной функции

Вычислить первообразную сложной функции

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Теоретическая часть

Понятие первообразной функции актуально в механике. Проблема нахождения функции по некоторой определённой производной этой же функции является задачей первообразной. Поэтому будем считать, что задачи по нахождению производных функций уже известны. Обычно понятие первообразной разбирают в рамках вопроса нахождения определённого интеграла.

Определение 1

Первообразная функция $F(x)$ или просто первообразная является таковой, если в любой точке $x$ из некоторого замкнутого интервала $X=(a,b)$ на числовом множестве (или на бесконечной прямой) $F(x)$ дифференцируема и $F'(x)=f(x)$.

Если известны основные элементарные производные, то задача нахождения первообразной разрешима.

Если $C$ – любая постоянная величина (константа), то $F(x)+C$ – тоже первообразная для $f(x)$. Это означает, что у функции имеется бесконечное множество первообразных, которые отличны друг от друга на постоянную величину, потому что производная от $C$ равна нулю. Графически первообразные одной функции будут представлять собой одинаковую кривую с параллельным сдвигом относительно друг друга в направлении оси ординат.

Две любые первообразные одной функции могут отличаться только на постоянное слагаемое. То есть $F_1(x)-F_2(x)=C$.

Неопределённый интеграл от какой-либо функции представляет общий вид (выражение) всех её первообразных. Заметим, что первообразная и неопределённый интеграл существуют только для непрерывных функций на заданном промежутке.

Найти общее выражение первообразных представляется возможным, если решить неопределённый интеграл от заданной функции.

Практическая часть

«Вычислить первообразную сложной функции» 👇

Для интегрирования сложных функций существует специальный способ – способ замены переменных.

Рассмотрим примеры. Будем пользоваться таблицей неопределённых интегралов.

Рисунок 1. Таблица неопределённых интегралов. Автор24 — интернет-биржа студенческих работ

Пример 1

Имеется функция

Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ

Введём замену. Пусть $t=ax$. Тогда:

Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ

Пример 2

Дана функция

Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ

Произведём замену $t=x^2+a^2$. Тогда

Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ

Пример 3

Имеется

Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ

Сделаем замену $t=sin x$.

Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ

Пример 4

Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ

Замена $t=x^2$.

Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 13.05.2023

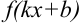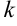Некоторыми сложными функциями будем считать функции вида , где и 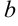— любые действительные числа. Так, 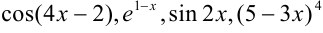— примеры некоторых сложных функций. В аргументе этих функций переменная 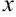находится только в первой степени!

Для нахождения интеграла от некоторых сложных функций будем использовать формулу: 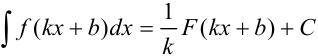. Ее правильность легко проверяется дифференцированием обеих частей.

Можно также применять следующий алгоритм:

1. Выбрать табличный интеграл, к которому сведется данный.
2. Вместо 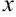в табличном интеграле подставить выражение 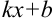из исходного интеграла.
3. В правую часть добавить множитель 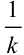, где 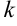— коэффициент перед .

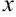Рассмотрим нахождение интеграла от некоторых сложных функций на примерах.

Пример №19.4.

Найдите .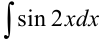

Решение:

Видим, что под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .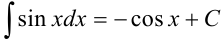

В нашем примере в качестве аргумента выступает угол 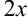. Выделим коэффициент 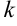, стоящий перед 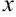: 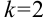, следовательно, в правую часть мы должны добавить множитель 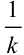, то есть 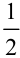. Тогда получим, что .

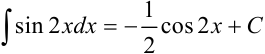Пример №19.5.

Найдите .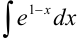

Решение:

Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .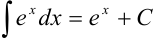

В примере в качестве аргумента выступает выражение 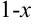. Выделим коэффициент 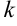, стоящий перед 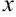: 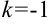, следовательно, в правую часть добавим множитель (-1). Тогда получим, что .

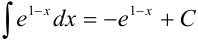Пример №19.6.

Найдите .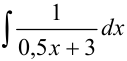

Решение:

Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .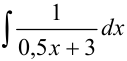

В примере в качестве аргумента выступает выражение 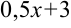. Выделим коэффициент 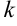, стоящий перед 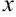: 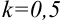, следовательно, в правую часть добавим множитель 1:0,5=2. Тогда получим, что .

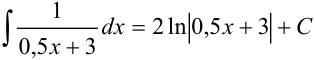Пример №19.7.

Найдите .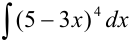

Решение:

Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .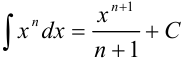

В примере в качестве аргумента выступает выражение 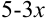. Выделим коэффициент 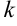, стоящий перед 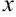: 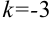, следовательно, в правую часть добавим множитель (-1/3). Тогда получим, что .

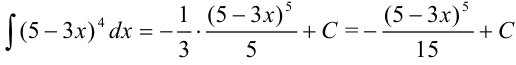Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Лекция 9. Понятие первообразной функции.  Первообразные элементарных
функций

1. Понятие первообразной

     Рассмотрим
две функции:  . Очевидно, производная первой функции равна второй функции, т.е.
.

   В таком случае функция f₁(x) 
называется первообразной функции (или первообразной для функции)  f₂(x). 
В общем виде: первообразные обозначаются заглавными буквами, чтобы их можно
было отличить от самой функции.

Определение:  функция  F(x)
называется первообразной функции f(x), если производная функции F(x) 
равна функции  f(x):

Fx f x

Следует учесть, что
равенство имеет смысл на том множестве, на котором обе функции существуют.  Например:

•      
функция  y sin x является
первообразной для функции   y
cos x , т.к. sin
x^
 cos
x ;

•       функция y cos xявляется
первообразной для функции   y
sin x , т.к. cosx^

sinx

sinx;

•       функция 
y 
2x 1 –  первообразная для
функции  y 
2 ;

•       функция
yln x–
первообразная для функции y_¹ на множестве x0 . И т.д. x

Задачи: 

Определить, является ли функция F(x) первообразной
для f(x):

Дано:  Fx
x³ 3x 1;   f x3x² 1       │ F(x) 
первообразная?

Решение:  Fx
x³ 3x 1^ 3x² 33x² 1
f x                                                       
Ответ:  да

2. Множество первообразных

  Теперь разберем важный момент: сколько первообразных
существует для заданной функции? Для этого рассмотрим функции:

F₁x 2sin x 
cos x;  F₂x
2sin x 
cos x 1;  F₃x
2sin x 
cos x 3;  f x
2cos x sin x

 Очевидно, что F₁^x
F₂^x
F₃^x
2cos x sin x 
f x

  Значит функции
F₁(x), F₂(x), F₃(x)  все являются
первообразными для функции f(x).  И подобных функций можно составить сколько
угодно, меняя лишь числа в конце.

  В общем виде:  для любой
заданной функции f(x) существует бесконечно много первообразных.  Все
они имеют общую часть, а отличаются лишь числами.  

   Все первообразные функции 
f(x) обозначаются  , где F(x) – их общая часть,  а C – некоторая постоянная
C const.

3. Правила нахождения первообразных

  Операция нахождения перообразной называется интегрированием.
Это операция над функцией, обратная операции дифференцирование.

   Для различных функций найдены их интегралы,
существуют таблицы интегралов. Но будем разбираться, как появились известные
формулы. Начнем, как и при дифференцировании, с нахождения первообразной
постоянной и степенной функции.

•      
Первообразная постоянной  C const. 
Для любого числа C первообразной будет функция y Cx , т.к.

Cx^ 
C

•      
Первообразная степенной функции yxⁿ .

Очевидно, что для любой заданной степенной функции ее
первообразная должна быть на порядок выше,

т.к. при дифференцировании степень понижается на единицу.
Поэтому, степень первообразной будет x^n1.

Например, для функции
yx² первообразная
будет третьей степени. Проверим: x³^ 
3x²– получили нужную
функцию, а от коэффициента «3» избавимся, разделив на него первообразную,
т.е.


3 
 1x3  1 3x2  x2 .  x 

 3  3              3

Тогда общая формула: для
степенной функции yxⁿ ее
первообразная находится по правилу:

  Эта формула справедлива для всех степенных функций, кроме
функции y 
x^1, т.к.
первообразная

^x11  ^x0 не имеет смысла.
Значит, формула справедлива для любого показателя, кроме -1. Для функции

11 0

yx 

^1
1 первообразная
имеет другой вид.

x

Таблица первообразных элементарных
функций

	Функция   f x	Первообразная   Fx C
1	Постоянная:                   C	Cx
2	Степенная:                  xn,  n1	xn1                        C n1
	1;    xn,  n1 x	ln x C,   x 0
3	Показательная:             ax                                          ex	ax                   C ln a ex C
4	Тригонометрические:  sin x	cos xC
	cosx	sin x C
	1           cos2 x	tgx C
	1            sin2 x	ctgx C
	Правила интегрирования
1	 f x	FxС
2	f x gx	Fx Gx C
3	Сложная функция:  f kxb	1 FkxbC k

Правила нахождения первообразной (правила
интегрирования)

   Правил всего три. В отличие от дифференцирования нет
правила нахождения первообразной от произведения функций и от частного функций.
При нахождении первообразной сложной функции аргументом (внутренней функцией)
является лишь линейная функция.

Правило 1.  Если
функция умножена на коэффициент –  
f x,
то ее первообразная  Fx;

Правило 2. Первообразная
суммы (разности) функций равна сумме (равности) их первообразных: т.е. для
функции f
x gxпервообразная:
FxGx.

Правило 3.Первообразная сложной функции. Для
функции f kxb
первообразная: ^{Fkxb}
. k

Пример. Для функции  найдем одну из ее
первообразных:

Fx x³ 
x² 
2x 
2sin x

Проверка:  

Производные от сложных функций.

Формула для нахождения производной от
сложной функции такова:

[f(φ(х))]`=f<sub>φ</sub>`(φ(x))
* φ`(x)

Например: у = (1-х²)³; у`=
3(1 –х<sup>2</sup>)<sup>2</sup>* (-2х) или у =sin<sup>2</sup>х;
у` = 2sinx * cosx.

Пример 7 . Найти dy, если у
=sin3х

Решение dy= у`
* dx = (sin3x)` dx = (cos3x) * 3dx = 3 cos3x dx.

Пример 8. Найти dy, если у
= 2^{х^2}/

Решение: dy = y` * dx = (2<sup>x^2</sup>)`
* dx = 2^{x^2}
ln2 * 2xdx

Производные высших порядков.

Пусть мы нашли от функции у = f(х)
ее производную у`=f
`(х). Производная от этой производной
и называется производной второго порядка
от функцииf(х) и обозначается
у“илиf “(х) или(d²y)
/ (dx²).
Аналогично определяются и
обозначаются: производная третьего
порядка у“` = f “`(x) = (d³y)
/ (dx³).

производная четвертого порядка у^IV
= f ^IV(x)
= (d⁴y)
/ (dx⁴).

производнаяn-oго
порядка у⁽ⁿ⁾
= f ⁽ⁿ⁾(x)
= (d ⁿ y)
/ (dxⁿ).

Пример: у = 5х⁴– 3х³+ 2х – 2.
Найти у“.

Решение. Находим в начале первую
производную: у`= 20х³– 9х²+2, потом вторую от первой
производной: у“= 60х²– 18х.

Пример. y=хsinx.Найти у“`.

Решение. y` = sinx + xcosx

y“ = cosx + cosx – x sinx = 2cosx – x sinx

y“` = -2sinx – sinx – x cosx = -3sinx – x cosx.

Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла.

Определение.ФункцияF(x)называется первообразной для функцииf(x)на интервале Х, если в
каждой точке этого интервала выполняется
условие

F ` (x)=f(x).

Например, для функции f(x)= 2х первообразной являетсяF(х)
= х²
для любых х Є (-∞, ∞).

Действительно, F`(x) = 2x = f(x).

F₁(x)
= x² +
2так же является первообразной дляf(x) = 2x, F₂(x)
= x² –
100 первообразная той же функцииf(x)
= 2x.

Теорема.ЕслиF₁(x)
иF₂(x)первообразные для функцииf(x)на некотором интервале Х, то найдется
такое число С, что справедливо равенство:

F₂(x)
= F₁(x)
+ C,

Или можно сказать так, две первообразные
для одной и той же функции отличаются
друг от друга на постоянное слагаемое.

Определение.Совокупность всех
первообразных для функцииf(x)на интервале Х называется неопределенным
интегралом от функцииf(x)и обозначаетсяf(x)dx,
где–
знак интеграла,f(x)–
подинтегральная функция,f(x)dx– подинтегральное выражение. Таким
образом

f(x)dx
= F(x) + C,

F(x)– некоторая первообразная
дляf(x),С – произвольная
постоянная. Операция нахождения
неопределенного интеграла от функции
называется интегрированием этой
функции.

Основные свойства неопределенного интеграла.

1. ((f(x)dx)`
   = f(x). Производная от неопределенного
   интеграла равна подынтегральной
   функции.

2. Дифференциал от неопределенного
   интеграла равен подинтегральному
   выражению. d(f(x)dx)
   = f(x)dx.

3. Неопределенный интеграл от дифференциала
   некоторой функции равен этой функции
   с точностью до постоянного слагаемого.

d(F(x))
= F(x) + C.

1. Постоянный множитель можно выносить
   за знак интеграла:

,
где к – число

1. Интеграл от суммы двух функций равен
   сумме интегралов от этих функций

(f(x)
+φ(x))dx = f(x)dx
+ φ(x)dx.

Для вычисления неопределенных интегралов
от функций используют таблицу
неопределенных интегралов, которая
приводиться ниже.

Таблица неопределенных интегралов.

1. х^αdx = [x^α+1
   / (α +1)] +C, α ≠ -1, α Є R

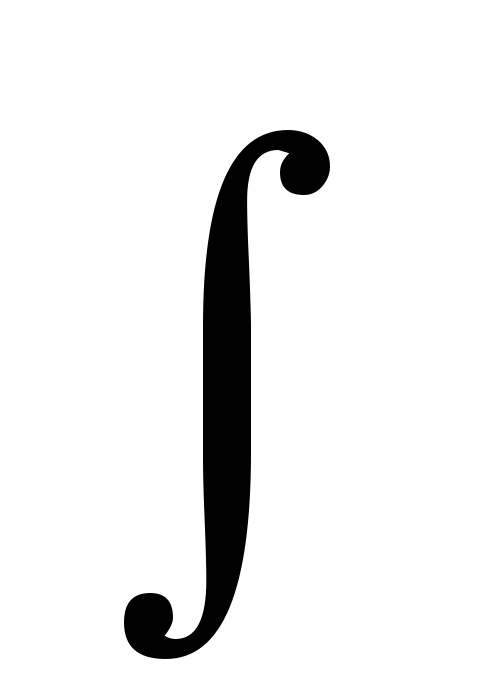2. dx/x
   = ln│x│+C

3. a^x
   = (a^x/ln
   a)+C, e^xdx
   = e^x+C

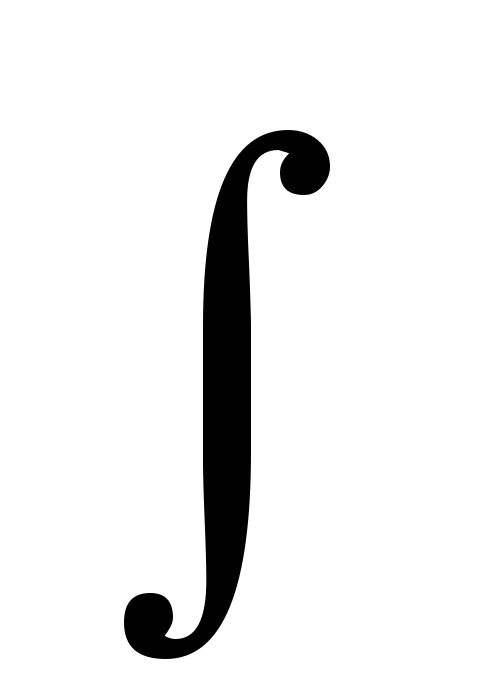4. sinx
   dx = -cosx + C

5. cosx
   dx = sinx + C

6. dx/(cosx)²
   = tgx + C

7. dx/(sinx)²
   = -ctgx + C

8. dx
   /²-x²)
   = (arcsin x/a) + C

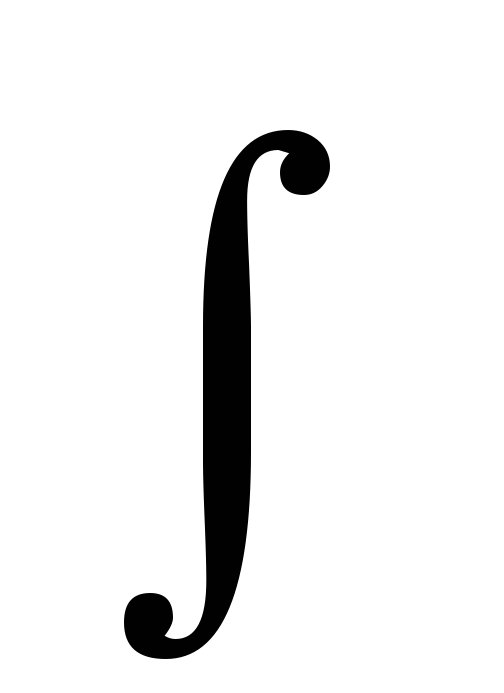9. dx
   /
   ²
   – x²)
   = (-arccos x/a) +C

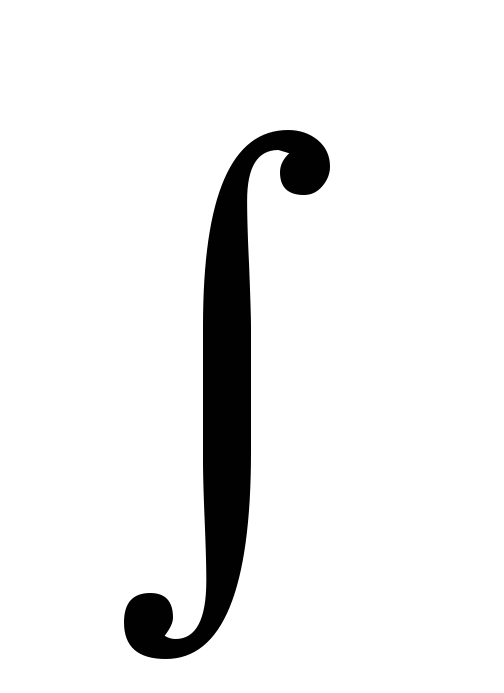10. dx
    / a²
    +x² =
    1/a arctg x/a +C

11. dx
    / a²
    +x² =
    – 1/a arcctg x/a +C

12. dx
    / a²
    -x² =
    1/2a ln │x+a/x-a│ +C

13. dx
    /
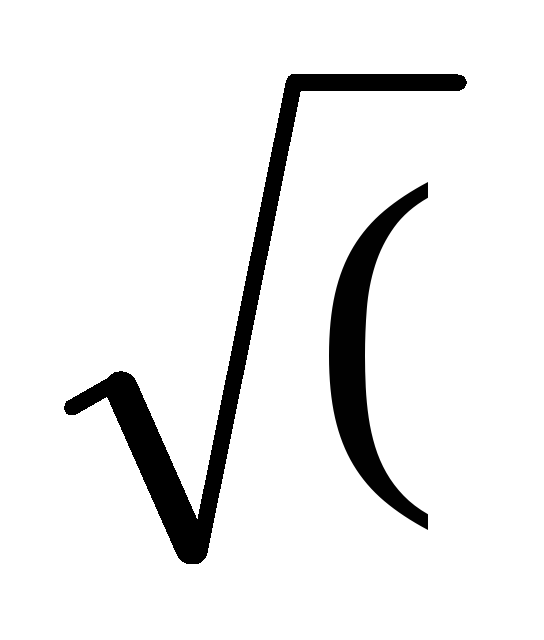    a²
    +x²)
    = ln │x+
    ²+x²)│
    +C.

Пример 1.Вычислить(2х²
-3-1)dx.

Решение. Воспользуемся свойствами 4 и
5 неопределенных интегралов и первой
табличной формулой.
(2х²
-3-1)dx= 2х²
dx – 3х^1/2
dx-dx=

= 2(x²/2)
– 3[(х^3/2*2)/3] – x + C =
x² –
2³
– x +C.

Пример 2.(2/-1/х + 4sinx)dx=2х^–1/2dx–ln
│х│ – 4cosx + C =

= 2[(x^1/2
*2)/1] – ln │x│ – 4 cosx +C = 4-ln│x│- 4cosx + C.

Для вычисления неопределенных интегралов
применяют следующие методы: метод
непосредственного интегрирования,
метод подстановки(метод замены
переменной), метод интегрирования по
частям.

Существуют элементарные функции
первообразные которых элементарными
функциями не являются. По этой причине
соответствующие неопределенные интегралы
называются «неберущимися» в элементарных
функциях, а сами функции не интегрируемыми
в элементарных функциях.

Например,
e
^{–x^2}
dx,sinх²
dx, cosх²
dx, sinx/x
dx, cosx/x
dx,dx/lnx
– «неберущиеся» интегралы , т.е. не
существует такой элементарной функции,
чтоF `(x) = e <sup>–x^2</sup>,
F ` (x) = sinx²
и т.д.

Соседние файлы в предмете Алгебра и начала анализа

• #
• #
• #
• #
• #

  02.05.20142.2 Mб9Лекции Золотых Г.А.ps

• #
• #
• #
• #
• #
• #