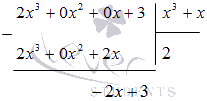Задача
нахождения неопределенного интеграла
дробно рациональной функции сводится
к интегрированию простейших дробей.
Поэтому рекомендуем для начала
ознакомиться с разделом теории разложение
дроби на простейшие.
Пример.
Найти
неопределенный интеграл .
Решение.
Так
как степень числителя подынтегральной
функции равна степени знаменателя, то
для начала выделяем целую часть,
проводя деление
столбиком многочлена на многочлен:
Поэтому, 
Разложение
полученной правильной рациональной
дроби на
простейшие дроби имеет вид.
Следовательно,
Полученный
интеграл представляет собой интеграл
простейшей дроби третьего типа. Забегая
немного вперед, отметим, что взять его
можно методом подведения
под знак дифференциала.
Так
как ,
то.
Поэтому
Следовательно,
Теперь
перейдем к описанию методов интегрирования
простейших дробей каждого из четырех
типов.
Интегрирование
простейших дробей первого типа
Для
решения этой задачи идеально подходит метод
непосредственного интегрирования:
Пример.
Найти
множество первообразных функции
Решение.
Найдем
неопределенный интеграл ,
используя свойства первообразной,
таблицу первообразных и правило
интегрирования.
К
началу страницы
Интегрирование
простейших дробей второго типа
Для
решения этой задачи также подходит
метод непосредственного интегрирования:
Пример.
Найдите
неопределенный интеграл 
Решение.
К
началу страницы
Интегрирование
простейших дробей третьего типа
Для
начала представляем неопределенный
интеграл 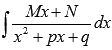
виде суммы:
Первый
интеграл берем методом подведения под
знак дифференциала:
Поэтому,
У
полученного интеграла преобразуем
знаменатель:
Следовательно,
Формула
интегрирования простейших дробей
третьего типа принимает вид:
Пример.
Найдите
неопределенный интеграл .
Решение.
Используем
полученную формулу:
Если
бы у нас не было этой формулы, то как бы
мы поступили:
9. Интегрирование простейших дробей четвертого типа
Первый
шаг – подводим под знак дифференциала:
Второй
шаг – нахождение интеграла вида 
Интегралы подобного вида находятся с
использованием рекуррентных формул.
(Смотрите разделинтегрирование
с использованием рекуррентных формул).
Для нашего случая подходит следующая
рекуррентная формула:
Пример.
Найдите
неопределенный интеграл
Решение.
Для
данного вида подынтегральной функции
используем метод подстановки. Введем
новую переменную (смотрите
раздел интегрирование
иррациональных функций):
После
подстановки имеем:
Пришли
к нахождению интеграла дроби четвертого
типа. В нашем случае имеем коэффициенты М
= 0, р = 0, q = 1, N = 1 и n
= 3.
Применяем рекуррентную формулу:
После
обратной замены получаем
результат:
10. Интегрирование тригонометрических функций.
Множество
задач сводится к нахождению интегралов
трансцендентных функций, содержащих
тригонометрические функции. В данной
статье сгруппируем наиболее часто
встречающиеся виды подынтегральных
функций и на примерах рассмотрим методы
их интегрирования.
-
Начнем
с интегрирования синуса, косинуса,
тангенса и котангенса.
Из
таблицы первообразных сразу заметим,
что и
.
Метод
подведения под знак дифференциалапозволяет
вычислить неопределенные интегралы
функций тангенса и котангенса:
К
началу страницы
-
Поясним,
как были найдены формулыи
,
находящиеся в таблице первообразных.
Разберем
первый случай, второй абсолютно
аналогичен.
Воспользуемся методом
подстановки:
Пришли
к задаче интегрирования
иррациональной функции. Здесь нам
также поможет метод подстановки:
Осталось
провести обратную замену иt
= sinx:
К
началу страницы
-
Отдельно
хочется остановиться на интегралах,
содержащих степени тригонометрических
функций, вида.
Подробно
о принципах их нахождении можете
ознакомиться в разделеинтегрирование
с использованием рекуррентных формул.
Если изучите вывод этих формул, то без
особого труда сможете брать интегралы
вида,
гдеm и n –
натуральные числа.
К
началу страницы
-
Когда
тригонометрические функции идут в
комбинациях с многочленами или
показательными функциями, то
применяется метод
интегрирования по частям. В этом
разделе даны рекомендации для нахождения
интегралов,
.
К
началу страницы
-
Максимум
творчества приходится вкладывать,
когда подынтегральная функция содержит
тригонометрические функции с различными
аргументами.
Здесь
на помощь приходят основные формулы
тригонометрии. Так что выписывайте их
на отдельный листочек и держите перед
глазами.
Пример.
Найти
множество первообразных функции 
Решение.
Формулы
понижения степени дают и
.
Поэтому
Знаменатель
представляет собой формулу синуса
суммы, следовательно,
Приходим
к сумме трех интегралов.
К
началу страницы
-
Подынтегральные
выражения, содержащие тригонометрические
функции, иногда можно свести к дробно
рациональным выражениям, используя
стандартную тригонометрическую
подстановку.
Выпишем
тригонометрические формулы, выражающие
синус, косинус, тангенс через тангенс
половинного аргумента:
При
интегрировании нам также понадобится
выражение дифференциала dx через
тангенс половинного угла.
Так
как 
то
То
есть, ,
где.
Пример.
Найти
неопределенный интеграл .
Решение.
Применим
стандартную тригонометрическую
подстановку:
Таким
образом, .
Разложение
на простейшие дробиподынтегральной
функции приводит нас к сумме двух
интегралов:
Осталось
провести обратную замену :
11.
Рекуррентные формулы – это формулы,
выражающие n-ый
член последовательности через предыдущие
члены. При нахождении интегралов они
не редко используются.
Мы
не ставим целью перечислить все
рекуррентные формулы, а хотим дать
принцип их получения. Вывод этих формул
основан на преобразовании подынтегральной
функции и применении метода
интегрирования по частям.
К
примеру, неопределенный интеграл можно
взять, используя рекуррентную формулу.
Вывод
формулы 
Используя
формулы тригонометрии, можно записать:
Полученный
интеграл найдем методом интегрирования
по частям. В качестве функции u(x)возьмем cosx,
следовательно, .
Поэтому,
Возвращаемся
к исходному интегралу:
То
есть,
Что
и требовалось показать.
Аналогично
выводятся следующие рекуррентные
формулы:
-
Для
нахождения интегралов видаиспользуется
рекуррентная формула,n –
натуральное число. -
Для
нахождения интегралов видаиспользуется
рекуррентная формула.
-
Для
нахождения интегралов видаиспользуется
рекуррентная формула.
-
Для
нахождения интегралов видаиспользуется
рекуррентная формула.
Пример.
Найти
неопределенный интеграл .
Решение.
Используем
рекуррентную формулу из четвертого
пункта (в нашем примере n
= 3):
Так
как из таблицы первообразных имеем ,
то
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интегрирование рациональных функций — операция взятия неопределённого интеграла от рациональной функции. Известно, что первообразная рациональной функции выражается в виде суммы рациональных функций, натуральных логарифмов и арктангенсов.[1] Обычно такое интегрирование выполняется при помощи разложения дроби на простейшие, однако иногда могут использоваться и другие способы, например метод Остроградского.
Разложение на простейшие[править | править код]
Самым известным способом интегрирования рациональной функции является разложение дроби на простейшие. Впервые оно было использовано Исааком Барроу для вычисления интеграла от секанса.[2]
Из алгебры известно, что любую рациональную функцию можно представить как сумму многочлена и конечного числа дробей определённого вида, называемых простейшими. Простейшая дробь над действительными числами — это дробь одного из следующих двух видов:
Каждая из таких дробей затем интегрируется отдельно. Таким образом, разложение дроби на простейшие сводит задачу интегрирования произвольной рациональной функции к интегрированию простейших дробей.[3]
Разложение дроби на простейшие строится следующим образом. Пусть требуется построить разложение дроби 






Разложение правильной дроби может иметь лишь простейшие слагаемые определённого вида, который зависит только от многочлена 
(здесь
и
— кратности соответствующих множителей, то есть количество раз, которое множитель входит в произведение).
Все простейшие дроби в разложении содержат в знаменателе степень одного из таких множителей, причём эта степень меньше или равна кратности соответствующего множителя. К примеру: если в разложении 

Аналогично, если в разложении 

Общий вид разложения правильной дроби на простейшие представляет сумму всех таких сумм для каждого множителя в разложении многочлена 
При этом некоторые слагаемые могут быть равны нулю.
Общий вид разложения дроби нужен для наиболее известного способа разложения дроби на простейшие — метода неопределённых коэффициентов. Его суть заключается в составлении уравнений на неизвестные коэффициенты разложения. Записывается равенство правильной дроби и её разложения на простейшие с неопределёнными коэффициентами. Затем каким-либо способом составляются уравнения на эти коэффициенты и система из уравнений решается.[4]
Наиболее очевидный способ составления уравнений — это умножить обе части на многочлен 

Процедуру разложения на простейшие дроби проще всего описать на примерах.
Пример 1. Приравнивание коэффициентов при одинаковых степенях

Записываем общий вид её разложения на простейшие с неопределёнными коэффициентами.
Умножаем на 
Раскрываем скобки
Приравниваем коэффициенты при одинаковых степенях:
Получили систему уравнений. Решаем её. Из первого уравнения:
Подставляем во второе и третье
Складываем уравнения
Из первого уравнения последней системы:
Из полученного в начале соотношения на 
Все коэффициенты разложения найдены.
Пример 2. Подстановка корней знаменателя
Уравнения получаемые простым приравниваем коэффициентов при одинаковых степенях часто довольно сложные. Для получения более простых уравнений часто используют подстановки вместо 
Умножаем на 
Удобнее всего подставлять значения, обнуляющие слагаемые. Подставим 1.
Подставим 2.
Подстановка корней знаменателя помогает очень легко находить коэффициенты дробей со старшей степенью в знаменателе. Если мы бы приравнивали коэффициенты при равных степенях, уравнения бы были гораздо сложнее. Однако, как видно из примера, для нахождения остальных коэффициентов нужно использовать другие приёмы.
Для нахождения коэффициента при первой степени знаменателя можно использовать подстановку бесконечности.
Умножим обе части на 
Подставим бесконечность. Под подстановкой бесконечности здесь понимается предел при стремлении 
В свою очередь предел при стремлении аргумента к бесконечности очень просто определяется: если степень числителя больше степень знаменателя, то предел — 
Вернёмся к нашему примеру. Подставим бесконечность.
Оставшийся коэффициент можно найти приравниванием коэффициента при одинаковой степени 

Приравниваем свободные члены.
Все коэффициенты найдены.
Последний приём также довольно удобен на практике: старший и свободный член легко получить без раскрытия скобок, поэтому этот приём применяется наряду с подстановками.
Пример 3. Подстановка комплексных корней знаменателя
Корни многочленов с отрицательным дискриминантом не являются действительными. Однако ничего не мешает подставить в уравнение комплексный корень.
Умножим на знаменатель.
Подставляем 
Подставим 
А теперь приравняем действительную и мнимую часть чтобы получить уравнение с действительными числами.
Подстановка сопряжённого корня 
Коэффициент 
Коэффициент 
Умножаем на 
Подставляем бесконечность.
Все коэффициенты найдены.
Вообще подставлять можно абсолютно любое значение, не обязательно корень знаменателя или бесконечность. В особо трудных случаях это может быть проще, чем рассчёт и приравнивание коэффициентов при одинаковых степенях 
Пример 4. Разложение простыми преобразованиями
Иногда разложение на простейшие можно получить просто преобразовывая выражения.

Пример 5. Метод прикрытия Хевисайда и метод вычетов
.
Таким образом, задача была сведена к интегрированию простейших дробей.
Табличные интегралы[править | править код]
Несколько интегралов от рациональных функций принято запоминать, чтобы далее сводить к ним более сложные.[6]
Последние 2 интегралы называются высокими логарифмами и их запоминание не обязательно, поскольку они могут быть сведены разложением дроби на простейшие ко второму интегралу. Интеграл от многочлена, который появляется после разложения на простейшие неправильной дроби, может быть сразу рассчитан при помощи первой формулы.
Интегрирование дробей вида  [править | править код]
[править | править код]
Дроби такого вида интегрируются простым занесением линейного двучлена под дифференциал.[7]
В зависимости от значения 
Если 
Если 
Интегрирование дробей вида  [править | править код]
[править | править код]
Сначала рассмотрим дробь вида 
Для интегрирования таких дробей применяется выделение полного квадрата знаменателя.[8] Прибавим к 


Мы свели интеграл к табличному; конкретный табличный интеграл определяется знаком 
Если 

Если 

Если 
Для интегрирования дробей вида 


Производная числителя есть 

.
Затем прибавляем такое число, чтобы это выражение стало равно числителю.
В таком виде и записываем числитель в интеграле.
Второй интеграл уже был рассмотрен в предыдущем пункте. Осталось взять первый. Так как в числителе стоит производная знаменателя, мы без труда можем занести знаменатель под дифференциал.
Описанный метод интегрирования работает для любой дроби с квадратным трёхчленом в знаменателе, а не только с отрицательным дискриминантом. Таким образом, для дробей с двучленом с положительным дискриминантом мы рассмотрели два способа интегрирования.
Интегрирование дробей вида  [править | править код]
[править | править код]
Дробь 
Левый интеграл является табличным:
Правый же интеграл является самым сложным из рассмотренных здесь. Сразу же выделим полный квадрат в знаменателе. Задача сводится к взятию следующего интеграла:
Рассмотрим два способа его взятия.
Рекуррентное соотношение[править | править код]
Обозначим 

Тогда
Интеграл 


Так как интегралы такого вида встречаются довольно редко, обычно эту рекуррентную формулу не запоминают, а просто каждый раз снова выводят. Заметим, что в формуле не накладывается никаких ограничений на знак 
Тригонометрическая подстановка[править | править код]
Интегрирование такого вида дробей также возможно при помощи тригонометрической подстановки.
Рассмотрим для начала дробь вида
Здесь есть важное отличие от рекуррентной формулы: та не зависела от знака дискриминанта и одинаково работала в любом случае; здесь же мы сразу полагаем дискриминант знаменателя отрицательным и поэтому после выделения полного квадрата можем представить 


Выполним замену 

Данный интеграл довольно легко берётся с помощью последовательного применения формул понижения степени в случае чётной степени косинуса, и занесения косинуса под дифференциал в случае нечётной. В результате у нас получится линейная комбинация степеней синусов от чётного угла.
Далее необходимо сделать обратную замену. Для получения красивых выражений применяется следующая уловка. Выражение 







Формулы для синусов и косинусов можно и просто запомнить: синус есть деление линейного двучлена из полного квадрата на корень квадратного трёхчлена, а косинус — деление константы (точнее её корня), которая прибавляется к полному квадрату.[10]
Существует вариация этого метода и для трёхчленов с положительным дискриминантом.
В такой ситуации можно сделать гиперболическую замену.
Затем аналогично приходим к интегралу от гиперболического косинуса в чётной степени и аналогично интегрируем его. Итоговое выражение состоит из гиперболических синусов и линейных слагаемых. В линейных слагаемых мы делаем обратную замену
Для того, чтобы выразить гиперболические синусы, применяем аналогичный приём:
На самом деле тригонометрические и гиперболические замены могут быть и другими. Для случая отрицательного дискриминанта возможны следующие замены:
Для случая положительного следующие:
Наиболее удобны здесь замены на тангенсы и котангенсы, поскольку они приводят интеграл к интегралу от синуса или косинуса в некоторой степени, который берётся довольно просто. Остальные же замены приводят к куда более сложным интегралам.
Комплексное разложение на простейшие[править | править код]
Если в коэффициентах дробей допускать комплексные числа, то разложение на простейшие заметно упрощается. В комплексных числах правильную дробь можно разложить в сумму одних только дробей вида 
Использование комплексного разложения позволяет проинтегрировать дробь практически устно. Все методы вещественного разложения дроби работают и с комплексным разложением. Недостатком является то, что итоговый интеграл содержит логарифмы и дроби с комплексными числами и приведение этого выражения к выражению содержащему только вещественные числа требует дальнейших преобразований.
Пример 1. С логарифмом
Строим комплексное разложение на простейшие. Искать коэффициенты будем методом прикрытия Хевисайда.
При 
При 
При 
При 
Умножаем на 
Далее интегрируем.
Теперь нам нужно избавиться от комплексных значений внутри логарифмов. Для этого складываем функции с сопряжёнными значениями.
Интеграл найден.
Пример 2. С арктангенсом
Находим разложение на простейшие
После очевидного интегрирования имеем:
Сгруппируем отдельно действительные и мнимые слагаемые:
Как известно, арктангенс комплексного переменного выражается через логарифм:
Это даёт нам возможность переписать второе слагаемое через арктангенс:
Для нахождения интеграла рациональной функции комплексного переменного, комплексное разложение на простейшие используется напрямую без дальнейшего преобразования выражений. Все табличные интегралы верны и для комплексных функций, с тем лишь изменением, что арктангенс и логарифм модуля заменяются соответственно на комплесный многозначный логарифм и комплексный многозначный арктангенс.
Общий вид интеграла рациональной функции[править | править код]
Из вышеприведённых методов для интеграла от рациональной функции можно составить общий вид.



Из этого общего вида легко можно видеть, что интеграл от дроби, не имеющей кратных корней, есть сумма одних только арктангенсов и логарифмов. В свою очередь, если кратные корни есть, то в рациональной части интеграла кратности этих корней уменьшаются на 1.
Метод Остроградского[править | править код]
Если сумму логарифмов и арктангенсов представить как интеграл некоторой правильной дроби без кратных корней (эту дробь можно определить просто взяв производную), то получится следующая формула.
,
называемая формулой Остроградского. На этой формуле основан ещё один метод интегрирования рациональных функций — метод Остроградского. Он позволяет свести задачу к интегрированию рациональной дроби со знаменателем без кратных неприводимых множителей, которая значительно проще.
Суть метода заключается в следующем. Пусть нам нужно проинтегрировать рациональную функцию. Запишем для неё формулу Остроградского (как выше). Знаменатели дробей из формулы нам известны, числители имеют степень меньше знаменателей. Это даёт нам возможность записать в знаменатели многочлены с неопределёнными коэффициентами.
Теперь мы можем найти эти коэффициенты методом неопределённых коэффициентов. Продифференцируем это равенство и приведём к общему знаменателю. Тогда мы можем приравнять числители, приравнять коэффициенты при равных степенях и решить систему. Разумеется, тут можно использовать все те упрощения, что использовались при разложении дробей, вроде подстановок корней или подстановки бесконечности. Таким образом, задача будет сведена к интегрированию дроби со знаменателем без кратных дробей. Дробь же со знаменателем без кратных корней намного проще интегрировать. Все её коэффициенты разложения можно получить методом Хевисайда и подстановками комплексных корней.
Пример
Запишем формулу Остроградского.
Дифференцируем.
Вторую дробь можно сократить на 
Приведём к общем знаменателю
Приравниваем числители.
Приравняем коэффициенты при старшей степени.
Это даёт нам возможность в будущем вновь использовать приравнивание коэффициентов при старшей степени.
Здесь очевидны две подстановки. Подставим 
Подставим 
Теперь приравняем старшие и младшие коэффициенты.
Сложим.
Получили 3 уравнения.
Вычтем из первого второе.
Теперь сложим первое и третье.
Из последнего уравнения
Таким образом,
Последний интеграл легко берётся:
В итоге
Метод Остроградского удобен при большом количестве кратных корней. Однако сильно задачу он не упрощает, система уравнений получается не менее сложная, чем при обычном разложении на простейшие.
Метод Остроградского позволяет найти рациональную часть интеграла при помощи одних только алгебраических операций даже не зная разложения знаменателя. Пусть 






См. также[править | править код]
- Список интегралов от рациональных функций
- Методы интегрирования
- Разложение рациональной дроби на простейшие
- Метод Остроградского
Примечания[править | править код]
- ↑ Зорич, 2012, с. 392.
- ↑ Rickey, 1980.
- ↑ Фихтенгольц, 2003, с. 48.
- ↑ Кудрявцев, 2003, с. 501.
- ↑ Bauldry, 2018, с. 429.
- ↑ Кудрявцев, 2003, с. 459.
- ↑ Кудрявцев, 2003, с. 504.
- ↑ 1 2 Фихтенгольц, 2003, с. 41.
- ↑ Кудрявцев, 2003, с. 505.
- ↑ Dawkins.
- ↑ Кудрявцев, 2003, с. 503.
- ↑ Кудрявцев, 2003, с. 509.
Ссылки[править | править код]
- Partial Fraction Expander
Литература[править | править код]
- Зорич В. А. Математический анализ. Часть 1. — 6-е изд. — М.: МЦНМО, 2012. — 702 p.
- Кудрявцев Л. Д. Курс математического анализа. В 3-х томах. Том 1. Дифференциальное и интегральное исчисления функций многих переменных. — М.: Дрофа, 2003. — 704 p.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3-х томах. Том 2. — 8-е изд.. — М.: ФИЗМАТЛИТ, 2003. — 864 p. — ISBN 5-9221-0157-9.
- Rickey V. F., Tuchinsky Ph. M. An Application of Geography to Mathematics: History of the Integral of the Secant (англ.) // Mathematics Magazine : журнал. — 1980. — May (vol. 53, no. 3). — P. 162–166.
- Bauldry W.C. Partial Fractions via Calculus (англ.) // Daniel Alpay Problems, Resources, and Issues in Mathematics Undergraduate Studies : журнал. — 2018. — 9 May (vol. 28, iss. 5). — P. 425–437. — ISSN 1051-1970. — doi:10.1080/10511970.2017.1388312.
- Dawkins P. Integrals Involving Quadrtics (англ.). Дата обращения: 5 июля 2021.
Прежде, чем приступить к интегрированию простейших дробей для нахождения неопределенного интеграла дробно рациональной функции, рекомендуется освежить в памяти раздел «Разложение дроби на простейшие».
Найдем неопределенный интеграл ∫2×3+3×3+xdx .
Решение
Выделим целую часть, проведя деление столбиком многочлена на многочлен, учитывая тот факт, что степень числителя подынтегральной функции равна степени знаменателя:
Поэтому 2×3+3×3+x=2+-2x+3×3+x . Мы получили правильную рациональную дробь -2x+3×3+x , которую теперь разложим на простейшие дроби -2x+3×3+x=3x-3x+2×2+1 . Следовательно,
∫2×3+3×3+xdx=∫2+3x-3x+2×2+1dx=∫2dx+∫3xdx-∫3x+2×2+1dx=2x+3lnx-∫3x+2×2+1dx
Мы получили интеграл простейшей дроби третьего типа. Взять его можно методом подведения под знак дифференциала.
Так как dx2+1=2xdx , то 3xdx=32dx2+1 . Поэтому
∫3x+2×2+1dx=∫3xx2+1dx+∫2×2+1=32∫dx2+1×2+1+2∫dxx2+1=32lnx2+1+2arctg x+C1
Следовательно,
∫2×3+3×3+xdx=2x+3lnx-∫3x+2×2+1dx=2x+3lnx-32lnx2+1-2arctan x+C, где С=-С1
Опишем методы интегрирования простейших дробей каждого из четырех типов.
Интегрирование простейших дробей первого типа Ax-a
Используем для решения этой задачи метод непосредственного инетгрирования:
∫Ax-adx=A∫dxx-a=A·lnx-a+C
Найдите множество первообразных функции y=32x-1.
Решение
Испльзуя правило интегрирования, свойства первообразной и таблицу первообразных, найдем неопределенный интеграл ∫3dx2x-1: ∫fk·x+bdx=1k·Fk·x+b+C
∫3dx2x-1=3∫dx2x-12=32∫dxx-12=32lnx-12+C
Ответ: ∫3dx2x-1=32lnx-12+C
Интегрирование простейших дробей второго типа Ax-an
Здесь также применим метод непосредственного интегрирования:∫Ax-andx=A∫x-a-ndx=A-n+1x-a-n+1+C=A1-nx-an-1+C
Необходимо найти неопределенный интеграл ∫dx2x-37 .
Решение
∫dx2x-37=∫dx2x-327=127∫x-32-7dx==127·1-7+1·x-32-7+1+C=127·-6·x-326+C==12·-6·26·x-326+C=-112·12x-36+C
Ответ: ∫dx2x-37=-112·12x-36+C
Интегрирование простейших дробей третьего типа Mx+Nx2+px+q, D=p2-4q<0
Первым шагом представим неопределенный интеграл ∫Mx+Nx2+px+q в виде суммы:
∫Mx+Nx2+px+qdx=∫Mxx2+px+qdx+N∫dxx2+px+q
Для того, чтобы взять первый интеграл, используем метод подведения под знак дифференциала:
∫Mxx2+px+qdx=dx2+px+q=2x+pdx=2xdx+pdx⇒2xdx=dx2+px+q-pdx⇒Mxdx=M2dx2+px+q-pM2dx==∫M2dx2+px+q-pM2dxx2+px+q==M2∫dx2+px+qx2+px+q-pM2∫dxx2+px+q==M2lnx2+px+q-pM2∫dxx2+px+q
Поэтому,
∫Mx+Nx2+px+qdx=∫Mxx2+px+qdx+N∫dxx2+px+q==M2lnx2+px+q-pM2∫dxx2+px+q+N∫dxx2+px+q==M2lnx2+px+q+2N-pM2·∫dxx2+px+q
Мы получили интеграл ∫dxx2+px+q. Проведем преобразование его знаменателя:
∫dxx2+px+q=∫dxx2+px+p22-p22+q==∫dxx+p22-p24+q=∫dxx+p22-p24+q==∫dxx+p22+4q-p24=24q-p2·arctg2x+p24q-p2+C1
Следовательно,
∫Mx+Nx2+px+qdx=M2lnx2+px+q+2N-pM2·∫dxx2+px+q==M2lnx2+px+q+2N-pM2·24q-p2·arctg2x+p24q-p2+C1
Формула интегрирования простейших дробей третьего типа принимает вид:
∫Mx+Nx2+px+qdx=M2lnx2+px+q+2N-pM4q-p2·arctg2x+p24q-p2+C
Необходимо найти неопределенный интеграл ∫2x+13×2+6x+30dx.
Решение
Применим формулу:
∫2x+13×2+6x+30dx=13∫2x+1×2+2x+10dx=M=2,N=1,p=2,q=10==1322lnx2+2x+10+2·1-2·24·10-22arctg2x+224·10-22+C==13lnx2+2x+10-19arctgx+13+C
Второй вариант решения выглядит следующим образом:
∫2x+13×2+6x+30dx=13∫2x+1×2+2x+10dx=d(x2+2x+10=(2x+2)dx==13∫2x+2-1×2+2x+10dx=13∫d(x2+2x+10)x2+2x+10=13∫dxx2+2x+10==преобразуем знаменатель=13lnx2+2x+10-13∫d(x)x+12+9==13lnx2+2x+10-19arctgx+13+C
Ответ: ∫2x+13×2+6x+30dx=13lnx2+2x+10-19arctgx+13+C
Интегрирование простейших дробей четвертого типа Mx+N(x2+px+q)n, D=p2-4q<0
Первым делом выполняем подведение под знак дифференциала:
∫Mx+Nx2+px+qdx=d(x2+px+q)=(2x+p)dx==M2∫d(x2+px+q)(x2+px+q)n+N-pM2∫dx(x2+px+q)n==M2(-n+1)·1(x2+px+q)n-1+N-pM2∫dx(x2+px+q)n
Затем находим интеграл вида Jn=∫dx(x2+px+q)n с использованием рекуррентных формул. Информацию о рекуррентных формулах можно посмотреть в теме «Интегрирование с использованием рекуррентных формул».
Для решения нашей задачи подходит рекуррентная формула вида Jn=2x+p(n-1)(4q-p2)(x2+px+q)n-1+2n-3n-1·24q-p2·Jn-1.
Необходимо найти неопределенный интеграл ∫dxx5x2-1 .
Решение
∫dxx5x2-1=∫x-5(x2-1)-12dx
Мы будем использовать для этого вида подынтегральной функции метод подстановки. Введем новую переменную x2-1=z2x=(z2+1)12dx=z(z2+1)-12dx
Получаем:
∫dxx5x2-1=∫x-5(x2-1)-12dx==∫(z2+1)-52·z-1·z·(z2+1)-12dz=∫dz(z2+1)3
Пришли к нахождению интеграла дроби четвертого типа. В нашем случае имеем коэффициенты М = 0, р = 0, q = 1, N = 1 и n = 3. Применяем рекуррентную формулу:
J3=∫dz(z2+1)3=2z+0(3-1)·(4·1-0)·z2+13-1+2·3-33-1·24·1-0·∫dz(z2+1)2==z4(z2+1)2+342z(2-1)·(4·1-0)·(z2+1)2-1+2·2-32-11·24·1-0·∫dzz2+1==z4(z2+1)2+38zz2+1+38arctg(z)+C
После обратной замены z=x2-1 получаем результат:
∫dxx5x2-1=x2-14×4+38×2-1×2+38arctgx2-1+C
Ответ: ∫dxx5x2-1=x2-14×4+38×2-1×2+38arctgx2-1+C
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Интегрирование простейших рациональных дробей
Напомним, что дробно-рациональными называют функции вида
$$
f(x) = frac{P_n(x)}{Q_m(x)},
$$
в общем случае являющиеся отношением двух многочленов %%P_n(x)%% и %%Q_m(x)%%.
Если %%m > n geq 0%%, то рациональную дробь называют правильной, в противном случае — неправильной. Используя правило деления многочленов, неправильную рациональную дробь можно представить в виде суммы многочлена %%P_{n – m}%% степени %%n – m%% и некоторой правильной дроби, т.е.
$$
frac{P_n(x)}{Q_m(x)} = P_{n-m}(x) + frac{P_l(x)}{Q_n(x)},
$$
где степень %%l%% многочлена %%P_l(x)%% меньше степени %%n%% многочлена %%Q_n(x)%%.
Таким образом, неопределенный интеграл от рациональной функции можно представить суммой неопределенных интегралов от многочлена и от правильной рациональной дроби.
Интегралы от простейших рациональных дробей
Среди правильных рациональных дробей выделяют четыре типа, которые относят к простейшим рациональным дробям:
- %%displaystyle frac{A}{x – a}%%,
- %%displaystyle frac{A}{(x – a)^k}%%,
- %%displaystyle frac{Ax + B}{x^2 + px + q}%%,
- %%displaystyle frac{Ax + B}{(x^2 + px + q)^k}%%,
где %%k > 1%% — целое и %%p^2 – 4q < 0%%, т.е. квадратные уравнения не имеют действительных корней.
Вычисление неопределенных интегралов от дробей первых двух типов
Вычисление неопределенных интегралов от дробей первых двух типов не вызывает затруднений:
$$
begin{array}{ll}
int frac{A}{x – a} mathrm{d}x &= Aint frac{mathrm{d}(x – a)}{x – a} = A ln |x – a| + C, \
\
int frac{A}{(x – a)^k} mathrm{d}x &= Aint frac{mathrm{d}(x – a)}{(x – a)^k} = A frac{(x-a)^{-k + 1}}{-k + 1} + C = \
&= -frac{A}{(k-1)(x-a)^{k-1}} + C.
end{array}
$$
Вычисление неопределенного интегралов от дробей третьего типа
Дробь третьего типа сначала преобразуем, выделив полный квадрат в знаменателе:
$$
frac{Ax + B}{x^2 + px + q} = frac{Ax + B}{(x + p/2)^2 + q – p^2/4},
$$
так как %%p^2 – 4q < 0%%, то %%q – p^2/4 > 0%%, которое обозначим как %%a^2%%. Заменив также %%t = x + p/2, mathrm{d}t = mathrm{d}x%%, преобразуем знаменатель и запишем интеграл от дроби третьего типа в форме
$$
begin{array}{ll}
int frac{Ax + B}{x^2 + px + q} mathrm{d}x &= int frac{Ax + B}{(x + p/2)^2 + q – p^2/4} mathrm{d}x = \
&= int frac{A(t – p/2) + B}{t^2 + a^2} mathrm{d}t = int frac{At + (B – A p/2)}{t^2 + a^2} mathrm{d}t.
end{array}
$$
Последний интеграл, используя линейность неопределенного интеграла, представим в виде суммы двух и в первом из них введем %%t%% под знак дифференциала:
$$
begin{array}{ll}
int frac{At + (B – A p/2)}{t^2 + a^2} mathrm{d}t &= Aint frac{t mathrm{d}t}{t^2 + a^2} + left(B – frac{pA}{2}right)int frac{mathrm{d}t}{t^2 + a^2} = \
&= frac{A}{2} int frac{mathrm{d}left(t^2 + a^2right)}{t^2 + a^2} + – frac{2B – pA}{2}int frac{mathrm{d}t}{t^2 + a^2} = \
&= frac{A}{2} ln left| t^2 + a^2right| + frac{2B – pA}{2a} text{arctg}frac{t}{a} + C.
end{array}
$$
Возвращаясь к исходной переменной %%x%%, в итоге для дроби третьего типа получаем
$$
int frac{Ax + B}{x^2 + px + q} mathrm{d}x = frac{A}{2} ln left| x^2 + px + qright| + frac{2B – pA}{2a} text{arctg}frac{x + p/2}{a} + C,
$$
где %%a^2 = q – p^2 / 4 > 0%%.
Вычисление интеграла 4 типа сложно, поэтому в этом курсе не рассматривается.
Интегрирование рациональных функций (рациональных дробей). Первая часть.
Материал, изложенный в этой теме, опирается на сведения, представленные в теме “Рациональные дроби. Разложение рациональных дробей на элементарные (простейшие) дроби”. Очень советую хотя бы бегло просмотреть эту тему перед тем, как переходить к чтению данного материала. Кроме того, нам будет нужна таблица неопределенных интегралов.
Напомню пару терминов. О их шла речь в соответствующей теме, посему тут ограничусь краткой формулировкой.
Отношение двух многочленов $frac{P_n(x)}{Q_m(x)}$ называется рациональной функцией или рациональной дробью.
Рациональная дробь называется правильной, если $n < m$, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если $n ≥ m$) дробь называется неправильной.
Элементарными (простейшими) рациональными дробями именуют рациональные дроби четырёх типов:
- $frac{A}{x-a}$;
- $frac{A}{(x-a)^n}$ ($n=2,3,4, ldots$);
- $frac{Mx+N}{x^2+px+q}$ ($p^2-4q < 0$);
- $frac{Mx+N}{(x^2+px+q)^n}$ ($p^2-4q < 0$; $n=2,3,4,ldots$).
Примечание (желательное для более полного понимания текста): показатьскрыть
Примеры рациональных дробей (правильных и неправильных), а также примеры разложения рациональной дроби на элементарные можно найти тут. Здесь нас будут интересовать лишь вопросы их интегрирования. Начнём с интегрирования элементарных дробей. Итак, каждый из четырёх типов указанных выше элементарных дробей несложно проинтегрировать, используя формулы, указанные ниже. Напомню, что при интегрировании дробей типа (2) и (4) предполагается $n=2,3,4,ldots$. Формулы (3) и (4) требуют выполнение условия $p^2-4q < 0$.
$$
begin{equation}
int frac{A}{x-a} dx=Acdot ln |x-a|+C
end{equation}
$$
$$
begin{equation}
intfrac{A}{(x-a)^n}dx=-frac{A}{(n-1)(x-a)^{n-1}}+C
end{equation}
$$
$$
begin{equation}
intfrac{Mx+N}{x^2+px+q} dx= frac{M}{2}cdot ln (x^2+px+q)+frac{2N-Mp}{sqrt{4q-p^2}}arctgfrac{2x+p}{sqrt{4q-p^2}}+C
end{equation}
$$
Для $intfrac{Mx+N}{(x^2+px+q)^n}dx$ делается замена $t=x+frac{p}{2}$, после полученный интерал разбивается на два. Первый будет вычисляться с помощью внесения под знак дифференциала, а второй будет иметь вид $I_n=intfrac{dt}{(t^2+a^2)^n}$. Этот интеграл берётся с помощью рекуррентного соотношения
$$
begin{equation}
I_{n+1}=frac{1}{2na^2}frac{t}{(t^2+a^2)^n}+frac{2n-1}{2na^2}I_n, ; nin N
end{equation}
$$
Вычисление такого интеграла разобрано в примере №7 (см. третью часть).
Схема вычисления интегралов от рациональных функций (рациональных дробей):
- Если подынтегральная дробь является элементарной, то применить формулы (1)-(4).
- Если подынтегральная дробь не является элементарной, то представить её в виде суммы элементарных дробей, а затем проинтегрировать, используя формулы (1)-(4).
Указанный выше алгоритм интегрирования рациональных дробей имеет неоспоримое достоинство – он универсален. Т.е. пользуясь этим алгоритмом можно проинтегрировать любую рациональную дробь. Именно поэтому почти все замены переменных в неопределённом интеграле (подстановки Эйлера, Чебышева, универсальная тригонометрическая подстановка) делаются с таким расчётом, чтобы после оной замены получить под интералом рациональную дробь. А к ней уже применить алгоритм. Непосредственное применение этого алгоритма разберём на примерах, предварительно сделав небольшое примечание.
Примечание
Формулы (1)-(4) предполагают, что коэффициент перед $x$ (в формулах (1) и (2)) и коэффициент перед $x^2$ (в формулах (3) и (4)) равен единице. Но как быть, если этот коэффициент не равен единице? В этом случае достаточно просто вынести его за скобки:
$$frac{3x+7}{5x^2+10x+9}=frac{3x+7}{5left(x^2+2x+frac{9}{5}right)}=frac{frac{3}{5}x+frac{7}{5}}{x^2+2x+frac{9}{5}}.$$
Кстати сказать, это касается не только элементарных дробей. Например, если требуется разложить дробь $frac{4x^2+6x+7}{(2x+9)(3x^2+5x+18)}$, то её представим в такой форме:
$$
frac{4x^2+6x+7}{(2x+9)(3x^2+5x+18)}=frac{4x^2+6x+7}{2cdotleft(x+frac{9}{2}right)cdot 3 cdot left(x^2+frac{5}{3}x+6right)}=
frac{4x^2+6x+7}{6cdotleft(x+frac{9}{2}right)left(x^2+frac{5}{3}x+6right)}=\
=frac{frac{4}{6}x^2+frac{6}{6}x+frac{7}{6}}{left(x+frac{9}{2}right)left(x^2+frac{5}{3}x+6right)}
=frac{frac{2}{3}x^2+x+frac{7}{6}}{left(x+frac{9}{2}right)left(x^2+frac{5}{3}x+6right)}.
$$
В дальнейших примерах я затрону случай, когда коэффициент перед старшим членом многочлена в знаменателе не равен $1$. Но каждый раз этот случай будет разрешён по стандартной схеме: вынести “мешающий” коэффициент за скобки и перенести его в числитель (или вообще вынести за знак интеграла).
Перейдём к примерам. Первый пример – тренировочный, на использование формул интегрирования элементарных дробей (пока что без использования формулы №4, она будет рассмотрена отдельно).
Пример №1
Найти интегралы:
- $intfrac{7dx}{x+9}$;
- $intfrac{11dx}{(4x+19)^8}$;
- $intfrac{4x+7}{x^2+10x+34}dx$.
Решение
1) Для нахождения интеграла $intfrac{7dx}{x+9}$ можно сразу применить формулу (1):
$$
intfrac{7dx}{x+9}=7ln|x+9|+C.
$$
В принципе, этот интеграл несложно получить без механического применения формулы (1). Если вынести константу $7$ за знак интеграла и учесть, что $dx=d(x+9)$, то получим:
$$
intfrac{7dx}{x+9}=7cdot intfrac{dx}{x+9}=7cdot intfrac{d(x+9)}{x+9}=|u=x+9|=7cdotintfrac{du}{u}=7ln|u|+C=7ln|x+9|+C.
$$
Для детальной информации рекомедую посмотреть тему “Интегрирование подстановкой (внесение под знак дифференциала)”. Там подробно поясняется, как решаются подобные интегралы. Кстати, формула (1) доказывается теми же преобразованиями, что были применены в этом пункте при решении “вручную”.
2) Вновь есть два пути: применить готовую формулу или обойтись без неё. Если применять формулу (2), то следует учесть, что коэффициент перед $x$ (число 4) придется убрать. Для этого оную четвёрку просто вынесем за скобки:
$$
intfrac{11dx}{(4x+19)^8}=intfrac{11dx}{left(4left(x+frac{19}{4}right)right)^8}=
intfrac{11dx}{4^8left(x+frac{19}{4}right)^8}=intfrac{frac{11}{4^8}dx}{left(x+frac{19}{4}right)^8}.
$$
Теперь настал черёд и для применения формулы (2):
$$
intfrac{frac{11}{4^8}dx}{left(x+frac{19}{4}right)^8}=-frac{frac{11}{4^8}}{(8-1)left(x+frac{19}{4} right)^{8-1}}+C=
-frac{frac{11}{4^8}}{7left(x+frac{19}{4} right)^7}+C=-frac{11}{7cdot 4^8 left(x+frac{19}{4} right)^7}+C.
$$
Можно обойтись и без применения формулы (2). И даже без вынесения константы $4$ за скобки. Если учесть, что $dx=frac{1}{4}d(4x+19)$, то получим:
$$
intfrac{11dx}{(4x+19)^8}=11intfrac{dx}{(4x+19)^8}=frac{11}{4}intfrac{d(4x+19)}{(4x+19)^8}=|u=4x+19|=\
=frac{11}{4}intfrac{du}{u^8}=frac{11}{4}int u^{-8};du=frac{11}{4}cdotfrac{u^{-8+1}}{-8+1}+C=\
=frac{11}{4}cdotfrac{u^{-7}}{-7}+C=-frac{11}{28}cdotfrac{1}{u^7}+C=-frac{11}{28(4x+19)^7}+C.
$$
Подробные пояснения по нахождению подобных интегралов даны в теме “Интегрирование подстановкой (внесение под знак дифференциала)”.
3) Нам нужно проинтегрировать дробь $frac{4x+7}{x^2+10x+34}$. Эта дробь имеет структуру $frac{Mx+N}{x^2+px+q}$, где $M=4$, $N=7$, $p=10$, $q=34$. Однако чтобы убедиться, что это действительно элементарная дробь третьего типа, нужно проверить выполнение условия $p^2-4q < 0$. Так как $p^2-4q=10^2-4cdot 34=-16 < 0$, то мы действительно имеем дело с интегрированием элементарной дроби третьего типа. Как и в предыдущих пунктах есть два пути для нахождения $intfrac{4x+7}{x^2+10x+34}dx$. Первый путь – банально использовать формулу (3). Подставив в неё $M=4$, $N=7$, $p=10$, $q=34$ получим:
$$
intfrac{4x+7}{x^2+10x+34}dx = frac{4}{2}cdot ln (x^2+10x+34)+frac{2cdot 7-4cdot 10}{sqrt{4cdot 34-10^2}} arctgfrac{2x+10}{sqrt{4cdot 34-10^2}}+C=\
=2cdot ln (x^2+10x+34)+frac{-26}{sqrt{36}} arctgfrac{2x+10}{sqrt{36}}+C
=2cdot ln (x^2+10x+34)+frac{-26}{6} arctgfrac{2x+10}{6}+C=\
=2cdot ln (x^2+10x+34)-frac{13}{3} arctgfrac{x+5}{3}+C.
$$
Решим этот же пример, но без использования готовой формулы. Попробуем выделить в числителе производную знаменателя. Что это означает? Мы знаем, что $(x^2+10x+34)’=2x+10$. Именно выражение $2x+10$ нам и предстоит вычленить в числителе. Пока что числитель содержит лишь $4x+7$, но это ненадолго. Применим к числителю такое преобразование:
$$
4x+7=2cdot 2x+7=2cdot (2x+10-10)+7=2cdot(2x+10)-2cdot 10+7=2cdot(2x+10)-13.
$$
Теперь в числителе появилось требуемое выражение $2x+10$. И наш интеграл можно переписать в таком виде:
$$
intfrac{4x+7}{x^2+10x+34} dx= intfrac{2cdot(2x+10)-13}{x^2+10x+34}dx.
$$
Разобьём подынтегральную дробь на две. Ну и, соответственно, сам интеграл тоже “раздвоим”:
$$
intfrac{2cdot(2x+10)-13}{x^2+10x+34}dx=int left( frac{2cdot(2x+10)}{x^2+10x+34}-frac{13}{x^2+10x+34} right); dx=\
=int frac{2cdot(2x+10)}{x^2+10x+34}dx-intfrac{13dx}{x^2+10x+34}=2cdotint frac{(2x+10)dx}{x^2+10x+34}-13cdotintfrac{dx}{x^2+10x+34}.
$$
Поговорим сперва про первый интеграл, т.е. про $int frac{(2x+10)dx}{x^2+10x+34}$. Так как
$$d(x^2+10x+34)=(x^2+10x+34)’dx=(2x+10)dx,$$
то в числителе подынтегральной дроби расположен дифференциал знаменателя. Короче говоря, вместо выражения $(2x+10)dx$ запишем $d(x^2+10x+34)$.
Теперь скажем пару слов и о втором интеграле. Выделим в знаменателе полный квадрат: $x^2+10x+34=(x+5)^2+9$. Кроме того, учтём $dx=d(x+5)$. Теперь полученную нами ранее сумму интегралов можно переписать в несколько ином виде:
$$
2cdotint frac{(2x+10)dx}{x^2+10x+34}-13cdotintfrac{dx}{x^2+10x+34}
=2cdotint frac{d(x^2+10x+34)}{x^2+10x+34}-13cdotintfrac{d(x+5)}{(x+5)^2+9}.
$$
Если в первом интеграле сделать замену $u=x^2+10x+34$, то он примет вид $intfrac{du}{u}$ и возьмётся простым применением второй формулы из таблицы неопределенных интегралов. Что же касается второго интеграла, то для него осуществима замена $u=x+5$, после которой он примет вид $intfrac{du}{u^2+9}$. Это чистейшей воды одиннадцатая формула из таблицы неопределенных интегралов. Итак, возвращаясь к сумме интегралов, будем иметь:
$$
2cdotint frac{d(x^2+10x+34)}{x^2+10x+34}-13cdotintfrac{d(x+5)}{(x+5)^2+9}
=2cdotln(x^2+10x+34)-frac{13}{3}arctgfrac{x+5}{3}+C.
$$
Мы получили тот же ответ, что и при применении формулы (3), что, собственно говоря, неудивительно. Вообще, формула (3) доказывается теми же методами, кои мы применяли для нахождения данного интеграла. Полагаю, что у внимательного читателя тут может возникнуть один вопрос, посему сформулирую его:
Вопрос №1
Если к интегралу $int frac{d(x^2+10x+34)}{x^2+10x+34}$ применять вторую формулу из таблицы неопределенных интегралов, то мы получим следующее:
$$
int frac{d(x^2+10x+34)}{x^2+10x+34}=|u=x^2+10x+34|=intfrac{du}{u}=ln|u|+C=ln|x^2+10x+34|+C.
$$
Почему же в решении отсутствовал модуль?
Ответ на вопрос №1
Вопрос совершенно закономерный. Модуль отсутствовал лишь потому, что выражение $x^2+10x+34$ при любом $xin R$ больше нуля. Это совершенно несложно показать несколькими путями. Например, так как $x^2+10x+34=(x+5)^2+9$ и $(x+5)^2 ≥ 0$, то $(x+5)^2+9 > 0$. Можно рассудить и по-иному, не привлекая выделение полного квадрата. Так как $10^2-4cdot 34=-16 < 0$, то $x^2+10x+34 > 0$ при любом $xin R$ (если эта логическая цепочка вызывает удивление, советую посмотреть графический метод решения квадратных неравенств). В любом случае, так как $x^2+10x+34 > 0$, то $|x^2+10x+34|=x^2+10x+34$, т.е. вместо модуля можно использовать обычные скобки.
Все пункты примера №1 решены, осталось лишь записать ответ.
Ответ:
Пример №2
Найти интеграл $intfrac{7x+12}{3x^2-5x-2}dx$.
Решение
На первый взгляд подынтегральая дробь $frac{7x+12}{3x^2-5x-2}$ очень похожа на элементарную дробь третьего типа, т.е. на $frac{Mx+N}{x^2+px+q}$. Кажется, что единcтвенное отличие – это коэффициент $3$ перед $x^2$, но ведь коэффициент и убрать недолго (за скобки вынести). Однако это сходство кажущееся. Для дроби $frac{Mx+N}{x^2+px+q}$ обязательным является условие $p^2-4q < 0$, которое гарантирует, что знаменатель $x^2+px+q$ нельзя разложить на множители. Проверим, как обстоит дело с разложением на множители у знаменателя нашей дроби, т.е. у многочлена $3x^2-5x-2$.
У нас коэффициент перед $x^2$ не равен единице, посему проверить условие $p^2-4q < 0$ напрямую мы не можем. Однако тут нужно вспомнить, откуда взялось выражение $p^2-4q$. Это всего лишь дискриминант квадратного уравнения $x^2+px+q=0$. Если дискриминант меньше нуля, то выражение $x^2+px+q$ на множители не разложишь. Вычислим дискриминант многочлена $3x^2-5x-2$, расположенного в знаменателе нашей дроби: $D=(-5)^2-4cdot 3cdot(-2)=49$. Итак, $D > 0$, посему выражение $3x^2-5x-2$ можно разложить на множители. А это означает, что дробь $frac{7x+12}{3x^2-5x-2}$ не является элементаной дробью третьего типа, и применять к интегралу $intfrac{7x+12}{3x^2-5x-2}dx$ формулу (3) нельзя.
Ну что же, если заданная рациональная дробь не является элементарной, то её нужно представить в виде суммы элементарных дробей, а затем проинтегрировать. Короче говоря, след воспользоваться схемой интегрирования рациональных дробей. Как разложить рациональную дробь на элементарные подробно написано тут. Начнём с того, что разложим на множители знаменатель:
$$
3x^2-5x-2=0;\
begin{aligned}
& D=(-5)^2-4cdot 3cdot(-2)=49;\
& x_1=frac{-(-5)-sqrt{49}}{2cdot 3}=frac{5-7}{6}=frac{-2}{6}=-frac{1}{3};\
& x_2=frac{-(-5)+sqrt{49}}{2cdot 3}=frac{5+7}{6}=frac{12}{6}=2.\
end{aligned}\
3x^2-5x-2=3cdotleft(x-left(-frac{1}{3}right)right)cdot (x-2)=3cdotleft(x+frac{1}{3}right)(x-2).
$$
Подынтеральную дробь представим в таком виде:
$$
frac{7x+12}{3x^2-5x-2}=frac{7x+12}{3cdotleft(x+frac{1}{3}right)(x-2)}=frac{frac{7}{3}x+4}{left(x+frac{1}{3}right)(x-2)}.
$$
Теперь разложим дробь $frac{frac{7}{3}x+4}{left(x+frac{1}{3}right)(x-2)}$ на элементарные:
$$
frac{frac{7}{3}x+4}{left(x+frac{1}{3}right)(x-2)}
=frac{A}{x+frac{1}{3}}+frac{B}{x-2}=frac{A(x-2)+Bleft( x+frac{1}{3}right)}{left(x+frac{1}{3}right)(x-2)};\
frac{7}{3}x+4=A(x-2)+Bleft( x+frac{1}{3}right).
$$
Чтобы найти коэффициенты $A$ и $B$ есть два стандартных пути: метод неопределённых коэффициентов и метод подстановки частных значений. Применим метод подстановки частных значений, подставляя $x=2$, а затем $x=-frac{1}{3}$:
$$
frac{7}{3}x+4=A(x-2)+Bleft( x+frac{1}{3}right).\
x=2;; frac{7}{3}cdot 2+4=A(2-2)+Bleft( 2+frac{1}{3}right); ; frac{26}{3}=frac{7}{3}B;; B=frac{26}{7}.\
x=-frac{1}{3};; frac{7}{3}cdot left(-frac{1}{3} right)+4=Aleft(-frac{1}{3}-2right)+Bleft( -frac{1}{3}+frac{1}{3}right); ;
frac{29}{9}=-frac{7}{3}A;; A=-frac{29cdot 3}{9cdot 7}=-frac{29}{21}.\
$$
Так как коэффициенты найдены, осталось лишь записать готовое разложение:
$$
frac{frac{7}{3}x+4}{left(x+frac{1}{3}right)(x-2)}=frac{-frac{29}{21}}{x+frac{1}{3}}+frac{frac{26}{7}}{x-2}.
$$
В принципе, можно такую запись оставить, но мне по душе более аккуратный вариант:
$$
frac{frac{7}{3}x+4}{left(x+frac{1}{3}right)(x-2)}=-frac{29}{21}cdotfrac{1}{x+frac{1}{3}}+frac{26}{7}cdotfrac{1}{x-2}.
$$
Возвращаясь к исходному интегралу, подставим в него полученное разложение. Затем разобьём интеграл на два, и к каждому применим формулу (1). Константы я предпочитаю сразу выносить за знак интеграла:
$$
intfrac{7x+12}{3x^2-5x-2}dx
=intleft(-frac{29}{21}cdotfrac{1}{x+frac{1}{3}}+frac{26}{7}cdotfrac{1}{x-2}right)dx=\
=intleft(-frac{29}{21}cdotfrac{1}{x+frac{1}{3}}right)dx+intleft(frac{26}{7}cdotfrac{1}{x-2}right)dx
=-frac{29}{21}cdotintfrac{dx}{x+frac{1}{3}}+frac{26}{7}cdotintfrac{dx}{x-2}dx=\
=-frac{29}{21}cdotlnleft|x+frac{1}{3}right|+frac{26}{7}cdotln|x-2|+C.
$$
Ответ: $intfrac{7x+12}{3x^2-5x-2}dx=-frac{29}{21}cdotlnleft|x+frac{1}{3}right|+frac{26}{7}cdotln|x-2|+C$.
Пример №3
Найти интеграл $intfrac{x^2-38x+157}{(x-1)(x+4)(x-9)}dx$.
Решение
Нам нужно проинтегрировать дробь $frac{x^2-38x+157}{(x-1)(x+4)(x-9)}$. В числителе расположен многочлен второй степени, а в знаменателе – многочлен третьей степени. Так как степень многочлена в числителе меньше степени многочлена в знаменателе, т.е. $2 < 3$, то подынтегральная дробь является правильной. Разложение этой дроби на элементарные (простейшие) было получено в примере №3 на странице, посвящённой разложению рациональных дробей на элементарные. Полученное разложение таково:
$$
frac{x^2-38x+157}{(x-1)(x+4)(x-9)}=-frac{3}{x-1}+frac{5}{x+4}-frac{1}{x-9}.
$$
Нам останется только разбить заданный интеграл на три, и к каждому применить формулу (1). Константы я предпочитаю сразу выносить за знак интеграла:
$$
intfrac{x^2-38x+157}{(x-1)(x+4)(x-9)}dx=intleft(-frac{3}{x-1}+frac{5}{x+4}-frac{1}{x-9} right)dx=\=-3cdotintfrac{dx}{x-1}+
5cdotintfrac{dx}{x+4}-intfrac{dx}{x-9}=-3ln|x-1|+5ln|x+4|-ln|x-9|+C.
$$
Ответ: $intfrac{x^2-38x+157}{(x-1)(x+4)(x-9)}dx=-3ln|x-1|+5ln|x+4|-ln|x-9|+C$.
Продолжение разбора примеров этой темы расположено во второй части.

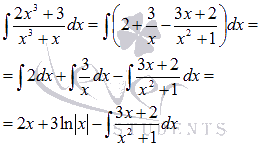























 и
и ,
,

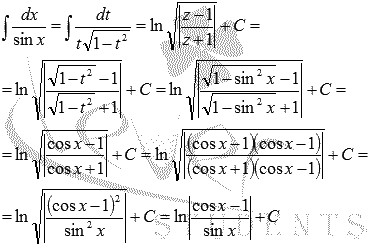

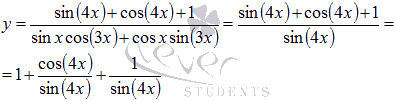






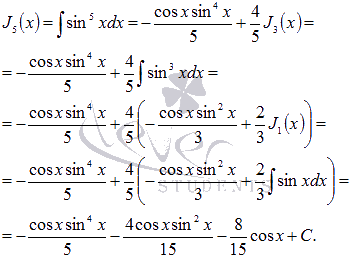





 используется
используется