Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Интеграл косинуса
Интеграл косинуса по таблице интегрирования основных элементарных функций равен:
$$ int cos x dx = sin x + C $$
Словами это запомнить легче и звучит так: интеграл косинуса равен сумме синуса и константы. Выполним разбор частных примеров.
| Пример 1 |
|
Найти интеграл от косинуса 2х: $$ int cos 2x dx $$ |
| Решение |
|
2х под косинусом называется двойным углом. Из-за того, что аргумент косинуса равен $ 2x $, то нельзя сразу применить формулу. Нужно чтобы $ 2x $ находилось и под знаком дифференциала. Выполним подведение $ 2x $ под дифференциал: $$ frac{1}{2}int cos 2x d(2x) = frac{1}{2}sin 2x + C $$ Перед интегралом появилась дробь $ frac{1}{2} $, так как $ d(2x) = 2 dx $ и нам необходимо уничтожить лишнюю двойку. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ int cos 2x dx = sin 2x + C $$ |
| Пример 2 |
| Найти интеграл от произведения синуса и косинуса: $$ int sin x cos x dx $$ |
| Решение |
|
Данный интеграл можно взять двумя методами: подведением $ sin x $ под знак дифференциала $ cos x dx = d(sin x) $ или заменой $ t = sin x, dt = cos x dx $ Проще будет решить внесением под дифференциал. Получаем: $$ int sin x cos x dx = int sin x d(sin x) = frac{sin^2 x}{2} + C $$ |
| Ответ |
| $$ int sin x cos x dx = frac{sin^2 x}{2} + C $$ |
| Пример 3 |
| Вычислить интеграл косинуса от 0 до пи: $$ int_0^pi cos x dx $$ |
| Решение |
|
Выражение стоящее под знаком интеграла полностью готово к непосредственному интегрированию. Но стоит заметить, что интеграл определенный, а это значит нужно воспользоваться дополнительно формулой Ньютона-Лейбница: $ int_a^b f(x) dx = F(b) – F(a) $, где $ F(x) $ – это первообразная функции. $$ int_0^pi cos x dx = sin x bigg |_0^pi = sinpi – sin 0 = -1 – 0 = -1 $$ |
| Ответ |
| $$ int_0^pi cos x dx = -1 $$ |
| Пример 4 |
| Найти интеграл от косинуса в квадрате: $$ int cos^2 x dx $$ |
| Решение |
|
Непосредственно взять интеграл не получится, так как косинус в квадрате не является табличной функцией, поэтому воспользуемся еще одной формулой понижения степени: $$ cos^2 x = frac{1+ cos 2x}{2} $$ Подставляем правую часть формулы в интеграл: $$ int cos^2 x dx = int frac{1+cos 2x}{2} dx = frac{1}{2} int (1+cos 2x) dx = $$ $$ = frac{1}{2}int 1dx + frac{1}{2} int cos 2x dx = frac{1}{2}x + frac{1}{4}sin 2x + C $$ |
| Ответ |
| $$ int cos^2 x dx = frac{1}{2}x + frac{1}{4}sin 2x + C $$ |
Неопределенный интеграл от косинуса cos (x) равен синусу. Для первоначальной косинуса к правой стороне добавляем постоянную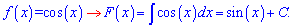
Постоянную определяют с дополнительного условия на первоначальную.
График косинуса имеет вид
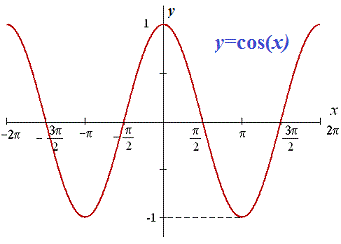Само по себе определение интеграла косинуса достаточно простое. Но как только задают вычислить интеграл косинуса двойного угла, тройного или половины угла, сразу возникают трудности в половины студентов. Выведем формулу интегрирования для функции cos (k*x). Для применения табличной формулы интегрирования надо внести коэффициент под дифференциал, что может привести к изменению самого интеграл. Поэтому одновременно необходимо разделить на этот коэффициент.
.
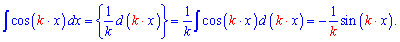Зная приведенную формулу, проинтегрировать косинус двойного угла сможет каждый школьник 10, 11 класса. Все что необходимо это подставить 2 или 3 в интеграл
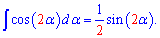
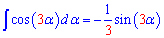и по индукции следующие интегралы
int(sin(k*x)=-1/k*cos(k*x).
Приведенная формула позволяет вычислить интеграл от косинуса половины угла
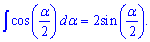и интеграл от косинуса одной трети угла
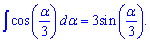В этих случаях коэффициент, стоящий при переменной в косинусе при интегрировании становится обратным значением перед синусом.
Распространенные примеры интегрирования косинуса
Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинус
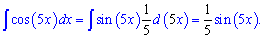
Пример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрирование
Пример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интеграл
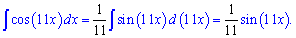
Пример 4. Найти интеграл функции y= cos (x/5).
Решение: Записываем неопределенный интеграл
Пример 5. Найти интеграл функции y= cos (x/6).
Решение: Проинтегрируем по приведенной выше формуле
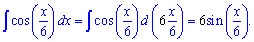Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.
Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинуса
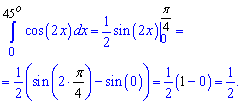
Пример 7. Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрирования
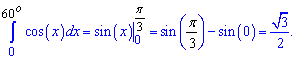
Пример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1.
Решение: Находим первоначальную
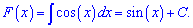С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
Подставляем полученную постоянную в уравнение
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
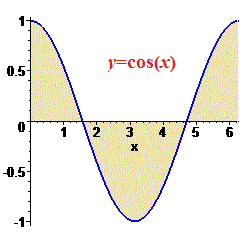
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
Находим определенный интеграл в указанных пределах
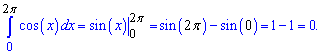Он равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
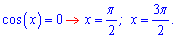Таким образом площадь необходимо искать на трех промежутках
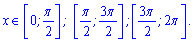Ось абсцисс можем записать функцией y = 0. Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = – cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy). Вычисляем площадь интегрированием в указаных пределах
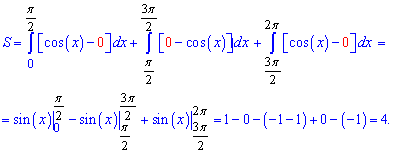Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
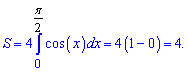На этом знакомство с интегрированием косинуса завершается. Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса. Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
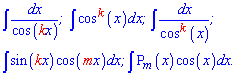Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории “Интегрирование функций“.
На практике часто приходится вычислять интегралы трансцендентных функций, которые содержат тригонометрические функции. В рамках этого материала мы опишем основные виды подынтегральных функций и покажем, какие методы можно использовать для их интегрирования.
Интегрирование синуса, косинуса, тангенса и котангенса
Начнем с методов интегрирования основных тригонометрических функций – sin, cos, tg, ctg. Используя таблицу первообразных, сразу запишем, что ∫sin xdx=-cos x+C, а ∫cos xdx=sin x+C.
Для вычисления неопределенных интегралов функций tg и ctg можно воспользоваться подведением под знак дифференциала:
∫tg xdx=∫sin xcos xdx=d(cos x)=-sin xdx==-∫d(cos x)cos x=-lncos x+C∫ctg xdx=∫cos xsin xdx=d(sin x)=cos xdx==∫d(sin x)sin x=lnsin x+C
Как же у нас получились формулы ∫dxsin x=ln1-cos xsin x+C и ∫dxcos x=ln1+sin xcos x+C, взятые из таблицы первообразных? Поясним только один случай, поскольку второй будет понятен по аналогии.
Используя метод подстановки, запишем:
∫dxsin x=sinx=t⇒x=arcsin y⇒dx=dt1-t2=dtt1-t2
Здесь нам нужно интегрировать иррациональную функцию. Берем тот же метод подстановки:
∫dtt1-t2=1-t2=z2⇒t=1-z2⇒dt=-zdz1-z2==∫-zdzz1-z2·1-z2=∫dzz2-1=∫dz(z-1)(z+)==12∫dzz-1-12∫dzz+1=12lnz-1-12z+1+C==12lnz-1z+1+C=lnz-1z+1+C
Теперь производим обратную замену z=1-t2 и t = sin x:
∫dxsin x=∫dtt1-t2=lnz-1z+1+C==ln1-t2-11-t2+1+C=ln1-sin2 x-11-sin2 x+1+C==lncos x-1cos x+1+C=ln(cos x-1)2sin2x+C==lncos x-1sin x+C
Отдельно разберем случаи с интегралами, которые содержат степени тригонометрических функций, таких, как ∫sinn xdx, ∫cosn xdx, ∫dxsinn x, ∫dxcosn x.
О том, как их правильно вычислять, можно прочесть в статье об интегрировании с использованием рекуррентных формул. Если вы знаете, каким образом выведены эти формулы, то легко сможете брать интегралы вроде ∫sinn x·cosm xdx с натуральными m и n.
Если у нас имеется комбинация тригонометрических функций с многочленами или показательными функциями, то их придется интегрировать по частям. Советуем прочесть статью, посвященную методам нахождения интегралов ∫Pn(x)·sin (ax)dx, ∫Pn(x)·cos (ax)dx, ∫ea·x·sin (ax)dx, ∫ea·x·cos (ax)dx.
Наиболее сложными являются задачи, в которых подынтегральная функция включает в себя тригонометрические функции с разными аргументами. Для этого нужно пользоваться основными формулами тригонометрии, так что желательно помнить их наизусть или держать запись под рукой.
Найдите множество первообразных функции y=sin (4x)+2cos2 (2x)sin x·cos (3x)+2cos2x2-1·sin (3x).
Решение
Воспользуемся формулами понижения степени и запишем, что cos2x2=1+cos x2, а cos22x=1+cos 4×2. Значит,
y=sin (4x)+2cos2 (2x)sin x·cos (3x)+2cos2x2-1·sin (3x)=sin (4x)+2·1+cos 4x2sin x·cos (3x)+2·1+cos x2-1·sin (3x)==sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)
В знаменателе у нас стоит формула синуса суммы. Тогда можно записать так:
y=sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)=sin (4x)+cos(4x)+1sin(4x)==1+cos (4x)sin (4x)
У нас получилась сумма 3-х интегралов.
∫sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)dx==∫dx+cos(4x)dxsin (4x)+∫dxsin (4x)==x+14ln∫d(sin(4x))sin(4x)+14lncos (4x)-1sin (4x)==14lnsin (4x)+14lncos (4x)-1sin (4x)+C=x+14·lncos4x-1+C
В некоторых случаях тригонометрические функции, находящиеся под интегралом, можно свести к дробно рациональным выражениям с использованием метода стандартной подстановки. Для начала возьмем формулы, которые выражают sin, cos и tg через тангенс половинного аргумента:
sin x=2tgx21+tg2x2, sin x=1-tg2x21+tg2x2, tg x=2tgx21-tg2x2
Также нам нужно будет выразить дифференциал dx через тангенс половинного угла:
Поскольку dtgx2=tgx2’dx=dx2cos2x2, то
dx=2cos2x2dtgx2=2dtgx21cos2x2=2dtgx2cos2x2+sin2x2cos2x2=2dtgx21+tg2x2
Таким образом, sin x=2z1+z2, cos x1-z21+z2, tg x2z1-z2, dx=2dz1+z2 при z=tgx2.
Найдите неопределенный интеграл ∫dx2sin x+cos x+2.
Решение
Используем метод стандартной тригонометрической подстановки.
2sin x+cos x+2=22z1+z2+1-z21+z2=z2+4z+31+z2⇒dx2sin x+cos x+2=2dz1+z2z2+4z+31+z2=2dzz2+4z+3
Получим, что ∫dx2sin x+cos x+2=2dzz2+4z+3.
Теперь мы можем разложить подынтегральную функцию на простейшие дроби и получить сумму двух интегралов:
∫dx2sin x+cos x+2=2∫2dzz2+4z+3=2∫121z+1-1z+3dz==∫dzz+1-∫Cz+3=lnz+1-lnz+3+C=lnz+1z+3+C
Далее производим обратную замену z=tgx2:
∫dx2sin x+cos x+2=lnz+1z+3+C=lntgx2+1tgx2+3+C
Ответ: ∫dx2sin x+cos x+2=lntgx2+1tgx2+3+C
Важно отметить, что те формулы, которые выражают фукнции через тангенс половинного аргумента, не являются тождествами, следовательно, получившееся в итоге выражение lntgx2+1tgx2+3+C – это множество первообразных функции y=12sin x+cos x+2 только на области определения.
Для решения других типов задач можно использовать основные методы интегрирования.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Подставим все в формулу интегрирования по частям и приведем интеграл к табличному, тогда будем иметь:
Методы не применяются для интегрирования функций вида
; 
; 
; 
;
; 
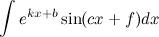, т.е. от тригонометрических функций,
умноженных на многочлен. Такие интегралы интегрируются по частям.
При нахождении интегралов от тригонометрических функций используется ряд методов:
Использование тригонометрических формул Понижение степени подынтегральной функции Метод замены переменной Универсальная тригонометрическая подстановка
При работе с тригонометрическими функциями следует помнить, что:
Косинус – это четная функция, то есть 
, минус исчезает без всяких последствий.
Синус – функция нечетная: 
– здесь минус, наоборот – не пропадает, а выносится.
Использование тригонометрических формул
Пример34
Найти интеграл. 
Используем формулу: 
и метод подведения под знак дифференциала
Пример 35
Найти интеграл 
Для упрощения подынтегральной функции воспользуемся тригонометрическими функциями. Затем с помощью свойств интеграла приведем данный интеграл к табличному виду.
Пример 36
Найти интеграл. 
Используем формулу: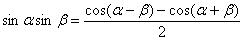 
и метод подведения под знак дифференциала.
Пример 37
Найти интеграл. 
Используем формулу:
Пример 38
Найти неопределенный интеграл
Используем формулы преобразования произведения функций сначала для произведения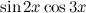 
, а затем для произведения синусов в каждом из интегралов :
В результате искомый интеграл будет равен
Понижение степени подынтегральной функции
Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в чётных степенях. Для понижения степени используют
тригонометрические формулы 
, 
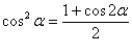и , причем последняя формула чаще используется в обратном
направлении:
Интеграл вида ʃ sinn (x) cosm (x), где n и m – чётные числа, решается методом
понижения степени подынтегральной функции.
Пример 39
Найти интеграл
|
∫cos2xdx = ∫1+cos2x2 |
dx = |
21 |
∫(1 + cos2x)dx = 21 x + 21 sin2x + C |
|
|
Используем формулу: |
||||
|
Пример 40 |
||||
|
Найти интеграл |
dx = |
21 ∫(1 −cos3x)dx = 21 x −31 sin3x + C |
||
|
∫sin2 23 xdx = ∫1−cos3x2 |
||||
|
Используем формулу: |
Пример 41
Найти интеграл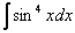 
Выражаем sin4 x как (sin2 x)2 и применяем формулу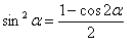
Используем формулу 
В третьем слагаемом снова понижаем степень с помощью формулы 
.
Пример 42
Найти интеграл 
Метод замены переменной
Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в нечётных степенях.
Общие рекомендации :
1.за t нужно обозначить функцию, которая находится в знаменателе.
2.за t нужно обозначить ту функцию, которая, является более сложной.
3.Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за t – обозначить другую функцию
Интеграл вида ʃ sinn (x) cosm (x), где n или m – нечётные числа, решается методом замены переменной
Пример 43
Найти интеграл 
Проведем замену:
Примечание: здесь можно было сделать замену 
, но гораздо выгоднее обозначить за 
весь знаменатель.
Пример 44
Найти интеграл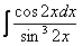 
Проводим замену 
Пример 45
Найти интеграл 
Проведем замену: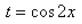 
Пример 46
Найти интеграл
Представляем cos3 x dx как cos2 x cos x dx, а cos2x выражаем через синус с помощью основного тригонометрического тождества: 
Делаем замену:
Пример 47
Найти интеграл 
Преобразуем подынтегральное выражение:
Проведем замену:
Пример 48
Найти интеграл 
Проведем замену:
Пример 49
Найти неопределенный интеграл 
Для вычисления исходного интеграла введем замену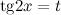 
, тогда
Подставляя это в искомый интеграл, получим
Сделаем обратную замену
Пример 50
Найти неопределенный интеграл 
Преобразуем подынтегральную функцию, используя основное тригонометрическое тождество
Введем замену 
, тогда исходный интеграл примет вид
Сделаем обратную замену и окончательно получим
Пример 51
Найти неопределенный интеграл 
Преобразуем подынтегральную функцию, используя вначале формулу для синуса двойного угла:
а затем, формулу для понижения степени
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка 
– это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Интегралами, где нужно применить универсальную тригонометрическую подстановку, являются интегралы вида:
, 
, 
, 
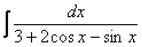и т.д.
Указанная замена позволяет свести интеграл от тригонометрической функции к интегралу от рациональной функции.
При этом следует учесть, что из равенства 
получаем:
;
Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под синусом и косинусом, т.е., в общем виде, если присутствуют функции вида:
sin(kx), cos(kx), делается подстановка tg(kx/2) = t. Еще раз, при sin2x ‒ tg(2x/2), при sin3x ‒ tg(3x/2) и т.д.
Пример 52
Найти неопределенный интеграл 
Воспользуемся универсальной тригонометрической подстановкой:
Пример 53
Найти неопределенный интеграл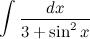 
Для решения данного интеграла сделаем упрощенную тригонометрическую замену, положив что
выразим из равенства
то есть 
Подставим все в искомый интеграл
Сделаем обратную замену
Пример 54
Найти неопределенный интеграл 
Преобразуем подынтегральную функцию следующим образом:
Для нахождения первого интеграла будем использовать универсальную тригонометрическую замену
Тогда первый интеграл преобразуется следующим образом
Разложим подынтегральную функцию полученного интеграла на элементарные дроби:
Приведем к общему знаменателю дроби в правой части равенства и приравниваем числители:
Приравнивая коэффициенты при соответствующих степенях, получим такую систему для нахождения 
и 
Тогда подынтегральная функция имеет следующее разложение на простые дроби
а соответствующий интеграл равен
Делаем обратную замену
Окончательно искомый интеграл равен:
Пример 55
Найти неопределенный интеграл. 
Перед применением универсальной тригонометрической подстановки необходимо понизить степени в знаменателе при помощи формул
, 
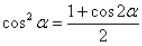
Универсальная тригонометрическая подстановка:
Применение универсальной тригонометрической подстановки часто приводит к длинным и трудоемким вычислениям. Поэтому на практике универсальной тригонометрической подстановки стараются избегать (если возможно).
В ряде случаев целесообразно свести подынтегральное выражение, содержащее sinn(α) и cosm(α), к tg(α) и ее производной 1/cos2(α) т.е. произвести замену:
. Для этого можно воспользоваться формулами
; 
.
Метод работает, если сумма показателей степеней n+m ‒ целое четное отрицательное число .
Пример56
Найти неопределенный интеграл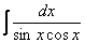 
Пример57
Найти неопределенный интеграл 
Замена tgх =t (чтобы не запутаться)
Пример58
Найти неопределенный интеграл 
Пример59
Найти неопределенный интеграл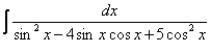 
Пример60
Найти неопределенный интеграл 
|
Пример61 |
||||||||||||||
|
Интеграл из примера55 |
||||||||||||||
|
= |
= |
= |
||||||||||||
|
4 2 − 5 2 |
(4 2 − 5 2 ) 2 |
(4 2 − 5) 2 |
||||||||||||
|
( ) |
= |
2 |
1 |
2 |
1 |
1 |
2 − √5 |
|||||||
|
= |
4 2 − 5 |
= |
= 4 2 − 5 = |
2 |
(2 )2 − (√5)2 |
= 2 |
2√5 |
2 + √5 + = |
||||||
|
= 4√1 |
5 22 +−√√55 + |
Решение значительно быстрее и проще.
6.Интегралы от дробей
Суть методов решения интегралов от дроби сводится к преобразованию дроби в сумму элементарных дробей табличного вида:
1.
2.
3.
4.
5.
6.
Для преобразования дроби используется комплекс приемов, основными из которых будут выделение полного квадрата, подстановка, разложение на множители, с дальнейшим преобразованием в сумму элементарных дробей.
Для решения интегралов от дроби можно придерживаться следующего алгоритма:
|
Определяем тип подынтегрального выражения. |
||||||
|
1. |
Для простейших дробей вида |
применяется способ подведения функции |
||||
|
под знак дифференциала с дальнейшим интегрированием с помощью таблицы. |
||||||
|
( + ) |
||||||
|
( + ) |
( + )−+ |
, |
||||
|
∫( + ) = ∫( + ) |
= |
−+ |
+ |
Примеры:
|
2. Для дробей вида |
, |
, |
, |
(коэффициенты |
a и c не равны нулю) также применяется способ подведения функции под знак дифференциала с дальнейшим интегрированием с помощью таблицы. (Формулы 2 – 6, см. выше).
Примеры:
|
3. Для дробей вида |
сначала представляем |
|
интеграл в виде суммы: |
Первый интеграл берем методом подведения под знак дифференциала:
|
В интегралах вида |
выделяем в знаменателе полный квадрат и приводим |
||||
|
выражение к табличному виду. |
|||||
|
В ряде случаев, неразложимый многочлен |
целесообразно представить в |
||||
|
необходимо вынести коэффициент за знак интеграла, |
|||||
|
виде полного квадрата (перед этим |
( |
+ + ) |
|||
|
поделив все выражение на ) по формуле: |
и свести интеграл к виду:
,
или
Пример62
Найти неопределенный интеграл 
Квадратный трехчлен, который стоит в знаменателе подынтегральной функции, не
раскладывается на множители 
. Поэтому для нахождения данного интеграла выделим в знаменателе полный квадрат.
Пример63
Найти неопределенный интеграл 
. Для начала вынесем двойкуиз под знака радикала:
т.е. вида
В подкоренном выражении выделяем полный квадрат:
Поэтому
Пример64
4. Для дробей вида 
используют метод интегрирования по частям n раз, каждый раз понижая степень знаменателя и применяя предыдущие способы. Вычисления получаются очень длинные и долгие. Или пользуемся рекуррентными формулами.
5. Дроби( ) , у которых многочлены и в числителе и в знаменателе,
( ) , где Pn(x) и Pm(x) многочлены степени n и m соответственно, перед
собственно взятием интеграла необходимо разложить на множители, а затем, преобразовать в сумму элементарных дробей.
Определяем что дробь правильная. Правильной называется дробь, у которой степень числителя меньше степени знаменателя. Если дробь неправильная, то выделяем целую часть, с оставшейся частью работаем как с правильной дробью.
Раскладываем знаменатель правильной дроби на множители и преобразуем дробь в сумму элементарных дробей.
Для преобразования дроби в сумму элементарных дробей в большинстве случаев используют метод неопределенных коэффициентов.
Метод неопределенных коэффициентов.
|
т.е. |
|||||
|
Любую дробь вида |
( + )( + )( + ) |
можно представить в виде |
|||
|
2+ + |
|||||
|
2 + + |
|||||
|
( + )( + )( + ) = |
+ + + + + , |
+ ++ + +
|
где A, B, C неизвестные коэффициенты. |
|||||||||||||||||||||||
|
Приводим правую часть уравнения к общему знаменателю: |
|||||||||||||||||||||||
|
+ |
= |
( + )( + ) + ( + )( + ) ( + )( + ) |
, |
||||||||||||||||||||
|
+ |
+Тогда |
+ |
( + )( + )( + ) |
||||||||||||||||||||
|
+ |
|||||||||||||||||||||||
|
2 |
+ + |
( + )( + ) + ( + )( + ) + ( + )( + ) |
|||||||||||||||||||||
|
( + )( + )( + ) |
( + )( + )( + ) |
||||||||||||||||||||||
|
2 |
+ + = ( + )( + ) + ( + )( + ) ( + )( + ) |
||||||||||||||||||||||
|
Если дроби равны= и равны их знаменатели, то должны быть равны и их числители, |
: |
||||||||||||||||||||||
|
+ + = |
|||||||||||||||||||||||
|
= 2 |
Раскрываем скобки |
( + ) + + 2 + |
( + ) + = |
||||||||||||||||||||
|
+ |
( + ) + + 2 + |
||||||||||||||||||||||
|
= ( + + ) |
+ |
( + + + + + ) + ( + + ) |
|||||||||||||||||||||
|
= + + |
|||||||||||||||||||||||
|
Приравниваем коэффициенты в выражениях: |
|||||||||||||||||||||||
|
= ( + ) |
+ ( + ) + ( + ) |
||||||||||||||||||||||
|
= + + |
|||||||||||||||||||||||
|
Решая систему уравнений, находим неизвестные коэффициенты A, B, C и раскладываем |
|||||||||||||||||||||||
|
2 |
+ + |
||||||||||||||||||||||
|
дробь на сумму элементарных дробей: |
+ |
||||||||||||||||||||||
|
( + )( + )( + ) |
+ |
+ |
|||||||||||||||||||||
|
он приравнивается к |
( |
+ + ) |
квадратный. |
многочлен вида: |
|||||||||||||||||||
|
Если в знаменателе встречается= |
+неразложимый+ |
||||||||||||||||||||||
|
( + )( |
+ |
1 + ) |
2 |
+ |
|||||||||||||||||||
|
12 |
, где |
– неразложимый квадратный многочлен (D<0), то |
|||||||||||||||||||||
|
( + )( |
сумме дробей по формуле: |
||||||||||||||||||||||
|
+ + ) |
+ |
( |
+ + ) |
||||||||||||||||||||
|
Если в знаменателе2 |
встречаются= |
+кратные2 |
множители. |
вида: |
|||||||||||||||||||
|
1 |
, |
1 |
2 |
1 |
2 |
||||||||||||||||||
|
( 1+ ) |
то они раскладываются по формуле: |
||||||||||||||||||||||
|
( + ) = |
+ |
2 + + |
+ ( + ) + |
( + )2 |
+ + |
( + ) |
Пример65
Найти неопределенный интеграл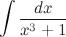 
Преобразуем подынтегральную функцию, расписав знаменатель согласно формуле сокращенного умножения для суммы кубов:
Тогда интеграл примет вид:
Далее разложим подынтегральную функцию на простые дроби с неопределенными коэффициентами. В нашем случае имеет место следующее разложение:
Найдем неопределенные коэффициенты, для этого приведем к общему знаменателю дроби в правой части равенства, а затем приравняем соответствующие числители
Далее приравняем коэффициенты при соответствующих степенях
Подставим, выраженные через 
, коэффициенты 
и 
во второе уравнение системы:
, тогда 
, а 
Таким образом, искомый интеграл будет равен:
|
1 |
1 |
(2 − 1) − 3 |
|||||||
|
= 3 |
| + 1| − 6 |
2 − + 1 |
= |
||||||
|
1 |
1 |
2 − 1 |
−3 |
= |
|||||
|
= 3 |
| + 1| − 6 |
2 |
− + 1 − |
6 |
2 − + 1 |
||||
|
1 |
1 |
| |
2 |
1 |
|||||
|
= 3 |
| + 1| − 6 |
− + 1| + 2 |
2 − + 1 |
Квадратный трехчлен, стоящий в знаменателе последнего интеграла, не раскладывается на
|
множители |
1 |
1 |
2 |
. Поэтому для его нахождения выделим в |
||||||||
|
1 |
||||||||||||
|
знаменателе полный квадрат: |
||||||||||||
|
3 + 1 |
= = 3 |
| + 1| − 6 |
| |
− + 1| + |
2 2 − + 1 = |
|||||||
|
1 |
| + 1| − |
1 |
| |
2 |
1 |
+ 3 = |
||||||
|
= 3 |
6 |
2 |
− + 1| + 2 |
( − 1)2 |
||||||||
|
1 |
| + 1| − |
1 |
| |
1 |
1 |
2 |
4 |
|||||
|
= 3 |
6 |
− + 1| + 2 |
3 |
3 |
+ = |
|||||||
|
1 |
| + 1| − |
1 |
| |
2 |
1 |
4 |
2 |
4 |
||||
|
= 3 |
6 |
− + 1| + √3 |
√3 + |
Пример66
Найти неопределенный интеграл 
Дробь является правильной
Раскладываем знаменатель на множители, используя формулу сокращенного умножения
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Приводим дробь к общему знаменателю:
Составим и решим систему:
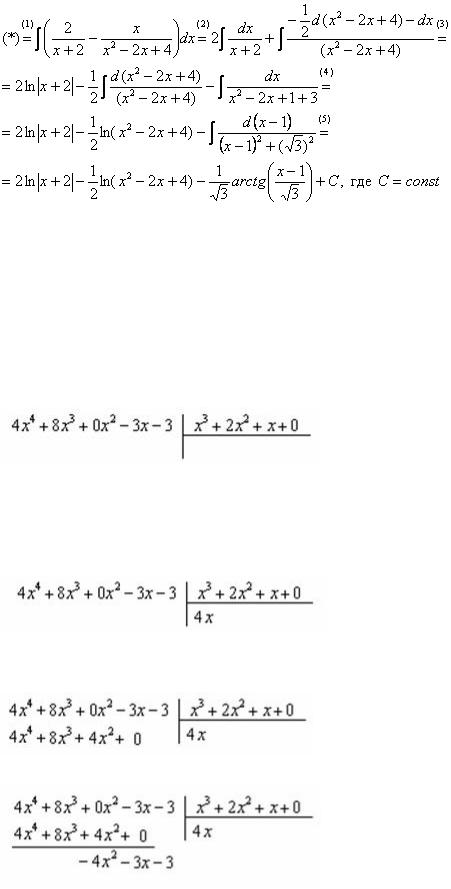
Пример67
Найти неопределенный интеграл 
Данная дробь является неправильной.
Основной метод решения интеграла с неправильной дробно-рациональной функцией – это
деление числителя на знаменатель.
Сначала рисуем «заготовку» для деления:
ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами
Теперь маленькая задачка, на какой множитель нужно умножить 
, чтобы получить 
? Очевидно, что на 
:
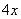Далее умножаем 
сначала на 
, потом – на 
, потом – на 
, потом – на 0 и записываем результаты слева:
Проводим черточку и производим вычитание (из верха вычитаем низ):
Старшая степень остатка 
равна двум, старшая степень делителя
– больше, она равна трём, значит, больше разделить не удастся. Если бы
изначально унас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.
Итак, у нас получилась целая часть плюс остаток:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
6. Неопределенные интегралы иррациональных функций вида 
находятся методом подстановки.
В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:
|
1. |
Если p – целое число, то принимают |
, где N – общий знаменатель чисел m и n. |
||||||||||
|
2. |
– целое число, то |
, где N – знаменатель числа p. |
||||||||||
|
Если + |
||||||||||||
|
знаменатель |
+ p |
– целое число, то вводят новую переменную |
, где N – |
|||||||||
|
3. |
Если |
+ |
||||||||||
|
числа . |
||||||||||||
|
привести к виду: |
± |
, |
− |
которые можно |
||||||||
|
Очень часто в вычислениях встречаются дроби вида |
||||||||||||
|
+ − |
+ |
|||||||||||
|
+ = |
+ |
= + |
− + = − + |
|||||||||
|
+ − |
− |
− |
||||||||||
|
− = |
− |
= − |
+ − = − − |
+ − = −1 + − = − − |
||||||||
|
+ − |
− |
|||||||||||
|
− = |
− |
= − |
+ − = + − |
Пример68
Найти неопределенный интеграл 
То есть, m = -1, n = 1, p = 1/2. Так как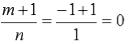 
– целое число, то вводим новую
переменную 
(N = 2 – знаменатель числа p). Выражаем х через z:
Выполняем подстановку в исходный интеграл:
Пример 69
Найти неопределенный интеграл 
Проведем замену: 
. Навешиваем дифференциалы на обе части:
Вот почему дифференциалы нужно именно НАВЕШИВАТЬ на обе части и добросовестно
раскрывать эти дифференциалы. Немало чайников здесь формально напишет 
и допустит ошибку.
Пример70
Найти неопределенный интеграл 
Проведем замену: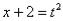 
Навешиваем дифференциалы на обе части:
С числителем разобрались. Что делать с 
в знаменателе? Берем нашу замену 
и выражаем из неё: 
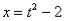Если 
, то 
Пример71
Найти неопределенный интеграл 
Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.
Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в
виде 
: . Нас будут интересовать знаменатели степеней. Записываем эти знаменатели: 2, 3, 3.
Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше.
Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать.
Замена в рассматриваемом интеграле будет следующей: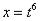 
Оформляем решение:
Проведем замену:
Содержание:
- Формула
- Примеры вычисления интеграла косинуса
Формула
$$int cos x d x=sin x+C$$
Интеграл от косинуса равен синусу плюс константа интегрирования.
Примеры вычисления интеграла косинуса
Пример
Задание. Найти неопределенный интеграл $int 2 cos x d x$
Решение. Согласно
свойствам интеграла, константу можно выносить за интеграла, тогда будем иметь:
$$int 2 cos x d x=2 int cos x d x=2 sin x+C$$
Ответ.$int 2 cos x d x=2 sin x+C$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти интеграл $int(cos x+3) d x$
Решение. Интеграл от суммы функций равен
сумме интегралов от каждой из функций, то есть
$$int(cos x+3) d x=int cos x d x+int 3 d x$$
Интеграл от косинуса равен синусу, а интеграл от константы – константе, умноженной на
, то есть получаем:
$$int(cos x+3) d x=int cos x d x+int 3 d x=sin x+3 x+C$$
Ответ. $int(cos x+3) d x=sin x+3 x+C$
Читать дальше: интеграл тангенса.
