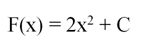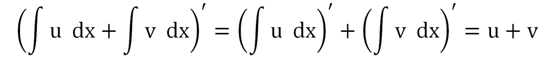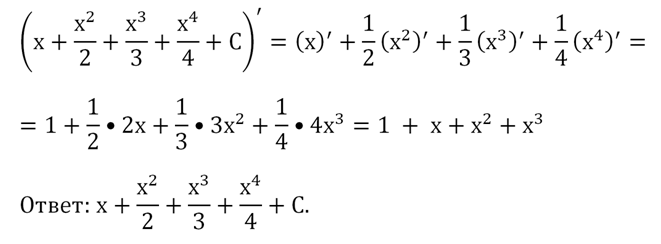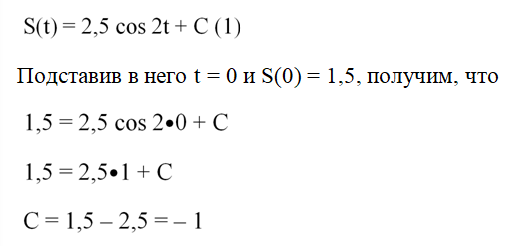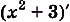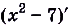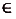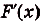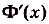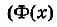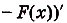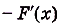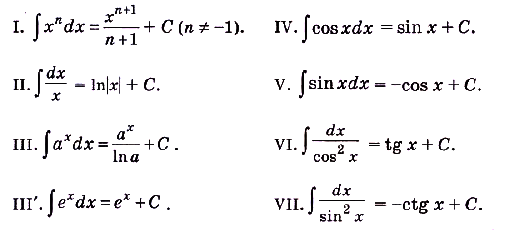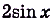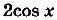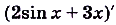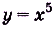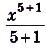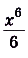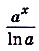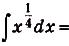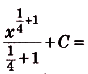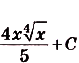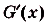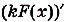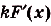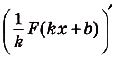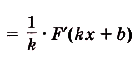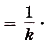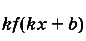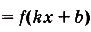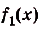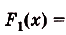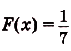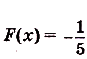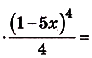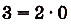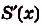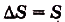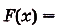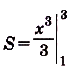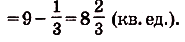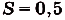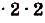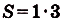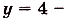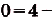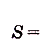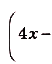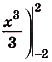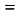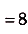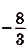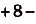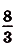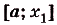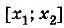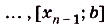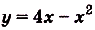Как найти первообразную функции в интеграле

План урока:

Понятие первообразной

Бесконечное количество первообразных

Неопределенный интеграл

Таблица первообразных

Правила вычисления интегралов

Физический смысл неопределенного интеграла

Понятие первообразной

Ранее мы познакомились с важнейшим понятием математического анализа – производной. Она имеет большое практическое значение, в частности, с ее помощью можно определить скорость тела, если известен закон его передвижения. Например, если путь, пройденный автомобилем, можно вычислить с помощью функции S = t², то его скорость в любой момент времени может быть рассчитана по формуле

Однако на практике значительно чаще встречается прямо противоположная задача. Известно, как меняется скорость тела, и найти требуется путь, пройденный им. В таком случае необходимо по производной определить ту функцию, которая «подверглась» дифференцированию.

Задание. Известна производная функции у(х):

В этом примере мы выполнили операцию, обратную дифференцированию. В математическом анализе он называется интегрированием. Если интегрируют некоторую произвольную функцию f(х), то в итоге получают новую функцию, которую чаще всего обозначают как F(x). Её называют первообразной функции f(x).

Приведем несколько примеров первообразной:

Последний пример показывает, что иногда первообразная может и совпадать с исходной функцией.

Задание. Докажите, что функция

Первообразные встречаются и в ряде практических задач, особенно в тех, где рассматривается движение тел.

Задание. Автомобиль Buggati Veyron разгоняется от 0 до 40 м/с за 4 секунды. Какое расстояние проедет эта машина за эти 4 секунды, если разгон осуществляется равномерно?

Решение: Если за 4 секунды машина разгоняется до 30 м/с, то за одну секунду она увеличивает скорость на

Примечание – в будущем мы научимся более строго решать такие задачи, и «угадывать» подходящую первообразную не придётся.

Бесконечное количество первообразных

Рассмотрим функцию

Оказывается, что g₁ также является первообразной для у. То есть у одной функции у = 4х³ есть сразу две первообразных:g = x⁴и g = x⁴ + 1! Более того, можно доказать, что у любой функции есть бесконечное количество первообразных!

Действительно, рассмотрим сразу все функции

где С – некоторая константа, то есть параметр. В данном случае можно сказать, что мы рассматриваем не одну функцию, а семейство функций. Продифференцируем g:

Мы видим, что у всех функций из этого семейства, независимо от значения параметра С, производная одинакова. Здесь С может принимать любое действительное значение. Так как действительных чисел бесконечно много, то и количество функций, образующих семейство, также бесконечно. И все они являются первообразными для у = 4х³.

Данная особенность операции интегрирования может быть сформулирована в виде следующей теоремы:

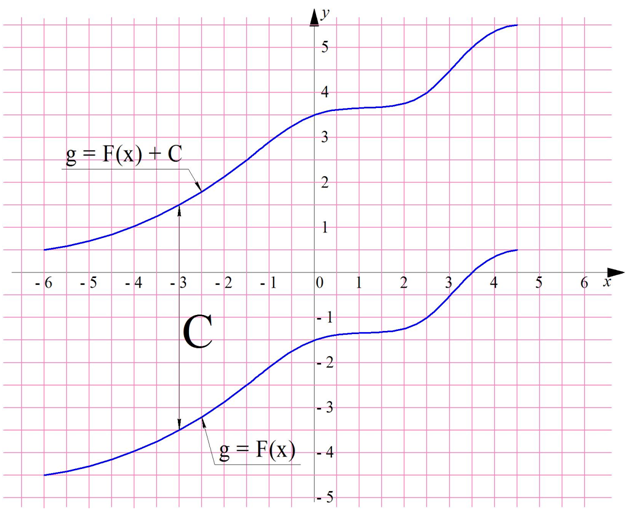
Можно дать и графическую иллюстрацию этого правила. Построим произвольный график g = F(x). Далее построим ещё один график

Очевидно, что он может быть получен параллельным переносом первого графика на С единиц вверх:

Теперь в какой-нибудь точке х₀ проведем касательные к обоим графикам первообразных. Очевидно, что они будут иметь одинаковый угол наклона, так как по сути тоже могут быть получены параллельным переносом:

Если же углы наклона касательных совпадают, то и производные в этих точках также равны.

В связи с наличием у каждой функции бесконечного количества первообразных их часто записывают в общем виде. Например, пусть надо записать первообразную для

Однако 2х² – это лишь одна из бесконечного множества первообразных. Все вместе они образуют семейство, которое записывается так:

Неопределенный интеграл

Каждая математическая операция имеет какое-то особое обозначение. Например, чтобы показать, что мы дифференцируем некоторую функцию, мы ставим после неё штрих (и при необходимости берем в скобки):

Напомним, что операция нахождения первообразной называется интегрированием. Для ее обозначения используется особый знак – интеграл. Например, мы знаем, что первообразная для у = х² – это семейство функций вида

Рассмотрим элементы записанного нами равенства:

Исходная функция – это та самая функция, для которой необходимо найти первообразную, то есть интегрируемая функция. Справа от знака «равно» как раз записывается первообразная. Сразу после первообразной надо писать «+ С». Тем самым мы показываем, что у интегрируемой функции есть бесконечное количество первообразных.

После интегрируемой функции стоит так называемый дифференциал dх (читается как «дэ икс»). В данном случае он указывает, что именно буквой х мы обозначаем переменную в интегрируемой функции. Его значение мы разберем несколько позже. Пока что надо запомнить, что после интегрируемой функции необходимо писать «dx». В целом вся запись

читается так: «интеграл от два икс по дэ икс равен икс в квадрате плюс цэ».

В чем разница между первообразной и интегралом? Первообразная – это функция, при дифференцировании которой получается исходная функция. Интеграл же – это не функция, а целое семейство функций (или их множество), которое включает в себя сразу все первообразные интегрируемой функции.

Так как интегрирование – это действие, обратное дифференцированию, то мы можем проверить результат своих вычислений. Пусть мы записали, что

Получили подынтегральное выражение. Значит, мы всё сделали правильно.

Здесь важно заметить, что в математике существует сразу несколько видов интегралов, каждый из которых имеет разное определение. Здесь описан так называемый «неопределенный интеграл». Несложно догадаться, что существует ещё и «определенный интеграл», который мы рассмотрим на следующих уроках. Теперь можно дать следующее определение:

Задание. Найдите неопределенный интеграл

Решение. Вспомним таблицу производных элементарных функций. Производная синуса равна косинусу:

Заметим, что непосредственно из определения следует важное свойство неопределенного интеграла – производная интеграла равна его подынтегральному выражению:

Грубо говоря, операции интегрирования дифференцирования «сокращают» друг друга.

Задание. Вычислите производную:

Таблица первообразных

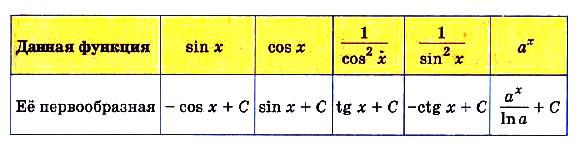
Как же вычислять интегралы? Проще всего начать с тех функций, которые уже есть в таблице производных. Напомним, как она выглядит:

Из определения первообразной следует, что для тех функций, которые указаны во втором столбце таблицы, одной из первообразных является соответствующая функция из первого столбца. То есть можно составить такую таблицу первообразных:

Обратите внимание на третью строку снизу. Здесь произошло небольшое изменение – вместо первообразной lnx мы записали ln |x|, то есть использовали модуль числа. Дело в том, что функция

определена при любом значении аргумента, кроме нуля. В то же время функция

не определена при отрицательных значениях х, так как под знаком логарифма не может стоять отрицательное число. Однако области определения интегрируемой функции и ее первообразной должны совпадать. Использование модуля обеспечивает выполнение этого условия.

Полученная нами таблица интегралов не совсем удобна. Предположим, нам надо проинтегрировать функцию

отличающуюся от интересующей нас функции лишь множителем перед х⁵.

Однако можно догадаться, что в качестве подходящей первообразной можно взять функцию

В связи с этим есть смысл немного подкорректировать таблицу первообразных таким образом, чтобы в первом столбце стояли стандартные функции без неудобных множителей. В результате таблица примет следующий вид:

Можно доказать, что каждое равенство в третьем столбце является справедливым. Возьмем, например, равенство

Получили подынтегральное выражение, а это значит, что равенство справедливо. Таким же образом можно доказать и все остальные равенства в таблице.

Задание. Вычислите неопределенный интеграл:

Решение. Этот интеграл присутствует в таблице (7-ая строка), а потому мы просто переписываем равенство из неё:

Задание. Найдите первообразную функции

Правила вычисления интегралов

Что делать в том случае, если надо вычислить интеграл, которого нет в таблице? Существует три несложных правила интегрирования, которые могут помочь в такой ситуации.

Докажем это правило. Для этого просто продифференцируем правую часть равенства:

Получили именно то выражение, которое стоит под знаком интеграла в левой части равенства. Это значит, что формула справедлива.

Рассмотрим пример использования этого правила. Пусть надо найти первообразную функции

Здесь мы представили исходный интеграл как сумму двух более простых интегралов, которые являются табличными

Обратите внимание, что мы не стали складывать константы интегрирования С как подобные слагаемые и писать 2С. Дело в том, что С – это некоторое произвольное число. Но если сложить два произвольных числа, то в итоге получится третье произвольное число, которое также будет обозначаться как С! Поэтому обычно константу С просто дописывают в самом конце решаемого примера.

Естественно, что правило сложения интегралов работает и в случае суммы не двух, а большего количества слагаемых.

Задание. Вычислите неопределенный интеграл

Возможна ситуация, когда мы не уверены в правильности полученного решения. В таком случае можно легко проверить себя, просто продифференцировав получившийся интеграл. В итоге мы должны получить исходную функцию (подынтегральное выражение):

Следующее правило позволяет выносить множитель из-под знака интеграла.

Для доказательства тождества снова продифференцируем его левую часть:

Получили как раз то выражение, которое стоит под интегралом справа. Следовательно, формула верна.

Рассмотрим несколько простейших примеров использования этого метода интегрирования неопределенных интегралов:

Естественно, что правила 1 и 2 можно комбинировать друг с другом, решая более сложные примеры.

Задание. Вычислите неопределенный интеграл от квадратичной функции

Первые два правила достаточно просты и напоминают аналогичные правила дифференцирования. А вот третий метод вычисления неопределенного интеграла более сложный.

Проиллюстрируем его на примере. Пусть надо найти первообразную для функции

Но в нашем случае под знаком косинуса стоит не х, а выражение 5х + 7, являющееся линейной функцией. Поэтому, согласно правилу, мы должны написать впервообразной не sinx, а sin (5x + 7), то есть изменить аргумент. Также надо добавить перед синусом «поправочный множитель», равный 1/k, то есть в нашем случае 1/5:

Проверим себя. Продифференцируем получившуюся первообразную. При этом мы используем правило дифференцирования сложной функции:

Получили ту самую функцию, которую и надо было проинтегрировать.

Приведем ещё несколько примеров использования правила 3:

Напомним, что при изучении производной мы познакомились также с правилами дифференцирования произведения, дроби и сложной функции. Используя их, мы могли найти производную для почти любой функции, которую только могли записать. С решением неопределенных интегралов ситуация значительно сложнее. С помощью приведенных трех правил не получится вычислить такие интегралы, как

Более того, в записанной нами таблице интегралов отсутствует ряд элементарных функций, поэтому мы не сможем даже проинтегрировать такую простую функцию, как

Дело в том, что задача интегрирования является значительно более сложной, чем задача дифференцирования. Отметим три момента. Во-первых, в нашей школьной таблице интегралов, содержащей всего 11 формул, указаны лишь самые простые элементарные функции. Существуют справочники, где в качестве табличных указаны интегралы десятков, а то и сотен функций. Во-вторых, есть и более сложные правила интегрирования, которые изучаются уже в институте. В-третьих, существуют такие элементарные функции, первообразную которых в принципе невозможно записать, используя элементарные функции (синус, косинус, логарифм и т.п.). В связи с этим приходится вводить в рассмотрение новые специальные функции, а также использовать приближенные методы вычислений.

Физический смысл неопределенного интеграла

Напомним физический смысл производной – если известен закон движения материальной точки, то есть некоторая функция S(t), то производная этого закона будет выражать скорость тела в момент времени t:

Отсюда прямо вытекает физический смысл первообразной. Если известен закон изменения скорости v(t), то его первообразная будет являться законом движения S(t). Точнее говоря, законом движения будет являться только одна из первообразных, так как их существует бесконечно много.

Задача. Скорость тела в произвольный момент времени t может быть вычислена по закону

Найдите закон движения материальной точки S(t). Известно, что в начальный момент времени тело находилось в точке с координатой 1,5, то есть S(0) = 1,5.

Решение. Нам надо просто проинтегрировать функцию v(t):

Интеграл вычислен, но это ещё не закон движения, ведь в нем присутствует константа интегрирования. Как от неё избавиться? Надо использовать условие, согласно которому S(0) = 1,5. В общем виде закон движения имеет вид

Мы нашли конкретное значение константы интегрирования. С учетом этого закон движения (1) примет вид:

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие «интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Ранее вы ознакомились с операцией дифференцирования: нахождения производной по данной функции. Не менее важна и обратная ей операция — интегрирование: нахождение функции по её производной.

Пусть дано функцию такую, что в каждой точке х некоторого промежутка . В этом случае функцию f(x) называют производной функции F(x), a — первообразной для f(x).

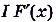
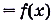
Функция F(x) называется первообразной функции на промежутке , если для каждого значения х из этого промежутка F'(x) = f(x).

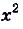
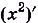
Например, на всей числовой оси (т. е. на R] функция F(x) = является первообразной для f(x) = 2х, ибо = 2х; F(x) = sin х есть первообразной для f(x) = cos х, ибо (sin х)’ = cos х.

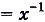
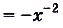
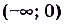
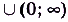
Функция F(x) является первообразной для например на [1; 5]. Но не на R, поскольку F'(O) не существует, и не на , поскольку это не промежуток.

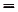
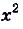
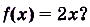
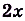
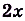
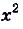
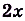
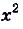
Одна ли функция является первообразной для Нет. Ведь и и и т. д. Каким бы ни было число С (произвольная постоянная), функция — первообразная для, ибо ( )‘

Существуют ли другие функции, отличные от , первообразные для ? Нет.

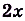
Теорема. (Основное свойство первообразных.) Каждая первообразная для функции ) имеет вид F(x) + С, где — одна из этих первообразных, а С — произвольная постоянная.

Доказательство 1. Пусть—одна из первообразных для функции на промежутке , т. е. для каждого :.

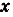
По правилу нахождения производной суммы

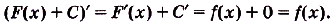
Этим доказано» что какая бы ни была постоянная С, если — первообразная для , то и — первообразная для

Пусть и — две любые первообразные для функции

на промежутке, т. е. и для каждого . Тогда

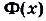
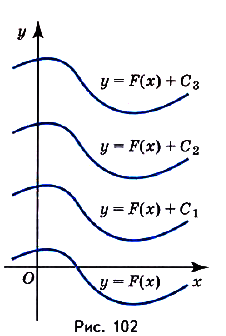
Как видим, функция такая, что в каждой точке её производная равна 0.

Такое свойство имеет только определённая на функция, которая ни возрастает, ни убывает на этом промежутке. Ведь если бы на некоторой части промежутка эта функция возрастала или убывала, то там её производная была бы соответственно положительная или отрицательная. (Подробнее обоснование этого факта даётся в строгих курсах математического анализа.) Итак, , где С — постоянная, т. е. .

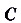
Этим доказано, что если — одна из первообразных для функции , то каждая из функций также её первообразная и других первообразных для ) не существует. Геометрически это означает, что графики любых двух первообразных для функции такие, что их можно совместить параллельным переносом вдоль оси ординат (рис. 102).

— общий вид первообразных для функции .

Каждая первообразная рассматривается на некотором промежутке. Если же для краткости его не указывают, то имеют в виду промежуток максимально возможной длины. В частности, если функция ) определена на и промежуток не указано, то речь идет о её первообразной также на .

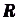
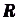
Операцию нахождения производной данной функции называют дифференцированием. Обратная ей операция — нахождение первообразной — называется интегрированием.

Используя формулы дифференцирования (с. 218), составим таблицу первообразных. Советуем запомнить её.

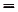
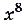
Обосновать эту таблицу можно дифференцированием функции из её второй строки. Пользуясь таблицей, можно сразу писать, что, например, для функции первообразной есть и т.д.

Множество всех первообразных функции часто называют неопределённым интегралом этой функции и обозначают символом (читают: интеграл эф от икс де икс).

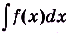
Выражение «проинтегрировать функцию» обозначает то же, что и «найти первообразную для функции » .

То есть, если — первообразная для функции , а —произвольное число, то .

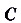
Слово интеграл в переводе с латинского языка означает целый. Почему его так назвали, вы поймёте, когда ознакомитесь с определённым интегралом (см. с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении 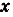имеет не одно числовое значение, а бесконечно много.

Таблицу первообразных, с помощью символа неопредёлен-ного интеграла можно записать так:

Примеры с решением

Пример №1

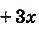
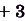
Докажите, что функция является первообразной для функции .

Доказательство..

Имеем . Итак, по определению, функция — первообразная для функции

Пример №2

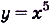
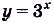
Найдите первообразную для функции : а) ; б) ;

Решение:

Воспользуемся таблицей первообразных.

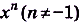
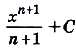
а) Первообразной для функции есть функция .

Для функции 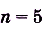, поэтому .

б) Первообразной для функции 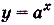есть функция

Для функции 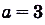поэтому .

Пример №3

Найдите для функции такую первообразную, чтобы её график проходил через точку Р (2; 5).

Решение:

Пользуясь таблицей, найдём общий вид первообразных: Поскольку график искомой первообразной проходит через точку Р (2; 5), то , отсюда С = 3.

Следовательно, .

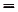
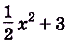
Ответ..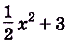

Пример №4

Проинтегрируйте функцию .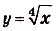

Решение:

Нахождение первообразных

Выведем несколько правил, подобных правилам дифференцирования, которые облегчают нахождение первообразных.

I. Если и — первообразные для функций ) и, то — первообразная для функции .

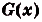
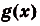
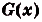
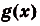
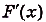
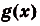
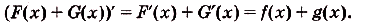
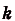
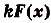
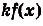
Действительно, если и . то

. Если — первообразная для функции , a — произвольное число, то — первообразная для функции .

Ведь .

Если —первообразная для функции , a ,b — произвольные числа , то — первообразная для функции .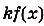

»

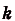
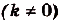
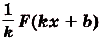
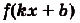
Ведь

Пример №5

Найдите первообразную для функции:

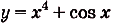
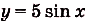
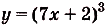
а) ; б) ; в) .

Решение:

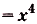
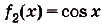
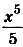
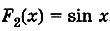
а) Для функций и первообразными являются соответственно и .

Поэтому для суммы данных функций общий вид первообразных

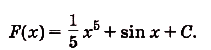
б) По правилу II: .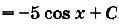

в) Одной из первообразных для функции ,согласно правилу III, является функция . Общий вид первообразных для данной функции

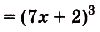
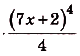
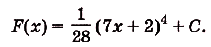
К нахождению первообразных сводятся прежде всего задачи, обратные тем, которые решаются с помощью производной. Рассмотрим пример..

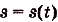
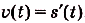
Если известен закон прямолинейного движения тела ,то для нахождения его скорости в момент t нужно найти производную: . Здесь дан закон движения и требуется найти его скорость. Для механики не менее важно уметь решать обратную задачу: по заданной в каждый момент скорости определять закон движения.

Задача №1.

Точка движется прямолинейно с переменной скоростью 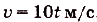. За перые 4 с она прошла 80 м. Найдите закон движения точки.

Решение:

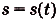
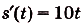
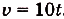
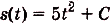
Искомый закон движения выражается такой функцией, что . Здесь s(t) — первообразная для функции . Общий вид всех таких первообразных . Поскольку за 4 с точка прошла 80м, то 80 = 5-16 + С, отсюда С = 0.

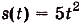
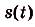
Ответ. Искомый закон движения точки , где t — время в секундах, — расстояние в метрах.

Примеры других применений первообразной рассмотрим в следующих параграфах.

С помощью неопределённого интеграла правила интегрирования записываются так:

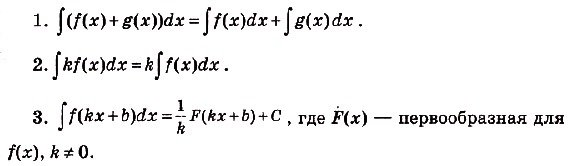
Пример №6

Найдите одну из первообразных для функции:

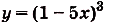
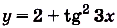
а); б).

Решение:

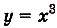
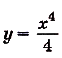
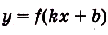
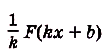
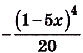
а) Для функции одной из первообразных есть функция . Учитывая то, что первообразной для функции есть функция , запишем искомую первообразную: ;

б) преобразуем сначала формулу, задающую функцию:

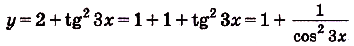
Тогда .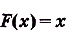

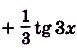
Пример №7

Тело движется прямолинейно с ускорением .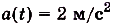

Определите скорость данного движения как функцию от времени f, если в момент t = 0 она равнялась 3 м/с.

Решение:

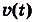
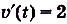
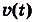
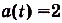
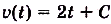
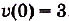
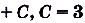
Ускорение — производная скорости. Поэтому если — искомая скорость, то . Следовательно,) — первообразная для функции , поэтому . Поскольку , то .

Ответ. .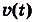

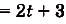
Первообразная и площадь криволинейной трапеции

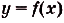
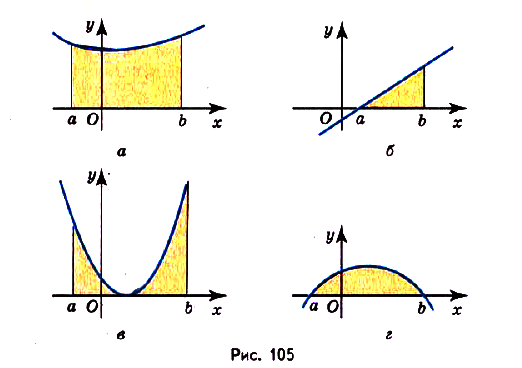
Пусть на координатной плоскости задан график непрерывной функции , принимающей на промежутке [а; Ь) только неотрицательные значения. Фигуру, ограниченную таким графиком, осью абсцисс и прямыми х = а и х = Ь, называют криволинейной трапецией.

Криволинейную трапецию называют также под графиком функции 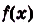на [а; Ь].

Несколько криволинейных трапеций изображено на (рис. 105).

Каждая криволинейная трапеция имеет определённую площадь (это доказано в строгих курсах математического анализа). Эти площади можно находить с помощью первообразных.

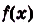
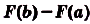
Теорема. Площадь криволинейной трапеции, образованной графиком функции ) на промежутке [а; Ь], равна , где — первообразная для функции на [а; b].

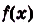
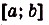
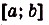
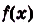
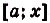
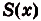
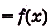
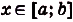
Доказательство. Рассмотрим произвольную криволинейную трапецию, образованную графиком функции на (риc. 106). Пусть х — произвольная точка отрезка , а S(x) — площадь криволинейной трапеции, образованной графиком функции на . Понятно, что — функция от х. Докажем, что для каждого .

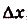
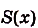
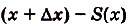
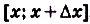
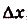
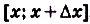
Дадим переменной х приращение , тогда функция получит приращение (pиc. 107). Это — площадь криволинейной трапеции, образованной графиком функции на промежутке , она приближённо равна площади прямоугольника с основанием , и высотой f(t), где t — некоторое число из промежутка . Поскольку функция f(x) непрерывна, такое число t обязательно найдётся.

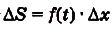
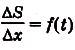
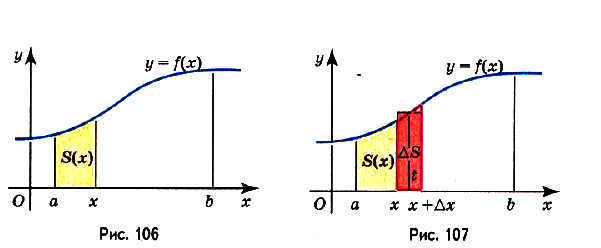
Следовательно, откуда .

Если , то и , ибо функция непрерывна. Поэтому если , то , т. е. .

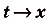
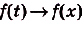
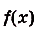
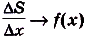
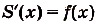
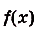
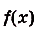
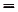
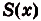
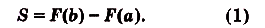
Как видим, функция S(x) — первообразная для на [а; Ь]. Поэтому если F(x) — какая-либо другая первообразная для ) на [a; b], то S(x) = F(x) + С, где С — постоянная. Чтобы определить С, учтём, что S(a) 0, ибо при х — а криволинейная трапеция, образованная графиком функции f(x) на [a; х], вырождается в отрезок; его площадь равна 0. Имеем: 0 = F(a) + С, отсюда С = -F(a). Следовательно,= F(х) — F(a). Если в это равенство подставим значение х = Ь, то получим площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]:

Значение выражения F(b) — F(a) вычисляют часто, поэтому для удобства его записывают ещё и так:.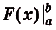.Итак, формула (1) приобретает вид:

Задача №2.

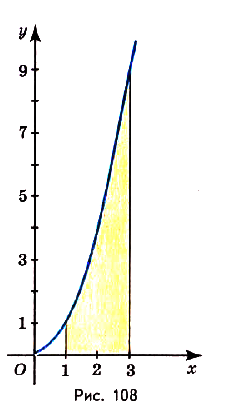
Найдите площадь криволинейной трапеции, образованной графиком функции 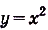на промежутке [1; 3].

Решение:

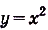
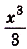
На (рис) 108 изображена фигура, площадь которой нужно найти. Для функции первообразной есть . Следовательно, искомая площадь

Задача №3.

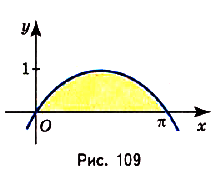
Найдите площадь фигуры, ограниченной одной аркой синусоиды и осью абсцисс (риc. 109).

Решение:

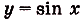
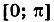
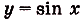
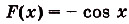
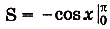
Надо найти площадь криволинейной трапеции, образованной графиком функции на промежутке . Для функции первообразной есть функция . Следовательно, искомая площадь= 1 — (-1) — 2 (кв. ед.).

Пользуясь термином «криволинейная трапеция следует иметь в виду, что «криволинейная трапеция» не всегда является трапецией (риc. 109) и не всегда она криволинейная(риc. 105, б). А вообще она — не геометрическая фигура в научном понимании. Любое движение отображает каждую фигуру на равную ей фигуру такого же вида. А если «криволинейную трапецию *, например, изображенную на (рис 108), повернуть на 90°, она отображается на фигуру, которая не является криволинейной трапецией. Поэтому вместо «криволинейная трапеция» говорят и пишут «подграфик функции».

Задача №4.

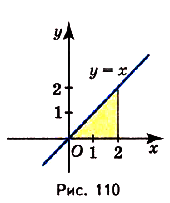
Найдите площадь криволинейной трапеции, образованной графиком функции у = х на [0; 2].

Решение:

Данная криволинейная трапеция — прямоугольный треугольник с катетами 2 и 2 (риc. 110). Его площадь 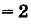(кв. ед.).

Ответ. 2кв. ед.

Задача №5.

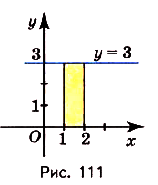
Найдите площадь криволинейной трапеции, образованной графиком функции у -3 на [1,2].

Заданная криволинейная трапеция — прямоугольник с измерениями 1 и 3 (риc. 111). Его площадь 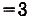(кв. ед.).

Ответ. 3 кв. ед.

Задача №6.

Найдите площадь фигуры, ограниченной графиком функции 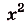и осью абсцисс.

Решение:

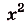
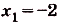
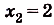
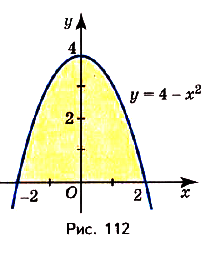
Найдем абсциссы точек пересечения графика данной функции с осью Ох. В этих точках ордината функции равна нулю:, отсюда , (риc. 112). Значит, надо найти площадь криволинейной трапеции, образованной

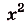
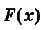
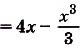
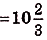
графиком функции на [-2; 2].Одна из первообразных для данной функции .Поэтому искомая площадь кв,ед.

Ответ. 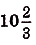кв.ед.

Определённый интеграл

Рассмотрим другой подход к определению площади криволинейной трапеции.

Пусть дана криволинейная трапеция, образованная графиком функции f(x) на [a;b] (рис. 117). Разобьём отрезок [а; Ь] точками 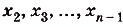на n равных отрезков:

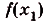
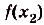
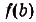
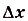
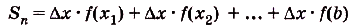
Построим на первом из этих отрезков прямоугольник высотой , на втором — прямоугольник высотой ,…, на n—м — прямоугольник высотой . В результате получим ступенчатый многоугольник, составленный из n прямоугольников. Пусть основание каждого из построенных прямоугольников равно ; тогда площадь всего ступенчатого многоугольника

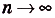
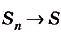
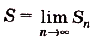
Суммы такого вида называют интегральными суммами функции f(x) на [а; Ь]. Полученную интегральную сумму можно считать приближённым значением площади S криволинейной трапеции, образованной графиком функции f(x) на [а; Ь]. При этом если то (риc. 118). Пишут: .

He только задача о нахождении площади криволинейной трапеции, но и много других важных прикладных задач приводят к вычислению пределов подобных интегральных сумм. Поэтому для такого понятия введено специальное название и обозначение.

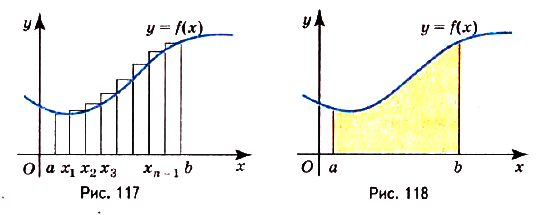
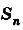
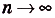
Предел интегральной суммы функции f(x) на отрезке [а; Ь], если , называют определённым интегралом функции f(x) от а до Ь.

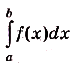
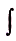
Его обозначают символом (читают: интеграл от а до b эф от икс де икс). Здесь числа а и b пределы интегрирования, — знак интеграла, f(x) — подинтегральная функция, х —переменная интегрирования.

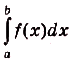
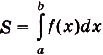
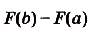
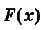
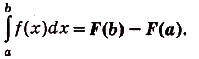
Следовательно, площадь криволинейной трапеции, образованной графиком функции f(x) на [а; Ь], равна , т. е.. Как доказано в предыдущем пункте, эта площадь равна , где — первообразная для функции f(x). Поэтому

Это — формула Ньютона—Лейбница, основная формула математического анализа. Она даёт возможность решать много разных интересных и содержательных задач — абстрактных и прикладных, в частности — и очень важных. Решали такие задачи сотни математиков еще задолго до создания математического анализа. Но для каждой задачи раньше они находили отдельный оригинальный способ решения. Найдя и обосновав формулу Ньютона—Лейбница, учёные получили общий и очень эффективный способ решения таких задач. Не случайно открытие формулы Ньютона—Лейбница специалисты считают самым важным открытием XVII века.Рационализировать вычисления определённых интегралов часто помогает такое их с в о й с т в о:

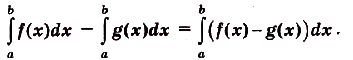
Справедливость этой формулы вытекает из следующих преобразований:

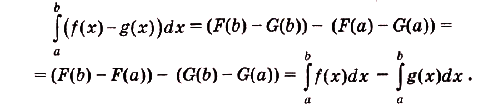
Задача №7.

Найдите площадь фигуры, ограниченной графиками функций 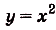и

Решение:

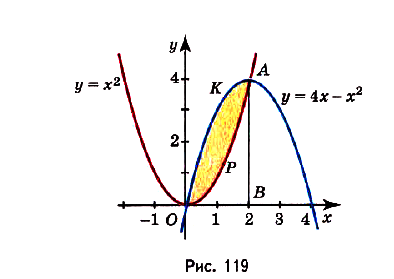
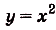
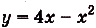
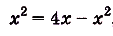
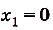
Построим графики данных функций (рис. 119). Надо найти площадь закрашенной фигуры. Она равна разности площадей фигур ОВАК и ОВАР. Границы интегрирования — абсциссы точек О и А, в которых пересекаются графики функций, т. е. значения х удовлетворяющие системе уравнений и . Из системы получим уравнение корни которого и

Следовательно, искомая площадь

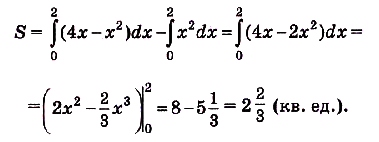
Ответ. 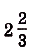кв. ед.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Первообразной для функции $f(x)$ называется такая функция $F(x)$, для которой выполняется равенство: $F'(x)=f(x)$

Таблица первообразных

Первообразная нуля равна $С$

Функция	Первообразная
$f(x)=k$	$F(x)=kx+C$
$f(x)=x^m, m≠-1$	$F(x)={x^{m+1}}/{m+1}+C$
$f(x)={1}/{x}$	$F(x)=ln|x|+C$
$f(x)=e^x$	$F(x)=e^x+C$
$f(x)=a^x$	$F(x)={a^x}/{lna}+C$
$f(x)=sinx$	$F(x)-cosx+C$
$f(x)=cosx$	$F(x)=sinx+C$
$f(x)={1}/{sin^2x}$	$F(x)=-ctgx+C$
$f(x)={1}/{cos^2x}$	$F(x)=tgx+C$
$f(x)=√x$	$F(x)={2x√x}/{3}+C$
$f(x)={1}/{√x}$	$F(x)=2√x+C$

Если $y=F(x)$ – это первообразная для функции $y=f(x)$ на промежутке $Х$, то $у$ $у=f(x)$ бесконечно много первообразных и все они имеют вид $y=F(x)+C$

Правила вычисления первообразных:

1. Первообразная суммы равна сумме первообразных. Если $F(x)$ – первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ – первообразная для $f(x)+g(x)$.
2. Постоянный множитель выносится за знак первообразной. Если $F(x)$ – первообразная для $f(x)$, а $k$ – постоянная величина, то $k$ $F(x)$ – первообразная для $k$ $f(x)$.
3. Если $F(x)$ – первообразная для $f(x)$, $а, k, b$ – постоянные величины, причем $k≠0$, то ${1}/{k}$ $F(kx+b)$ – это первообразная для $f(kx+b)$.

Связь между графиками функции и ее первообразной:

1. Если график функции $f (x) > 0$ на промежутке, то график ее первообразной $F(x)$ возрастает на этом промежутке.
2. Если график функции $f (x) < 0$ на промежутке, то график ее первообразной $F(x)$ убывает на этом промежутке.
3. Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий (или наоборот).

Неопределенный интеграл

Если функция $у=f(x)$ имеет на промежутке $Х$ первообразную $у=F(x)$, то множество всех первообразных $у=F(x)+С$, называют неопределенным интегралом функции $у=f(x)$ и записывают:

$∫f(x)dx$

Определенный интеграл – это интеграл с пределами интегрирования (на отрезке)

$∫_a^bf(x)dx$, где $a,b$ – пределы интегрирования

Площадь криволинейной трапеции или геометрический смысл первообразной

Площадь $S$ фигуры, ограниченной осью $Oх$, прямыми $х=а$ и $х=b$ и графиком неотрицательной функции $у=f(x)$ на отрезке $[a;b]$, находится по формуле

$S=∫_a^bf(x)dx$ 

Формула Ньютона – Лейбница

Если функция $у=f(x)$ непрерывна на отрезке $[a;b]$, то справедливо равенство

$∫_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)$, где $F(x)$ – первообразная для $f(x)$