Как найти первообразную от суммы

Содержание:

• Формула
• Примеры вычисления интеграла суммы

Формула

Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов слагаемых.

Данное правило распространяется и на случай, когда слагаемых больше, чем два.

Примеры вычисления интеграла суммы

Читать дальше: интеграл разности функций.

ВИДЕО УРОК

Что такое первообразная и как она считается ?

ПРИМЕР:

Найдём производную:

f(x) = x³.

Находим её, пользуясь формулой:

Откуда

Это и есть определение
первообразной.

Аналогично запишем и
такое выражение:

Обобщим это правило и
выведем следующую формулу:

При   n = –1 
первообразная функция определяется следующим образом:
Учитывая,
что

а производная

Первообразной функции называется такая функция, производная которой равна
исходной функции.

Функция

y = F(x)

называется первообразной функции

y = f(x)

на промежутке  Х, если для любого  х ∈ Х  выполняется равенство:

F(x) = f(x).

Таблица первообразных
функций.

К каждому выражению в правой части таблицы необходимо прибавить константу.

Правила нахождения первообразных функций.

1. Первообразная функция суммы (разности) равна сумме (разности)
первообразных функций.

F(x + у) = F(x) + F(у),

F(x – у) = F(x) – F(у).

ПРИМЕР:

Найти первообразную для функции

у
= 4х³ + cos x.

РЕШЕНИЕ:

Первообразная суммы равна сумме
первообразных, тогда надо найти первообразную для каждой из представленных
функций.

f(x) = 4x³,  F(x)
= x⁴.

f(x) = cos x,  F(x) = sin x.

Тогда первообразная исходной
функции будет

у
= х⁴ + sin x

или любая функция вида

у
= х⁴ + sin x + C.

2. Если  F(x) –
первообразная для  f(x), то

k F(x)–
первообразная для функции  k f(x).

(Коэффициент можно выносить за функцию).

ПРИМЕР:

Найти первообразную для функции

у
= 8 sin x.

РЕШЕНИЕ:

Первообразной для  sin x  служит
минус  cos x.
Тогда первообразная исходной функции примет вид:

у
= –8 cos x.

ПРИМЕР:

Найти первообразную для функции

у
= 3x² + 4х + 5.

РЕШЕНИЕ:

Первообразной для  x²  служит

Первообразной для  x  служит

Первообразной для  1  служит  x.

Тогда первообразная исходной
функции примет вид:

у
= x³ + 2x² + 5 x.

3. Если  y = F(x) – первообразная для функции

y = f(x),

то первообразная для функции

y = f(kx + m)

служит функция

y = ¹/_k F(kx + m).

ПРИМЕР:

Найти первообразную для функции

у
= cos (7x).

РЕШЕНИЕ:

Первообразной для  cos x  служит  sin x. Тогда первообразная для функции

cos (7x)

будет функция

ПРИМЕР:

Найти первообразную для функции

у
= sin ^x/₂.

РЕШЕНИЕ:

Первообразной для  sin x  служит минус  cos x. Тогда первообразная для функции

у
= sin ^x/₂

будет функция

ПРИМЕР:

Найти первообразную для функции

у
= (–2х + 3)³.

РЕШЕНИЕ:

Первообразной для  x³  служит

Тогда первообразная для исходной
функции

у
= (–2х + 3)³.

будет функция

ПРИМЕР:

На этой странице вы узнаете:

• Родственные связи первообразной. Как первообразная связана с производной?
• Одна функция, но много ее первообразных. Как такое происходит?

Понятие первообрвообразной

Легко догадаться, что термин “первоОбразная” происходит от двух слов: первый и образ. Первым образом у автомобиля была повозка, а у пюре — картофель.

Вернемся к математике.

Ранее мы уже рассматривали, что такое Производная и как найти её.  Давайте быстро вспомним, что нахождение производной или дифференцирование — это совершение математической операции над функцией. То есть, следуя определенным правилам, любая функция может быть преобразована в новую функцию, которая и будет производной.  

В обычной жизни, совершая несколько действий, мы можем преобразовать муку в тесто, а затем и в пирожки. Но разобрать готовый пирожок на муку у нас уже не получится. Зато в математике всегда можно вернуться на шаг назад: сложили два числа — вычтем обратно, возвели в степень — извлечем корень. 

Похожим образом мы можем поступить с функцией. 

Возьмем любую функцию, например, f(x) = x² и найдем для нее производную f'(x) = 2x — получилась новая функция. Теперь для того, чтобы вернуться на шаг назад, нам нужно найти первообразную от новой функции (f'(x) = 2x).

Первообразной для функции f(x) называется такая функция F(x), для которой выполняется равенство: F'(x) = f(x). 

То есть, если взять производную от первообразной какой-либо функции, получится сама эта функция. Процесс нахождения множества первообразных называется интегрированием.

F'(x) = f(x)

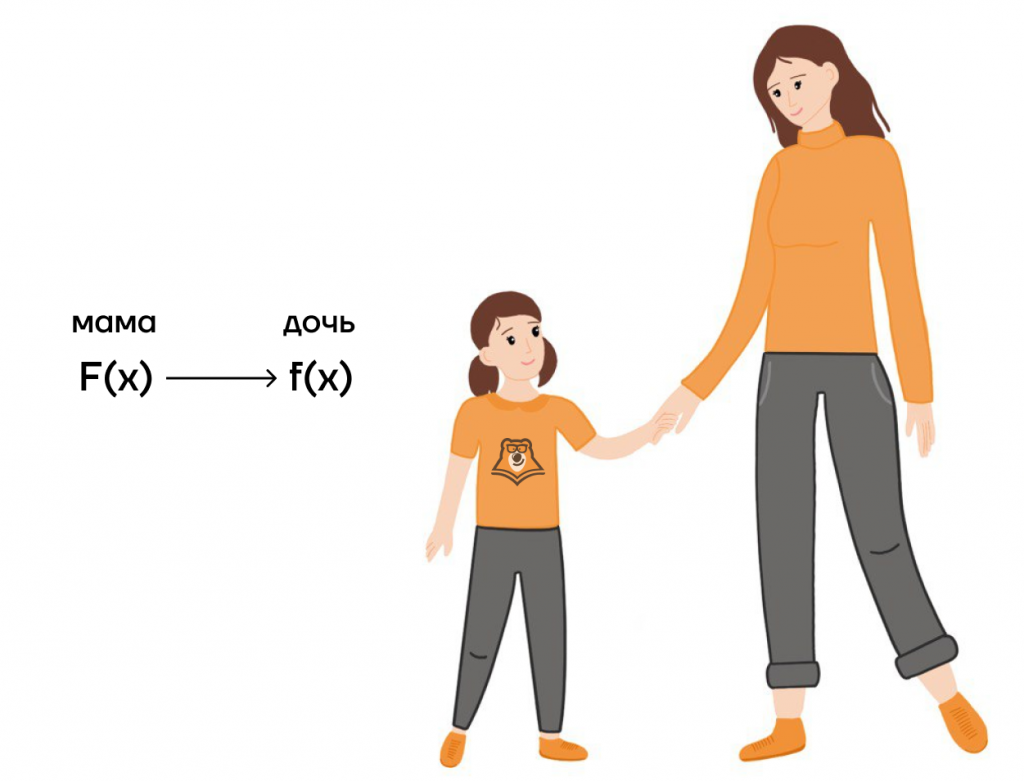
Для нахождения первообразных существует специальная таблица. В ней приведены первообразные для каждой функции. А чтобы убедиться в этом, можно найти производную от первообразной и сравнить с функцией. Они будут одинаковые.

Таблица первообразных

 Где С — произвольное число

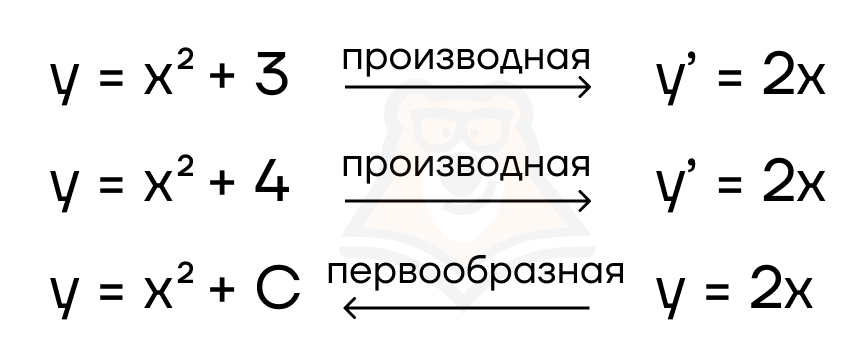
Важно:  F(x) первообразная f(x) только на том промежутке, где F(x) и f(x) существуют. То есть, (F(x) = frac{1}{2} * ln (2x) + C) первообразная (f(x) = frac{1}{2}x) на промежутке 2х > 0 (rightarrow) x > 0

Рассмотрим нахождение первообразной от следующей функции
y = 2x³

Применим правило интегрирования для степенной функции из таблицы первообразных

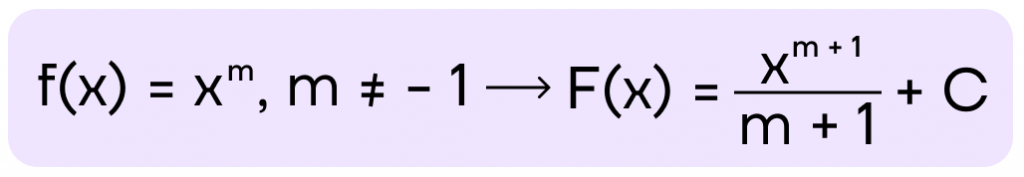
(F(x) = frac{2x^4}{4} + C)
(F(x) = frac{1}{2} x^4 + C)

Правила нахождения первообразных:

1. Если нужно найти первообразную от произведения числа на функцию, то первообразной выражения будет произведение этого числа на первообразную функции.

a*f(x) (rightarrow) a*F(x)

Пример:
f(x) = 4x (rightarrow F(x) = 4 * frac{x^2}{2} = 2x^2)

1. Если нужно найти первообразную от суммы/разности двух функций, то первообразной выражения будет сумма/разность первообразных этих двух функций. 

g(x) (pm) f(x) (rightarrow) G(x) (pm) F(x)

Пример:
f(x) = x² + 2 (rightarrow F(x) = frac{x^3}{3} + 2x)

Фактчек

• Первообразной для функции f(x) называется такая функция F(x), для которой выполняется равенство: F'(x) = f(x)
• Для нахождения первообразных существует специальная таблица первообразных
• Правила нахождения первообразных:
  a*f(x) (rightarrow) a*F(x)
  g(x) (pm) f(x) (rightarrow) G(x) (pm) F(x)

Проверь себя

Задание 1.
Найдите первообразную функции y = 4x⁵

1. F(x) = 20x⁴
2. (F(x) = frac{1}{3}x^6)
3. (F(x) = frac{1}{3}x^5)
4. (F(x) = frac{2}{3}x^6)

Задание 2.
Найдите первообразную функции y = 4

1. F(x) = 4x
2. F(x) = x
3. (F(x) = frac{1}{2}x^2)
4. (F(x) = frac{1}{2}x)

Задание 3.
Найдите первообразную функции (y = 2sin x)

1. F(x)= x
2. (F(x) = -2cos x)
3. (F(x) = frac{1}{2}cos x)
4. (F(x) = -2sin x)

Задание 4.
Найдите первообразную функции y = 2^x

1. (F(x) = frac{2^x}{ln2})
2. F(x) = ln2
3. F(x) = 2
4. F(x) = x²

Ответы: 1. — 4; 2. — 1; 3. — 2; 4. -1

Первообразной для функции $f(x)$ называется такая функция $F(x)$, для которой выполняется равенство: $F'(x)=f(x)$

Таблица первообразных

Первообразная нуля равна $С$

Функция	Первообразная
$f(x)=k$	$F(x)=kx+C$
$f(x)=x^m, m≠-1$	$F(x)={x^{m+1}}/{m+1}+C$
$f(x)={1}/{x}$	$F(x)=ln|x|+C$
$f(x)=e^x$	$F(x)=e^x+C$
$f(x)=a^x$	$F(x)={a^x}/{lna}+C$
$f(x)=sinx$	$F(x)-cosx+C$
$f(x)=cosx$	$F(x)=sinx+C$
$f(x)={1}/{sin^2x}$	$F(x)=-ctgx+C$
$f(x)={1}/{cos^2x}$	$F(x)=tgx+C$
$f(x)=√x$	$F(x)={2x√x}/{3}+C$
$f(x)={1}/{√x}$	$F(x)=2√x+C$

Если $y=F(x)$ – это первообразная для функции $y=f(x)$ на промежутке $Х$, то $у$ $у=f(x)$ бесконечно много первообразных и все они имеют вид $y=F(x)+C$

Правила вычисления первообразных:

1. Первообразная суммы равна сумме первообразных. Если $F(x)$ – первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ – первообразная для $f(x)+g(x)$.
2. Постоянный множитель выносится за знак первообразной. Если $F(x)$ – первообразная для $f(x)$, а $k$ – постоянная величина, то $k$ $F(x)$ – первообразная для $k$ $f(x)$.
3. Если $F(x)$ – первообразная для $f(x)$, $а, k, b$ – постоянные величины, причем $k≠0$, то ${1}/{k}$ $F(kx+b)$ – это первообразная для $f(kx+b)$.

Связь между графиками функции и ее первообразной:

1. Если график функции $f (x) > 0$ на промежутке, то график ее первообразной $F(x)$ возрастает на этом промежутке.
2. Если график функции $f (x) < 0$ на промежутке, то график ее первообразной $F(x)$ убывает на этом промежутке.
3. Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий (или наоборот).

Неопределенный интеграл

Если функция $у=f(x)$ имеет на промежутке $Х$ первообразную $у=F(x)$, то множество всех первообразных $у=F(x)+С$, называют неопределенным интегралом функции $у=f(x)$ и записывают:

$∫f(x)dx$

Определенный интеграл – это интеграл с пределами интегрирования (на отрезке)

$∫_a^bf(x)dx$, где $a,b$ – пределы интегрирования

Площадь криволинейной трапеции или геометрический смысл первообразной

Площадь $S$ фигуры, ограниченной осью $Oх$, прямыми $х=а$ и $х=b$ и графиком неотрицательной функции $у=f(x)$ на отрезке $[a;b]$, находится по формуле

$S=∫_a^bf(x)dx$ 

Формула Ньютона – Лейбница

Если функция $у=f(x)$ непрерывна на отрезке $[a;b]$, то справедливо равенство

$∫_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)$, где $F(x)$ – первообразная для $f(x)$

Первообразная функции и общий вид

20 июля 2015

Этот урок — первый из серии видео, посвященных интегрированию. В нём мы разберём, что такое первообразная функции, а также изучим элементарные приёмы вычисления этих самых первообразных.

На самом деле здесь нет ничего сложного: по существу всё сводится к понятию производной, с которым вы уже должны знакомы.:)

Сразу отмечу, что, поскольку это самый первый урок в нашей новой теме, сегодня не будет никаких сложных вычислений и формул, но то, что мы изучим сегодня, ляжет в основу гораздо более сложных выкладок и конструкций при вычислении сложных интегралов и площадей.

Кроме того, приступая к изучению интегрирования и интегралов в частности, мы неявно предполагаем, что ученик уже, как минимум, знаком к понятиям производной и имеет хотя бы элементарные навыки их вычисления. Без четкого понимания этого, делать в интегрировании совершенно нечего.

Однако здесь же кроется одна из самых частых и коварных проблем. Дело в том, что, начиная вычислять свои первые первообразные, многие ученики путают их с производными. В результате на экзаменах и самостоятельных работах допускаются глупые и обидные ошибки.

Поэтому сейчас я не буду давать четкого определения первообразной. А взамен предлагаю вам посмотреть, как она считается на простом конкретном примере.

Что такое первообразная и как она считается

Допустим, нам необходимо посчитать следующую производную:

[fleft( x right)={{x}^{3}}]

Мы знаем такую формулу:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

Считается эта производная элементарно:

[{f}’left( x right)={{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}}]

Посмотрим внимательно на полученное выражение и выразим ${{x}^{2}}$:

[{{x}^{2}}=frac{{{left( {{x}^{3}} right)}^{prime }}}{3}]

Но мы можем записать и так, согласно определению производной:

[{{x}^{2}}={{left( frac{{{x}^{3}}}{3} right)}^{prime }}]

А теперь внимание: то, что мы только что записали и есть определением первообразной. Но, чтобы записать ее правильно, нужно написать следующее:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

Аналогично запишем и такое выражение:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

Если мы обобщим это правило, то сможем вывести такую формулу:

[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]

Теперь мы можем сформулировать четкое определение.

Первообразной функции называется такая функция, производная которой равна исходной функции.

Вопросы о первообразной функции

Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:

1. Допустим, хорошо, эта формула верна. Однако в этом случае при $n=1$ у нас возникают проблемы: в знаменателе появляется «ноль», а на «ноль» делить нельзя.
2. Формула ограничивается только степенями. Как считать первообразную, например, синуса, косинуса и любой другой тригонометрии, а также констант.
3. Экзистенциальный вопрос: а всегда ли вообще можно найти первообразную? Если да, то как быть с первообразной суммы, разности, произведения и т.д.?

На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.

Решение задач со степенными функциями

Давайте попробуем посчитать такое выражение:

[{{x}^{-1}}to frac{{{x}^{-1+1}}}{-1+1}=frac{1}{0}]

Как видим, данная формула для ${{x}^{-1}}$ не работает. Возникает вопрос: а что тогда работает? Неужели мы не можем посчитать ${{x}^{-1}}$? Конечно, можем. Только давайте для начала вспомним такое:

[{{x}^{-1}}=frac{1}{x}]

Теперь подумаем: производная какой функции равна $frac{1}{x}$. Очевидно, что любой ученик, который хоть немного занимался этой темой, вспомнит, что этому выражению равна производная натурального логарифма:

[{{left( ln x right)}^{prime }}=frac{1}{x}]

Поэтому мы с уверенностью можем записать следующее:

[frac{1}{x}={{x}^{-1}}to ln x]

Эту формулу нужно знать, точно так же, как и производную степенной функции.

Итак, что нам известно на данный момент:

• Для степенной функции — ${{x}^{n}}to frac{{{x}^{n+1}}}{n+1}$
• Для константы — $=constto cdot x$
• Частный случай степенной функции — $frac{1}{x}to ln x$

Идем далее. Что нам еще может потребоваться? Конечно же, правило вычисления первообразных от суммы и от разности. Запишем так:

[fleft( x right)to Fleft( x right)]

[gleft( x right)to Gleft( x right)]

[f+gto F+G]

[f-g=F-G]

[ccdot fto ccdot Fleft( c=const right)]

А если простейшие функции мы начнем умножать и делить, как тогда посчитать первообразную произведения или частного. К сожалению, аналогии с производной произведения или частного здесь не работают. Какой-либо стандартной формулы не существует. Для некоторых случаев существуют хитрые специальные формулы — с ними мы познакомимся на будущих видеоуроках.

Однако запомните: общей формулы, аналогичной формуле для вычисления производной частного и произведения, не существует.

Решение реальных задач

Задача № 1

[fleft( x right)={{x}^{2}}+5{{x}^{4}}]

Давайте каждую из степенных функций посчитаем отдельно:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[5{{x}^{4}}to 5cdot frac{{{x}^{5}}}{5}={{x}^{5}}]

Возвращаясь к нашему выражению, мы запишем общую конструкцию:

[Fleft( x right)=frac{{{x}^{3}}}{3}+{{x}^{5}}]

Задача № 2

[fleft( x right)=frac{x+1}{x}]

Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:

[fleft( x right)=frac{x}{x}+frac{1}{x}=1+frac{1}{x}]

Мы разбили дробь на сумму двух дробей.

Посчитаем:

[Fleft( x right)=1cdot x+ln x]

[Fleft( x right)=x+ln x]

Хорошая новость состоит в том, что зная формулы вычисления первообразных, вы уже способны считать более сложные конструкции. Однако давайте пойдем дальше и расширим наши знания еще чуть-чуть. Дело в том, что многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к ${{x}^{n}}$, могут быть представлены в виде степени с рациональным показателем, а именно:

[sqrt{x}={{x}^{frac{1}{2}}}]

[sqrt[n]{x}={{x}^{frac{1}{n}}}]

[frac{1}{{{x}^{n}}}={{x}^{-n}}]

Все эти приемы можно и нужно комбинировать. Степенные выражения можно

• умножать (степени складываются);
• делить (степени вычитаются);
• умножать на константу;
• и т.д.

Решение выражений со степенью с рациональным показателем

Пример № 1

[fleft( x right)=7sqrt{x}+sqrt[4]{x}]

Посчитаем каждый корень отдельно:

[]

[sqrt{x}={{x}^{frac{1}{2}}}to frac{{{x}^{frac{1}{2}+1}}}{frac{1}{2}+1}=frac{{{x}^{frac{3}{2}}}}{frac{3}{2}}=frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[sqrt[4]{x}={{x}^{frac{1}{4}}}to frac{{{x}^{frac{1}{4}}}}{frac{1}{4}+1}=frac{{{x}^{frac{5}{4}}}}{frac{5}{4}}=frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Итого всю нашу конструкцию можно записать следующим образом:

[Fleft( x right)=7cdot frac{2cdot {{x}^{frac{3}{2}}}}{3}+frac{5cdot {{x}^{frac{5}{4}}}}{4}=frac{14cdot {{x}^{frac{3}{2}}}}{3}+frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Пример № 2

[fleft( x right)=frac{1}{sqrt{x}}-frac{1}{{{x}^{3}}}]

Запишем:

[frac{1}{sqrt{x}}={{left( sqrt{x} right)}^{-1}}={{left( {{x}^{frac{1}{2}}} right)}^{-1}}={{x}^{-frac{1}{2}}}]

Следовательно, мы получим:

[Fleft( x right)=frac{{{x}^{-frac{1}{2}+1}}}{-frac{1}{2}+1}=frac{{{x}^{frac{1}{2}}}}{frac{1}{2}}=2{{x}^{frac{1}{2}}}=2sqrt{x}]

[frac{1}{{{x}^{3}}}={{x}^{-3}}to frac{{{x}^{-3+1}}}{-3+1}=frac{{{x}^{-2}}}{-2}=-frac{1}{2{{x}^{2}}}]

Итого, собирая все в одно выражение, можно записать:

[Fleft( x right)=2sqrt{x}+frac{1}{2{{x}^{2}}}]

Пример № 3

[fleft( x right)=sqrt[4]{x}-xsqrt{x}+1]

Для начала заметим, что $sqrt[4]{x}$ мы уже считали:

[sqrt[4]{x}to frac{4{{x}^{frac{5}{4}}}}{5}]

[xsqrt{x}={{x}^{1}}cdot {{x}^{frac{1}{2}}}={{x}^{frac{3}{2}}}]

[{{x}^{frac{3}{2}}}to frac{{{x}^{frac{3}{2}+1}}}{frac{3}{2}+1}=frac{2cdot {{x}^{frac{5}{2}}}}{5}]

[1to x]

Перепишем:

[Fleft( x right)=frac{4{{x}^{frac{5}{4}}}}{5}-frac{2{{x}^{frac{5}{2}}}}{5}+x]

Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.

Решение более сложных примеров

Задача № 1

[fleft( x right)={{left( sqrt[3]{x}-2 right)}^{2}}]

Вспомним формулу квадрата разности:

[{{left( a-b right)}^{2}}={{a}^{2}}-ab+{{b}^{2}}]

Давайте перепишем нашу функцию:

[fleft( x right)=left( sqrt[3]{x} right)-2cdot sqrt[3]{x}cdot 2+4]

[fleft( x right)={{x}^{frac{2}{3}}}-4{{x}^{frac{1}{3}}}+4]

Первообразную такой функции нам сейчас предстоит найти:

[{{x}^{frac{2}{3}}}to frac{3cdot {{x}^{frac{5}{3}}}}{5}]

[{{x}^{frac{1}{3}}}to frac{3cdot {{x}^{frac{4}{3}}}}{4}]

[4to 4x]

Собираем все в общую конструкцию:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x]

Задача № 2

[fleft( x right)={{left( frac{1}{x}-2 right)}^{3}}]

В этом случае нам нужно раскрыть куб разности. Вспомним:

[{{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}cdot b+3acdot {{b}^{2}}-{{b}^{3}}]

С учетом этого факта можно записать так:

[fleft( x right)=frac{1}{{{x}^{3}}}-3cdot frac{1}{{{x}^{2}}}cdot 2+3cdot frac{1}{x}cdot 4-8]

Давайте немного преобразуем нашу функцию:

[fleft( x right)={{x}^{-3}}-6{{x}^{-2}}+12cdot {{x}^{-1}}-8]

Считаем как всегда — по каждому слагаемому отдельно:

[{{x}^{-3}}to frac{{{x}^{-2}}}{-2}]

[{{x}^{-2}}to frac{{{x}^{-1}}}{-1}]

[{{x}^{-1}}to ln x]

[8to 8x]

Запишем полученную конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x-8x]

Задача № 3

[fleft( x right)=frac{{{left( x+sqrt{x} right)}^{2}}}{x}]

Сверху у нас стоит квадрат суммы, давайте его раскроем:

[frac{{{left( x+sqrt{x} right)}^{2}}}{x}=frac{{{x}^{2}}+2xcdot sqrt{x}+{{left( sqrt{x} right)}^{2}}}{x}=]

[=frac{{{x}^{2}}}{x}+frac{2xsqrt{x}}{x}+frac{x}{x}=x+2{{x}^{frac{1}{2}}}+1]

Далее все легко:

[xto frac{{{x}^{2}}}{2}]

[{{x}^{frac{1}{2}}}to frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[1to x]

Давайте напишем итоговое решение:

[Fleft( x right)=frac{{{x}^{2}}}{x}+frac{4{{x}^{frac{3}{2}}}}{3}+x]

А теперь внимание! Очень важная вещь, с которой связана львиная доля ошибок и недопониманий. Дело в том, что до сих пор считая первообразные с помощью производных, приводя преобразования, мы не задумывались о том, чему равна производная константы. А ведь производная константы равна «нулю». А это означает, что можно записать такие варианты:

1. ${{x}^{2}}to frac{{{x}^{3}}}{3}$
2. ${{x}^{2}}to frac{{{x}^{3}}}{3}+1$
3. ${{x}^{2}}to frac{{{x}^{3}}}{3}+C$

Вот это очень важно понимать: если производная функции всегда одна и та же, то первообразных у одной и той же функции бесконечно много. Просто к нашим первообразным мы можем дописывать любые числа-константы и получать новые.

Неслучайно, в пояснении к тем задачам, которые мы только что решали, было написано «Запишите общий вид первообразных». Т.е. уже заранее предполагается, что их не одна, а целое множество. Но, на самом деле, они отличаются лишь константой $C$ в конце. Потому в наших задачах мы исправим то, что мы не дописали.

Еще раз переписываем наши конструкции:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x+C]

В таких случаях следует дописывать, что $C$ — константа — $C=const$.

Во второй нашей функции мы получим следующую конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x+C]

И последняя:

[Fleft( x right)=frac{{{x}^{2}}}{2}+frac{4{{x}^{frac{3}{2}}}}{3}+x+C]

И вот теперь мы действительно получили то, что от нас требовалось в исходном условии задачи.

Решение задач на нахождение первообразных с заданной точкой

Сейчас, когда мы знаем о константах и об особенностях записи первообразных, вполне логично возникает следующий тип задач, когда из множества всех первообразных требуется найти одну-единственную такую, которая проходила бы через заданную точку. В чем состоит эта задача?

Дело в том, что все первообразные данной функции отличаются лишь тем, что они сдвинуты по вертикали на какое-то число. А это значит, что какую бы точку на координатной плоскости мы не взяли, обязательно пройдет одна первообразная, и, причем, только одна.

Итак, задачи, которые сейчас мы будем решать, сформулированы следующем образом: не просто найти первообразную, зная формулу исходной функции, а выбрать именно такую из них, которая проходит через заданную точку, координаты которой будут даны в условии задачи.

Пример № 1

[fleft( x right)=5{{x}^{4}}+6{{x}^{3}}-2x+6]

[M=left( -1;4 right)]

Для начала просто посчитаем каждое слагаемое:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

[{{x}^{3}}to frac{{{x}^{4}}}{4}]

[xto frac{{{x}^{2}}}{2}]

[6to 6x]

Теперь подставляем эти выражения в нашу конструкцию:

[Fleft( x right)=5cdot frac{{{x}^{5}}}{5}+6cdot frac{{{x}^{4}}}{4}-2cdot frac{{{x}^{2}}}{2}+6x+C]

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+C]

Эта функция должна проходить через точку $Mleft( -1;4 right)$. Что значит, что она проходит через точку? Это значит, что если вместо $x$ поставить везде $-1$, а вместо $Fleft( x right)$ — $-4$, то мы должны получить верное числовое равенство. Давайте так и сделаем:

[4={{left( -1 right)}^{5}}+frac{3cdot {{left( -1 right)}^{4}}}{2}-{{left( -1 right)}^{2}}+6cdot left( -1 right)+C]

Мы видим, что у нас получилось уравнение относительно $C$, поэтому давайте попробуем его решить:

[4=-1+frac{3}{2}-1-6+C]

[C=4+6+2-frac{3}{2}=10,5]

Давайте запишем то самое решение, которое мы искали:

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+10,5]

Пример № 2

[fleft( x right)={{left( x-3 right)}^{2}}]

[M=left( 2;-1 right)]

В первую очередь необходимо раскрыть квадрат разности по формуле сокращенного умножения:

[fleft( x right)={{x}^{2}}-6x+9]

Считаем:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[xto frac{{{x}^{2}}}{2}]

[9to 9x]

Исходная конструкция запишется следующим образом:

[Fleft( x right)=frac{{{x}^{3}}}{3}-6cdot frac{{{x}^{2}}}{2}+9x+C]

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x+C]

Теперь давайте найдем $C$: подставим координаты точки $M$:

[-1=frac{8}{3}-12+18+C]

Выражаем $C$:

[C=-1-6-2frac{2}{3}=-9frac{2}{3}]

Осталось отобразить итоговое выражение:

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x-9frac{2}{3}]

Решение тригонометрических задач

В качестве финального аккорда к тому, что мы только что разобрали, предлагаю рассмотреть две более сложные задачи, в которых содержится тригонометрия. В них точно так же потребуется найти первообразные для всех функций, затем выбрать из этого множества одну-единственную, которая проходит через точку $M$ на координатной плоскости.

Забегая наперед, хотел бы отметить, что тот прием, который мы сейчас будем использовать для нахождения первообразных от тригонометрических функций, на самом деле, является универсальным приемом для самопроверки.

Задача № 1

[fleft( x right)=frac{1}{{{cos }^{2}}x}]

[M=left( frac{text{ }!!pi!!text{ }}{text{4}};-1 right)]

Вспомним следующую формулу:

[{{left( text{tg}x right)}^{prime }}=frac{1}{{{cos }^{2}}x}]

Исходя из этого, мы можем записать:

[Fleft( x right)=text{tg}x+C]

Давайте подставим координаты точки $M$ в наше выражение:

[-1=text{tg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[-1=1+C]

[C=-2]

Перепишем выражение с учетом этого факта:

[Fleft( x right)=text{tg}x-2]

Задача № 2

[fleft( x right)=frac{1}{{{sin }^{2}}x}]

[M=left( -frac{text{ }!!pi!!text{ }}{text{4}};2 right)]

Тут будет чуть сложнее. Сейчас увидите, почему.

Вспомним такую формулу:

[{{left( text{ctg}x right)}^{prime }}=-frac{1}{{{sin }^{2}}x}]

Чтобы избавится от «минуса», необходимо сделать следующее:

[{{left( -text{ctg}x right)}^{prime }}=frac{1}{{{sin }^{2}}x}]

Вот наша конструкция

[Fleft( x right)=-text{ctg}x+C]

Подставим координаты точки $M$:

[2=-text{ctg}left( -frac{text{ }!!pi!!text{ }}{4} right)+C]

[2=text{ctg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[2=1+C]

[C=1]

Итого запишем окончательную конструкцию:

[Fleft( x right)=-text{ctg}x+1]

Вот и все, о чем я хотел сегодня вам рассказать. Мы изучили сам термин первообразных, как считать их от элементарных функций, а также как находить первообразную, проходящую через конкретную точку на координатной плоскости.

Надеюсь, этот урок хоть немного поможет вам разобраться в этой сложной теме. В любом случае, именно на первообразных строятся неопределенные и неопределенные интегралы, поэтому считать их совершенно необходимо. На этом у меня все. До новых встреч!

Смотрите также:

1. Таблица первообразных
2. Интегрирование по частям
3. Решение задач B12: №448—455
4. Что такое ЕГЭ по математике 2011 и как его сдавать
5. Задача B4: случай с неизвестным количеством товара
6. Задача B15: что делать с квадратичной функцией