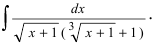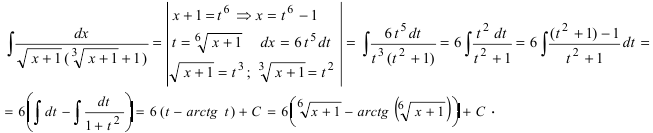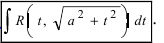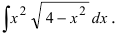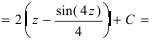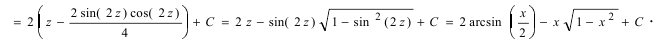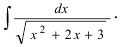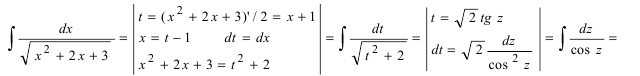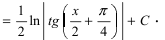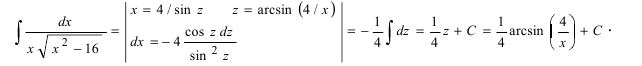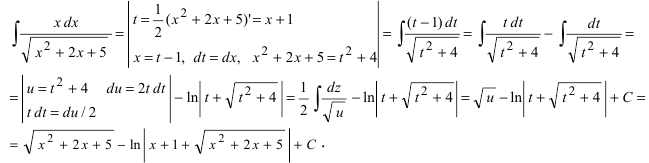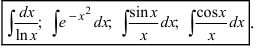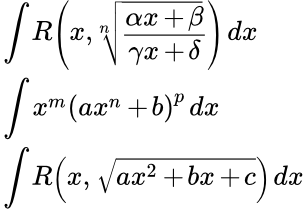Как найти первообразную от дроби с квадратным корнем в знаменателе?
Знаток
(295),
закрыт
1 год назад
Сергей Алексеев
Оракул
(86916)
3 года назад
Корень квадратный да и не только квадратный, любой, можно заменить дробной степенью. например 1/ корень квадратный их х = 1/х^(1/2). См свойства корней. Дальше если 1/2 написать с минусом то мы в обще можем избавиться от дроби. Причем не изменим значение выражения. 1/х^(1/2)= х (-1/2) . Дальше по формуле интегрирования получаем что первообразная = ((х^(-1/2+1))/(-1/2+1))+С . Ещё, если у вас скажем 3/x^(1/2) то можно записать 3*1/х^(1/2) . Потом 3 выносим за знак интеграла и дальше действуем по схеме выше. Правда- давайте пример, так проще будет.

Пример 8
|
∫ |
1 |
dx = ∫ |
(lnx +1)′ dx = 2 |
+C . |
|||
|
lnx +1 |
|||||||
|
x |
lnx +1 |
lnx +1 |
|
I. Интегралы вида ∫ |
dx |
или ∫ |
dx |
берутся с помощью вы- |
||
|
ax2 +bx + c |
||||||
|
ax2 +bx + c |
деления полного квадрата для квадратного трехчлена и использование табличных интегралов № 8 – 11.
Пример 9
|
∫ |
dx |
= ∫ |
dx |
= ∫ |
dx |
= ∫ |
d(x +1) |
= |
|
x2 + 2x +5 |
x2 + 2x +1+ 4 |
(x +1)2 + 4 |
(x +1)2 + 22 |
= 12arctg x 2+1+C .
В случае с квадратным корнем только на последнем шаге применяется другой табличный интеграл (10-11 вместо 8-9).
Пример 10
|
dx |
d(x +1) |
|||||||||||||
|
∫ |
= ∫ |
= ln(x +1+ x |
2 |
+ 2x +5)+C . |
||||||||||
|
x |
2 |
+ 2x +5 |
(x +1) |
2 |
+ 4 |
|||||||||
Замечание. Так как у нас подкоренное выражение, очевидно, положительно, то выражение под знаком логарифма тоже положительно и проще избавиться в ответе от знака модуля.
|
II. Интегралы вида ∫ |
kx + e |
∫ |
kx + e |
||
|
dx или |
dx берутся с помо- |
||||
|
ax2 +bx + c |
|||||
|
ax2 +bx + c |
щью выделения в числителе производной от квадратного трехчлена в знамена-
теле (ax2 +bx +c)′ = 2ax +b: kx + e = A(2ax +b)+ B, где А и B находятся мето-
дом неопределенных коэффициентов (раскрываются скобки и после приведения подобных членов приравниваются коэффициенты при x и свободные чле-
10

ны, что дает систему двух линейных уравнений относительно А и В, определитель которой всегда отличен от нуля); подставив полученное выражение в числитель и почленно разделив, мы сводим первые слагаемые к формулам (1.6) или (1.7), а вторые будут интегралами I типа.
Пример 11
∫x24−x6−x9+5dx .
Применим, описанный выше метод:
(x2 −6x +5)′ = 2x −6, 4x −9= A(2x −6)+ B, 4x −9= 2Ax + (−6A + B),
приравнивая коэффициенты при одинаковых степенях x, выписываем систему для определения коэффициентов
|
2A = 4, |
A = 2, |
|
−6A + B = −9, |
B = 6A −9=3, |
значит,
4x −9= 2(2x −6)+3.
Отметим, что в простых случаях с целыми числами A, B можно сразу найти A и B подбором т.е. а) на что нужно умножить 2x, чтобы получить 4x, очевидно, A=2; б) подставив в первое равенство A=2, уже раскрыв скобки 4x 12 легко ответить, какое число надо добавить к 12, чтобы получить 9, это позволяет найти B=3. Тогда
|
4x −9 |
2(2x −6)+3 |
2x −6 |
dx |
|||||||||||||||||||||||
|
∫ |
dx = ∫ x2 −6x +5 dx = 2∫ |
dx |
+3∫ |
= |
||||||||||||||||||||||
|
x2 −6x +5 |
x2 −6x +5 |
x2 −6x +5 |
||||||||||||||||||||||||
|
= 2∫ |
(x2 −6x +9)′ |
dx +3∫ |
d(x −3) |
2 |
3 1 |
x −3− 2 |
||||||||||||||||||||
|
x2 −6x +5 |
= 2ln |
x |
−6x +5 |
+ 2 |
2ln |
+C = |
||||||||||||||||||||
|
(x −3)2 − 4 |
x −3+ 2 |
|||||||||||||||||||||||||
|
3ln |
x −5 |
|||||||||||||||||||||||||
|
= 2ln |
x2 −6x +5 |
+ |
+C . |
|||||||||||||||||||||||
|
x −1 |
||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||
11

Аналогичный пример с квадратным корнем отличается только применением последнего частного случая внесения под знак дифференциала и иного табличного интеграла.
Пример 12
|
∫ |
9 |
− 4x |
dx = ∫ |
2(6− 2x)−3 |
dx = 2∫ |
(6x − x2 −5)′ |
||||||||||||||
|
dx − |
||||||||||||||||||||
|
6x |
− x |
2 |
6x − x |
2 |
−5 |
6x − x |
2 |
|||||||||||||
|
−5 |
−5 |
|||||||||||||||||||
|
−3∫ |
d(x −3) |
4 |
−3arcsin |
x −3 |
+C . |
|||||||||||||||
|
= |
6x − x2 −5 |
|||||||||||||||||||
|
4−(x −3) |
2 |
|||||||||||||||||||
|
2 |
Проверьте, что из-за смены знака квадратного трехчлена и знака числителя по сравнению с предыдущим примером А не изменится, а B сменит знак.
§5. Интегрирование рациональных дробей
Определение. Правильной рациональной дробью называется отношение двух многочленов
|
Qm (x) |
= bm xm + +b1x +b0 |
, |
(1.8) |
|
Pn (x) |
an xn + + a1x + a0 |
если степень многочлена в числителе меньше степени многочлена в знаменателе, то есть при m < n . Если дробь неправильная, то разделив уголком, всегда можно выделить целую часть и добавить остаток, деленный на многочлен Pn (x)
в знаменателе.
Пример 13
|
∫ |
x5 |
|||
|
dx . |
||||
|
x2 +9 |
||||
|
Так как степень числителя больше степени знаменателя, значит подынте- |
||||
|
гральная рациональная дробь неправильная: Q (x) = x5 |
, |
P (x) = x2 |
+9, |
|
|
5 |
2 |
m =5> 2= n. При делении уголком на каждом шаге степень многочлена понижается на n = 2, и, как только она станет меньше двух, процесс останавливаем.
12

−9x3
−9x3 −81x
81x
В нашем случае целая часть равна x3 −9x , а остаток 81x , поэтому
x2x+5 9 = x3 −9x + x812 +x9 .
Тогда
|
x5 |
81x |
||||||||||||||||||||
|
dx = |
x3 −9x + |
dx = |
x3dx − |
||||||||||||||||||
|
∫x |
2 |
+9 |
∫ |
x |
2 |
+9 |
∫ |
||||||||||||||
|
xdx |
x |
4 |
x |
2 |
1 |
(x |
2 |
′ |
4 |
2 |
|||||||||||
|
−9∫xdx + 81∫ |
= |
−9 |
+81 |
∫ |
+9) dx |
= 0,25x |
− 4,5x |
+ |
|||||||||||||
|
x2 +9 |
4 |
2 |
2 |
x2 +9 |
+40,5ln(x2 +9) +C .
Замечание. Первоначальный интеграл свелся к сумме трех интегралов, первые два из которых (от целой части) берутся как табличные, а последний сводится к выделению в числителе производной от знаменателя ((1.6)), но пока в сумме есть хотя бы один интеграл, произвольную постоянную С не пишут, т.к. она содержится в нем, и появляется в ответе только после взятия последнего интеграла.
Рассмотрим теперь общую схему интегрирования рациональных дробей.
1.Если дробь неправильная, то выделить целую часть (пример 13.).
2.Разложить знаменатель, если это возможно, на множители:
Pn (x) = an xn + an−1xn−1 + + a1x + a0 = an (x − x1) (x − x2)k
|
2 + |
p1x |
+ |
q1) |
(x2 |
+ p x + q )s |
, |
(1.9) |
|||||||
|
(x |
2 |
2 |
||||||||||||
|
где x1 является простым корнем многочлена Pn (x), x2 |
̶корнем кратности k, а |
|||||||||||||
|
дискриминантыD = p2 |
− 4q |
, D = p2 |
− 4q |
отрицательны, им у квадратных |
||||||||||
|
1 |
1 |
1 |
2 |
2 |
2 |
трехчленов соответствуют пары комплексно-сопряженных корней. Отметим, что по основной теореме алгебры у каждого многочлена, в области комплексных чисел, существует хотя бы один корень, отсюда вытекает, что у многочлена нечетной степени с действительными коэффициентами точно будет хотя бы один действительный корень, но нахождение корней для многочленов старших
13
степеней и соответствующее разложение (1.9) на множители на практике часто затруднительно. Например, чтобы разложить на множители многочлен четвер-
той степени P4 = x4 + 4 , у которого нет действительных корней, нужно догадаться добавить и отнять 4x2 , то есть дополнить до полного квадрата.
P4 = x4 + 4x2 + 4 − 4x2 = (x2 + 2)2 −(2x)2 = (x2 − 2x + 2)(x2 + 2x + 2),
проверьте, что оба дискриминанта отрицательны.
3.Пусть по формуле (1.9) знаменатель разложен на множители. Пра-
|
вильную рациональную дробь |
R(x) |
, где |
R(x) ̶остаток, полученный при деле- |
||
|
P |
(x) |
||||
|
n |
нии многочленов (или, если изначально была правильная дробь, многочлен
R(x) = Qm (x)) можно разложить на сумму простейших дробей. Кроме того,
без ограничения общности, можно считать многочлен Pn (x) приведенным, ко-
гда первый коэффициент равен единице (так как мы можем первый коэффициент an ≠ 0 перенести в числитель). Тогда разложение будет иметь вид:
|
R(x) |
= |
A1 |
+ + |
B1 |
+ |
B2 |
+ + |
Bk |
+ + |
Cx + D |
+ |
|||||||
|
P (x) |
x − x |
x − x |
(x − x |
)2 |
(x − x |
)k |
x2 + p x + q |
|||||||||||
|
n |
1 |
2 |
2 |
2 |
1 |
1 |
||||||||||||
|
+ |
С1x + D1 |
+ + |
Cs x + Ds |
. |
(1.10) |
|||||||||||||
|
x2 + p x + q |
2 |
(x2 |
+ p x + q )s |
|||||||||||||||
|
2 |
2 |
2 |
При разложении мы руководствовались следующими правилами:
•каждому корню соответствует столько слагаемых, какова его кратность;
•для действительных корней в числителях ставятся константы;
•для квадратных трехчленов с отрицательными дискриминантами в числителях ставятся линейные выражения, то есть многочлены первой степени.
Отметим, что все коэффициенты разложения: A1, ,Ds необходимо обо-
значать разными буквами, их можно просто нумеровать A1,A2, ,An , так как их количество совпадает со степенью многочлена знаменателя Pn (x) равной n .
4. Метод неопределенных коэффициентов, который заключается в следующем:
а) привести к общему знаменателю полученное разложение. Заметим, что дополнительные множители можно выписывать по разложению на множители (1.9) (только без an );
б) раскрыть скобки и привести подобные члены в правой части;
в) приравнять коэффициенты при одинаковых степенях переменной xk , k = 0,1,…,n −1, при этом получится система n уравнений с n неизвестными
A1,A2, ,An ;
14
г) решить полученную в пункте в) систему n уравнений с n неизвестными и найти её единственное решение (доказано, что основной определитель этой системы отличен от нуля);
д) подставить найденные коэффициенты A1,A2, ,An в (1.10).
5. Добавив к найденному разложению на сумму простейших дробей целую часть (если она была для первоначальной неправильной дроби), почленно проинтегрировать.
Пример 14
|
∫ |
6x3 +10x2 + 6x +15dx . |
|
x4 + 2x3 +5x2 |
Решение
1) рациональная дробь правильная, поэтому начинаем с пункта 2.
2) разложим многочлен в знаменателе на множители: x4 + 2x3 +5x2 = x2(x2 + 2x +5), так как D = 4− 20= −16< 0, то квадратный мно-
гочлен на линейные множители в области действительных чисел разложить нельзя.
3) разложимисходную правильную рациональную дробьна суммупростейших:
|
6x3 +10x2 + 6x +15 |
= |
A |
+ |
A |
+ |
A x + A |
. |
|
|
x2(x2 |
+ 2x +5) |
1 |
2 |
3 |
4 |
|||
|
x |
x2 |
x2 + 2x +5 |
||||||
4) приведем дроби, стоящие в правой части к общему знаменателю, раскроем скобки и приведем подобные члены, тогда
|
6x3 +10x2 + 6x +15= A x3 |
+ 2A x2 |
+5A x + A x2 |
+ 2A x +5A + A x3 |
+ A x2 |
, |
||||
|
1 |
1 |
1 |
2 |
2 |
2 |
3 |
4 |
||
|
6x3 +10x2 + 6x +15= (A + A )x3 |
+ (2A + A + A )x2 |
+ (5A + 2A )x +5A , |
|||||||
|
1 |
3 |
1 |
2 |
4 |
1 |
2 |
2 |
Приравняв коэффициенты при одинаковых степенях x , получим систему
|
A |
+ A |
= 6, |
A = 6− A , |
A = 6, |
|||
|
1 |
3 |
3 |
1 |
3 |
|||
|
2A1 + A2 |
+ A4 =10, |
A4 |
=10− 2A1 − A2, |
A4 |
= 7, |
||
|
+ 2A2 |
= 6, |
5A1 = 6− 2A2, |
A1 = 0, |
||||
|
5A1 |
|||||||
|
5A2 |
=15. |
A2 |
=3, |
A2 |
=3. |
||
В данном примере система, также, как и приведение её методом Гаусса к треугольному виду ( если расположить неопределенные коэффициенты в по-
15
|
рядке A3,A4,A1,A2 ), двигаясь снизу вверх найдем A2 , затем A1,A4 и A3 . Под- |
||||||
|
ставив найденные коэффициенты в разложение из п. 3), получим |
||||||
|
6x3 +10x2 + 6x +15 |
= |
3 |
+ |
6x + 7 |
. |
|
|
x2(x2 + 2x +5) |
x2 |
x2 + 2x +5 |
||||
|
∫ |
6x3 +10x2 +6x +15 |
3 |
6x +7 |
|||||||||||||||||||||||||||||||
|
5) |
2 |
2 |
dx = |
+ |
dx = |
|||||||||||||||||||||||||||||
|
x |
(x |
+ 2x +5) |
2 |
x |
2 |
+ |
2x +5 |
|||||||||||||||||||||||||||
|
∫ x |
||||||||||||||||||||||||||||||||||
|
dx 3(2x + 2)+1 |
−2 |
(x |
2 |
+ |
2x |
+ |
′ |
dx |
||||||||||||||||||||||||||
|
=3∫x2 + ∫ x2 + 2x +5 dx = 3∫x |
dx + 3∫ |
5) |
dx + ∫ |
= |
||||||||||||||||||||||||||||||
|
x2 + 2x +5 |
(x +1)2 + 4 |
|||||||||||||||||||||||||||||||||
|
= − |
3 |
+3ln(x2 + 2x +5)+ |
1arctg |
x +1 |
+C |
. (пример 9). |
||||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||
|
Решим пример 11 ∫ |
4x −9 |
|||||||||||||||||||||||||||||||||
|
dx по общей схеме. |
||||||||||||||||||||||||||||||||||
|
x2 −6x +5 |
||||||||||||||||||||||||||||||||||
|
Решение. 1) дробь правильная; |
||||||||||||||||||||||||||||||||||
|
2)x2 −6x +5= 0, по теореме Виета x =1, |
x |
= 5 и x2 −6x +5= (x −1)(x −5); |
||||||||||||||||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||||||||||
|
3) |
4x −9 |
= |
A1 |
+ |
A2 |
; |
||||||||||||||||||||||||||||
|
(x −1)(x −5) |
x −1 |
x −5 |
||||||||||||||||||||||||||||||||
4) 4x −9= A1(x −5)+ A2(x −1).
Если все корни многочлена в знаменателе действительны и различны, то можно сразу найти неопределенные коэффициенты, полагая по очереди x равным найденным в пункте 2 корням. В нашем случае
|
а) при x =1 |
4−9= A (1−5)+ A 0, |
−4A = −5, |
A = |
5 |
; |
|
|
1 |
2 |
1 |
1 |
4 |
||
|
б) при x = 5 |
20−9 = A 0+ A (5−1) |
, 4A =11, |
A =11. |
|||
|
1 |
2 |
2 |
2 |
4 |
||
Поэтому, минуя остальные подпункты 4), сразу получим
|
4x −9 |
5 |
11 |
|||
|
4 |
4 |
||||
|
= |
+ |
. |
|||
|
(x −1)(x −5) |
x −1 |
x −5 |
|||
|
16 |

|
5 |
11 |
|||||||||||||||||||||
|
5) |
4x −9 |
dx = |
4 |
+ |
4 |
dx = 5 d(x −1) |
+11 d(x −5) = |
|||||||||||||||
|
∫x |
2 |
−6x +9 |
∫ |
x −5 |
4∫ x −1 |
4 ∫ x −5 |
||||||||||||||||
|
x −1 |
||||||||||||||||||||||
|
5ln |
x −1 |
+ 11ln |
x −5 |
+С . |
||||||||||||||||||
|
4 |
4 |
|||||||||||||||||||||
Замечание 1. Сравним данный ответ с ответом на с. 10, полученного с помощью выделения в числителе производной от знаменателя, но упростив тот первоначальный ответ с помощью свойств логарифма, можно свести его к новому ответу. Такая ситуация при взятии интеграла разными методами типична: ответы получаются часто совершенно на первый взгляд разные, но отличаются друг от друга на константу (см. лемму о первообразных).
Замечание 2. Отметим, что чем больше степень многочлена в знаменателе, тем выгоднее применение предложенного метода нахождения неопределенных коэффициентов (в случае разложения этого многочлена только на различные линейные множители). В качестве упражнения, возьмите с помощью этого ме-
тода ∫ 2x3 −3x2 +7x +5 dx (полагая по очереди x = 0, x =1, x = −1, x = 2). x(x −1)(x +1)(x − 2)
Приведем еще один метод интегрирования выражений, содержащих ко-
|
рень из квадратного трехчлена, а именно, |
метод неопределенных коэффициен- |
|||||||||||
|
тов |
для |
нахождения |
интегралов |
вида |
∫ |
Pn (x) |
dx |
или |
||||
|
ax |
2 |
|||||||||||
|
+bx + c |
||||||||||||
|
∫Pn (x) |
ax2 +bx + cdx , где Pn (x) |
многочлен степени n. |
Отметим, что второй |
интеграл сводится к первому умножением и делением на 
|
Pn (x) |
dx |
||||||||||||||
|
dx = Qn−1 |
(x) |
ax |
2 |
+bx + c + L |
, |
||||||||||
|
∫ |
∫ |
||||||||||||||
|
ax2 |
+bx + c |
ax2 |
+bx + c |
||||||||||||
где Qn−1(x) ̶некоторый многочлен, степени на единицу меньшей степени многочлена Pn (x), L ̶некоторая константа.
Продифференцировав обе части записанного равенства, получим
17

|
Pn (x) |
ax + |
b |
L |
||||||||||||
|
2 |
|||||||||||||||
|
= Qn′−1(x) |
ax2 +bx + c |
+Qn−1(x) |
+ |
, |
|||||||||||
|
ax2 +bx + c |
ax2 +bx |
ax2 +bx + c |
|||||||||||||
|
+ c |
откуда при умножении правой и левой частей на 
Pn (x)=Qn′−1(x)(ax2 +bx + c)+ Qn−1(x) ax + b2 + L,
которое должно выполняться тождественно. Это условие даёт возможность определения коэффициентов многочлена Qn−1(x) и константы L обычным ме-
тодом неопределенных коэффициентов. Отметим также, что система уравнений для определения этих коэффициентов будет иметь треугольный вид.
Пример 15
|
2 |
2 |
4 |
3 |
2 |
||||||||||||||
|
∫x2 |
dx = ∫ |
x |
(x |
+ 2x + 2) |
dx = ∫ |
x |
+ 2x |
+ 2x |
dx. |
|||||||||
|
x2 + 2x + 2 |
||||||||||||||||||
|
2 |
||||||||||||||||||
|
2 |
||||||||||||||||||
|
x |
+ 2x + 2 |
x |
+ 2x + 2 |
В соответствии с рассмотренным методом запишем равенство
|
∫ |
x4 |
+ 2x3 + 2x |
2 |
+L∫ |
dx |
|||||||
|
dx = (Ax3 + Bx2 |
+Cx + D) x2 + 2x + 2 |
. |
||||||||||
|
2 |
x |
2 |
||||||||||
|
x + 2x + 2 |
+ 2x + 2 |
Продифференцируем это равенство:
|
x4 + 2x3 + 2x2 |
|||||||||||||
|
= (3Ax2 |
+ 2Bx +C) x2 |
+ 2x + 2 + (Ax3 + Bx2 + Cx + D) |
|||||||||||
|
x2 + 2x + 2 |
|||||||||||||
|
x +1 |
+ |
L |
|||||||||||
|
x2 + 2x + 2 |
x2 + 2x + 2 |
и, умножив обе его части на 
x4 + 2x3 + 2x2 = (3Ax2 + 2Bx +C )(x2 + 2x + 2) +(Ax3 + Bx2 +Cx + D)(x +1)+ L.
18
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Универсального способа решения иррациональных уравнений нет, так как их класс отличается количеством. В статье будут выделены характерные виды уравнений с подстановкой при помощи метода интегрирования.
Для использования метода непосредственного интегрирования необходимо вычислять неопределенные интегралы типа ∫kx+bp dx, где p является рациональной дробью, k и b являются действительными коэффициентами.
Найти и вычислить первообразные функции y=13x-13.
Решение
По правилу интегрирования необходимо применить формулу ∫f(k·x+b)dx=1k·F(k·x+b)+C, а таблица первообразных говорит о том, что имеется готовое решение данной функции. Получаем, что
∫dx3x-13=∫(3x-1)-13dx=13·1-13+1·(3x-1)-13+1+C==12(3x-1)23+C
Ответ: ∫dx3x-13=12(3x-1)23+C.
Имеют место быть случаи, когда можно использовать метод подведения под знак дифференциала. Это решается по принципу нахождения неопределенных интегралов вида ∫f'(x)·(f(x))pdx, когда значение p считается рациональной дробью.
Найти неопределенный интеграл ∫3×2+5×3+5x-776dx.
Решение
Отметим, что dx3+5x-7=x3+5x-7’dx=(3×2+5)dx. Тогда необходимо произвести подведение под знак дифференциала с использованием таблиц первообразных. Получаем, что
∫3×2+5×3+5x-776dx=∫(x3+5x-7)-76·(3×2+5)dx==∫(x3+5x-7)-76d(x3+5x-7)=x3+5x-7=z==∫z-76dz=1-76+1z-76+1+C=-6z-16+C=z=x3+5x-7=-6(x3+5x-7)6+C
Ответ: ∫3×2+5×3+5x-776dx=-6(x3+5x-7)6+C.
Решение неопределенных интегралов предусматривает формулу вида ∫dxx2+px+q, где p и q являются действительными коэффициентами. Тогда необходимо выделить полный квадрат из-под корня. Получаем, что
x2+px+q=x2+px+p22-p22+q=x+p22+4q-p24
Применив формулу, расположенную в таблице неопределенных интегралов, получаем:
∫dxx2±α=lnx+x2±α+C
Тогда вычисление интеграла производится:
∫dxx2+px+q=∫dxx+p22+4q-p24==lnx+p2+x+p22+4q-p24+C==lnx+p2+x2+px+q+C
Найти неопределенный интеграл вида ∫dx2x2+3x-1.
Решение
Для вычисления необходимо вынести число 2 и расположить его перед радикалом:
∫dx2x2+3x-1=∫dx2x2+32x-12=12∫dxx2+32x-12
Произвести выделение полного квадрата в подкоренном выражении. Получим, что
x2+32x-12=x2+32x+342-342-12=x+342-1716
Тогда получаем неопределенный интеграл вида 12∫dxx2+32x-12=12∫dxx+342-1716==12lnx+34+x2+32x-12+C
Ответ: dxx2+3x-1=12lnx+34+x2+32x-12+C
Интегрирование иррациональных функций производится аналогичным способом. Применимо для функций вида y=1-x2+px+q.
Найти неопределенный интеграл ∫dx-x2+4x+5.
Решение
Для начала необходимо вывести квадрат знаменателя выражения из-под корня.
∫dx-x2+4x+5=∫dx-x2-4x-5==∫dx-x2-4x+4-4-5=∫dx-x-22-9=∫dx-(x-2)2+9
Табличный интеграл имеет вид ∫dxa2-x2=arcsinxa+C, тогда получаем, что ∫dx-x2+4x+5=∫dx-(x-2)2+9=arcsinx-23+C
Ответ: ∫dx-x2+4x+5=arcsinx-23+C.
Процесс нахождения первообразных иррациональных функций вида y=Mx+Nx2+px+q, где имеющиеся M, N, p, q являются действительными коэффициентами, причем имеют схожесть с интегрированием простейших дробей третьего типа. Это преобразование имеет несколько этапов:
подведение дифференциала под корень, выделение полного квадрата выражения под корнем, применение табличных формул.
Найти первообразные функции y=x+2×2-3x+1.
Решение
Из условия имеем, что d(x2-3x+1)=(2x-3)dx и x+2=12(2x-3)+72, тогда (x+2)dx=12(2x-3)+72dx=12d(x2-3x+1)+72dx.
Рассчитаем интеграл: ∫x+2×2-3x+1dx=12∫d(x2-3x+1)x2-3x+1+72∫dxx2-3x+1==12∫(x2-3x+1)-12d(x2-3x+1)+72∫dxx-322-54==12·1-12+1·x2-3x+1-12+1+72lnx-32+x-32-54+C==x2-3x+1+72lnx-32+x2-3x+1+C
Ответ: ∫x+2×2-3x+1dx=x2-3x+1+72lnx-32+x2-3x+1+C.
Поиск неопределенных интегралов функции ∫xm(a+bxn)pdx осуществляется при помощи метода подстановки.
Для решения необходимо ввести новые переменные:
- Когда число p является целым, тогда считают, что x=zN, а N является общим знаменателем для m, n.
- Когда m+1n является целым числом, тогда a+bxn=zN, а N является знаменателем числа p.
- Когда m+1n+p является целым числом, то необходим ввод переменной ax-n+b=zN, а N является знаменателем числа p.
Найти определенный интеграл ∫1x2x-9dx.
Решение
Получаем, что ∫1x2x-9dx=∫x-1·(-9+2×1)-12dx. Отсюда следует, что m=-1, n=1,p=-12, тогда m+1n=-1+11=0 является целым числом. Можно ввести новую переменную вида -9+2x=z2. Необходимо выразить x через z. На выходы получим, что
-9+2x=z2⇒x=z2+92⇒dx=z2+92’dz=zdz-9+2x=z
Необходимо произвести подстановку в заданный интеграл. Имеем, что
∫dxx2x-9=∫zdzz2+92·z=2∫dzz2+9==23arctgz3+C=23arcctg2x-93+C
Ответ: ∫dxx2x-9=23arcctg2x-93+C.
Для упрощения решения иррациональных уравнений применяются основные методы интегрирования.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Преподаватель который помогает студентам и школьникам в учёбе.
Интегрирование иррациональных функций с примерами решения
Содержание:
Интегрирование иррациональных функций.
Определение 1. Функция вида
Пример 1.
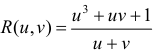
п.1. Интегралы вида:
Пусть s – общий знаменатель дробей 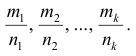
делает подинтегральную функцию рациональной.
Пример 2.
Пример 3
п.2. Интегралы вида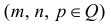
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а) p∈Z – интегралы рассмотрены в п.1.
б) 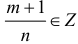
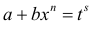
в) 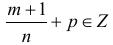
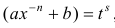
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).
Пример 4.
Пример 5.
п.3. Интегралы вида 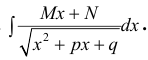
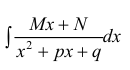
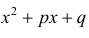
Пример 6.
п 4. Интегралы вида 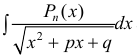
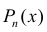
Для вычисления интегралов используют равенство:
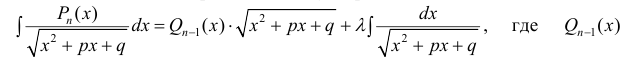
- Заказать решение задач по высшей математике
Пример 7.
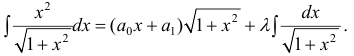
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях.
Решив систему (3), получим :
(сравни с примером 5).
п.5. Интегралы вида
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
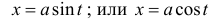
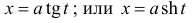
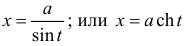
Пример 8.
Пример 9.
Интегрирование некоторых иррациональных функций
1. Интегралы вида 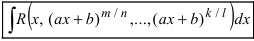
Интегралы такого типа вычисляются по следующей схеме:
- -у дробей
находят наименьший общий знаменатель, который обозначим через р;
- – проводят замену
.
В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.
Пример:
Вычислить
Решение:
В данном примере 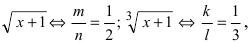
2. Интегралы вида 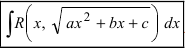
Такие интегралы путем замены 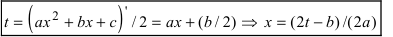
1. 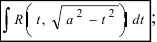
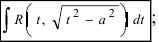
Для вычисления этих интегралов применяют следующие тригонометрические замены
1. 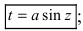
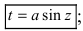
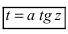
Пример:
Вычислить
Решение:
Данный интеграл соответствует интегралам типа 1., поэтому
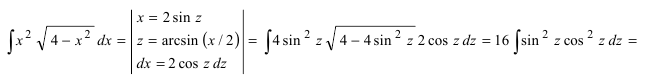
Пример:
Вычислить
Решение:
Воспользуемся указанной выше заменой
(интеграл вычислен в п. 2а)
Пример:
Вычислить
Решение:
Пример:
Вычислить
Решение:
Воспользуемся указанной выше заменой
Понятие о неберущихся интегралах
Определение: Интегралы, первообразные которых не выражаются через элементарные функции, называются неберущимися:
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
Интегрирование иррациональных функций: способы и примеры решений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Рассмотрим интегралы от иррациональных функций, то есть функций, содержащих переменную (обычно икс) под корнем или, что то же самое — в дробной степени. Интегралы от таких функций с помощью подстановок приводятся к интегралам от рациональных функций и могут быть проинтегрированы окончательно.
В подынтегральном выражении — различные дробно-рациональные функции
Разберём интегралы, где в подынтегральном выражении переменная присутствует под корнем. В формально обобщённом виде речь идёт об интегралах вида

В примерах мы увидим, что переменная икс, присутствующая под корнем, присутствует там без степени. В примере 3 икс присутствует также в квадрате, но при этом — не по корнем. То есть корни отдельно, степени — отдельно.
В этом случае важное значение имеет наименьшее общее кратное чисел λ , . μ (или общий знаменатель, если эти числа дробные). Обозначим это наименьшее общее кратное (общий знаменатель) через n . Рассматриваемые интегралы от иррациональных функций можно найти, используя следующую подстановку:
Тогда каждая дробная степень «икса» выразится через целую степень «тэ» и подынтегральная функция преобразуется в рациональную функцию от «тэ».
Пример 1. Найти интеграл от иррациональной функции 
Решение. Преобразуем все корни икса в степени. Выписываем степени при иксе в подынтегральном выражении — все, которые там находим:

Находим наименьшее общее кратное знаменателей этих чисел: 4.
Поэтому используем следующую подстановку:
Подставляем и преобразуем:
Возвращаясь к переменной икс, окончательно находим:

Пример 2. Найти интеграл от иррациональной функции 
Решение. Используем следующую подстановку:
Подставляем и преобразуем:
Интегрируем и получаем:
Возвращаясь к переменной икс, окончательно находим:

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 3. Найти интеграл от иррациональной функции 
Пример 4. Найти интеграл от иррациональной функции

Корень из квадратного трёхчлена и подстановки Эйлера
Если дан интеграл иррациональной функции вида

то есть в подынтегральном выражении — корень из квадратного трёхлчена, то можно воспользоваться подстановками Эйлера.

В зависимости от характера корней квадратного уравнения используются следующие подстановки Эйлера.
1. Если x 1 , x 2 — действительные числа (не комплексные), то используется подстановка
(первая подстановка Эйлера).
2. Если x 1 , x 2 — комплексные числа и a > 0 , то используется подстановка
(вторая подстановка Эйлера).
3. Если x 1 , x 2 — комплексные числа и c > 0 , то используется подстановка
(третья подстановка Эйлера).
Пример 5. Найти интеграл от иррациональной функции 
Решение. Разложим квадратный трёхчлен на множители:
Используем первую подстановку Эйлера:
Интегрируем и получаем:
Возвращаясь к переменной икс, сначала долго занимаемся преобразованием выражений, а затем окончательно находим:
Пример 6. Найти интеграл от иррациональной функции 
Используем вторую подстановку Эйлера:
Интегрируем и получаем:

Возвращаясь к переменной икс, окончательно находим:

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 7. Найти интеграл от иррациональной функции 
(использовать третью подстановку Эйлера).
Интегралы от дифференциального бинома и подстановки Чебышева

где m, n, p — рациональные числа (целые или дробные), называются интегралами от дифференциального бинома. В примерах мы увидим, что в подынтегральных выражениях переменная икс присутствует не только под корнем: она под корнем, но ещё и в степени. В этом главное отличие рассматриваемых интегралов от тех, которые были рассмотрены в первом параграфе.
Чтобы найти такие интегралы, используются подстановки Чебышева.
1. Если p — целое число, то используется подстановка

где k — наименьшее общее кратное знаменателей m и n.
2. Если 

где s — знаменатель дроби p .
3. Если 

где s — знаменатель дроби p .
Русский математик П.Л. Чебышев доказал, что только в перечисленных трёх случаях интеграл от дифференциальных биномов с рациональными показателями степени выражается через элементарные функции.
Пример 8. Найти интеграл от иррациональной функции 
Преобразуем корни в степени и избавимся от дроби:
Здесь p = -1 (целое число). Чтобы избавиться от степени икса в скобках, сделаем промежуточную подстановку


Теперь сделаем следующую подстановку:
Подставляем и получаем:
Возвращаемся к переменной z :

Возвращаясь к переменной икс, окончательно находим:

Пример 9. Найти интеграл от иррациональной функции 
Преобразуем корни в степени и избавимся от дроби:

Здесь m = 3 , n = 2 , 

Cделаем промежуточную подстановку


Теперь, чтобы избавиться от дробной степени выражения в скобках, сделаем следующую подстановку:

Интегрируем и получаем:

Возвращаемся к переменной z :

Возвращаясь к переменной икс, окончательно находим:

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 10. Найти интеграл от иррациональной функции 

Частный случай квадратичных иррациональностей
Рассмотрим интеграл от иррациональной функции вида

где в знаменателе — квадратный корень из квадратного трёхчлена.
Чтобы проинтегрировать любой интеграл такого вида, необходимо уметь находить интегралы 

Формула для нахождения первого из них:

Второй интеграл находится по формуле

Формулы (2 и (3) можно условно считать табличными интегралами. Если в подкоренном выражении интеграла (1) выделить полный квадрат, то при a > 0 это выражение примет вид
После подстановки t = x – m в первом случае интеграл (1) приводится к интегралу (3), во втором – к интегралу (2).
Пример 11. Найти интеграл от иррациональной функции
Решение. Выделим в подкоренном выражении полный квадрат:
Произведя теперь подстановку
причём при интегрировании воспользовались формулой (3). Возвращаясь к старой переменной, окончательно получим
Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 12. Найти интеграл от иррациональной функции
Методы интегрирования иррациональных функций (корней)
Иррациональная функция от переменной – это функция, которая образована из переменной и произвольных постоянных с помощью конечного числа операций сложения, вычитания, умножения (возведения в целочисленную степень), деления и извлечения корней. Иррациональная функция отличается от рациональной тем, что иррациональная функция содержит операции извлечения корней.
Существует три основных типа иррациональных функций, неопределенные интегралы от которых приводятся к интегралам от рациональных функций. Это интегралы, содержащие корни произвольных целочисленных степеней из дробно-линейной функции (корни могут быть различных степеней, но от одной и той же, дробно-линейной функции); интегралы от дифференциального бинома и интегралы с квадратным корнем из квадратного трехчлена.
Важное замечание. Корни многозначны!
При вычислении интегралов, содержащих корни, часто встречаются выражения вида , где – некоторая функция от переменной интегрирования . При этом следует иметь в виду, что . То есть, при t > 0 , |t| = t . При t 0 , |t| = – t . Поэтому, при вычислении подобных интегралов, нужно отдельно рассматривать случаи t > 0 и t 0 . Это можно сделать, если писать знаки или там, где это необходимо. Подразумевая, что верхний знак относится к случаю t > 0 , а нижний – к случаю t 0 . При дальнейшем преобразовании, эти знаки, как правило, взаимно сокращаются.
Возможен и второй подход, при котором подынтегральную функцию и результат интегрирования можно рассматривать как комплексные функции от комплексных переменных. Тогда можно не следить за знаками в подкоренных выражениях. Этот подход применим, если подынтегральная функция является аналитической, то есть дифференцируемой функцией от комплексной переменной. В этом случае и подынтегральная функция и интеграл от нее являются многозначными функциями. Поэтому после интегрирования, при подстановке численных значений, нужно выделить однозначную ветвь (риманову поверхность) подынтегральной функции, и для нее выбрать соответствующую ветвь результата интегрирования.
Далее, по возможности, мы будем применять первый подход, и следить за знаком подкоренных выражений.
Дробно-линейная иррациональность
Это интегралы с корнями от одной и той же дробно-линейной функции:
,
где R – рациональная функция, – рациональные числа, m1, n1, . ms, ns – целые числа, α, β, γ, δ – действительные числа.
Такие интегралы сводится к интегралу от рациональной функции подстановкой:
, где n – общий знаменатель чисел r1, . rs .
Корни могут быть не обязательно от дробно-линейной функции, но и от линейной ( γ = 0 , δ = 1 ), или от переменной интегрирования x ( α = 1 , β = 0 , γ = 0 , δ = 1 ).
Вот примеры таких интегралов:
, .
Интегралы от дифференциальных биномов
Интегралы от дифференциальных биномов имеют вид:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Такие интегралы сводятся к интегралам от рациональных функций в трех случаях.
1) Если p – целое. Подстановка x = t N , где N – общий знаменатель дробей m и n .
2) Если – целое. Подстановка a x n + b = t M , где M – знаменатель числа p .
3) Если – целое. Подстановка a + b x – n = t M , где M – знаменатель числа p .
В остальных случаях, такие интегралы не выражаются через элементарные функции.
Иногда такие интегралы можно упростить с помощью формул приведения:
;
.
Интегралы, содержащие квадратный корень из квадратного трехчлена
Такие интегралы имеют вид:
,
где R – рациональная функция. Для каждого такого интеграла имеется несколько методов решения.
1) С помощью преобразований привести к более простым интегралам.
2) Применить тригонометрические или гиперболические подстановки.
3) Применить подстановки Эйлера.
Рассмотрим эти методы более подробно.
1) Преобразование подынтегральной функции
Применяя формулу , и выполняя алгебраические преобразования, приводим подынтегральную функцию к виду:
,
где φ(x), ω(x) – рациональные функции.
Подробнее >>>
Далее выделяя целую часть у ω(x) и раскладывая остаток на простейшие дроби, получаем интегралы трех типов.
I тип
Интеграл вида:
,
где Pn(x) – многочлен степени n .
Такие интегралы находятся методом неопределенных коэффициентов, используя тождество:
.
Дифференцируя это уравнение и приравнивая левую и правую части, находим коэффициенты Ai .
Подробнее >>>
II тип
Интеграл вида:
,
где Pm(x) – многочлен степени m .
Подстановкой t = ( x – α ) –1 этот интеграл приводится к предыдущему типу. Если m ≥ n , то у дроби следует выделить целую часть.
Подробнее >>>
III тип
Здесь мы делаем подстановку:
.
После чего интеграл примет вид:
.
Далее, постоянные α, β нужно выбрать такими, чтобы в знаменателе коэффициенты при t обратились в нуль:
B = 0, B1 = 0 .
Тогда интеграл распадается на сумму интегралов двух видов:
,
,
которые интегрируются подстановками:
u 2 = A1t 2 + C1 ,
v 2 = A1 + C1 t –2 .
Подробнее >>>
2) Тригонометрические и гиперболические подстановки
В некоторых случаях, применение тригонометрических и гиперболических подстановок приводит к более коротким вычислениям. Для их применения, с помощью линейной подстановки, квадратный трехчлен под знаком интеграла нужно привести к сумме или разности квадратов. Затем нужно применить одну из тригонометрических или гиперболических подстановок. Основные подстановки перечислены ниже. Более подробно они рассматриваются на странице:
Тригонометрические и гиперболические подстановки >>>
Для интегралов вида , a > 0 ,
имеем три основные подстановки:
;
;
;
Для интегралов , a > 0 ,
имеем следующие подстановки:
;
;
;
И, наконец, для интегралов , a > 0 ,
подстановки следующие:
;
;
;
3) Подстановки Эйлера
Также интегралы могут быть сведены к интегралам от рациональных функций одной из трех подстановок Эйлера:
, при a > 0 ;
, при c > 0 ;
, где x1 – корень уравнения a x 2 + b x + c = 0 . Если это уравнение имеет действительные корни.
Эллиптические интегралы
В заключении рассмотрим интегралы вида:
,
где R – рациональная функция, . Такие интегралы называются эллиптическими. В общем виде они не выражаются через элементарные функции. Однако встречаются случаи, когда между коэффициентами A, B, C, D, E существуют соотношения, при которых такие интегралы выражаются через элементарные функции.
Ниже приводится пример, связанный с возвратными многочленами. Вычисление подобных интегралов выполняется с помощью подстановок:
.
Пример
.
Здесь при x > 0 ( u > 0 ) берем верхний знак ′ + ′. При x 0 ( u 0 ) – нижний ′ – ′.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 02-04-2015 Изменено: 30-01-2018
Интегрирование иррациональных функций с примерами решения
Содержание:
Интегрирование иррациональных функций.
Определение 1. Функция вида
Пример 1. 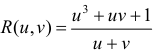
п.1. Интегралы вида:
Пусть s – общий знаменатель дробей 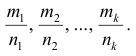
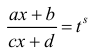
делает подинтегральную функцию рациональной.
Пример 2. 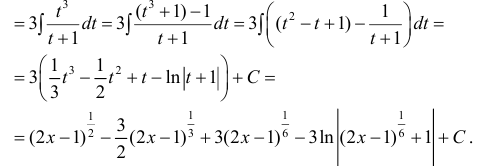
Пример 3
п.2. Интегралы вида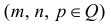
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а) p∈Z — интегралы рассмотрены в п.1.
б) 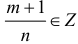
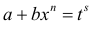
в) 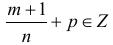
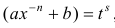
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).
Пример 4. 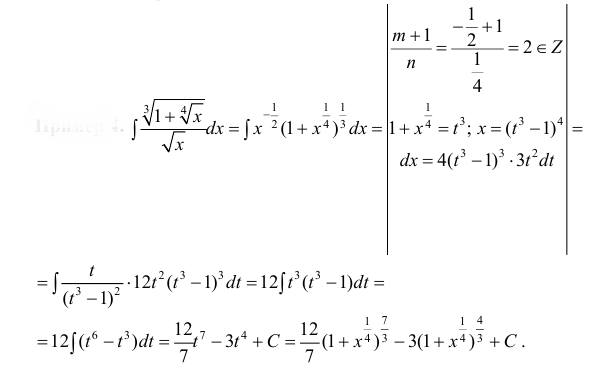
Пример 5. 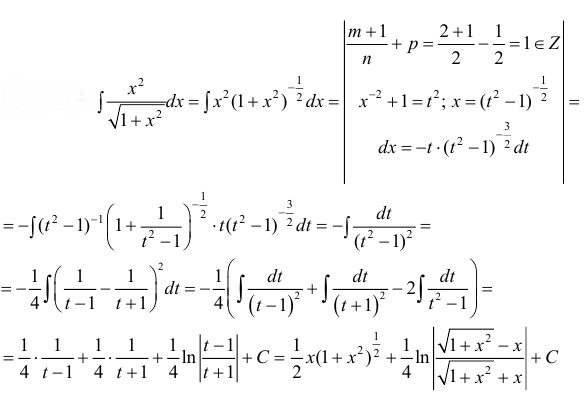
п.3. Интегралы вида 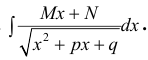
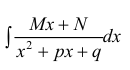
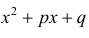
Пример 6.
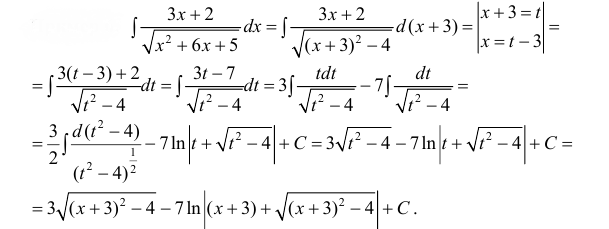
п 4. Интегралы вида 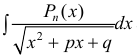
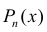
Для вычисления интегралов используют равенство:
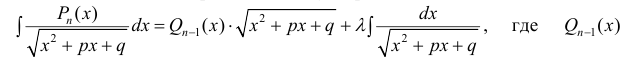
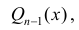
Пример 7. 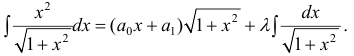
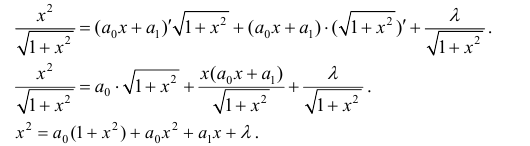
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях. 
Решив систему (3), получим :
(сравни с примером 5).
п.5. Интегралы вида 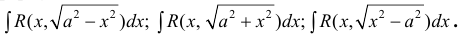
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
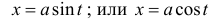
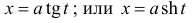
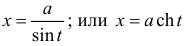
Пример 8.
Пример 9.
Интегрирование некоторых иррациональных функций
1. Интегралы вида 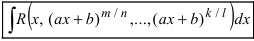
Интегралы такого типа вычисляются по следующей схеме:
- -у дробей
находят наименьший общий знаменатель, который обозначим через р;
- — проводят замену
.
В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.
Пример:
Вычислить
Решение:
В данном примере 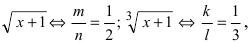
2. Интегралы вида 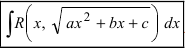
Такие интегралы путем замены 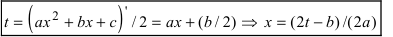
1. 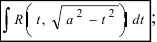
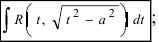
Для вычисления этих интегралов применяют следующие тригонометрические замены
1. 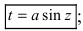
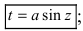
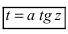
Пример:
Вычислить
Решение:
Данный интеграл соответствует интегралам типа 1., поэтому
Пример:
Вычислить
Решение:
Воспользуемся указанной выше заменой
(интеграл вычислен в п. 2а)
Пример:
Вычислить
Решение:
Пример:
Вычислить
Решение:
Воспользуемся указанной выше заменой
Понятие о неберущихся интегралах
Определение: Интегралы, первообразные которых не выражаются через элементарные функции, называются неберущимися:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:
http://1cov-edu.ru/mat_analiz/integrali/neopredelennie/irratsionalnye/
http://www.evkova.org/integrirovanie-irratsionalnyih-funktsij




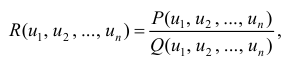
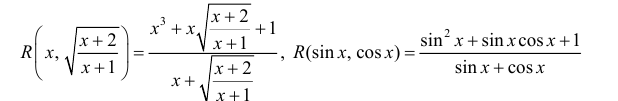

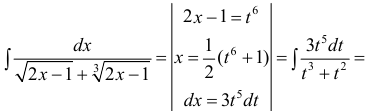
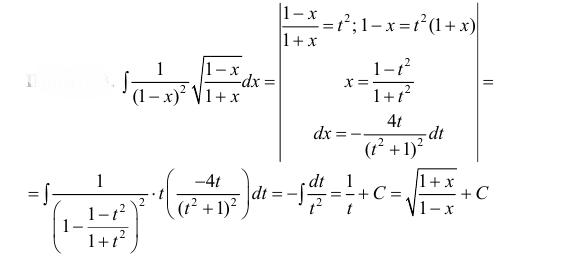
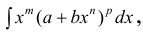
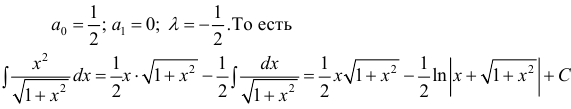
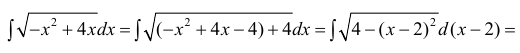
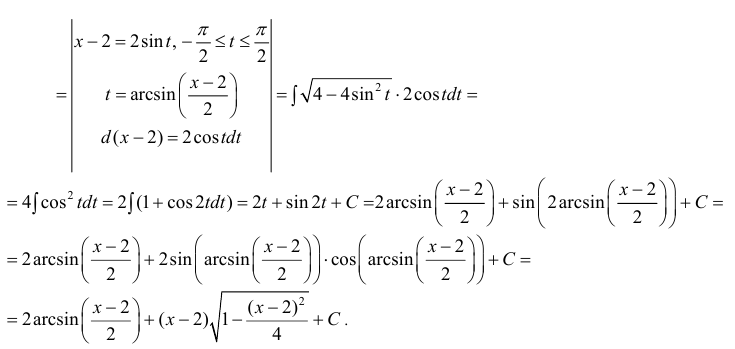

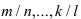 находят наименьший общий знаменатель, который обозначим через р;
находят наименьший общий знаменатель, который обозначим через р;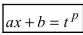 .
.