Как найти первообразную умножения - Сайт, где вы сможете решить свои вопросы

Общая информация

В математике существуют функции, которые не поддаются интегрированию простыми методами. Некоторые алгоритмы также неприменимы в этом случае. Специалисты рекомендуют освоить нахождение первообразной на простых примерах. Этот принцип называется переходом от простого к сложному. Невозможно, не зная основ, переходить к решению сложных задач.

На начальных этапах обучения следует руководствоваться некоторыми правилами и алгоритмами. Их нужно освоить, и безошибочно решать простые задачи. Кроме того, следует разобраться в основном предназначении интеграла, и понять его геометрический смысл. Очень часто новички пытаются найти первообразную сложной функции. Некоторые пользуются информацией из интернета, которая бывает недостоверной. Но у них ничего не получается. Объяснение такому поражению — неверное обучение и отсутствие опыта.

Использование интеграла

Во многих дисциплинах применяется интеграл. Он обозначается литерой или символом «∫”, и считается единицей дифференциального исчисления. Выражение (функция), которое идет после этого знака, называется подынтегральным. Его ограничением является знак дифференциала, т. е. «dx» или «dy». Под дифференциалом стоит переменная, по которой происходит поиск первообразной. Интегралом функции вида z = y (x) называется функция вида Y (x) с учетом константы «С» (Y (x) + C). Необходимо отметить, что Y (x) + C является первообразной функции y (x), которая была получена при дифференцировании.

Интегрирование очень часто применяется для нахождения площадей разнообразных фигур, когда невозможно воспользоваться какой-либо формулой. Например, площадь криволинейной трапеции следует искать толь при помощи операции интегрирования. Кроме того, при помощи данного метода выполняется нахождение объемов тел, пройденного пути при равноускоренном движении и т. д.

Следует отметить, что интегралы бывают двух типов: неопределенные и определенные. Вторые отличаются от первых конечным результатом, который является не первообразной, а некоторым численным значением. Если интеграл определенный, то необходимо воспользоваться формулой Ньютона — Лейбница, подставив в нее некоторые значения или границы. Она имеет такой вид с ограничениями a и b: F (y) = F (b) — F (a). Значение определенного интеграла соответствует разности первообразных, в которые подставляются верхняя и нижняя границы.

Интегралы бывают также собственными и несобственными. К первому типу относятся определенные интегралы, ограничениями которого являются область интегрирования и его подынтегральное выражение. Несобственный — интеграл определенного типа, который ограничен подынтегральным выражением или областью его интегрирования.

Геометрический смысл интеграла — площадь трапеции криволинейного типа. Стороной или сторонами фигуры являются кривые прямые. В этом случае найти площадь не удастся, поскольку формулы для этого не предусмотрены. Криволинейной называется плоская фигура, которая ограничена системой координат, неотрицательной функцией, а также прямыми. Значения ограничений нужно подставлять в формулу Ньютона — Лейбница. Фигура состоит из множества частей прямоугольной формы. При интегрировании их площади складываются, образуя общую площадь S.

Методика нахождения первообразной

Определение первообразной зависит от самой функции. Если она является элементарной, то для этого используется только простейший алгоритм, состоящий из двух шагов. Первым этапом является упрощение выражения, а вторым — определение исходной функции по таблице интегралов.

Некоторые выражения имеют свойство инвариантности, т. е. остаются неизменными при дифференцировании и интегрировании (экспонента в степени, которой является аргумент — e^x). В случае, когда подынтегральное выражение является сложным, то нужно применять специальный метод интегрирования по частям. Методика позволяет находить решения с высокой долей вероятности. Однако бывают функции очень сложные. При этом нужно применять метод замены, а затем правило интегрирования по частям.

Теорема имеет такую формулировку: первообразная сложной функции F (z, y) соответствует произведению ее составных элементов без интеграла, последнего элемента по первому. Следствие из нее — формула, позволяющая искать производную сложной функции. Пусть даны две непрерывные функции z = z (x) и y = y (x), имеющие производные. Соотношение необходимо рассматривать следующим образом: d (zy) = zdy + ydz. Нужно найти первообразные двух частей: ∫d (zy) = ∫(zdy + ydz). Произведение двух функций равно zy = ∫zdy + ∫ydz. Окончательная формула интегрирования по частям имеет такой вид: ∫zdy = zy — ∫ydz.

Формула применяется, когда невозможно найти первообразную какой-либо функции. Примером для интегрирования по частям является y = x * e^(2x). Однако не во всех случаях можно разобраться, когда стоит применять формулу. Ведь при неверном пути решения задания можно потерять много времени. Специалисты классифицировали функции, которые необходимо интегрировать по частям:

Любой логарифм, умноженный на переменную или многочлен с неизвестным [z = (x² — 2x) * ln (x — 2)].
Произведение переменной (многочлена с неизвестным) на функцию, имеющую экспоненциальный или показательный вид [f = (y — 2)^(3) — e^y].
Частное (деление) или произведение аргумента на тригонометрическое выражение [y = x * cos (2x²)].
Дробь, в которой числитель и знаменатель состоит из переменных [v = (x² — 3x + 7) / x⁴ — 5x³ + 12x + 7)].

Необходимо также отметить, что в первом и во втором видах сложных функций, необязательно должно быть произведение. Оно может рассматриваться в виде дроби, умноженной на выражение.

Например, уравнение с натуральным логарифмом y = ln (x) / (x² — 4) можно записать в виде произведения (1 / (x² — 4)) * ln (x). Для нахождения первообразной умножения длинного натурального логарифма на переменную также нужно применять этот метод.

В некоторых случаях необходимо осуществлять замену выражения, которое находится под знаком интеграла, а затем, в зависимости от самой замены, находить значение по таблице первообразных или использоваться способ интегрирования по частям. Очень важно правильно определить алгоритм решения, поскольку он избавит от циклического разложения на множители и прочих операций.

Примеры решения

Необходимо вычислить интеграл функции v = x * ln (x). Если границы не обозначены, то интеграл является неопределенным. Для этого следует воспользоваться универсальным алгоритмом нахождения первообразной по частям:

Преобразования не нужно выполнять. Подынтегральное выражение состоит из произведения функций, которые являются табличными.
Обозначения: z = ln (x), y = x, dz = [ln (x)]’ = (1/x)dx, dy = [x]’ = dx.
Подставить в формулу: ∫zdy = zy — ∫ydz = ln (x) * x — ∫(x * (1/x))dx = ln (x) * x — ∫dx = ln (x) * x — x + С= x (ln (x) — 1) + С.
Если воспользоваться онлайн-калькулятором интегралов, то видно, что решения совпадают. Следовательно, задача решена правильно.

Нужно проинтегрировать функцию u = (x — 9) * e^(3x). Следует обратить внимание на выражение e^(3x), поскольку оно является сложным. Для решения рекомендуется применить также универсальный алгоритм:

Необходимость в упрощении выражения отсутствует.
Ввести обозначения: z = x — 9, dy = e^(3x), dz = dx и y = ∫(e^(3x))dx = (1/3) * e^(3x).
Интегрирование: ∫zdy = zy — ∫ydz = (1/3) * (x — 9) * e^(3x) — (1/3) * ∫(e^(3x))dx =(1/3) * (x — 9) * e^(3x) — (1/3) * (1/3) * e^(3x) + С = [(e^(3x) * (3x — 28)) / 9] + С.

Если проверить результат с помощью INTEGRAL CALCULATOR, то решения совпадут. Очень важно анализировать функции, и следить за знаками. Например, необходимо также учитывать, что e^(-x) является также сложной. Ее первообразная соответствует -e^(-x).

Таким образом, интегрирование по частям следует применять в том случае, когда обыкновенные методы поиска первообразной не дают результата. Метод используется для понижения сложности подынтегрального выражения. Его можно применять неограниченное количество раз для одной функции.

Источник

Время на прочтение
10 мин

Количество просмотров 49K

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

К сожалению, так сложилось, что многим (и мне) она, порой кажется, слишком сложной, недоступной, наукой для избранных. Между тем, так только кажется ! Безусловно, она требует интеллектуального напряжения, памяти, воображения и много чего ещё, как и многие другие интеллектуальные занятия.

Отличительными особенностями её являются:

использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),
логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),
последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),
высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин
Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы
Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т.д.)
Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук
Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными
Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее
Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т.д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Во введении к книге «Развитие понятия интеграла» известный историк математики профессор Фёдор Андреевич Медведев так охарактеризовал сущность интегрирования и процесс его развития в науке «… Интегрирование представляет собой абстрактное выражение разнообразнейших способов измерения величин, и по мере вовлечения в человеческое познание всё новых и новых объектов реальной действительности математики создают всё более и более общие схемы интеграционных процессов с тем, чтобы охватить всё расширяющийся круг объектов, подлежащих измерению» [1].

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

2. Геометрический и аналитико-алгебраический смысл интегрирования

Естественным образом, возникает два вида задач, которые отражают два смысла интегрирования: — геометрический и аналитико-алгебраический. Первый – отыскание площади плоской фигуры под произвольной кривой (квадратура) и отыскание объёма (кубатура). Второй – подсчёт суммарного значения некой переменной величины [2], которая изменяется, принимает различные значения сообразно единицам времени, длины и т.д.

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].
В случае с вещественными числами.
- Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.
- Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.
- В случае с отрицательными числами (-2,3 × 4,3), умножение — сумма произведений и разворот числовой оси или иными словами отражение суммарного значения произведения — в данном случае числа 9,89 относительно начала отсчёта, то есть числа ноль, в результате получаем -9,89.
В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».
Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где a=x_0 а b=x_n .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

$lim_{n rightarrow +infty} S(x) = S_1(Delta x_1) + S_2(Delta x_2) + … + S_n(Delta x_n) quad (ii.2)$

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

3. Интуитивные способы отыскания значения интеграла

Итак, каким же образом вычислить интегральную сумму ? Можно попробовать несколько способов:

Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

Функция является числовой, то есть область определения и область значений являются числовыми — принимают числовые значения (более точно — вещественные значения).
Функция непрерывна и принимает значения в каждой точке с соответствующим значением переменной (к примеру, в точкесуществует значение функции , а в точке значение
Функция может иметь любое выражение. Мы можем иметь набор значений функции в соответствующих точках в виде таблицы (функция задана таблично). Или функция может быть явно задана в виде аналитического выражения (к примеру, в случае с функцией от одной вещественной переменной — , и т.д.).
Функция может описывать зависимость величины любой природы — физической, биологической, экономической и т.д.

Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

$v(t) = S'(t) = lim_{t rightarrow 0} frac{Delta S}{Delta t} quad (iv. 1)$

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

$int_{a}^{b} f(x) dx quad (iv. 6)$

[1]. Медведев Ф.А. Развитие понятия интеграла. — М.: Наука, 1974. С. 4

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для A(x) и f(x) одно и тоже. Далее, мы покажем, что f(x) производная A(x) , то есть можно записать или .

[7]. То есть . К примеру, пусть функция задана выражением . Тогда, при x_2 = 2 , , а значение . Если. Тогда, при x_2 = 2 , , а значение .

[8]. Пусть имеется точка, число 7 и 10, чтобы найти величину промежутка между этими значениями надо найти разность то есть 10 — 7 = 3.

Источник

Интегрирование по частям

Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.

Формула для неопределенного интеграла:

$$ int udv = uv – int vdu $$

Формула для определенного интеграла:

$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} – int limits_{a}^{b} vdu $$

Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.

Пример 1

Найти интеграл $ int xe^xdx $

Решение

Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $

Подставляем найденные значения в первую формулу интегрирования и получаем

$$ int xe^x dx = xe^x – int e^x dx = xe^x – e^x + C. $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int xe^x dx = xe^x – e^x + C $$

Пример 2

Найти интеграл $ int xcos x dx $

Решение

В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $.

Подставим функции $ u $ и $ v $ в первую формулу

$$ int x cos x dx = x sin x – int sin x dx = x sin x + cos x + C. $$

Ответ

$$ int x cos x dx = x sin x + cos x + C $$

Пример 3

Вычислить интеграл $ int limits_1 ^e xln x dx $

Решение

В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения

$$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$

Осталось подставить это в формулу

$$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e – int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} – 0 – frac{1}{2} int limits_1 ^e xdx = $$

$$ =frac{e^2}{2} – frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} – frac{1}{2}(frac{e^2}{2} – frac{1}{2}) = frac{e^2}{2} – frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$

Ответ

$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$

Пример 4

Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $

Решение

По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет “на руку”. Поэтом поступаем так

$$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$

Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу

$$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 – int limits_0 ^1 frac{3^x dx}{ln 3} = $$

$$ = frac{18}{ln 3} – frac{5}{ln 3} – frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} – frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$

Ответ

$$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$

Источник

Первообразная функции и общий вид

20 июля 2015

Этот урок — первый из серии видео, посвященных интегрированию. В нём мы разберём, что такое первообразная функции, а также изучим элементарные приёмы вычисления этих самых первообразных.

На самом деле здесь нет ничего сложного: по существу всё сводится к понятию производной, с которым вы уже должны знакомы.:)

Сразу отмечу, что, поскольку это самый первый урок в нашей новой теме, сегодня не будет никаких сложных вычислений и формул, но то, что мы изучим сегодня, ляжет в основу гораздо более сложных выкладок и конструкций при вычислении сложных интегралов и площадей.

Кроме того, приступая к изучению интегрирования и интегралов в частности, мы неявно предполагаем, что ученик уже, как минимум, знаком к понятиям производной и имеет хотя бы элементарные навыки их вычисления. Без четкого понимания этого, делать в интегрировании совершенно нечего.

Однако здесь же кроется одна из самых частых и коварных проблем. Дело в том, что, начиная вычислять свои первые первообразные, многие ученики путают их с производными. В результате на экзаменах и самостоятельных работах допускаются глупые и обидные ошибки.

Поэтому сейчас я не буду давать четкого определения первообразной. А взамен предлагаю вам посмотреть, как она считается на простом конкретном примере.

Что такое первообразная и как она считается

Допустим, нам необходимо посчитать следующую производную:

[fleft( x right)={{x}^{3}}]

Мы знаем такую формулу:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

Считается эта производная элементарно:

[{f}’left( x right)={{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}}]

Посмотрим внимательно на полученное выражение и выразим ${{x}^{2}}$:

[{{x}^{2}}=frac{{{left( {{x}^{3}} right)}^{prime }}}{3}]

Но мы можем записать и так, согласно определению производной:

[{{x}^{2}}={{left( frac{{{x}^{3}}}{3} right)}^{prime }}]

А теперь внимание: то, что мы только что записали и есть определением первообразной. Но, чтобы записать ее правильно, нужно написать следующее:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

Аналогично запишем и такое выражение:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

Если мы обобщим это правило, то сможем вывести такую формулу:

[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]

Теперь мы можем сформулировать четкое определение.

Первообразной функции называется такая функция, производная которой равна исходной функции.

Вопросы о первообразной функции

Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:

Допустим, хорошо, эта формула верна. Однако в этом случае при $n=1$ у нас возникают проблемы: в знаменателе появляется «ноль», а на «ноль» делить нельзя.
Формула ограничивается только степенями. Как считать первообразную, например, синуса, косинуса и любой другой тригонометрии, а также констант.
Экзистенциальный вопрос: а всегда ли вообще можно найти первообразную? Если да, то как быть с первообразной суммы, разности, произведения и т.д.?

На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.

Решение задач со степенными функциями

Давайте попробуем посчитать такое выражение:

[{{x}^{-1}}to frac{{{x}^{-1+1}}}{-1+1}=frac{1}{0}]

Как видим, данная формула для ${{x}^{-1}}$ не работает. Возникает вопрос: а что тогда работает? Неужели мы не можем посчитать ${{x}^{-1}}$? Конечно, можем. Только давайте для начала вспомним такое:

[{{x}^{-1}}=frac{1}{x}]

Теперь подумаем: производная какой функции равна $frac{1}{x}$. Очевидно, что любой ученик, который хоть немного занимался этой темой, вспомнит, что этому выражению равна производная натурального логарифма:

[{{left( ln x right)}^{prime }}=frac{1}{x}]

Поэтому мы с уверенностью можем записать следующее:

[frac{1}{x}={{x}^{-1}}to ln x]

Эту формулу нужно знать, точно так же, как и производную степенной функции.

Итак, что нам известно на данный момент:

Для степенной функции — ${{x}^{n}}to frac{{{x}^{n+1}}}{n+1}$
Для константы — $=constto cdot x$
Частный случай степенной функции — $frac{1}{x}to ln x$

Идем далее. Что нам еще может потребоваться? Конечно же, правило вычисления первообразных от суммы и от разности. Запишем так:

[fleft( x right)to Fleft( x right)]

[gleft( x right)to Gleft( x right)]

[f+gto F+G]

[f-g=F-G]

[ccdot fto ccdot Fleft( c=const right)]

А если простейшие функции мы начнем умножать и делить, как тогда посчитать первообразную произведения или частного. К сожалению, аналогии с производной произведения или частного здесь не работают. Какой-либо стандартной формулы не существует. Для некоторых случаев существуют хитрые специальные формулы — с ними мы познакомимся на будущих видеоуроках.

Однако запомните: общей формулы, аналогичной формуле для вычисления производной частного и произведения, не существует.

Решение реальных задач

Задача № 1

[fleft( x right)={{x}^{2}}+5{{x}^{4}}]

Давайте каждую из степенных функций посчитаем отдельно:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[5{{x}^{4}}to 5cdot frac{{{x}^{5}}}{5}={{x}^{5}}]

Возвращаясь к нашему выражению, мы запишем общую конструкцию:

[Fleft( x right)=frac{{{x}^{3}}}{3}+{{x}^{5}}]

Задача № 2

[fleft( x right)=frac{x+1}{x}]

Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:

[fleft( x right)=frac{x}{x}+frac{1}{x}=1+frac{1}{x}]

Мы разбили дробь на сумму двух дробей.

Посчитаем:

[Fleft( x right)=1cdot x+ln x]

[Fleft( x right)=x+ln x]

Хорошая новость состоит в том, что зная формулы вычисления первообразных, вы уже способны считать более сложные конструкции. Однако давайте пойдем дальше и расширим наши знания еще чуть-чуть. Дело в том, что многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к ${{x}^{n}}$, могут быть представлены в виде степени с рациональным показателем, а именно:

[sqrt{x}={{x}^{frac{1}{2}}}]

[sqrt[n]{x}={{x}^{frac{1}{n}}}]

[frac{1}{{{x}^{n}}}={{x}^{-n}}]

Все эти приемы можно и нужно комбинировать. Степенные выражения можно

умножать (степени складываются);
делить (степени вычитаются);
умножать на константу;
и т.д.

Решение выражений со степенью с рациональным показателем

Пример № 1

[fleft( x right)=7sqrt{x}+sqrt[4]{x}]

Посчитаем каждый корень отдельно:

[]

[sqrt{x}={{x}^{frac{1}{2}}}to frac{{{x}^{frac{1}{2}+1}}}{frac{1}{2}+1}=frac{{{x}^{frac{3}{2}}}}{frac{3}{2}}=frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[sqrt[4]{x}={{x}^{frac{1}{4}}}to frac{{{x}^{frac{1}{4}}}}{frac{1}{4}+1}=frac{{{x}^{frac{5}{4}}}}{frac{5}{4}}=frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Итого всю нашу конструкцию можно записать следующим образом:

[Fleft( x right)=7cdot frac{2cdot {{x}^{frac{3}{2}}}}{3}+frac{5cdot {{x}^{frac{5}{4}}}}{4}=frac{14cdot {{x}^{frac{3}{2}}}}{3}+frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Пример № 2

[fleft( x right)=frac{1}{sqrt{x}}-frac{1}{{{x}^{3}}}]

Запишем:

[frac{1}{sqrt{x}}={{left( sqrt{x} right)}^{-1}}={{left( {{x}^{frac{1}{2}}} right)}^{-1}}={{x}^{-frac{1}{2}}}]

Следовательно, мы получим:

[Fleft( x right)=frac{{{x}^{-frac{1}{2}+1}}}{-frac{1}{2}+1}=frac{{{x}^{frac{1}{2}}}}{frac{1}{2}}=2{{x}^{frac{1}{2}}}=2sqrt{x}]

[frac{1}{{{x}^{3}}}={{x}^{-3}}to frac{{{x}^{-3+1}}}{-3+1}=frac{{{x}^{-2}}}{-2}=-frac{1}{2{{x}^{2}}}]

Итого, собирая все в одно выражение, можно записать:

[Fleft( x right)=2sqrt{x}+frac{1}{2{{x}^{2}}}]

Пример № 3

[fleft( x right)=sqrt[4]{x}-xsqrt{x}+1]

Для начала заметим, что $sqrt[4]{x}$ мы уже считали:

[sqrt[4]{x}to frac{4{{x}^{frac{5}{4}}}}{5}]

[xsqrt{x}={{x}^{1}}cdot {{x}^{frac{1}{2}}}={{x}^{frac{3}{2}}}]

[{{x}^{frac{3}{2}}}to frac{{{x}^{frac{3}{2}+1}}}{frac{3}{2}+1}=frac{2cdot {{x}^{frac{5}{2}}}}{5}]

[1to x]

Перепишем:

[Fleft( x right)=frac{4{{x}^{frac{5}{4}}}}{5}-frac{2{{x}^{frac{5}{2}}}}{5}+x]

Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.

Решение более сложных примеров

Задача № 1

[fleft( x right)={{left( sqrt[3]{x}-2 right)}^{2}}]

Вспомним формулу квадрата разности:

[{{left( a-b right)}^{2}}={{a}^{2}}-ab+{{b}^{2}}]

Давайте перепишем нашу функцию:

[fleft( x right)=left( sqrt[3]{x} right)-2cdot sqrt[3]{x}cdot 2+4]

[fleft( x right)={{x}^{frac{2}{3}}}-4{{x}^{frac{1}{3}}}+4]

Первообразную такой функции нам сейчас предстоит найти:

[{{x}^{frac{2}{3}}}to frac{3cdot {{x}^{frac{5}{3}}}}{5}]

[{{x}^{frac{1}{3}}}to frac{3cdot {{x}^{frac{4}{3}}}}{4}]

[4to 4x]

Собираем все в общую конструкцию:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x]

Задача № 2

[fleft( x right)={{left( frac{1}{x}-2 right)}^{3}}]

В этом случае нам нужно раскрыть куб разности. Вспомним:

[{{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}cdot b+3acdot {{b}^{2}}-{{b}^{3}}]

С учетом этого факта можно записать так:

[fleft( x right)=frac{1}{{{x}^{3}}}-3cdot frac{1}{{{x}^{2}}}cdot 2+3cdot frac{1}{x}cdot 4-8]

Давайте немного преобразуем нашу функцию:

[fleft( x right)={{x}^{-3}}-6{{x}^{-2}}+12cdot {{x}^{-1}}-8]

Считаем как всегда — по каждому слагаемому отдельно:

[{{x}^{-3}}to frac{{{x}^{-2}}}{-2}]

[{{x}^{-2}}to frac{{{x}^{-1}}}{-1}]

[{{x}^{-1}}to ln x]

[8to 8x]

Запишем полученную конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x-8x]

Задача № 3

[fleft( x right)=frac{{{left( x+sqrt{x} right)}^{2}}}{x}]

Сверху у нас стоит квадрат суммы, давайте его раскроем:

[frac{{{left( x+sqrt{x} right)}^{2}}}{x}=frac{{{x}^{2}}+2xcdot sqrt{x}+{{left( sqrt{x} right)}^{2}}}{x}=]

[=frac{{{x}^{2}}}{x}+frac{2xsqrt{x}}{x}+frac{x}{x}=x+2{{x}^{frac{1}{2}}}+1]

Далее все легко:

[xto frac{{{x}^{2}}}{2}]

[{{x}^{frac{1}{2}}}to frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[1to x]

Давайте напишем итоговое решение:

[Fleft( x right)=frac{{{x}^{2}}}{x}+frac{4{{x}^{frac{3}{2}}}}{3}+x]

А теперь внимание! Очень важная вещь, с которой связана львиная доля ошибок и недопониманий. Дело в том, что до сих пор считая первообразные с помощью производных, приводя преобразования, мы не задумывались о том, чему равна производная константы. А ведь производная константы равна «нулю». А это означает, что можно записать такие варианты:

${{x}^{2}}to frac{{{x}^{3}}}{3}$
${{x}^{2}}to frac{{{x}^{3}}}{3}+1$
${{x}^{2}}to frac{{{x}^{3}}}{3}+C$

Вот это очень важно понимать: если производная функции всегда одна и та же, то первообразных у одной и той же функции бесконечно много. Просто к нашим первообразным мы можем дописывать любые числа-константы и получать новые.

Неслучайно, в пояснении к тем задачам, которые мы только что решали, было написано «Запишите общий вид первообразных». Т.е. уже заранее предполагается, что их не одна, а целое множество. Но, на самом деле, они отличаются лишь константой $C$ в конце. Потому в наших задачах мы исправим то, что мы не дописали.

Еще раз переписываем наши конструкции:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x+C]

В таких случаях следует дописывать, что $C$ — константа — $C=const$.

Во второй нашей функции мы получим следующую конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x+C]

И последняя:

[Fleft( x right)=frac{{{x}^{2}}}{2}+frac{4{{x}^{frac{3}{2}}}}{3}+x+C]

И вот теперь мы действительно получили то, что от нас требовалось в исходном условии задачи.

Решение задач на нахождение первообразных с заданной точкой

Сейчас, когда мы знаем о константах и об особенностях записи первообразных, вполне логично возникает следующий тип задач, когда из множества всех первообразных требуется найти одну-единственную такую, которая проходила бы через заданную точку. В чем состоит эта задача?

Дело в том, что все первообразные данной функции отличаются лишь тем, что они сдвинуты по вертикали на какое-то число. А это значит, что какую бы точку на координатной плоскости мы не взяли, обязательно пройдет одна первообразная, и, причем, только одна.

Итак, задачи, которые сейчас мы будем решать, сформулированы следующем образом: не просто найти первообразную, зная формулу исходной функции, а выбрать именно такую из них, которая проходит через заданную точку, координаты которой будут даны в условии задачи.

Пример № 1

[fleft( x right)=5{{x}^{4}}+6{{x}^{3}}-2x+6]

[M=left( -1;4 right)]

Для начала просто посчитаем каждое слагаемое:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

[{{x}^{3}}to frac{{{x}^{4}}}{4}]

[xto frac{{{x}^{2}}}{2}]

[6to 6x]

Теперь подставляем эти выражения в нашу конструкцию:

[Fleft( x right)=5cdot frac{{{x}^{5}}}{5}+6cdot frac{{{x}^{4}}}{4}-2cdot frac{{{x}^{2}}}{2}+6x+C]

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+C]

Эта функция должна проходить через точку $Mleft( -1;4 right)$. Что значит, что она проходит через точку? Это значит, что если вместо $x$ поставить везде $-1$, а вместо $Fleft( x right)$ — $-4$, то мы должны получить верное числовое равенство. Давайте так и сделаем:

[4={{left( -1 right)}^{5}}+frac{3cdot {{left( -1 right)}^{4}}}{2}-{{left( -1 right)}^{2}}+6cdot left( -1 right)+C]

Мы видим, что у нас получилось уравнение относительно $C$, поэтому давайте попробуем его решить:

[4=-1+frac{3}{2}-1-6+C]

[C=4+6+2-frac{3}{2}=10,5]

Давайте запишем то самое решение, которое мы искали:

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+10,5]

Пример № 2

[fleft( x right)={{left( x-3 right)}^{2}}]

[M=left( 2;-1 right)]

В первую очередь необходимо раскрыть квадрат разности по формуле сокращенного умножения:

[fleft( x right)={{x}^{2}}-6x+9]

Считаем:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[xto frac{{{x}^{2}}}{2}]

[9to 9x]

Исходная конструкция запишется следующим образом:

[Fleft( x right)=frac{{{x}^{3}}}{3}-6cdot frac{{{x}^{2}}}{2}+9x+C]

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x+C]

Теперь давайте найдем $C$: подставим координаты точки $M$:

[-1=frac{8}{3}-12+18+C]

Выражаем $C$:

[C=-1-6-2frac{2}{3}=-9frac{2}{3}]

Осталось отобразить итоговое выражение:

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x-9frac{2}{3}]

Решение тригонометрических задач

В качестве финального аккорда к тому, что мы только что разобрали, предлагаю рассмотреть две более сложные задачи, в которых содержится тригонометрия. В них точно так же потребуется найти первообразные для всех функций, затем выбрать из этого множества одну-единственную, которая проходит через точку $M$ на координатной плоскости.

Забегая наперед, хотел бы отметить, что тот прием, который мы сейчас будем использовать для нахождения первообразных от тригонометрических функций, на самом деле, является универсальным приемом для самопроверки.

Задача № 1

[fleft( x right)=frac{1}{{{cos }^{2}}x}]

[M=left( frac{text{ }!!pi!!text{ }}{text{4}};-1 right)]

Вспомним следующую формулу:

[{{left( text{tg}x right)}^{prime }}=frac{1}{{{cos }^{2}}x}]

Исходя из этого, мы можем записать:

[Fleft( x right)=text{tg}x+C]

Давайте подставим координаты точки $M$ в наше выражение:

[-1=text{tg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[-1=1+C]

[C=-2]

Перепишем выражение с учетом этого факта:

[Fleft( x right)=text{tg}x-2]

Задача № 2

[fleft( x right)=frac{1}{{{sin }^{2}}x}]

[M=left( -frac{text{ }!!pi!!text{ }}{text{4}};2 right)]

Тут будет чуть сложнее. Сейчас увидите, почему.

Вспомним такую формулу:

[{{left( text{ctg}x right)}^{prime }}=-frac{1}{{{sin }^{2}}x}]

Чтобы избавится от «минуса», необходимо сделать следующее:

[{{left( -text{ctg}x right)}^{prime }}=frac{1}{{{sin }^{2}}x}]

Вот наша конструкция

[Fleft( x right)=-text{ctg}x+C]

Подставим координаты точки $M$:

[2=-text{ctg}left( -frac{text{ }!!pi!!text{ }}{4} right)+C]

[2=text{ctg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[2=1+C]

[C=1]

Итого запишем окончательную конструкцию:

[Fleft( x right)=-text{ctg}x+1]

Вот и все, о чем я хотел сегодня вам рассказать. Мы изучили сам термин первообразных, как считать их от элементарных функций, а также как находить первообразную, проходящую через конкретную точку на координатной плоскости.

Надеюсь, этот урок хоть немного поможет вам разобраться в этой сложной теме. В любом случае, именно на первообразных строятся неопределенные и неопределенные интегралы, поэтому считать их совершенно необходимо. На этом у меня все. До новых встреч!

Смотрите также:

Таблица первообразных
Интегрирование по частям
Решение задач B12: №448—455
Что такое ЕГЭ по математике 2011 и как его сдавать
Задача B4: случай с неизвестным количеством товара
Задача B15: что делать с квадратичной функцией

Источник

Что такое интеграл — это умножение
- - Понятие умножения
  - Понятие площади
  - Умножение по частям
  - Проблема с числами
  - Описываем изменение
  - Насколько большая эта “часть”?
  - А что по поводу начала и конца?
  - Где же “часть”, и каково ее значение?
  - Понимание записи интеграла
  - Как это понимать
  - Бесплатный сюрприз: новые идеи
  - Как читать интегралы
  - Что это нам дало?
«Где в практической жизни используется интеграл?» — Яндекс Кью
- - - О сообществе
Неопределенные интегралы — Задача 3
Расчет 2 Справка

Что такое интеграл — это умножение

Интегралы чаще всего описываются как “площадь под кривой”. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это “нахождение площади прямоугольника”. Нахождение площади — это одно из полезных применений умножения, но не его суть. Интегралы помогают нам комбинировать числа тогда, когда умножение бессильно.

Так я размышлял про себя на парах математики в ВУЗе:

“Интегралы позволяют нам ‘умножать’ изменяющиеся числа. Мы привыкли к “3 × 4 = 12”, но что если одно из чисел изменяется? Мы не можем умножать меняющиеся числа, поэтому используем интегралы вместо умножения.

Вы услышите много разговоров насчет площади — но это всего лишь один из способов визуализировать умножение. Ключом является не площадь, а идея объединения множеств воедино. Конечно, мы можем интегрировать (“умножать”) длину и ширину, чтобы получить площадь на плоскости. Но мы также можем интегрировать скорость и время, чтобы получить расстояние, или длину, ширину и высоту для получения объема.

Когда мы хотим использовать обычное умножение, но не можем, мы достаем свое оружие и начинаем интегрировать. Площадь — это всего лишь прием визуализации, не зацикливайтесь на нем слишком сильно. А теперь давайте учить математику!”

И вот он, мой момент истины: интегрирование — это улучшенная версия умножения, которая работает с изменяющимися величинами. Давайте изучать интегралы в таком свете.

Понятие умножения

Вот как во все времена и эпохи понимали умножение:

Если речь идет о натуральных числах (3 × 4), умножение — это повторяющееся сложение.
С вещественными числами (3.12 × √2 ), умножение — это масштабирование.
В случае с отрицательными числами (-2.3 × 4.3), умножение — это поворот и масштабирование.
С комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около “применения” одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Понятие площади

Площадь — очень тонкое понятие. На данный момент, давайте представим площадь как визуальную интерпретацию умножения:

Мы можем “применять” числа на разных осях друг к другу (3 применяется к 4) и получить результат (12 единиц площади). Свойства каждого вводного значения (длина и длина) превратились в результат (единицы площади).

Легко, правда? Не так, как кажется на первый взгляд. Умножение может привести к “отрицательному результату” (3×(-4) = -12), которого не существует.

Мы понимаем график как представление умножения, и используем эту аналогию из-за удобства. Если бы все были слепыми, и в мире не существовало диаграмм, мы бы все равно хорошо справлялись с умножением. Площадь — это всего лишь интерпретация.

Умножение по частям

А теперь давайте умножим 3 × 4.5:

Что происходит? Ну, 4.5 — это не целочисленное число, но мы же можем воспользоваться “частичным” умножением. Если 3×4 = 3 + 3 + 3 + 3, то

3 × 4.5 = 3 + 3 + 3 + 3 + 3×0.5 = 3 + 3 + 3 + 3 + 1.5 = 13.5

Мы берем 3 (значение) 4.5 раза. Таким образом, мы объединили 3 с 4 полными сегментами (3 × 4 = 12), а также одним частичным сегментом (3 × 0.5 = 1.5).

Мы так привыкли к умножению, что даже забываем, как здорово оно работает. Мы можем разбить число на единицы (целые или частичные), умножать каждый кусочек и складывать результаты. Заметьте, как мы легко расправились с дробной частью? Это и есть начало интегрирования.

Проблема с числами

Числа не всегда ведут себя постоянно для наших расчетов. Сценарии типа “Вы ехали 3 часа со скоростью 30 км/ч” не имеют ничего общего с реальностью. Так условия описываются просто для удобства.

Формулы по типу “расстояние = скорость × время” только маскируют проблему; нам все еще нужно брать постоянные числа и умножать. А как узнать пройденное расстояние, если наша скорость постоянно изменялась во времени?

Описываем изменение

Первым испытанием для нас будет описание изменяющегося числа. Мы можем просто сказать: “Моя скорость менялась с 0 до 30 км/ч”. Это не совсем точно: как быстро она изменялась? Были ли изменения плавными?

Давайте будем точны: моя скорость в каждый момент времени равнялась удвоенному количеству секунд. В 1 секунду я двигался со скоростью 2 км/ч. Во 2 секунду скорость уже была 4 км/ч, в 3 секунду — уже 6 км/ч, и так далее:

Вот теперь у нас есть хорошее описание, достаточно подробное, чтобы знать свою скорость в каждый момент времени. Формальное описание звучит как “скорость — это функция времени”, и оно означает, что мы можем взять любой момент времени (t) и узнать нашу скорость в тот момент (“2t” км/ч).

(Это, конечно, не дает ответа на вопрос, почему скорость и время связаны. Я могу ускоряться за счет гравитации, или ослик может толкать меня сзади. Мы всего лишь установили, что с изменением времени изменяется и скорость).

Наше произведение “расстояние = скорость × время”, возможно, лучше написать так:

расстояние = скорость(t) × t

где скорость (t) — это скорость в любой момент времени. В нашем случае скорость (t) = 2t, так что мы пишем:

расстояние = 2t × t

Но это уравнение выглядит странно! “t” по-прежнему выглядит как единичный момент, который нужно выбирать (например, t=3 секунды), а значит и скорость (t) примет единичное значение (6 км/ч). А это нехорошо.

При обычном умножении, мы можем взять одну скорость и предположить, что она одинаковая во всем прямоугольнике. Но изменяющаяся скорость требует совмещения скорости и времени по частям (секунда за секундой). В каждый момент ситуация может быть разной.

Вот как это выглядит в большой перспективе:

Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и “масштабируем ее”.
Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные посекундно.

Мы видим, что обычное умножение — это частный случай интегрирования, когда количество пройденных метров не изменяется.

Насколько большая эта “часть”?

Насколько велика “часть”, при прохождении дистанции по частям? Секунда? Миллисекунда? Наносекунда?

Ответ навскидку: достаточно мала, чтобы значение было постоянным все время. Нам не нужна идеальная точность.

Более длинный ответ: такие понятия, как пределы, были придуманы, чтобы помочь в покусочном умножении. Принося пользу, они просто решают проблему и отвлекают от сути “объединения величин”. Мне очень не нравится, что пределы проходят в самом начале матанализа, еще перед тем, как студенты вникнут в проблему, которую они решают.

А что по поводу начала и конца?

Скажем, мы исследуем интервал от 3 до 4 секунд.

Скорость вначале (3×2 = 6 км/ч) отличается от скорости в конце (4×2 = 8 км/ч). Так какое же значение мне брать при вычислении “скорости × время”?

Решением будет разбить наши кусочки времени на достаточно мелкие отрезки (от 3.00000 до 3.00001 секунд), пока разность скоростей от начала до конца интервала будет для нас незначительной. Опять же, это более длинный разговор, но “поверьте мне”, что это временной отрезок, который делает разницу незначительной.

На графике представьте, что каждый интервал — это одна точка на прямой. Вы можете нарисовать ровную линию к каждой скорости, и ваша “площадь” будет представлять собой множество отрезков, которое и будет измерять умножение.

Где же “часть”, и каково ее значение?

Разделение части и ее значения далось мне нелегко.

“Часть” — это интервал, который мы рассматриваем (1 секунда, 1 миллисекунда, 1 наносекунда). “Позиция” — это то, где начинается секундный, миллисекундный или наносекундный интервал. Значение — это наша скорость в той позиции.

Например, рассмотрим интервал от 3.0 до 4.0 секунд:

“Ширина” отрезка времени составляет 1.0 секунду
Позиция (начальное время) равно 3.0
Значение (скорость(t)) — это скорость(3.0) = 6.0 км/ч

Опять же, матанализ учит нас сокращать интервал до тех пор, пока разница между значениями в начале и конце интервала будет на столько мала, что ею можно пренебречь, считая этот интервал «точкой». Не выпускайте из вида большую картинку: мы умножаем набор частей.

Понимание записи интеграла

У нас есть здравая идея “покусочного умножения”, но мы никак не можем ее выразить. “Расстояние = скорость(t) × t” все еще выглядит, как обычное уравнение, где t и скорость(t) принимают одно единственное значение.

В матанализе мы пишем это соотношение как

расстояние = ∫скорость(t)dt

знак интеграла (s-образная кривая) означает, что мы умножаем покусочно и суммируем значения в одно.
dt представляет временной “интервал”, который мы рассматриваем. Его называют “дельта t” а не “d раз по t”.
t представляет положение dt (если dt — это промежуток от 3.0 до 4.0, то t равно 3.0)
скорость(t) — это значение, на которое мы умножаем (скорость(3.0) = 6.0))

У меня есть парочка претензий к этой записи:

То, как здесь используются буквы, немного смущает. “dt” выглядит как “d раз по t” в отличие от любого уравнения, которое вы ранее видели.
Мы пишем скорость(t) × dt, вместо скорость(t_dt) × dt. Последний вариант четко указывает, что мы исследуем “t” на конкретном участке “dt”, а не какое-то глобальное “t”
Вы часто встретите ∫скорость(t), без dt. Это вообще помогает легко забыть, что мы выполняем покусочное умножение двух элементов.

Похоже, уже поздно менять форму записи интегралов. Просто запомните эту идею насчет “умножения” чего-то, что изменяется.

Как это понимать

Когда я вижу вот это:

расстояние = ∫скорость(t)dt

Я думаю “Расстояние равно скорости t раз (читая левую часть первой) или “совместите скорость и время, чтобы получить расстояние” (читая правую часть первой).

В уме я перевожу “скорость(t)” как скорость и “dt”, и это превращается в умножение, при условии, что скорости позволено изменяться. Представление интегрирования подобным образом помогает мне сконцентрироваться на том, что на самом деле происходит (“Мы совмещаем скорость и время, чтобы получить расстояние!”) вместо зацикливания на деталях действия.

Бесплатный сюрприз: новые идеи

Интегралы — это очень глубокая идея, также, как и умножение. У вас могло появиться много вопросов, основанных на этой аналогии:

Если интегралы умножают изменяющиеся величины, есть ли что-то, что делит их? (ДА — производные).
Являются ли интегралы (умножение) и производные (деление) взаимообратными? (Да, с некоторыми тонкостями).
Можем ли мы преобразовать уравнение “расстояние = скорость × время” в “скорость = расстояние / время”? (Да).
Можем ли мы совмещать несколько величин одновременно? (Да — это называется многократное интегрирование).
Влияет ли как-то порядок совмещения на результат? (Обычно нет).

Как только вы начнёте воспринимать интегралы как “улучшенное умножение”, вы сразу начнете задумываться о таких вещах, как “улучшенное деление”, “повторное интегрирование” и так далее. Застряв на “площади под кривой”, вы не уловите связи между этими темами. (Математических заучек видение “площади под кривой” и “угла наклона кривой” обратными понятиями ставит в тупик).

Как читать интегралы

У интегралов масса применений. Одним из них является объяснение того, что две величины были “умножены” для получения результата.

Вот как мы представляем площадь круга с помощью интегралов:

Площадь = ∫Длина окружности (r) · dr = ∫2πr · dr = π · r²

Нам бы очень хотелось взять площадь кривой умножением. Но мы не можем — высота изменяется в каждой ее точке. Если мы “развернем” круг, мы увидим, что частичка площади под каждой порцией радиуса будет равна “радиус × отрезок окружности”. Мы можем описать эту связь с помощью интеграла (как описано выше).

А вот как интеграл описывает идею, что “масса = плотность × объем”:

масса = ∫_Vρ(r) ∙ dv

Что здесь сказано? Греческая буква «ро» («ρ») — это функция плотности, которая говорит нам, насколько плотен материал в определенном положении. Так, r∙dv — это частичка объема, который мы рассматриваем. Так что мы умножаем маленький кусочек объема (dv) на плотность в том интервале ρ(r), и потом складываем все эти части, чтобы получить массу.

Мы привыкли просто умножать плотность на объем, но если плотность изменяется, то нужно интегрировать. Индекс V просто означает “интеграл объема”, что по сути является тройным интегралом длины, ширины и высоты! Интеграл предполагает четыре “умножения”: 3 для поиска объема, и еще одно для умножения на плотность.

Что это нам дало?

Сегодняшней целью было не научное понимание интегральных исчислений. Наша цель — расширить модель мышления, и получить представление об интеграле как о надстройке над такими низкоуровневыми операциями как сложение, вычитание, умножение и деление.

Рассматривайте интегралы как улучшенный способ умножения: вычисления станут проще, и вам под силу станут понятия типа кратного интеграла и производной. Приятных вычислений!

Перевод статьи «A Calculus Analogy: Integrals as Multiplication».

«Где в практической жизни используется интеграл?» — Яндекс Кью

Математика и математики

О сообществе

Математика и математики

Сообщество практикующих математиков разного уровня. Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!

Неопределенные интегралы — Задача 3

Одним из полезных свойств неопределенных интегралов является правило постоянного кратного числа. Это правило означает, что вы можете вытащить константы из интеграла, что может упростить задачу. Например, интеграл от 2x + 4 равен 2, умноженному на интеграл от x + 2. Однако важно, чтобы из интеграла извлекались только константы, а не переменные.

Другим свойством является степенное правило первообразных (помните, что взятие интеграла от чего-либо равнозначно антидифференцированию). Правило мощности утверждает, что первообразная a x ⁿ равно x ⁿ⁺¹ /n + c, где c — некоторая константа.

Для первообразных не существует правила произведения или частного, поэтому для решения интеграла от произведения необходимо умножить или разделить две функции.

неопределенный интеграл
первообразная
антидифференциация
дифференцирование

Давайте рассмотрим более сложные примеры. Я хочу найти некоторые первообразные. В этом примере я не собираюсь проверять свою антидифференцировку дифференцированием. Помните, что вы всегда можете это сделать, если не уверены в своем ответе. Это хорошая привычка. Позвольте мне вернуться к этому позже, когда я почувствую, что наша работа немного более подвержена ошибкам. На этот раз пропустим.

Итак, здесь я хочу антидифференцировать x³ раз (2x² минус 3). Теперь помните, что для антидифференциации нет правила произведения. Вы не можете просто антидифференцировать каждого из этих парней и умножать их продукты. Вы должны умножить через.

Так давайте. Если я умножу это, я получу x³, умноженное на 2x², то есть 2x в 5-м. Помните, что вы добавляете показатели степени. Итак, 2x в 5-м минус 3x³. Намного лучше. Теперь я могу антидифференцировать это, просто отделив его и получив константы.

Итак, сначала давайте разделим его на сумму. У меня 2x к 5-му dx плюс интеграл от -3x³ dx. Итак, что я только что сделал, так это воспользовался правилом сумм. У вас есть интеграл от суммы, он равен сумме интегралов. Теперь я воспользуюсь правилом постоянного умножения, чтобы извлечь 2 и -3 из каждого из этих интегралов соответственно. 2-кратный интеграл от x до 5-го dx минус 3-кратный интеграл от x³.

Теперь у меня есть каждый из этих интегралов в форме, в которой я могу применить это свойство; х к н. Интеграл равен 1 на n плюс 1, x на n плюс 1. Итак, здесь, где мое n равно 5, n плюс 1 будет 6. Таким образом, это будет 2 раза 1/6 x до 6-го минус 3 раза 1/4x до 4-го. Здесь n равно 3, поэтому n плюс 1 будет 4. Затем я добавляю свой плюс c в конце.

Осталось только упростить дроби. 2 на 6 равно 1/3, 3/4 x до четвертой плюс c. На этот раз мы не проверяем. Так что, надеюсь, это правильный ответ. 1/3x до шестой минус 3/4x до четвертой плюс c. Это первообразные этой функции.

Давайте сделаем еще один. Теперь у нас есть частное двух функций. Точно так же, как нет правила произведения для антидифференциации, нет и правила частного.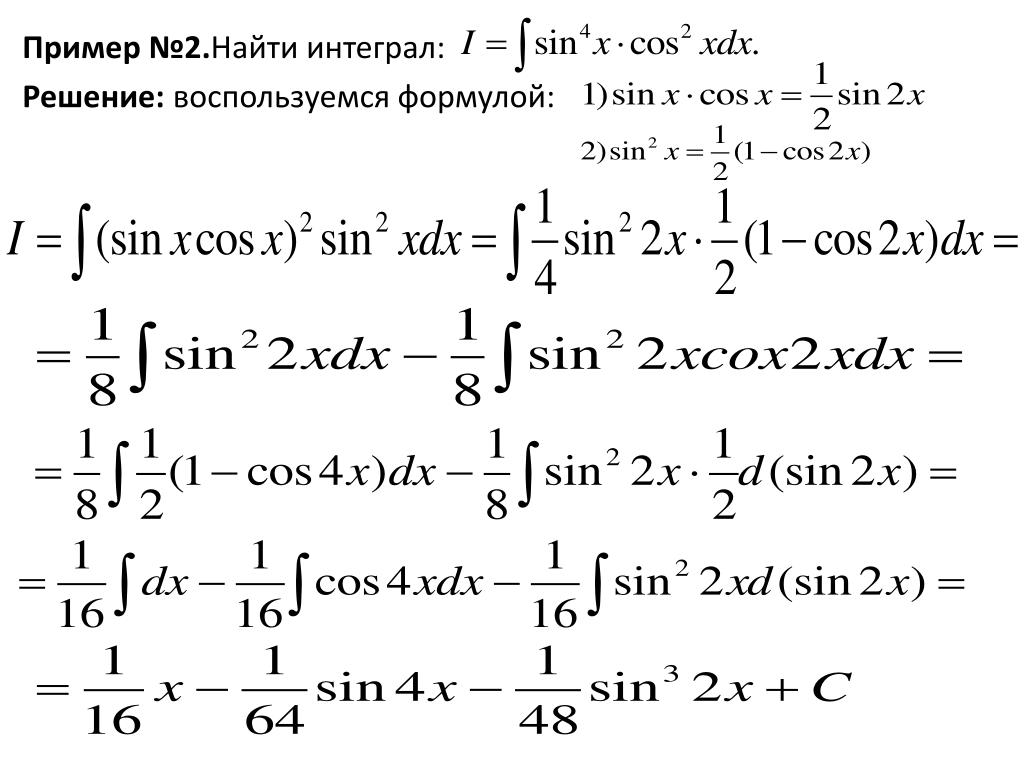 Так что вам действительно нужно объединить их, чтобы получить сумму или разность степеней x.

Это первое, что я собираюсь сделать. Я собираюсь записать каждое из них как просто степени x. У меня 22x³ минус 4 на кубический корень из x такой же, как x в 1/3dx. Итак, это равно; теперь, что я могу сделать, я могу по существу распределить этот x на 1/3 по каждому из этих терминов. Подумайте об этом так. Думайте об этом как 22x³ на x в 1/3 минус 4 на x в 1/3.

Итак, позвольте мне упростить каждое из них, чтобы у меня была одна степень х. У меня 22x³ больше x на 1/3 равно x на 3 минус 1/3. 3 равно 9/3. 9/3 минус 1/3 равно 8/3 минус 4. Тогда 4 на x до 1/3 равно x до -1/3. Так что это гораздо более удобная форма для целей интеграции. У меня каждое из них записано как степень х. Теперь я могу отделить сумму.

Итак, это один термин. Другой — уведомление, я сказал «сумма», хотя здесь стоит знак «минус». Я могу втянуть этот негатив внутрь. Это то же самое, что добавить -4x к -1/3. Итак, от -4x до -1/3. Затем я могу вытащить константы наружу.

Очень скоро я буду делать эти два шага за один шаг. Когда-то вы привыкнете ко всем свойствам, а пока я их разделяю. Так что я хочу вытащить это -4. Интеграл от -1/3 до х.

Теперь у меня есть каждый интеграл как интеграл от некоторой степени x. Так что помните, х к 8/3, я должен добавить 1 к показателю степени, что становится 11 на 3. Итак, х на 11 на 3. Я должен разделить на 11 на 3, что то же самое, что умножить на обратное ; 3/11, минус 4. Я должен сделать то же самое с x до -1/3. Я добавляю 1. -1/3 плюс 1 равно 2/3. Так что я получаю х к 2/3. Мне нужно разделить на 2/3, что то же самое, что умножить на 3/2, а затем я добавлю букву «с» в конце.

Произошли некоторые отмены. 22 и 11 отменяются, остается 2. 2 умножить на 3, это 6, 6x до 11/3, минус, здесь у меня есть отмена. 4 и 2 сокращаются, оставляя 2. 2 умножить на 3 снова — это 6 x до 2/3, а затем плюс c. Это мои первообразные; 6x до 11/3 минус 6x до 2/3 плюс c.

Расчет 2 Справка

Студенты, нуждающиеся в помощи по исчислению 2, получат большую пользу от нашей интерактивной программы.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по исчислению 2.
Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы быстро получите много помощи по Calculus 2.
Получите помощь сегодня с нашей обширной коллекцией необходимой информации по исчислению 2.

Исчисление 2 продолжается математическим исследованием изменений, впервые представленным студентам во время Исчисления 1. Курс охватывает интеграцию, применение интегрирования и ряды, а также рассматривает и расширяет понятия, введенные в Исчислении 1, такие как пределы и производные. Это преимущественно курс математики на уровне колледжа, и большинство студентов, которые проходят этот курс, делают это либо на первом, либо на втором курсе. Поскольку «Исчисление 2» является продолжением «Исчисления 1», рекомендуется, чтобы учащиеся проходили два курса последовательно. Хотя Calculus 2 обычно не является обязательным курсом в колледже, он настоятельно рекомендуется студентам, изучающим математику или любую другую область, требующую продвинутых математических понятий, таких как инженерное дело, физика или экономика. Нужен ли вам репетитор по математическому анализу в Атланте, репетитор по математическому анализу в Хьюстоне или в Сан-Франциско, работа один на один с экспертом может быть именно тем, что вам нужно для учебы.

Бесплатный инструмент обучения Learn by Concept от The Varsity Tutors предлагает учебные материалы для студентов, которым нужна помощь в изучении Calculus 2 или которые просто хотят повторить предмет. Инструмент обучения построен как интерактивная учебная программа с рядом разделов и тем, подробно описывающих исчисление 2. Нажав на любую тему, вы перейдете к серии примеров вопросов с несколькими вариантами ответов. Затем вы можете просмотреть образец вопроса и возможные ответы, решить проблему и выбрать ответ, который вы считаете правильным. Правильный ответ указан под вариантами ответов, что позволяет вам проверить правильность своего ответа. Varsity Tutors предлагает ресурсы, такие как бесплатные практические тесты по исчислению II, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторах по исчислению II.

Было бы полезно просто задавать вопросы и ответы, но инструмент «Узнай по концепции» делает больше. Подробное пошаговое описание того, как прийти к правильному ответу, прилагается к каждому примерному вопросу, что помогает упростить задачу. Эти описания показывают каждое уравнение, концепцию и теорию, которые применимы к проблеме, будь то получение производной функции или просто переписывание уравнения. Если вы дали неправильный ответ, вы можете выяснить, где вы ошиблись, и что вам нужно сделать, чтобы в будущем задать правильный вопрос. Если вы дали правильный ответ с первой попытки, вы можете проверить свою работу, чтобы убедиться, что понимаете, почему ваш ответ был правильным.

Если вы только начали изучать Calculus 2 или готовитесь к выпускному экзамену, вы можете использовать инструмент «Учиться по концепции» в качестве учебного пособия. Инструмент охватывает широкие единицы деривативов; интегралы; лимиты; параметрический, полярный и векторный; и серии в исчислении. Это также входит в особенности в каждой категории. Вы можете пройти весь блок сразу или сосредоточиться на одной теме или подтеме. Благодаря тысячам примеров вопросов по Calculus 2 в базе данных средств обучения охвачены все возможные темы. В дополнение к справочному разделу по исчислению II и репетиторству по исчислению II вы также можете рассмотреть некоторые из наших карточек с исчислением II.

Инструмент «Обучение по концепции» лучше всего использовать вместе с другими инструментами обучения. Прохождение бесплатного полного практического теста поможет вам определить, какие темы Calculus 2 вы уже знаете и на чем следует сосредоточить свое внимание. Пройдя один из сотен бесплатных тематических практических тестов по исчислению 2, вы также можете использовать карточки по тем же темам. Практические тесты и карточки можно сортировать по категориям или настраивать в соответствии с вашими потребностями.

Источник

Общая информация

Использование интеграла

Методика нахождения первообразной

Рекомендации специалистов

Примеры решения

0. Предисловие

1. Предпосылки возникновения интегрирования

2. Геометрический и аналитико-алгебраический смысл интегрирования

3. Интуитивные способы отыскания значения интеграла

4. Отыскание значения интеграла через отыскание первообразной

Интегрирование по частям

Первообразная функции и общий вид

Что такое первообразная и как она считается

Вопросы о первообразной функции

Решение задач со степенными функциями

Решение реальных задач

Задача № 1

Задача № 2

Решение выражений со степенью с рациональным показателем

Пример № 1

Пример № 2

Пример № 3

Решение более сложных примеров

Задача № 1

Задача № 2

Задача № 3

Решение задач на нахождение первообразных с заданной точкой

Пример № 1

Пример № 2

Решение тригонометрических задач

Задача № 1

Задача № 2

Что такое интеграл — это умножение

Понятие умножения

Понятие площади

Умножение по частям

Проблема с числами

Описываем изменение

Насколько большая эта “часть”?

А что по поводу начала и конца?

Где же “часть”, и каково ее значение?

Понимание записи интеграла

Как это понимать

Бесплатный сюрприз: новые идеи

Как читать интегралы

Что это нам дало?

«Где в практической жизни используется интеграл?» — Яндекс Кью

О сообществе

Неопределенные интегралы — Задача 3

Расчет 2 Справка

Вам также может понравиться

Как найти вакансии в гомеле

Псково печерский монастырь как найти

Как найти тангенс угла соотношение сторон

Добавить комментарий Отменить ответ