Как найти первообразную в фотоматч

PhotoMath: помощник в школьной математике?

Как часто мучительно найденный икс в итоге не сходится с ответом в учебнике. Но эту проблему поможет решить приложение PhotoMath.

Недавно мы цитировали профессора Кита Девлина, говорившего о том, что школьная математика устарела, потому что телефоны, которые мы носим в кармане, решают уравнения быстрее любого человека. Компания MicroBlink с помощью приложения для смартфонов PhotoMath сделала ещё один шаг к сближению телефонов и школьных уравнений. PhotoMath решает за вас примеры – нужно только сфотографировать страницу с заданием.

Приложение можно установить бесплатно на телефоны с iOS или Windows Phone, версия под Android будет готова к началу 2015 года. Программа распознает напечатанный текст с листа учебника и, немного хуже, с экрана компьютера. С примерами, написанными от руки, PhotoMath пока не справляется.

Правильное решение выдаётся за несколько секунд, а дальше можно посмотреть, как именно решалось уравнение, шаг за шагом. Приложение поддерживает арифметические действия, дроби, корни и степени и простые линейные уравнения. По мнению разработчиков, PhotoMath делает математику проще, потому что не просто решает задачи, но и учит пользователя, как решать их самостоятельно.

Компания MicroBlink несколько лет разрабатывала собственную систему распознавания текста, а теперь начала придумывать ей различные применения. Сначала было приложение PhotoPay, которое позволяет оплачивать счета с помощью их сканирования. Информация с телефона передаётся в банк, который оплачивает счёт автоматически. Теперь их система распознавания добралась и до школ.

Похоже, что PhotoMath устроит революцию в школьной математике. Бесплатное приложение, работающее под всеми основными платформами, довольно быстро дойдёт и до наших школ. Люди, уже попробовавшие его в деле, отмечают, что у программы есть свои пределы – длинные уравнения не всегда влезают в красную рамку, или наоборот – другие примеры «заползают» в эту рамку и мешают сканированию. Но это, разумеется, случается не так уж часто.

Конечно, кому-то это приложение поможет понять ранее непонятые алгоритмы, но есть подозрения, что большинство просто будет переписывать правильные ответы в тетрадь, аргументируя это тем, что математика им всё равно никогда больше не пригодится. Как справится с этим наша, ориентированная на решение примеров, школьная математика? Не доказывает ли появление PhotoMath, что в этой системе что-то нужно менять? Если же новые технологии так и будут существовать совместно со старой учебной программой, то в каком качестве?

Источник

Photomatch как посчитать производную

Лень, как известно, двигатель прогресса. А мобильный сегмент — реактивный двигатель. Ведь это устройство практически всегда (а у тебя — всегда) под рукой. Лентяям и двоечникам компания PhotoPay сделала шикарный подарок — бесплатное (!) приложение для решения уравнений и функций при одном лишь наведении…

Приложение Photomath вызвало большой резонанс в некоторых сообществах (лепра, например). На фоне общей деградации умственных способностей нынешнего поколения, есть мнение, что подобные приложения до конца угробят «молодых и талантливых», которые после этого идут в инженеры и проектируют мотор барабан мб3. Он, кстати, используется для ленточных конвееров и стоит довольно существенный суммы — до 85 тысяч рублей. Различаются они, по большей части, по длине рабочей части и мощности электродвигателя. Вообще, доля правды во всем этом есть, однако стоит заметить, что при изобретении калькулятора люди не разучились считать.

Photomath выпущено для всех популярных мобильных ОС — Android, Windows Phone 8/8.1, iOS. Самый весомый плюс приложения в том, что оно не только показывает правильный ответ, но ход решения. На момент написания статьи Photomath «понимает» дроби, десятичные числа, линейные уравнения и несколько функций, логарифмов. Списанное наспех задание в тетрадке не покатит — приложение распознает только печатный текст.

Еще одно преимущество перед онлайн-шпаргалками — приложение работает без подключения к интернету. В последней версии улучшили сканер для камер без автофокусировки. В целом, приложение прекрасно подходит для учащихся 1-8 классов. Высшую математику с ним, конечно, не решить

— Нет русского языка
— Если страница просвечивает, программа может «захватить» часть уравнения с другой стороны листа.
— Дифференциалы и лимиты пока не ищу
— Иногда очень долго распознает текст

Вычисляет производную заданной функции.

Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, – вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.

Калькулятор производных

Производная функции

Синтаксис описания формул

В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, – — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.

педагогическая практика

Среди математических калькуляторов Photomath, безусловно, занимает особое место. Во-первых, он предназначен для андроидов. Во-вторых, задание можно не вводить, а сканировать.

Достаточно навести камеру на математическую задачу и Photomath покажет результат, причём с пошаговыми инструкциями, как это решается.

Photomath поддерживает арифметику, целые числа, дроби, десятичные числа, корни, алгебраические выражения, линейных уравнений, неравенств, квадратных уравнений, логарифмы, тригонометрию, производные, интегралы и многое другое.

А теперь из области фантастики.

Ещё один плюс данного приложения — умение распознать рукописный шрифт.

Проверено вашим покорным слугой.

Между тем, педагоги прекрасно понимают, что любое новое изобретение может быть использовано как во благо, так и во вред. Конечно, такой калькулятор облегчит расчёты в лабораторной работе, обработку больших массивов.

Однако мы прекрасно понимаем, что подобные приложения могут и помешать учащимся шаг за шагом познавать глубинные секреты математики.

Помню, как в школе мы соревновались, кто представит учителю больше вариантов решения тригонометрического уравнения. И пятёрки мы получали не только за правильные ответы, но и за самые изящные варианты.

Учителю математики придётся думать, как сделать так, чтобы это и другие новшества помогли ученикам в их успешной учёбе.

Так или иначе их не скроешь.

Хотелось бы узнать мнение учителей математики.

Источник

Интегралы для чайников: как решать, правила вычисления, объяснение

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Свойства определенного интеграла

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

App Store PhotoMath: карманный решебник по алгебре

«Решите систему уравнения, принимая во внимание следующее неравенство…», – с этим сталкивались все. Кому-то математика в школе давалась легко, а для кого-то она так и осталась чем-то далеким и непостижимым. Как ни крути, иногда умение считать деньги не спасает от необходимости решения сложных математических уравнений и неравенств. «Смартфон» дословно переводится как «умный телефон» и благодаря стороннему софту ему можно доверить даже самые сложные задачи.

Приложение PhotoMath всего за несколько секунд поможет решить сложные алгебраические уравнения, неравенства и задачи, показав подробный ход расчетов.

Эволюция калькуляторов началась еще в середине прошлого века. О микрокомпьютере Электроника МК-52 мечтал практически каждый учащийся старших классов и, уж тем более, студент. Потом появились инженерные калькуляторы и на прилавках стали мелькать недешевые помощники Citizen, Casio и Assistant. Одни были оснащены лишь минимальным количеством тригонометрических функций, другие (дорогие и редкие модели) даже строили графики.

С появление смартфонов потребность в них отпала, но сотни различных приложений-калькуляторов по-прежнему оставались бессильными против самостоятельного решения поставленной задачи.

Приложение PhotoMath умеет не только самостоятельно рассчитывать требуемое значение «икс и игрик», но и показывает весь ход решения. Все, что потребуется от вас – навести камеру на уравнение и подождать несколько секунд.

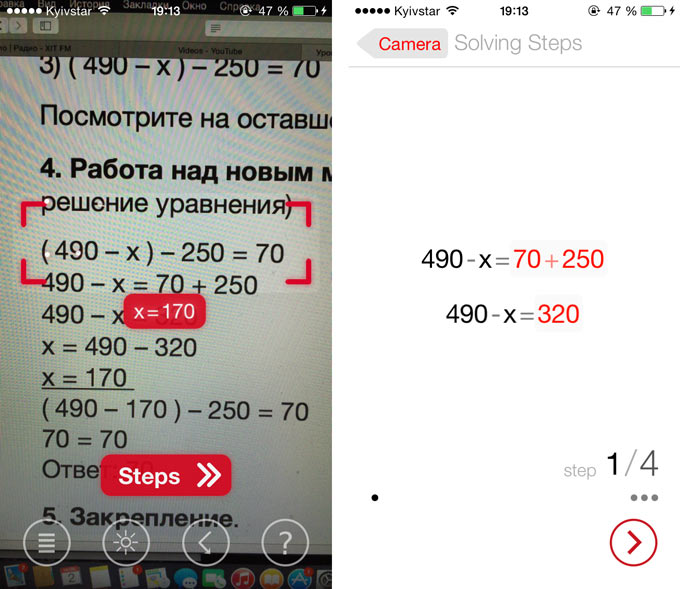
Появление на экране различных точек означает, что приложение распознает «увиденные» символы. Если PhotoMath все понятно, он тут же выдаст правильный ответ. Для того, чтобы увидеть ход решения достаточно нажать клавишу Steps (Шаги).

Весь ход решения будет представлен в виде нескольких последовательных шагов, последним из которых станет результат решения.

PhotoMath автоматически сохраняет историю всех, когда-либо решенных примеров. Количество настроек сведено к минимум и единственное, что может сделать пользователь – включить/отключить вспышку.

При работе с приложением следует учитывать ряд его особенностей:

– PhotoMath распознает исключительно печатный текст (поддержку рукописного разработчики планируют внедрить в ближайшее время);
– следите за качеством изображения примера или неравенства;
– приложение с трудом справляется со сложными уравнениями и неравенствами, но идеально решает простые линейные уравнения;
– распознавание с экрана компьютера/планшета проходит хуже, чем с бумаги.

Учитывая полную бесплатность приложения, отсутствие навязчивой рекламы и действительно интересную задумку, PhotoMath заслуживает весьма высокой оценки. Текущая версия 1.1.0 работает стабильно, но, как и любой человек, учится решать более сложные и запутанные математические задачи.

iPhone: Бесплатно [Скачать из App Store]

Источник

Обзор Photomath — больше, чем просто калькулятор

Школьные и студенческие годы для большинства людей раньше были мучительными по многим причинам, но одной из самых главных всегда оставалась математика. Простая арифметика, превращающаяся в многоэтажные интегральные уравнения — вот что заставляло ненавидеть этот предмет. Именно поэтому в App Store все чаще стали появляться приложения, помогающие решить математические выражения любого рода. Сегодня посмотрим на Photomath — незаменимого помощника в решении уравнений.

Главное преимущество приложения в том, что вводить огромные уравнения с множеством символов вовсе не обязательно — Photomath с легкостью распознает печатный текст, причем делает это весьма быстро. Просто открой приложение и наведи камеру на выражение, а программа все сделает за тебя.

На экране сразу появится решаемое уравнение и ответ. Photomath только 1 раз из 10 ошиблось при распознавании текста — отличный результат, учитывая еще и то, как быстро эта операция происходит. Разработчики также учли возможность промаха и добавили функцию редактирования выражений — если приложение неправильно читает нужный текст, ты всегда можешь поправить распознаваемое уравнение.

Отличным дополнением ко всему этому является возможность самостоятельно ввести нужное выражение, ведь написанный от руки текст Photomath пока не умеет распознавать. Разработчики обещают в скором времени устранить как этот недостаток, так и ограничение по сложности решаемых задач. Так, приложение решает простые линейные уравнения и системы с двумя неизвестными, а также считает логарифмы и частично интегралы. И все это с подробными пошаговыми инструкциями.

Photomath без сомнений можно назвать идеальным помощником как для школьников, так и для их родителей, ведь вспомнить то, что учил с десяток лет назад (да еще и с такой неохотой), — задача не из легких. К тому же разработчики утверждают, что создали приложение скорее как пример доступности технологии, нежели в образовательных целях.

Photomath

Источник

Сколько бы ни было приложений в App Store, как бы ни варьировалось их качество, время от времени там появляются совсем неординарные проекты. Вспомнить хотя бы переводчик с дополненной реальностью Word Lens или CamFind, которая распознает предметы на фото. На днях в магазине приложений Apple появилась еще одна интересная разработка: PhotoMath — приложение, которое решает математические задачи, используя камеру вашего смартфона.

Принцип работы приложения предельно прост: вы берете в руки смартфон с запущенным PhotoMath, наводите камеру на какую-либо математическую формулу, а затем смотрите результат вычислений на дисплее. Эх, такую бы штуку мне, когда я в школе учился…

Однако приложение пригодится не только тем, кто не хочет думать и решать самостоятельно. Помимо полученного результата, PhotoMath также распишет весь процесс решения уравнения по шагам. Это может помочь не только ученику, но и, например, родителям, которые решат проверить его домашнее задание.

На данный момент в приложении конечно же есть и свои ограничения: так, к примеру, PhotoMath умеет решать только не сложные дроби, десятичные числа, линейные уравнения и стандартную арифметику. Тем не менее разработчики обещают улучшать приложение и дальше, что в теории позволит совершать сложные расчеты всего за несколько секунд. К сожалению, распознавание текста (в данном случае формул) тоже нельзя назвать идеальным, но очень хорошим — запросто. PhotoMath умеет распознавать лишь печатный текст, написанные уравнения “от руки” ему даются крайне тяжело (конечно, если они не написаны типографским шрифтом). Но и этот недостаток разработчики обещают довести до рабочего состояния.

На данный момент приложение абсолютно бесплатно и доступно для смартфонов на iOS, а также Windows Phone. Версия для Android обещает появиться в скором будущем. Как заверяют разработчики, приложение было создано все же не в образовательных целях, а как пример доступности технологии. Поэтому пока еще рано совсем “отключать” мозг и решать все с помощью смартфона. Тем не менее демонстрация, я считаю, получилась хорошей. Остается только пожелать разработчикам удачи в их нелегком деле.

А как вам подобное решение? Пригодилось бы такое приложение, когда вы еще учились в школе? Делитесь мнением в комментариях!

bold{mathrm{Basic}}	bold{alphabetagamma}	bold{mathrm{ABGamma}}	bold{sincos}	bold{gedivrightarrow}	bold{overline{x}spacemathbb{C}forall}	bold{sumspaceintspaceproduct}	bold{begin{pmatrix}square&square\square&squareend{pmatrix}}	bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx} ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square} left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec alpha beta gamma delta zeta eta theta iota kappa lambda mu nu xi pi rho sigma tau upsilon phi chi psi omega A B Gamma Delta E Z H Theta K Lambda M N Xi Pi P Sigma T Upsilon Phi X Psi Omega sin cos tan cot sec csc sinh cosh tanh coth sech arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge (square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset vee wedge neg oplus cap cup square^{c} subset subsete superset supersete int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x} (2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5) (1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1) mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить} arcsin sin sqrt{square} 7 8 9 div arccos cos ln 4 5 6 times arctan tan log 1 2 3 – pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

• int xln(x)dx
  

• int sin (2x)dx
  

• int frac{x}{x^2+1}dx
  

• int cos (sqrt{x})dx
  

• int sin ^2(x)+cos ^2(x)dx
  

• int :xe^xdx
  

• Показать больше

Описание

Поэтапное решение первообразной функции

antiderivative-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

Advanced Math Solutions – Integral Calculator, trigonometric substitution

In the previous posts we covered substitution, but standard substitution is not always enough. Integrals involving…

Read More

Введите Задачу

Сохранить в блокнот!

Войти